Existence and Ulam stability for fractional differential equations of mixed Caputo-Riemann derivatives

1.   Introduction

The fractional differential equations have drawn much attention due to their applications in a number of fields such as physics, mechanics, chemistry, biology, economics, biophysics, etc, see ^[16,32]. Some physical phenomena such as the fractional oscillator equations and fractional Euler-Lagrange equations with mixed fractional derivatives can be found in ^[10,12,31]. Once a model of fractional differential equation for the real problem have been constructed, people faced the issue of how to solve this model. In many circumstances, finding the exact solution to the fractional differential equation is quite challenging. As a result, researchers must identify as many aspects of the problem's solution as possible. Is there a solution to the problem, for example? Is the solution unique if there is a one? Hence the study of existence and uniqueness solutions for fractional differential equations with initial and boundary conditions appealed many scientists and mathematicians ^{[2,3,4,19,20,21,25,27,30]}. Some existence results for fractional differential equations with integral boundary conditions can be found in ^[17,28,29]. Recently, the existence theorem for fractional differential equations involving mixed fractional derivatives have been studied by many authors ^[5,6,8]. More specifically, Abbas ^[1] proved the existence and uniqueness of solution for a boundary value problem of fractional differential equation of the form

where $\; \alpha \in(m-1, m], \; m\geq 2,$ and $^{C} D^{\alpha}, ^{C}D^{\beta}$ are the Caputo fractional derivatives. Alghamdi et al.^[7] studied new existence and uniqueness results for three-point boundary value problem of sequential fractional differential equations given by

where $^{C}D^{\beta}$ is Caputo fractional derivative. Song et al. ^[34] used the coincidence degree theory while proving the existence of solutions of the following nonlinear mixed fractional differential equation with the integral boundary value problem:

where $^{C}D^{\alpha}_{1-}$ and $D^{\beta}_{0+}$ are respectively the left Caputo fractional derivative and the right Riemann–Liouville fractional derivative. Sousa et al. ^[35] investigated the existence and uniqueness of mild and strong solutions of fractional semilinear evolution equations, by means of the Banach fixed point theorem and the Gronwall inequality. The notion of Ulam stability has been studied and expanded in many ways. There have been a number of articles published on this subject that have yielded a number of conclusions ^[11,23,24]. Ibrahim ^[18] examined Ulam stability for the Cauchy differential equation of fractional order in the unit disk. Chen et al. ^[13] studied the Ulam-Hyers stability of solutions for linear and nonlinear nabla fractional Caputo difference equations when $0 < v \leq 1$ on finite intervals. The linear case has the form

and the non-linear case has the form

Muniyappan and Rajan ^[26] discussed Hyers-Ulam and Hyers-Ulam-Rassias stability for the following fractional differential equation with boundary condition

where $D^{\alpha}$ is Caputo fractional derivative of order $\alpha$. Dai et al. ^[14] researched the Ulam–Hyers and Ulam–Hyers–Rassias stability of nonlinear fractional differential equations with integral boundary condition which has the form

where $D^{\alpha}$ is Caputo derivative and $I^{\beta}_{0+}(.)$ is the Riemann–Liouville fractional integral.

In this paper, we consider the nonlinear fractional differential equations wich has the form

with initial conditions

where $f:J\times \mathbb R\rightarrow \mathbb R$, $1 < \alpha\leq 2, \; 0 < \beta\leq1,$ $^{C}D^{\alpha}$ is the Caputo fractional derivative, and $^{R}D^{\beta}$ is the Riemann fractional derivative. New existence and uniqueness results are obtained by driving the corresponding Green's function of problem (1.1) and (1.2) with the help of the Schauder theorem and Banach contraction principle. Furthermore, the Ulam–Hyers and Ulam–Hyers–Rassias stability for Eq (1.1) is briefly described. Finally, some examples are given to demonstrate the application of our main results.

2.   Preliminaries

Let us give some definitions and lemmas that are basic and needed at various places in this work.

Definition 2.1. ^[9] Let $f$ be a function which is defined almost everywhere $(a.e.)$ on $[a, b]$, If $\alpha > 0$, then:

provided that this integral (Lebesgue) exists.

Definition 2.2. ^[22] The Riemann-Liouville fractional derivative oforder $\alpha > 0$ for a function function $f : [0, \infty) \rightarrow \mathbb{R}$, is defined as

where $n = [\alpha] + 1, [\alpha]$ denotes the integer part of the real number $\alpha$.

Definition 2.3. ^[32] For a continuous function $f : [0, \infty) \rightarrow \mathbb{R}$, the Caputo derivative of fractional order $\alpha$ is defined as

provided that $f^{(n)}$ exists, where $n = [\alpha] + 1, [\alpha]$ denotes the integer part of the real number $\alpha$.

Lemma 2.4. ^[32] Let $f(t) \in L_{1}[a,b]$ and $\alpha,\beta \geq 0$. Then

Moreover, if $f(t) \in C[a, b]$, then the above identity is true for all $t \in [a, b]$.

Lemma 2.5. ^[9] Let $\alpha > 0$, $n$ be the smallest integer $n > \alpha$ and let $f(t)\in L(a, b)$. If $_{a}^{t}D^{\alpha-1}f$ exists and is absolutely continuous on $[a, b]$, then $_{a}^{a^+}D^{\alpha-i}f = k_i$ exists for $i = 1, 2, ..., n$; $_{a}^{t}D^{\alpha}f$ exists $a.e.$ on $[a, b]$, is in $L(a, b)$ and

Furthermore, the inequality holds everywhere on $(a, b]$, if in addition, $f(t)$ is continuous on $(a, b]$.

Lemma 2.6. ^[22] Let $\alpha > 0$. If we assume $y \in C(0, 1)\cap L_{1}(0, 1)$, then the Caputo fractional differential equation

has the solution

where $c_i\in \mathbb{R}, i = 0, 1, 2, ..., n-1$, and $n = [\alpha]+1.$

Lemma 2.7. ^[22] Let $y \in C(0, 1)\cap L_{1}(0, 1)$ with fractional derivative of order $\alpha > 0$ that belongs to $C(0, 1)\cap L_{1}(0, 1).$ Then

for $c_i\in \mathbb{R}, i = 0, 1, 2, ..., n-1,$ where $n$ is the smallest integer greater than or equal to $\alpha.$

Lemma 2.8. ^[9,32] Let $\alpha$, $\beta \in \mathbb{R}$, $\beta > -1.$ If $t > a$, then

Definition 2.9. ^[32] The two-parametric Mittag-Leffler function is defined as

Theorem 2.10. ^[15] (Arzela-Ascoli Theorem). If $X$ is compact and $f\subseteq C(X)$, then $f$ totally is bounded if and only if f is bounded and equicontinuous.

Theorem 2.11. ^[15] (Schauder fixed point theorem). Let X be a Banach space and let $M \subseteq X$ be nonempty, convex, and closed. If $T: M \rightarrow M$ is compact, then T has a fixed point

Theorem 2.12. ^[36] (Contraction mapping principle). Let M be a Banach space. If $T: M \rightarrow M$ is a contraction, then$T$ has a unique fixed point in M.

For the definitions of Ulam-Hyers stable and Ulam-Hyers-Rassias stable see ^[33].

Definition 2.13. The Eq (1.1) is Ulam-Hyers stable if there exists a real number $c_f > 0$ such that for each $\varepsilon > 0$ and for each solution $z \in C^{1}(J, \mathbb{R})$ of the inequality

there exists a solution $y\in C^{1}(J, \mathbb{R})$ of Eq (1.1) with

Definition 2.14. The Eq (1.1) is Ulam-Hyers-Rassias stable with respect to $\varphi \in C(J, \mathbb{R}_+)$ if there exists a real number $c_f > 0$ such that for each $\varepsilon > 0$ and for each solution $z \in C^{1}(J, \mathbb{R})$ of the inequality

there exists a solution $y\in C^{1}(J, \mathbb{R})$ of Eq (1.1) with

Lemma 2.15. Let $f\in C[0, 1]$, $\; y\in C^{1}[0, 1]$, then the initial value problem (1.1) and (1.2) has a solution

where $G(t, s)$ is the Green's function described by

where

Proof. By applying the Lemma 2.5 and 2.7, we may reduce Eq (1.1) to an equivalent equation

Operate both sides of Eq (2.4) by operator $D$, we get

Then the solution of Eq (2.5) is

Using the initial conditions (1.2), we find that

Substituting the values of $c_1$ and $k_1$ in Eq (2.6), we have

The converse of the lemma follows from a direct computation. Hence, the proof is completed.

3.   Main results

In this section, we prove the existence and uniqueness of solution for the problem (1.1) and (1.2) in the Banach space $C$ by applying Banach contraction principle and Schauder fixed point theorem.

Let $C([0, 1], \mathbb{R})$ denote the Banach space of all continuous functions from $[0, 1]$ into $\mathbb{R}$ with the norm defined by

To prove the main results, we need the following assumptions:

$\bf{(H1)}$ There exists a positive constants $\gamma_1, \gamma_2$ such that $\big|f(t, y(t))\big|\leq \gamma_1+\gamma_2 |y(t)|$, for each $t \in J$ and all $y \in \mathbb{R}$.

$\bf{(H2)}$ There exists a positive constant $k$ such that $\big|f(t, x(t))-f(t, y(t))\big|\leq k |x(t)-y(t)|,$

for each $t \in J$ and all $x, y \in \mathbb{R}$.

$\bf{(H3)}$ There exists an increasing function $\varphi \in C(J, \mathbb{R}_+)$ and there exists $\nu_{\varphi} > 0$ such that for any $t\in J$, we have

For convenience, we define the following notations:

The existence result can be obtained by the Schauder fixed point theorem.

Theorem 3.1. Assume $f:J\times \mathbb{R}\rightarrow \mathbb{R}$ is continuous and satisfies (H1). Then the problem (1.1) and (1.2) has a solution.

Proof. Consider an operator $T$ defined on $C(J)$ by

By the continuity of the functions $G(t, s)$ and $f (t, y(t))$, we have $Ty \in C(J)$ for any $y \in C(J)$. We define the set $B_r = \{ y(t) \in C(J, \mathbb{R}):\left\|y \right\| \leq r\}$ and choose $r \geq \dfrac{\gamma_1 \Lambda_{1}}{(1-\gamma_2 \Lambda_{1})}$. First, we have to show that $TBr \subseteq Br$, for $y \in B_r$. Now, consider

Then

and so

Therefore, we have

which implies that

Hence, $TBr \subseteq Br$.

Next, we need to prove that T is a completely continuous operator. For this purpose we fix,

$Q = \sup_{t\in J} \left|f(s, y(s))\right|$, where $y \in B_r$, and $t, \tau \in J$ with $t < \tau$. Then

Therefore,

and so

Let $t \rightarrow \tau$, the right-hand side of the above inequality tends to zero. Thus, $T$ is uniformly bounded and equicontinuous. Therefore by th Arzela-Ascoli implies that $T$ is completely continuous. Hence, by Schauder's fixed point theorem, the problem (1.1) and (1.2) has a solution on $C(J, \mathbb R)$. Now, we use the contraction principle mapping to investigate uniqueness results for (1.1) and (1.2).

Theorem 3.2. Suppose that (H2) holds. If

where $\Lambda_{2} = \dfrac{(\lambda+e^{-\lambda}-1)}{\lambda}$, then the problem (1.1) and (1.2) has a unique solution.

Proof. Let $x, y \in C(J, \mathbb R)$. Then

and so

Therefore,

Then

Hence

Using the condition (3.1), we conclude that $T$ is a contraction mapping. Hence Banach contraction principle guarantees that $T$ has a fixed point which is the unique solution of the problem (1.1) and (1.2). The proof is complete.

4.   Stability theorems

In this section, we study Ulam-Hyers and Ulam-Hyers-Rassias stability of our problem (1.1) and (1.2).

Theorem 4.1. Assume that $f:J \times R \rightarrow R$ is a continuous function and $\bf{(H2)}$ holds with $k \mu < 1$. Then the problem (1.1) and (1.2) is Ulam-Hyers stable.

Proof. Let $z(t) \in C(J, \mathbb{R})$ be a solution of the inequality (2.1), and there exists a solution $y\in C(J, \mathbb{R})$ of Eq (1.1). Then, we have

From inequality (2.1), for each $t \in J$, we get

by $\bf{(H2)}$, for each $t \in J$, we obtain

Then from Eq (4.1) we conclude that

If $c_f = \dfrac{ E_{1, \alpha+\beta}(-\lambda)}{1-k\mu},$ then inequality

holds. Thus the problem (1.1) and (1.2) is Ulam-Hyers stable.

Theorem 4.2. Assume that $f:J \times R \rightarrow R$ is a continuous function and $\bf{(H2)}$, $\bf{(H3)}$ holds with $k \mu < 1$. Then the problem (1.1) and (1.2) is Ulam-Hyers-Rassias stable.

Proof. Let $z(t) \in C(J, \mathbb{R})$ be a solution of the inequality (2.2), and there exists a solution $y\in C(J, \mathbb{R})$ of Eq (1.1). From inequality (2.2), for each $t \in J$, we have

by using the hypothesis $\bf{(H2)}$, for each $t \in J$, we get

Then the use of Eq (4.2) implies that

Set $c_{f} = \dfrac{ \nu_{\varphi}}{1-k\mu}$. The inequality

holds. The problem (1.1) and (1.2) is Ulam-Hyers-Rassias stable.

5.   Examples

In this section, we give two examples to illustrate the usefulness of our main results.

Example 5.1. Consider the following fractional initial value problem:

Here, $\alpha = 1.2,$ $\beta = 0.2,$ and $\lambda = 1$. By Lipschitz condition, we obtain $k = 0.25$. To estimate the contraction mapping, apply Theorem 3.2 to get $k\mu = 0.1499975 < 1$. This proves the problem (5.1) has a unique solution.

By Theorem 4.1, we have

which shows the problem (5.1) is Ulam-Hyers stable.

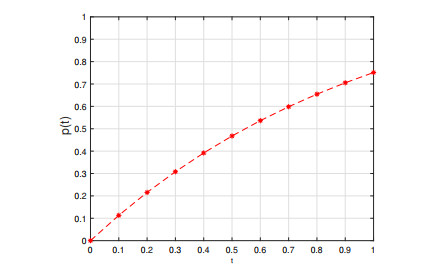
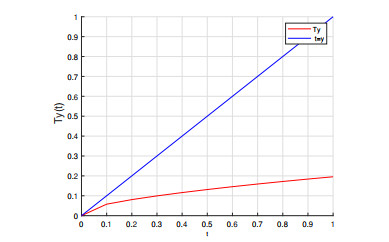
Now, to analyze the behavior of the operator $T$, one can see that $|f(t, y(t))| \leq 0.2103677$ and $|Ty(t)| \leq 0.2103677 \; \; \zeta_{3}$, (see Figure 1).

Example 5.2. Consider the following fractional initial value problem:

Here, $\; \alpha = 1.5, \; \beta = 0.5, \; \lambda = 1,$ and $k = \frac{5}{6}$. By a direct calculation, one can obtain that

$k\mu = 0.298856 < 1$. Then by Theorem 3.2, the problem (5.2) has a unique solution.

Furthermore, by Theorem 4.1, the problem (5.2) is Ulam-Hyers stable with

Now, to illustrate the obtained results for Ulam-Hyers and Ulam-Hyers-Rassias stability, we consider the following cases:

${\textbf Case I:}$ We start by computing the value of $p(t) = |z(t)-y(t)|$ for $y = 1$. From the Eq (2.1), we have

Therefor, by Theorem 4.1, the problem (5.2) has a solution $z$ satisfying

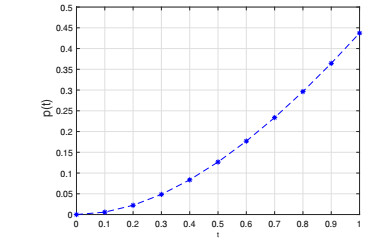
${\textbf Case II:}$ We estimate the value $p(t)$ for $y = 1$ and $\varphi(t) = t$, from the Eq (2.2), we obtain $\varepsilon = 0.83333$. By Theorem 4.2, the problem (5.2) is Ulam-Hyers-Rassias stable with

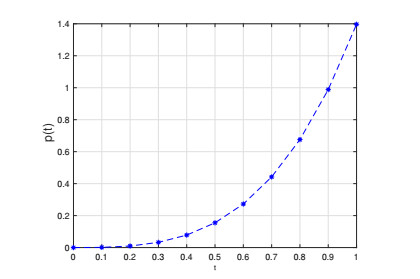
Now, we estimate the value $p(t)$ for $y = 1$ when the function $\varphi(t) = e^{ t}$. The problem (5.2) is Ulam-Hyers-Rassias stable with

6.   Conclusions

In this research, we examined the solution of nonlinear fractional differential equations with integral initial conditions. By means of the Shauder fixed point theorem and contraction mapping principle, we proved the existence and uniqueness of solutions for a nonlinear problem. In addition, the Hyers-Ulam and Hyers-Ulam-Rassias stability of the problem (1.1) and (1.2) are studied. Lastly, we presented several examples to demonstrate the use of our main theorems.

Conflict of interest

The authors declare no conflict of interest.