Study of implicit-impulsive differential equations involving Caputo-Fabrizio fractional derivative

1.   Introduction and definitions

Assume that $\mathcal{A}$ represents the family of analytic functions in the open unit disc

For $f_{1}$, $f_{2}\in \mathcal{A},$ we say that $f_{1}$ subordinate to $f_{2}$ in $\mathcal{U}$, indicated by

if there exists a Schwarz function $w$, defined by

that satisfies the condition

Indeed, it is known that

Moreover, if the function $f_{2}$ is univalent in $\mathcal{U}$ then

Let the class $\mathcal{P}$ be defined by

The class of all functions in the normalized analytic function class $\mathcal{A}$ that are univalent in $\mathcal{U}$ is also denoted by the symbol $\mathcal{S}$. The maximization of the non-linear functional $\left \vert a_{3}-\mu a_{2}^{2}\right \vert$ or other classes and subclasses of univalent functions has been the subject of a number of established results and these results are known as Fekete-Szegö problems, see ^[1]. If $f\in \mathcal{S}$ and of the form (1.1), then

and the result $\left \vert a_{3}-\mu a_{2}^{2}\right \vert$ are sharp (see ^[1]). The Fekete-Szegö problems have a rich history in literature and for complex number $\mu$.

In the area of geometric function theory (GFT), the $q$-calculus and fractional $q$-calculus have been extensively employed by scholars who have developed and investigated a number of novel subclasses of analytic, univalent and bi-univalent functions. Jackson ^[2,3] first proposed the concept of the $q$-calculus operator and gave the definition of the $q$ -difference operator $D_{q}$ in 1909. In instance, Ismail et al. were the first to define a class of $q$-starlike functions in open unit disc $\mathcal{U}$ using $D_{q}$ in ^[4]. The most significant usages of $q$ -calculus in the perspective of GFT was basically furnished and the basic (or $q$-) hypergeometric functions were first used in GFT in a book chapter by Srivastava (see, for details, ^[5]). See the following articles ^[6,7,8,9,10] for more information about $q$-calculus operator theory in GFT.

Now we review some fundamental definitions and ideas of the $q$ -calculus, we utilize them to create some new subclasses in this paper.

For a non-negative integer $l$, the $q$-number $[l]_{q},$ $(0 < q < 1)$, is defined by

and the $q$-number shift factorial is given by

For $q\rightarrow 1^{-},$ then $[l]!$ reduces to $l!$.

The $q$-generalized Pochhammer symbol is defined by

The $q$-gamma function $\Gamma _{q}$ is defined by

The $q$-generalized Pochhammer symbol is defined by

Remark 1. For $q\rightarrow 1^{-},$ then $[l]_{q, k}$ reduces to $\left(l\right) _{k} = \frac{\Gamma (l+k)}{\Gamma (l)}$.

Definition 1. Jackson ^[3] defined the $q$-integral of function $f(z)$ as follows:

Jackson ^[2] introduced the $q$-difference operator for analytic functions as follows:

Definition 2. ^[2] For $f\in \mathcal{A},$ the $q$-difference operator is defined as:

Note that, for $n\in \mathbb{N}$, $z\in \mathcal{U}$ and

Let $\mathcal{A}_{p}$ stand for the class of analytic functions with the form

in the open unit disk $\mathcal{U}$. More specifically, $\mathcal{A}_{1} = \mathcal{A}$ and

Consider the $q$-difference operator for $f\in \mathcal{A}_{p}$ as follows:

Definition 3. ^[11] For $f\in \mathcal{A}_{p},$ the $q$-difference operator is defined as:

Note that, for $n\in \mathbb{N}$, $z\in \mathcal{U}$ and

Let $\mathcal{S}^{\ast }\left(p\right)$ represents the class of $p$-valent starlike functions and every $f\in \mathcal{S}^{\ast }\left(p\right),$ if

and $\mathcal{K}\left(p\right)$ represents the class of $p$-valent convex functions and every $f\in \mathcal{K}(p),$ if

These conditions are equivalent in terms of subordination as follows:

and

The aforementioned two classes can be generalized as follows:

and

where $\varphi \left(z\right)$ is a real part function that is positive and is normalized by the rule

and $\varphi$ maps $\mathcal{U}$ onto a space that is symmetric with regard to the real axis and starlike with respect to $1.$ If $p = 1,$ then

and

These two classes $\mathcal{S}^{\ast }\left(\varphi \right)$ and $\mathcal{ K}\left(\varphi \right)$ defined by Ma ^[12].

A function $f\in \mathcal{A}_{p},$ is called $p$-valently starlike of order $\alpha$ ($0\leq\alpha < 1$) with complex order $b\in \mathbb{C} \backslash \{0\},$ if it satisfies the inequality

The class $\mathcal{S}_{p}^{\ast}(\alpha, b)$ denotes the collection of all $f\in \mathcal{A}_{p}$ functions that satisfy the aforementioned condition.

A function $f\in \mathcal{A}_{p},$ is called $p$-valently convex function of order $\alpha$ $(0\leq \alpha < 1)$ with complex order $b\in \mathbb{C} \backslash \{0\},$ if it satisfies the inequality

The class $\mathcal{K}_{p}(\alpha, b)$ denotes the collection of all functions $f\in \mathcal{A}_{p}$ that satisfy the aforementioned condition.

Note that

Kargar et al. ^[13] investigated the classes $\mathcal{S}_{p}\left(\alpha, \beta \right)$ for $f\in \mathcal{A}_{p}$ and defined as follows:

For $0\leq \alpha < 1 < \beta$ and $b\in \mathbb{C} \backslash \{0\},$ then the function $f\in \mathcal{A}_{p}$ belongs to the class $\mathcal{K}_{b, p}\left(\alpha, \beta \right)$ if it satisfies the inequality

If $p = 1,$ then $\mathcal{K}_{b, p}\left(\alpha, \beta \right) = \mathcal{K} _{b}\left(\alpha, \beta \right)$, studied by Kargar et al. in ^[13] and if $\beta \rightarrow \infty$ in above definition, $\mathcal{K} _{b, p}\left(\alpha, \beta \right) = \mathcal{K}_{b, p}\left(\alpha, b\right)$.

Recently, Bult ^[14] used the definition of subordination and defined new subclasses of $p$-valent starlike and convex functions associated with vertical strip domain as follows:

and

where

and

Bult ^[14] determined the coefficient bounds for functions belonging to these new classes.

On the basis of the geometrical interpretation of their image domains, numerous subclasses of analytic functions have established using the concept of subordination. Right half plane ^[15], circular disc ^[16], oval and petal type domains ^[17], conic domain ^[18,19], leaf-like domain ^[20], generalized conic domains ^[21], and the most important one is shell-like curve ^{[22,23,24,25]} are some fascinating geometrical classes we obtain with this domain. The function

is essential for the shell-like shape, where

The image of unit circle under the function $h$ gives the conchoid of Maclaurin's, due to the function

The function given in (1.3) has the following series representation:

where

and $u_{n}$ produces a Fibonacci series of coefficient constants that are more closely related to the Fibonacci numbers.

Taking motivation from the idea of circular disc and shell-like curves, Malik et al. ^[26] defined new domain for analytic functions which is named as cardioid domain. A new class of analytic functions is defined associated with cardioid domain, for more detail, see ^[26].

Definition 4. ^[26] Assume that $\mathcal{CP}\left(L, N\right)$ represents the class of functions $p$ that are defined as

where $\overline{p}\left(L, N, z\right)$ is defined by

with $-1 < N < L\leq 1$, $\tau = \frac{1-\sqrt{5}}{2}$ and $z\in \mathcal{U}$.

To understand the class $\mathcal{CP}\left(L, N\right)$, an explanation of the function $\overline{p}\left(L, N, z\right)$ in geometric terms might be helpful in this instance. If we denote

and

then the image $\overline{p}\left(L, N, e^{i\theta }\right)$ of the unit circle is a cardioid like curve defined by

where

and

Moreover, we observe that

and

According to (1.5), the cusp of the cardioid-like curve is provided by

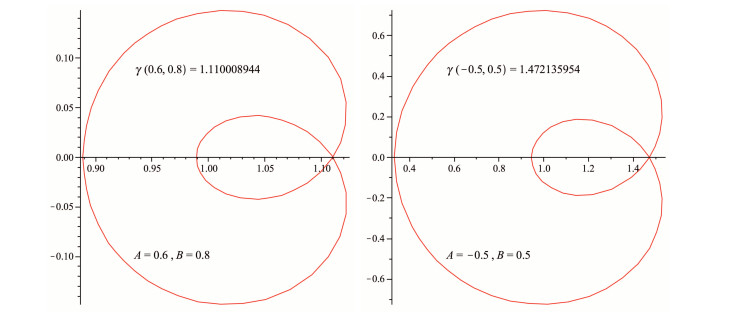
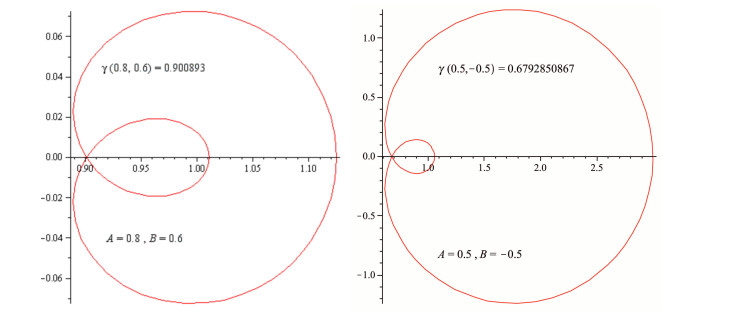
The image of each inner circle is a nested cardioid-like curve if the open unit disc $\mathcal{U}$ is considered a collection of concentric circles with origin at the center. As a result, the open unit disc $\mathcal{U}$ is mapped onto a cardioid region by the function $\overline{p}(L, N, z)$. This means that $\overline{p}\left(L, N;\mathcal{U}\right)$ is a cardioid domain. The above discussed cardioid like curve with different values of parameters can be seen in Figures 1 and 2.

The relationship $N < L$ links the parameters $L$ and $N$. The cardioid-like curve is flipped by its voilation, as seen in the figures below.

See Figure 3, if collection of concentric circles having origin as center. Thus, the function $\overline{p}(L, N, z)$ maps the open unit disk $\mathcal{U}$ onto a cardioid region. See ^[26] for more details about cardioid region.

The operator theory of quantum calculus is the primary result of this research. Using standard uses in quantum calculus operator theory and the $q$ -difference operator, we develop numerous novel $q$-analogous of the differential and integral operators. We construct a large number of new classes of $q$-starlike and $q$-convex functions using these operators and study some interesting characteristics of the corresponding analytic functions. In this paper, we gain inspiration from recent research by ^[14,26,27] and define two new classes of $p$-valent starlike, convex functions connected with the cardioid domain using the $q$-difference operator.

Influenced by recent studies ^[14,26,27], we defined two new classes of $p$-valent starlike, convex functions related with cardioid domain.

Definition 5. The function $f$ of the form (1.1) related with cardioid domain, represented by $\mathcal{S}_{p}^{\ast }\left(L, N, q, b\right),$ is defined to be the functions $f$ such that

where, $b\in \mathbb{C} \backslash \{0\}$ and $\overline{p}\left(L, N;z\right)$ is given by (1.4).

Definition 6. The function $f$ of the form (1.1) related with cardioid domain, represented by $\mathcal{K}_{p}\left(L, N, q, b\right),$ is defined to be the functions $f$ such that

where $b\in \mathbb{C} \backslash \{0\}$ and $\overline{p}\left(L, N;z\right)$ is given by (1.4) and $\mathcal{K}_{p}\left(L, N, q, b\right)$ is the class of convex functions of order $b$ related with cardioid domain.

Special cases:

(i) For $q\rightarrow 1^{-}, b = 1$ and $p = 1$, in Definition 5, we have known class $\mathcal{S}^{\ast }\left(L, N\right)$ of starlike functions associated with cardioid domain proved by Zainab et al. in ^[27].

(ii) For $q\rightarrow 1^{-}, L = 1, N = -1$, $b = 1$ and $p = 1$ in Definition 5, then class $\mathcal{S}_{p}^{\ast }\left(L, N, q, b\right) = S\mathcal{L}$ and this class is defined on starlike functions associated with Fibonacci numbers, introduced and studied by Sokół in ^[28].

(iii) For $q\rightarrow 1^{-},$ $L = 1,$ $N = -1$, $b = 1$ and $p = 1$ in Definition 6 then class $\mathcal{K}_{p}\left(L, N, q, b\right) = \mathcal{K},$ and this family is referred to as a class of convex functions connected with Fibonacci numbers.

There are four parts to this article. In Section $1$, we briefly reviewed some basic concepts from geometric function theory, quantum calculus, and cardioid domain, studied the $q$-difference operator, and finally discussed this operator to define two new subclasses of multivalent $q$-starlike and $q$-convex functions. The established lemmas are presented in Section $2$. Our main results and some known corollaries will be presented in Section $3$, then some concluding remarks in Section $4$.

2.   A set of lemmas

By utilizing the following lemmas, we will determine our main results.

Lemma 1. ^[26] Let the function $\overline{p}\left(L, N;z\right),$ defined by (1.4). Then,

(i) For the disc $\left \vert z\right \vert < \tau ^{2}$, the function $\overline{p}\left(L, N;z\right)$ is univalent.

(ii) If $h(z)\prec \overline{p}\left(L, N;z\right),$ then ${Re} h(z) > \alpha,$ where

where

and

(iii) If

then

where

(iv) Let $h(z)\prec \overline{p}\left(L, N;z\right)$ and of the form $h(z) = 1+\sum \limits_{n = 1}^{\infty }h_{n}z^{n}.$ Then

Lemma 2. ^[29] Let $h\in \mathcal{P},$ such that $h(z) = 1+\sum \limits_{n = 1}^{\infty }c_{n}z^{n}.$ Then

and

Lemma 3. ^[30] Let $h\in \mathcal{P},$ such that

Then for any complex number $v$

and the result is sharp for

Lemma 4. ^[31] Let the function $g$ given by

be convex in $\mathcal{U}$. Also let the function $f$ given by

be analytic in $\mathcal{U}.$ If

then

For the recently described classes of multivalent $q$-starlike ($\mathcal{S} _{p}^{\ast }\left(L, N, q, b\right))$ and multivalent $q$-convex ($\mathcal{K} _{p}\left(L, N, q, b\right)$) functions, we get sharp estimates for the coefficients of Taylor series, Fekete-Szegő problems and coefficient inequalities.

3.   Main results

In the following theorems, we investigate the functions $f(z)$ which can be used to find the sharpness of the results of this article.

Theorem 5. A function $f\in \mathcal{A}_{p}$ given by (1.1) is in the class $\mathcal{S}_{p}^{\ast }\left(L, N, q, b\right)$ if and only if there exists an analytic function $S$,

where, $\overline{p}\left(L, N, 0\right) = 1,$ such that

Proof. Let $f\in \mathcal{S}_{p}^{\ast }\left(L, N, q, b\right)$ and

Then by integrating this equation we obtain (3.1). Conversely, if given by (3.1) with an analytic function $S(z)$ such that $S(z)\prec \overline{p}\left(L, N, z\right),$ then by logarithmic differentiation of (3.1) we obtain

Therefore we have

and $f\in \mathcal{S}_{p}^{\ast }\left(L, N, q, b\right)$. □

The initial coefficient bounds $\left\vert a_{p+1}\right\vert$ and $\left\vert a_{p+2}\right\vert$ for the functions $f\in \mathcal{S} _{p}^{\ast }\left(L, N, b\right)$ are investigated in Theorem 6 using the Lemma 2.

Theorem 6. Let $f\in \mathcal{S}_{p}^{\ast }\left(L, N, q, b\right)$ be given by (1.1)$,$ $-1\leq N < L\leq 1.$ Then

These bounds are sharp.

Proof. Let $f\in \mathcal{S}_{p}^{\ast }\left(L, N, q, b\right)$, and of the form (1.1). Then

where

By applying the concept of subordination, there exists a function $w$ with

such that

Let

Since

then

Also consider the function

Let $\tau z = \alpha _{0},$ then

This implies that

It is simple to observe from (3.5) that

Since $f\in \mathcal{S}_{p}^{\ast }\left(L, N, b\right),$ then

It is simple to show that by utilizing (3.3) and comparing the coefficients from (3.7) and (3.8), we get

Applying modulus on both side, we have

Now again comparing the coefficients from (3.7) and (3.8), we have

where

It shows that $v > 2$ which is satisfied by the relation $L > N.$ Hence, by applying Lemma 2, we obtain the required result.

Result is sharp for the function

where $\overline{p}\left(L, N, \right)$ defined in (1.4). □

Letting $q\rightarrow 1^{-},$ $b = 1$ and $p = 1$ in Theorem 6, we get the known corollary proved in ^[32] for starlike functions connected with cardioid domain.

Corollary 1. ^[32] Let $f\in \mathcal{S}^{\ast }\left(L, N\right)$ be given by (1.2)$,$ $-1\leq N < L\leq 1.$ Then

Fekete-Szegö problem $\left\vert a_{p+2}-\mu a_{p+1}^{2}\right\vert$ for the functions $f\in \mathcal{S}_{p}^{\ast }\left(L, N, b\right)$ are investigated in Theorem 7.

Theorem 7. Let $f\in \mathcal{S}_{p}^{\ast }\left(L, N, q, b\right)$ and of the form (1.1). Then

This result is sharp.

Proof. Since $f\in \mathcal{S}_{p}^{\ast }\left(L, N, q, b\right),$ we have

where $w$ is Schwarz function such that $w(0)$ and $|w(z)| < 1$ in $\mathcal{U}$. Therefore

and after some simple calculation, we have

Comparing the coefficients of both sides, we get

This implies that

where

By using (iv) of Lemma 1 for

we have the required result. The equality

holds for $f_{\ast }$ given in (3.11). Consider $f_{0}$: $\mathcal{U} \rightarrow \mathbb{C}$ defined as:

where, $\overline{p}\left(L, N;z\right)$ is defined in ($1.4$). Hence

This demonstrates $f_{0}\in \mathcal{S}_{p}^{\ast }\left(L, N, q, b\right)$. Hence the equality

holds for the function $f_{0}$ given in (3.12). □

Letting $q\rightarrow 1^{-},$ $b = 1$ and $p = 1$ in Theorem 7, we get the known corollary proved in ^[32] for starlike functions associated with cardioid domain.

Corollary 2. ^[32] Let $f\in \mathcal{S}^{\ast }\left(L, N\right)$ and of the form (1.2). Then

This result is sharp.

Coefficient inequality for the class $\mathcal{S}_{p}^{\ast }\left(L, N, b\right)$:

Theorem 8. For function $f\in \mathcal{A}_{p},$ given by (1.1), if $f\in \mathcal{S}_{p}^{\ast }\left(L, N, q, b\right),$ then

Proof. Suppose $f\in \mathcal{S}_{p}^{\ast }\left(L, N, q, b\right)$ and the function $S(z)$ define by

Then by Definition 5, we have

where, $b\in \mathbb{C} \backslash \{0\}$ and $\overline{p}\left(L, N;z\right)$ is given by (1.4). Hence, applying the Lemma 4, we get

where

and by (2.1), we have

Also from (3.13), we find

Since $a_{p} = 1,$ in view of (3.16), we obtain

Applying (3.14) into (3.17), we get

For $n = 1, 2, 3$, we have

and

respectively. Applying the equality (3.15) and using the mathematical induction principle, we obtain

This evidently completes the proof of Theorem 8. □

The initial coefficient bounds $\left\vert a_{p+1}\right\vert$ and $\left\vert a_{p+2}\right\vert$ for the functions $f\in \mathcal{K} _{p}\left(L, N, q, b\right)$ are investigated in Theorem 9 using the Lemma 2.

Theorem 9. Let $f\in \mathcal{K}_{p}\left(L, N, q, b\right)$ be given by (1.1)$,$ $-1\leq N < L\leq 1.$ Then

These bounds are sharp.

Proof. Let $f\in \mathcal{K}_{p}\left(L, N, q, b\right)$, and be of the form (1.1). Then

where

By applying the concepts of subordination, there exists a function $w$ with

such that

Let

Since

then

Also consider the function

Let $\tau z = \alpha _{0}.$ Then

This implies that

It is simple to observe from (3.21) that

Since $f\in \mathcal{K}_{p}\left(L, N, q, b\right),$ then

It is simple to show that by utilizing (3.19) and comparing the coefficients from (3.23) and (3.24), we get

Applying modulus on both side, we have

Now again comparing the coefficients from (3.7) and (3.8), we have

where

it shows that $v > 2$ which is satisfied by the relation $L > N.$ Hence, by applying Lemma 2, we obtain the required result.

Result is sharp for the function

where $\overline{p}\left(L, N, \right)$ defined in (1.4). □

Fekete-Szegö problem $\left\vert a_{p+2}-\mu a_{p+1}^{2}\right\vert$ for the functions $f\in \mathcal{K}_{p}\left(L, N, q, b\right)$ are investigated in Theorem 10.

Theorem 10. Let $f\in \mathcal{K}_{p}\left(L, N, q, b\right)$ and be of the form (1.1). Then

This result is sharp.

Proof. Since $f\in \mathcal{K}_{p}\left(L, N, b\right),$ we have

where $w$ is Schwarz function such that $w(0)$ and $|w(z)| < 1$ in $\mathcal{U}$. Therefore

and after some simple calculation, we have

Comparing the coefficients of both sides, we get

This implies that

where

By using (iv) of Lemma 1 for

we have the required result. The equality

holds for $f_{\ast }$ given in (3.25). Consider the function $f_{0}$: $\mathcal{U}\rightarrow \mathbb{C}$ be defined as:

where, $\overline{p}\left(L, N;z\right)$ is defined in ($1.4$). Hence and

□

Theorem 11. Let $f\in \mathcal{A}_{p},$ be given by (1.1). If $f\in \mathcal{K}_{p}\left(L, N, b\right),$ then

Proof. We can obtain Theorem 11, by using the same technique of Theorem 8. □

4.   Conclusions

In this article, we have used the ideas of cardioid domain, multivalent analytic functions, and $q$-calculus operator theory to define the new subfamilies of multivalent $q$-starlike and $q$-convex functions. In Section $1$, we discussed some basic concepts from geometric functions, analytic functions, multivalent functions, $q$-calculus operator theory, and the idea of the cardioid domain. We also define two new classes of $p$-valent starlike, convex functions connected with the cardioid domain using the $q$ -difference operator. The already known lemmas are presented in Section $2$. In Section $3$, for the class $\mathcal{S}_{p}^{\ast }\left(L, N, q, b\right)$, we investigated sharp coefficient bounds, Fekete-Szegö functional, and coefficient inequalities. Same type of results also studied for the class $\mathcal{S}_{p}^{\ast }\left(L, N, q, b\right)$. The research also demonstrated how the parameters, including some new discoveries, expand and enhance the results.

For future studies, researchers can use a number of ordinary differential and $q$-analogous of difference and integral operators and can define a number of new subclasses of multivalent functions. By applying the ideas of this article, many new results can be found. The idea presented in this article can be implemented on papers ^[33,34,35], and researchers can discuss the new properties of multivalent functions associated with the cardioid domain.

Use of AI tools declaration

The authors declare that they did not employ any artificial intelligence in the execution of this work.

Acknowledgments

The authors extend their appreciation to the Arab Open University for funding this work through research fund No. (AOURG-2023-007).

Conflict of interest

All the authors claim to have no conflicts of interest.