Financing constraints change of China's green industries

1.   Introduction

The accurate analysis and interpretation of mechanisms and events in various nonlinear systems arising in fluid mechanics, nonlinear optical fibers and applied sciences heavily relies on the discovery of exact solutions of nonlinear equations. Various methods have been utilized by scholars to identify exact solutions of several types to nonlinear partial differential equations (PDEs). In the quest to analyze PDE solitons, researchers have utilized a range of analytical methods that includes inverse scattering approach ^[1], reduction methods ^[2], ansatz technique ^[3], and other techniques ^[4]. The bilinear method is powerful technique used to find analytic solutions to PDEs of nonlinear type. Bilinear method is often referred to as the Hirota bilinear method, a term coined after Hirota's original proposal in 1971. Bilinear type operators are unique type of Backlund transformations which gives a unified approach to finding the Backl$\ddots{u}$nd transformation solutions of the PDEs. This is primary concept of the manuscript. The bilinear method has since evolved to create more comprehensive solutions, including lumps^[5], breathers ^[6], rogue waves ^[7], and other interaction solutions ^[8,9]. Further, Cheng et al have studied N-solitons of the (2+1)-D generalized KdV model in ^[10]. Similarly for some more useful and excellent works on asymptotics for solitons in large order limit, the reader is referred to ^[11,12]. We consider the following three component nonlinear $(3+1)$-dimensional generalized breaking soliton system (gBSS) ^[13]

where $\alpha$ is a constant. The (3+1)-dimensional gBSS is a mathematical model that describes the behavior of nonlinear waves in three-dimensional space and time. It consists of three components: dispersion, nonlinearity, and dissipation. Dispersion refers to the spreading of waves, nonlinearity refers to the interaction between waves, and dissipation refers to the loss of energy by waves. These three components interact to produce a variety of phenomena, such as soliton formation and wave breaking.

Whenever two or more than two solitons overlap, and interact in evolution system, they can either collide elastically or pass through each other. During a soliton-soliton collision, the solitons maintain their amplitude, speed, and path, except for a phase shift. This behavior is due to the balance between nonlinearity and dispersion, which allows the solitons to interact without changing their properties.

Nonlinear physical systems can support multiple solitons that can coexist and interact with each other. The interaction between solitons is a natural response of the system and can lead to complex dynamics. The shapes and arrangements of natural phenomena such as plants, streams, mountains, and many others can fall into a vast category of naturally occurring phenomena known as bifurcation. Bifurcation refers to the emergence of complex behavior from the interaction between multiple solitons, leading to the creation of intricate patterns and structures. Solitons capable of splitting or combining during soliton interactions are called bifurcation solitons, and they can effectively replicate the bifurcation phenomenon of nonlinear processes. Recently, a Y-type soliton, the simplest bifurcation soliton, was discovered by two-soliton fusion ^[14,15]. In physics, lump wave refer to a type of wave solution that behaves like a localized lump or a pulse of energy that travels through a medium. These waves can arise in nonlinear systems where the wave speed depends on the amplitude of the wave, leading to wave packets that retain their shape and energy as they propagate. In mathematics, the term may refer to a particular type of solution of partial differential equations, such as the Korteweg–de Vries equation, which describes the propagation of nonlinear waves in dispersive media ^[16,17]. The lump wave solution of this equation is a localized solution that behaves like a soliton, maintaining its shape and speed over time. Overall, the concept of lump wave solutions has important applications in various fields, including physics, mathematics, and engineering. In ^[18], researchers presented the dynamics bright as well as dark lump solutions for a novel BKP-Boussinesq model in (3+1)-dimensions. Additionally, lump and rogue waves for Broer Kaup Kupershmidt model is studied by the authors in ^[19]. The coexistence of rogue waves, M-shaped solitons, and other types of solitons were reported in ^[20].

2.   Bilinear form

Here we present the bilinear form (BF) of the suggested system. To calculate BF of the proposed Eq (1.1), in ^[13] authors have selected $\lambda = \delta = 3\beta$ and $\gamma = 6\alpha$, then substituting these into Eq (1.1), and obtained the following

Now upon the substitution of $\mathcal{U} = \phi_{x} = 2(\ln\; \varUpsilon)_{xx}$ and $\mathcal{V} = \phi_{y} = 2(\ln\, \varUpsilon)_{xy}$, where $\phi = \varpi_{x} = \; 2(\ln\, \varUpsilon)_{x}, \varUpsilon, \phi$ and $\varpi$ are real functions of $(x, y, z, t)$, the following bilinear form is obtained

In Hirota $\mathcal{D}-$operator form above equation can be written as

Where the $\mathcal{D}-$operator is defined as

where $x = (x_{1}, x_{2}, \ldots, x_{\mathcal{K}}), \, x^{\prime} = (x_{1}^{\prime}, x_{2}^{\prime}, \ldots, x_{\mathcal{Q}}^{\prime}),$denotes vectors and $\zeta_{1}, \zeta_{2}, \ldots, \zeta_{\mathcal{Q}}\in$ $Z^{+}$. There will be two various types of exact solutions for the suggested equation which are presented below

3.   First order soliton

Here we begin the study on soliton solutions from the first order soliton of proposed model Eq (1.1), first we calculate constraint condition. In order to calculate the constraint condition we consider the following function

where

Now inserting Eq (3.1) in Eq (1.1) except nonlinear terms, and after doing so solving the resulting equation for $\lambda_{\varsigma}$, we get

for obtaining soliton of the first order, one can consider auxiliary function $\varUpsilon$ as follows

where $\mathcal{K}_{1} = \varrho_{1}x+\zeta_{1}y+\gamma_{1}z-\lambda_{1}t$, putting Eq (3.4) into Eqs (2.4) and (2.5) repectively we obtained the first order soliton solutions as follows

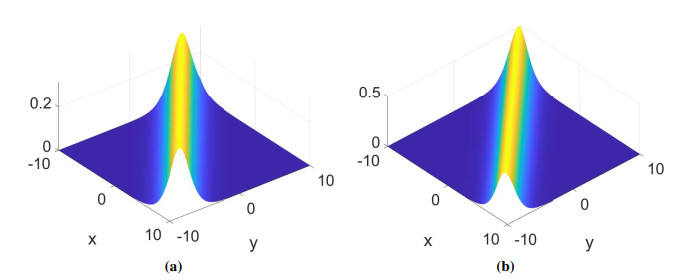
Equation (3.5) is visualized in Figure 1a, while the exact solution Eq (3.6) is presented in Figure 1b, where one soliton is observed.

4.   Second order soliton with bifurcation

Here, we find the soliton solution of second order. Therefore we take the $\varUpsilon$ as sum of the two exponential functions and its product in the form of

here the $\mathcal{K}_{\varsigma}$, with $\varsigma = 1, 2$ can be obtained from the Eq (3.2). Next we put Eq (4.1) into Eq (2.2) and solve the obtained result for the dispersion coefficient (DC) $\mathfrak{R}_{12}$, hence we get

where $\mathcal{P}_{12} = -\varrho_{1}+\varrho_{2}-\zeta_{1}+\zeta_{2}-\gamma_{1}+\gamma_{2}$, $\mathcal{Q}_{12} = \varrho_{1}-\varrho_{2}+\zeta_{1}-\zeta_{2}+\gamma_{1}-\gamma_{2}$ and $\mathcal{R}_{12} = \varrho_{1}+\varrho_{2}+\zeta_{1}+\zeta_{2}+\gamma_{1}+\gamma_{2}$. In more general format the Eq (4.2) can be written as

in the similar fashion the second-order dispersion coefficient $\mathfrak{R}_{12}$ can be expressed generally as

where $1\leq\sigma < \varOmega\leq2$. Next to obtain the exact soliton solution of order two, we substitute Eq (4.1) with Eq (4.2) into Eqs (2.4) and (2.5) respectively, we obtained the following two second order solutions

Where $\mathcal{M} = 1+e^{\mathcal{H}_{1}}+e^{\mathcal{H}_{2}}+\mathfrak{R}_{12}e^{\mathcal{H}_{1}+\mathcal{H}_{2}}$. The first solution (4.5) is visualized in Figure 2, while the second solution (4.6) is graphically depicted in Figure 3 by using suitable parameters values. In these figures one can observe the X-type soliton solutions.

4.1.   Bifurcation of second order soliton

In this part, we present the bifurcation in soliton of third order with the consideration of the dispersion coefficient $\mathfrak{R}_{12} = 0$ in Eq (5.1), therefore $\varUpsilon$ takes the form

to get the bifurcation of soliton of order two, we first insert Eq (4.7) into Eq (2.4) and then into Eq (2.5). After obtaining the exact solutions we simulate them with consideration of proper values of parameters which are presented in Figures 4 and 5, where the y-type soliton is observed.

5.   Solitons of order three and bifurcation

In this part, we calculate and demonstrate the soliton solution of order three. To do so, we consider the function $\varUpsilon$ in following form

where $\mathcal{K}_{\varsigma}, \varsigma = \{1, 2, 3\}$ follows from Eq (3.2). Further, one can verify that the $\mathfrak{R}_{123}$ satisfy the following relation

Generally, the function $\varUpsilon$ for the soliton of order three can be expressed as

where $1\leq\sigma < \varOmega < \varphi.$ The first soliton solution of order three can be acquired by inserting Eq (5.1) with Eq (5.2) into Eq (2.4). The graphical visualization of first solution with proper parameters is shown in the Figure 6. In similar way, the second soliton solution of order three can be acquired by putting Eq (5.1) with Eq (5.2) into Eq (2.5). The graphical visualization of second solution with proper parameters is shown in the Figure 7. In Figure 6, we have considered various values of $\zeta_3$, where we observe its affects on the dynamics of wave. Similarly, in Figure 7, the $\zeta$ is varied which reveals that the increase in this parameter contracts the waves to small region.

5.1.   Bifurcation of third order soliton

In this part, we would like to include the bifurcation of third order soliton by supposing the DC to be zero, and will see its affects on the dynamics of third order soliton of such supposition. So, first consider $\mathfrak{R}_{12} = 0$ in Eq (5.1), so $\varUpsilon$ become

where $\mathfrak{R}_{13}$ and $\mathfrak{R}_{23}$ can be collected from Eq (4.4). Next to get the bifurcation of third order soliton we insert Eq (5.3) into Eq (2.4), and after doing so graphically present the obtained result is depicted in Figure 8. Similarly to find the bifurcation of the second third order soliton, put Eq (5.3) into the Eq (2.5). The obtained result is graphically presented in Figure 9 with suitable parameters. Further we set $\mathfrak{R}_{13} = 0$ in Eq (5.1), so that the auxiliary function $\varUpsilon$ takes the form

where the DCs $\mathfrak{R}_{12}$ and $\mathfrak{R}_{23}$ can be found from Eq (4.4). To observe the bifurcation with $\mathfrak{R}_{13} = 0$, we insert Eq (5.4) into the Eq (2.4) and then into Eq (2.5) which are simulated with suitable parameters in Figures 10 and 11 respectively.

In Figure 8, it can be seen that at $\zeta_3 = 1.1$ the tuning fork shaped soliton is observed. Further, in Figure 9, complex type bifurcated soliton is observed. Figure 10 shows the combined x-y-type solitons dynamics and Figure 11 shows the x-type soliton solution.

6.   Fourth order solitons with bifurcation

This part presents the supposition of $\varUpsilon$ in a appropriate way to get fourth-order solitons solution of suggested Eq (1.1). To get so, we consider $\varUpsilon$ as presented below:

where in Eq (6.1), $\mathfrak{R}_{\delta\varUpsilon}$ follow Eq (4.4) and $\mathfrak{R}_{\delta\varUpsilon\varphi}$ satisfy Eq (5.2). Moreover, it can be found that the fourth order DC satisfy:

One can obtain fourth-order solitons solution by substituting Eq (6.1) with Eq (6.2) in the Eqs (2.4) and (2.5). The graphical demonstrations of the fourth order solitons with suitable parameters are visualized in the Figures 12 and 13.

6.1.   Bifurcation in fourth order solitons

Here, we suppose various dispersion coefficients as zeros due to which bifurcation is obtained of the suggested Eq (1.1). To do so, we suppose $\mathcal{R}_{12} = 0$ in the auxiliary function, so we obtain

where in Eq (6.3), $\mathfrak{R}_{134}$ and $\mathfrak{R}_{234}$ satisfy Eq (5.2). Solution of bifurcation of fourth-order solitons can be acquired by substituting Eq (6.3) in the Eqs (2.4) and (2.5). The physical demonstrations of the bifurcation of fourth order soliton with suitable parameters are visualized in the Figures 14 and 15. Further we suppose the DC $\mathcal{R}_{12} = \mathcal{R}_{23} = \mathcal{R}_{34}$ as zeros. So we get the following form of $\varUpsilon$

Solution of bifurcation of fourth-order solitons can be acquired by substituting Eq (6.4) in the Eqs (2.4) and (2.5). The physical demonstrations of the bifurcation of fourth order soliton with suitable parameters are visualized in the Figures 16 and 17.

7.   Various soliton structures

In this section, we derive various soliton structures including lump wave, interaction and M as well as W shaped solitons with the consideration of suitable auxiliary functions.

7.1.   Lump waves

This part presents the lump wave solutions of the suggested (3+1)-dimensional gBSS by choosing the transformation in the form ^[21,22]

On substituting Eq (7.1) in Eq 3.2, and equating the coefficients of variables $x, \; y, \; z$ and $t$ along with the combinations of them as well as various powers, we obtained a system comprised of algebraic equations. The solution of the obtained system yields the following values

Next inserting the parameter values Eq (7.2) into Eq (7.1), and then putting into Eqs (2.4) and (2.5) we obtained two exact solutions. The dynamics of the exact solutions Eqs (2.4) and (2.5) are presented in Figure 18 with suitable parameters.

7.2.   Interaction of M-M shaped with dark soliton

In this, we aim to present the interaction of two M-shaped solitons with the dark soliton solution. For the achievement of our result we use the transformation in the following form

Next, inserting Eq (7.3) into Eq (3.2), and equating the like powers and of the exponential, trigonometric and hyperbolic functions along with the combinations of them, we obtained system comprised of algebraic equations. On solving the algebraic system, we obtain following:

Here the parameters $\varsigma_{14}$ and $\beta$ should be greater than $0$. Further, inserting the parameter values Eq (7.4) into Eq (7.3), and then putting into Eqs (2.4) and (2.5) we obtained two exact solutions of the interaction. The interaction of M-M and dark soliton solutions are presented in Figure 19.

7.3.   M and W shaped solitons

In this part of manuscript, we study the M-shaped and W-shaped soliton solutions. To reach the goal, we use the transformation in the following form

On putting Eq (7.5) into Eq (3.2), and comparing the coefficients of same powers of the hyperbolic and trigonometric functions along with the combinations of them, we obtained a system comprised of algebraic equations. On solving the algebraic system gives:

Here $\beta\neq 0$. Further, inserting the parameter values presented in Eq (7.6) into Eq (7.5), and then putting into Eqs (2.4) and (2.5) we obtained two exact solutions of M and W shaped respectively, which are simulated in Figure 20.

8.   Conclusions

In the context of nonlinear evolution processes, it is not uncommon for certain characteristics to display unusual and remarkable properties. Our study has revealed that the displacement of solitons exhibits asymmetric resonant phenomena before and after bifurcation in a system defined by gBSS. This suggests that during interactions, the energy reflected by the amplitudes may shift. To explore this, we employed the Hirota bilinear approach to study gBSS and obtained novel solutions by considering different types of auxiliary functions. Our analysis includes the study of multi-solitons, multiple bifurcations solitons, lump wave, M-shaped solitons, and the interaction of M-M shaped with dark soliton. Additionally, we observed several novel hybrid solitons, such as tuning fork-shaped, X-Y shaped, and double Y shaped solitons.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Conflict of interest

All authors declare that they have no conflict of interest.