Does FinTech drive asymmetric risk spillover in the traditional finance?

1.   Introduction

Finance has been accompanied by risks since its birth. Unsystematic risk can be prevented and resolved by means of diversified investment, but the systemic risk is the eternal theme of financial study ^[1]. In recent years, FinTech has been regarded as one of the most important innovations in finance, and it is expected to reshape the industry by cutting costs, improving the quality of financial services, and creating a more diverse and stable financial landscape ^[2,3]. Technological developments in infrastructure, big data, data analysis, and mobile devices enable FinTech firms to get rid of the intermediary role of traditional financial institutions through unique and personalized services ^[4,5]. However, on the dark side, FinTech has the potential to amplify the contagion, pro-cyclicality and volatility of markets, which would destabilize the financial system ^[6]. The 14th "Five-Year Plan" voted by the Fourth Session of the 13th National People's Congress emphasized, "We must develop financial technology steadily... strengthen financial innovation risk assessment". In reality, different traditional industries possess different characteristics and have different links with FinTech, so it is necessary to study the asymmetric risk spillover impact that FinTech drives on traditional finance.

The rapid development of FinTech has caused a great impact on traditional financial businesses, such as the terminology conversion, credit conversion, income conversion and risk conversion ^[7,8]. The literature summarizes three reasons why FinTech and traditional financial institutions are intrinsically related: first, the two compete in similar market segments ^[9]; second, the two cooperate closely ^[10]; Third, the investment of traditional financial institutions in FinTech companies is increasing ^[4,11]. For banks, Cheng & Qu ^[12] believe that the external influence of FinTech mainly affects commercial banks through the competitive effect and technology spillover effect. Almost every component of the banking value chain is sensitive to information and time, benefiting from the innovative use of digital technology ^[13]. For the security industry, online stock trading reduces operating costs to the maximum extent by processing each stock transaction online, and provides differentiated services at the lowest feasible transaction cost to achieve competitive advantage ^[14] For the insurance industry, FinTech is committed to establishing more direct relationships between insurance companies and customers, using data analysis to calculate and match risks, and simplifying the medical insurance billing process ^[4]. On the other hand, the multiple interconnections between FinTech and traditional financial institutions makes the inherent risks of FinTech institutions possibly spread to traditional financial institutions, thus resulting in systemic risks. Li, Li, Zhu, Yao, & Casu ^[15] found that the tail risk spillover between FinTech and traditional financial institutions is indeed different.

A large number of scholars have studied the risks of the FinTech industry. Pi, Hu, Lu, & Chen ^[16] believe that the integration of finance and technology has greatly rebuilt the risk characteristics of the financial system itself. Based on the existing research and the reality of the FinTech development, it is possible for FinTech to trigger traditional financial risks such as credit risk, liquidity risk and operational risk ^[17,18], as well as risks containing non-financial factors such as basic information technology and technical ethics due to its own characteristics ^[19]. The impact of digital technology is particularly obvious. Once there are technical loopholes, it may lead to information technology risks such as data theft, privacy infringement, website attacks, and bring serious economic loss to customers and enterprises ^[20,21]. Wei, Deng, Huang, Han, & Jing ^[22] specially studied the risk factors of FinTech, among which the 12 most important factors are information system security risk, product risk, investment risk, business risk, legal risk, compliance risk, transaction payment security risk, infringement risk, economic and market status risk, capital risk, acquisition risk and tax risk. In terms of risk control, Fuster, Plosser, Schnabl, & Vickey ^[23] propose that FinTech innovation can use advanced technologies including biometrics and voice recognition to reduce labor, capital and time costs, thus reducing internal fraud risk and systemic risk. Brown & Piroska ^[24] suggest that instead of containing fintech, the sandbox is designed in a way that advances risk washing of fintech even if it is disguised as risk taming.

From the perspective of risk measurement methods, the previous literature can be roughly divided into two categories. The first type is text analysis. For example, the LDA topic model is used to identify risk factors faced by FinTech companies from text ^[22]. The second type is to calculate the tail risk, such as obtaining the expected value at risk (EVAR) by calculating the tail risk of the FinTech stock index using the expectation regression model containing lagging returns and macroeconomic risk factors ^[25]. For example, the conditional value at risk method is used to measure the risk spillover effect between the online lending industry and different types of platforms ^[26,27], and the Conditional Autoregressive Value at Risk model is used to measure Bitcoin's risk ^[28,29].

The aforementioned literature provides a wealth of materials for the research of this paper, and also leaves enough room for improvement. First, the systemic risks of FinTech and traditional finance are measured. The measurement of systemic risk has been improved in recent papers. In this paper, we take the Shanghai Composite index as the systematic index, and measure the asymmetric conditional value at risk (CoVaR) under the framework of the DCC-GJR-GARCH model. Based on the previous measurement result, we can forwardly calculate the systemic risk of FinTech and the traditional financial industry after effectively fitting the marginal distribution of the industry's return rate data, so that we can analyze the evolution of the risk. Second, the systematic risk series are divided to obtain ΔCoVaR at different frequencies. Time range is a must consider when we discuss the financial industry, for example, the transaction needs to be divided into high-frequency and low-frequency categories, and risks need to be divided into short-term and long-term categories. Most of the existing literature focuses on a certain period of time, while this paper uses the wavelet analysis method to further subdivide the series into five frequencies, and discusses the risk spillover from the FinTech industry to the traditional financial industries at different frequencies. Third, the heterogeneity of risk spillover from FinTech to traditional finance under different risk states is discussed. When the industry itself is at different risk stages, the spillover impact may be different. Based on this, this paper uses the quantile-on-quantile regression model to study the heterogeneity of impact and verify its asymmetric risk spillover relationship under different risk quantiles of both FinTech and traditional financial industries. We finally draw the following conclusions: first, in general, the peak of the positive risk spillover impact of FinTech on the traditional industries is mainly concentrated in the high quantile of FinTech, while the peak of the negative impact is mainly concentrated in the low quantile of FinTech. Second, the risk spillover impact direction of FinTech on the five traditional financial industries mainly changes from the negative to the positive under high trading frequency and low trading frequency, and takes a U-shape in medium trading frequency.

The remaining structure of this paper is arranged as follows: the second part is materials and methods, which describes the research strategies and methods used in this paper, as well as the description of variables and the data trend analysis. The third part is the empirical results, including the CoVaR of each industry obtained by the DCC-GJR-GARCH model, and the risk spillover effect that FinTech drives on traditional financial industries under different frequencies and risk conditions. The fourth part is the discussion of the empirical results, which further analyzes and compares the heterogeneity of the impact intensity and direction change of the risk spillover impact. The fifth part is the conclusion of this paper.

2.   Materials and methods

2.1.   Research strategy and methods

2.1.1.   DCC-GJR-GARCH-CoVaR model

The concept of CoVaR is derived from VaR (Value at Risk), and its economic meaning is the total value at risk borne by one institution when another institution takes risks ^[30]. VaR refers to the maximum potential loss faced by an institution within a certain holding period and at a certain confidence level. A general function of VaR is:

According to the definition, a general function of CoVaR is:

The overall risk taken by industry i in the case of risk in industry j is ${{\mathrm{C}}{\mathrm{o}}{\mathrm{V}}{\mathrm{a}}{\mathrm{R}}}_{{\mathrm{q}}}^{{\mathrm{i}}{\mathrm{j}}}$. If we want to exclude industry i's own risk and calculate the risk increment brought by industry j, then we can use the following index:

The DCC-GARCH model is mainly used to describe the dynamic change relationship and mutual influence between different variables. The core steps are as follows: 1) calculating the single variable GARCH model first; 2) calculating the dynamic correlation coefficient parameter ρ between the two variables. Therefore, the starting point of DCC-GARCH model is to build GARCH model ^[31].

In this paper, following Singhal & Ghosh ^[32] and Jiang, Nie, & Monginsidi ^[33]; ARMA (p, q)-DCC-GJR-GARCH model considering the leverage effects in the financial markets are employed. We use the ARMA (p, q) form to construct the mean model:

where ${{\mathrm{r}}}_{{\mathrm{t}}}$ is the return of an industry, p and q are the lagged order of the elements of AR(p) and MA(q) process, ${\mathtt{ε}}_{{\mathrm{t}}}$ is the residual term, c is the constant variable, ${\mathtt{ν}}_{{\mathrm{t}}}$ is the standardizes residuals and ${\mathtt{σ}}_{{\mathrm{t}}}$ is the conditional variance term. The conditional variance of GJR model can be described as:

where ${{\mathrm{d}}}_{{\mathrm{t}}-1}$ is the dummy variable; when ${\mathtt{ε}}_{{\mathrm{t}}-1} < 0$, ${{\mathrm{d}}}_{{\mathrm{t}}-1} = 1$, otherwise, ${{\mathrm{d}}}_{{\mathrm{t}}-1} = 0$. If ${\mathtt{η}}\ne 0$, there exist the leverage effects.

The basic assumption of the DCC model is that it is the normal distribution ${\mathrm{N}}(0, {\mathrm{E}}[{{\mathrm{r}}}_{{\mathrm{t}}}{{\mathrm{r}}}_{{\mathrm{t}}}^{{\mathrm{\text{'}}}}\left|{{\mathrm{I}}}_{{\mathrm{t}}-1}\right])$, and the variance matrix is denoted as ${{\mathrm{H}}}_{{\mathrm{t}}} = {{\mathrm{D}}}_{{\mathrm{t}}}{{\mathrm{R}}}_{{\mathrm{t}}}{{\mathrm{D}}}_{{\mathrm{t}}}$, where the diagonal matrix ${{\mathrm{D}}}_{{\mathrm{t}}} = {\mathrm{d}}{\mathrm{i}}{\mathrm{a}}{\mathrm{g}}[\sqrt{{{\mathrm{h}}}_{1, {\mathrm{t}}}}, \sqrt{{{\mathrm{h}}}_{2, {\mathrm{t}}}}]$ is the time-varying standard deviation matrix, ${{\mathrm{h}}}_{{\mathrm{i}}, {\mathrm{t}}}$ is conditional covariance (${\mathtt{σ}}_{{\mathrm{t}}}^{2})$ which can be obtained through GJR-GARCH model in Eq (6). ${{\mathrm{R}}}_{{\mathrm{t}}}$ is the conditional correlation coefficient matrix of the standardized returns, ${\mathtt{τ}}_{{\mathrm{t}}} = {{\mathrm{D}}}_{{\mathrm{t}}}^{-1}{{\mathrm{r}}}_{{\mathrm{t}}}$

The matrix ${{\mathrm{R}}}_{{\mathrm{t}}}$ can be decomposed as

where ${{\mathrm{Q}}}_{{\mathrm{t}}}$ is the time-varying covariance matrix of standardized returns.

and then we can obtain the DCC (1, 1) model:

where ${\mathrm{w}} = (1-{\mathtt{α}}-{\mathtt{β}})\stackrel{-}{{\mathrm{Q}}}$; $\stackrel{-}{{\mathrm{Q}}} = {\mathrm{E}}\left({\mathtt{τ}}_{{\mathrm{t}}}{{\mathtt{τ}}{\mathrm{\text{'}}}}_{{\mathrm{t}}}\right)$ is the unconditional variance matrix; and it meets ${\mathtt{α}}+{\mathtt{β}} < 1$.

We can obtain the dynamic conditional correlation coefficient shown as:

Under the framework of DCC-GJR-GARCH, we have obtained dynamic correlation parameters, then the function of $\Delta {\mathrm{C}}{\mathrm{o}}{\mathrm{V}}{\mathrm{a}}{\mathrm{R}}$ can be written as:

2.1.2.   The wavelet analysis method

Compared with ordinary discrete wavelet transform, the maximum overlap discrete wavelet transform (MODWT) has no excessive requirements for data length and higher resolution. Scholars often use this method to decompose time series data in empirical research ^[34,35]. Based on this, this paper uses MODWT to decompose the original time series. The following is the process of the wavelet decomposition. Firstly, it is assumed that all-time series variables Z(t) in this paper follow a specific structure, as shown in Eq (13):

where j represents the decomposition level, and k represents the translation parameter; ${\mathtt{ω}}_{{\mathrm{j}}, {\mathrm{k}}}\left({\mathrm{t}}\right)$ is the father wavelet, which is applied for the trend components in Eq (13); ${\mathtt{φ}}_{{\mathrm{j}}, {\mathrm{k}}}\left({\mathrm{t}}\right)$ is the mother wavelet, which stands for the degree of deviation from the trend; ${{\mathrm{s}}}_{{\mathrm{j}}, {\mathrm{k}}}$ represents scaling coefficients; ${{\mathrm{d}}}_{{\mathrm{j}}, {\mathrm{k}}}$ represents detail coefficients. ${{\mathrm{s}}}_{{\mathrm{j}}, {\mathrm{k}}}$ and ${{\mathrm{d}}}_{{\mathrm{j}}, {\mathrm{k}}}$ can be further expressed by ${\mathtt{ω}}_{{\mathrm{j}}, {\mathrm{k}}}\left({\mathrm{t}}\right)$ and ${\mathtt{φ}}_{{\mathrm{j}}, {\mathrm{k}}}\left({\mathrm{t}}\right)$, as shown in Eqs (14) and (15):

where ${{\mathrm{d}}}_{{\mathrm{j}}, {\mathrm{k}}}$ is the scale deviation from the smooth process; ${{\mathrm{s}}}_{{\mathrm{j}}, {\mathrm{k}}}$ is the smooth behavior of data j = 1…n that is connected with a location t and scale [2^(j-1), 2^j].

Secondly, in this paper, the maximum overlap discrete wavelet transform (MODWT) is used to decompose the original time series at multiple scales so that the functional expressions of the father wavelet and the mother wavelet can be obtained, as shown in Eqs (16) and (17):

Finally, the original time series in Eq (13) can be rewritten into the form of Eq (18):

where ${{\mathrm{D}}}_{{\mathrm{j}}}\left({\mathrm{t}}\right)$ represents the decomposed time series; ${{\mathrm{S}}}_{{\mathrm{j}}}\left({\mathrm{t}}\right)$ represents the residual term.

To sum up, after the wavelet transformation, the research data in this paper can be transformed from the original time series to data with different frequencies under five timescales, D1–D5, where D1 represents the highest frequency and D5 represents the lowest frequency, and these are helpful for a more comprehensive study on the $\Delta {\mathrm{C}}{\mathrm{o}}{\mathrm{V}}{\mathrm{a}}{\mathrm{R}}$ under different transaction frequencies.

2.1.3.   The quantile-on-quantile regression method

Scholars have dug out many methods to investigate spillover effects such as VAR model, state-space model, and PTSR model ^[36,37,38]. This paper hopes to get more detailed and targeted conclusions, so we attempt to progress empirical analysis at different quantile distribution level. Compared with the traditional OLS regression method and the quantile regression analysis (QRA) method, the quantile-on-quantile regression (QQR) method can more effectively and comprehensively analyze the impact of FinTech on $\Delta {\mathrm{C}}{\mathrm{o}}{\mathrm{V}}{\mathrm{a}}{\mathrm{R}}$ of traditional financial industries. Although QRA can provide more information about tail dependence, i.e., it can capture the influence between return rates and $\Delta {\mathrm{C}}{\mathrm{o}}{\mathrm{V}}{\mathrm{a}}{\mathrm{R}}$ in different degrees and the correlation structure between variables, it may ignore that the risk spillover effect of FinTech can affect the interaction of different financial industries. The QQR method, however, can comprehensively study the heterogeneous effect of the spillover effect under different quantiles on $\Delta {\mathrm{C}}{\mathrm{o}}{\mathrm{V}}{\mathrm{a}}{\mathrm{R}}$ in different quantiles, and flexibility is the main advantage of the QQR method ^[39]. Furthermore, the asymmetric effects of $\Delta {\mathrm{C}}{\mathrm{o}}{\mathrm{V}}{\mathrm{a}}{\mathrm{R}}$ of FinTech at different quantiles on $\Delta {\mathrm{C}}{\mathrm{o}}{\mathrm{V}}{\mathrm{a}}{\mathrm{R}}$ of traditional financial industries at different quantiles are negligible in this paper. In summary, after referring to the method of Sim & Zhou ^[40], this paper adopts the QQR method to analyze the asymmetric risk spillover effect that FinTech drives on traditional financial industries under different quantiles. This model has two key advantages: (a) providing more accurate and detailed empirical results; (b) overcoming the shortcomings of the conventional linear regression model and the quantile regression analysis and captures more factors of uncertainty ^[41,35]. The following is an introduction to the QQR method. The specific model is shown in Eq (19):

where, ${{\mathrm{T}}{\mathrm{F}}}_{{\mathrm{i}}, {\mathrm{t}}}$ represents the $\Delta {\mathrm{C}}{\mathrm{o}}{\mathrm{V}}{\mathrm{a}}{\mathrm{R}}$ of traditional financial industries in period t, and n = 1, 2, 3, 4, 5 representing bank, multi-finance, security, insurance and real estate; ${{\mathrm{F}}{\mathrm{t}}{\mathrm{e}}}_{{\mathrm{t}}}$ represents the $\Delta {\mathrm{C}}{\mathrm{o}}{\mathrm{V}}{\mathrm{a}}{\mathrm{R}}$ of FinTech industry in period t; ${\mathtt{θ}}$ represents the ${\mathtt{θ}}$th quantile; ${\mathtt{μ}}_{{\mathrm{t}}}^{{\mathtt{θ}}}$ stands for the residual under quantile ${\mathtt{θ}}$; ${{\mathtt{β}}}^{{\mathtt{θ}}}(\cdot)$ is an unknown function form lacking prior information.

In order to calculate the unknown relationship function ${{\mathtt{β}}}^{{\mathtt{θ}}}(\cdot)$ between FinTech and traditional financial industries in Eq (19), this paper first uses the first-order Taylor expansion to expand the regression model, and the specific form is shown in Eq (20):

where ${{\mathtt{β}}}^{{\mathtt{θ}}}\left({{\mathrm{F}}{\mathrm{t}}{\mathrm{e}}}^{\mathtt{φ}}\right)$ is the value of ${\mathrm{F}}{\mathrm{t}}{\mathrm{e}}$ ($\Delta {\mathrm{C}}{\mathrm{o}}{\mathrm{V}}{\mathrm{a}}{\mathrm{R}}$ of FinTech) at the quantile ${\mathtt{φ}}$, and ${{\mathtt{β}}}^{{\mathtt{θ}}}{\mathrm{\text{'}}}\left({{\mathrm{F}}{\mathrm{t}}{\mathrm{e}}}_{{\mathrm{t}}}^{\mathtt{φ}}\right)$ is the partial derivative of ${{\mathtt{β}}}^{{\mathtt{θ}}}\left({{\mathrm{F}}{\mathrm{t}}{\mathrm{e}}}_{{\mathrm{t}}}^{\mathtt{φ}}\right)$ with respect to ${{\mathrm{F}}{\mathrm{t}}{\mathrm{e}}}_{{\mathrm{t}}}$, which can be seen as a marginal benefit. Meanwhile, since all variables in Eq (20) are functions of ${\mathtt{θ}}$ and ${\mathtt{φ}}$, ${{\mathtt{β}}}^{{\mathtt{θ}}}\left({{\mathrm{F}}{\mathrm{t}}{\mathrm{e}}}^{\mathtt{φ}}\right)$ and ${{\mathtt{β}}}^{{\mathtt{θ}}}{\mathrm{\text{'}}}\left({{\mathrm{F}}{\mathrm{t}}{\mathrm{e}}}^{\mathtt{φ}}\right)$ can be regarded as the functions of ${\mathtt{θ}}$ and ${\mathtt{φ}}$ in Eq (20), so that Eq (20) can be simplified as Eq (21):

Then, by substituting Eq (21) into Eq (19), Eq (22) can be further obtained:

where ${{\mathtt{β}}}_{0}({\mathtt{θ}}, {\mathtt{φ}})+{{\mathtt{β}}}_{1}({\mathtt{θ}}, {\mathtt{φ}})({{\mathrm{F}}{\mathrm{t}}{\mathrm{e}}}_{{\mathrm{t}}}-{{\mathrm{F}}{\mathrm{t}}{\mathrm{e}}}^{\mathtt{φ}})$ is the linear part of $\Delta {\mathrm{C}}{\mathrm{o}}{\mathrm{V}}{\mathrm{a}}{\mathrm{R}}$ of traditional financial industries of the conditional quantile ${\mathtt{θ}}$, which can be seen that these parameters change with the change of the quantile, effectively reflecting the impact of $\Delta {\mathrm{C}}{\mathrm{o}}{\mathrm{V}}{\mathrm{a}}{\mathrm{R}}$ of FinTech at the ${\mathtt{θ}}$th quantile on traditional financial industries at the ${\mathtt{θ}}$th quantile.

Finally, this paper uses the estimators of ${{\mathrm{F}}{\mathrm{t}}{\mathrm{e}}}_{{\mathrm{t}}}$ and ${{\mathrm{F}}{\mathrm{t}}{\mathrm{e}}}^{\mathtt{φ}}$ to replace the original estimators, and uses ${b}_{0}$ and ${b}_{1}$ to replace the estimated coefficients ${{\mathtt{β}}}_{0}$ and ${{\mathtt{β}}}_{1}$ in the local linear regression. In this way, the original problem can be transformed into a minimization problem. The specific solution formula is shown in Eq (23), and the values of ${{\mathtt{β}}}_{0}({\mathtt{θ}}, {\mathtt{φ}})$ and ${{\mathtt{β}}}_{1}({\mathtt{θ}}, {\mathtt{φ}})$ can be finally obtained. Eq (23) is as follows:

where ${\rho }_{\theta }\left(u\right)$ is a quantile loss function, and ${\rho }_{\theta }\left(u\right) = u(\theta -I(u < 0)$; I(∙) is a commonly used indicator function; K(∙) represents the kernel function, which is widely used for parameter estimation due to its simplicity and effectiveness. Therefore, this paper adopts the Gaussian kernel function to weight the adjacent observations of ${{\mathrm{F}}{\mathrm{t}}{\mathrm{e}}}^{\mathtt{φ}}$. In addition, the weight of the neighborhood observations is inversely proportional to the distanced observations in the distribution of ${\widehat{Fte}}_{t}$, which can be represented by the empirical distribution function of ${F}_{m}\left({\widehat{Fte}}_{t}\right)$ in Formula (24):

It should be noted that the key to kernel function regression is the choice of bandwidth. Therefore, by referring to relevant literature, this paper finally decides that the bandwidth parameter is 0.05, so as to weight the observation values near the quantile.

2.2.   Variable description and data trend analysis

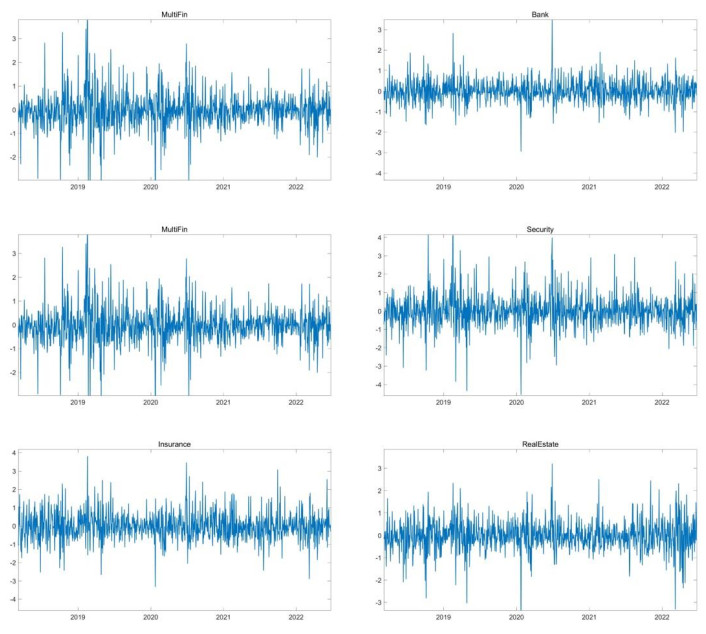
In order to study the systematic risk spillover impact of FinTech on the traditional financial industries, this paper selects six industries in China, that is, FinTech, Bank, Multi-Finance (MultiFin), Security, Insurance and Real Estate as the research objects. The research sample is the daily yield data from March 12^th of 2018 to June 30^th of 2022, of which the FinTech data is from Vanke FinTech Index. The index reflects the integrative development of innovative technologies, such as finance and Intellectual Technology. The statistical objectives of the index include listed companies specialized in technology service, equipment manufacture, etc. in the field of finance. The time period is chosen based on the data availability as the FinTech Index was constructed from Marth 12^th of 2018. The index reflects the integrative development of innovative technologies, such as finance and Intellectual Technology. We take the logarithmic of the prices and differentiate it, then multiply it by 100 to get the yield. The yield trend of the six industries is shown in Figure 1.

We can see from Figure 1 that the volatility of returns of all industries is within the (−4, +4) range. Among them, the returns of the FinTech industry are concentrated in the (−2, +2) range, and that of the traditional financial industries are concentrated in the (−1, +1) range. However, there are many extreme values, such as the security industry close to +400% and −400%. Since we need to calculate the systemic risk of each industry, we introduce Shanghai Composite Index as the systematic index, and then make descriptive statistics on all variables, as shown in Table 1.

Table 1 gives much information. The mean of all variables is around 0, the standard deviation of Shanghai Stock Exchange index is the smallest, and the standard deviation of financial technology is the largest. The results of the Jarque-Bera test show that all variables are far greater than 0, which means that they are not normally distributed. Among them, Shanghai Composite Index, FinTech, Multi-Finance and Real Estate are left biased, while Bank, Security and Insurance are right biased. Moreover, the kurtosis of all variables is greater than 3, showing a sharp kurtosis, which is a typical characteristic distribution of financial time series. The ADF test results in the last line confirm that all variables are stable. In order to preliminarily observe whether there is a linear correlation between the variables for further processing, the correlation test results we obtained are shown in Table 2.

It can be seen from Table 2 that the returns of all industries have a strong positive correlation with Shanghai Composite Index. The correlations between FinTech and traditional financial industries are above 0.3, of which the correlation with Security is the highest (0.7760) and the correlation with Bank is the lowest (0.4262). To a certain extent, it reflects the close internal relationship between FinTech and traditional finance.

3.   Empirical results

3.1.   The overall impact of FinTech on traditional finance

In this part, we first obtain the $\Delta {\mathrm{C}}{\mathrm{o}}{\mathrm{V}}{\mathrm{a}}{\mathrm{R}}$ of each industry according to the model mentioned in Section 2.1.1, as shown in Figure 2.

The maximum of the six industries mainly appeared at the beginning of 2020, while Bank, Security and Insurance also reached a peak in the middle of 2020. However, in 2021, the six industries entered in a low state. It is reported in "China's systemic financial risks in the first half of 2021" that, at the macro level, the risk of major disasters of China's financial system has repeatedly touched the short-term risk warning domain since the impact of the epidemic, but the trend value gradually fell in the first quarter of 2021. At the micro level, systemic risks are obviously concentrated in the banking industry, which is the financial hub, rising rapidly in the first half of 2020 and then declining. The report believes that excessive concentration of risks in traditional financial sectors such as banks in the post COVID-19 pandemic era will create certain hidden dangers, and the lack of breadth and depth of the capital market has restricted the channels for clearing and sharing risks.

3.2.   The heterogeneous impact of FinTech on traditional finance

3.2.1.   The heterogeneous impact of FinTech on Bank

This section reflects the heterogeneous risk spillover impact of FinTech on Bank with frequencies D1–D5. The specific impact parameter estimation results are shown in Figure 3, where (a)–(e) represent D1–D5, respectively.

We can summarize the heterogeneous risk spillover impact of FinTech on Bank from Figure 3. In most cases, the coefficient is around 0, which indicates that the risk spillover impact is not strong in the short term, but when Bank is at low and high quantiles, the impact is quite different. Under D1, when Bank is at the low quantile (0–0.2), the impact has a significant intensity change, from −3 (at the low quantile) to −1 (at the high quantile). Under D2, when Bank is at the low quantile (0.2–0.4), the coefficient starts to increase to about 6 at the 0.8 quantile. Under D3, the positive impact intensities of both sides are large, that is, when Bank is at the low quantile (0.2–0.4), the impact coefficient is about 2, and when Bank is at the high quantile (0.9–1), the coefficient reaches 4.2. Under D4, when the bank is at the low quantile (0–0.1), the impact coefficient gradually changes from −6 (at the low quantile) to 0 (at the high quantile). Under D5, when bank is at the low quantile (0.3–0.4), the impact coefficient gradually increases from −2 (at the low quantile) to +1.5 (at the high quantile); when Bank is at the high quantile (0.9–1), the coefficient gradually decreases from +1.2 to 0.

By comparing the risk spillover impact characteristics of FinTech on Bank in different time periods in Figure 3, we have the following findings. First, from the perspective of impact direction, in most cases, it has a positive impact close to 0, but there is obvious heterogeneity at both ends of Bank. Second, from the perspective of the peak impact intensity, the peak of the positive impact intensity is under D2, and the peak of the negative impact intensity is under D4, which indicates that FinTech has the largest risk spillover impact on Bank in the medium term. Third, from the perspective of the quantile where the peak occurs, the positive peak is most likely to occur at the high quantile of Bank, and the negative peak is most likely to occur at the low quantile of Bank. Fourth, from the perspective of the change form of the impact direction, the main form is from the negative to the positive, and the turning point mainly occurs at the low quantile of Bank.

3.2.2.   The heterogeneous impact of FinTech on MultiFin

This section reflects the heterogeneous risk spillover impact of FinTech on MultiFin with frequencies D1–D5. The specific impact parameter estimation results are shown in Figure 4, where (a)–(e) represent D1–D5, respectively.

We can summarize the heterogeneous risk spillover impact of the FinTech on MultiFin from Figure 4. In most cases, the impact is around +1, and when MultiFin is at the low quantile (0–0.2), there is no significant impact coefficient, and the difference between the middle and the two ends is large. Under D1, when MultiFin is at the middle (0.3–0.5), the impact coefficient changes from −4 at the low quantile of FinTech to −2 in the high quantile, while when MultiFin is at the middle quantile (0.5–0.6), the impact coefficient reaches the positive peak of 2. Under D2, in most cases, the impact is around 0, while when MultiFin is at the middle (0.4–0.6), the coefficient starts to increase to about 10 at the 0.8 quantile. Under D3, the positive impact intensities of both ends are large, that is, when MultiFin is at the low quantile (0.2–0.4), the impact coefficient is about 3, and when MultiFin is at the high quantile (0.9–1), the coefficient reaches 4. Under D4, when MulthFin is at the low quantile (0.1–0.2), the impact coefficient gradually changes from −2 (at the low quantile) to 0 (at the high quantile). Under D5, when MultiFin is at the middle (0.4–0.6), the impact coefficient gradually increases from −1 (at the low quantile) to +3 (at the high quantile); When MultiFin is at the middle and high quantile (0.6–0.8), the impact coefficient gradually decreases from +1.2 to 0; when MultiFin is at the high quantile (0.9–1), the impact coefficient is almost around +1.

By comparing the risk spillover impact characteristics of FinTech on MultiFin under different time periods in Figure 4, we have the following findings. First, from the perspective of impact direction, in most cases, it is a positive impact close to +1. Second, from the perspective of the peak impact intensity, the peak of the positive impact intensity is under D2, and the peak of the negative impact intensity is under D1, which indicates that FinTech has the largest risk spillover impact on the bank in the short term. Third, from the perspective of the quantile where the peak occurs, both the positive peak and the negative peak occur at the low quantile of MultiFin. Fourth, from the perspective of the change form of the influence direction, the main form is from the negative to the positive, and the turning point mainly occurs at the middle quantile of MultiFin.

3.2.3.   The heterogeneous impact of FinTech on Security

This section reflects the heterogeneous risk spillover impact of FinTech on Security with frequencies D1–D5. The specific impact parameter estimation results are shown in Figure 5, where (a)–(e) represent D1–D5, respectively.

We can summarize the heterogeneous risk spillover impact of FinTech on Security from Figure 5. Under D1, the impact coefficients are at the positive area, on the whole, showing a wave shape. When Security is at (0.3–0.5) and (0.6–0.8), the impact coefficient reaches a peak of 1.6, while when Security is at (0.6–0.7) and (0.8–1), the impact coefficient reaches a low peak of 2.5. Under D2, in most cases, FinTech has a positive risk spillover impact on security, but when Security is at the middle quantile (0.4), the impact coefficient reaches a negative peak of −0.5, and when Security is at the high quantile (0.9–1), the impact coefficient reaches a positive peak of 2.3. Under D3, in most cases, FinTech has a positive risk spillover impact on Security, with a strong positive impact at both ends, that is, when Security is at the low quantile (0.3–0.5), the impact coefficient is about 2.6, and when Security is at the high quantile (0.9–1), the coefficient reaches 2.5. Under D4, in most cases, the impact is positive, and the positive impact intensities at both ends are large, that is, when Security is at the low quantile (0.1–0.3), the impact coefficient reaches the positive peak of about 1.5, while when Security is at the high quantile (0.9–1), the coefficient reaches 1.4, and when Security is at the middle quantile (0.4–0.8), the coefficient is about 0. Under D5, in most cases, the impact is positive. When Security is at the low quantile (0.1–0.2), the impact coefficient gradually increases from −1 (at the low quantile) to +2.6 (at the high quantile); when Security is at the middle quantile (0.3–0.7), the impact coefficient gradually decreases from +1.2 to 0 minus; when Security is at the high quantile (0.7–1), the impact coefficient rises from 0 to about 1.5.

By comparing the risk spillover impact characteristics of the FinTech industry on Security in different time periods in Figure 5, we have the following findings. First, from the perspective of impact direction, most of the cases are positive. Second, from the perspective of impact intensity peak, the positive impact intensity peak is at D3 and D5, and the negative impact intensity peak is at D5, which indicates that the risk spillover impact in the long-term is the largest. Third, from the perspective of the quantile where the peak occurs, both the positive peak and the negative peak are easy to appear at the low and high quantile of the security. Fourth, from the change form of the impact direction, it is mainly U-shaped.

3.2.4.   The heterogeneous impact of FinTech on Insurance

This section reflects the heterogeneous risk spillover impact of FinTech on Insurance with frequencies D1–D5. The specific impact parameter estimation results are shown in Figure 5, where (a)–(e) represent D1–D5, respectively.

We can summarize the heterogeneous risk spillover impact of FinTech on Insurance from Figure 6. Under D1, the impact coefficient is about 0 in most cases. When Insurance is at the low quantile (0.4–0.6), the impact coefficient reaches a negative peak of −2 when FinTech is at the low quantile (0.3–0.7), and reaches a positive peak of 2.5 when Fintech is at the high quantile (0.7–1). Under D2, it is about 0 in most cases, showing a U-shape. However, when Insurance is at the middle quantile (0.3–0.5), the impact coefficient reaches the negative peak of −1. When Insurance is at the high quantile (0.9–1), the impact coefficient reaches the positive peak of 3.4. Under D3, in most cases, the impact is positive. When Insurance is at the high quantile (0.8–1), the impact coefficient is about 3.8, while when Insurance is at the middle quantile (0.5–0.6), the coefficient reaches the negative peak value −1. Under D4, when Insurance is at the low quantile (0.2–0.3), the impact coefficient reaches a negative peak of −3, and then gradually rises. When Insurance is at the high quantile (0.9–1), the coefficient reaches a positive peak of 2.5. Under D5, when Insurance is at the low quantile (0.1–0.2), the impact coefficient gradually increases from −1 (at the low quantile) to +1.8 (at the high quantile).

By comparing the risk spillover impact characteristics of FinTech on Insurance in different time periods in Figure 6, we have the following findings. First, from the perspective of the impact direction, it is a positive impact in most cases. Second, from the perspective of impact intensity peak, the positive peak is at D3, and the negative peak is at D4, which indicates that in the medium term, FinTech has the largest risk spillover impact on Insurance. Third, from the perspective of the quantile where the peak occurs, both the positive peak and the negative peak tend to occur at the low quantile and the high quantile of Insurance. Fourth, from the perspective of the change direction, the short-term is U-shaped, while the long-term is from the negative to the positive.

3.2.5.   The heterogeneous impact of FinTech on Real Estate

This section reflects the heterogeneous risk spillover impact of FinTech on Real Estate with frequencies D1–D5. The specific impact parameter estimation results are shown in Figure 7, where (a)–(e) represent D1–D5, respectively.

We can summarize the heterogeneous risk spillover impact of FinTech on Real Estate from Figure 7. In most cases, the impact coefficient is around 0, and the coefficient at both ends is obviously heterogeneous. Under D1, when Real Estate is at the low quantile (0.1–0.3), the impact coefficient gradually increases from −2 (at the low quantile of FinTech) to +2 (at the high quantile); when Real Estate is at the high quantile (0.9–1), the impact coefficient reaches a positive peak of 2.5. Under D2, when Real Estate is at the low quantile (0.1–0.3) and the high quantile (0.8–1), the impact coefficient reaches 4.5. Under D3, when Insurance is at the low quantile (0.1–0.2) and FinTech is at the high quantile (0.8–1), and when Insurance is at the high quantile (0.9–1) and FinTech is at the low quantile (0.1–0.3), the impact coefficient reaches a positive peak of about 5. Under D4, when Insurance is at the low quantile (0.1–0.2), the impact coefficient reaches a negative peak of −6, and then gradually rises. When Insurance is at the high quantile (0.9–1), the coefficient reaches a positive peak of 2.5. Under D5, when Insurance is at the low quantile (0.1–0.2) and FinTech is at the high quantile (0.8–1), the impact coefficient reaches a positive peak of 2.6; when FinTech is at the low quantile (0.2–0.4), the impact coefficient gradually increases from −2 (at the low quantile of Insurance) to 1.8 (at the high quantile).

By comparing the risk spillover impact characteristics of FinTech on Real Estate under different time periods in Figure 7, we have the following findings. First, from the perspective of the impact direction, it is a positive impact in most cases. Second, from the perspective of impact intensity peak, the positive peak is at D3, and the negative peak is at D4, which indicates that in the medium term, FinTech has the largest risk spillover impact. Third, from the perspective of the quantile where the peak occurs, both the positive peak and the negative peak tend to occur at the low and high quantile of Real Estate. Fourth, from the impact direction change form, it is mainly U-shaped.

3.3.   Discussion of the empirical results

This part is the further analysis and discussion of the empirical results we obtained above.

First, in general, the peak of the positive risk spillover impact of FinTech on the traditional industries is mainly concentrated in the high quantile (the high-risk area) of FinTech, while the peak of the negative impact is mainly concentrated in the low quantile (the low-risk area) of FinTech. Under the condition of the past development and the present internal macroeconomy, FinTech in China is exposed to higher risk than traditional finance ^[25]. Specific to the five industries, we can find that the impact directions for Bank, Multi Finance, Insurance and Real Estate are mainly from the negative to the positive, and the turning points are concentrated in the middle-risk area of FinTech. The impact for Security is mainly from the positive to the negative and then the positive, in a U-shape. This finding can be explained as follows. When FinTech's own risk is low, it shows a more obvious privilege in information technology. The use of big data and artificial intelligence technology solves the problems of information asymmetry, reduces the high financing cost, increases the cost of credit default, and improves management efficiency ^[42]. At this stage, FinTech has made up for the shortcomings of traditional finance and reduced the risks of the latter to a certain extent. Therefore, our empirical results show that the peak of negative impact is mainly concentrated in the low-risk area of FinTech. However, when FinTech's own risk is high, which means its liquidity risk, leverage, maturity mismatch and operational risk are all high, it is unable to make up for its information advantage. Moreover, FinTech has strengthened the infection of risk among various assets, so the network effect and long tail effect will further amplify the risk. Therefore, our empirical results show that the positive impact peak is mainly concentrated in the high-risk areas of FinTech. This result is consistent with what Li et al. ^[15] discovered that the spillover effect is stronger in economic recession.

Second, from the perspective of the trading frequency, the risk spillover impact volatility of FinTech on the five traditional financial industries mainly changes from the negative to the positive in high-frequency and low-frequency trading, and takes a U-shape in medium-frequency trading. The impact intensity of risk spillover varies significantly from different frequencies. Specifically, under high-frequency trading, the effects for Bank and Multi Finance are stronger; Under low-frequency trading, the effects on Insurance and Real Estate are greater. Li, Yang, & Huang ^[43] verify that FinTech enterprises can react quickly to signals issued by the central bank and they can help reallocate the market's resources. In recent years, commercial banks have developed more short-term intermediate businesses in order to improve their income ^[44]. These businesses, especially the development and operation of financial derivatives which need to use Internet and digital technology, have brought great risks to banks, and are more vulnerable to FinTech ^[45]. Multi Finance can promote enterprises to rapidly become a banking institution and a quasi-listed enterprise. In recent years, it has changed from the traditional mode to the Internet integration mode. Therefore, in the short term, the impact for Bank and Multi Finance is strong. Compared with the first two industries, the business of Insurance always lasts longer, especially the contract period of life insurance is as long as several decades, and so is Real Estate. Just as Lee et al. ^[4] suggests that the business model of Insurance FinTech is the most commonly accepted by traditional insurance industry. The two industries possess the characteristic of low liquidity, so the risk spillover effects of FinTech on Insurance and Real Estate are strong in low-frequency transactions.

4.   Conclusions

Based on the return rates of FinTech and the five traditional financial industries from 2019 to 2022, this paper uses the DCC-GJR-GARCH-COVAR model to measure systemic risk, and then uses wavelet analysis method and quantile-on-quantile regression model to analyze the asymmetry of risk spillover effect of FinTech on the traditional financial industries under different frequencies and risk states. We draw the following conclusions.

First, in general, the peak of the positive risk spillover impact of FinTech on the traditional industries is mainly concentrated in the high quantile (the high-risk area) of FinTech, while the peak of the negative impact is mainly concentrated in the low quantile (the low-risk area) of FinTech. Specific to the five industries, we can find that the impact directions for Bank, Multi Finance, Insurance and Real Estate are mainly from the negative to the positive, and the turning points are concentrated in the middle risk area of FinTech. The impact for Security is mainly from the positive to the negative and then the positive, in a U-shape.

Second, from the perspective of the trading frequency, the risk spillover impact volatility of FinTech on the five traditional financial industries mainly changes from the negative to the positive in high-frequency and low-frequency trading, and takes a U-shape in medium-frequency trading. The impact intensity of risk spillover varies significantly from different frequencies. Specifically, under high-frequency trading, the effects for Bank and Multi Finance are stronger; Under low-frequency trading, the effects on Insurance and Real Estate are greater.

According to our findings, we suggest that the policymakers should attach importance to the risk regulation of the FinTech industry, especially in an economic recession period. Also, the eye should be kept on different traditional financial industries and their trading frequencies to reach the precise regulation objective.

This paper stands at a macro perspective to study the risk spillover effect that FinTech drives on traditional finance. We believe more details can be dug out if the traditional financial industries are isolated to discuss. In addition to trading frequency and risk state, the spillover effect under more conditions such as management quality or information service are worth discovering.

Acknowledgements

This research is supported by the Humanities and Social Sciences Research Planning Fund 19YJA790075 of the Ministry of Education of China

Conflict of interest

The authors declare no conflict of interest.