The dynamics of a stochastic SEI model with standard incidence and infectivity in incubation period

1.   Introduction

In recent years, the investigation of infectious disease has increased dramatically and became an hot topic of research, attempts have been made to develop realistic mathematical models for the transmission dynamics of infectious diseases ^[1,2,3,4]. In the research of epidemic, the related models have been revealed as very useful tools to predict how the process of disease transmission, and provided some suggestions for the epidemic prevention and control work. During this period, Anderson and May first proposed a ordinary differential system to describe a classical SEIR model ^[5]. Later, Cooke and Van Den Driessche considered a disease transmission model of SEIRS type with exponential demographic structure ^[6]. Zhao et al. studied an SEIR epidemic disease model with time delay and nonlinear incidence rate ^[7]. Abta et al. gave a comparison of a delayed SIR model and its corresponding SEIR model in terms of global stability ^[8]. Furthermore, there exists a non-exhaustive list of papers on the epidemic dynamics of deterministic SEIR models (see e.g., ^{[9,10,11,12,13]} references therein). In addition, as a special epidemic, the propagation force of COVID-19 is extremely high, which transmit people of all ages, especially those with low immunity or with underlying disease. In everyday life, the transmission of human-to-human is possible going on quietly and rapidly when a susceptible individual touches the saliva or droplets sprayed from a person who has positive nucleic acid tests, symptomatic person, virus carrier et al., and manifest corresponding clinical symptoms, such as cough, fever et al., this adds great difficulties and obstacles to controlling the spread of the disease ^[14,15,16]. Although the high-risk groups have been quarantined timely, there still posses contagiousness during the latent period of the COVID-19, therefore, it is significant to investigate the model on COVID-19 with infectivity in incubation period. Based on the transmission and control of COVID-19, Jiao et al. put forward a deterministic SEI epidemic model with infectivity in incubation period as follows

and investigated the local and global asymptotically stable at equilibrium points by the basic reproduction number respectively ^[17]. Besides, in view of the rationality of the variables on the total population, we consider the standard incidence instead of the bilinear law incidence function that echoes the classical epidemic model proposed by White and Comiskey ^[18], which greatly increases the complexity and challenge in the course of the research for the SEI models. Thus the improved system can be expressed as

where $N$ represents the total population that include the numbers of the susceptible population $S$, exposed population $E$ and infected population $I$; $\Lambda$ stands for the number of individuals entering the susceptible population during the general population; $\beta$, $\delta$ and $\gamma$ denote by the transition rate from $S$ to $E$, $E$ to $I$ and $I$ to recovered individuals respectively; $\mu$, $0 < \theta_{1} < 1$, $0 < \theta_{2} < 1$ and $\sigma$ are natural death rate, the homestead-isolation rate of the susceptible, the infective effect of the exposed in incubation period and the hospitalized rate of $I$ separately. And the basic reproduction number of system (1.2) is $R_{0} = \frac{\beta(1-\theta_{1})\left[\delta+\theta_{2}(\gamma+\sigma+\mu)\right]-\delta(\gamma+\sigma)}{\mu(\gamma+\sigma+\mu+\delta)}$.

However, there exists some shortcomings and limitations in portraying the dynamics of infectious disease models by deterministic cases, after all, in the process of disease transmission, it is inevitably restricted and affected by random factors. Therefore, it is necessary to study the stochastic system on infectious disease models. Based on biological and mathematical perspective, there are some possible approaches to introduce random factors to the models ^{[19,20,21,22,23,24,25,26,27,28]}. Here, we mainly refer to three approaches. The first one is through time Markov chain model as environment noises in HIV epidemic ^[29,30]. The second is through parameters perturbation which is a standard technique in stochastic population modelling, and there is an intensive papers on this approach. For example, Dalal et al. analysed a stochastic HIV model and the stochasticity is introduced by the death rate of healthy cells, the death rate of infected cells and the death rate of infective virus particles perturbation respectively ^[31]. Gray et al. extended the classical SIS epidemic model from a deterministic framework to a stochastic one by considering the the disease transmission coefficient affected by the noises ^[32]. The last one to consider stochastic epidemic system is to robust the positive equilibria of deterministic models ^[33,34].

Inspired by existing literatures ^[35,36], by replacing $-\mu$, $-\delta$, $-\gamma$ by $-\mu+\alpha_{1}\dot{B}_{1}$, $-\delta+\alpha_{2}\dot{B}_{2}$, $-\gamma+\alpha_{3}\dot{B}_{3}$ respectively. This is only one simple approach in introducing stochasticity into this model. Ideally we would also like to introduce stochastic environmental variation into the other parameters, but to do this would make the analysis much too difficult. Therefore, we present a stochastic SEI system with standard incidence and infectivity in incubation period in this paper as follows:

where $\alpha_{i} > 0$ and $B_{i}$ are independent Brownian motions for $i = 1, 2, 3$. Based on some stochastic analysis technique and Lyapunov functions ^[37,38,39], we explore some dynamics for this model.

This paper is organized as follows. In Section 2, some necessary preliminaries are recalled and the theorem concerning the uniquely existence of the global positive solution for the system (1.3) is proved. In Section 3, the sufficient conditions of the unique stationary measure, the extinction and the asymptotic behavior around the two equilibriums are established. In Section 4, the numerical simulations are obtained to illustrate the presented results.

2.   Preliminaries

Let $(\Omega, \mathcal{F}, \mathbb{P})$ be a complete probability space endowed with a filtration $\{\mathcal{F}_{t}\}_{t\geq 0}$ that satisfies the usual conditions. Denote by $\mathbb{R}^{3}_{+} = \{x^{T} = (x_{1}, x_{2}, x_{3})\in\mathbb{R}^{3}|x_{i} > 0, i = 1, 2, 3\}$ for real set $\mathbb{R}$ and $C^{2}(\mathbb{R}_{+}^{3}, \mathbb{R})$ the family of all real-valued functions $V(x, t)$: $\mathbb{R}_{+}^{3}\rightarrow \mathbb{R}$ such that they are twice differentiable in $x$ and once in $t$.

Assume $E_{d}$ denotes d-dimensional Euclidean space, and $X(t)\in E_{d}$ be a time-homogeneous strong Markov process such that

and its diffusion matrix is $(a_{ij})$ with $a_{ij} = \sum_{s = 1}^{k}f_{s}^{i}(x)f_{s}^{j}(x)$.

Lemma 2.1. ^[37] Assume that there exists a bounded domain $U\subseteq E_{d}$ with regular boundary $\Upsilon$, having the following properties:

$(i)$ there is a constant $C_{1} > 0$ such that $\sum_{i, j = 1}^{d}a_{ij}(x)\zeta_{i}\zeta_{j}\geq C_{1}\|\zeta\|$ for any $x\in U$, $\zeta\in R^{d}$.

$(ii)$ there is a nonnegative $C_{2}$-function $V$ such that $LV\leq-C_{2}$ for any $x\in E_{d}/U$ and positive constant $C_{2}$.

Then the Markov process $X(t)$ has a stationary measure $\pi(\cdot)$ with density in $E_{d}$ satisfies $\lim\limits_{t\rightarrow \infty}P_{t}(x, B) = \pi(B)$for any $B\in \mathcal{B}(E_{d})$ and for any $x\in E_{d}$, let $f(x)$ be a function integrable with respect to the measure $\pi$, it yields

Next, we investigate the existence and uniqueness of the global solution in $\mathbb{R}_{+}^{3}$.

Theorem 2.1. For any initial value $(S(0), E(0), I(0))\in \mathbb{R}_{+}^{3}$, the system (1.3) exists a unique globalsolution $(S(t), E(t), I(t))\in \mathbb{R}_{+}^{3}$ for $t\geq0$ almost surely.

Proof. Define $V(S, E, I)\in C^{2}(\mathbb{R}_{+}^{3}, \mathbb{R}_{+})$ by

From Itô formula, it follows

where $L_{0} = \Lambda+\beta(1-\theta_{1})+\delta+\frac{(p+2)\alpha_{1}^{2}+\alpha_{2}^{2}+p\alpha_{3}^{2}}{2}$.

Based on the fact that drift coefficients satisfy the locally Lipschitz conditions, hence, there exists a unique local solution $(S(t), E(t), I(t))$ $(t\in[0, \tau_{e}])$ for any given positive initial value $(S(0), E(0), I(0))$ and explosion time $\tau_{e}$. One claims $\tau_{e} = \infty$. In fact, let $m_{0}$ be sufficiently large to make sure the initial value entirely belongs to the interval $\left[\frac{1}{m_{0}}, m_{0}\right]$. In addition, define a stopping time for each $m\geq m_{0}$ as follows:

It is not difficult to verify the sequence $\{\tau_{m}\}$ is increasing against the variable $m$, denote by $\tau_{\infty} = \lim\limits_{m\rightarrow \infty}\tau_{m}$, further, $\tau_{\infty}\leq \tau_{e}$ a.s., next, one will present $\tau_{\infty} = \infty$, which indicates the global existence of $(S(t), E(t), I(t))$. To fulfill the judgment, by integrating (2.1) from $0$ to $\tau_{m}\wedge T$ and taking the expectation of both sides, it yields

Meanwhile, together with

one comes to a conclusion that $\mathbb{P}(\tau_{\infty} = \infty) = 1$, which implies (1.3) exists a unique global solution ^[38].

3.   The dynamics

For system (1.2), by complicated calculations, there exist two equilibriums with $Q_{0}(S_{0}, 0, 0)$ for $S_{0} = \frac{\Lambda}{\mu}$, and $Q_{*}(S_{*}, E_{*}, I_{*})$ (see Appendix A) provided the basic reproduction number $R_{0} > 1$, where

Next, we research the stationary distribution of system (1.3).

Theorem 3.1. Assume $R_{0} > 1$ and $0 < L_{0}^{*} < \min\{L_{1}^{*}S_{*}^{2}, L_{2}^{*}E_{*}^{2}, L_{3}^{*}I_{*}^{2}\}$, then system (1.3) possesses a unique stationary measure provided

Proof. Let $(S(t), E(t), I(t))$ is the unique positive solution of system (1.3) with the initial value $(S(0), E(0), I(0))\in \mathbb{R}_{+}^{3}$. If $R_{0} > 1$, obviously, system (1.2) has equilibrium $(S_{*}, E_{*}, I_{*})$ that satisfies

Define

where $V_{i}\geq0$ for $i = 1, \cdots, 4$, $h_{j} > 0$ for $j = 1, 2$ and

By applying the Itô formula and (3.1), it obtains

similarly, one gives

and

Further, by the expression of $LV_{i}$ for $i = 1, \cdots, 4$, it follows

where

Since $h_{1} = \frac{\beta(1-\theta_{1})S_{*}}{2\mu}$, $h_{2} = \frac{h_{1}(\gamma+\sigma+2\mu)}{2\delta}$, therefore, $\Psi_{i}\geq0$ for $i = 1, 2, 3$.

In order to present a better estimate of $LV$, one divides $\mathbb{R}_{+}^{3}$ into eight domains:

Case 1. $(S, E, I)\in\Im_{i}$, $i = 1, 2$. Further, it deduces $(S-S_{*})(E-E_{*})\geq0$, $(S-S_{*})(I-I_{*})\geq0$, $(E-E_{*})(I-I_{*})\geq0$, then

Case 2. $(S, E, I)\in\Im_{i}$, $i = 3, 4$. One obtains $(S-S_{*})(E-E_{*})\geq0$, $(S-S_{*})(I-I_{*})\leq0$, $(E-E_{*})(I-I_{*})\leq0$, together with $2ab\leq a^{2}+b^{2}$ for $a, b\in\mathbb{R}$, it follows

and

Case 3. $(S, E, I)\in\Im_{i}$, $i = 5, 6$. One obtains $(S-S_{*})(E-E_{*})\leq0$, $(S-S_{*})(I-I_{*})\geq0$, $(E-E_{*})(I-I_{*})\leq0$, together with $2ab\leq a^{2}+b^{2}$ for $a, b\in\mathbb{R}$, it yields

Case 4. $(S, E, I)\in\Im_{i}$, $i = 7, 8$. One obtains $(S-S_{*})(E-E_{*})\leq0$, $(S-S_{*})(I-I_{*})\leq0$, $(E-E_{*})(I-I_{*})\geq0$, similarly

Based on the above discussion of different situations, one comes to a conclusion that

In view of $L_{0}^{*} < \min\{L_{1}^{*}S_{*}^{2}, L_{2}^{*}E_{*}^{2}, L_{3}^{*}I_{*}^{2}\}$, therefore, the ellipsoid

Assume $U$ be a any bounded neighborhood of the ellipsoid $\Re$ satisfies the closure $\bar{U}\subseteq \mathbb{R}_{+}^{3}$, further, there exists a constant $C_{2} > 0$ such that $LV\leq-C_{2}$.

Let $\xi = \min\{S^{2}, E^{2}, I^{2}, SE, SI, EI:(S, E, I)\in\bar{U}\}$, denote the diffusion matrix of system (1.3) by $A$, for any $\eta = (\eta_{1}, \eta_{2}, \eta_{3})^{T}$, it deduces $\eta^{T}A\eta\geq \xi\eta^{T}A_{0}\eta$, where

and

By complicated calculations, it claims that the matrix $A_{0}$ is positive definite endowed with three positive real characteristic roots $\lambda_{i}$ for $i = 1, 2, 3$, this implies that there exists a $\zeta = (\zeta_{1}, \zeta_{2}, \zeta_{3})^{T}\in\mathbb{R}^{3}$ and $C_{1} > 0$ such that $\zeta^{T}A\zeta\geq C_{1}\|\zeta\|$. From above discussion, it obtains according to Lemma 2.1 that system (1.3) possesses a unique stationary measure.

Theorem 3.2. Assume $\Lambda-\mu-\frac{\alpha_{1}^{2}}{2} < 0$, then the disease of system (1.3) will become extinct exponentially with probability one.

Proof. Let $V(t) = \ln(S+E+I)$, by applying Itô formula, it follows

where

By comparison theorem, it has

Integrating the above inequality from $0$ to $t$, it follows from the strong law of large numbers for local martingales in ^[19] that

which implies that $\lim\limits_{t\rightarrow \infty}S(t) = \lim\limits_{t\rightarrow \infty}E(t) = \lim\limits_{t\rightarrow \infty}I(t) = 0, a.s.$.

While $Q_{0}(S_{0}, 0, 0)$ and $Q_{*}(S_{*}, E_{*}, I_{*})$ are no longer the equilibriums of system (1.3), we still can explore the asymptotic behavior of the solutions of system (1.3) around these two equilibriums of the deterministic system (1.2) from different aspects, the result is obtained as follows.

Theorem 3.3. Assume $R_{0} < 1$ and $K_{*} = \min\{K_{1}, K_{2}, K_{3}\} > 0$ with

then the solution $(S(t), E(t), I(t))$ of (1.3) with the initial value $(S(0), E(0), I(0))$ $\in \mathbb{R}_{+}^{3}$ satisfies

Proof. $R_{0} < 1$ indicates the system (1.2) admits a unique equilibrium $(S_{0}, 0, 0)$. To consider the asymptotic behavior of system (1.2) around $(S_{0}, 0, 0)$, define $V = V_{1}+V_{2}\in C^{2}(\mathbb{R}_{+}^{3}, \mathbb{R}_{+})$ with

From the Itô formula and (3.1), it obtains

and

Combine (3.2) with (3.3), one obtains

In view of $K_{0} = \min\{K_{1}, K_{2}, K_{3}\} > 0$, it is not difficult to give

Integrating and taking expectation both sides of (3.4), one derives

furthermore, it yields

Remark 3.1. Theorem 3.3 illustrates that the solution of system (1.3) fluctuates near the equilibrium $Q_{0}(S_{0}, 0, 0)$ of system (1.2), and decreases as the variable $\alpha_{1}$ and $\beta$ decrease, which means that the epidemic is dying out and will not further spread in the society.

Theorem 3.4. Assume $R_{0} > 1$ and $H_{*} = \min\{H_{1}, H_{2}, H_{3}\} > 0$, then the solution $(S(t), E(t), I(t))$ of system (1.3) with the initial value $(S(0), E(0), I(0))\in \mathbb{R}_{+}^{3}$ has the property

where

Proof. System (1.2) admits the equilibrium $(S_{*}, E_{*}, I_{*})$ since $R_{0} > 1$. Define

where

Based on the Itô formula, it obtains

Similarly, it deduces

and

Therefore, it follows

Since the uncertainty of $S-S_{*}\geq0$, $S-S_{*}\leq0$, $E-E_{*}\geq0$, $E-E_{*}\leq0$, for a better estimate of $LV$, one derives

By adoptting the same principle in (3.7), one yields

and

Substituting (3.7)–(3.9) into (3.6), it follows

Since $H_{*} = \min\{H_{1}, H_{2}, H_{3}\} > 0$, then

Integrating from $0$ to $t$, taking expectation both sides of (3.11), and combining with $0\leq\mathbb{E}V(S(t), E(t), I(t))$, one deduces

which guarantees $(3.5)$ holds.

Remark 3.2. Theorem 3.4 indicates that the solution of system (1.3) disturbs around the equilibrium $Q_{*}(S_{*}, E_{*}, I_{*})$ of system (1.2), this implies the epidemic will continue to spread in the society.

Theorem 3.5. Assume $R_{0} > 1$ and $B_{*} = \min\{B_{1}, B_{2}, B_{3}\} > 0$, then the solution $(S(t), E(t), I(t))$ of (1.3) with the initial value $(S(0), E(0), I(0))\in \mathbb{R}_{+}^{3}$ has the property

where

Proof. System (1.2) admits the equilibrium $(S_{*}, E_{*}, I_{*})$ since $R_{0} > 1$. Define $V = V_{1}+V_{2}+V_{3},$ where

Based on Itô formula and $ab\leq\frac{1}{2}\left[(2a)^{2}+\left(\frac{b}{2}\right)^{2}\right]$, it obtains

Taking a similar way, it deduces

Therefore, it follows

According to $B_{*} = \min\{B_{1}, B_{2}, B_{3}\} > 0$, one obtains

which implies (3.12) holds by utilizing a same method to the proof of $(3.5)$.

Remark 3.3. Theorem 3.5 describes that the solution of system (1.3) vibrates around $\left(\frac{4\mu+\beta(1-\theta_{1})}{2B_{1}}, \frac{\delta+\mu}{B_{2}}E_{*}, \frac{\gamma+\sigma+\mu}{2B_{3}}I_{*}\right)$, this implies the epidemic will be lasting spread in the society.

4.   Examples and computer simulations

In this section, we introduce mainly some examples and numerical simulations to support the main results. To illustrate the main presented results, we use Milstein$^{\prime}$s higher order method in ^[20] to simulate the dynamics of system (1.3) with given the parameters and initial value. The corresponding discretization equations are

where $N_{k} = S_{k}+E_{k}+I_{k}$ and $\xi_{1, k}, \xi_{2, k}, \xi_{3, k}, k = 1, 2, ..., n$ are independent Gaussian random variables $N(0, 1)$, and $\alpha^2_{i}, \; i = 1, 2, 3$ are intensities of white noises.

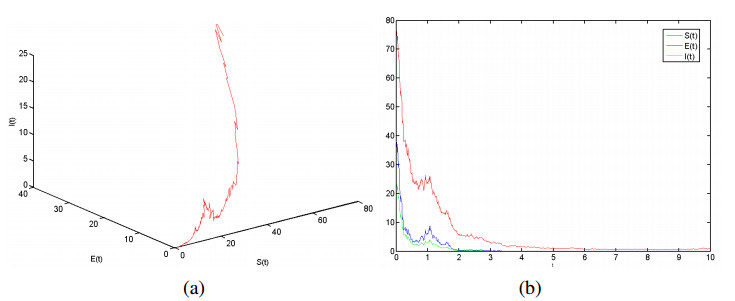
Example 4.1. Let us illustrate the extinction of the disease for the epidemic in Theorem 3.2. Choosing the initial value $(S(0), E(0), I(0)) = (75, 35, 22)$ and

which implies $R_{0} = \frac{\beta(1-\theta_{1})\left[\delta+\theta_{2}(\gamma+\sigma+\mu)\right]-\delta(\gamma+\sigma)}{\mu(\gamma+\sigma+\mu+\delta)} = 0.23 < 1$ and $\Lambda-\mu-\frac{\alpha_{1}^{2}}{2} = -0.16125 < 0$. It follows from Theorem 3.2. that system (1.3) becomes extinct exponentially with probability one. The simulations of system (1.3) is shown in Figure 1(a). Meanwhile, the numerical simulations of the different samples $S(t)$, $E(t)$ and $I(t)$ are shown in Figure 1(b).

Example 4.2. Let us illustrate the asymptotic behavior of the solutions of system (1.3) in Theorem 3.3. Choosing the initial value $(S(0), E(0), I(0)) = (95, 40, 25)$ and

this implies that $R_{0} = 0.03 < 1$, $K_{1} = \mu-\frac{3\beta(1-\theta_{1})}{2}-\alpha_{1}^{2} = 0.29$, $K_{2} = \frac{\delta}{2}+\mu-\frac{\beta(1-\theta_{1})+\alpha_{1}^{2}+\alpha_{2}^{2}}{2} = 0.58$ and $K_{3} = \gamma+\sigma+\mu-\frac{\delta+\alpha_{1}^{2}+\alpha_{3}^{2}}{2} = 1.71$. It follows from Theorem 3.3 that system (1.3) is asymptotic stable around $Q_{0}(S_{0}, 0, 0) = (\frac{100}{17}, 0, 0)$. The simulation of system (1.3) is shown in Figure 2. Meanwhile, the numerical simulations of the different samples $S(t)$, $E(t)$ and $I(t)$ are shown in Figure 3(a)–(c), respectively.

Example 4.3. Let us illustrate the asymptotic behavior of the solutions of system (1.3) in Theorem 3.5. Choosing the initial value $(S(0), E(0), I(0)) = (5, 4, 1)$ and

which implies $B_{1} = \frac{5(2\mu-\delta)}{8}-\frac{3\alpha_{1}^{2}}{2} = 0.13$, $B_{2} = \frac{3(\delta+2\mu)}{8}-\frac{2\alpha_{1}^{2}+\alpha_{2}^{2}}{2} = 0.76$, $B_{3} = \gamma+\sigma+\mu-\frac{\delta+\alpha_{1}^{2}+\alpha_{3}^{2}}{2} = 0.07$ and $R_{0} = 1.06 > 1$. Obviously, the conditions of Theorem 3.5 are satisfied. The simulations of system (1.3) is shown in Figure 4(a). Meanwhile, the numerical simulations of the different samples $S(t)$, $E(t)$ and $I(t)$ are shown in Figure 4(b).

5.   Conclusion and simple discussion

The outbreak of the COVID-19 epidemic disease brought profound changes unseen in a century to the world. Even although it caused great losses to the national economy, it promoted human progress to a certain extent. With the unremitting efforts of all mankind, the COVID-19 has been gradually controlled, however, there still exists some gaps and inadequacies on the theory of this epidemic. In order to compensate partly for these shortcomings, this paper is committed to focusing on the dynamics for a class of stochastic SEI epidemic model (1.3). Firstly, we obtain a unique global positive solution of nonlinear stochastic system (1.3). Secondly, based on Lyapunov technique and inequalities, we explore its unique stationary measure around the positive equilibrium $Q_{*}(S_{*}, E_{*}, I_{*})$ of deterministic system (1.2). Thirdly, we establish the sufficient conditions to ensure the disease will become extinct exponentially with probability one, and study the asymptotic behavior near the equilibrium $Q_{0}(S_{0}, 0, 0)$ and $Q_{*}(S_{*}, E_{*}, I_{*})$ respectively. Noting that Jiao et al. in ^[17] proved the infection-free equilibrium point and positive equilibrium point of model (1.1) is asymptotically stable respectively. Compared to the results in ^[17], it it not difficult to see that these conclusions obtained for stochastic model (1.3) in this paper is richer and the calculations is more challenging. Therefore, it is meaningful to explore the dynamics of model (1.3). To some extent, the results in this paper may provide a theoretical basis for the current epidemic prevention and control work of our country, and further save some human, financial and physical resources possibly, which may make contribute to the economic development.

Acknowledgments

The work is supported by the Research Start-up Fund (No.180141051218) and the National Cultivating Fund (No.2020-PYJJ-012) of Luoyang Normal University.

Conflict of interest

All authors declare no conflicts of interest in this paper.

Appendix A

In order to show the equilibriums of system (1.2), let

Adding the first two equations of system (5.1), it follows

From the third equation of system (5.1), it yields

If $E = 0$, combine (5.2) and (5.3), then $S = \frac{\Lambda}{\mu}$ and $I = 0$. Therefore, $Q_{0}(S_{0}, 0, 0)$ is an equilibrium of system (1.2), where $S_{0} = \frac{\Lambda}{\mu}$.

Substituting (5.3) into the second equation of system (5.1), it has

which deduces that

Further, Substituting (5.2) into (5.4), it gives

Obviously, based on (5.2) and (5.3), it is not difficult to compute that

and

It is worth noting that $S$, $E$, $I$ make sense provide

In other words, when $R_{0} > 1$, then $Q_{*}(S_{*}, E_{*}, I_{*})$ introduced in Section 3 is anther equilibrium of system (1.2).