Periodic solution for inertial neural networks with variable parameters

1.   Introduction

In this paper, we consider the following neutral-type inertial neural networks:

where $t\geq0, \; i\in I = \{1, 2, \cdots, n\},$

$x_i(t)$ denotes the state of $ith$ neuron at time $t$, $\tau > 0$ is a constant, $c_i(t)$ is a continuous $T-$periodic function on $\mathbb{R}$, $f_j:\mathbb{R}\rightarrow \mathbb{R}$ is a continuous function which denotes activation function, $a_i > 0$ is a constant which denotes the damping coefficient, $b_i > 0$ is a constant which denotes the strength of different neuron, constants $c_{ij} > 0$ and $d_{ij} > 0$ denote the connection strengths, $\tau_{j}(t) > 0$ is a continuous $T-$periodic function on $\mathbb{R}$ which is a variable delay, $I_i:\mathbb{R}\rightarrow \mathbb{R}$ is a continuous $T-$periodic function which denotes an external input. Let $\hat{\tau} = \max_{t\in \mathbb{R}}\{\tau, \tau_{j}(t)\}\; j\in I$. The initial conditions of (1.1) are

When $c_i(t) = 0$ in system (1.1), then system (1.1) is a classic inertial neural networks (INNs) which has been studied due to its extensive applications in image encryption, secure communication, information science and so on, see e.g. ^[1,2,3]. For globally exponential stability and dissipativity of INNs, see ^{[4,5,6,7,8,9,10,11,12]}. For periodic solution problems of INNs, see ^[13,14]. For synchronization of INNs, see ^[15,16].

System (1.1) belongs to neutral functional differential equation (NFDE) which is a class of equation depending on past as well as present values, but which involve derivatives with delays as well as the function itself. Lots of models in many fields including electronics, biology, physics, mechanics and economics can be described by NFDE. Specifically, a large class of electrical networks can be well modeled by NFDE which have broad applications in automatic control, high speed computers, robotics and so on, see ^[17,18]. The operator $A_i$ defined by (1.2) is called $D-$operator. The properties of $D-$operator are crucial for studying periodic solution of system (1.1). Hale ^[19] pointed out that the stability of $D-$operator has important application in dynamic behaviours of neutral-type system. In this paper, we will use the properties of $D-$operator for studying periodic solution problems of system (1.1).

So far, to the best of our knowledge, there are few results for the periodic solution problems to INNs with $D-$operators. In very recent years, Aouiti etc. ^[20] studied a neutral-type inertial neural networks with mixed delay and impulsive perturbations. Duan etc. ^[21] studied a neutral-type BAM inertial neural networks with mixed time-varying delays. However, in ^[20,21], neutral terms are $f_j(x_j'(t-\sigma_{ij}(t)))$ and $f_j(v_j'(t-\sigma_{j}(t)))$, respectively. Neutral term in system (1.1) is derivative of $D-$operator $A_i$. Since neutral terms in ^[20,21] are not $D-$operator forms, the Lyapunov functionals are complicated and the proofs are very difficult. However, in the present paper, we can use the properties of $D-$operator for constructing a simple Lyapunov functional and the proof is easy.

The main contributions of our study are as follows:

(1) We first use Lemma 2.1 for studying neutral-type INNs.

(2) For studying the asymptotic stability of neutral-type INNs, we change a second-order system into an equivalent first-order system by proper variable substitution.

(3) Since system (1.1) contain $D-$operators and delays, obtaining the asymptotic stability of periodic solution is very difficult. We will construct proper Lyapunov functionals and develop some new mathematical analysis technique for overcoming the above difficulty.

The following sections are organized as follows: Section 2 gives preliminaries and main Lemmas. Section 3 gives the existence results of periodic solutions. The asymptotic stability of periodic solutions is obtained in Section 4. In Section 5, a numerical example is given to show the feasibility of our results. Finally, Section 6 concludes the paper.

2.   Preliminary and main Lemmas

Denote $f_{0} = \max_{t\in\mathbb{R}}|f(t)|, \; C_T = \{x:x\in C(\mathbb{R}, \mathbb{R}^n), x(t+T)\equiv x(t)\}, \; C_T^1 = \{x:x\in C^1(\mathbb{R}, \mathbb{R}^n), x'\in C_T\}$, $T$ is a given positive constant. The norm $||\cdot||$ of $n$ dimensional Euclidean space is standard in this paper.

Lemma 2.1. ^[22] Let

If $|c(t)|\neq1$, then operator $A$ has continuous inverse $A^{-1}$ on $\mathcal{C}_T$, satisfying

(1)

(2)

(3)

where $\mathcal{C}_{T}$ is $T-$periodic continuous function space, $c_{0} = \max_{t\in[0, T]}|c(t)|, \; \; \sigma = \min_{t\in[0, T]}|c(t)|.$

Remark 2.1. When $c(t)$ is a constant $c$, we give the following Lemma:

Lemma A. ^[23] Let $A:C_T\rightarrow C_T, \; (Ax)(t) = x(t)-cx(t-\tau)$, where $\tau > 0$ and $c$ are constants, $C_T$ is a $T-$periodic continuous function space. If $|c|\neq1$, then operator $A$ has continuous inverse $A^{-1}$ on $C_T$, satisfying

and

Obviously, Lemma A is a special case of Lemma 2.1. In a very recent paper, Xu and Du ^[24] studied a neutral-type INNs by using Lemma A. In the present paper, we will use Lemma 2.1 for studying neutral-type INNs. We greatly improve the results in ^[24]. In the present paper, since Lemma 2.1 is more complicated than Lemma A, we discuss the existence of periodic solution in two cases (see Theorem 3.1). The proof is simple for the existence of periodic solution in ^[24]. Furthermore, since the neutral-type $A_i$ in this paper is more general, the proof of asymptotic stability of periodic solutions is more difficult than the corresponding one in ^[24].

Lemma 2.2. ^[25] Suppose that X and Y are two Banach spaces, and $L:D(L)\subset X\rightarrow Y,$ is a Fredholm operator with index zero. Furthermore, $\Omega\subset X$ is an open bounded set and $N:\bar{\Omega}\rightarrow Y$ is $L$-compact on $\bar{\Omega}$. if all the following conditions hold:

$(1)$ $Lx\neq\lambda Nx, \rm\forall x\in\partial\Omega\cap D(L), \forall \lambda\in(0, 1),$

$(2)$ $Nx\notin ImL, \rm\forall x\in\partial\Omega\cap KerL,$

$(3)$$deg\{QN, \Omega\cap KerL, 0\}\neq 0$,

then equation $Lx = Nx$ has a solution on $\bar{\Omega}\cap D(L).$

Throughout the paper, the following assumptions hold. There exist constants $p_j, l_j\geq0$ and $K > 0$ such that

(H$_1$) $|f_j(x)|\leq p_j, \; j\in I, \; \forall x\in\mathbb{R},$

(H$_2$) $x_jf_j(x_j) < 0\; \mathrm{for}\; x_j\in(-\infty, -K)\cup(K, +\infty), \; j\in I,$

(H$_3$) $|f_j(x)-f_j(y)|\leq l_j|x-y|, \; j\in I, \; \forall x, y\in\mathbb{R}.$

3.   Existence of periodic solutions

Theorem 3.1. Suppose that $\int_0^TI_i(s)ds = 0$, $\int_0^T\varphi_i^2(s)ds\neq0$, $|c_i(t)|\neq1$ for all $t\in \mathbb{R}, \; i\in I$, and assumptions $\text{(H} _1)–\text{(H} _2)$ hold, where $\varphi_i(t)$ is defined by (3.3). Then system (1.1) has at least one $T$-periodic solution, if

where $c_{0, i} = \max_{t\in[0, T]}|c_i(t)|, \; c_{1, i} = \max_{t\in[0, T]}|c_i'(t)|, \; \sigma_{0, i} = \min_{t\in[0, T]}|c_i(t)|, \; k_{1, i} = (1+c_{0, i})Tb_i, \; k_{2, i} = (1+c_{0, i})T\Big(\sum_{j = 1}^n(c_{ij}+d_{ij})p_j+|I_i|_0\Big).$

Proof. Define a linear operator

where $x = (x_1, \cdots, x_n)^T, \; Lx = (L_1x_1, \cdots, L_nx_n)^T, \; Ax = (A_1x_1, \cdots, A_nx_n)^T$, then

and a nonlinear operator

where $D(L) = \{x|x\in C_{T}^1\}.$ $\forall x\in \text{Ker}L$, we have $(x(t)-c(t)x(t-\tau))'' = {\bf0},$ where $c(t) = \mathrm{diag}\{c_(t), \cdots, c_n(t)\}$. Thus,

where $a_1, \; a_2\in \mathbb{R}^n$. Since $x(t)-c(t)x(t-\tau)\in C_T$, then $a_1 = {\bf0}.$ Let $\varphi(t) = (\varphi_1(t), \cdots, \varphi_n(t))^T$ be a solution of

where $\varphi_i(t)$ satisfies $\int_0^T\varphi_i^2(t)dt\neq0.$ We get

Obviously, $ImL$ is a closed in $C_{T}$ and $\text{dimKer}L = \text{codimIm}L = n$, So $L$ is a Fredholm operator with index zero. Define continuous projectors $P, \; Q$

and

Let

Similar to the proof of ^[22], nonlinear operator $N$ is $L$-compact on $\overline{\Omega}$, where $\Omega\subset C_T$ is an open bounded set.

Consider the operator equation $Lx = \lambda Nx, \lambda\in(0, 1)$, where $L$ and $N$ are defined by (3.1) and (3.2), respectively. Then, we have

Integrate both sides of (3.4) on $[0, T]$, we have

We show that there exists a point $t_1\in[0, T]$ such that

where $K$ is defined by assumption (H$_2$). If $x_i(t) > K, \; t\in\mathbb{R}, \; i\in I,$ it follows by assumption (H$_2$) that

which contradicts (3.5). On the other hand, if $x_i(t) < -K, \; t\in\mathbb{R}, \; i\in I$, we have the same contradiction. Hence, (3.6) holds. Thus,

Multiplying both sides of (3.4) by $(A_ix_i)(t)$ and integrating them over $[0, T],$ combining with (3.7) and assumption (H$_1$), we have

From $[A_ix_i](t) = x_i(t)-c_i(t)x_i(t-\tau)$, we have

then from Lemma 2.1 and (3.8), if $c_{0, i} < \frac{1}{2}$ we have

In view of $\frac{T^\frac{1}{2}k_{1, i}^\frac{1}{2}}{1-c_{0, i}}+\frac{c_{1, i}T}{1-c_{0, i}} < 1$, there exists a constant $M_1 > 0$ which is independent of $\lambda$ such that

Similarly, for $\sigma_{0, i} > 1$, by $\frac{T^\frac{1}{2}k_{1, i}^\frac{1}{2}}{\sigma_{0, i}-1}+\frac{c_{1, i}T}{\sigma_{0, i}-1} < 1$, there exists a constant $M_2 > 0$ which is independent of $\lambda$ such that

Combining (3.7) with the last two inequalities (3.9) and (3.10), we get

Thus, $||x||\leq\sqrt{n}M$ and condition (1) of Lemma 2.2 holds. Take $\Omega_1 = \{ x|x\in KerL, \; Nx\in ImL\}, \forall x\in \Omega_1$, then $x_i(t) = a_0\varphi_i(t), \; a_0\in \mathbb{R}, \; i\in I$ satisfies

When $c_{0, i} < \frac{1}{2},$ we have

We claim that

Otherwise, $\forall t\in[0, T], \; a_0\varphi_i(t) > K$, from assumption (H$_2$), we have

which is contradiction to (3.11). When $\sigma_{0, i} > 1,$ similar to the above proof, $a_0$ is also bounded. Hence $\Omega_1$ is a bounded set and condition (2) of Lemma 2.2 holds. Let $\Omega = \{x\in C_T:||x||\leq \sqrt{n}M+1\}$. Take the homotopy

where $H(x, \mu) = (H_1(x_1, \mu), \cdots, H_n(x_n, \mu))^T, \; QNx = (Q_1N_1x_1, \cdots, Q_nN_nx_n)^T$. For $x\in \partial \Omega \cap KerL$ and $\mu\in[0, 1]$, we have $x_iH(x_i, \mu)\neq 0, \; i\in I.$ So we have

Applying Lemma 2.2, we reach the conclusion.

By standard discussions for functional differential equation, we have the following theorem for the unique existence of periodic solution to system (1.1).

Theorem 3.2. Suppose all the conditions of Theorem 3.1 and assumption (H$_3$) hold. Then system (1.1) has unique $T-$periodic solution.

Remark 3.1. The dynamic behaviours of INNs have been widely studied, see e.g. ^[4,5,6,13]. However, there exist few results for the existence of periodic solutions to neutral-type INNs. In this paper, we obtain the existence of periodic solutions for system (1.1) by using coincidence degree theory and Lemma 2.1, see Theorems 3.1 and 3.2.

4.   Asymptotic behaviours of periodic solution

For obtaining the asymptotic stability of periodic solution to system (1.1), we change system (1.1) into a first-order system. Let

where $\xi_i > 0$ is a constant. Then system (1.1) is changed into the following system:

where $t\geq0,$ with initial conditions

Definition 4.1. If $w^*(t) = (x^*_1(t), \cdots, x^*_n(t), y^*_1(t), \cdots, y^*_n(t))^\top$ is a periodic solution of system (4.1) and $w(t) = (x_1(t), \cdots, x_n(t), y_1(t), \cdots, y_n(t))^\top$ is any solution of system (4.1) satisfying

We say $w^*(t)$ is globally asymptotic stable.

Theorem 4.1. Under the conditions of Theorem 3.2, assume further that let $\iota_i > 0, \; \kappa_i > 0,$

where

where $\hat{l} = \max_{i\in I}l_i, \; \hat{c} = \max_{i, j\in I}c_{ij}, \; \hat{d} = \max_{i, j\in I}d_{ij}$. Then system (4.1) has unique $T-$periodic solution $w^*(t) = (x^*_1(t), \cdots, x^*_n(t), y^*_1(t), \cdots, y^*_n(t))^\top$ which is globally asymptotic stable.

Proof. Based on Theorem 3.2, system (4.1) has unique $T-$periodic solution $w^*(t)$. Assume that $w(t)$ is any solution of system (4.1). Let

Derivation of (4.4) along the solution of (4.1) gives

In view of (4.2) and (4.3), for any $\varepsilon > 0$ with $\iota_i-\varepsilon > 0$ and $\kappa_i-\varepsilon > 0$, there exists a positive constant $\mathbb{T}$ (enough large) such that

and

From (4.5)–(4.7), we have

Construct the following Lyapunov functional for system (4.1):

Differentiating it along the solution of system (4.1) which together with (4.8), we have

Integrate both sides of (4.9) on $[\mathbb{T}, \infty)$, then

Using Barbalat's Lemma ^[26], we have

Hence, the periodic solution $w^*(t)$ of (4.1) is globally asymptotic stable.

Remark 4.1. When $|c_i(t)| = 1$ in system (1.1), there are no results for the existence and stability of periodic solutions. In ^[27], the authors obtained the properties of neutral operator in critical case. After that, Du, Lu and Liu ^[28] studied periodic solution for neutral-type neural networks in the critical case. We will study system (1.1) in the case of $|c_i(t)| = 1$ in the future work.

Remark 4.2. In this paper, using Mawhin's continuation theorem and Lemma 2.1, we obtain the existence of periodic solution to system (1.1). Furthermore, using Lyapunov method and the properties of $D-$operator, we obtain asymptotic stability of periodic solution to system (1.1). We first use Lemma 2.1 for studying neutral-type INNs, our methods are different from ones of ^[20,21,24].

5.   A numerical example

For $i, j = 1$ and $n = 1,$ consider the following system of model (1.1):

Let $y_1(t) = (A_1x_1)'(t)+\xi_1x_1(t),$ then (5.1) is changed into

where

Obviously, $(x_1, y_1)^T = (0, 0)^T$ is a solution of system (5.2). After a simple calculation, then $T = \frac{\pi}{5}, \; l_1 = 0.2, \; c_{0, 1} = 0.01, \; c_{1, 1} = 0.1, \; k_{1, 1} = (1+c_{0, 1})Tb_1\approx0.06$. Obviously, assumptions (H$_1$)–(H$_3$) hold. Now, we check the following conditions in Theorem 3.1:

Finally, we check conditions (4.2) and (4.3) hold:

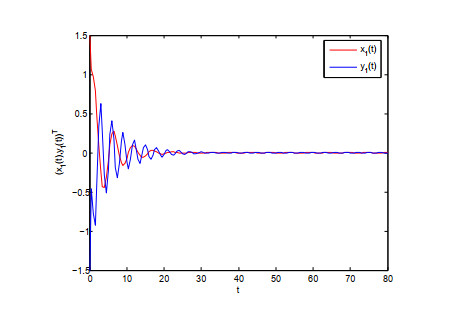
Hence, all assumptions of Theorems 3.1, 3.2 and 4.1 hold. It follows from Theorem 4.1 that the solution $(0, 0)^T$ of system (5.2) is globally asymptotic stable. The corresponding numerical simulations are presented in Figure 1.

6.   Conclusions

In this paper, we discussed the existence and asymptotic stability of the periodic solution for a neutral-type inertial neural networks. First, the sufficient conditions that ensure the existence of periodic solution were obtained by using Mawhin's continuation theorem and Lemma 2.1. Then, Lyapunov method was used to establish the criteria for the globally asymptotic stability of the periodic solution. It should be pointed out that Lemma 2.1 is important for estimating the range of solutions. Finally, a numerical test has been given to illustrate the effectiveness of the proposed criterion.

The proposed methods in this article can also be used to study other types of neural networks, such as impulse neural networks, stochastic neural networks and so on. The above problems are our future research directions.

Acknowledgments

The authors would like to express the sincere appreciation to the editor and reviewers for their helpful comments in improving the presentation and quality of the paper.

Conflict of interest

The authors confirm that they have no conflict of interest.