Dynamic behaviors for reaction-diffusion neural networks with mixed delays

1.   Introduction

As the vector of many diseases, mosquitoes are listed as one of the most lethal animals to humans in the world. With the development of people's understanding and research on mosquito-borne diseases, mosquito control is considered to be the key to suppress the spread of such diseases. In addition to the traditional physical and chemical means of mosquito control, in recent years, biological control methods have also received a lot of attention. For example, using the sterile insect technique or the Wolbachia driven mosquito control technique to release sterile mosquitoes or Wolbachia-infected mosquitoes into the field are common means of biological control ^{[4,5,6,7,8,23,30]}.

Mathematical models are widely used to study the transmission and control of mosquito-borne diseases. On the one hand, mathematical models are used to study the interaction between people and mosquitoes in the transmission process of different types of mosquito-borne diseases ^{[10,11,21,28]}, and on the other hand, they are also used to explore the interaction between wild mosquitoes and the released sterile mosquitoes or Wolbachia-infected mosquitoes ^{[1,9,13,14,15,18,19,29]}. In recent years, some researchers have focused on the release strategy of sterile mosquitoes and Wolbachia-infected mosquitoes, considering the suppression effect of the release behavior on the wild mosquito population in different situations ^{[12,16,17,20,22,24,25,26,27,31,32,33,34,35]}. Some of the mosquito population suppression models currently studied ^{[25,26,31,32]} are based on an interaction model of two types of mosquitoes (wild mosquitoes and sterile mosquitoes) constructed by Cai et al. in ^[9] as follows

where $w(t)$ and $g(t)$ are the number of the wild and sterile mosquitoes in the field at time $t$, respectively. $a$ is the birth rate per wild mosquito and it follows logistic growth. $\xi_i$ and $\mu_i, i = 1, 2$ are the density dependent and independent death rate, respectively. Further, $B(\cdot)$ is the release rate of the sterile mosquitoes.

It is noted that model (1.1) did not distinguish different stages of the mosquito's life cycle, and the growth of wild and sterile mosquitoes are both affected by intraspecific competition. However, we know that the intraspecific competition of mosquitoes mainly exists in the aquatic stage, while adult mosquitoes are little affected. Then, a revised model was developed in ^[19]

where $1-\xi_1w(t)$ describes the density dependent survival probability of wild mosquitoes. Based on model (1.2), a series of mosquito population suppression models were proposed and studied ^[20,35].

It is widely known that a mosquito's life cycle consists of several stages which include egg, larva, pupa in an aquatic phase and adult in an aerial phase. In addition, the released mosquitoes are mainly sterile males or Wolbachia-infected males and they compete with wild male mosquitoes and occupying the opportunity to mate with wild female mosquitoes ^[16]. Therefore, in mathematical modelling, it is better to consider different growth stages of mosquitoes and distinguish male and female groups.

In this work, we attempt to give and study a kind of mosquito population suppression model with sex and stage structure. The rest of this paper is arranged as follows: in Section 2, based on previous research, we give several mosquito population suppression models with life stage and sex structure. In Section 3, we study the dynamic behavior of the established models, and establish sufficient conditions for successful suppression and partial suppression of wild mosquito population. Then, in Section 4, a series of numerical examples are presented to illustrate the theoretical results we obtained. Finally, a brief conclusion is given in Section 5.

2.   Model formulation

According to the life cycle of mosquitoes, the following compartmental model was considered in ^[2].

where $E(t), M(t), F(t)$ and $M_s(t)$ denote the density of mosquito in aquatic phase, the fertile adult males, the fertile adult females and the sterilized adult males at time $t$, respectively. $u(\cdot)$ stands for a releasing function. Model parameters are all positive constants, and their biological meaning can be referred to Table 1.

To reduce the dimension of the model, the authors of ^[2] assumed that the time dynamics of the mosquitoes in aquatic phase and the adult males compartments are fast, so the equations of $E(\cdot)$ and $M(\cdot)$ are at equilibrium. That is, $E = \frac{\beta_EF}{\frac{\beta_EF}{K}+\nu_E+\delta_E}, \, M = \frac{(1-\nu)\nu_E}{\delta_M}E$. Then, they deduced the following simplified version ^[2]

The authors in ^[2] have demonstrated the reliability of the above simplified model through numerical analysis by comparing the dynamics of adult female mosquitoes in the original and simplified systems. The numerical solutions of fertile adult female mosquitoes were found to be very close, indicating that the simplified model is reliable.

In the work ^[2], in addition to using the optimization method to study the release strategy, the authors studied the dynamical behavior of system (2.2) for the case $u(\cdot) = 0$, that is, sterile mosquitoes are released only once and no longer replenished. However, we know that the suppression of mosquito population requires a large number of sterile mosquitoes to be released several times, which is a relatively long-term continuous release behavior. In this paper, we will study a mosquito population suppression model incorporating stage and sex structure based on model (2.2). In addition, by employing the modeling ideas in ^[24], we consider $M_s(t)\geq 0$ as the density of sterile mosquitoes which are sexually active in the field at time $t$, then a non-autonomous mosquito population suppression model is obtained as follows

A special case of model (2.3) is $M_s(t)\equiv m$. Yu et al. proposed the concept of the sexual lifespan of sterile mosquitoes in ^[25], ^[26], ^[31] and ^[32]. When the release period of sterile mosquitoes is equal to its sexual lifespan, the number of sexually active sterile mosquitoes in the field $M_s(t)$ is a constant value $m$ if its natural death is ignored. Then, the mosquito population suppression model (2.3) reduces to

which is a autonomous equation.

In addition, based on the work ^[2], we further investigate the suppression effect of long-term constant release of sterile mosquitoes on the wild mosquito population. Therefore, we let $u(\cdot)\equiv u$, here $u$ is a positive constant, then system (2.2) becomes another special case of model (2.3) as follows

In this paper, we will study dynamic behaviors of the non-autonomous mosquito population suppression model (2.3) and its two special cases (2.4) and (2.5), and mainly discuss the threshold conditions for successful suppression of mosquito population and the conditions for sustainable survival of mosquitoes.

3.   Main results

3.1.   Preliminaries

As in ^[16], to simplify the expression of the model, we let

then model (2.3) becomes

If no biological control measure is introduced and there are only wild mosquitoes in the field, that is $M_s(t) = 0$, then system (2.3) can be written as

Obviously, when $A\leq CD\delta_F$, system (3.2) has no positive equilibrium and the extinction equilibrium $F = 0$ is globally asymptotically stable.

In this work we assume that

then system (3.2) has a unique positive equilibrium $F^* = \frac{C}{B}(\frac{A}{CD\delta_F}-1)$ which is globally asymptotically stable.

For the case $M_s(t)\equiv m > 0$, (2.4) is a autonomous equation, and we can also discuss its equilibria. To get positive equilibria of (2.4), we need to consider the following algebraic equation

which is equivalent to

Thus, the existence and the number of positive equilibria of model (2.4) are equivalent to that of the following quadratic equation

where $A_1(m) = \delta_FB(D+mHB), \; A_2 = A+\delta_FCD, \; A_3 = \frac{AC}{B}.$

Using the discriminant $\triangle (m) = A_2^2-4A_1(m)A_3$, we introduce a threshold of the release amount

which satisfies $\triangle (m^*) = 0$.

According to ^[16], we have the following conclusions.

Lemma 1. When $A > CD\delta_F$, the nonnegative equilibria of model (2.4) can be classified as follows:

(i) If $0 < m < m^*$, then model (2.4) has three equilibria: $F = 0$,

(ii) If $m = m^*$, then model (2.4) has two equilibria: $F = 0$ and

(iii) If $m > m^*$, then the extinction equilibrium $F = 0$ is the unique equilibrium of model (2.4).

Remark 1. Since $A_1(m)$ is strictly monotonically increasing with respect to $m$, while $F_{2}(m)$ is strictly monotonically decreasing with respect to $m$ in $(0, m^*)$, we have

3.2.   General non-autonomous case

We first study the dynamics of (2.3) for the case when the number of sexual active sterile mosquitoes in the field, $M_s(t)$, is a given nonnegative continuous function.

Let $F(t, M_s, t_0, F_0)$ be a solution of (2.3) through $(t_0, F_0)$, then $F(t, M_s, t_0, F_0) \in C^1([t_0, \infty), [0, \infty))$ satisfies (2.3) on $[t_0, \infty)$ and $F(t_0) = F_0$.

According to equation (2.3), it is clear that $\frac{dF(t)}{dt}|_{F = 0} = 0$, and

then we get the following conclusion.

Lemma 2. For any $t_0\geq 0$ and $F_0 > 0$, the solution $F(t, M_s, t_0, F_0)$ of (2.3) is positive and $\limsup_{t\rightarrow \infty}F(t)\leq F^*$.

In the following, we investigate the stability of the extinction equilibrium $F = 0$. For convenience, let

Theorem 1. If $A > CD\delta_F$, $m_0 > 0$ and $M_s(t)\leq m^*, t\geq0$, then the extinction equilibrium $F = 0$ of model (2.3) is locally asymptotically stable, and $\lim_{t\rightarrow \infty}F(t, M_s, t_0, F_0) = 0$ if $0 < F_0 < F_1(m_0)$. In addition, $F(t) = F(t, M_s, t_0, F_0)\geq F^*(m^*), t\geq t_0$ if $F_0\geq F^*(m^*)$.

Proof. We first prove that the extinction equilibrium $F = 0$ of model (2.3) is locally stable. Since $m_0 > 0$, according to Lemma 1 and the properties of $G(F, m)$ defined in (3.3), we know that $G(F, m_0) > 0$ for all $F\in(0, F_1(m_0))$. Then, for any $\delta\in (0, F_1(m_0))$, the following inequality

holds.

We claim that

If it does not hold, then there must exist $t_1 > t_0$ such that $F(t_1) = \delta$ and $0 < F(t) < \delta, t_0\leq t < t_1$, thus $F'(t_1)\geq 0$. However, according to (2.3) and (3.4), we have

A contradiction occurs. Therefore, $F = 0$ is locally stable.

We further prove the attractivity of $F = 0$. From (3.5), we have that for any $0 < F(t_0) < \delta$, $\overline{F} = \limsup_{t\rightarrow \infty}F(t, M_s, t_0, F_0) \leq \delta$. By the fluctuation lemma, there exists a time sequence $\{\omega_k\}$ such that $\lim_{k\rightarrow \infty}F(\omega_k) = \overline{F}, \lim_{k\rightarrow \infty}F'(\omega_k) = 0$. Taking the limit in (2.3) along $\{\omega_k\}$ gives

and consequently

which leads to $\overline{F} = 0$ or $\frac{A\overline{F}}{(B\overline{F}+C)[D\overline{F}+m_0H(B\overline{F}+C)]}\geq\delta_F$. According to (3.4), the second case cannot occur, then $\overline{F} = 0$ and $\lim_{t\rightarrow \infty}F(t, M_s, t_0, F_0) = 0$. Thus, $F = 0$ is locally asymptotically stable. Noting the arbitrariness of $\delta$, which can be sufficiently close to $F_1(m_0)$, we can get $\lim_{t\rightarrow \infty}F(t, M_s, t_0, F_0) = 0$ if $0 < F_0 < F_1(m_0)$.

Next, we prove that: $F_0\geq F^*(m^*)\Rightarrow F(t) = F(t, M_s, t_0, F_0)\geq F^*(m^*), t\geq t_0$. If it does not hold, then there must exist $\tilde{t} > t_0$ and $\bar{t}\in (t_0, \tilde{t})$ such that $F(\tilde{t}, M_s, t_0, F_0) < F^*(m^*)$ and $F(\bar{t}, M_s, t_0, F_0) = F^*(m^*)$. We consider the following comparison equation of (2.3)

Since $0 < m_0\leq M_s(t)\leq m^*, t\geq0$, we have $f(F(t), M_s(t))- \delta_FF\geq f(F(t), m^*)- \delta_FF$. We also know that $F^*(m^*)$ is an equilibrium of (3.7), so the solution of (3.7) passing through $(\bar{t}, F^*(m^*))$ is $\tilde{F}(t, m^*, \bar{t}, F^*(m^*)) = F^*(m^*)$. According to the comparison principle, we obtain that the solution of (2.3) passing through $(\bar{t}, F^*(m^*))$ satisfies

which contradicts to $F(\tilde{t}, M_s, t_0, F_0) < F^*(m^*)$ and $\bar{t}\in (t_0, \tilde{t})$. The proof is completed.

Remark 2. Theorem 1 shows that when the initial population size of wild mosquitoes is not large ($F_0 < F_1(m_0)$), even if the release intensity of sterile mosquitoes is not strong ($M_s(t)\leq m^*$), the mosquito population can be successfully suppressed. However, if the initial size of mosquito population is large ($F_0\geq F^*(m^*)$), the same release intensity will lead to the failure of mosquito population suppression.

In the following, we try to determine a release intensity to ensure successful suppression of mosquito population for large initial population size. Let

Theorem 2. If $A > CD\delta_F$, $m_0 > 0$ and $\underline{M_s} > m^*$, then the extinction equilibrium $F = 0$ of model (2.3) is globally asymptotically stable.

Proof. Since $m_0 > 0$, the extinction equilibrium $F = 0$ of model (2.3) is locally asymptotically stable from the proof of Theorem 1. We only need to show that $F = 0$ is globally attractive. According to Lemma 1, for any $t_0\geq 0$ and $F_0 > 0$, $\overline{F} = \limsup_{t\rightarrow \infty}F(t, M_s, t_0, F_0)$ exists.

We now show that $\overline{F} = 0$. If it does not hold, then $\overline{F} > 0$. By the fluctuation lemma, there exists a time sequence $\{\tau_k\}$ such that $\lim_{k\rightarrow \infty}F(\tau_k) = \overline{F}, \lim_{k\rightarrow \infty}F'(\tau_k) = 0$. In addition, since $m_0 > 0$ and $\underline{M_S} > m^*$, there must be a subsequence $\{\bar{\tau}_k\}\subseteq\{\tau_k\}$ such that $\lim_{k\rightarrow \infty}M_s(\bar{\tau}_k) > m^*$. Taking the limit in (2.3) along $\{\bar{\tau}_k\}$ gives

which leads to $G(\overline{F}, m^*) < 0$. However, from Lemma 1 and the properties of $G(F, m)$ defined in (3.3), we know that $G(F, m^*)\geq0$ for $F\in(0, \infty)$, then a contradiction occurs. Therefore, $\overline{F} = 0$, and for any $t_0\geq 0$ and $F_0 > 0$, $\lim_{t\rightarrow \infty}F(t, M_s, t_0, F_0) = 0$ holds. The proof is completed.

Remark 3. Theorem 2 shows that when we increase the release intensity of sterile mosquitoes so that $m_0 > 0$ and $\underline{M_s} > m^*$, the mosquito population can always be successfully suppressed. This result can be conveniently applied in practice.

3.3.   Autonomous special cases

In this subsection, we investigate two special cases of the autonomous models (2.4) and (2.5), and mainly study the dynamic behavior.

3.3.1.   Dynamics of model (2.4)

For model (2.4), the release period of the sterile mosquito is equal to its sexual lifespan, and the number of sexually active sterile mosquitoes in the field remains unchanged, that is, $M_s(t)\equiv m$. We have the following results for (2.4).

Theorem 3. If $A > CD\delta_F$ and $0 < m < m^*$, then the dynamics of model (2.4) has the following conclusions:

(i) $F = 0$ is uniformly stable and $\lim_{t\rightarrow \infty}F(t, m, t_0, F_0) = 0$ if $0 < F_0 < F_1(m)$.

(ii) $F = F_1(m)$ is unstable.

(iii) $F = F_2(m)$ is uniformly stable, and $\lim_{t\rightarrow \infty}F(t, m, t_0, F_0) = F_2(m)$ if $F_0 > F_1(m)$.

Proof. From Lemma 1, when $0 < m < m^*$, model (2.4) has three equilibria: $F = 0$, $F = F_1(m)$ and $F = F_2(m)$.

(ⅰ) This conclusion can be verified by slightly modifying the proof of the same result in Theorem 1. In fact, if we replace $m_0$ and $M_S$ by $m$, then we can deduce the conclusion (ⅰ).

(ⅱ) The instability of $F_1(m)$ follows directly from the attractivity of $F_0 = 0$.

(ⅲ) We first show that for any $t_0\geq0$ and $\delta\in(0, F_2(m)-F_1(m))$, if $|F_2(m)-F_0| < \delta$, then

If it does not hold, then there must exist $t_1 > t_0$ such that $|F(t_1, m, t_0, F_0)-F_2(m)| = \delta$ and $|F(t, m, t_0, F_0)-F_2(m)| < \delta$ for $t_0\leq t < t_1$. There are two possible cases: $F(t_1) = F_2(m)+\delta$ and $F(t_1) = F_2(m)-\delta$. If $F(t_1) = F_2(m)+\delta$, then we have $F'(t_1)\geq 0$ and $F(t) < F_2(m)+\delta$ for $t_0\leq t < t_1$. Substitute $t_1$ into (2.4), and we can obtain

and consequently

which can be further reduced to $G(F_2(m)+\delta, m)\leq0$. However, $G(F, m) > 0$ for all $F > F_2(m)$, which is a contradiction. For the second case, if $F(t_1) = F_2(m)-\delta$ and $F(t) > F_2(m)-\delta$ for $t_0\leq t < t_1$, through similar discussions, we can get $G(F_2(m)-\delta, m)\geq0$. However, $G(F, m) < 0$ for all $F_1(m) < F < F_2(m)$, which is also a contradiction. Thus, $F_2(m)$ is uniformly stable.

Now we further prove its attractivity. To this end, we only need to show

In fact, by (3.8), for any $\delta\in(0, F_2(m)-F_1(m))$ and $F_0 > F_1(m)+\delta$, we can get $F(t, m, t_0, F_0) > F_1(m)+\delta, t\geq t_0$. Then, $\underline{F} = \liminf_{t\rightarrow \infty}F(t, 0, t_0, F_0)\geq F_1(m)+\delta$, and there must be a monotonic time sequence $\{t_k\}$ satisfying $\lim_{k\rightarrow \infty}t_k = \infty$, such that $\lim_{k\rightarrow \infty}F(t_k) = \underline{F}$ and $\lim_{k\rightarrow \infty}F'(t_k) = 0$. Taking limit on both sides of (2.4) along $\{t_k\}$, and we can get

which can be further reduced to $G(\underline{F}, m) = 0$. Since $\underline{F}\geq F_1(m)+\delta > F_1(m)$, and $G(F, m) = 0$ if and only if $F = F_2(m)$ for $F > F_1(m)$, we can deduce $\underline{F} = F_2(m)$. In addition, according to Lemma 2, we know $\overline{F} = \limsup_{t\rightarrow \infty}F(t, m, t_0, F_0)$ exists and is finite. By similar discussion, we can derive $\overline{F} = F_2(m)$. Then, we have $\underline{F} = \overline{F} = F_2(m)$ which verifies (3.10). The proof is completed.

As $m$ increases to $m^*$, these two positive equilibria $F = F_1(m)$ and $F = F_2(m)$ coincide as the unique positive equilibrium $F^*(m^*)$. When $m > m^*$, the extinction equilibrium $F = 0$ is the only equilibrium of (2.4). By discussions similar to the above, we can obtain the following conclusions.

Theorem 4. (1) If $A > CD\delta_F$ and $m = m^*$, then the extinction equilibrium $F = 0$ of (2.4) is uniformly stable, and $\lim_{t\rightarrow \infty}F(t, m^*, t_0, F_0) = 0$ if $0 < F_0 < F^*(m^*), t_0\geq 0$. In addition, the unique positive equilibrium $F = F^*(m^*)$ is globally asymptotically stable from the right-side, and $\lim_{t\rightarrow \infty}F(t, m^*, t_0, F_0) = F^*(m^*)$ if $F_0 > F^*(m^*), t_0\geq 0$.

(2) If $m > m^*$, then the unique equilibrium $F = 0$ of (2.4) is globally asymptotically stable.

Remark 4. According to Theorem 3 and 4, as the value of $m$ changes, the attraction domain of the stable extinction equilibrium $F = 0$ is different. This indicates that under a specific release intensity, the initial size of mosquito population determines whether the mosquito population can be finally suppressed. The larger the $m$, the larger the corresponding attraction area of $F = 0$, and the more likely the mosquito population will be suppressed.

3.3.2.   Dynamics of model (2.5)

Next, we investigate the effect of long-term constant releases of sterile mosquitoes on the suppression of wild mosquito population based on system (2.5).

Clearly, for any $t_0\geq 0$, if $F(t_0) > 0, M_s(t_0) > 0$, then $F(t) > 0, M_s(t) > 0$ for all $t\geq t_0$. In addition, $F(t)\leq\max\{F(t_0), F^*\}, M_S(t)\leq\max\{M_s(t_0), \frac{u}{\delta_s}\}$ hold for $t\geq t_0$.

By choosing the Dulac function $B(F, M_s) = \frac{1}{F^2}$, we can deduce

where $f$ and $g$ are the functions at the right end of equations in system (2.5).

Noting that if $\delta_F < \delta_s$ (this assumption is consistent with the actual situation), then $\frac{\partial (fB)}{\partial F}+\frac{\partial (gB)}{\partial M_s} < 0$ for $(F, M_s)\in R_2^+$, thus system (2.5) has no closed orbits in $R_2^+$.

It is easy to know that system (2.5) has a boundary equilibrium $E_0(0, M_s^*)$, where $M_s^* = \frac{u}{\delta_s}$. To study positive equilibria of (2.4), we consider the algebraic equation

which is equivalent to

Therefore, the existence and number of positive equilibria of model (2.5) are equivalent to the existence and number of positive roots of the following quadratic equation

where $\tilde{A_1}(u) = \delta_FB(D+\frac{u}{\delta_s}HB)$, and $A_2, A_3$ are the same as in Lemma 1.

By introducing a threshold for the release rate

we can get the following conclusion by similar discussion in Lemma 1.

Lemma 3. When $A > CD\delta_F$, the nonnegative equilibria of system (2.5) can be classified as follows:

(i) If $0 < u < u^*$, then system (2.5) has three equilibria: $E_0(0, M_s^*)$, $E_1(F_1(u), M_s^*)$ and $E_2(F_2(u), M_s^*)$, where

(ii) If $u = u^*$, then system (2.5) has two equilibria: $E_0(0, M_s^*)$ and $E^*(F^*(u^*), M_s^*)$, where

(iii) If $u > u^*$, then the boundary equilibrium $E_0(0, M_s^*)$ is the unique equilibrium of system (2.5).

We now investigate the stability of these equilibria. The Jacobian matrix of system (2.5) has the form

where

Obviously, $J_{11}(E_0) = -\delta_F$, thus the boundary equilibrium $E_0(0, M_s^*)$ of system (2.5) is a node which is locally asymptotically stable. In particular, If $u > u^*$, then the unique equilibrium $E_0(0, M_s^*)$ is globally asymptotically stable.

When $0 < u < u^*$, we have $\frac{AF_i}{\left[DF_i(BF_i+C)+HM_s^*(BF_i+C)^2 \right]} = \delta_F, i = 1, 2$, where $F_i = F_i(u)$. It is clear that $J_{12}(E_i) < 0$. Let

then

Since $F_i+\frac{C}{B} = \frac{A_2}{2\tilde{A_1}(u)}\Big{[}1\mp\sqrt{1-\frac{\tilde{A_1}(u)}{\tilde{A_1}(u^*)}}\Big{]}$, $A_2 = A+\delta_FCD < 2A, \; A_3 = \frac{AC}{B}$, $\tilde{A_1}(u^*) = \frac{A_2^2}{4A_3} = \frac{A_2^2B}{4AC}$ and $\tilde{A_1}(u) < \tilde{A_1}(u^*)$, we can further get

Noting that

then we can easily get $J_{11}(E_2) < 0$, and the positive equilibrium $E_2(F_2(u), M_s^*)$ is a locally asymptotically stable node.

Let

thus

In addition, by $\tilde{A_1}(u^*) = \frac{A_2^2}{4A_3} = \frac{A_2^2B}{4AC}$, we get

Because $\tilde{A_1}(u) = \delta_FB(D+\frac{u}{\delta_s}HB) < \tilde{A_1}(u^*)$ for $0 < u < u^*$, we have $\frac{\tilde{A_1}(u)}{\tilde{A_1}(u^*)}\in(0, 1)$. Let $y = \sqrt{1-\frac{\tilde{A_1}(u)}{\tilde{A_1}(u^*)}}$ and $N = \frac{A}{\delta_FCD}$, then $N > 1$,

and

Consider $w(y) = \frac{2Ny}{N-1+(N+1)y^2}$, and by direct calculation, we can get that $w'(y) = \frac{2N(N-1)-2N(N+1)y^2}{[N-1+(N+1)y^2]^2} = 0$ has only one positive root $y = \sqrt{\frac{N-1}{N+1}}$, and $w(y)$ is strictly monotonically increasing on $(0, \frac{N-1}{N+1}]$ with $w(\frac{N-1}{N+1}) = 1$. Then, $w(y) < 1$ for any $0 < y < \frac{N-1}{N+1}$ and $T_{E_1}(u) > 0$. The positive equilibrium $E_1(F_1(u), M_s^*)$ is an unstable saddle.

When $u$ increases to $u = u^*$, these two positive equilibria $E_1(F_1(u), M_s^*)$ and $E_2(F_2(u), M_s^*)$ coincide as the unique positive equilibrium $E^*(F^*(u^*), M_s^*)$, which is a saddle node.

In summary, we have the following results.

Theorem 5. If $A > CD\delta_F$ and $\delta_F < \delta_s$, then we have the following conclusions for model (2.5).

(i) If $0 < u < u^*$, then the boundary equilibrium $E_0(0, M_s^*)$ is a locally asymptotically stable node, $E_1(F_1(u), M_s^*)$ is an unstable saddle, while $E_2(F_2(u), M_s^*)$ is a locally asymptotically stable node.

(ii) If $u = u^*$, then the unique positive equilibrium $E^*(F^*(u^*), M_s^*)$ is an unstable saddle node.

(iii) If $u > u^*$, then the unique equilibrium $E_0(0, M_s^*)$ is globally asymptotically stable.

4.   Numerical simulation

In this section, some numerical examples are presented to confirm the theoretical results we obtained in last section. Most parameter values are taken from ^[2], ^[3] and ^[23] (see Table 2).

We apply the calculation method in ^[2] and ^[3] for the environmental capacity of eggs $K$, where an island of 74 ha (hectares) was considered. The male population was estimated to be 69 ha$^{-1}$, then they assumed that the number of adult wild males was $M^* = F^* = 69\times 74 = 5106$ when the population reaches a stable state. By direct calculation, they got the eggs number at the stable state was $E^* = \frac{\delta_M M^*}{(1-\nu)\nu_E}\approx 2.0023\times10^4$. Because $F^* = \frac{\nu \nu_EE^*}{\delta_F} = \frac{(\nu_E+\delta_E)E^*}{\beta_E(1-E^*/K)}$ holds, the approximate value of environmental capacity can be deduced as

It is easy to verify that $A = 0.0625 > \delta_FCD\approx0.0008$ and $m^* = \frac{(A-CD\delta_F)^2}{4A{CD\delta_F}}\frac{D}{HB}\approx9.5123\times10^4$. Without releasing sterile mosquitoes, the number of wild adult female ones will stabilize at $F^* = \frac{C}{B}(\frac{A}{CD\delta_F}-1)\approx1.2094\times10^4$.

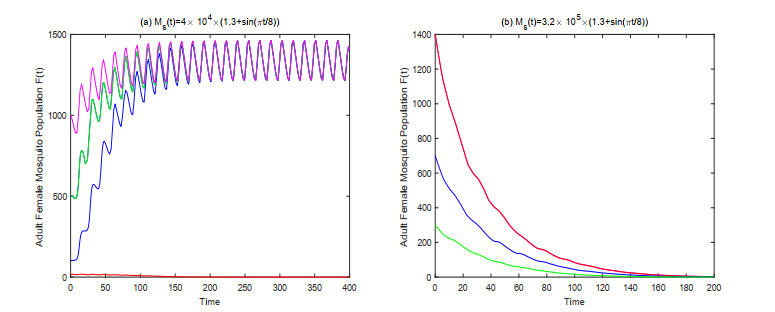
For the general non-autonomous case, we first take $M_s(t) = 4\times 10^4\times(1.3+\sin(\pi t/8))$ for model (2.3). By direct calculation, we get $m_0 = \inf_{t\in (0, \infty)} M_s(t) = 1.2\times 10^4$ and $M_s(t)\leq 9.2\times 10^4 < m^*, t\geq0$. From Figure 1(a), we can see that the extinction equilibrium $F = 0$ is locally asymptotically stable (which is consistent with the conclusion of Theorem 1), and there is also a positive periodic solution that is locally stable. That is, the model presents bistability phenomenon. When increasing the release intensity of sterile mosquitoes to $M_s(t) = 3.2\times 10^5\times(1.3+\sin(\pi t/8))$, we have $\underline{M_S} = \liminf_{t\rightarrow \infty}M_S(t) = 9.6\times 10^4 > m^*, t\geq0$. According to Theorem 2, the extinction equilibrium $F = 0$ is globally asymptotically stable (see Figure 1(b)).

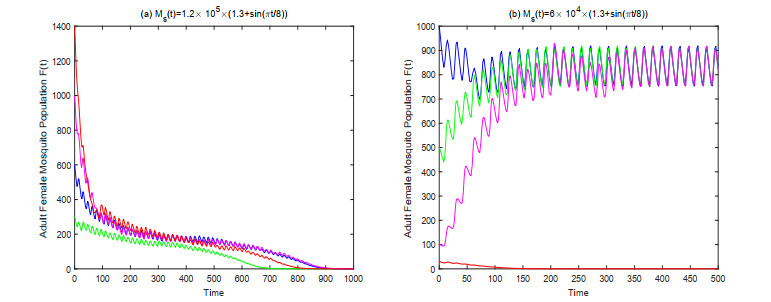
Comparing the constraints for the function $M_s(t)$ in Theorem 1 ($M_s(t)\leq m^*$) and Theorem 2 ($\underline{M_S} > m^*$), we note that there are other cases of $M_s(t)$. To this end, we consider special forms for $M_s(t)$ such that its function values distributed on both sides of the threshold $m^*$. We choose two forms: $M_s(t) = 1.2\times 10^5\times(1.3+\sin(\pi t/8))$ and $M_s(t) = 6\times 10^4\times(1.3+\sin(\pi t/8))$, which both satisfy $\underline{M_S} < m^* < \overline{M_S}$. From Figure 2, we can see that for the former one, $F = 0$ is globally asymptotically stable (see Figure 2(a)), while bistability phenomenon is present for the latter form (see Figure 2(b)). This also shows that the conditions in Theorem 1 and 2 are sufficient but not necessary.

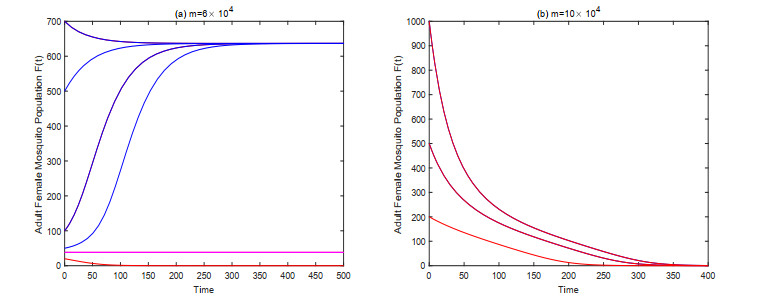
For the autonomous cases, we first verify the results we get for model (2.4). Select $0 < m = 6\times 10^4 < m^*\approx9.5123\times10^4$, from Figure 3(a), we find that the extinction equilibrium $F = 0$ is locally asymptotically stable. In addition, there are also two positive equilibria and the larger one is locally stable. As the release intensity increases to $m = 10\times 10^4 > m^*$, the extinction equilibrium $F = 0$ becomes globally asymptotically stable (see Figure 3(b)). These are consistent with the conclusions in Theorem 3 and 4.

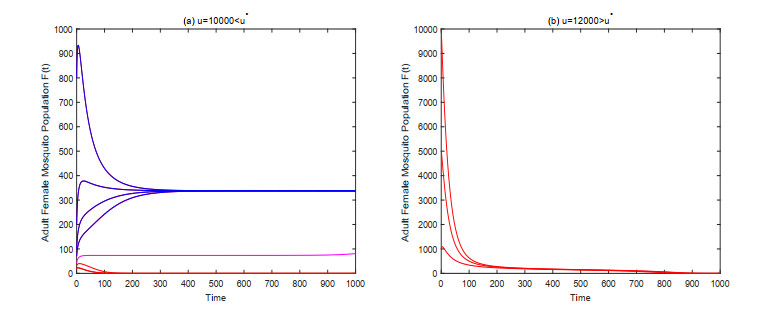
Then for system (2.5), we get the threshold for the release rate $u^* = \frac{m^*}{\delta_s}\approx 1.1415\times 10^4$. By taking $u = 1\times 10^4 < u^*$, Figure 4(a) also shows bistability phenomenon, and both the wild mosquito-extinction equilibrium $E_0(0, M_s^*)$ and the larger positive equilibrium $E_2(F_2, M_s^*)$ are locally stable. The wild mosquito-extinction equilibrium $E_0(0, M_s^*)$ becomes globally asymptotically stable when the release rate increases to $u = 1.2\times 10^4 > u^*$ (see Figure 4(b)).

In addition to the two modes described by models (2.4) and (2.5), there is another common release mode of sterile mosquitoes in practice, namely, impulsive release, which means that the release function $u(\cdot)$ in (2.2) is a sum of Dirac deltas. Now let's study this situation numerically. We assume that sterile mosquitoes are released with amount of $\sigma$ at discrete times $t = kT, k = 0, 1, 2, \cdots$, where $T$ is the release period, then the number of sterile mosquitoes in the environment satisfies

Obviously, system (4.1) has a unique positive periodic solution $\widetilde{M_s}(t)$ which is globally asymptotically stable, where

In addition, the expression for the solution of system (4.1) is $M_s(t) = (M_s(0^+)-\widetilde{M_s}(0^+))\exp(-\delta_s t)+\widetilde{M_s}(t)$, then we can deduce $\lim\limits_{t\rightarrow \infty} {M_s}(t) = \widetilde{M_s}(t)$. Since what we want to study is the asymptotic behavior of the population development system of wild mosquitoes, we let ${M_s}(t) = \widetilde{M_s}(t)$.

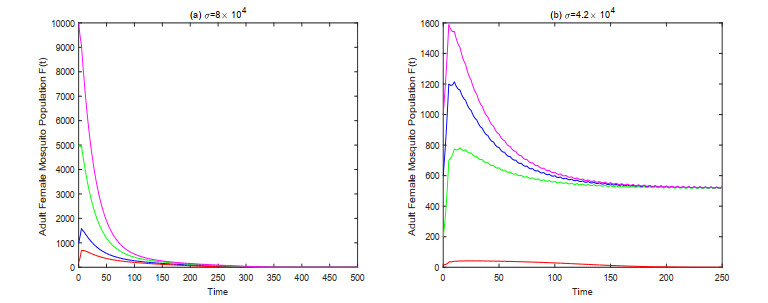
Fix a release period $T = 5$. When we select $\sigma = 8\times 10^4$, by simple calculating, we can get $\widetilde{M_s}(t) > m^*, t\geq 0$. Then we can see that the extinction equilibrium is globally asymptotically stable (see Figure 5(a)). When choose $\sigma = 4.2\times 10^4$, then we can get $\liminf_{t\rightarrow \infty}\widetilde{M_s}(t) < m^*$, and we find that in addition to the extinction equilibrium, there is also a locally stable positive periodic solution(see Figure 5(b)).

5.   Conclusions

In this paper, we studied a kind of mosquito population suppression model, taking into account the stage structure of mosquito growth as well as the sex structure. First, we constructed a non-autonomous mosquito population suppression model (2.3) by taking the number of sexually active sterile mosquitoes released into the field as a given function $M_s(t)$. Then we considered a special case, that is, the release period of the sterile mosquito is equal to its sexual lifespan. The non-autonomous model (2.3) is transformed into a one-dimensional ordinary differential equation model (2.4). Finally, continuing the work in ^[2], we considered another special case and investigated a two-dimensional mosquito population suppression system (2.5).

For the non-autonomous mosquito population suppression model (2.3), we determined a critical value $m^*$ for $M_s(t)$. If $m_0 > 0$ and $M_s(t)\leq m^*, t\geq0$, then the extinction equilibrium $F = 0$ is locally but not globally asymptotically stable (Theorem 1). While when $m_0 > 0$ and $\underline{M_S} > m^*$, then the extinction equilibrium $F = 0$ becomes globally asymptotically stable (Theorem 2). For the one-dimensional ordinary differential equation model (2.4), if $0 < m < m^*$, both the extinction equilibrium $F = 0$ and the larger positive equilibrium $F_2(m)$ are locally stable (Theorem 3). If $m = m^*$, the unique positive equilibrium $F = F^*(m^*)$ is semi-stable. While if $m > m^*$, then the unique equilibrium $F = 0$ becomes globally asymptotically stable (Theorem 4). For the two-dimensional mosquito population suppression system (2.5), we also found a critical value $u^*$ of the release rate $u$. Through dynamic analysis, we finally obtained conclusions similar to model (2.4) (Theorem 5). Finally, we provided a series of numerical examples to verify our theoretical results.

In this work, we just gave sufficient conditions for successful suppression and persistence of mosquito population for the non-autonomous model (2.3). In the numerical example, we also found that mosquito populations can be eliminated with a relatively weak release function $M_s(t)$. In the future research, we will try new research methods to obtain sufficient and necessary conditions for mosquito population suppression.

In addition, to reduce the difficulty of mathematical analysis, when constructing model (5), we omitted the equations for the aquatic stage population and the adult male mosquito population under specific assumptions, and only used the model parameters to characterize the stage and sex structure of the wild mosquito population. This may make the characterization of these structures less precise. Therefore, in future research, we will use high-dimensional models to accurately depict the stage and gender structures of mosquitoes and study various release strategies.

Acknowledgments

This work is supported by the National Natural Science Foundation of China (11901502), Program for Innovative Research Team (in Science and Technology) in University of Henan Province (21IRTSTHN014), Natural Science Foundation of Henan Province(222300420016) and Nanhu Scholars Program for Young Scholars of XYNU.

Conflict of interest

The authors declare no conflicts of interest in this paper.