1.
Introduction
Compared to traditional surgery, the advantages of minimally invasive surgery are minor trauma, minor infection, and minor pain [1], a trend of surgical treatment in modern medicine. In modern minimally invasive surgery technology, the endoscope and specialist instruments are inserted into the internal cavity through a small incision in the surgical site. The images captured by the endoscope are displayed on the screen in real-time [2]. The surgeon can monitor the patient's entire operation through the endoscopic transmission of images and can determine the patient's surgical condition [3]. For traditional minimally invasive surgery, there are still limitations in obtaining image information from the endoscope, such as the narrow field of view, uneven illumination and high reflection intensity, and the difficulty in obtaining depth information of the target area and locating the endoscope accurately. Under such complex environmental conditions, higher requirements are put forward for computer vision processing systems. Therefore, SLAM system is innovatively applied to the field of minimally invasive surgery to solve the bottleneck faced by modern minimally invasive surgery [4]. The endoscope acts as a robot in the field of minimally invasive surgery. It moves through the cavity of the human body, measures spatial information of the visible area of the cavity, completes the reconstruction of soft tissue, and displays it to the doctor. Minimally invasive surgery can help doctors make the right decisions by combining SLAM with better positioning of the endoscope and depth of the target area. It has crucial research significance and application value [5].
The concept of minimally invasive surgery and the issue of visual SLAM were first proposed in 1983 and 1986, respectively. The use of vision technology based on endoscope images in minimally invasive surgery has obvious advantages without introducing additional equipment to the already very complex surgical device [6]. SLAM is most frequently used in minimally invasive surgery in the abdomen, where deformation and tissue movement are minimal. At the initial stage of application, SLAM was added to the algorithm as an auxiliary means for positioning [7]. In 2009, Grasa et al. used monocular laparoscopy to generate a sparse map of the environment from SLAM and then estimated the three-dimensional information of the scene through sequential images. In 2009 and 2010, the Mountney P team respectively proposed the application of an SLAM system based on the monocular endoscope and binocular endoscope in minimally invasive surgery for endoscope positioning and 3D modeling, and the monocular system based on the framework of SLAM to establish a motion model to estimate the motion of the camera and soft tissue effectively [8]. The binocular system constructs a 3D texture model of a minimally invasive surgery environment, a method model of dynamic view expansion [9]. In recent years, there have been more and more studies on the application of visual SLAM in minimally invasive surgery [10,11,12], most of which are devoted to solving the bottleneck of minimally invasive surgery. Vision-based techniques are good at restoring 3D structures and estimating endoscope motion. However, this research has a long way to go to solve the problems of accuracy [13].
This paper mainly studies visual SLAM in minimally invasive surgery. For the deficiencies of traditional minimally invasive surgery, visual SLAM technology is used to complete the positioning and 3D mapping of the endoscope [14,15]. In combination with the K-means algorithm and the Super point algorithm, the feature information of the image in the inner cavity is extracted. It solves the problem that it is difficult to obtain the depth information of the target area and accurately locate the endoscope position in the environment with narrow vision, uneven illumination and high reflection intensity of minimally invasive surgical endoscope. Then, the iterative nearest point method was used to estimate the position and attitude of the endoscope. Finally, the stereo matching method was used to reconstruct the lumen image, and the point cloud image of the surgical area was recovered. Improve surgical accuracy and shorten the surgical time, thus optimizing the operation of the entire system [16].
The structure of this paper is as follows. Section 2 discusses the visual SLAM and the method of extracting image features through Superpoint algorithm, as well as the method of extracting image feature points based on Superpoint algorithm and k-means algorithm. In Section 3, experiments are carried out to verify the effectiveness of our proposed method. Section 4 summarizes the whole article.
2.
Materials and methods
2.1. Feature extraction
2.1.1. Superpoint algorithm network
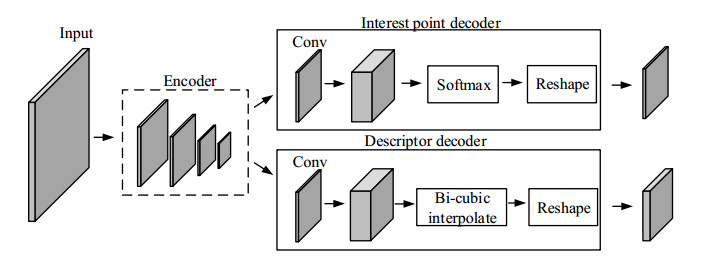
The final output of the Super point (self supervised interest point detection and description) algorithm is the feature point algorithm with descriptors [17]. The network diagram is shown in Figure 1.
In this network, the initial feature detector is obtained by training the basic graph with undisputed feature points in a self-supervised way, and the image feature information is further extracted by the neural network. The stability of feature extraction is improved while the sensitivity of the feature extraction algorithm to illumination is reduced. The network is divided into two parts [18], the network for detecting basic graph corners and the network for extracting image features and outputting descriptors. The specific steps are as follows:
(1) Feature point detector pre-training. For an image, it is difficult to define which points are the real feature points, but if it is a simple graph with defined corner positions, it is easy to determine the truth. Therefore, the pre-training is carried out by extracting undisputed feature points from an unlabelled virtual simple image, obtaining pseudo-truths, and using the resulting pseudo-truths to determine the true feature points. Then, the pseudo-true values are combined with the true values to retrain the feature detector to obtain the extracted feature. The resulting pseudo-truths are combined with the true values to retrain the feature detector to obtain the extracted feature point model.
(2) The feature point detection network is divided into two parts: encoding and decoding. Image coding is to input the image to be processed into the shared coding network and reduce the dimension of the image to reduce the computation of the network. After dimensionality reduction, the image size is 1/8 of the original image. The main function of the encoder in the network is to map the input image to the spatial tensor, which has a smaller spatial dimension and larger channel depth. A probability is calculated for each pixel, which represents the probability that this pixel is a feature point. When decoding feature points, subpixel convolution is adopted to avoid the possibility of network overload caused by excessive computation in the process of extracting feature points. The input dimension of the decoder is RHc×Wc×65 (65 is the number of channels, and A non-feature point is added to the local area of the original picture 8×8), and the output dimension is RH×W. After normalization of the exponential function, When the non-feature points are removed, the image is deformed to change the dimension from RHc×Wc×64 to RH×W. As shown in Figure 2. The true value of the feature points at the position of, and then the truth value of the feature detector is trained to get the optimized detector. Then the optimized detector is used to re-detect the features and get the image with the feature points, and the image of the superposition feature points is taken as the final output feature graph [19].
(3) Description sub detection network. Extracting the descriptor is a decoding operation. The descriptors are obtained from feature points. First, the image size and feature point position are normalized. (x,y) and K are used to represent the coordinates and number of feature points, respectively, and the normalized feature points are formed into A tensor with scale 1×1×K×(x,y). The actual positions of feature points on a certain channel in the tensor are obtained by inverse normalization, and the pixel positions are complemented by bilinear interpolation to avoid non-integer pixel positions. Output a complete descriptor with a complete dimension 1×C×1×K, where C is the number of channels. Finally, the unit length is described by the L2 normalization operation. As shown in Figure 3. The descriptors of feature points can be calculated through the above steps and output by the deep learning network. However, this result may not satisfy the characteristics that the distance between the same feature points is as close as possible, the distance between different feature point descriptors is as far as possible, and the truth value cannot be determined. We know the pose transformation between a pair of images for homography transformation, and we can calculate the corresponding relationship of feature points. It can calculate the loss of any pair of feature points, and further optimization can make the obtained descriptor conform to its feature
2.1.2. Superpoint algorithm combined with the k-means algorithm
K-Means clustering algorithm will use all the data as a whole, the initial clustering center is K randomly selected points in the whole, and the other data into the center of the minimum Euclidean distance, but this is not the final result of dividing. Each data needs to recalculate the bunch distance between the point and point and average to recalculate the clustering center for K a new round of the division of data clusters. The clustering stops until the clustering result of each time remains unchanged or reaches the preset maximum number of iterations. This clustering algorithm presets K categories in clustering without knowing the specific information of these C categories and the type of data to be clustered. The algorithm divides the data to be clustered into these K categories on the basis of minimizing the error function. In the case of processing massive data, the clustering does not depend on the pre-defined classes [20].
After the Super point algorithm extracts the feature points and descriptors of the image, the heatmap of the feature map can be obtained. Each feature point in the heatmap has an index value, and the K-means method is used to cluster these index values. When feature points are matched, a confidence probability of a correct match is set for each index value. According to this probability, whether this point is the correct match of the points to be matched is determined. Set the maximum number of matching point pairs and match according to the index of feature points. When all feature points are matched, or the maximum number of matching points is reached, the matching graph is output. The K-means clustering algorithm is applied to avoid the successful matching between the reflective spot and the strong light point in the inner cavity and reduce the probability of mismatching. Because the k-means algorithm is very simple, very fast, time complexity is nearly linear, and it is suitable for mining large-scale datasets, combining it with the super point algorithm not only improves the matching degree, but also shortens the time it takes to compute the k-means algorithm.
2.2. Endoscopic pose estimation
The pose estimation process is actually to find the corresponding point between the 2D image and the 3D spatial position. When representing an object's 3D spatial position and orientation, a coordinate system rotating with the object is usually established with the object as the coordinate origin. The transformation relationship between the rotating coordinate system and the reference coordinate system can determine the spatial position of the object. That is, the solution of pose estimation discusses the transformation relationship between coordinate systems.
In visual SLAM, there are usually two methods to estimate the pose of the sensor. One is to use a linear method to estimate the pose information of the visual sensor. After obtaining the initial pose, the pose information is further optimized by constructing and solving the least square problem. The other is to directly integrate the position of the space point and the position of the sensor to solve the pose information. In the estimation of the pose information of the endoscope, since the position of the endoscope is not continuous and uniform, the first method is selected to solve the pose information of the endoscope. The initial pose is estimated first, and then the results are optimized to increase the accuracy and robustness of the SLAM system.
The iterative closest point (ICP) is a standard algorithm that estimates pose between completed 3D Point pairs. Suppose there are a pair of 3D point pairs matched and their centroids:
where: p1,p2,...pn is the two-dimensional coordinate of the target point.
To perform pose estimation is actually to find a Euclidean transform that satisfies:
The result of the above formula is solved through the algebraic method of singular value decomposition, and the error term of the point i is defined as:
Constructing the least-squares problem:
Solve the above equation and get R and t, minimizing the sum of squares of errors. Calculate the centroids coordinates of each point:
The rotation matrix and translation vector are calculated according to the following formula:
Define matrix:
W=U∑VT can be obtained by singular value decomposition of Eq (7), where ∑ is the diagonal matrix of singular values. When the rank is full, the rotation matrix can be solved as:
Substitute the solved rotation matrix into Eq (8) to solve the translation vector.
2.3. Reconstruction of regional point clouds
Firstly, the disparity value of the target region is obtained and optimized by the SGBM stereo matching method; Secondly, the depth value is calculated by using the parallax value to form the depth image; Finally, the 3D point cloud data are obtained by further calculation.
Parallax refers to that when binocular stereo vision obtains two frames of images at the same time through the left and right cameras, the corresponding relationship between features is established at the imaging points on the left and right imaging planes of the camera through the corresponding three-dimensional space points so that the human eye can feel the depth. Observe the imaging difference of the image on the camera plane. This difference is called parallax. In short, parallax describes the horizontal pixel difference between the corresponding imaging points of the left and right eyes [21].
There is a point P(X,Y,Z) in the world coordinate system, stereo vision to capture the image parallax produce process as shown in Figure 3, when the left and right eye of the camera to get the world coordinates of the same spatial point P, the position of the two imaging points due to the existence of the error will not identical, when choosing the left camera as a benchmark, to obtain the current position of parallax need to put the right mesh projection to the left eye, The distance between the right target coordinate and the left target is obtained by calibration, so this projection process is equivalent to the projection of the left target to the point (x−Tx,y) in the world coordinate system. We use the similar triangle mathematics principle; the parallax obtained is d=xl−xr. After stereoscopic correction of binocular vision, a point is identified on the left, and a matching point can be found along the opposite pole line.
The parallax values in the parallax map can be calculated to obtain the corresponding depth values. The depth map shows the form of the image by integrating these depth values. The depth map contains the depth information of each pixel value, and the pixel value in the depth map is the depth value. According to the geometric relation of parallel binocular vision, the relation between parallax value and object depth information is as follows:
where: dep represents image depth information; f is the normalized focal length, which is the parameter fx in the endoscope's internal parameter matrix; b is the baseline length, that is, the distance between the optical centers of the two cameras left and right of the endoscope; xlandxrare the distances between the imaging points on the left and right imaging planes and the left and right edges of the image. The calculation formula of parallax value and depth value can be derived as follows:
where, d is the parallax value of pixel points. Since the right side of the equation is known, the depth value is easy to calculate. By analyzing the above formula, it can be concluded that the closer the point in the image is to the imaging plane, the greater the parallax in the left and right cameras, and vice versa.
According to the coordinate transformation relation, the transformation relation between the world coordinate system and the pixel coordinate system can be obtained as follows:
where: The first matrix on the right of the equation is the endoscope internal parameter; matrix R and t are rotation matrices and shift vectors, respectively. The camera coordinate system coincides with the origin of the world coordinate system. If there is no translation or rotation during the transition between the two coordinate systems, the object has the same depth in the two coordinate systems. The depth information of each point is directly presented in the depth map. The depth information can be used to calculate the corresponding point cloud data, namely the three-dimensional spatial information of pixels, through the coordinate transformation relationship between the above world coordinate system and the image coordinate system:
The calculated data can be saved in the created point cloud data, and the point cloud image can be displayed by using some libraries. The depth image of point cloud data can be calculated through the reverse calculation of the above operations.
3.
Results
3.1. Image feature extraction and analysis
In order to verify whether the improved algorithm has better feature extraction and matching effect in the strong reflection environment in minimally invasive surgery, the feature extraction results of the improved algorithm and the improved algorithm in the lumen environment are compared, and the simulation results are compared and analyzed. The original image pairs for feature extraction are shown in a) and b) Figure 5. By comparing the feature extraction results of various methods on the image pairs, the effectiveness of the improved extraction network is shown [22].
The results of image feature extraction using the original Super point algorithm are shown in c) in Figure 5, and the results of feature extraction using the improved Super point algorithm are shown in d) in Figure 5. As can be seen from the figure, the number of feature points extracted by the Super point algorithm in the inner cavity environment under a strong reflection environment is more and more uniform than that extracted by the traditional algorithm, but there are too many failed matching points and many invalid points. These matching failed points and invalid points are caused by the narrow field of vision, uneven lighting and high reflection intensity of minimally invasive surgical endoscope, The numerical value of the depth map physically means the distance from the camera. A lot of black and a lot of white are similar distances from you. The feature points are difficult to extract, and the resolution of the depth map is low, which reduces the number of feature points that can be extracted. False matching situations are reasonable. However, the distribution of feature points extracted by the improved Super point algorithm is more uniform, and effective features can be extracted from the edge part of the insufficient light. e) in Figure 5 is the matching result of feature points extracted by the original Super point algorithm, and f) in Figure 5 is the matching result of feature points extracted by the improved Super point algorithm. It can be easily seen from the figure that the improved algorithm has a better matching effect on feature points, and the number of invalid feature points is 0, which is better than the original algorithm and the traditional algorithm. As can be seen from Figure 5 and Table 1, after the Super point algorithm and clustering algorithm are combined and improved, the number of feature extraction effects of the inner cavity image increases and is evenly distributed, without any redundant points that fail to be matched successfully, and the percentage of successfully matched points in the total number of extractions is the highest and the false matching rate is the lowest. Although the proportion of effective points extracted by SIFT, SURF and ORB algorithms can reach 100%, their speed is very slow when there are too many matching points, and there are many wrong matching point pairs. The original Superpoint algorithm can not only ensure the number of feature points, but also ensure the speed, but it has a very low proportion of effective points. Compared with the traditional feature extraction algorithm and the original Super point algorithm, it shows the best effect.
Table 1 shows the numerical results of each algorithm. From the two indicators of Extracting time and Match time in the table, the time of the improved algorithm is significantly shorter than that of other algorithms, which also proves that the improved algorithm has the minimum time consumption, the maximum number of matching success points and the minimum mismatch rate, and the effective point ratio is significantly improved compared with that before the improvement.
3.2. Positioning of the endoscope
Different from large-scale scenarios, when the endoscope is in the special environment of minimally invasive surgery, the estimation of the position information of the endoscope only needs numerical values. Since the movement process of the endoscope is irregular, it is not meant to form the map of its position information [23]. In this topic, will the SLAM system of camera pose estimation algorithm used in endoscopic minimally invasive surgery, using the image information of the real environment of minimally invasive surgery for endoscopic frame only when the estimate judgment in endoscopic movement between rotation and translation in the process of calculation is accurate, lumen mapping results of image feature points as shown in Figure 6.
The blue point in Figure 6 is the feature point of the current frame, and the green point is the feature point of the next frame. The current frame is directly processed without any operation. The position difference between blue and green is why the camera moves when shooting different frames, and the red point is the position of the green point after the rotation matrix and the motion vector move left. The distance between blue dots and red dots is smaller than that between green dots, with an average error of 5.43 pixels.
3.3. Reconstruction of regional point clouds
The disparity image and depth image before and after optimization are obtained by using the algorithm in this chapter as follows:
Figure 7 shows the point cloud before and after optimization of the lumen image in the actual scene, which is displayed in the gray form, and the cavity area is more obvious. The image information with too dark illumination in the original image has the condition that the visual difference has not been calculated, so the depth value cannot be calculated, which is reflected as the whole area in the point cloud image. The point cloud image before optimization has obvious segmentation lines. After optimization, this phenomenon is weakened, and most of the information is effectively restored. The details of the main areas are more delicate, and some smaller blood vessels that are not easy to extract can also be restored [24].
Figure 8 is a pure point cloud image without adding mesh and texture. The color depth in the figure indicates the distance between the point and the endoscope. Although the edge results of the disparity map and depth map are not satisfactory, it can be seen from b) of Figures 7 and 8 that the reconstruction method adopted can have a good effect on the restoration of images in the lumen environment.
As can be seen from a) and b) in Figure 9, except for the empty part with extremely weak light, the image has a filling effect, and the edge is partially optimized. Although the "boundary" between the core area and the fat part of the image does not have an excellent restoration result, the edge is smoothed. c) is a pure point cloud image without mesh and texture, and the depth of color in the figure represents the distance between the point and the endoscope. d) is the point cloud diagram of the inner cavity image in the real scene. In the case of the image information with a too-dark light in the original image, the parallax value is not calculated, so the depth value cannot be calculated, which is reflected in the point cloud image as the empty area in the figure. Most of the information in the image can be effectively restored. The details of the main areas are delicate, and some small vessels that are not easy to be extracted can also be recovered. The reconstruction method used in this paper can restore the image in the inner cavity with good effect.
4.
Conclusions
In view of the problem that it is difficult to obtain depth information on the target area and accurately locate the position of the endoscope in the environment of the narrow field of vision, uneven illumination, and high reflection intensity of minimally invasive surgery endoscope, the method based on the combination of K-means and Super point algorithm is first used to extract image feature points and match. Compared with the traditional algorithm, the simulation results are more accurate and stable. Compared with the Super point, the logarithm of successful matching points is increased by 32.69%, the proportion of effective points is increased by 25.28%, the false matching rate is reduced by 0.64%, and the extraction time is reduced by 1.98%. In the real minimally invasive surgery scene, the feature points in the endovascular image were mapped to verify the accuracy of the calculated rotation and translation, with an average error of 5 pixels. Finally, the stereo matching algorithm is used to calculate the disparity map of the original image, and then the disparity map is used to calculate the depth information so as to calculate the point cloud image with depth information, which can well reconstruct the small features such as blood vessels in the image, and also have a good reconstruction effect on the edge part of the insufficient light [25].
Acknowledgments
Funding: This research was supported by the Natural Science Foundation of Heilongjiang Province (LH2019F024), China, 2019–2022, and Key R & D Program Guidance Projects of Heilongjiang Province (Grant No. GZ20210065), 2021–2024
Conflict of interest
The authors declare there is no conflict of interest.









 DownLoad:
DownLoad:











