Existence and uniqueness solutions of fuzzy integration-differential mathematical problem by using the concept of generalized differentiability

1.   Introduction

The predator-prey model has always been an important research content of biomathematics, because a predator-prey relationship is widespread in nature ^[1,2,3,4]. Among the population growth laws, the Allee effect is an important biological phenomenon. W. Allee proposed the famous Allee effect to describe the phenomenon that low-density populations are prone to extinction ^[5]. Since then, the predator-prey model with the Allee effect has received extensive attention from scholars. Cooperative hunting is also widespread in nature, such as gray wolves, chimpanzees, banded mongooses, lions, etc. ^[6,7]. They all hunt collectively.

In ^[8], R. Yadav et al. studied a predator-prey model with the Allee effect and hunting cooperation, that is

$u(t)$ and $v(t)$ are densities of prey and predator, respectively. $r$, $K$ and $u_0$ represent intrinsic growth rate, carrying capacity and Allee effect parameter of prey, respectively. The term $\frac{(\lambda+a v) u^2 }{1 +A(\lambda+a v) u^2}$ is the functional response function including the hunting cooperation in predator, with capturing rate $\lambda$, handling time $A$ and hunting cooperation parameter $a$. $e$ and $m$ are conversion efficiency and death rate of a predator. Make the changes $u = K\tilde{u}$, $v = \frac{r}{\lambda}\tilde{v}$, $t = \frac{1}{rK}\tilde{t}$, $\alpha = \frac{a r}{\lambda ^2}$, $\beta = \frac{\text{N0}}{K}$, $\sigma = \frac{m}{K^2 e \lambda }$, $h = A K^2 \lambda$, $\eta = \frac{K e \lambda }{r}$, and drop "$\tilde{\; \; }$", the model (1.1) is changed into

The authors mainly studied the Turing pattern of the model (1.2) by applying the amplitude equation through weakly nonlinear analysis ^[8]. The model (1.2) shows the spiral and target patterns.

In the inter-population interaction, time delay often occurs, such as gestation delay, maturation time, capturing time, and so on. Some scholars have discussed the dynamic properties of predator-prey models with time delay, mainly focusing on Hopf bifurcation ^[9,10,11]. They obtained that time delay may affect the stability of equilibria, and induce Hopf bifurcation ^[12,13,14]. In particular, in the reaction-diffusion predator-prey model with time delay, there may be spatially homogeneous and inhomogeneous periodic solutions, but the stable periodic solutions are often spatially homogeneous in the numerical simulation. This is not consistent with the actual situation, because in the real world, the spatial distribution of the population is difficult to reach a completely uniform state, that is, a stable spatial homogeneous periodic solution. This is one of our motivations, that is, will there be stably spatially inhomogeneous periodic solutions for the delayed reaction-diffusion predator-prey model.

In addition, due to the limited resources and the competition within the population, many scholars have chosen the Logistic growth law to describe the growth law of the prey population. Logistic growth law is mainly applicable to the predator-prey model in the form of an ordinary differential equation, and it is assumed that the spatial distribution of resources is uniform. However, in fact, the spatial distribution of resources is often nonuniform, and the population competition among prey is often spatially nonlocal competition ^[15,16]. To describe this phenomenon, the authors ^[17,18] modified the $\frac{u}{K}$ as $\frac{1}{K} \int_{\Omega}G(x, y)u(y, t)dy$ with some kernel function $G(x, y)$. In ^[19], D. Geng and H. Wang studied the normal form of double-Hopf bifurcation for a predator-prey model with nonlocal competition with nonlocal effect. In ^[21], Liu et al. studied a delayed diffusive predator-prey model with group defense effect and nonlocal competition and observed stably spatially inhomogeneous oscillations. In ^[20] the authors analyzed a diffusive predator-prey model with nonlocal competition from the perspective of bifurcation. In this paper, we want to study what new dynamic phenomena will appear when adding spatial nonlocal competition in the model (1.2), and what impact it will have on the distribution of prey and predator densities. This is another motivation for our work.

Motivated by above, we studied the following model

where $d_1$ and $d_2$ are diffusive coefficients. $\tau$ is the gestation delay in predator. $\int_{\Omega}G(x, y)u(y, t)dy$ represents the nonlocal competition effect. The kernel function is

which is widely used ^[20,21]. This is based on the assumption that the competition strength among prey individuals in the habitat is the same. The region $\Omega = (0, l\pi)$ with $l > 0$ just for the convenience of calculation.

The article is structured as follows. In Section 2, the stability and existence of Hopf bifurcation for the models with and without nonlocal competition are studied. In Section 3, the parameters that determine the properties of Hopf bifurcation are given. In Section 4, some numerical simulations are shown. In Section 5, a short conclusion is given.

2.   Stability analysis

The authors obtain that the system (1.3) has at least one coexisting equilibrium $(u_*, v_*)$ when $\frac{\beta ^2}{\beta ^2 h+1} < \sigma < \frac{1}{h+1}$ and $\beta < 1$ in ^[8], where $u_*$ is the root of the following equation falling in the interval $(\beta, 1)$,

and $v_* = \frac{u_* (1-u_*) (u_*-\beta)}{\sigma }$. In the following, we just denote the coexisting equilibrium as $(u_*, v_*)$.

2.1.   The model with nonlocal competition

Linearize system (1.3) at $E_*(u_*, v_*)$

where

and $\hat{u} = \frac{1}{l\pi}\int_{0}^{l\pi}u(y, t)dy$. The characteristic equations are

where

$\mathbb{N}$ and $\mathbb{N}_0$ represent the positive integer set and the non-negative integer set.

When $\tau = 0$, the characteristic equations are as follow

Make the following hypothesis

Under the hypothesis ${\bf{(H_1)}}$, $E_*(u_*, v_*)$ is locally asymptotically stable when $\tau = 0$.

Next, we will discuss the case of $\tau > 0$.

Lemma 2.1. Assume ${\bf{(H_1)}}$ holds, the following results hold.

● Equation (2.3) has a pair of purely imaginary roots $\pm i\omega^+_n$ at $\tau^{j, +}_n$ for $j \in \mathbb{N}_0$ and $n\in\mathbb{W}_1$.

● Equation (2.3) has two pairs of purely imaginary roots $\pm i\omega^\pm_n$ at $\tau^{j, \pm}_n$ for $j \in \mathbb{N}_0$ and $n\in\mathbb{W}_2$.

● Equation (2.3) has no purely imaginary root for $n\in\mathbb{W}_3$.

Where $\pm i\omega^\pm_n$, $\tau^{j, \pm}_n$, $\mathbb{W}_1$, $\mathbb{W}_2$ and $\mathbb{W}_3$ are defined in (2.8) and (2.9).

Proof. Let $\mbox{i}\omega$ ($\omega > 0$) be a solution of Eq (2.3), then

Obviously. $\text{cos}\omega\tau = \frac{\omega ^2 (b_2 E_n+G_n)-M_n G_n}{G_n^2+b_2^2 \omega ^2}$, $\text{sin}\omega\tau = \frac{\omega \left(E_n G_n+M_n b_2-b_2 \omega ^2\right)}{G_n^2+b_2^2 \omega ^2}$. It leads to

Let $z = \omega^2$, then (2.6) becomes

and the roots of (2.7) are $z^{\pm} = \frac{1}{2}[-H_n \pm \sqrt{H_n^2-4J_nK_n}]$, where $H_n = E_n^2-2 M_n-b_2^2$, $J_n = M_n+G_n$, and $K_n = M_n-G_n$. If ${\bf{(H_1)}}$ holds, $J_n > 0\; (n \in \mathbb{N}_0)$. By direct calculation, we have

Define

and

It is easy to verify the conclusion in the Lemma 2.1.

Next, we verify the transversal condition for the existence of Hopf bifurcation.

Lemma 2.2. Assume ${\bf{(H_1)}}$ holds. Then $\mathit{\text{Re}}(\frac{d \lambda} {d \tau})|_{\tau = \tau^{j, +}_n} > 0$, $\mathit{\text{Re}} (\frac{d \lambda} {d \tau})|_{\tau = \tau^{j, -}_n} < 0$ for $n \in \mathbb{S}_1\cup \mathbb{S}_2$ and $j \in \mathbb{N}_0$.

Proof. By (2.3), we have

Then

Therefore, $\text{Re}(\frac{d \lambda} {d \tau})|_{\tau = \tau^{j, +}_n} > 0$, $\text{Re} (\frac{d \lambda} {d \tau})|_{\tau = \tau^{j, -}_n} < 0$.

Denote $\tau_* = min\{\tau^0_n|\; n\in\mathbb{S}_1\cup \mathbb{S}_2\}$. We have the following theorem.

Theorem 2.1. For system (1.3), assume ${\bf{(H_1)}}$ holds.

● $E_*(u_*, v_*)$ is locally asymptotically stable for $\tau > 0$ when $\mathbb{S}_1\cup \mathbb{S}_2 = \varnothing$.

● $E_*(u_*, v_*)$ is locally asymptotically stable for $\tau \in [0, \tau_*)$ when $\mathbb{S}_1\cup \mathbb{S}_2\neq \varnothing$.

● $E_*(u_*, v_*)$ is unstable for $\tau \in (\tau_*, \tau_*+\varepsilon)$ for some $\varepsilon > 0$ when $\mathbb{S}_1\cup \mathbb{S}_2\neq \varnothing$.

● Hopf bifurcation occurs at $(u_*, v_*)$ when $\tau = \tau^{j, +}_n$ $(\tau = \tau^{j, -}_n)$, $j\in \mathbb{N}_0$, $n \in \mathbb{S}_1\cup \mathbb{S}_2$. In addition, the spatially homogeneous (inhomogeneous) periodic solutions occur when $\tau = \tau^{j, \pm}_0$ ($\tau = \tau^{j, \pm}_n$, $n > 0$).

2.2.   The model without nonlocal competition

The model (1.3) without nonlocal competition is as follow

Linearize system (2.10) at $E_*(u_*, v_*)$

The characteristic equations are

where

When $\tau = 0$, the characteristic equations are as follow

Make the following hypothesis

Under the hypothesis ${\bf{(H_2)}}$, $E_*(u_*, v_*)$ is locally asymptotically stable when $\tau = 0$.

Remark 2.1. It is easy to obtain that $\tilde{A}_0-b_2 = E_0-b_2$, $\tilde{B}_0+\tilde{C}_0 = M_0+G_0$, $\tilde{E}_n-b_2-(E_n-b_2) = -\hat{a} > 0$ and $\tilde{M}_n+\tilde{G}_n-(M_n+G_n) = -\hat{a}\left(d_2\frac{n^2}{l^2}+\eta \sigma -b_2\right)$ for $n \in \mathbb{N}$. Hence, under condition $\frac{d_2}{l^2}+\eta \sigma -b_2\geq 0$, hypothesis ${\bf{(H_1)}}$ can deduce ${\bf{(H_2)}}$.

Through a similar process, we have the following results. Define

Corollary 2.1. Assume ${\bf{(H_2)}}$ holds, the following results hold.

● Equation (2.12) has a pair of purely imaginary roots $\pm i\omega^+_n$ at $\tau^{j, +}_n$ for $j \in \mathbb{N}_0$ and $n\in\mathbb{S}_1$.

● Equation (2.12) has two pairs of purely imaginary roots $\pm i\omega^\pm_n$ at $\tau^{j, \pm}_n$ for $j \in \mathbb{N}_0$ and $n\in\mathbb{S}_2$.

● Equation (2.12) has no purely imaginary root for $n\in\mathbb{S}_3$.

The transversal condition is also valid.

Corollary 2.2. Assume ${\bf{(H_2)}}$ holds. Then $\mathit{\text{Re}}(\frac{d \lambda} {d \tau})|_{\tau = \tau^{j, +}_n} > 0$, $\mathit{\text{Re}} (\frac{d \lambda} {d \tau})|_{\tau = \tau^{j, -}_n} < 0$ for $n \in \mathbb{\widetilde{S}}_1\cup \mathbb{\widetilde{S}}_2$ and $j \in \mathbb{N}_0$.

Denote $\tilde{\tau}_* = min\{\tau^0_n|\; n\in\mathbb{\widetilde{S}}_1\cup \mathbb{\widetilde{S}}_2\}$. We have the following theorem.

Corollary 2.3. For the model (2.10), assume ${\bf{(H_2)}}$ holds.

● $E_*(u_*, v_*)$ is locally asymptotically stable for $\tau > 0$ when $\mathbb{\widetilde{S}}_1\cup \mathbb{\widetilde{S}}_2 = \varnothing$.

● $E_*(u_*, v_*)$ is locally asymptotically stable for $\tau \in [0, \tilde{\tau}_*)$ when $\mathbb{\widetilde{S}}_1\cup \mathbb{\widetilde{S}}_2\neq \varnothing$.

● $E_*(u_*, v_*)$ is unstable for $\tau \in (\tilde{\tau}_*, \tilde{\tau}_*+\varepsilon)$ for some $\varepsilon > 0$ when $\mathbb{\widetilde{S}}_1\cup \mathbb{\widetilde{S}}_2\neq \varnothing$.

● Hopf bifurcation occurs at $(u_*, v_*)$ when $\tau = \tau^{j, +}_n$ $(\tau = \tau^{j, -}_n)$, $j\in \mathbb{N}_0$, $n \in \mathbb{\widetilde{S}}_1\cup \mathbb{\widetilde{S}}_2$. In addition, the spatially homogeneous (inhomogeneous) periodic solutions occur when $\tau = \tau^{j, \pm}_0$ ($\tau = \tau^{j, \pm}_n$, $n > 0$).

3.   Property of Hopf bifurcation

By the work ^[22,23], we study the property of Hopf bifurcation. For fixed $j\in \mathbb{N}_0$ and $n\in \mathbb{S}_1\cup \mathbb{S}_2$, we denote $\tilde{\tau} = \tau^{j, \pm}_n$. Let $\bar{u}(x, t) = u(x, \tau t)-u_*$ and $\bar{v}(x, t) = v(x, \tau t)-v_*$. Drop the bar, (1.3) can be written as

We rewrite system (3.1) as following system

where $\alpha_1 = \frac{2 v_* (\alpha v_*+1) \left(3 h u_*^2 (\alpha v_*+1)-1\right)}{\left(h u_*^2 (\alpha v_*+1)+1\right)^3}-2 u_*+2$, $\alpha_2 = -\frac{2 \left(u_*^3 (\alpha h v_*+h)+2 \alpha u_* v_*+u_*\right)}{\left(h u_*^2 (\alpha v_*+1)+1\right)^3}$, $\alpha_3 = -\frac{2 u_*^2 \left(\alpha +\alpha h u_*^2\right)}{\left(h u_*^2 (\alpha v_*+1)+1\right)^3}$, $\alpha_4 = -\frac{24 h u_* v_* (\alpha v_*+1)^2 \left(h u_*^2 (\alpha v_*+1)-1\right)}{\left(h u_*^2 (\alpha v_*+1)+1\right)^4}$, $\alpha_5 = \frac{6 u_*^4 (\alpha h v_*+h)^2+4 h u_*^2 \left(5 \alpha ^2 v_*^2+6 \alpha v_*+1\right)-4 \alpha v_*-2}{\left(h u_*^2 (\alpha v_*+1)+1\right)^4}$, $\alpha_6 = \frac{4 \alpha u_* \left(h^2 u_*^4 (\alpha v_*+1)+2 \alpha h u_*^2 v_*-1\right)}{\left(h u_*^2 (\alpha v_*+1)+1\right)^4}$, $\alpha_7 = \frac{6 \alpha ^2 h u_*^4 \left(h u_*^2+1\right)}{\left(h u_*^2 (\alpha v_*+1)+1\right)^4}$, $\beta_1 = -\frac{2 \eta v_* (\alpha v_*+1) \left(3 h u_*^2 (\alpha v_*+1)-1\right)}{\left(h u_*^2 (\alpha v_*+1)+1\right)^3}$, $\beta_2 = \frac{2 \eta \left(u_*^3 (\alpha h v_*+h)+2 \alpha u_* v_*+u_*\right)}{\left(h u_*^2 (\alpha v_*+1)+1\right)^3};\beta_3 = \frac{2 \alpha \eta u_*^2 \left(h u_*^2+1\right)}{\left(h u_*^2 (\alpha v_*+1)+1\right)^3}$, $\beta_4 = \frac{24 \eta h u_* v_* (\alpha v_*+1)^2 \left(h u_*^2 (\alpha v_*+1)-1\right)}{\left(h u_*^2 (\alpha v_*+1)+1\right)^4}$, $\beta_5 = -\frac{2 \eta \left(3 u_*^4 (\alpha h v_*+h)^2+2 h u_*^2 \left(5 \alpha ^2 v_*^2+6 \alpha v_*+1\right)-2 \alpha v_*-1\right)}{\left(h u_*^2 (\alpha v_*+1)+1\right)^4}$, $\beta_6 = -\frac{4 \alpha \eta u_* \left(h^2 u_*^4 (\alpha v_*+1)+2 \alpha h u_*^2 v_*-1\right)}{\left(h u_*^2 (\alpha v_*+1)+1\right)^4}$, $\beta_7 = -\frac{6 \alpha ^2 \eta h u_*^4 \left(h u_*^2+1\right)}{\left(h u_*^2 (\alpha v_*+1)+1\right)^4}$.

Define the real-valued Sobolev space $X: = \left\{(u, v)^T: u, v\in H^2(0, l\pi), \; (u_x, v_x)|_{x = 0, l\pi} = 0 \right\},$ the complexification of $X$ is $X_{\mathbb{C}}: = X \oplus \mbox{i}X = \left\{x_1+\mbox{i}x_2|\; x_1, x_2\in X\right\}.$ The inner product $< \tilde{u}, \tilde{v} > : = \int_{0}^{l\pi} \overline{u_1} v_1dx+ \int_{0}^{l\pi} \overline{u_2} v_2dx$ is for $\tilde{u} = (u_1, u_2)^{T}$, $\tilde{v} = (v_1, v_2)^{T}$, $\tilde{u}, \tilde{v}\in X_{\mathbb{C}}$. The phase space $\mathbb{C}: = C([-1, 0], X)$ is with the sup norm, then we can write $\phi_t \in \mathbb{C}$, $\phi_t(\theta) = \phi(t+\theta)$ or $-1\leq \theta \leq0$. Denote $\beta_n^{(1)}(x) = (\gamma_n(x), 0)^T$, $\beta_n^{(2)}(x) = (0, \gamma_n(x))^T$, and $\beta_n = \{\beta_n^{(1)}(x), \beta_n^{(2)}(x) \}$, where $\{\beta_n^{(i)}(x) \}$ is an orthonormal basis of $X$. We define the subspace of $\mathbb{C}$ as $\mathbb{B}_n: = \mbox{span}\{ < \phi(\cdot), \beta_n^{(j)} > \beta_n^{(j)}| \phi \in \mathbb{C}, j = 1, 2 \}$, $n\in\mathbb{N}_0$. There exists a $2\times2$ matrix function $\eta^n(\sigma, \tilde{\tau})$ $-1\le \sigma \le0$, such that $-\tilde{\tau} D\frac{n^2}{l^2} \phi(0)+\tilde{\tau}L(\phi) = \int_{-1}^{0}d \eta^n(\sigma, \tau) \phi(\sigma)$ for $\phi \in \mathbb{C}$. The bilinear form on $\mathbb{C}^* \times \mathbb{C}$ is defined by

for $\phi \in \mathbb{C}$, $\psi \in \mathbb{C}^*$. Define $\tau = \tilde{\tau}+\mu$, then the system undergoes a Hopf bifurcation at $(0, 0)$ when $\mu = 0$, with a pair of purely imaginary roots $\pm \mbox{i}\omega_{n_0}$. Let $A$ denote the infinitesimal generators of semigroup, and $A^*$ be the formal adjoint of $A$ under the bilinear form (3.3). Define the following function

Choose $\eta_{n_0}(0, \tilde{\tau}) = \tilde{\tau}[(-n_0^2/l^2)D+L_1+L_3 \delta(n_{n_0})]$, $\eta_{n_0}(-1, \tilde{\tau}) = -\tilde{\tau} L_2$, $\eta_{n_0}(\sigma, \tilde{\tau}) = 0$ for $-1 < \sigma < 0$. Let $p(\theta) = p(0)e^{\mbox{i}\omega_{n_0} \tilde{\tau} \theta}\; \; (\theta \in[-1, 0])$, $q(\vartheta) = q(0)e^{-\mbox{i}\omega_{n_0} \tilde{\tau} \vartheta}\; \; (\vartheta \in[0, 1])$ be the eigenfunctions of $A(\tilde{\tau})$ and $A^*$ corresponds to $i \omega_{n_0} \tilde{\tau}$ respectively. We can choose $p(0) = (1, p_1)^T$, $q(0) = M(1, q_2)$, where $p_1 = \frac{1}{a_2}(\mbox{i}\omega_{n_0}+d_1 n_0^2/l^2-a_1-\hat{a}\delta(n_0))$, $q_2 = \frac{e^{-\mbox{i} \tau \omega_{n_0} }}{b_1}\left(-\hat{a} \delta(n_0)-a_1+\frac{d_1 n^2}{l^2}+\mbox{i} \omega_{n_0} \right)$, and $M = (1+p_1 q_2+\tilde{\tau}q_2(b_1 +b_2 p_1)e^{-\mbox{i}\omega_{n_0} \tilde{\tau}})^{-1}$. Then (3.1) can be rewritten in an abstract form

where

respectively, for $\phi = (\phi_1, \phi_2)^T \in \mathbb{C}$ and $\hat{\phi}_1 = \frac{1}{l\pi}\int_{0}^{l\pi}\phi dx$. Then the space $\mathbb{C}$ can be decomposed as $\mathbb{C} = P\oplus Q$, where $P = \{z p \gamma_{n_0}(x) +\bar{z} \bar{p} \gamma_{n_0}(x)|z \in \mathbb{C}\}$, $Q = \{\phi \in \mathbb{C} | (q\gamma_{n_0}(x), \phi) = 0\; \mbox{and}\; (\bar{q}\gamma_{n_0}(x), \phi) = 0 \}$. Then, system (3.6) can be rewritten as $U_t = z(t)p(\cdot)\gamma_{n_0}(x) +\bar{z}(t)\bar{p}(\cdot)\gamma_{n_0}(x)+ \omega(t, \cdot)$ and $\hat{U_t} = \frac{1}{l\pi}\int_{0}^{l\pi} U_t dx$, where

then, we have $\dot{z}(t) = \mbox{i}\omega){n_0} \tilde{\tau} z(t)+\bar{q}(0) < F(0, U_t), \beta_{n_0} >$. There exists a center manifold $\mathcal{C}_0$ and $\omega$ can be written as follow near $(0, 0)$.

Restrict the system to the center manifold is $\dot{z}(t) = \mbox{i}\omega_{n_0} \tilde{\tau} z(t)+g(z, \bar{z})$. Denote $g(z, \bar{z}) = g_{20}\frac{z^2}{2}+g_{11}z\bar{z} +g_{02}\frac{\bar{z}^2}{2}+g_{21}\frac{z^2\bar{z}}{2}+\cdots$. By direct computation, we have

where $I_2 = \int_{0}^{l\pi} \gamma^2_{n_0}(x) dx$, $I_3 = \int_{0}^{l\pi} \gamma^3_{n_0}(x) dx$, $I_4 = \int_{0}^{l\pi} \gamma^4_{n_0}(x) dx$, $\varsigma_1 = (\alpha_1+\xi (\alpha_2+\alpha_3 \xi))+\delta{n_0} (\beta -2 u_*)$, $\varsigma_2 = e^{-2 i \tau \omega _n} (\beta_1+\xi (\beta_2+\beta_3 \xi))$, $\varrho_1 = \frac{1}{4} ((2 \alpha_1+\alpha_2 (\overline{\xi} +\xi)+2 \alpha_3 \overline{\xi} \xi)+2 \delta{n_0} (\beta -2 u_*))$, $\varrho_2 = \frac{1}{4} (2 \beta_1+\beta_2 (\overline{\xi} +\xi)+2 \beta_3 \overline{\xi} \xi)$, $\kappa_{11} = 2 W_{11}^{(1)}(0) (2 \alpha_1+\alpha_2 \xi +\beta \delta{n_0}+\beta -2 (\delta{n_0}+1) u_*)+W_{20}^{(1)}(0) (2 \alpha_1+\alpha_2 \overline{\xi} +\beta \delta{n_0}+\beta -2 (\delta{n_0}+1) u_*)+2 W_{11}^{(2)}(0) (\alpha_2+2 \alpha_3 \xi)+W_{20}^{(2)}(0) (\alpha_2+2 \alpha_3 \overline{\xi})$, $\kappa_{12} = \frac{1}{2} (3 \alpha_4+\alpha_5 (\overline{\xi} +2 \xi)+\xi (2 \alpha_6 \overline{\xi} +\alpha_6 \xi +3 \alpha_7 \overline{\xi} \xi))$, $\kappa_{21} = 2 W_{11}^{(1)}(-1) (2 \beta_1+\beta_2 \xi) e^{-i \tau \omega _n}+2 W_{11}^{(2)}(-1) (\beta_2+2 \beta_3 \xi) e^{-i \tau \omega _n}+W_{20}^{(1)}(-1) (2 \beta_1+\beta_2 \overline{\xi}) e^{i \tau \omega _n}+W_{20}^{(2)}(-1) (\beta_2+2 \beta_3 \overline{\xi}) e^{i \tau \omega _n}$, $\kappa_{22} = \frac{1}{2} e^{-i \tau \omega _n} (3 \beta_4+\beta_5 (\overline{\xi} +2 \xi)+\xi (2 \beta_6 \overline{\xi} +\beta_6 \xi +3 \beta_7 \overline{\xi} \xi))$.

Now, we compute $W_{20}(\theta)$ and $W_{11}(\theta)$ for $\theta \in [-1, 0]$ to give $g_{21}$. By (3.7), we have

where

Compare the coeffcients of (3.8) with (3.9), we have

Then, we have

where $E_1 = \sum_{n = 0}^{\infty}E_1^{(n)}$, $E_2 = \sum_{n = 0}^{\infty}E_2^{(n)}$,

and $\hat{F}_{20} = 2(\varsigma_1, \varsigma_2)^T$, $\hat{F}_{11} = 2(\varrho_1, \varrho_2)^T$.

Thus, we can obtain

By the work ^[22], we can obtain the following theorem.

Theorem 3.1. For any critical value $\tau^j_n$ ($n\in \mathbb{S}, \; j \in \mathbb{N}_0$), we have the following results.

● When $\mu_2 > 0$ (resp. $< 0$), the Hopf bifurcation is forward (resp. backward).

● When $\beta_2 < 0$ (resp. $> 0$), the bifurcating periodic solutions on the center manifold are orbitally asymptotically stable (resp. unstable).

● When $T_2 > 0$ (resp. $T_2 < 0$), the period increases (resp. decreases).

4.   Numerical simulations

To analyze the effect of the Allee effect, hunting cooperation, nonlocal competition and time delay on the model (1.3), we carry out numerical simulations in this section which is done with Matlab. The numerical simulation of the systems is implemented by finite-difference methods. In the later numerical simulation, we select the initial value as $(u_0(x) = u_* +0.001cosx, v_0(x) = v_* -0.001cosx.)$, and have similar conclusions when we randomly select other initial values in the convergence domain. Fix the following parameters.

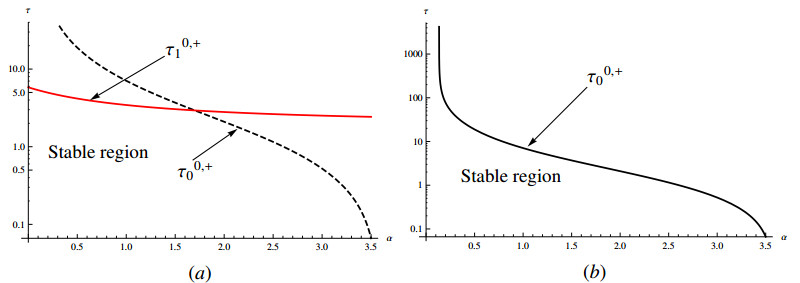
The bifurcation diagrams of models (1.3) and (2.10) are given in Figures 1 and 2. It can be seen that the coexistence equilibrium will change from stable to unstable with the appearance of periodic solutions. In the model (1.3), the inhomogeneous Hopf bifurcation curve $\tau_1^{0, +}$ exists, which implies that the stably spatially inhomogeneous periodic solutions may exist. But in the model (2.10), only the homogeneous Hopf bifurcation curve $\tau_0^{0, +}$ exists, which implies that only the spatially homogeneous periodic solutions may exist. This implies that the model (1.3) with nonlocal competition is more realistic than the model (2.10), since the existence of periodic solutions in the model (1.3) is spatially inhomogeneous. Because the prey and predator will continue to spread in space and move from the place with high survival pressure to the place with low survival pressure, thus forming a non-uniform periodic oscillation. Therefore, we should consider the nonlocal competition within the population when establishing the delayed reaction-diffusion predator-prey model. We can obtain that increasing the Allee effect parameter $\beta$ and hunting cooperation parameter $\alpha$ is not conducive to the stability of coexistence equilibrium points.

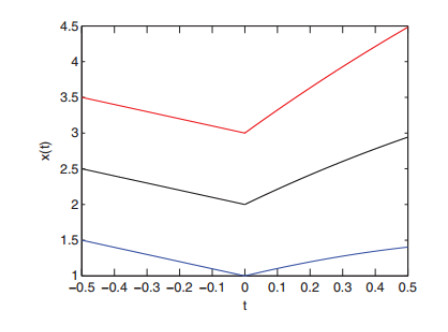
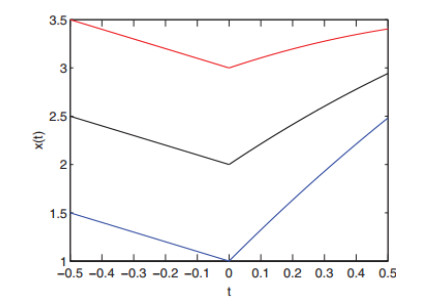
If we choose $\beta = 0.1$ and $\alpha = 1$, then $(u_*, v_*) = (0.5125, \; 0.3436)$ is the unique coexisting equilibrium and the hypothesis ${\bf{(H_1)}}$ holds. By direct computation, we have $\tau_* = \tau^0_1 \approx 3.4439 < \tau_0^0\approx 7.0688$. By Theorem 2.1, we know that $E_*(u_*, v_*)$ is locally asymptotically stable when $\tau \in [0, \tau_*)$ (Figure 3). It can be seen that the coexisting equilibrium $(u_*, v_*)$ is stable for models (1.3) and (2.10). For model (1.3), the Hopf bifurcation occurs when $\tau = \tau_*$. By Theorem 2.3, we have

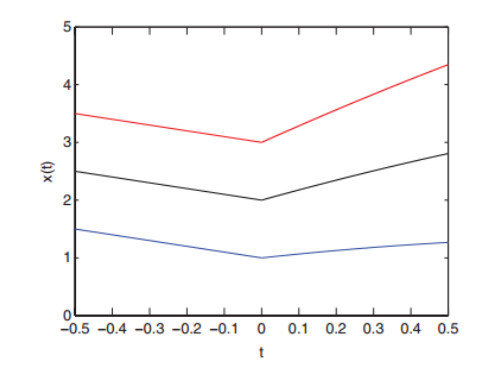
Hence, the stably spatially inhomogeneous bifurcating periodic solutions exist for $\tau > \tau_*$ (Figure 4). This means that increasing the time delay $\tau$ can affect the stability of the coexisting equilibrium $(u_*, v_*)$. In addition, the coexisting equilibrium $(u_*, v_*)$ changes from stable to unstable and the stably spatially inhomogeneous bifurcating periodic solutions appear for the model (1.3). But with the same parameters, the coexisting equilibrium $(u_*, v_*)$ is still stable for the model (2.10). Comparing Figure 4 and Figure 5, we can see that the nonlocal competition in prey can affect the dynamic properties of the predator-prey model and induce new dynamic phenomena (stably spatially inhomogeneous bifurcating periodic solutions).

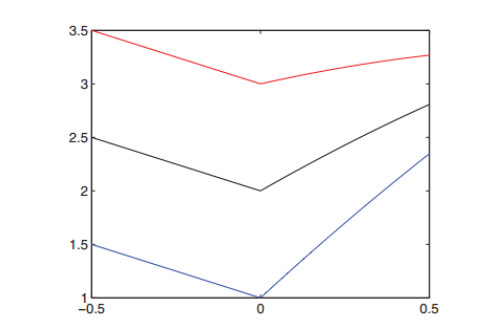
Continue to increase the time delay $\tau$ until it is larger than the critical value $\tau_0^{0, +}$, we can observe stable periodic solutions for both models (1.3) and (2.10). However, the stably spatially inhomogeneous bifurcating periodic solutions appear in model (1.3), and stably spatially homogeneous bifurcating periodic solutions appear in model (2.10). This also shows that nonlocal competition can affect the dynamic properties of the predator-prey model.

5.   Conclusions

In this paper, considering the self-diffusion of prey and predator, nonlocal competition in prey, and gestation delay in predators, we propose a delayed diffusive predator-prey model with the Allee effect and nonlocal competition in prey and hunting cooperation in predators. We study the local stability of coexisting equilibrium and existence of Hopf bifurcation by analyzing the distribution of eigenvalues. We also study the property of Hopf bifurcation: bifurcation direction, stability of the periodic solution, period of the periodic solution by center manifold theorem and normal form method.

Our analysis results are verified by numerical simulation, and the influence of the Allee effect, hunting cooperation, nonlocal competition and time delay on the model is analyzed. By numerical simulation, we obtain that increasing the Allee effect parameter $\beta$ and hunting cooperation parameter $\alpha$ will affect the stability of the coexistence equilibrium point, and there will be periodic solutions. The time delay can also affect the stability of coexisting equilibrium. When the time delay is less than the critical value, the coexistence equilibrium point is stable, and the densities of prey and predator will tend to the coexistence equilibrium. However, when the time delay is larger than the critical value, the coexistence equilibrium is unstable and the stable periodic solution appears. At this time, the density of prey and predator will produce periodic oscillation. The nonlocal competition in prey can affect the dynamic properties of the predator-prey model and induce new dynamic phenomena (stably spatially inhomogeneous bifurcating periodic solutions). Sometimes, the stability interval of a predator-prey model with nonlocal competition is smaller than that of a predator-prey model without nonlocal competition. This is also the reason why the predator-prey model with the nonlocal competition will have stably spatial inhomogeneous periodic solutions.

The main findings show that the Allee effect parameter $\beta$, hunting cooperation parameter $\alpha$, and time delay $\tau$ can significantly affect the stability of the coexistence equilibrium point, and can be used control the development of the population.

Acknowledgments

This research is supported by the Fundamental Research Funds for the Central Universities (Grant No.2572022DJ05), Postdoctoral program of Heilongjiang Province (No.LBHQ21060) and College Students Innovations Special Project funded by Northeast Forestry University. Data sharing is not applicable to this article as no datasets were generated or analyzed during the current study.

Conflict of interest

The authors declare there is no conflicts of interest.