Construction of functional brain connectivity networks from fMRI data with driving and modulatory inputs: an extended conditional Granger causality approach

1.   Introduction

In recent decades, there has been considerable focus on the control challenges associated with nonlinear systems, driven by the widespread occurrence of nonlinear behavior in modern control systems ^[1]. Various control strategies, including adaptive output feedback control, adaptive event-triggered control, adaptive backstepping control, and adaptive sliding mode control have been developed ^[2,3]. The backstepping control technique offers a systematic approach to tackling tracking control problems in nonlinear systems without the need to satisfy matching conditions. This technique involves breaking down the intricate nonlinear system into multiple subsystems and subsequently designing a virtual controller for each subsystem until the actual control law is derived ^[4]. In previous works, adaptive backstepping controllers and variable structure adaptive backstepping controllers were introduced to address the control problems of specific systems. However, for certain nonlinear systems, obtaining accurate dynamic models proves exceedingly challenging. To address this challenge, researchers have introduced neural networks (NNs) and fuzzy logic systems (FLSs) ^[5]. Given their ability to identify unknown nonlinear functions, the application of NNs and FLSs in the control of nonlinear systems has garnered significant interest and various studies in this domain have been conducted ^[6,7,8]. For example, an adaptive NN-based decentralized control approach has been formulated for interconnected nonlinear systems ^[9]. Additionally, an adaptive method has been reported for stochastic nonlinear systems by using fuzzy approximation and output feedback control ^[10]. However, it is important to clarify that the studies mentioned above did not consider the fault-tolerance aspect of the controlled system.

Actuators and sensors regularly experience operational disruptions and faults in real-world manufacturing environments, such as those involving flight control systems, satellite operations, and nuclear power facilities ^[11]. These faults can result in unsatisfactory system performance and, in severe cases, lead to instability. Ensuring system reliability and stability under all circumstances is crucial. As a result, it is crucial to devise an effective fault-tolerant control scheme that ensures the maintenance of stable and satisfactory control performance, even when faults are present ^[12]. Actuators ultimately age or breakdown entirely due to the increasing complexity and automation of modern control systems, particularly when they are subjected to demanding and prolonged continuous operations ^[13]. Actuator failures are common in many real-world applications, such as offshore ship-mounted cranes, two-stage chemical reactors and highly adaptable airplanes ^[14]. To minimize the negative impacts of faults on the system and get it as close to its pre-fault state as possible, fault-tolerant control is required. Adaptive control can simultaneously achieve optimal performance by dynamically modifying the controller design. As a result, combining fault-tolerant control with adaptive control has become a primary area of research to improve the security and dependability of industrial systems ^[15]. For instance, using the command filter technique, an adaptive fault-tolerant control issue for switched nonlinear systems has been reported ^[16]. Furthermore, an adaptive fault-tolerant control problem has been explored for a class of nonlinear large-scale systems under the impact of dead-zone nonlinearity ^[17]. In addition, under the influence of uncertainties in mismatched parameters and disturbances, an adaptive fault-tolerant control problem has been explored for nonaffine nonlinear systems ^[18]. A model-free adaptive fault-tolerant control technique, relying on NNs, has been documented for discrete-time nonlinear systems in the presence of sensor faults ^[19]. Despite these accomplishments, to the best of our knowledge, there has been no attention given to fault-tolerant control considering input delay in the existing literature.

Moreover, input delays can stem from the inherent characteristics of the plant or external factors within the system, such as computation time or sensor measurements ^[20]. This occurrence has the potential to result in a decline in system performance, or even induce instability ^[21]. Recent efforts have introduced various approaches to tackle adaptive control schemes for nonlinear systems grappling with input delays ^[22,23]. In ^[24], the authors have presented a NN-based adaptive control strategy for nonlinear systems facing state constraints and input delays. For single-input single-output uncertain systems with unmodeled dynamics and encompassing unknown constant time delays, an adaptive controller has been formulated using a backstepping design ^[25]. To address the adaptive fuzzy tracking control problem for nonlinear systems with input delays and output constraints, Pade approximation has been employed ^[26]. Furthermore, the exploration of adaptive output tracking control for disturbed multiple-input multiple-output switched uncertain nonlinear systems with input delays has been reported ^[27]. The authors of ^[28] proposed an adaptive fuzzy control methodology specifically for high-order nonlinear time-delay systems characterized by input saturation and state constraints.

Inspired by these considerations, here, we have undertaken the challenge of formulating an adaptive controller for nonstrict-feedback nonlinear systems featuring actuator faults, external disturbances, and input delays. Notably, considering the existing literature, the following contributions distinguish this work:

(1) Compared with the existing results ^[1,15], this paper addresses the problem of nonlinear systems with a nonstrict-feedback structure. The proposed control scheme deals with both input delay and actuator faults in nonlinear systems. Instead of employing the auxiliary system from previous research ^[29], this study utilizes the Pade approximation method to address the issue of input delay. It introduces the variable $x_{n+1}$ to handle input delay, thereby simplifying the design process. In addition, external disturbance is also considered in this work. This demonstrates the versatility and real-world usefulness of the proposed control strategy.

(2) By utilizing the capabilities of radial basis function NNs, this study employs a backstepping method to create an adaptive fault-tolerant controller through the application of Lyapunov stability theory. The controller ensures that all signals in the closed-loop systems are bounded and tracking errors converge to a small area around the starting point. The effectiveness of the proposed method is confirmed through comparisons with existing results by using error assessment criteria.

This article is organized into the following sections. The problem formulation and preliminary information are provided in Section 2. Section 3 presents the main results. The results of the simulation are then covered in Section 4, and the conclusion is given in Section 5.

2.   System statement and preliminaries

Consider the following type of nonstrict-feedback nonlinear system with input delays and actuator faults:

where $x = [x_1, \ldots, x_n]^T$ is the state variable, $f_i(.)$ denotes the unknown nonlinear function with $f_i(0) = 0$, $v$ is the controller input to be designed, $u$ is the system input that is subject to actuator fault, $\tau$ is the input delay, which is a positive constant, $y$ is the system output, $d_i(.)$ represents the external disturbance, and $d_i(.)$ satisfies $|d_i(.)|\leq \bar{d}_i$, with $\bar{d}_i$ being the constant.

In this study, the input delay problem is addressed by estimating the input delay of the systems using the Pade approximation, as described in ^[30]. The Pade approximation is characterized as follows:

where $s$ is the Laplace variable and $\mathcal{L}\{u(v(t))\}$ is the Laplace transform of $u(t)$.

Describe the new variable $x_{n+1}$ as follows:

By the inverse Laplace transform and $\rho = \frac{2}{t_d}$, one has

By using (2.2)–(2.4), the system (2.1) can be rewritten as follows:

where $u(v(t))$ denotes the system input that is subject to actuator fault described by

where $\lambda(t, t_\lambda) \in [0, 1]$ indicates the effectiveness of the actuation. $v$ is a control signal, and $t_\lambda$ denotes the time instant at which an actuation effectiveness fault will occur. An uncontrollable additive actuation fault is represented by $u_r(t, t_r)$, and the instant an additive actuation fault occurs is indicated by $t_r$ ^[31].

By using (2.6), the nonlinear system (2.5) can be rewritten as follows:

Remark 2.1. $x_{n+1}$ is a newly introduced variable that manages the input delay. $x_{n+1}$ can be considered an intermediate rather than the system state variable ^[30].

The control goal is to formulate an adaptive fault-tolerant controller for the system (2.1) ensures that all signals within the closed-loop exhibit semi-globally uniformly ultimately bounded (SGUUB) behavior, and that the tracking error converges to a compact region around the origin. To achieve this goal, the following assumptions and lemmas are necessary.

Assumption 2.1. ^[1] The desired trajectory signal $y_d(t)$ and its time derivatives up to the $n$th order are assumed to be continuous and bounded.

Assumption 2.2. ^[31] The unknown time-varying functions $\lambda(t, t_\lambda)$ and $u_r(t, t_r)$ are bounded. Thus, there exist positive constants $\lambda_{\text{min}}$ and $u_{\text{max}}$ such that $\lambda_{\text{min}} < \lambda(t, t_\lambda) \leq 1$ and $|u_r(t, t_r)| \leq u_{\text{max}}$.

Remark 2.2. Assumption 2.1 ensures the boundedness of the reference signal $y_d(t)$ and its time derivatives $y^{(n)}_d(t)$, thus guaranteeing the boundedness of all variables throughout the backstepping derivation. This assumption is a standard practice in the design of adaptive controllers, has been demonstrated in various works, including ^[1,2,5,6]. The control gain $\lambda(t, t\lambda)$ and the uncontrollable additive actuation fault $u_r(t, t_r)$ are unknown, as stated in Assumption 2.2. As such, the traditional stability requirement is no longer applicable ^[31].

Radial basis function neural networks (RBFNNs). In this work, an RBFNN ^[32] is used to approximate the continuous function $f_i(X): \mathbb{R}^n \rightarrow \mathbb{R}$. The RBFNN is expressed in the following form:

where $X \in \Omega_X \subset \mathbb{R}^q$ represents the input vector and $W = [w_1, \ldots, w_l]^T \in \mathbb{R}^l$ denotes the weight vector of the RBFNN, where $l (>1)$ is the number of nodes. Additionally, $S(X) = [s_1(X), \ldots, s_l(X)]^T \in \mathbb{R}^l$ is the basis function vector, and $s_i(X)$ is given by

where $\mu_i = [\mu_{i1}, \ldots, \mu_{iq}]^T$ and $\zeta$ denotes the center and the width of the Gaussian function.

As illustrated in ^[32], the function $f(X)$ is continuous and defined on a compact set $\Omega_X$. For any $\varepsilon > 0$, there exists an RBFNN represented as $W^{*T}S(X)$ such that the following relationship holds:

where $\delta(X)$ represents the approximation error with $|\delta(X)| < \varepsilon$ i, $W^*$ is the ideal weight vector defined as

Lemma 2.1. ^[32] Let $S(X) = [s_1(X), \ldots, s_l(X)]^T$ denote the basis function vector of the RBFNN, and $X = [x_1, \ldots, x_n]^T$ represent the input vector. For an arbitrary integer $m \leq n$, let $X_m = [x_1, \ldots, x_m]^T$. The following inequality holds:

Lemma 2.2. ^[4] For all $(m, n) \in \mathbb{R}^{2}$ and $\epsilon > 0$, the following inequality holds:

where $p > 1$, $q > 1$, and $(p - 1)(q - 1) = 1$.

Remark 2.3. Lemma 2.1 explains an important and basic structural feature of RBFNNs. It is important to emphasize that, in the context of backstepping design, Lemma 2.1 plays a crucial role in managing the complete state variables ^[32].

3.   Adaptive fault-tolerant controller design and stability analysis

In this section, a design procedure for an adaptive fault-tolerant controller based on the backstepping method for the system (2.1) will be developed. The proposed design procedure consists of $n$ steps, designed for an $n$-th order system. To design the controller, the first step involves a change of coordinates given by

where $\alpha_{i-1}$ stands for the virtual control law that will be introduced later. To obtain the main results, the controller design process is separated into $n$ steps.

Step 1. By using (2.7) and (3.1), the time derivative of $e_1$ is given by

Choose the following Lyapunov function $V_1$ as follows:

where $e_1 = x_1 - y_d$, $r_1 > 0$ is a design constant, and $\tilde{\theta}_1 = \theta_1 - \hat{\theta}_1$ represents the estimation error, with $\hat{\theta}_1$ denoting the estimate of the unknown parameter $\theta_1$, defined as $\theta_1 = \|W_1^*\|^2$.

Then, by taking the time derivative of $V_1$, one has

where $\bar{f}_1(X_1) = f_1(x) + \frac{1}{2}e_1-\dot{y}_d$.

In (3.4), it is evident that $\bar{f}_1(X_1)$ contains the unknown smooth function $f_1$. Consequently, the RBFNN $W_1^{*T} S(X_1)$ is employed to characterize $\bar{f}_1(X_1)$ in such a way that, for any given constant $\varepsilon_1 > 0$,

where $X_1 = [x_1, \ldots, x_n]^T$, and $\delta_1(Z_1)$ represents the estimation error.

By utilizing Lemmas 2.1 and 2.2, one has

where $\theta_1 = \|W_1^*\|^2$, $Z_1 = [x_1]^T$, and $a_1 > 0$ is a constant.

By using Young's inequality, one has

where $\bar{d}_1 > 0$ is a constant.

The design of the virtual control law $\alpha_1$ is formulated as follows:

where $k_1 > 0$ and $a_1 > 0$ are the design parameters.

By using Lemma 2.2 and (3.8), one has

By incorporating (3.6)–(3.9) into (3.4), we have

Given that $\tilde{\theta}_1 = \theta_1-\hat{\theta}_1$, (3.10) becomes

The adaptive law $\dot{\hat{\theta}}_1$ is formulated as follows:

where $r_1 > 0$ and $a_1 > 0$ represent the design parameters.

By substituting (3.12) into (3.11), one has

Step $i$ ($i = 1, 2, \ldots, n-1$). According to (3.1) and (2.7), the time derivative of $e_i$ is given by

We can obtain the derivative of $\alpha_{i-1}$ as follows:

Consider a Lyapunov function as follows:

where $e_i = x_i - \alpha_{i-1}$, $\tilde{\theta}_i = \theta_i - \hat{\theta}_i$ is the estimation error, and $r_i > 0$ is a design constant.

Further, the dynamics of $V_i$ are given by

The derivative of $V_{i-1}$ is given as follows:

By incorporating (3.16) into (3.15), one has

where $\bar{f}_i(X_i) = f_i(x) - \dot{\alpha}_{i-1} + \frac{1}{2}e_i$. The function $\bar{f}_i(X_i)$ involves the unknown smooth function $f_i$. Consequently, the RBFNN $W_i^{*T} S_i(X_i)$ is utilized to approximate the unknown function $\bar{f}_i(X_i)$, ensuring that, for any positive $\varepsilon_i > 0$,

where $X_i = [x_1, \ldots, x_n, \hat{\theta}_1, \ldots, \hat{\theta}_{i-1}, \lambda_1, \ldots, \lambda_i]^T$.

Applying a similar approach as in (3.6), one has

where $Z_i = [x_1, \ldots, x_i, \hat{\theta}_1, \ldots, \hat{\theta}_{i-1}]^T$, $\theta_i = \|W_i^*\|^2$, and $a_i > 0$ is a design parameter.

Applying Young's inequality, we have

where $\bar{d}_i > 0$ is a constant.

The virtual control input signal $\alpha_i$ can be selected as follows:

where $k_i$ and $a_i$ are positive design constants.

By using Lemma 2.2 and (3.23), one has

By incorporating (3.21)–(3.24) into (3.19), we have

Given that $\tilde{\theta}_i = \theta_i-\hat{\theta}_i$, (3.25) becomes

The adaptive law $\dot{\hat{\theta}}_i$ can be selected as follows:

where $r_i$ and $\vartheta_i$ are positive design constants.

Moreover, by substituting (3.27) into (3.26), one has

Step $n$. According to (3.1) and (2.7), the time derivative of $e_n$ is given by

where $\alpha_{n-1}$ is defined as follows:

Take the Lyapunov function as follows:

where $\tilde{\theta}_n = \theta_n - \hat{\theta}_n$ represents the estimation error and $r_n > 0$ represents the design constant.

Further, the dynamics of $V_n$ are given by

The derivative of $V_{n-1}$ is given as follows:

By incorporating (3.29) into (3.28), one has

where $\bar{f}_n(X_n) = f_n(x) - \dot{\alpha}_{n-1} + \frac{1}{2}e_n$. The function $\bar{f}_n(X_n)$ involves the unknown smooth function $f_n$. Therefore, the RBFNN $W_n^{*T} S_n(X_n)$ is employed to estimate the unknown function $\bar{f}_n(X_n)$, ensuring that, for any positive $\varepsilon_n > 0$,

where $X_n = [x_1, \ldots, x_n, \hat{\theta}_1, \ldots, \hat{\theta}_{n-1}]^T$.

Applying a similar approach as in (3.6), one has

where $Z_n = [x_1, \ldots, x_n, \hat{\theta}_1, \ldots, \hat{\theta}_{n-1}]^T$, $\theta_n = \|W_n^*\|^2$, and $a_n > 0$ is a design parameter.

Applying Young's inequality, we have

where $\bar{d}_n > 0$ is a constant.

Utilizing Lemma 2.2 and considering Assumption 2.2, we have

The real control law $v$ can be selected as follows:

where $k_n$ and $a_n$ are positive design constants.

By using Lemma 2.2, Assumption 2.2 and (3.39), one has

By incorporating (3.36)–(3.40) into (3.34), we have

Given that $\tilde{\theta}_n = \theta_n-\hat{\theta}_n$, (3.41) becomes

The adaptive law $\dot{\hat{\theta}}_n$ can be selected as follows:

where $r_n$ and $\vartheta_n$ are positive design constants.

Furthermore, it results from substituting (3.43) into (3.42) and applying Assumption 2.2 that

Theorem 3.1. Consider the nonstrict feedback nonlinear system (2.1) with input delay and actuator faults under Assumptions 2.1 and 2.2, the real controller (3.39), the virtual control laws (3.8) and (3.23), and the adaptive laws (3.12), (3.27) and (3.43). The presented control scheme guarantees the achievement of the following control objectives: (1) The SGUUB nature of all variables within the closed-loop system. (2) The convergence of the system's tracking error to a compact region around the origin.

Proof. By studying the definition of $\tilde{\theta}_j$, one has

By substituting (3.45) into (3.44), we have

where $a_0 = 2m$, $m = \min\{k_1, \ldots, k_n\lambda_{\min}, \vartheta_1, \ldots, \vartheta_n\}$, and $b_0 = \sum_{j = 1}^{n}\left(\frac{\vartheta_j\theta_{j}^2}{r_j} +\frac{a^2_j}{2}+\frac{\epsilon^2_j}{2} + \frac{\bar{d}^2_j}{2}\right)+ \frac{u^2_{\max}}{2}$.

Integrating (3.46) over the interval $[0, t]$, we can derive the following inequality:

Considering the definition of $V_n$ in (3.31) and the inequality (3.47), it can be inferred that $e_i$ $(i = 1, \ldots, n)$ and $\theta_i$ $(i = 1, \ldots, n)$ are bounded. Taking $e_1 = x_1 - y_d$ and the boundedness of $e_1$ and $y_d$ into account, it implies that the state $x_1$ is bounded. For $e_i = x_i - \alpha_{i-1}$ and the definition of the virtual control signal $\alpha_i$ $(i = 1, \ldots, n-1)$ along with Assumption 2.1, it can be concluded that $x_i$ $(i = 2, \ldots, n)$ remains bounded. Additionally, from (3.39), it can be deduced that the control $v$ is also bounded. Therefore, all signals in the closed-loop system are SGUUB. Moreover, based on (3.47), one has

Hence, the proof is completed.

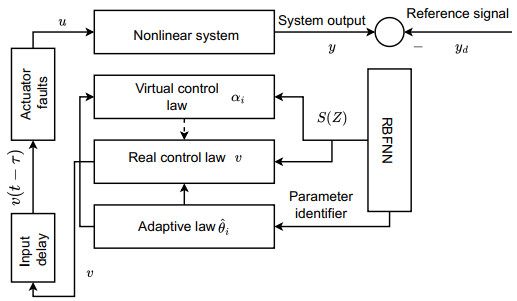
Figure 1 depicts the architecture of the control scheme that is being discussed.

Remark 3.1. Improved tracking performance is achievable by reducing the IC values. However, it is crucial to carefully select the appropriate ascertained. Furthermore, as can be ascertained from (3.46), the tracking error decreases as the parameters $k_i$, $\vartheta_i$ increase and $b_i$ decreases. It is important to keep in mind that selecting a sufficiently high value for $k_i$ and $\vartheta_i$ results in a larger control energy. Typically, both initial conditions and design parameters are determined through a trial-and-error method, where system performance is observed and adjustments are made accordingly. Therefore, it is essential to design the parameters appropriately in real-world engineering settings to achieve improved transient performance and efficient control action while avoiding excess control energy.

4.   Simulation results

In this section, the efficacy of the presented control schemes will be assessed through the two examples. The methodology outlined in Theorem 3.1 will be employed to formulate controllers to regulate the considered systems.

Example 4.1. Consider the following nonstrict-feedback nonlinear system:

where $f_1(x) = 1 - \cos(x_1x_3) + x_3+x_2$, $f_2(x) = x_1^2 x_3e^{-x^2_2}$, $f_3(x) = x_1x_2^2 e^{-x^2_3} + x_3 \sin(x_1x_2)$, $d_1(t) = 0.5\cos(t)$, $d_2(t) = \sin(0.5t)$, $d_3(t) = 0$, $\tau = 1.5s$.

The reference signal was set as $y_d = 0.5(\sin(t) + 0.5\sin(0.5t))$. The system input subject to actuator fault described by $u(v(t)) = \lambda(t, t_\lambda)v + u_r(t, t_r)$ with $\lambda(t, t_\lambda) = 0.4 + 0.6\exp(-0.2t)$, and $u_r(t, t_r) = \cos^2(x_1) x_2$. The following virtual control laws, real control law and, adaption laws are considered:

The center of the receptive field was chosen as $\mu_i = [-1.5, -1, -0.5, 0, 0.5, 1, 1.5]^T$ for $i = 1, 2, 3$, and the Gaussian function's width was set to $\zeta = 2$. In the simulation, the design parameters were determined using the trial-and-error method, as follows: $k_1 = k_2 = 3$, $k_3 = 6$, $a_1 = a_2 = a_3 = 3$, $\vartheta_1 = 1$, $\vartheta_2 = 1$, $\vartheta_3 = 1$, $r_1 = 1$, $r_2 = 1$, $r_3 = 1$. The simulation began with ICs set via the trial-and-error method as $[x_1(0), x_2(0), x_3(0)]^T = [0.5, 0.5, 0.5]^T$ and $[\hat{\theta}_1(0), \hat{\theta}_2(0), \hat{\theta}_3(0)] = [0, 0, 0]$.

The simulation results are depicted in Figures 2–7. Figure 2 illustrates the trajectories of the system output $y = x_1$ and the reference signal $y_d$. As observed in Figure 2, the output $y = x_1$ adeptly tracks the reference signal $y_d$ with bounded error, and the tracking error $e_1$ is depicted in Figure 3. The trajectories of $x_2$ and $x_3$ are presented in Figure 4. Figure 5 showcases the bounded adaptive laws $\hat{\theta}_1$, $\hat{\theta}_2$, and $\hat{\theta}_3$, while Figure 6 displays the control input $v$ and system input $u$. The simulation results affirm that the proposed controller ensures the boundedness of all signals within the closed-loop system.

In this study, the effectiveness of the proposed method was validated through a comparison with an existing control approach ^[29] that utilizes auxiliary systems to minimize the effects of input delay. In contrast to the established control method, the proposed approach integrates Pade approximation. The comparison results, illustrated in Figure 7, clearly demonstrate a slight yet consistent improvement in tracking error under the proposed control method relative to the existing approach ^[29].

Figures 2–7 collectively highlight that, through judicious parameter adjustments, the designed controller effectively constrains all closed-loop system signals. This validation demonstrates the effectiveness of the proposed controller.

Moreover, error assessment criteria ^[33] were employed to substantiate the effectiveness of the proposed method in comparison to the existing approach ^[29]. For a given pair of data points $(y_i(t), y_{id}(t))$ in the interval $t\in [1, P]$ with $P$ as the observations in the data set, the assessment error criteria were as follows:

where $\bar{y_{id}}$ represents the mean of $y_{id}(t)$.

The results, as depicted in Table 1, demonstrate a marginal improvement in the proposed control scheme relative to the existing control method ^[29]. This enhancement provides compelling evidence of the effectiveness of the proposed control approach.

Remark 4.1. Understanding the convergence dynamics of the system components is largely dependent on the time constant and half-life analyses. In Figure 2, the modest convergence speed for $x_1$ is indicated by a time constant of 19.6239 seconds, indicating that it takes about 0.3651 seconds to reach half of its initial value. In Figure 3, a longer time constant of 32.6245 seconds is shown by the tracking error ($e_1$), which suggests a slower rate of convergence with a half-life of roughly 0.2685 seconds. In Figure 5, $\hat{\theta}_1$, $\hat{\theta}_2$, and $\hat{\theta}_3$ are shown to have time constants of 121.8149 seconds, 11.4806 seconds, and 2.8463 seconds in that ratio. Additionally, the half-life of 0.0000 seconds that was consistently reported for each parameter points to nuances in their convergence dynamics that are not explained by the conventional half-life criterion of attaining half of the initial value.

Example 4.2. To further illustrate the effectiveness of the proposed method, the electromechanical system in ^[34] was employed. It is governed by the following dynamic equations:

where

and $\ddot{q}$, $\dot{q}$, $q$ stand for the link acceleration, velocity, and position, respectively. $V_{\epsilon}$ represents the input. $J = 0.001625$, $K_t = 0.9$, $m = 0.506$, $L_0 = 0.305$, $M_0 = 0.434$, $R_0 = 0.023$, $G = 9.8$, and $B_0 = 0.01625$. The physical meaning of the electromechanical system can be found in ^[34]. Defining $x_1 = q$, $x_2 = \dot{q}$, $x_3 = I$, and $u(v(t-\tau)) = V_{\epsilon}$, the (4.3) can be rewritten as follows:

where $f_1(x) = 0$, $f_2(x) = - \frac{N}{ M }\sin x_1 - \frac{B }{M }x_2 + \frac{B}{ M} \cos x_2 \sin x_3$, $f_3(x) = - \frac{K}{ L} x_2 -\frac{ R}{ L} x_3$, $d_1(t) = 0.2 \sin(t)$, $d_2(t) = 0$, $d_3(t) = sin(2t)$, $\tau = 1.5s$.

The reference signal is set as $y_d = 0.5\sin(t) -\cos(0.5t)$. The system input subject to actuator fault described by $u(v(t)) = \lambda(t, t_\lambda)v + u_r(t, t_r)$ with $\lambda(t, t_\lambda) = 0.4 + 0.6\exp(-0.2t)$, and $u_r(t, t_r) = \cos^2(x_1) x_2$. The following virtual control laws, real control law and adaption laws are considered:

The receptive field center is defined as $\mu_i = [-1.5, -1, -0.5, 0, 0.5, 1, 1.5]^T$ for $i = 1, 2, 3$, with a Gaussian function width of $\zeta = 2$. In the simulation, design parameters are determined through the trial-and-error method: $k_1 = 8$, $k_2 = 7$, $k_3 = 8$, $a_1 = a_2 = a_3 = 1$, $\vartheta_1 = 1$, $\vartheta_2 = 1$, $\vartheta_3 = 1$, $r_1 = 1$, $r_2 = 1$, $r_3 = 1$. ICs for the simulation are set by using the trial-and-error method: $[x_1(0), x_2(0), x_3(0)]^T = [0.5, 0.5, -0.5]^T$ and $[\hat{\theta}_1(0), \hat{\theta}_2(0), \hat{\theta}_3(0)] = [0, 0, 0]$.

The simulation outcomes are displayed in Figures 8–13. Figure 8 demonstrates the effective tracking of the output $y = x_1$ to the reference signal $y_d$ with bounded error. Further insights into the tracking error $e_1$ are provided in Figure 9. Trajectories of $x_2$ and $x_3$ are depicted in Figure 10. Figure 11 presents the bounded adaptive laws $\hat{\theta}_1$, $\hat{\theta}_2$, and $\hat{\theta}_3$, while Figure 12 exhibits the control input $v$ and system input $u$.

In this study, the effectiveness of the proposed method was validated through a comparison with an existing control approach ^[29] that utilizes auxiliary systems to minimize the effects of input delay. In contrast to the established control method, the proposed approach integrates Pade approximation. The comparison results, illustrated in Figure 13, clearly demonstrate a slight yet consistent improvement in tracking error under the proposed control method relative to the existing approach ^[29]. The simulation results affirm that the proposed controller ensures the boundedness of all signals within the closed-loop system. Figures 8–13 collectively highlight that, through judicious parameter adjustments, the designed controller effectively constrains all closed-loop system signals. This validation demonstrates the effectiveness of the proposed controller.

In this illustrative example, the error assessment criteria defined in Example 4.1 were utilized to establish the effectiveness of the proposed method as compared to the existing approach ^[29].

The results, as depicted in Table 2, demonstrate a marginal improvement in the proposed control scheme relative to the existing control method ^[29]. This enhancement provides compelling evidence of the effectiveness of the proposed control approach.

Remark 4.2. Comprehending the convergence dynamics of system elements heavily relies on the examination of time constants and half-life analyses. In Figure 8, the relatively moderate pace at which $x_1$ converges is indicated by a time constant of 2.6835 seconds, and it took about 0.0504 seconds to become half of its initial value. In Figure 9, the tracking error ($e_1$) demonstrates a lengthier time constant of 11.8472 seconds, suggesting a slower convergence rate with a half-life of approximately 0.1387 seconds. In Figure 11, $\hat{\theta}_1$, $\hat{\theta}_2$, and $\hat{\theta}_3$ have time constants of 23.7414 seconds, 3.7447 seconds, and 1.2005 seconds, respectively. Moreover, the consistently reported half-life of 0.0000 seconds for each parameter underscores intricacies in their convergence dynamics that are not fully explicable by the conventional half-life criterion associated with achieving half of the initial value.

5.   Conclusions

The adaptive control problem for nonstrict-feedback nonlinear systems with actuator faults, input delays, and external disturbances has been the primary focus of this study. The use of an RBFNN and the Padé approximation, respectively, helped to resolve the difficulties brought forth by input delay and unknown functions. An adaptive controller has been developed by applying the Lyapunov stability theorem with the backstepping approach. The tracking error of the suggested controller converges to a small neighborhood around the origin, guaranteeing the boundedness of all signals in the closed-loop system. The efficacy of the suggested control method has been confirmed by the simulation results. Future research will concentrate on nonlinear systems with sensors and actuator faults, including providing true and estimated values of the nonlinear function to improve overall performance.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This work was funded by the Princess Nourah bint Abdulrahman University Researchers Supporting Project number (PNURSP2024R528), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia.

Conflict of interest

The authors confirm no conflicts of interest.