Assessing agglomeration processes in Russian second-tier urban agglomerations

1.   Introduction

Important properties of the HSA, such as fast and accurate responses, a high force/mass ratio and relatively good stiffness, have attracted great interest in the HSA and its applications. In the last two decades, high-performance controller design of the HSA has attracted increasing attention due to the expanded performance requirements of technical systems in the industry ^[1,2,3,4].

A large number of machines driven by HSAs often work with high payloads in harsh and mostly external environments. As a result of variables of their environment, such as temperature, dust, humidity, wear, variable loads and disturbances, the HSA is usually subject to large uncertainties during operation. Hence, high-precision control of the HSA has always challenged researchers due to its unmodeled dynamics, large nonlinearities, parametric uncertainties, unmeasurable states in practice, etc. It is well known that it is impossible to determine most of the physical parameters of HSA components. While some HSA parameters are available only with certain accuracy, the other parameters are completely unknown. Dominant nonlinear sources existing in HSAs are impossibility of accurate determining parameters, which are very difficult to handle with high accuracy. These unknown parameters are caused by protection of proprietary data of individual manufacturers or indirect measuring and calculating, pressure losses, transient and turbulent flow conditions, friction, leakage characteristics, and generation discontinuous control signals to HSAs due to effects of saturation and changing the direction of servo valve. Furthermore, variable working conditions during operation, such as oil temperature, the bulk modulus, fluctuating supply pressure and pipe volume will lead to parameter changes, which worsen the existing control performances. These facts make it difficult to realize high-quality control of the HSA, which cannot be achieved without knowing the accurate HSA model ^[5,6,7,8].

Further, direct measurement of the whole HSA state vector is not feasible for practical implementation and in addition would require very expensive measurement equipment. It is more convenient to use control algorithms which apply methods based on state reconstruction rather than to perform direct measurements of the states ^[9].

In modern control theory, optimal control of the HSA plays a vital role in the controller design. Namely, the main challenge is to design optimal control algorithms that will affect the minimum energy consumption ^[10,11]. The optimal control design is an offline control technique that usually depends on perfect knowledge of the HSA model, which is not possible to obtain in most practical situations. Even if an approximated model of the HSA can be developed, the dynamic uncertainty, produced by the mismatch between the approximated model and the true HSA model, will degrade the control performance of the traditionally designed optimal controller ^[9,12]. Therefore, further research on the design of optimal controllers of HSAs is very important and our primary aim for this study.

The practical applicability of control algorithms is enhanced by the fact that nonlinear systems can be very precisely represented by linear models with online estimated dynamics ^[13,14]. Many modern engineering applications such as intelligent vehicles ^[15,16], modernized microgrids ^[17], microphone sensing ^[18], strain prediction for fatigue ^[19], maintaining the security of cyber–physical systems ^[20], robotic manipulation tasks ^[21], 2-degree-of-freedom helicopter ^[22] and requests for online controller design which rely on linear systems.

Adaptive dynamic programming (ADP) ensures an effective way to achieve high performance of the optimal controller which relies on adaptive control, optimal control and reinforcement learning ^{[9,23,24,25,26]}. ADP represents a kind of data-based control technique which can guarantee the stability of the feedback control system ^[9]. Recently, the field of ADP application has also been expanded to various research areas, including robotic systems, aerospace systems, guided missiles, spacecraft, etc. ^[27,28,29]. In circumstances of unknown system dynamics and unmeasurable states, of great interest is to use ADP techniques based on measured input/output data from linear systems, which are commonly called output feedback. A main benefit of the output feedback techniques is that knowledge of the HSA dynamics is not needed for their application. For an unknown HSA model, this indirect technique generates a sequence of suboptimal controllers which converge to the optimal control policy with an increasing number of iterations.

The implementation of ADP algorithms is usually based on periodic selection ^[30]. In order to save limited communication and computational resources, event-triggered strategies have recently started to be applied in control algorithms based on ADP ^{[31,32,33,34]}. Moreover, the number of updates of the control inputs in this way will be smaller compared to the periodic update of the controller, because it is updated only when necessary (e.g., when the performance of the system deteriorates). The implementation of event-triggered algorithms is based on aperiodic sampling. Several event-based controllers have been proposed in the literature, most of which are state-feedback controllers ^{[35,36,37,38,39]}. In contrast, this paper will consider the event-triggered ADP-based control problem of HSAs in the case where only output feedback is available.

This paper considers an online learning technique, where during operation, from measured input/output data, the controller learns to compensate unknown HSA dynamics, various disturbances and modeling errors, ensuring desired performances of the control system. The optimal control law is accomplished iteratively based on output feedback, state reconstruction and ADP. The unknown HSA model is first identified after which the algebraic Riccati equation (ARE) is iteratively solved. To ensure consistency of approximations and obtain unique solutions in each iteration step, some exploration noise must be added to control input to meet the requirements of the persistent excitation condition ^[40,41,42]. For exploration noise, some persistent excitation is usually applied such as white noise or pseudo random binary signals (PRBS). The selection of exploration noise is a non-trivial task for the most learning problems, as it can affect the accuracy of solutions, especially for large systems ^[43]. By applying the theory of experimental design, we will use the sum of sinusoidal signals as an exploration noise that will enable the output of the system to carry maximum information about the system, which will shorten the learning time, i.e., speed up the controller design process. Thus, the obtained input and output signals are used to reconstruct the state vector of the model, which is of great practical importance in relation to control techniques with direct state measurement that rely on a large number of sensors.

Due to implementation of the ADP-based control techniques, it is easier to realize data acquisition for the discrete-time HSA model in relation to its continuous-time model. ADP-based control methodology for discrete-time systems is proposed in ^[44].

We chose to use the measured input and output data to reconstruct the state vector of the discretized HSA model, after which ADP-based control can be implemented. The control law is learned iteratively and very efficiently provides solutions for optimal control of HSAs based only on measurements in real time. The main advantage of the proposed control methodology is avoiding the knowledge of system dynamics, which is very important under practical conditions.

By applying an event-based control strategy, the number of control input updates will be reduced relative to periodic update of the controller, because the controller is only updated when certain conditions are met. In this way, energy, computing and communication resources will be significantly preserved.

The rest of the paper is organized as follows. The problem of modelling an HSA with unknown dynamics is presented in Section 2. Event-triggered control based on ADP is shown in Section 3. Simulation results show the validity and effectiveness of the event-triggered ADP-based controller for HSAs in the presence of completely model uncertainty in Section 4. Finally, Section 5 gives the concluding remarks.

2.   Description of the HSA

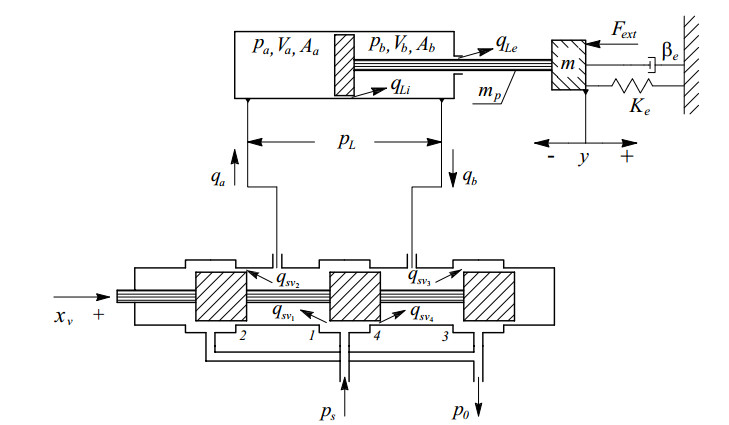
The HSA under study is shown in Figure 1, and it consists of a servo valve and a hydraulic cylinder. The analysis of the properties of the HSA comes out from the dynamics of its components, which involves the piston motion dynamics, pressure dynamics at the cylinder and servo valve dynamics. Hence, the model of the HSA is derived from complex nonlinear equations that depend on many parameters which cannot be accurately obtained ^[7,8].

See Table 1 for the description of the HSA parameters. Using the notation in Figure 1, and defining the area ratio of the piston $\alpha = A_b / A_a$ as well as $V_a = V_{a0} + y A_a$, $V_b = V_b0 + (L- y) \alpha A_a$ and $q_{Li} = c_{Li} (p_a-p_b)$, where $c_{Li}$ is the internal leakage flow coefficient; $c_{vi} > 0$ denote discharge coefficients, the sign function $\text{sg}(x) = \left\{ \begin{matrix} x & x \ge 0 \\ 0 & x < 0 \\ \end{matrix} \right.$ and assuming an external leakage negligible, the considered model can be described by the following equations:

According to Eqs (2.1)–(2.5), and by defining the state and input variables as

the governing nonlinear continuous-time dynamics of the HSA can be expressed in a state-space form as follows:

where $f(x(t))$ and $g(x(t), u(t))$ are the state dynamics and the input function, respectively:

where output function $\eta(x(t)) = x_1(t)$ and disturbance function $h(t) = \begin{bmatrix} h_1(t) & -F_{ext}/m_t+h_2(t) & h_3(t) & h_4(t) \end{bmatrix}$ include loads, unmodelled dynamics and parameter uncertainties.

One of the main nonlinearities of the cylinder model is the nonlinear friction force $F_f$, which consists of static friction, Coulomb friction and Stribeck effect of velocity. An extensive study related to acting friction forces upon the HSA can be found in ^[7]. Further, we consider the linearized model of the HSA, whose parameters are experimentally identified for different working points of the HSA (i.e., different positions and external load conditions) ^[8]. Now, the model equations are expressed in a more suitable way in terms of the load pressure:

which leads to simplified dynamic equations. At last, using the new state vector $\begin{bmatrix} x_1(t) & x_2(t) & x_3(t) \end{bmatrix}^T \triangleq \begin{bmatrix} y(t) & \dot{y}(t) & p_L(t) \end{bmatrix}^T$ allows us to express the HSA in a more compact form. Taking an operating point $x_0 \triangleq \begin{bmatrix} y_0 & \dot{y}_0 & p_{L0} \end{bmatrix}^T$, and assuming dominance of the first order term from the Taylor series expansion, the linearized continuous-time description of the reduced order is stated as follows

where $A = \begin{bmatrix} 0 & 1 & 0 \\ 0 & -\frac{B_C}{m_t} & \frac{A_a}{m_t} \\ 0 & -K_d & K_p \end{bmatrix}$, $B = \begin{bmatrix} 0 & 0 & K_x \end{bmatrix}^T$ and $C = \begin{bmatrix} 1 & 0 & 0 \end{bmatrix}$. The sensibility constants can be found as follows:

where the flow sensibility constants regarding the pressure at the cylinder chambers are stated as:

and the flow sensibility constants regarding the spool position are stated as

The previously mentioned valve sensibility constants are very significant in defining system stability and other dynamic characteristics ^[8]. Namely, the flow gain $K_x$ has a direct impact on the stability of the HSA, because it directly affects the gain constant in the open loop of the HSA. Further, direct impact on the damping ratio of the HSA has the flow-pressure constant $K_p$. Hence, the pressure sensibility $K_{p_x} = K_x / K_p$ is quite high, which explains the ability of the HSA to transfer large friction loads with a small error.

3.   Event-triggered ADP-based controller

Let us consider a linear continuous-time model of the HSA with unknown dynamics, as follows:

where $x(t) \in \mathbb{R}^n$, $u(t) \in \mathbb{R}^m$ and $y(t) \in \mathbb{R}^r$ are the system state vector, the control input vector, and the output vector, respectively. $A \in \mathbb{R}^{n \times n}$, $B \in \mathbb{R}^{n\times m}$ and $C \in \mathbb{R}^{r\times n}$ are unknown system matrices, assuming that $\left(A, B \right)$ is controllable and $\left(A, C \right)$ is observable.

For the HSA described by (3.1) and (3.2), the performance index is stated as

where $x_0 \in \mathbb{R}^n$ is an initial state, $Q = Q^T \ge 0$ and $R = R^T > 0$, with $(A, Q^{1/2} C)$ being observable.

A control law is also called a policy. The design objective is to find a linear optimal control policy in the form of

which minimizes the performance given by index (3.3). The optimal feedback gain matrix ${{K}^{*}}$can be determined as

where $P^* = \left(P^* \right)^T > 0$ is a unique symmetric positive definite solution of the well-known ARE

under conditions that the system matrices are accurately known, as well as conditions that the pair $(A, B)$ is controllable and the pair $(A, Q^{1/2}C)$ is observable ^[12]. It should be noted that this optimal control design is mainly applicable to low order simple linear systems. In fact, for high-order large scale systems, it is usually difficult to directly solve $P^*$ from (3.6), which is nonlinear in $P$.

Also, for practical implementation of the control system, it is easier to realize the data acquisition for discrete-time systems than for continuous-time systems. Consequently, we transform the continuous-time HSA into the following discrete-time HSA:

where $A_d = e^{Ah}$ and $B_d = \int\limits_0^h \left(e^{A\tau } d\tau \right) B$, where $h > 0$ is a specific sampling period, assuming $\omega_h = {2\pi}/h$ is the nonpathological sampling frequency whose existence is well known ^[45]. In other words, the controllability and observability of the original continuous-time HSA system is kept after discretization. Namely, if the state, input and output vectors at the sampled instant $kh$ are $x_k$, $u_k$ and $y_k$, respectively, then $\left(A_d, C \right)$ and $\left(A_d, Q^{1/2} C \right)$ are observable while $\left(A_d, B_d \right)$ is controllable.

As depicted in Figure 2, the ADP-based controller for the discretized HSA system consists of three parts: the state reconstruction, critic, and actor. The state reconstruction provides the relationship between the input/output data and the HSA states, which allows one to solve the optimal control problem of an HSA with unknown dynamics. Based on the input/output data, the critic part of the controller is designed to evaluate the performance of the control policy. The controller learns online in order to maximize its performance. Finally, the actor applies the improved control policy. The updates of the control actions are governed by an event-triggering mechanism to reduce the amount of data transmission from the controller to the HSA system.

The event-triggered design is based on a periodic sampling with a nonpathological $h > 0$. We use $\hat{u}_k$ to represent the sampled value of $u_k$, that is

where $\left\{ k_j \right\}_0^\infty$ is a monotonically increasing sequence of the sampling time instants, and the control input is only updated at the discrete-time instants: $k_0, k_1, k_2, \ldots$ For the convenience of discussions, define the sampling error of the input data as

Hence, the discrete-time system described by (3.7) and (3.8) can be rewritten as

Further, the performance index for the discretized system described by (3.7) and (3.8) is

where $Q_d = Qh$ and $R_d = Rh$. The optimal control low minimizing (3.13) is

where the discrete optimal feedback gain matrix is $K_d^* = \left(R + B_d^T P_d^* B_d \right)^{-1} B_d^T P_d^* A_d$, where $P_d^*$ is the unique symmetric positive definite solution to

Since (3.15) is nonlinear in $P_d^*$, it is difficult to directly solve $P_d^*$ for high-order large-scale systems. Nevertheless, many efficient algorithms have been developed to numerically approximate the solution of (3.15). One of such algorithms was developed by Hewer ^[46], and it is introduced in the form of Lemma 3.1.

Lemma 3.1. Let $K_0 \in \mathbb{R}^{m\times n}$ be any stability feedback gain matrix and $P_j$ be the symmetric positive definite solution of the Lyapunov equation

where $K_j$, $j = 1, 2, \ldots$ can be updated as follows:

Then, it holds that

1) $A_d - B_d K_j$ is a stability matrix

2) $P_d^* \le P_{j+1} \le P_j$

3) $\mathop {\lim }\limits_{j \to \infty } {K_j} = K_d^*$, $\mathop {\lim }\limits_{j \to \infty } {P_j} = P_d^*$.

By iteratively solving the Lyapunov equations given by (3.16), which is linear in $P_j$, and recursively updating the control policy $K_j$ by (3.17), the solution to the nonlinear equation given by (3.15) is numerically approximated ^[46]. It has been concluded that the sequences $\left\{ P_j \right\}_{j = 0}^\infty$ and $\left\{ K_j \right\}_{j = 0}^\infty$, computed from this algorithm, converge to $P_d^*$ and $K_d^*$, respectively. Moreover, for $j = 0, 1, \ldots$, $A_d - B_d K_j$ is a Schur matrix. It should be noted that the method by Hewers involves a model-based policy iteration (PI) algorithm, which cannot be directly applied to the problem studied in this paper since it is an offline algorithm which depends on the system parameters. To apply this algorithm online for the discretized HSA described by (3.7) and (3.8), we will develop the control algorithm based on ADP via output feedback, which does not depend on the knowledge of HSA matrices.

Motivated by ^[44,47], the discrete-time HSA described by (3.7) and (3.8) can be extended by using input/output sequences on the time horizon $[k-N, k-1]$ as follows:

where

and the observability index is $N = \max(\rho_u, \rho_v)$ where $\rho_u$ is the minimum integer which ensures that $U(\rho_u)$ has full column rank and $\rho_v$ is the minimum integer which ensures that $V(\rho_v)$ has full row rank ^[44]. Therefore, there exists a left inverse of $U(N)$, stated as $U^+(N) = \left[U^T(N) U(N) \right]^{-1} U^T(N)$. With the state reconstruction in (3.18), the idea of an ADP-based controller with output feedback can be applied to solve the optimal control problem of HSAs with unknown dynamics. A uniqueness of state reconstruction is stated in the form of Lemma 3.2 as follows ^[48].

Lemma 3.2. If the conditions of observability and controllability of the system described by (3.7) and (3.8) are fulfilled, then the states of the HSA are uniquely received in terms of measured inputs and outputs signals as follows:

where $\Theta = \begin{bmatrix} M_u & M_y \end{bmatrix}$ has full row rank, $M_u = V(N) - M_y T(N)$, $M_y = A_d^N U^+(N)$ and $z_k = \begin{bmatrix} \bar{u}_{k-1, k-N}^T & \bar{y}_{k-1, k-N}^T \end{bmatrix}^T \in \mathbb{R}^q$, where $q = N[\dim(u)+\dim(y)]$.

Now, based on (3.16) and (3.17), an online learning strategy using output feedback can be introduced in the form of $u^*_k = - \overline{K}_d z_k$, providing suboptimal property of the closed-loop system. The discrete-time model (3.11) can be stated as follows:

where $A_j = A_d - B_d K_j$. Setting $\bar{K}_j = K_j \Theta$ and $\bar{P}_j = \Theta^T P_j \Theta$, from (3.16) and (3.20), it can be obtained

where $\bar{H}_j^1 = B_d^T \bar{P}_j B_d$, $\bar{H}_j^2 = B_d^T \bar{P}_j A_d \Theta$, $\phi ^1 = \hat{u}_k^T \otimes \hat{u}_k^T -(z_k^T \otimes z_k^T)(\bar{K}_j^T \otimes \bar{K}_j^T)$ and $\phi ^2 = 2 \left[(z_k^T \otimes z_k^T)(I_q \otimes \bar{K}_j^T) + (z_k^T \otimes \hat{u}_k^T) \right]$.

The symbol $\otimes$ is used to denote a Kronecker product operator. The vector function $\text{vec}(V) = \begin{bmatrix} v_1^T & v_2^T & \ldots & v_m^T \end{bmatrix}^T$ is stated as an $mn$-vector formed by stacking the columns of $V \in \mathbb{R}^{n\times m}$ on top of one another, where $v_i \in \mathbb{R}^n$ denotes the columns of matrix $V$. For an arbitrary symmetric matrix $M \in \mathbb{R}^{n\times n}$, $\text{vecs}(M) = \left[m_{11}, 2m_{12}, \ldots, 2m_{1n}, m_{22}, 2m_{23}, \ldots, 2m_{n-1, n}, m_{nn} \right]^T \in \mathbb{R}^{n(n+1)/2}$ and for an arbitrary column vector $v \in \mathbb{R}^n$, $\tilde{v} = \left[v_1^2, v_1v_2, \ldots, v_1v_n, v_2^2, v_2v_3, \ldots, v_{n-1}v_n, v_n^2 \right]^T \in \mathbb{R}^{n(n+1)/2}$.

The convergence of the online learning control using output feedback is guaranteed under the rank condition stated in the form of Lemma 3.3 ^[47]. Lemma 3.3 is about the condition of persistent excitation in adaptive control theory ^[49,50].

Lemma 3.3. Let us suppose that for a sufficiently large $s \in \mathbb{Z}_+$, it holds that

where

then $\left(\bar{P}_j, \bar{H}_j^1, \bar{H}_j^2 \right)$ can be uniquely solved based on $\bar{K}_j$ and measurable online data during the period $k \in [k_0, k_s]$. Further, $\bar{K}_{j+1}$ is obtained as follows:

Some exploration noise $e_k$, which satisfies the persistent excitation condition, must be added into the input signal during the online learning phase due to the satisfaction of the rank condition given by (3.22), without affecting the convergence of the learning phase ^[43,51,52]. Note that (3.21) is called the policy evaluation, which is used to uniquely solve $\bar{P}_j$, and (3.24) is the policy improvement, which is used to update the control gain $\bar{K}_{j+1}$. Finally, we present the ADP-based online learning control algorithm in Figure 3.

It should be noted that solving (3.21) instead of (3.16), completely eliminates the original request on the accurate knowledge of the HSA dynamics. Now, we only need to measure $u_k$ and $y_k$. Namely, having in mind the expression for $z_k$, we can see that the control policy $\hat{u}_k = -\overline{K}_k^* z_k + \Delta_k$ contains only the previously measured input-output data. With the event-triggered control law $\hat{u}_k$, the system given by (3.20) is globally asymptotically stable (GAS) at the origin if

where $\alpha \in (0, 1)$ and $\eta$ is a positive constant satisfying $\eta \ge \lambda_{\max} \left(R_d + B_d^T \bar{P}_d B_d \right)$.

The convergence of the ADP-based control algorithm is presented in the form of Theorem 3.4. For Hurwitz feedback matrix $A - B K$, $K \in R^{m\times n}$ is called stabilizing feedback gain matrix for a linear system $\dot{x} = A x + B u$.

Theorem 3.4. If the condition of Lemma 3.3 is fulfilled, with some initial stabilizing feedback gain matrix $\overline{K}_0$, then the sequences $\left\{ \overline{P}_j \right\}_{j = 0}^{\infty }$ and $\left\{ \overline{K}_j \right\}_{j = 0}^{\infty}$ received from this algorithm, converge to their optimal values $\overline{P}^*$and $\overline{K}^*$, respectively ^[46,47].

Proof. If $P_{j}^{{}} = P_{j}^{T}$ represents the solution of (3.16), under the stability feedback gain matrix $\overline{K}_j$, then $K_{j+1}$ is uniquely obtained from (3.17). It can be easily shown that $\overline{P}_j$ and $\overline{K}_{j+1}$ fulfill (3.21) and (3.24). Now, setting $\overline{P}$ and $\overline{K}$ as solutions of (3.21) and (3.24), Lemma 3.3 provides that $\overline{P}_j = \overline{P}$ and $\overline{K}_{j+1} = \overline{K}$ are uniquely stated. Furthermore, from Lemma 3.1, we have that $\underset{j \to \infty}{\mathop{\lim }} \overline{K}_j = \overline{K}_d^*$ and $\underset{j \to \infty}{\mathop{\lim}} \overline{P}_j = \overline{P}_d^*$. The proof of convergence is proved.

The hybrid nature of the controller is shown in Figure 4. It is shown there that the feedback gain or policy is updated at discrete times by using (3.24) after the solution to (3.21) has been determined. On the other hand, the control input is a discrete time signal depending on the state $z(k)$ at each time $k$. From Figure 4, it can be seen that the control gains are updated at discrete times, but the control signal is piecewise continuous.

4.   Simulation results

In this section, we apply the proposed event-triggered ADP-based control design to the HSA. In the case of unknown dynamics and unmeasurable states of the HSA, it is meaningful to use the ADP-based method. Consequently, we conduct simulations on the HSA given by the linearized continuous-time description of (2.10) and (2.11) to show the effectiveness of the ADP-based control algorithm. A basic condition for energy savings in many hydraulically driven industrial systems is a high-quality design of event-triggered ADP control for the HSA.

For this purpose, the HSA is discretized by applying the periodic sampling period $h = {0.1}\ {\rm{s}}$ and the zero-order holder. The approximated optimal feedback gain and performance index for the discretized model of the HSA are iteratively obtained.

The effectiveness of the ADP-based control algorithm will be considered for the HSA model described by (2.10) and (2.11) with the following parameters: the viscous friction $B_C = {200} \ {\rm{N}}\ {\rm{s}}\ {\rm{m}}^{-1}$, the supply pressure $p_S = {45} \ {\rm{bar}}$, the tank pressure $p_0 = {1.6} \ {\rm{bar}}$, the bulk modulus of the fluid $\beta_e = 2 \times 10^8 \mathrm{~Pa}$, the total mass $m = {25}\ {\rm{kg}}$, the initial chamber volumes $V_{a0} = V_{b0} = 8.2 \times 10^{-6} \mathrm{~m}^3$, the load spring gradient $K_e = 10^{-1}$, the effective area of the head side of the piston $A_a=4.91 \times 10^{-4} \mathrm{~m}^2$, the effective area of the rod side of the piston $A_b=2.43 \times 10^{-4} \mathrm{~m}^2$, the internal leakage coefficient $c_{Li} = 5 \times 10^{-14}$, the piston stroke $L = {1} \ {\rm{m}}$ and discharge coefficients of valve orifices $c_{vi} = 1.15$, $i = \overline{1, 4}$.

For the purpose of demonstrating the event-triggered ADP method with the HSA, the weight matrices, $Q$ and $R$, are chosen to be identity matrices, the observability index is $N = 3$, initial state vector is $x_0 = \begin{bmatrix} 5 & -5 & -10 \end{bmatrix}$ and the convergence threshold $\varepsilon$ is selected as ${{10}^{-1}}$.

It should be noted that our event-driven ADP control design does not require exact knowledge of the HSA matrices. But, only for numerical verification via simulation, it is assumed that the system matrices in (2.10) and (2.11) are known.

To verify the benefits of the ADP based online learning controller, Figure 5 depicts the errors between $\bar{P}_j$ and $\bar{P}_d^*$ and $\bar{K}_j$ and $\bar{K}_d^*$, which indicate the convergence of $\bar{P}_j$ and $\bar{K}_j$.

The evolution of the maximum cost for HSA is shown in Figure 6(a), where $V_1$ is the maximum cost by using the initial control policy, and $V_7$ is the maximum cost by using the control policy after seven iterations. It can be seen that the approximated cost function $V_7$ has been remarkably reduced relative to the initial cost $V_1$. Figure 6(b) shows the 3D plot of the approximation error of the cost function. This error is close to zero which confirms that good approximation of the optimal cost function is achieved during the learning process.

The improved control policy and the initial control policy are compared in Figure 7(a). Further, Figure 7(b) shows the 3D plot of the difference between the approximated control obtained by using the online ADP-based control algorithm and the optimal control. This error is close to zero, which confirms that good approximation of the optimal input is also achieved during the learning process.

Figure 8 shows the control input and the states of the HSA system desribed by (2.10) and (2.11) by using the ADP-based controller with periodic sampling.

To illustrate the benefits of the event-triggered ADP method, the control input and the states of the original HSA system described by (2.10) and (2.11), as obtained by using the event-triggered ADP-based controller is shown in Figure 9.

The comparison of sampling numbers by using the event-triggered ADP controller versus the ADP controller with periodic sampling is shown in Figure 10.

It can be observed that similar control effects have been achieved by the two methods, however, for the event-triggered ADP method, the control input is updated only when the squared norm of the triggering error reaches the threshold, and it is kept constant otherwise. It is also shown that about $54\%$ communication between the controller and the HSA is reduced by using the event-triggered ADP method instead of the ADP method. The sequence of steps of event-triggered sampling is depicted in Figure 11.

5.   Conclusions

This paper has considered the event-triggered data-driven optimal controller of the HSA with completely unknown dynamics as based on an ADP framework. A basic advantage of the presented control methodology is its ability to avoid the knowledge of entire system dynamics, which is very important in real conditions. By using the output feedback and the state reconstruction method an applied ADP-based control technique has been shown to be a useful tool for digital implementation in a real HSA. For that purpose, a discrete-time control policy was iteratively learned based on the discretized HSA model. The learned control policy very efficiently ensures online solutions to data-driven optimal control problems for the HSA. The presented online control policy only uses measured input/output data to learn the optimal control gain. Then, to reduce the communication between the controller and the HSA, an output feedback event-triggered ADP controller has been designed. The simulation results have shown the validity and effectiveness of the applied control approach for the HSA.

Acknowledgments

This research was supported in part by the Serbian Ministry of Education, Science and Technological Development under grant 451-03-47/2023-01/200108, the National Natural Science Foundation of China under grants 61773181, 61976081, 62073001, 62103293 and 62203153,111 Project under grant B23008, the Fundamental Research Funds for the Central Universities under grant JUSRP51733B, the Anhui Provincial Key Research and Development Project under grant 2022i01020013 and the Natural Science Fund for Excellent Young Scholars of Henan Province under grant 202300410127.

Conflict of interest

The authors declare that there is no conflict of interest.