Constraint impulsive consensus of nonlinear multi-agent systems with impulsive time windows

1.   Introduction

Recently, distributed control of multi-agent systems has been substantial investigated in various fields, such as flocking, rendezvous, coordination, complex networks and so on ^[1,2,3]. Motivated by the advantage of strong robustness, high efficiency and low cost, many researchers pay more attentions on the applications of distributed multi-agent systems. However, there are still many unsolved issues that confuse people many years. In all of the issues, consensus problems of multi-agent systems have aroused wide concerns. To achieve consensus, designers usually devise the distributed control protocol of information exchanging only based on the local relative information ^[4,5,6].

Generally, there exist two classes of consensus problems: Leaderless consensus problems and leader-following consensus tracking problems. For leaderless consensus, all of the agents eventually achieve to an uncertain common value ^[7,8,9]. For leader-following consensus, the leader is preset and all of the other agents in networks converge to the value of the leader ^[10,11,12]. This is the advantage of leader-following consensus. By using the Lyapunov stability and graph theory, distributed leader-following consensus problem of second-order multi-agent systems with fixed directed topology and coupling delay was studied in ^[13]. In paper ^[14], the author established fractional order tracking consensus of nonlinear multi-agent systems with hybrid time-varying delay by using a heterogeneous impulsive method. In paper ^[15], the leader-following consensus problem was researched by an observer-based control protocol, which indicated that relative output measurements based on neighboring agents made an important influence for information exchange.

Meanwhile, impulsive control systems have sparked the interest of many researchers in recently years due to their widely applications on the consensus and cooperation problems of complex networks ^{[16,17,18,19,20]}. Compared with traditional method solving consensus problem, such as feedback control ^[21], event-triggered control ^[22] and adaptive control ^[23], impulsive control can decrease the redundancy between information exchanging and increase the robustness of distributed dynamic systems. Paper ^[24] only used the position information with time delays via impulsive protocol to achieve second-order consensus of multi-agent systems. In ^[25], second-order consensus with aperiodic impulsive protocol and time-varying delays was considered based on relative state measurements between the agent and the neighbors at a few discrete times.

The mentioned articles with impulsive protocol above are mostly described with fixed impulsive intervals, which means the impulsive instants have been required to design in advance. Due to the restriction of practical application and perturbation of external environment in real world, it is difficult to guarantee the precise impulsive input instants and we often need to choose variable instants in limit time intervals. Therefor, we propose the impulsive time windows in which the impulsive input instants can be changed randomly. The variable impulsive control protocol with impulsive time windows are effective and flexible which obtain larger control domain. However, there also exist some disadvantages. For example, impulsive time windows make the condition of system convergence more complicated and more conservative. If the impulsive intervals are more dense, it makes the impulsive time windows smaller which will be more difficult to implement. In past few years, stability and synchronization problems of neural networks have been studied intensely ^{[26,27,28,29,30]}. In paper ^[26], the problem of input-to-state stability of impulsive stochastic Cohen-Grossberg networks which contained mixed delays was investigated. A hybrid pinning impulsive control method with nonlinearly coupling function was considered in paper ^[29] for achieving synchronization of networks. Meanwhile, impulsive time windows have been widely concerned in stability, synchronization and consensus ^[31,32,33]. Since the impulsive instants could not be predicted in advance, the author analyzed the robust stability of neural networks with stochastic fuzzy delays in ^[34]. In ^[35], the impulsive control systems of periodically multiple state-jumps was studied in limited small time intervals. Paper ^[36] proposed variable impulsive protocol for first-order consensus of nonlinear multi-agent systems. For the advantage of impulsive time windows, it is interesting and practical to investigate the consensus problem with impulsive time windows.

In this paper, constraint impulsive protocol is also considered to prevent the jumping value beyond the secure setting. In all of the constraint methods, saturation is the most widely applied one. Because of saturation constraint, system with saturation impulse will increase the complexity of system structure and the difficulty of consensus problem analysis. However, it can protect the system avoiding too large impulsive jumping amplitude, which may destroy the system. Currently, there mainly exist three methods to disintegrate saturation function including method of combination convex, method of sector region and method of saturability. Compared with the last two methods, method of combination convex is easier and maturer. Through the introduction of the auxiliary matrix H, the saturated impulse input was transformed into a convex polyhedron which ensured stabilisation of time-varying structures dynamical systems in literature ^[37]. In paper ^[38], exponential stabilization for nonlinear delayed dynamic systems was investigated with a state-constraint impulsive control strategy. Compared with article ^[33], the constraint impulsive considered in this paper is more in line with the actual industrial application. Moreover, we use the central distance of the impulsive time windows to replace the impulsive interval through the whole paper, such that the constraint on the impulsive instant is reduced, so it is more meaningful.

The organization of this paper is introduced as follows. Fundamental preliminaries of notations and graph theory are introduced in section 2. Problem formulation of the nonlinear multi-agent systems and constraint impulsive protocol are given in section 3. Constraint impulsive consensus of multi-agent systems with impulsive time windows is analyzed in section 4, where the centre distance of adjacent or non-adjacent impulsive time windows is an important parameter for system convergence. Numerical examples that strongly support the effectiveness of the theoretical results are presented in section 5. The conclusion is given in section 6.

2.   Preliminaries

2.1.   Notations

Throughout this paper, ${\rm{R}}^n$ denotes the set of $n$-dimensional Euclidean space. For any square matrix $A\in {\rm{R}}^{N\times N}$, $A^ {\rm{T}}$ represents the transpose of $A$. $\mathbb{N_+}$ is the set of nonnegative natural numbers. $\mathcal{C}[\mathcal{X}, \mathcal{Y}]$ is a space of continuous mappings from space $\mathcal{X}$ to space $\mathcal{Y}$. Diagonal matrix $B$ is denoted as $diag[b_1, b_2, \cdots, b_n]$. $I_N$ denotes the N-dimensional identity matrix and $0_N$ denotes the N-dimensional zero matrix. $\textbf{1}_N$ indicates the N-dimensional column vector in which all the elements are equal to $1$. $A\otimes B$ indicates the Kronecker product between matrices $A$ and $B$. $\|\cdot\|$ is the Euclidean norm of vector or matrix. For any vector $x = (x_1, x_2, ..., x_n)^ {\rm{T}}$, the Euclidean norm is presented as $\|x\| = \sqrt{x_{1}^{2}+\cdot\cdot\cdot+x_{n}^{2}}$.

2.2.   Graph theory

Graph is a very important and practical tool to describe interconnected relation between agents. In this subsection, we will introduce some basic concepts. A directed graph $\mathcal{G} = (\mathcal{V}, \mathcal{E}, \mathcal{A})$ is a network with a finite set of nodes $\mathcal{V} = \{1, 2, 3, \cdots, N\}$, a set of edges $\mathcal{E} = \{(i, j):i, j\in\mathcal{V}\}\subseteq \mathcal{V} \times \mathcal{V}$ and a weighted coupling matrix $\mathcal{A} = [a_{ij}]\in {\rm{R}}^{N\times N}$. The entry $a_{ij}$ of matrix $\mathcal{A}$ represents the information communication between agent $i$ and agent $j$. If there is a path from node $i$ to node $j$, then $a_{ij}\geq 0$; otherwise, $a_{ij} = 0$. There are no repeated edges and self-loops. All the neighbors of $i$ are denoted as $N_{i} = \{j\in\mathcal{V}:(i, j)\in\mathcal{E}, i\neq j\}$. The out-degree of node $i$ in a directed graph is defined as $deg_{out}(i) = \sum_{j = 1}^{N}a_{ij}$. The corresponding diagonal matrix is $\mathcal{D} = diag[deg_{out}(1), deg_{out}(2), \cdots deg_{out}(N)]\in {\rm{R}}^{N\times N}$ which consists of the out-degree of each node. The Laplacian matrix of graph $\mathcal{G}$ is defined as $L = \mathcal{D}-\mathcal{A}$. For a directed graph $\mathcal{G}$, a Laplacian matrix $L = [l_{ij}]_{N\times N}$, where

Define $\bar{\mathcal{G}}$ as a directed graph consisting of graph $\mathcal{G}$ and an added node 0, where $\bar{\mathcal{V}} = \{0, 1, 2, ...N\}$, $\bar{\mathcal{E}} = \{(i, j):i, j\in\bar{\mathcal{V}}\}\subseteq \bar{\mathcal{V}} \times \bar{\mathcal{V}}$ and a weighted coupling matrix $\bar{\mathcal{A}} = [\bar{a}_{ij}]\in {\rm{R}}^{(N+1)\times (N+1)}$.

3.   Problem formulation

As we know, impulsive intervals make a great influence on the consensus of multi-agent systems via impulsive protocol and the assumption of impulsive interval is fixed. In this paper, impulsive time windows for consensus of multi-agent systems have been proposed, where the impulsive instants can be randomly changed in the impulsive time windows that are different from the traditional impulsive protocol. Actuator saturation is also considered for restraining the impulsive input beyond the threshold. These give us a new way to analysis the impulsive consensus problem.

Consider multi-agent systems with actuator saturation of nonlinear dynamic which are described by

$x_i(t) = (x_{i1}(t), x_{i2}(t), \cdots, x_{in}(t))^ {\rm{T}}\in {\rm{R}}^{n}$ is the state of agent $i$, where $i = \{1, 2, \cdots, N\}.$ $f(x_i(t), t): {\rm{R}}^n\times [0, +\infty)\to {\rm{R}}^n$ is a nonlinear function of agent $i$. $\mathrm{Sat}(u_i(t))\in {\rm{R}}^{n}$ is the control protocol of $i$th agent with saturation constraint which will be designed later. The initial condition $x_i(t_0)\in\mathcal{C}[t_0, {\rm{R}}^{n}]$.

Compared with the traditional control system where the control input is usually unconstrained, we will design a constrained input which is called the actuator saturation. The saturation function can be described as follow

where $u_i(t) = (u_{i1}(t), u_{i2}(t), \cdots, u_{in}(t))^ {\rm{T}}\in {\rm{R}}^{n}$, $i = \{1, 2, \cdots, N\}, \quad j = \{1, 2, \cdots, n\}$, and $\mathrm{Sat}(u_i(t)) = (\mathrm{Sat}(u_{i1}(t)), \mathrm{Sat}(u_{i2}(t)), \cdots \mathrm{Sat}(u_{in}(t))^ {\rm{T}}$.

The leader of multi-agent systems can be expressed as follows

where $x_0(t) = (x_{01}(t), x_{02}(t), \cdots, x_{0n}(t))^ {\rm{T}}\in {\rm{R}}^{n}$ is the state of leader node. Its initial condition is given as $x_0(t_0)\in \mathcal{C}[t_0, {\rm{R}}^{n}]$. In this paper, we assume the leader is the root node in graph $\bar{\mathcal{G}}$ that contains a spanning tree.

Definition 1. The multi-agent systems are said to achieve leader-following consensus for any initial states, if

where $i = \{1, 2, ..., N\}$.

Definite $\zeta_i(t) = \sum_{j\in N_i}^{N} a_{ij}(x_i(t)-x_j(t))+b_i(x_i(t)-x_0(t)).$ Then the impulsive control protocol of $i$th agent with a leader is designed as

Therefor the multi-agent systems via impulsive protocol and saturation constraint input can be described as

$c_k\in \rm {R}$ is the impulsive control gain at $t_k$. $b_i\in \rm {R}$ is a weight value from leader node to follower node $i$. $b_i > 0$, if there are information exchange between leader and $i$th follower, otherwise $b_i = 0$. $\delta(t)$ is the Delta function satisfying $\int_{-\infty}^{+\infty}\delta(t)dt = 1$. The instant $t_k$ satisfies $0\le t_0 < t_1\cdots < t_k < \cdots$ and $\lim_{k\to \infty}t_k = +\infty$. Suppose $x_i(t)$ is left continuous at $t_k$, then $\lim_{t \to t_k^-}x_i(t) = x_i(t_k^-) = x_i(t_k)$, $\lim_{t\to t_k^+}x_i(t) = x_i(t_k^+)$.

Define the error state between agent $i$ and leader as $e_i(t) = x_i(t)-x_0(t)$, then $e(t) = (e_1(t), e_2(t),$ $\cdots, e_N(t))^ {\rm{T}}\in {\rm{R}}^{Nn}$. System $(3.4)$ can be rewritten as

System $(3.5)$ can be described with the Kronecker product

where $\tilde{x}(t) = \{x_0(t), x_1(t)\cdots, x_N(t)\}$, $B = diag[b_1, b_2\cdots, b_N]\in {\rm{R}}^{N\times N}$ and $F(\tilde{x}(t), t) = [(f^ {\rm{T}}(x_1(t), t)-f^ {\rm{T}}(x_0(t), t)), (f^ {\rm{T}}(x_2(t), t)-f^ {\rm{T}}(x_0(t), t)), \cdot \cdot \cdot, (f^ {\rm{T}}(x_N(t), t)-f^ {\rm{T}}(x_0(t), t))]^ {\rm{T}}$.

Lemma 1. ^[38] Assume there exist two vectors $v, \mu\in {\rm{R}}^N$ satisfying $v = (v_1, v_2, \cdots, v_N)^\mathrm{T}, \mu = (\mu_1, \mu_2, \cdots, \mu_N)^\mathrm{T}$. Denote $F = \{F_i:i = 1, 2, \cdots, 2^N\}\in {\rm{R}}^{N\times N}$ is the set of diagonal matrices consisting of scalars 0 or 1. If $|\mu_i|\leq1$ for all $i$, then the constraint function $\mathrm{Sat}(v)\in co\{F_iv+F_i^-\mu: i = 1, 2, \cdots, 2^N\}$, where $F_i^- = I_N-F_i$. $\{F_iv+F_i^-\mu\}$ represents the vector consisting of the elements that some are from $v$ and the rest are from $\mu$. Define $e(t)\in {\rm{R}}^{N}$ and $E, H\in {\rm{R}}^{N\times N}$. If $\|He(t)\|_{\infty}\leq 1$, then $\mathrm{Sat}(Ee(t))\in co\{(F_iE+F_i^-H)e(t): i = 1, 2, \cdots, 2^N\}$. Moreover, if there exists $\kappa_i \in[0, 1]$ satisfying $\sum_{i = 1}^{2^N}\kappa_i = 1$, then the following equality $\mathrm{Sat}(Ee(t)) = \sum_{i = 1}^{2^N}\kappa_i(F_iE+F_i^-H)e(t)$ holds.

Lemma 2. ^[38] For any constant $\varepsilon > 0$, if there exist two vectors $a\in {\rm{R}}^{Nn}, b\in {\rm{R}}^{Nn}$, then the following inequality $2a^ {\rm{T}} b \leq \varepsilon a^ {\rm{T}} a + \varepsilon^{-1}b^ {\rm{T}} b$ holds.

Assumption 1. ^[18] The nonlinear function $f(x_i(t), t): {\rm{R}}^n\times [0, +\infty)\to {\rm{R}}^n$ satisfies the Lipschitz condition, if there exists a nonnegative constant $\theta$ satisfying

$\forall x_i(t), x_0(t)\in {\rm{R}}^n$ and $\theta$ is the Lipschitz constant.

Assumption 2. ^[36] The directed graph $\bar{\mathcal{G}}$ of leader-following communication topology contains a spanning tree rooted at the leader node $0$.

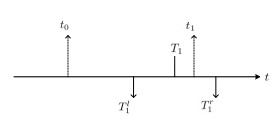
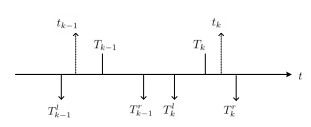
Assumption 3. ^[33] The time parameters of Figure 1 satisfy the relations as follow

where the interval $[T_k^l, T_{k}^r]$ is the $k$th impulsive time window. $T_{k}^{l}$, $T_{k}^{r}$, $T_{k}$ are the left endpoint, right endpoint and the center of the $k$th time window, respective.

The Lipschitz condition of Assumption 1 is used in Theorem 1 to deal with the nonlinear terms for obtaining a differential inequality. Assumption 2 guarantees all of the eigenvalues of matrix $L+B$ have positive real parts, and Assumption 3 ensures that there is one and only one impulsive instant in each impulsive time window where impulsive instant $t_k$ could happen everywhere and the adjacent impulsive time windows are independent with each other.

4.   Main results

4.1.   Consensus of impulsive time windows

In this subsection, the constraint impulsive consensus problem of multi-agent systems with impulsive time windows is investigated by using the Lyapunov function mathematical induction method. The impulsive instant $t_k$, left endpoint $T_k^l$ and right endpoint $T_k^r$ in impulsive time window satisfy Assumption $3$, and the relations of central positions, left endpoints, right endpoints and impulsive instants are shown in Figure 1 The interval $[T_k^l, T_{k}^r]$ indicates the possible range of impulsive instant $t_k$, which corresponds to the so-called impulsive time window. Now our main results are shown in the following theorem, which implies the admissible parameter $T_k$ in impulsive time window plays an important role for consensus of multi-agent systems.

Theorem 1. Under Assumption 1–3, the multi-agent systems via impulsive protocol can achieve consensus if there exist a positive definite matrix $P\in \mathrm{R^{Nn\times Nn}}$ and some positive scalars $\varepsilon, \alpha, \lambda_k < 1, \eta > 1$ satisfying the following conditions

(i) $\varepsilon P^2+\varepsilon^{-1}\theta^2I_{Nn}\leq\alpha P,$

(ii) $[(I_{Nn}+M_k)]^ {\rm{T}}P[(I_{Nn}+M_k)]\leq\lambda_k P,$

(iii) $\alpha(T_{k+1}-T_{k})+\ln(\lambda_k\eta) < 0,$

where $M_k = \sum_{i = 1}^{2^{Nn}}\kappa_i(F_i(c_k(L+B)\otimes I_n)+F_i^-H)$, $\theta$ is the Lipschitz constant, and $0 < T_{k+1}-T_{k} < \infty$ is the centre distance of adjacent impulsive time windows. Then multi-agent systems with constraint impulsive protocol can achieve consensus.

Proof. Consider a candidate Lyapunov function as

From Assumption 1 and Lemma 2, for $t\in(t_{k-1}, t_k]$, the right and upper Dini's derivative of V(t) along Eq (3.6) is

By differential inequality theorem ^[39], if scalar function $V(t)$ is continuous on $t\in(t_{k-1}, t_k]$, and the right-up Dini derivative $D^+V(t)$ exists and satisfies the differential inequality

where $V_0$ is the initial value of $V(t)$, then it follows that

On the other hand, when $t = t_{k}$, by Lemma 1, we can obtain

In the process of proving Theorem $1$, different results of $V(t)$ are obtained according to the relative position between $t$ and $t_k$. The impulsive instant $t_k$ can randomly change in the impulsive time window.

For $t\in[t_0, T_1]$, there are two cases (See Figure 2) to be discussed.

$\blacktriangle$ Case 1. When $t_0\leq t\leq t_1$.

It follows from (4.1) that

$\blacktriangle$ Case 2. When $t_1 < t \leq T_1$.

Combining (4.1) and (4.2), we can obtain

Therefore, combining (4.3) and (4.4), for $t\in[t_0, T_1],$ we have

where

The value of $m_k$ is decided by impulsive instant $t_k$.

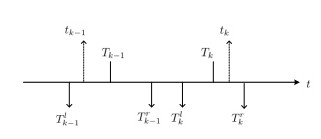
For $t\in(T_1, T_2]$, there are three cases (See Figure 3) to be discussed.

$\blacktriangle$ Case 1. When $T_1 < t\leq t_1$.

It follows from (4.1) that

$\blacktriangle$ Case 2. When $t_1 < t\leq t_2$.

Combining (4.1) and (4.2), we can obtain

$\blacktriangle$ Case 3. When $t_2 < t\leq T_2$.

Combining (4.1) and (4.2), we can obtain

Therefore, for $t\in(T_1, T_2],$ we have

where the decision value $m_k$ is defined in (4.6).

In general, for $t\in(T_{k-1}, T_k]$, we can derive

From condition (ⅲ), we have

Thus, for $t\in(T_{k-1}, T_k],$

Since $T_{1}-t_0 < \infty, T_{k}-T_{k-1} = \Delta_{k} < \infty$, $\lambda_{k}, m_k$ and $\theta$ are finite constants, then $V(t_{0})\exp(\alpha(T_1-t_{0})) \lambda_{k-1}^{m_{k-1}}\lambda_{k}^{m_{k}}\exp(\alpha(T_{k}-T_{k-1}))$ is a finite constant. $\frac{1}{\eta^{k-2}}\to 0$ as $k\to \infty$, which indicates the consensus error $e(t)$ is asymptotically stable at the origin. Then multi-agent systems (3.1) can achieve constraint impulsive consensus. Here the proof is completed.

Remark 1. This theorem indicates multi-agent systems (3.1) can achieve constraint impulsive consensus via impulsive time windows under suitable conditions. The Lipschitz parameter $\theta$, impulsive control gain $c_k$ and the centre distance $(T_{k+1}-T_k)$ of adjacent impulsive time windows play important roles for impulsive consensus. Usually we discuss the impulsive consensus in the interval $t\in (t_{k-1}, t_k], k\in\mathbb{N}_{+}$, but by using impulsive time windows we would change the interval to $t\in(T_{k-1}, T_k], k\in\mathbb{N}_{+}$, which is novel and flexible and gives us a new way to analysis the impulsive consensus problem. By expanding the central interval, we will deduce more interesting results in Theorem $2$.

Remark 2. The impulsive control gain $c_k$ and the centre distance $(T_{k+1}-T_k)$ of adjacent impulsive time windows are changing with $k$. If $c_k = c$ is time-invariant, $\Delta_k = T_{k}-T_{k-1} = \Delta$ is a fixed interval and $P = I_{Nn}$, then we can get easier conditions for constraint impulsive consensus

(ⅰ) $\varepsilon +\varepsilon^{-1}\theta^2\leq\alpha,$

(ⅱ) $\alpha\Delta+\ln(\lambda\eta) < 0,$

where $\lambda$ is the maximum eigenvalue of $(M+I_{Nn})^ {\rm{T}}(M+I_{Nn}).$

4.2.   Consensus of larger impulsive interval

In this subsection, we consider the interval $t\in[T_{2k-1}^l, T_{2k}^r]$. Only the odd central position $T_{2k-1}$ in impulsive time window has been used to prove the consensus of multi-agent systems. We just need to choose suitable impulsive instant $t_{2k-1}$in $[T_{2k-1}^{l}, T_{2k-1}^{r}]$. The restriction of impulsive instant $t_{2k}$ in impulsive time window $[T_{2k}^{l}, T_{2k}^{r}]$ can be released, and the random even impulsive instant $t_{2k}$ changes to more larger control range $(t_{2k-1}, t_{2k+1})$.

Theorem 2. Under Assumption 1–3, the multi-agent systems via impulsive protocol can achieve constraint impulsive consensus if there exist a positive definite matrix $P\in \mathrm{R^{Nn\times Nn}}$ and some positive scalars $\varepsilon, \alpha, \lambda_k < 1, \eta > 1$ satisfying the following conditions

(i) $\varepsilon P^2+\varepsilon^{-1}\theta^2I_{Nn}\leq\alpha P,$

(ii) $[(I_{Nn}+M_k)]^ {\rm{T}}P[(I_{Nn}+M_k)]\leq\lambda_k P,$

(iii) $\alpha(T_{2k+1}-T_{2k-1})+\ln(\lambda_{2k-1}\lambda_{2k}\eta) < 0,$

where $M_k$ has been definition in Theorem 1. Then multi-agent systems (3.1) can achieve impulsive consensus.

Proof. Consider a candidate Lyapunov function as

Similar to the process of proving Theorem 1, we can easily obtain (4.1) and (4.2). Combining (4.1) and (4.2), for $t\in (t_{k-1}, t_k]$, it yields

From condition (ⅲ), we can obtain

Using the result of Theorem 1, we consider two cases to prove the consensus of multi-agent systems.

$\blacktriangle$ Case 1. When $T_{2k-1} < t\leq T_{2k}$.

$\blacktriangle$ Case 2. When $T_{2k} < t\leq T_{2k+1}$.

Since $V(t_{0}), \theta, \lambda_{k}, m_k$ and $(T_k-T_{k-1}) = \Delta_k < \infty$ are finite constants. $\frac{1}{\eta^{k-1}}\to 0$ as $k\to \infty$, which indicates the consensus error $e(t)$ is asymptotically stable at the origin. Then multi-agent systems (3.1) can achieve constraint impulsive consensus. Here the proof is completed.

Remark 3. It follows from conditions of Theorem $2$ that the central position $T_{2k-1}$ of the impulsive time window has obvious influence for the impulsive consensus of multi-agent systems. And only the central position $T_{2k-1}$ of the impulsive time window is necessary. The impulsive instant $t_k$ and even central position $T_{2k}$ are not needed. From Theorem $2$, we need to choose the suitable odd impulsive instant in corresponding impulsive time window. However, the even impulsive instant $t_{2k}$ can be randomly changing in the larger interval $(t_{2k-1}, t_{2k+1})$ without any constraint and the corresponding impulsive time window is no more restriction on $t_{2k}$ which can be removed. This is one of the advantage of multi-agent systems with impulsive time windows that have been designed in this paper.

If we expand the central interval to larger range $t\in (T_{n_0(k-1)+1}, T_{n_0k+1}]$, There are more random impulsive instants out of constraint impulsive time windows. Here is the corollary.

Corollary 1. Under Assumption 1-3, the multi-agent systems via impulsive protocol can achieve consensus if there exist a positive definite matrix $P\in \mathrm{R^{Nn\times Nn}}$ and some positive scalars $\varepsilon, \alpha, \lambda_k < 1, \eta > 1$ satisfying the following conditions

(i) $\varepsilon P^2+\varepsilon^{-1}\theta^2I_{Nn}\leq\alpha P,$

(ii) $[(I_{Nn}+M_k)]^ {\rm{T}}P[(I_{Nn}+M_k)]\leq\lambda_k P,$

(iii) $\alpha(T_{kn_0+1}-T_{(k-1)n_0+1})+ \ln(\lambda_{(k-1)n_0+1}\lambda_{(k-1)n_0+2}\cdot \cdot \cdot\lambda_{kn_0}\eta) < 0,$

where $M_k$ has been definition in Theorem 1. Then multi-agent systems (3.1) can achieve constraint impulsive consensus.

Proof. From condition (ⅲ), we can get

Similar to the proof of Theorem 2, we will discuss $n_0$ situations of the consensus problem.

$\blacktriangle$ Case $1$. When $T_{n_0(k-1)+1} < t\leq T_{n_0(k-1)+2}$.

$\blacktriangle$ Case $2$. When $T_{n_0(k-1)+2} < t\leq T_{n_0(k-1)+3}$.

$\vdots$

$\blacktriangle$ Case $n_0$. When $T_{n_{0}k} < t\leq T_{n_{0}k+1}$.

Since $V(t_{0}), \theta, \lambda_{k}, m_k, n_0$ and $(T_k-T_{k-1}) = \Delta_k$ are finite constants. $\frac{1}{\eta^{k-1}}\to 0$ and $\frac{1}{\eta^{k}}\to 0$ as $k\to \infty$, which indicates the consensus error $e(t)$ is asymptotically stable at the origin. Then multi-agent systems (3.1) can achieve constraint impulsive consensus. Here the proof is completed.

Remark 4. Conditions of Theorem $1$ and Theorem $2$ are special cases of the inequation in Corollary $1$. When $n_0 = 1$, it corresponds to the fixed impulsive time windows in Theorem $1$. When $n_0 = 2$, the even impulsive instant $t_{2k}$ can be given anywhere in the interval $(t_{2k-1}, t_{2k+1})$ without the restriction of corresponding impulsive time window. When $n_0 = 3$, we just need to choose suitable impulsive instant $t_{3k-2}$ in the impulsive time window $[T_{3k-2}^l, T_{3k-2}^r]$, and the impulsive instants $t_{3k-1}, t_{3k}$ in $(t_{3k-2}, t_{3k+1})$ can be arbitrarily selected just satisfying $t_{3k-1} < t_{3k}$. The restriction of corresponding impulsive time windows has been released. By comparison, it concludes that lager $n_0$ allows for more arbitrary impulsive instants and removes more uncontrolled impulsive time windows. However lager $n_0$ corresponds to more complex inequality condition that is not good for system design. Therefor, we should choose suitable parameter $n_0$ according to practical application.

5.   Numerical simulations

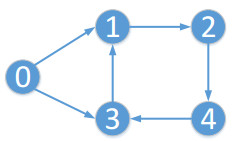
In this section, examples are given to illustrate the inequality conditions of Theorem 1 and Theorem 2 and to demonstrate the consensus of multi-agent systems. Consider the topology $\bar{\mathcal{G}}$ of five multi-agents which contains a leader agent. The communication of topology diagram is described in Figure 4.

For simplify, let $x_{i}(t) = x_{i}$, then the nonlinear system is described as

where $x_i\in {\rm{R}}^2, f(x_i, t) \in {\rm{R}}^2$, and take the Lipschitz constant $\theta = 2$. From Figure 4, the adjacency matrix and Laplacian matrix of topology $\bar{\mathcal{G}}$ are described as follow

and the matrix of the information exchange from leader to followers is

We suppose the impulsive gain $c_k = -1, \varepsilon = 2, \eta = 1.1, P = I_{Nn}$, $H = \rm{diag}[-0.2, -0.2, -0.2, -0.2]\otimes I_2$, $\kappa_1 = \kappa_2 = \kappa_3 = \kappa_4 = \kappa_5 = 0.2$ and the rest ones are 0. Then, we have

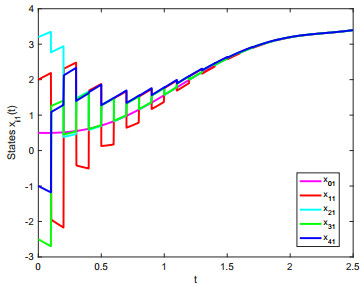
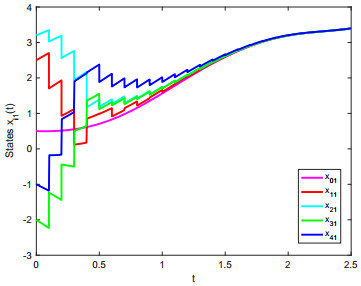
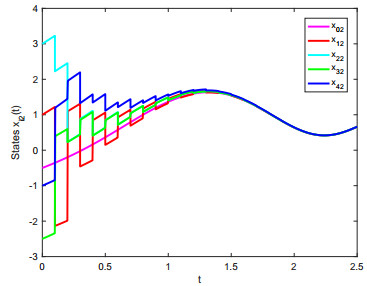
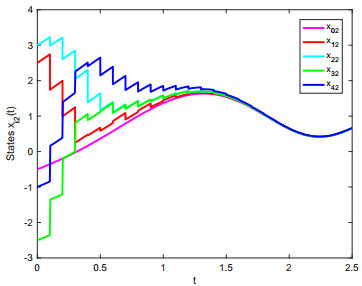
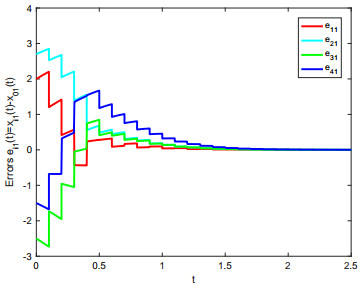
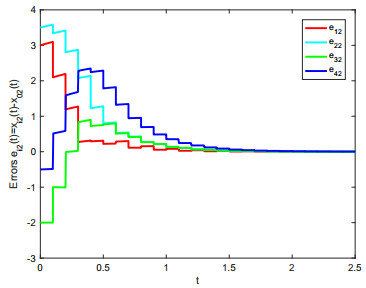
By numerical calculation, take $\alpha = \varepsilon +\varepsilon^{-1}\theta^2 = 4$. $\lambda_k = 0.5984$ is the maximum eigenvalue of $(M_k+I_{Nn})^ {\rm{T}}(M_k+I_{Nn})$ and the centre distance of adjacent impulsive time windows is deduced as $\Delta = T_k-T_{k-1} < -\frac{\ln(\lambda_k\eta)}{\alpha} = 0.1045$. We chose $\Delta = 0.1$. Then conditions of remark 2 can be easily obtained. When the conditions are satisfied, then all of the agents achieve constraint impulsive consensus with impulsive time windows. The results are shown from Figure 5 to Figure 10. Figure 5 to Figure 8 show the different convergence effects between unconstraint impulsive and constraint impulsive protocol. Figure 9 and Figure 10 show the error states of multi-agent systems with constraint impulsive protocol.

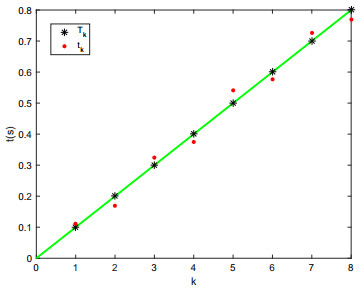
The relation between the impulsive instant $t_k$ and the central position $T_k$ is expressed in Figure 11. The diagram indicates that the impulsive instants $t_k$ are randomly distributed on both sides of the central position $T_k$.

Now, we analysis the holding condition of Theorem 2. Assuming $c_k = -1, \varepsilon = 2, \eta = 1.1, P = I_{Nn}$, and $\lambda_{2k} = \lambda_{2k-1} = 0.5984$, we can obtain

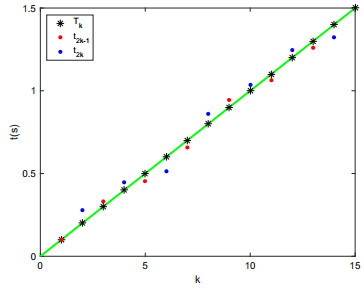
Then the constraint impulsive consensus of multi-agent systems can be achieved with impulsive time windows. Figure 12 expresses the relation between the impulsive instants $t_{2k}$, $t_{2k-1}$ and the central position $T_k$. Comparing the distance from different impulsive instant to corresponding central position, we could see $t_{2k}$ (blue point) has a larger variable range than $t_{2k-1}$ (red point). This is the one of the advantage of Theorem 2 which guarantees larger variable range of even impulsive instant.

6.   Conclusions

In this paper, the constraint impulsive consensus problem of nonlinear multi-agent systems in directed network with impulsive time windows is investigated. Based on algebraic graph theory, convex combination analysis, matrix theory and impulsive protocols, some sufficient conditions of impulsive consensus have been proposed. The simulations have demonstrated that constraint impulsive protocol with impulsive time windows is efficient and flexible for consensus. Constraint impulsive protocol may decrease the convergence rate, but it is more practical in industrial applications. It should be also pointed out that the centre distance of adjacent or non-adjacent impulsive time windows plays an important role for impulsive consensus. By comparison, the larger central interval is helpful to allow for more arbitrary impulsive instants without restriction of impulsive time windows but corresponds to more complex inequality conditions, so a good tradeoff of the centre interval is very essential. In the next future, the theory of impulsive time windows could be utilized to study Razumikhin stability for impulsive stochastic delay differential systems, stabilization of stochastic nonlinear delay systems with impulsive event-triggered feedback control, and moment exponential stability of stochastic nonlinear delay systems with impulse effects at random times with noise disturbances.

Acknowledgment

This work was supported by the National Natural Science Foundation of China under Grants 61873213 and 61633011, and in part by National Key Research and Development Project under Grant 2018AAA0100101.

Conflict of interest

The authors declare that they have no conflict and interests.