Bifurcation analysis, chaotic behaviors, and explicit solutions for a fractional two-mode Nizhnik-Novikov-Veselov equation in mathematical physics

1.   Introduction

Recent research has been focused more on the nonlinear time-dependent models that have been seen in different branches of science and engineering, namely, plasma physics ^[1], nano-fiber optics ^[2], magnetohydrodynamics ^[3], etc. There are different kinds of nonlinear fields such as the (3+1)-D Burger model ^[4], the Phi-four model ^[5], the Zoomeron system ^[6], the Chen-Lee-Liu equation ^[7], the iterated function system using interpolative Kannan operators ^[8], the generalized KP model ^[9], the KdV-burgers-Fisher equation ^[10], the Benjamin-Ono system ^[11], the Sawada-Kotera system ^[12], the generalized CBS-BK model ^[13], etc.

To solve these models, researchers use diverse analytical methods such as the Darboux transformation technique ^[14], the enhanced Kudryashov scheme ^[15], the generalized KP equation ^[16], the new Kudryashov's scheme ^[17], the fuzzy control approach ^[18], the Cauchy problem for matrix factorizations ^[19], the physics-informed neural networks approach ^[20], the modified alternative $\left(\frac{{\mathrm{G}}^{'}}{\mathrm{G}}\right)$-expansion algorithm ^[21], $\left(\frac{{\mathrm{G}}^{'}}{{\mathrm{G}}^{2}}\right)$ expansion method ^[22], the stochastic logical networks method ^[23], the first integral technique ^[24], METF technique ^[25], the modified extended direct algebraic method ^[26], Takagi-Sugeno fuzzy model approach to the nonlinear lateral dynamics ^[27], and many other methods ^[28,29,30].

Marwan and Jaradat obtained an innovative model named the next (2+1)-dimensional two-mode Nizhnik-Novikov-Veselov (TMNNV) equation, which represents a variety of physical processes occurring in diverse mediums, including biological membranes, optical fibers, modern strings, magnetoelectric dynamics, and inelastic fluids ^[31]. The nonlinear problems play a crucial role in the study of nonlinear wave propagation. The nonlinearity is prevalent across various fields of applied science, nonlinear dynamics, mathematical physics, and engineering, including biosciences, plasma physics, geochemistry, and fluid mechanics ^[32,33,34]. Nonlinear problems (NLPs) are significant equations because they are implemented for the mathematical modeling of numerous real-world applications ^[35,36]. In recent years, the calculus of NLPs has emerged as a prominent area of focus within nonlinear dynamics ^[37,38]. NLPs, which encompass more comprehensive forms of differential equations (DEs), significantly contribute to the qualitative analysis of many nonlinear wave propagation phenomena ^[39,40]. This work identifies bifurcation, multistability, quasi-periodic, and chaotic behavior in the fractional form of the stated model. Additionally, explicit solutions to this model are obtained. These solutions can be used to understand the system's dynamic properties better.

Outline of this work: Conversion to the ordinary differential form of the fractional TMNNV equation is presented in Section 2. Section 3 explains conformable fractional derivatives. In Section 4, the bifurcation analysis of the mentioned model is discussed. Section 5 determines the explicit solution by bifurcation analysis and plotting the 3-D and 2-D graph solutions. In Section 6, some specific figures illustrate quasi-periodic and chaotic behavior with multistability. Finally, conclusions are drawn in Section 7.

The novelty of this paper is that the bifurcation, finding the outcome, phase portraits, and multistability of the suggested model are not described by any other investigator before.

2.   Construction of the ordinary differential form of the TMNNV model

The (2+1)-dimensional TMNNV equation can be written in the next form ^[41]:

where $w = w(x, y, t)$ is the vector field with spatial variable $x, y,$ and temporal variable $t$. Here, ${\gamma }_{1}$ and ${\gamma }_{2}$ refer to the nonlinearity parameters, ${\alpha }_{1}$ and ${\alpha }_{2}$ denote the dispersion parameters, $\nu$ is the nonlinear interaction coefficient, $\rho$ corresponds to the higher-order interaction coefficient, and $p$ signifies the phase-velocity. Additionally, $\left|{\alpha }_{1}\right|\le 1$, $\left|{\alpha }_{2}\right|\le 1$, $\left|{\gamma }_{1}\right|\le 1$, and $\left|{\gamma }_{2}\right|\le 1$.

The time-fractional TMNNV equation Eq (1) can be written in the following way:

where $\beta \in (0, \mathrm{ }1]$. Consider a variable $\phi = \phi (x, y, t)$, which follows the next equation:

Using Eq (3), the time fractional TMNNV equation (2) converts into

Now, Eq (4) needs to be convert into an ordinary differential equation with the relation as

where $a, b,$ and $c$ are arbitrary parameters. We assume that ${\gamma }_{1} = {\gamma }_{2} = \gamma$ and ${\alpha }_{1} = {\alpha }_{2} = \alpha$, then using Eqs (4) and (5), we obtain the resulting shortened ordinary differential form:

where $a, b, c, p, \nu, \rho, \gamma,$ and $\alpha$ are arbitrary parameters and " $'$ " represents the derivative over the independent variable $\mu$.

3.   Characteristics of fractional derivative

Let $f:[0, \mathrm{\infty }]\to \mathbb{R}$ be a real function where $0 < \beta \le 1$; with the conformable fractional derivative of this function $f\left(\mathrm{q}\right)$ at a point $q > 0$ takes the following form ^[41]:

Assume that $f\left(q\right)$ and $g\left(q\right)$ are $\beta$-conformable differentiable functions while $q > 0$ and $0 < \beta \le 1$. Some important characteristics of fractional derivatives are listed below where $r$ is any constant and $s$ and $m$ are real constants.

(ⅰ) $\frac{{\partial }^{\mathtt{β}}}{\partial {q}^{\beta }}{q}^{n} = n{q}^{n-\beta }$, $\mathit{∀}n\in \mathbb{R}$.

(ⅱ) $\frac{{\partial }^{\mathtt{β}}}{\partial {q}^{\beta }}\left(\mathrm{r}\right) = 0$.

(ⅲ) $\frac{{\partial }^{\mathtt{β}}}{\partial {q}^{\beta }}sf\left(\mathrm{q}\right) = s\frac{{\partial }^{\mathtt{β}}}{\partial {q}^{\beta }}f\left(q\right)$.

(ⅳ) $\frac{{\partial }^{\mathtt{β}}}{\partial {q}^{\beta }}\left(sf\right(q)+mg(q\left)\right) = s\frac{{\partial }^{\mathtt{β}}}{\partial {q}^{\beta }}f\left(q\right)+\mathrm{m}\frac{{\partial }^{\mathtt{β}}}{\partial {q}^{\beta }}g\left(q\right)$.

(ⅴ) $\frac{{\partial }^{\mathtt{β}}}{\partial {q}^{\beta }}\left(g\right(q\left)f\right(q\left)\right) = g\left(q\right)\frac{{\partial }^{\mathtt{β}}}{\partial {q}^{\beta }}f\left(q\right)+f\left(q\right)\frac{{\partial }^{\mathtt{β}}}{\partial {q}^{\beta }}g\left(\mathrm{q}\right)$.

(ⅵ) $\frac{{\partial }^{\mathtt{β}}}{\partial {q}^{\beta }}\left(\frac{f\left(q\right)}{g\left(q\right)}\right) = \frac{g\left(q\right)\frac{{\partial }^{\mathtt{β}}}{\partial {q}^{\beta }}f\left(q\right)-f\left(q\right)\frac{{\partial }^{\mathtt{β}}}{\partial {q}^{\beta }}g\left(q\right)}{{g}^{2}\left(q\right)}, g\left(q\right)\ne 0$.

4.   Bifurcation analysis of the fractional TMNNV model

The bifurcation and phase representations ^[42,43] of the subsequent dynamical equation are discussed here. Let us assume that the differentiation of $R$ over the variable $\mu$ is equal to $Q$; then a prototype differential system can be written from Eq (6) as follows:

which has the first integral

where $k = \frac{{a}^{2}-\left({b}^{2}+{c}^{2}\right){p}^{2}}{\rho {b}^{3}\left(\mathrm{a}+\left(b+c\right)\alpha \right)}, l = \frac{\nu b\left(a+\left(b+c\right)\gamma \right)}{2\rho {b}^{3}\left(\mathrm{a}+\left(b+c\right)\alpha \right)}$, and $H(R, Q)$ and $h$ are the Hamiltonian function and constant, respectively.

Now, the bifurcation of the system (7) is discussed here with the arbitrary constants $a, b, c, p, \nu, \rho, \gamma$, and $\alpha$. A smooth homoclinic orbit of Eq (7) is seen which rises from the smooth solitary waves in Eq (2) ^[44,45]. Consider that ${\mathrm{l}\mathrm{i}\mathrm{m}}_{\mu \to -\mathrm{\infty }} R\left(\mu \right) = d$ and ${\mathrm{l}\mathrm{i}\mathrm{m}}_{\mu \to \mathrm{\infty }} R\left(\mu \right) = e$ of the outcome $R\left(cy+bx-\frac{a{t}^{\beta }}{\beta }\right) = R\left(\mu \right), (-\mathrm{\infty } < \mu < \mathrm{\infty })$, then:

(ⅰ) When $d = e$, $R\left(\mu \right)$ is represented as a homoclinic orbit of Eq (7), which connects with a solitary wave outcome of Eq (2).

(ⅱ) When $d\ne \mathrm{e}$, $R\left(\mu \right)$ is presumed to be a heteroclinic orbit of Eq (7), which connects with an antikink or a kink wave outcome of Eq (2).

Otherwise, a periodic orbit of Eq (7) connects with a periodic wave outcome of Eq (2).

Therefore, we can easily analyze the probable phase portraits of Eq (7) with different constants $a, b, c, p, \nu, \rho, \gamma,$ and $\alpha$.

By inserting ${R}^{'} = 0$ and ${Q}^{'} = 0$ into Eq (7), then for $k\ne 0$, this system will deliver two equilibrium points ${M}_{0}\left(\mathrm{0, 0}\right)$ and ${\mathrm{M}}_{1}\left(\frac{k}{l}, 0\right)$. Moreover, at $k = 0$, the system (7) provides one equilibrium point $M\left(\mathrm{0, 0}\right)$. Assume that $B\left({R}_{M}, {Q}_{\mathrm{M}}\right)$ be the matrix of coefficients of the system (7) at equilibrium points ${\mathrm{M}}_{j}(j = 0, \mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }1)$ and assume that $J\left({\mathrm{M}}_{j}\right) = \left|B({R}_{M}, {Q}_{M})\right|$. Therefore, we have $J\left({M}_{0}\right) = -k$, $J\left({M}_{1}\right) = k$, $\mathrm{T}\mathrm{r}\mathrm{a}\mathrm{c}\mathrm{e}\left(B\left({M}_{0}\right)\right) = 0$, $\mathrm{T}\mathrm{r}\mathrm{a}\mathrm{c}\mathrm{e}(B\left({M}_{1})\right) = 0$.

By exploring the bifurcations and the above outcomes, we can write the following categories:

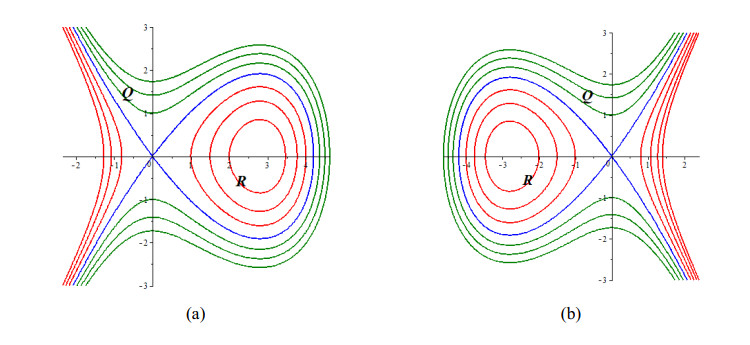
Category-1: For $k > 0,$ a saddle point and a center point can be seen of the nature at the points ${M}_{0}(0, 0)$ and ${M}_{1}\left(\frac{k}{l}, 0\right)$, respectively, while the equivalent phase portraits bifurcations of Eq (7) are imagined in Figure 1(a) and 1(b), respectively.

Figure 1.  The phase plot of the system (7) for (a) $k > 0, l > 0, \alpha = b = c = \gamma = \rho = p = \nu = 1, a = 3$ and (b) $k > 0, l < 0, \nu = -1, \alpha = b = c = \gamma = \rho = p = 1, a = 3$.

DownLoad: Full-Size Img PowerPoint

Category-2: For $k < 0,$ a center point and a saddle point can be seen of the nature at the points ${\mathrm{M}}_{0}(0, \mathrm{ }0)$ and ${M}_{1}\left(\frac{k}{l}, 0\right)$, respectively, while the equivalent phase portraits bifurcations of Eq (7) are drawn in Figure 2(a) and 2(b), respectively.

Figure 2.  The phase plot of the system (7) for (a) $k < 0, l > 0, \rho = \nu = -1, \alpha = b = c = \gamma = p = 1, a = 3$ and (b) $k < 0, l < 0, \rho = -1, \alpha = b = c = \gamma = p = \nu = 1, a = 3$.

DownLoad: Full-Size Img PowerPoint

Category-3: For $k = 0,$ a cusp point can be seen of the nature at the points ${M}_{0}(0, 0)$, while the equivalent phase portraits bifurcations of Eq (7) are drawn in Figure 3(a) and 3(b), respectively.

Figure 3.  The phase plot of system (7) for (a) $k = 0, l > 0, \alpha = \gamma = \rho = p = \nu = 1, c = 3, b = 4, a = 5$ and (b) $k = 0, l < 0, \rho = -1, \alpha = \gamma = p = \nu = 1, c = 3, b = 4, a = 5$.

DownLoad: Full-Size Img PowerPoint

A complete classification of equilibrium points is shown in Table 1.

Table 1.  The Bifurcations Categories Summary.

Figure	State points
	$(0, \mathrm{ }0)$	$(2.8, \mathrm{ }0)$	$(-2.8, \mathrm{ }0)$
1(a)	Unstable and saddle	Stable and center	-
1(b)	Unstable and saddle	-	Stable and center
2(a)	Stable and center	-	Unstable and saddle
2(b)	Stable and center	Unstable and saddle	-
3(a)	cusp point	-	-
3(b)	cusp point	-	-

---

 | Show Table

DownLoad: CSV

5.   Explicit solution for the proposed model

We aim to delve into the various explicit wave outcomes for the time fractional TMNNV model. For simplicity, the energy stage of the Hamiltonian is stated by taking ${h}_{0} = H\left(\mathrm{0, 0}\right) = 0$ and ${h}_{1} = H\left(\frac{k}{l}, 0\right) = -\frac{{k}^{3}}{6{l}^{2}}$.

5.1.   Investigating category-1 in Section 4

5.1.1.   Case-Ⅰ

For $k > 0, l > 0$, $R\left(\mu \right)$ is expected to be a homoclinic orbit of Eq (7) at ${M}_{0}\left(\mathrm{0, 0}\right)$ defined by $H(R, Q) = {h}_{0}$, where Eq (2) provides a valley-type smooth solitary wave ^[42,43] outcome shown in Figure 1(a). By employing $H(R, Q) = {h}_{0} = 0$ into Eq (8), we have

From the initial equation of the system (7) with Eqs (3), (5), and (9), we obtain

where $\mu = cy+bx-\frac{a{t}^{\beta }}{\beta }, k = \frac{{a}^{2}-\left({b}^{2}+{c}^{2}\right){p}^{2}}{\rho {b}^{3}\left(\mathrm{a}+\left(b+c\right)\alpha \right)} > 0, l = \frac{\nu b\left(a+\left(b+c\right)\gamma \right)}{2\rho {b}^{3}\left(\mathrm{a}+\left(b+c\right)\alpha \right)} > 0,$ and ${\mu }_{0}$ is an integrating constant.

A combo dark-bright bell wave ^[46,47] can be found in Figure 4 for the valley-type smooth solitary wave outcome Eq (10) with $\beta = 0.1, \mathrm{ }0.4, \mathrm{ }0.9;b = -1, {\mu }_{0} = 0, a = c = p = \nu = \rho = 1, \gamma = \alpha = 0.5.$

Figure 4.  Visualization of Eq (10) for $b = -1, {\mu }_{0} = 0, a = c = p = \nu = \rho = 1, \gamma = \alpha = 0.5$.

DownLoad: Full-Size Img PowerPoint

5.1.2.   Case-Ⅱ

For $k > 0, l < 0$, $R\left(\mu \right)$ is a homoclinic orbit of Eq (7) at ${\mathrm{M}}_{0}\left(\mathrm{0, 0}\right)$ defined by $H(R, Q) = {h}_{0}$, where Eq (2) provides a valley-type smooth solitary wave ^[42,43] outcome shown in Figure 1(b). By inserting $H(R, Q) = {h}_{0} = 0$ into Eq (8), we obtain

From the initial equation of the system (7) with Eqs (3), (5), and (11), we obtain

where $\mu = cy+bx-\frac{a{t}^{\beta }}{\beta }, k = \frac{{a}^{2}-\left({b}^{2}+{c}^{2}\right){p}^{2}}{\rho {b}^{3}\left(\mathrm{a}+\left(b+c\right)\alpha \right)} > 0, l = \frac{\nu b\left(a+\left(b+c\right)\gamma \right)}{2\rho {b}^{3}\left(\mathrm{a}+\left(b+c\right)\alpha \right)} < 0$, and ${\mu }_{0}$ is an integrating constant.

A combo bright-dark bell wave ^[42,43] can be found in Figure 5 for the valley-type smooth solitary wave outcome equation (12) with $\beta = 0.1, 0.4, 0.9;b = \nu = -1, {\mu }_{0} = 0, a = c = p = \rho = \gamma = 1, \alpha = 0.5.$

Figure 5.  Visualization of Eq (12) for $b = v = -1, {\mu }_{0} = 0, a = c = p = \rho = \gamma = 1, \alpha = 0.5$.

DownLoad: Full-Size Img PowerPoint

5.1.3.   Case-Ⅲ

For $k > 0, l > 0$ or $k > 0, l < 0$, Eq (2) provides a family of smooth periodic wave outcomes defined by $H\left(R, Q\right) = h, h\in \left({h}_{1}, 0\right)$ (shown in Figure 1(a) and 1(b)).

For $k > 0, l > 0$, the expression of the closed domain of the system (7) is written below and displayed in Figure 1(a):

where $\left({R}_{1}, 0\right), \left({R}_{2}, 0\right),$ and $\left({R}_{3}, 0\right)$ are the intersecting points of the graph defined by $H\left(R, Q\right) = h, h\in \left({h}_{1}, 0\right)$ on the $R$-axis and holds the condition ${R}_{1} < R < {R}_{2} < {\mathrm{R}}_{3}$. From the initial equation of the system (7) with Eqs (3), (5), and (13), we obtain the formula of the periodic outcome as follows ^[48]:

where $\mu = cy+bx-\frac{a{t}^{\beta }}{\beta }, k = \frac{{a}^{2}-\left({b}^{2}+{c}^{2}\right){p}^{2}}{\rho {b}^{3}\left(\mathrm{a}+\left(b+c\right)\alpha \right)} > 0, l = \frac{\nu b\left(a+\left(b+c\right)\gamma \right)}{2\rho {b}^{3}\left(\mathrm{a}+\left(b+c\right)\alpha \right)} > 0$, and ${\mu }_{0}$ is an integrating constant.

Periodic wave can be found in Figure 6 for the periodic wave outcome equation (14) with $\beta = 0.1, 0.6, 0.9;b = {R}_{1} = -1, {\mu }_{0} = 0, a = c = p = \nu = \rho = 1, \gamma = \alpha = 1, {R}_{2} = 2, {R}_{3} = 3.$

Figure 6.  Visualization of Eq (14) for $b = {R}_{1} = -1, {\mu }_{0} = 0, a = c = p = \nu = \rho = \gamma = \alpha = 1, {R}_{2} = 2, {R}_{3} = 3$.

DownLoad: Full-Size Img PowerPoint

For $k > 0, l < 0$, a similar study can be found in Figure 1(b). Assume that $\left({R}_{4}, 0\right), \left({R}_{5}, 0\right),$ and $\left({R}_{6}, 0\right)$ are the touching points of the graph defined by $H\left(R, Q\right) = h, h\in \left({h}_{1}, 0\right)$ on the $R$-axis and holds the condition ${R}_{4} < R < {R}_{5} < {R}_{6}$. We obtain the formula of the periodic outcome as follows ^[49]:

where $\mu = cy+bx-\frac{a{t}^{\beta }}{\beta }, k = \frac{{a}^{2}-\left({b}^{2}+{c}^{2}\right){p}^{2}}{\rho {b}^{3}\left(\mathrm{a}+\left(b+c\right)\alpha \right)} > 0, l = \frac{\nu b\left(a+\left(b+c\right)\gamma \right)}{2\rho {b}^{3}\left(\mathrm{a}+\left(b+c\right)\alpha \right)} < 0$, and ${\mu }_{0}$ is an integrating constant.

A periodic wave pattern can be found for the outcome equation (15), which is almost like the periodic wave of the outcome equation (14).

5.2.   Investigating category-2 in Section 4

5.2.1.   Case-Ⅰ

For $k < 0, l > 0$, $R\left(\mu \right)$ is expected to be a homoclinic orbit of Eq (7) at the stable point ${M}_{1}\left(\frac{k}{l}, 0\right)$ defined by $H(R, Q) = {h}_{1}$, and Eq (2) provides a valley-type smooth solitary wave ^[44,45] outcome shown in Figure 2(a). By substituting $H(R, Q) = {h}_{1}$ into Eq (8), we have

From the initial equation of the system (7), with Eqs (3), (5), and (16), we obtain the following solution, which is like that shown in Figure 4.

where $\mu = cy+bx-\frac{a{t}^{\beta }}{\beta }, k = \frac{{a}^{2}-\left({b}^{2}+{c}^{2}\right){p}^{2}}{\rho {b}^{3}\left(\mathrm{a}+\left(b+c\right)\alpha \right)} < 0, l = \frac{\nu b\left(a+\left(b+c\right)\gamma \right)}{2\rho {b}^{3}\left(\mathrm{a}+\left(b+c\right)\alpha \right)} > 0$, and ${\mu }_{0}$ is an integrating constant.

5.2.2.   Case-Ⅱ

For $k < 0, l < 0$, $R\left(\mu \right)$ is supposed to be a homoclinic orbit of Eq (7) at the stable point ${M}_{1}\left(\frac{k}{l}, 0\right)$ is defined by $H(R, Q) = {h}_{1}$, and Eq (2) provides a valley-type smooth solitary wave outcome shown in Figure 2(b). By taking $H(R, Q) = {h}_{1}$ into Eq (8), we have

From the initial equation of the system (7) with Eqs (3), (5), and (18), we obtain the following solution which is like that shown in Figure 4.

where $\mu = cy+bx-\frac{a{t}^{\beta }}{\beta }, k = \frac{{a}^{2}-\left({b}^{2}+{c}^{2}\right){p}^{2}}{\rho {b}^{3}\left(\mathrm{a}+\left(b+c\right)\alpha \right)} < 0, l = \frac{\nu b\left(a+\left(b+c\right)\gamma \right)}{2\rho {b}^{3}\left(\mathrm{a}+\left(b+c\right)\alpha \right)} < 0$, and ${\mu }_{0}$ is an integrating constant.

5.2.3.   Case-Ⅲ

For $k < 0, l > 0$ or $k < 0, l < 0$, Eq (2) provides a family of smooth periodic wave outcomes defined by $H\left(R, Q\right) = h, h\in \left(0, {h}_{1}\right)$, drawn in Figure 2(a) and 2(b), respectively. In addition, this periodic outcome is identical to the outcomes in Eqs (14) and (15).

5.3.   Investigating category-3 in Section 4

5.3.1.   Case-Ⅰ

For $k = 0, l > 0$, $R\left(\mu \right)$ is assumed to be an unrestricted orbit of Eq (7) at ${\mathrm{M}}_{0}\left(\mathrm{0, 0}\right)$ defined by $H(R, Q) = {h}_{0}$, and Eq (2) provides a soliton solution shown in Figure 3(a). By inserting $H(R, Q) = {h}_{0} = 0$ into Eq (8), we have

From the initial equation of the system (7) with Eqs (3), (5), and (20), we obtain the following soliton outcome:

where $\mu = cy+bx-\frac{a{t}^{\beta }}{\beta }, l = \frac{\nu b\left(a+\left(b+c\right)\gamma \right)}{2\rho {b}^{3}\left(\mathrm{a}+\left(b+c\right)\alpha \right)} > 0$, and ${\mu }_{0}$ is an integrating constant.

A combo bright-dark bell wave with singularity can be found in Figure 7 for the soliton solution equation (21) with $\beta = 0.1, 0.25, 0.9;{\mu }_{0} = 0, a = b = c = \nu = \rho = 1, p = \frac{1}{\sqrt{2}}, \gamma = 1, \alpha = 0.5.$

Figure 7.  Visualization of Eq (21) for ${\mu }_{0} = 0, a = b = c = \nu = \rho = 1, p = \frac{1}{\sqrt{2}}, \gamma = 1, \alpha = 0.5$.

DownLoad: Full-Size Img PowerPoint

5.3.2.   Case-Ⅱ

For $k = 0, l < 0$, $R\left(\mu \right)$ is an unrestricted orbit of Eq (7) at ${\mathrm{M}}_{0}\left(\mathrm{0, 0}\right)$ defined by $H(R, Q) = {h}_{0}$, and Eq (2) provides a similar soliton solution shown in Figure 3(b). By substituting $H(R, Q) = {h}_{0} = 0$ into Eq (8), we have

From the initial equation of the system (7) with Eqs (3), (5), and (22), we obtain the following soliton outcome which has a similar nature as shown in Figure 7:

where $\mu = cy+bx-\frac{a{t}^{\beta }}{\beta }, l = \frac{\nu b\left(a+\left(b+c\right)\gamma \right)}{2\rho {b}^{3}\left(\mathrm{a}+\left(b+c\right)\alpha \right)} < 0$, and ${\mu }_{0}$ is an integrating constant.

6.   Quasi-periodic and chaotic behaviors

Nonlinear models can exhibit chaotic behavior ^[50] when they experience bifurcations, leading to various dynamic properties. We saw in the previous section that the planar dynamical structure equation (7) does not exhibit chaotic properties, but it does when an external disturbance is added. Accordingly, for the dynamical system (7), perturbation takes the following shape:

with perturbed term $F\left(\mu \right)$. In the context of phase portraits and multistability ^[49], quasi-periodic and chaotic behavior can be explored by considering the following three types of perturbation terms with diverse parameters. It is noted that chaotic waves demonstrate irregular, non-repeating structures and are highly sensitive to initial values. On the other hand, quasi-periodic waves frequently occur in coupled oscillators or systems with several degrees of freedom and have intricate but predictable structures that are not exactly repeatable. Some remarkable graphical representations, such as 3D phase portraits, 2D phase portraits, Poincaré plots, and time series plots, will be included to reach our destinations. Wave structures like these can be found in many natural phenomena, such as ocean waves, climate models, optics, telecommunications, plasma physics, and biological rhythms.

(ⅰ) Trigonometric function: Let $F\left(\mu \right) = 1.5\mathrm{c}\mathrm{o}\mathrm{s}\left(3.9\mu \right)$, then the phase portrait and multistability of Eq (24) are exposed in Figures 8 and 11, respectively, for $\alpha = 1, \rho = 4, \gamma = 2, p = 4, a = 1, b = 0.5, c = 0.5$, and $v = 2$. Figure 8 shows that the system is chaotic, as evidenced by its irregular behavior and absence of regular patterns. Figure 11 shows that the system follows chaotic patterns due to its sensitivity to initial values.

Figure 8.  Outlook of the perturbation equation (24) for $F\left(\mu \right) = 1.5\mathrm{cos}\left(3.9\mu \right)$ with initial value $\left(R\left(0\right), Q\left(0\right)\right) = (0.1, 0.1)$.

DownLoad: Full-Size Img PowerPoint

Figure 9.  Outlook of the perturbation equation (24) for $F\left(\mu \right) = 3.5{e}^{\frac{-{\left(0.12\mu \right)}^{2}}{2}}$ with initial value $\left(R\left(0\right), Q\left(0\right)\right) = (0.2, \mathrm{ }0.2)$.

DownLoad: Full-Size Img PowerPoint

Figure 10.  Outlook of the perturbation equation (24) for $F\left(\mu \right) = 1.4\mathrm{c}\mathrm{o}\mathrm{s}\mathrm{h}\left(0.04\mu \right)$ with initial value $\left(R\left(0\right), Q\left(0\right)\right) = \left(0.2, \mathrm{ }0.2\right)$.

DownLoad: Full-Size Img PowerPoint

Figure 11.  Multistability of the perturbation equation (24) for $\left(\mu \right) = 1.5\mathrm{cos}\left(3.9\mu \right)$.

DownLoad: Full-Size Img PowerPoint

(ⅱ) Gaussian function: Let $F\left(\mu \right) = 3.5{e}^{\frac{-{\left(0.12\mu \right)}^{2}}{2}}$, then the phase portrait and multistability of Eq (24) are exposed in Figures 9 and 12, respectively, for parameters $\alpha = 1, \rho = 4, \gamma = 2, p = 4, a = 1, b = 0.5, c = 0.5,$ and $v = 2$. Figures 9 and 12 represent quasi-periodic structures, evidenced by the periodic irregularity of the wave.

Figure 12.  Multistability of the perturbation equation (24) for $F\left(\mu \right) = 3.5{e}^{\frac{-{\left(0.12\mu \right)}^{2}}{2}}$.

DownLoad: Full-Size Img PowerPoint

(ⅲ) Hyperbolic function: Let $F\left(\mu \right) = 1.4\mathrm{c}\mathrm{o}\mathrm{s}\mathrm{h}\left(0.04\mu \right)$, then the phase portrait and multistability of Eq (24) are exposed in Figures 10 and 13, respectively for parameters $\alpha = 1, \rho = 4, \gamma = 2, p = 4, a = 1, b = 0.5, c = 0.5,$ and $v = 2$. Figures 10 and 13 represent quasi-periodic structures, as evidenced by the wave's periodic irregularity.

Figure 13.  Multistability of the perturbation equation (24) for $F\left(\mu \right) = 1.4\mathrm{c}\mathrm{o}\mathrm{s}\mathrm{h}\left(0.04\mu \right)$.

DownLoad: Full-Size Img PowerPoint

7.   Conclusions

We apply bifurcation theory to the TMNNV model for the first time to uncover bifurcations, discrete solutions, phase portraits, and multistability under different parameters. 3D with density and 2D plots are used to identify and visualize unique wave patterns, such as combined bright-dark and dark-bright bell waves, periodic waves, and bright solitons. Additionally, quasi-periodic and chaotic behaviors are studied, along with multistability, showing how they are strongly dependent on initial conditions and parameter settings. The findings shed light on the dynamics of these nonlinear systems, providing valuable insights into their behavior. Based on this analysis and graphical representation, future physical experiments or observations can be conducted to validate these predicted complex dynamics and their practical applications.

Author contributions

Noor Alam: Formal analysis, Software; Mohammad Safi Ullah: Validation, Methodology; Jalil Manafian: Investigation, Writing–review & editing; Khaled H. Mahmoud: Software, Writing–review & editing; A. SA. Alsubaie: Formal analysis, Writing–review & editing; Hamdy M. Ahmed: Supervision, Software; Karim K. Ahmed: Resources, Writing–review & editing; Soliman Alkhatib: Mathematical analysis, Writing–review & editing. All authors have read and agreed to the published version of the manuscript.

Use of Generative-AI tools declaration

The authors declare they have used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

The authors extend their appreciation to Taif University, Saudi Arabia, for supporting this work through project number (TU-DSPP-2024-106).

Funding

This research was funded by Taif University, Saudi Arabia, Project No. (TU-DSPP-2024-106).

Conflict of interest

The authors declare that they have no competing interests.