In this paper, we studied the dynamical behavior of various phases of breast cancer using the Caputo Fabrizio (CF) fractional order derivative operator. The Picard-Lindelof (PL) method was used to investigate the existence and uniqueness of the proposed system. Moreover, we investigated the stability of the system in the sense of Ulam Hyers (UH) criteria. In addition, the two-step Adams-Bashforth (AB) technique was employed to simulate our methodology. The fractional model was then simulated using real data, which includes reported breast cancer incidences among females of Saudi Arabia from 2004 to 2016. The real data was used to determine the values of the parameters that were fitted using the least squares method. Also, residuals were computed for the integer as well as fractional-order models. Based on the results obtained, the CF model's efficacy rates were greater than those of the existing classical model. Graphical representations were used to illustrate numerical results by examining different choices of fractional order parameters, then the dynamical behavior of several phases of breast cancer was quantified to show how fractional order affects breast cancer behavior and how chemotherapy rate affects breast cancer behavior. We provided graphical results for a breast cancer model with effective parameters, resulting in fewer future incidences in the population of phases Ⅲ and Ⅳ as well as the disease-free state. Chemotherapy often raises the risk of cardiotoxicity, and our proposed model output reflected this. The goal of this study was to reduce the incidence of cardiotoxicity in chemotherapy patients while also increasing the pace of patient recovery. This research has the potential to significantly improve outcomes of patients and provide information of treatment strategies for breast cancer patients.
Citation: Anil Chavada, Nimisha Pathak. Transmission dynamics of breast cancer through Caputo Fabrizio fractional derivative operator with real data[J]. Mathematical Modelling and Control, 2024, 4(1): 119-132. doi: 10.3934/mmc.2024011
| [1] | Ihtisham Ul Haq, Nigar Ali, Hijaz Ahmad . Analysis of a chaotic system using fractal-fractional derivatives with exponential decay type kernels. Mathematical Modelling and Control, 2022, 2(4): 185-199. doi: 10.3934/mmc.2022019 |
| [2] | Rashid Jan, Normy Norfiza Abdul Razak, Sania Qureshi, Imtiaz Ahmad, Salma Bahramand . Modeling Rift Valley fever transmission: insights from fractal-fractional dynamics with the Caputo derivative. Mathematical Modelling and Control, 2024, 4(2): 163-177. doi: 10.3934/mmc.2024015 |
| [3] | Saïd Abbas, Mouffak Benchohra, Johnny Henderson . Random Caputo-Fabrizio fractional differential inclusions. Mathematical Modelling and Control, 2021, 1(2): 102-111. doi: 10.3934/mmc.2021008 |
| [4] | Anil Chavada, Nimisha Pathak, Sagar R. Khirsariya . A fractional mathematical model for assessing cancer risk due to smoking habits. Mathematical Modelling and Control, 2024, 4(3): 246-259. doi: 10.3934/mmc.2024020 |
| [5] | Ihtisham Ul Haq, Nigar Ali, Shabir Ahmad . A fractional mathematical model for COVID-19 outbreak transmission dynamics with the impact of isolation and social distancing. Mathematical Modelling and Control, 2022, 2(4): 228-242. doi: 10.3934/mmc.2022022 |
| [6] | Muhammad Nawaz Khan, Imtiaz Ahmad, Mehnaz Shakeel, Rashid Jan . Fractional calculus analysis: investigating Drinfeld-Sokolov-Wilson system and Harry Dym equations via meshless procedures. Mathematical Modelling and Control, 2024, 4(1): 86-100. doi: 10.3934/mmc.2024008 |
| [7] | Lusong Ding, Weiwei Sun . Neuro-adaptive finite-time control of fractional-order nonlinear systems with multiple objective constraints. Mathematical Modelling and Control, 2023, 3(4): 355-369. doi: 10.3934/mmc.2023029 |
| [8] | Naveen Kumar, Km Shelly Chaudhary . Position tracking control of nonholonomic mobile robots via $ H_\infty $-based adaptive fractional-order sliding mode controller. Mathematical Modelling and Control, 2025, 5(1): 121-130. doi: 10.3934/mmc.2025009 |
| [9] | M. Haripriya, A. Manivannan, S. Dhanasekar, S. Lakshmanan . Finite-time synchronization of delayed complex dynamical networks via sampled-data controller. Mathematical Modelling and Control, 2025, 5(1): 73-84. doi: 10.3934/mmc.2025006 |
| [10] | Abduljawad Anwar, Shayma Adil Murad . On the Ulam stability and existence of $ L^p $-solutions for fractional differential and integro-differential equations with Caputo-Hadamard derivative. Mathematical Modelling and Control, 2024, 4(4): 439-458. doi: 10.3934/mmc.2024035 |
In this paper, we studied the dynamical behavior of various phases of breast cancer using the Caputo Fabrizio (CF) fractional order derivative operator. The Picard-Lindelof (PL) method was used to investigate the existence and uniqueness of the proposed system. Moreover, we investigated the stability of the system in the sense of Ulam Hyers (UH) criteria. In addition, the two-step Adams-Bashforth (AB) technique was employed to simulate our methodology. The fractional model was then simulated using real data, which includes reported breast cancer incidences among females of Saudi Arabia from 2004 to 2016. The real data was used to determine the values of the parameters that were fitted using the least squares method. Also, residuals were computed for the integer as well as fractional-order models. Based on the results obtained, the CF model's efficacy rates were greater than those of the existing classical model. Graphical representations were used to illustrate numerical results by examining different choices of fractional order parameters, then the dynamical behavior of several phases of breast cancer was quantified to show how fractional order affects breast cancer behavior and how chemotherapy rate affects breast cancer behavior. We provided graphical results for a breast cancer model with effective parameters, resulting in fewer future incidences in the population of phases Ⅲ and Ⅳ as well as the disease-free state. Chemotherapy often raises the risk of cardiotoxicity, and our proposed model output reflected this. The goal of this study was to reduce the incidence of cardiotoxicity in chemotherapy patients while also increasing the pace of patient recovery. This research has the potential to significantly improve outcomes of patients and provide information of treatment strategies for breast cancer patients.
As per medical experts, breast cancer is characterized by the abnormal development and division of cells inside the breast tissue. This condition poses a significant risk to health and is mostly seen in the female population. According to [1], compared to other types of cancer, the most people get breast cancer. It kills breast tissue and cells, causing the breasts to grow out of control and change shape. Several risk factors have been found that put women at a higher chance of getting breast cancer. Dietary habits, personal experience of malignancy, alcohol consumption, smoking, weight status, dense breast tissue, physical inactivity, reproductive history (including pregnancy and breastfeeding), menstrual history, genetic predisposition, racial background, life span history, specific breast changes, and getting older are all factors to consider. The main clinical presentations of breast cancer include lymphadenopathy, nipple discharge, nipple retraction, breast/nipple pain, presence of flaky skin on the breast/nipple, skin irritation, appearance of skin dimpling with erythema, changes in breast form or size, localized breast tissue thickening, and either complete or partial breast swelling. Tumor, node, and metastatic stages are used by medical professionals to evaluate a patient's cancer state and calculate their prospects of remission.
The odds of recovery are higher at earlier stages. Bisphosphonates, bone marrow transplants, gene therapy, hormone therapy, immunotherapy, surgery, stem cell therapy, targeted cancer medications, radiation, and complementary and alternative treatments are only a few of the therapeutic methods that have been created to prevent cancer. Chemotherapy is the most popular kind of treatment for the aforementioned conditions, and it uses medications to destroy cancer cells. The medications used in chemotherapy are either administered intravenously to the patient or taken orally, with some efficacy but potential cardiac risks. Cardiotoxicity is a negative side effect that may affect both adults and children [2]. Mathematical models are employed to analyze the complicated dynamics of illnesses and offer precise outcomes for infection reduction and control.
One of the most rapidly expanding subfields of mathematical analysis is called fractional calculus, and it is concerned with the study of both derivatives and integrals of any arbitrary order [3,4]. The nonlocality is a major advantage of the nonclassical derivatives that helps in the depiction of memory and hereditary characteristics of the system. As most of the biological processes involve the memory effect in the study of the epidemiological model fractional derivatives play a vital role.
Recent advancements suggest that fractional interpreters exhibit superior accuracy, utility, and reliability compared to the conventional derivative method. Contemporary fractional derivative operators are now being formulated in order to elucidate practical phenomena. Many mathematical models including integer and fractional order have been created in the literature for the detailed analysis of various diseases such as diabetes [5,6], breast cancer [7], cancer treatment model [8,9], HIV/AIDS [10,11], lung cancer [12], Covid-19 [13,14,15], and in several other scientific and technological disciplines such as biology [16,17,18], chemistry [19], engineering [20,21,22,23,24,25,26], and most of the references cited therein.
The various techniques, such as the analytical methods [27,28,29], the semi-analytic methods [30,31,32,33,34,35], and the numerical methods [36,37,38,39,40,41] are found in the literature for solving fractional differential equations. Moreover, in [42], the solution of the fractional Sawada-Kotera-Ito equation using Caputo and Atangana-Baleanu (AB) derivatives have been derived. In [43], a robust computational analysis of residual power series involving general transform to solve fractional differential equations has been proposed. Abdeljawad et al. in [44] derived a higher-order extension of AB fractional operators with respect to another function and a Gronwall-type inequality. In [45], the authors provide studies on the coupled snap system with integral boundary conditions in the G-Caputo sense. The authors in [46], studied the nonlocal multi-order implicit differential equation involving Hilfer fractional derivative on unbounded domains. In [47], an efficient variable step-size rational method for stiff, singular, and singularly perturbed problems has been given. The development of the reproducing kernel Hilbert space algorithm for the numerical pointwise solution of the time-fractional nonlocal reaction-diffusion equation is provided in [48].
In fractional calculus, a number of fractional operators are offered for the study of real issues. In contrast, these operators have a power law kernel and can merely partly simulate physical obstacles. Caputo and Fabrizio (CF) [49] introduced a unique fractional operator with a nonsingular kernel to address these issues and constraints. This revolutionary operator's results are more appropriate and have several applications. In [50], the authors studied the fractional mathematical modeling of the human liver. Ullah et al. in [51] analyzed a fractional model for the dynamics of tuberculosis infection. In [52], the authors proposed fractional cancer treatment. In [53], the authors studied the application of the CF derivative to a cancer model with unknown parameters. Ngungu et al. in [54] focused on mathematical epidemiological modeling and analysis of monkeypox dynamics with non-pharmaceutical intervation using real data from the UK. In [55], the authors developed the mathematical modeling of the immune-chemotherapeutic treatment of breast cancer under some control parameters, and the majority of the references listed therein have adequately represented the diseases transmission process with therapy and unidentified parameters.
The breast cancer classical mathematical model was categorized into five epidemiological groups by authors in [56]. However, it fails to optimally capture nonlocal behavior for the dynamics of the cancer, and the deviation between the real data and the data obtained through the simulation of the classical model is found to be large. Moreover, the freedom of having access to the real data is the chief motivation behind detailed analysis of the breast cancer model under the CF fractional-order differential operator. These precise fractional calculus findings and consequences drive us to examine and analyze the dynamics of breast cancer using actual data, which are reported cases in Saudi Arabia from 2004 to 2016 [57]. It is noteworthy to mention that, unlike several previous studies, we have diligently ensured dimensional uniformity throughout the process of fractionalization.
The following is the outline of article: Section 2 explains the fractional calculus requirements for system analysis. Section 3 uses a CF framework to develop a fractional order model for breast cancer. Section 4 gives the Picard-Lindelof (PL) technique and the fixed-point theorem to investigate the existence and uniqueness of a proposed system. In Section 5, we numerically investigate the dynamics of the proposed model with variation in input parameters. Finally, final observations are offered in the concluding portion.
Definition 2.1. Let f∈H1(ι1,ι2) and 0<r<1, then the CF fractional derivative [49] is defined as follows:
| (cf0DrtN)(t)=P(r)1−r∫tι1N′(δ)exp[−r(t−δ)1−r]dδ, | (2.1) |
where P(r) is a normalizing function with the property that P(0)=P(1)=1.
Definition 2.2. [58] If 0<r<1, then the CF fractional integral of order r of a function N is:
| (cf0IrtN)(t)=2(1−r)(2−r)P(r)N(t)+2r(2−r)P(r)∫t0N(δ)dδ. | (2.2) |
Authors in [56] classified the breast cancer model into five epidemiological categories. During the initial medical report, the overall population of breast cancer patients was divided into phases 1 and 2 (S12), phase 3 (S3), phase 4 (S4), disease-free state (SR), and cardiotoxic (SE) subpopulations. The traditional system is described as:
| {dS12dt=Δ−(ρ+ν)S12,dS3dt=Γ+νS12+ψSR−(σ+μ+κ+χ)S3,dS4dt=Ω+μS3+ϕSR−(τ+ω+δ)S4,dSRdt=ρS12+σS3+τS4−(ψ+ϕ+ζ)SR,dSEdt=ζSR+ωS4+κS3−ηSE, | (3.1) |
where the following are the parameters of the system (3.1): Δ: people who have been diagnosed with cancer at stages 1 and 2; Γ: people suffering with stage 3 cancer; Ω: cancer patients in the fourth stage; ρ: chemotherapy recovery in phases 1 and 2; σ: chemotherapy recovery at stage 3; τ: chemotherapy recovery at stage 4; μ: people in worse health enter the stage 4 population; ν: people in worse health enroll in class S3; κ: patients undergoing severe treatment that induces cardiotoxicity; ω: people undergoing treatment for stage 4 cancer who suffer cardiotoxicity; ζ: at the disease-free stage, patients who have had extensive chemotherapy, which leads to cardiotoxicity; χ: cancer-related death at stage 3; δ: cancer-related death at stage 4; η: cardiotoxic patients' mortality rate; ψ: people who regress to stage 3; ϕ: people who regress to stage 4.
Now, to better approximate the spread of breast cancer with varying treatment rates into various compartments and to quantitatively demonstrate the influence of the above-mentioned parameters, the integer order model must be replaced by a fractional order model. The goal of this research is to extend the traditional system (3.1) by adding a fractional time derivative operator that allows for the analysis of memory effects in an arbitrary-order system. During the process of fractionalization, the dimensional consistency for each of the equations in the model has been maintained. We place the fractional order power r on each time-dimensional parameter to make the equal time dimension (time−r) on both sides of the model. The proposed breast cancer transmission model, which includes the CF derivative, is offered as:
| {cf0DrtS12=Δr−(ρr+νr)S12,cf0DrtS3=Γr+νrS12+ψrSR−(σr+μr+κr+χr)S3,cf0DrtS4=Ωr+μrS3+ϕrSR−(τr+ωr+δr)S4,cf0DrtSR=ρrS12+σrS3+τrS4−(ψr+ϕr+ζr)SR,cf0DrtSE=ζrSR+ωrS4+κrS3−ηrSE, | (3.2) |
with initial conditions: S12(0)=S120,S3(0)=S30,S4(0)=S40,SR(0)=SR0,SE(0)=SE0.
The present study aims to thoroughly examine the fractional system. The PL technique was used to investigate the presence and singularity of the offered solutions for the system (3.2). To begin the process, the system (3.2) is transformed into an integral equation with arbitrary order by applying (2.2) to both sides, resulting in
| {S12(t)−S12(0)=cfIrt{N1(t,S12)},S3(t)−S3(0)=cfIrt{N2(t,S3)},S4(t)−S4(0)=cfIrt{N3(t,S4)},SR(t)−SR(0)=cfIrt{N4(t,SR)},SE(t)−SE(0)=cfIrt{N5(t,SE)}, | (4.1) |
where
| N1(t,S12)=Δr−(ρr+νr)S12,N2(t,S3)=Γr+νrS12+ψrSR−(σr+μr+κr+χr)S3,N3(t,S4)=Ωr+μrS3+ϕrSR−(τr+ωr+δr)S4,N4(t,SR)=ρrS12+σrS3+τrS4−(ψr+ϕr+ζr)SR,N5(t,SE)=ζrSR+ωrS4+κrS3−ηrSE, |
are contractions with respect to the functions S12,S3,S4,SR, and SE, respectively. Applying (2.2) on (4.1), we obtain
| {S12(t)−S12(0)=Ω(r)N1(t,S12)+ω(r)∫t0N1(y,S12)dy,S3(t)−S3(0)=Ω(r)N2(t,S3)+ω(r)∫t0N2(y,S3)dy,S4(t)−S4(0)=Ω(r)N3(t,S4)+ω(r)∫t0N3(y,S4)dy,SR(t)−SR(0)=Ω(r)N4(t,SR)+ω(r)∫t0N4(y,SR)dy,SE(t)−SE(0)=Ω(r)N5(t,SE)+ω(r)∫t0N5(y,SE)dy, | (4.2) |
where
| Ω(r)=2(1−r)(2−r)P(r),ω(r)=2r(2−r)P(r). |
By Picard's iterative algorithm,
| {S12n+1(t)=Ω(r)N1(t,S12n)+ω(r)∫t0N1(y,S12n)dy,S3n+1(t)=Ω(r)N2(t,S3n)+ω(r)∫t0N2(y,S3n)dy,S4n+1(t)=Ω(r)N3(t,S4n)+ω(r)∫t0N3(y,S4n)dy,SRn+1(t)=Ω(r)N4(t,SRn)+ω(r)∫t0N4(y,SRn)dy,SEn+1(t)=Ω(r)N5(t,SEn)+ω(r)∫t0N5(y,SEn)dy. | (4.3) |
The solutions are achieved as follows:
| limn→∞S12n(t)=S12(t), limn→∞S3n(t)=S3(t), limn→∞S4n(t)=S4(t), limn→∞SRn(t)=SR(t), limn→∞SEn(t)=SE(t). |
To demonstrate the existence of the solution, we use the PL approach and the Banach fixed point theorem.
Let
| N∗1=supC[a,b1]‖ |
where
| \begin{align*} \mathbb {C}[a,b_1] & = [t-a, t+a]\times [\mathbb{S}_{12}-b_1, \mathbb{S}_{12}+b_1] = \mathbb{A} \times \mathbb {B}_1, \\ \mathbb {C}[a,b_2] & = [t-a, t+a]\times [\mathbb{S}_3-b_2, \mathbb{S}_3+b_2] = \mathbb{A} \times \mathbb {B}_2, \\ \mathbb {C}[a,b_3] & = [t-a, t+a]\times [{\mathbb{S}_{4}}-b_3, {\mathbb{S}_{4}}+b_3] = \mathbb{A} \times \mathbb {B}_3, \\ \mathbb {C}[a,b_4] & = [t-a, t+a]\times [{\mathbb{S}_{R}}-b_4, {\mathbb{S}_{R}}+b_4] = \mathbb{A} \times \mathbb {B}_4, \\ \mathbb {C}[a,b_5] & = [t-a, t+a]\times [{\mathbb{S}_{E}}-b_5, {\mathbb{S}_{E}}+b_5] = \mathbb{A} \times \mathbb {B}_5. \end{align*} |
Consider a uniform norm on \mathbb {C}[a, b_\iota], (\iota = 1, 2, 3, 4, 5) as given by
| \left \| U(t) \right \|_\infty = \sup\limits_{t \in [t-a,t+a]}\left | U(t) \right |. |
We define the Picard operator as:
| \triangle : \mathbb {C}(\mathbb{A},\mathbb {B}_1, \mathbb {B}_2, \mathbb {B}_3, \mathbb {B}_4, \mathbb {B}_5)\rightarrow \mathbb {C}(\mathbb{A},\mathbb {B}_1, \mathbb {B}_2, \mathbb {B}_3, \mathbb {B}_4, \mathbb {B}_5) |
described by
| \triangle (U(t)) = U_{0}(t) + \Omega(r) N(t, U(t)) + \omega (r) \int_{0}^{t} N(y,U(y))dy, |
where
| \begin{align*} \begin{aligned} U(t)& = \left\{\mathbb{S}_{12}(t), \mathbb{S}_3(t), {\mathbb{S}_{4}}(t), {\mathbb{S}_{R}}(t), {\mathbb{S}_{E}}(t)\right\},\\ U_0(t)& = \left\{ \mathbb{S}_{12}(0), \mathbb{S}_3(0), {\mathbb{S}_{4}}(0), {\mathbb{S}_{R}}(0), {\mathbb{S}_{E}}(0)\right\}, \\ N(t,U(t))& = \left\{ N_1(t,\mathbb{S}_{12}),N_2(t,\mathbb{S}_3),N_3(t,{\mathbb{S}_{4}}),N_4(t,{\mathbb{S}_{R}}),N_5(t,{\mathbb{S}_{E}}) \right\}.\end{aligned} \end{align*} |
We consider the solutions to the problem under examination are bounded within a time interval, that is,
| \left \| U(t) \right \|_\infty \leqslant max \left\{ b_1,b_2,b_3,b_4,b_5\right\} = b. |
Let
| N^{*} = max \left\{ N^{*}_1,N^{*}_2,N^{*}_3,N^{*}_4,N^{*}_5\right\}, |
and \exists t_0 , so t\leqslant t_0 , then
| \begin{align*} & \left \| \triangle U(t)-U_{0}(t) \right \| \\ & = \left \| \Omega(r)N(t,U(t))+\omega(r) \int_{0}^{t} N(y,U(y))dy \right \|\\ & \leqslant \Omega(r)\left \| N(t,U(t)) \right \|+\omega(r) \int_{0}^{t} \left \| N(y,U(y))\right \|dy \\ & \leqslant \left ( \Omega(r)+\omega(r)t \right )N^{*} \\ & \leqslant \left ( \Omega(r)+\omega(r)t_{0} \right )N^{*}\\ & \leqslant \mu^{*}N^{*} \\&\leqslant b, \end{align*} |
where
| \mu^{*} = \left ( \Omega(r)+\omega(r)t_{0} \right ) \leqslant \frac{b}{N^{*}}. |
Further, we prove the following equality:
| \left \| \triangle U_1 - \triangle U_2 \right \| = \sup\limits_{t \in \mathbb{A}} \left | U_1(t)-U_2(t) \right |. |
Using the Picard operator, we get
| \begin{align*} &\left \| \triangle U_1 - \triangle U_2 \right \|\\ & = \left \| \Omega(r) \left\{N(t,U_1(t)) -N(t,U_2(t))\right\} \right.\\ & \left . \quad +\omega(r) \int_{0}^{t} \left\{N(y,U_1(y))-N(y,U_2(y))\right\} dy \right \|\\ & \leqslant \Omega(r) \left \| N(t,U_1(t)) -N(t,U_2(t)) \right \| \\ &\quad +\omega(r) \int_{0}^{t}\left \| N(y,U_1(y))-N(y,U_2(y)) \right \| dy\\ & \leqslant \Omega(r) \gamma^{*} \left \| U_1(t) -U_2(t)\right \| +\omega(r) \gamma^{*}\int_{0}^{t}\left \|U_1(y)-U_2(y)\right \| dy\\ & \leqslant \left(\Omega(r)+\omega(r)t_{0}\right)\gamma^{*}\left \|U_1(y)-U_2(y)\right \| \\ & \leqslant \mu^{*} \gamma^{*}\left \|U_1(y)-U_2(y)\right \| \end{align*} |
with \gamma^{*} < 1. Since N is a contraction, then \mu^{*}\gamma^{*} < 1 , so the discussed operator \Delta is a contraction. Hence, system (3.2) has a unique solution.
In this section, we discuss the Ulam-Hyres (UH) stabiity (such as [59,60]) of the proposed fractional model (3.2) using the notion of nonlinear functional analysis. For the sake of simplicity we consider the proposed model (3.2) as:
| \begin{gather} \left\{\begin{array}{ll} {}^{\mathsf{cf}}_{0} D^{r}_{t} \mathbb{B}(t) = \Theta \left(t, \mathbb{B}(t)\right),\\ \quad \mathbb{B}(0) = \mathbb{B}_0 \geq 0, \end{array}\right. \end{gather} | (5.1) |
where
| \begin{align*} \mathbb{B}(t)& = \left(\mathbb{S}_{12}(t), \mathbb{S}_3(t), {\mathbb{S}_{4}}(t), {\mathbb{S}_{R}}(t), {\mathbb{S}_{E}}(t)\right)^{T},\\ \mathbb{B}_0& = \left(\mathbb{S}_{12_0},\mathbb{S}_{3_0}, {\mathbb{S}_{4_0}},{\mathbb{S}_{R_0}}, {\mathbb{S}_{E_0}}\right)^{T},\\ \Theta (t, \mathbb{B}(t))& = \left( N_1, N_2, N_3, N_4, N_5\right)^{T}. \end{align*} |
Applying fractional integral (2.2) on (5.1), we get
| \begin{equation} \mathbb{B}(t) = \mathbb{B}_{0} + \Omega(r) \Theta (t, \mathbb{B}(t)) + \omega (r) \int_{0}^{t} \Theta (\delta, \mathbb{B}(\delta))d\delta. \end{equation} | (5.2) |
Definition 5.1. The proposed system (3.2) is UH stable if \exists \overline{\mu} > 0 with the following property. For any \epsilon > 0 and \overline {\mathbb{B}} \in \mathsf{B} (Banach space), if
| \begin{equation} \left | {}^{\mathsf{cf}}_{0} D^{r}_{t} \overline{\mathbb{B}}(t) - \Theta \left(t, \overline{\mathbb{B}}(t)\right) \right |\leq \epsilon, \end{equation} | (5.3) |
then \exists \mathbb{B} \in \mathsf{B} satisfies system (3.2) with initial condition
| \mathbb{B}(0) = \overline{\mathbb{B}}(0) = \overline{\mathbb{B}}_0, |
such that
| \left \| \overline{\mathbb{B}}-\mathbb{B} \right \| \leq \overline{\mu}\epsilon. |
where
| \begin{gather*} \label{CFMP} \left\{\begin{array}{ll} \quad \overline{\mathbb{B}}(t) = \left(\overline{\mathbb{S}}_{12}(t), \overline{\mathbb{S}}_3(t), \overline{\mathbb{S}}_{4}(t), \overline{\mathbb{S}}_{R}(t), \overline{\mathbb{S}}_{E}(t)\right)^{T},\\ \quad \mathbb{B}_0 = \left( \overline{\mathbb{S}}_{12_0}, \overline{\mathbb{S}}_{3_0}, {\overline{\mathbb{S}}_{4_0}}, {\overline{\mathbb{S}}_{R_0}},{\overline{\mathbb{S}}_{E_0}}\right)^{T},\\ \Theta (t, \overline{\mathbb{B}}(t)) = \left(\overline{N}_1, \overline{N}_2, \overline{N}_3, \overline{N}_4, \overline{N}_5\right)^{T},\\ \quad \epsilon = max (\epsilon_{j})^T; \; \; \; j = 1,2,3,4,5, \\ \quad \overline{\mu} = max (\overline{\mu}_{j})^T;\; \; \; j = 1,2,3,4,5. \end{array}\right. \end{gather*} |
Remark 5.1. Consider a small perturbation k \in \mathsf{C}[0, \mathsf{T}] , such that k(0) = 0 along with the following property : \left | k(t) \right |\leq \overline{\epsilon } , for t \in [0, \mathsf{T}] and \overline{\epsilon} > 0 ,
Lemma 5.1. [10] The solution \overline{\mathbb{B}}_k(t) of the perturbed system
| \begin{align} {}^{\mathsf{cf}}_{0} D^{r}_{t} \overline{\mathbb{B}}(t) = \Theta \left(t, \overline{\mathbb{B}}(t)\right)+ k(t),\quad \overline{\mathbb{B}}(0) = \overline{\mathbb{B}}_{0}, \end{align} | (5.4) |
saisfies the relation:
| \left \| \overline{\mathbb{B}}_k(t)- \overline{\mathbb{B}}(t) \right\|\leq \Phi\overline{\epsilon}, |
where
| \begin{align*} \Phi & = \Omega (r)+\omega (r)T,\\ k(t) & = \left( k_1(t), k_2(t), k_3(t), k_4(t), k_5(t)\right)^T. \end{align*} |
Proof. Applying fractional integral (2.2) on (5.4), we get
| \begin{align} \overline{\mathbb{B}}_k(t) = & \overline{\mathbb{B}}_{0} + \Omega(r) \Theta \left(t, \overline{\mathbb{B}}(t)\right) + \omega (r) \int_{0}^{t} \Theta \left (\delta, \overline{\mathbb{B}}(\delta)\right)d\delta\\& + \Omega(r) k(t) + \omega (r) \int_{0}^{t} k(\delta) d\delta. \end{align} | (5.5) |
Also,
| \begin{align} \overline{\mathbb{B}}(t) & = \overline{\mathbb{B}}_{0} + \Omega(r) \Theta \left(t, \overline{\mathbb{B}}(t)\right) + \omega (r) \int_{0}^{t} \Theta \left (\delta, \overline{\mathbb{B}}(\delta)\right)d\delta. \end{align} | (5.6) |
Using Remark 5.1,
| \begin{align*} \left \| \overline{\mathbb{B}}_k(t)- \overline{\mathbb{B}}(t) \right \| &\leq \Omega(r) \left |k(t) \right| + \omega (r) \int_{0}^{t} \left |k(\delta) \right| d\delta \\ &\leq \left ( \Omega (r)+\omega (r)T \right)\overline{\epsilon} \\& = \Phi \overline{\epsilon}. \end{align*} |
This completes the proof.
Theorem 5.1. [10] The proposed fractional system (3.2) is UM stable if
| \left \| \overline{\mathbb{B}}(t)-\mathbb{B}(t) \right \| \leq \overline{\mu} \overline{\epsilon}. |
Proof. Let \overline{\mathbb{B}} be the solution of (5.3) and, due to uniqueness, \mathbb{B} be a unique solution of the system (5.1), then
| \begin{align*} \begin{aligned} \left\|\overline{\mathbb{B}}(t)- {\mathbb{B}}(t) \right\| \leq& \left\|\overline{\mathbb{B}}_h (t)- \overline{\mathbb{B}}(t) \right\| +\left\|\overline{\mathbb{B}}_h (t) - {\mathbb{B}}(t) \right\| \\ \leq& \Phi \overline{\epsilon}+\Omega(r) \left \| \Theta ( t,\overline{\mathbb{B}}(t)) - \Theta ( t,\mathbb{B}(t))\right\| \\ & +\omega (r) \int_{0}^{t} \left \| \Theta ( \delta,\overline{\mathbb{B}}(\delta)) - \Theta ( \delta,\mathbb{B}(\delta))\right\| d\delta + \Phi \overline{\epsilon}\\ \leq& 2 \Phi \overline{\epsilon} + \Phi \overline{\delta} \left \|\overline{\mathbb{B}}(t))-\mathbb{B}(t)) \right \|,\end{aligned} \end{align*} |
which implies that
| \left\|\overline{\mathbb{B}}(t)- {\mathbb{B}}(t) \right\|\leq \frac{2 \Phi \overline{\epsilon}}{1-\Phi \overline{\delta}} = \overline{\mu}\overline{\epsilon}, |
where
| \overline{\mu} = \frac{2 \Phi}{1-\Phi \overline{\delta}}. |
Hence, the considered fractional system (3.2) is UM stable.
The present part of the paper provides an approximate solution for the fractional order model (3.2) using two-step fractional Adams-Bashforth technique [37]. We discretized model (3.2) as follows:
| \begin{equation} \begin{aligned} {\mathbb{S}_{12}}_{\iota+1}& = {\mathbb{S}_{12}}_\iota + M_1(r) N_1(t_\iota,{\mathbb{S}_{12}}_\iota,{\mathbb{S}_3}_\iota,{\mathbb{S}_{4}}_\iota,{\mathbb{S}_{R}}_\iota,{\mathbb{S}_{E}}_\iota)- M_2(r)\\& \quad N_1(t_{\iota-1},{\mathbb{S}_{12}}_{\iota-1},{\mathbb{S}_3}_{\iota-1},{\mathbb{S}_{4}}_{\iota-1},{\mathbb{S}_{R}}_{\iota-1},{\mathbb{S}_{E}}_{\iota-1}),\\ {\mathbb{S}_3}_{\iota+1}& = {\mathbb{S}_3}_\iota + M_1(r) N_2(t_\iota,{\mathbb{S}_{12}}_\iota,{\mathbb{S}_3}_\iota,{\mathbb{S}_{4}}_\iota,{\mathbb{S}_{R}}_\iota,{\mathbb{S}_{E}}_\iota)- M_2(r) \\& \quad N_2(t_{\iota-1},{\mathbb{S}_{12}}_{\iota-1},{\mathbb{S}_3}_{\iota-1},{\mathbb{S}_{4}}_{\iota-1},{\mathbb{S}_{R}}_{\iota-1},{\mathbb{S}_{E}}_{\iota-1}),\\ {\mathbb{S}_{4}}_{\iota+1}& = {\mathbb{S}_{4}}_\iota + M_1(r) N_3(t_\iota,{\mathbb{S}_{12}}_\iota,{\mathbb{S}_3}_\iota,{\mathbb{S}_{4}}_\iota,{\mathbb{S}_{R}}_\iota,{\mathbb{S}_{E}}_\iota)- M_2(r) \\& \quad N_3(t_{\iota-1},{\mathbb{S}_{12}}_{\iota-1},{\mathbb{S}_3}_{\iota-1},{\mathbb{S}_{4}}_{\iota-1},{\mathbb{S}_{R}}_{\iota-1},{\mathbb{S}_{E}}_{\iota-1}),\\ {\mathbb{S}_{R}}_{\iota+1}& = {\mathbb{S}_{R}}_\iota + M_1(r) N_4(t_\iota,{\mathbb{S}_{12}}_\iota,{\mathbb{S}_3}_\iota,{\mathbb{S}_{4}}_\iota,{\mathbb{S}_{R}}_\iota,{\mathbb{S}_{E}}_\iota)- M_2(r)\\& \quad N_4(t_{\iota-1},{\mathbb{S}_{12}}_{\iota-1},{\mathbb{S}_3}_{\iota-1},{\mathbb{S}_{4}}_{\iota-1},{\mathbb{S}_{R}}_{\iota-1},{\mathbb{S}_{E}}_{\iota-1}),\\ {\mathbb{S}_{E}}_{\iota+1}& = {\mathbb{S}_{E}}_\iota + M_1(r) N_5(t_\iota,{\mathbb{S}_{12}}_\iota,{\mathbb{S}_3}_\iota,{\mathbb{S}_{4}}_\iota,{\mathbb{S}_{R}}_\iota,{\mathbb{S}_{E}}_\iota)- M_2(r)\\& \quad N_5(t_{\iota-1},{\mathbb{S}_{12}}_{\iota-1},{\mathbb{S}_3}_{\iota-1},{\mathbb{S}_{4}}_{\iota-1},{\mathbb{S}_{R}}_{\iota-1},{\mathbb{S}_{E}}_{\iota-1}),\\ \end{aligned} \end{equation} | (6.1) |
where
| M_1(r) = \left(\frac{1-r}{P(r)}+\frac{3rh}{2P(r)}\right) |
and
| M_2(r) = \left(\frac{1-r}{P(r)}+\frac{rh}{2P(r)}\right). |
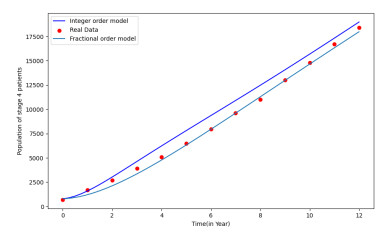
The dynamical behavior of the proposed fractional system (3.2) is investigated numerically using (6.1) for the approximate solution of the state variables {\mathbb{S}_{12}}(t), \mathbb{S}_3(t), {\mathbb{S}_{4}}(t), {\mathbb{S}_{R}}(t) , and {\mathbb{S}_{E}}(t) in (3.2). We take the initial values as {\mathbb{S}_{12}}(0) = 30000, \ \mathbb{S}_3(0) = 12300, \ {\mathbb{S}_{4}}(0) = 783, \ {\mathbb{S}_{R}}(0) = 334, \ {\mathbb{S}_{E}}(0) = 10 and parameters values: \Delta = 14000, \ \Gamma = 80, \ \Omega = 90, \ \mu = 0.01, \ \nu = 0.034, \ \psi = 0.03, \ \phi = 0.3, \ \omega = 0.1, \ \zeta = 0.2, \ \chi = \delta = \eta = 0.0256 [56], \rho = 0.149 (fitted), \ \kappa = 0.09 (fitted), \ \sigma = 0.47 (fitted) , and \tau = 0.01(fitted) , as fitted with real data. In Figure 1, we used real data [57] from Kingdom of Saudi Arabia from 2004 to 2016 to fit the classical model (3.1) and the suggested fractional order model (3.2). This demonstrates that the fractional model better matches the actual data and may be used to forecast future instances than the classical model. Figure 2 shows a long-term estimate of the cases based on a fractional model. Here, we can see from Figure 2 that the data fits the model curve well, and we can also see that the number of long-term behavior cases grows in an exponential way over time. This case could be scary because the number of cases could go up even more in the next few years if the health department does not use the right treatment methods to get rid of breast cancer.
Figures 3–7 show how the model compartments change over time ( t = 50 years) as the fractional-order r varies for each compartment. We discovered that the memory index r has a significant impact on the breast cancer model's solution route, and that controlling r gives us a lot of control over the way breast cancer behaves in all subgroups. Figures 8–11 show the solution of the proposed CF model while adjusting the input parameter \kappa . We found that raising this quantity makes fewer people get cancer in stage 3, stage 4, and disease-free states, implying that the cancer mortality rate would be reduced. However, increasing \kappa increases the number of people who are cardiotoxic, increasing the risk of cardiac mortality.
The diagram shown in Figures 12–14 illustrates the effects of rigorous chemotherapy on patients diagnosed with stage 4. This treatment approach has been found to potentially contribute to higher rates of morbidity and death within the population, particularly among those who experience cardiotoxicity. By intensifying the administration of chemotherapy to individuals in phase 4, populations with disease-free status, and those experiencing cardiotoxicity, it becomes evident that stage 4 and disease-free individuals exhibit significant improvements in disease reduction. However, the same level of improvement is not observed in individuals with cardiotoxicity. The adverse effects of chemotherapy have been shown to significantly increase the risk of developing cardiovascular complications in individuals. The simulations provide a visual representation of the parameters' functions, facilitating comprehension of strategies to reduce cancer and cardiac mortality rates in cancer patient healthcare facilities.
Figures 15–18 depict the simulation of the model compartment in the disease-free condition with intense treatment. The findings show a little rise in the cardiotoxicity population, whereas there are minor reductions in the population of phases 3, 4, and the disease-free state. Figure 15 shows that there is minimal improvement in the decline of instances in phase 3 sufferers. Figure 16 shows a significant decrease in cases among phase 4 patients. Figure 17 shows a significant drop in the number of patients in the disease-free state, but Figure 18 shows a modest rise in the number of instances of cardiotoxicity. The CF operator demonstrates a 66.64% improvement in the accuracy of estimating actual data compared to the classical order model as determined by
| \begin{align*} \begin{aligned} \frac{\text{classical model norm - fractional model norm}}{\text{classical model norm}} & = \frac{11045.11902 -3685 }{11045.11902 }\\& = 0.6664.\end{aligned} \end{align*} |
We developed a mathematical model in a fractional framework for breast cancer in this research to study the impact of treatment at various phases, incorporating the CF derivative and various chemotherapy rates. The PL technique is established for the system's existence and uniqueness. We have constructed some results for UH stability and have shown that our proposed model is UH stable. The numerical simulations supported our approach using the two-step AB algorithm. Through graphical representations, we illustrated the impact of fractional order and the effect of chemotherapy rates on breast cancer dynamics. Using real incidence data, the CF operator demonstrates a 66.64% improvement in the accuracy of estimating actual data compared to the classical order model. Notably, we identified effective parameters ( \kappa, \omega , and \zeta ) associated with reduced occurrences of stages 3 and 4 as well as disease-free states in breast cancer modeling. Our results emphasized the increased risk of cardiotoxicity linked with chemotherapy, indicating that pretreatment may be beneficial in mitigating such risks. Our research seeks to reduce cardiotoxicity prevalence among chemotherapy patients and improve their recovery rates, with implications for public health decision-making. Furthermore, by elucidating breast cancer mechanisms through the CF operator, our study paves the way for targeted therapies to minimize cardiotoxicity, thereby improving patient outcomes and guiding future breast cancer treatment strategies. In future work, we want to leverage our actual data-oriented estimated parameter values to anticipate breast cancer patients utilizing various models and fractional derivative operators. Using the provided data, certain optimal controls may also be added in the same model.
The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.
We thank the editors and the referees for their valuable comments.
All authors confirm that they have no competing interests related to this article.
| [1] |
C. Fitzmaurice, D. Dicker, A. Pain, H. Hamavid, M. Moradi-Lakeh, M. F. MacIntyre, et al., The global burden of cancer 2013, JAMA Oncol., 1 (2015), 505–527. https://doi.org/10.1001/jamaoncol.2015.0735 doi: 10.1001/jamaoncol.2015.0735

|
| [2] |
I. Vasiliadis, G. Kolovou, D. P. Mikhailidis, Cardiotoxicity and cancer therapy, Angiology, 65 (2014), 369–371. https://doi.org/10.1177/0003319713498298 doi: 10.1177/0003319713498298

|
| [3] | I. Podlubny, Fractional differential equations, Academic Press, 1999. |
| [4] | K. M. Owolabi, A Atangana, Mathematical modelling and analysis of fractional epidemic models using derivative with exponential kernel, CRC Press, 2020. |
| [5] |
S. R. Khirsariya, J. P. Chauhan, G. S. Hathiwala, Study of fractional diabetes model with and without complication class, Results Control Optim., 12 (2023), 100283. https://doi.org/10.1016/j.rico.2023.100283 doi: 10.1016/j.rico.2023.100283

|
| [6] |
S. R. Khirsariya, S. B. Rao, G. S. Hathiwala, Investigation of fractional diabetes model involving glucose-insulin alliance scheme, Int. J. Dyn. Control, 12 (2023), 1–14. https://doi.org/10.1007/s40435-023-01293-4 doi: 10.1007/s40435-023-01293-4

|
| [7] |
J. E. Solís-Pérez, J. F. Gómez-Aguilar, A. Atangana, A fractional mathematical model of breast cancer competition model, Chaos Solitions Fract., 127 (2019), 38–54. https://doi.org/10.1016/j.chaos.2019.06.027 doi: 10.1016/j.chaos.2019.06.027

|
| [8] |
M. Farman, M. Batool, K. S. Nisar, A. S. Ghaffari, A. Ahmad, Controllability and analysis of sustainable approach for cancer treatment with chemotherapy by using the fractional operator, Results Phys., 51 (2023), 106630. https://doi.org/10.1016/j.rinp.2023.106630 doi: 10.1016/j.rinp.2023.106630

|
| [9] |
C. Xu, M. Farman, A. Akgül, K. S. Nisar, A. Ahmad, Modeling and analysis fractal order cancer model with effects of chemotherapy, Chaos Solitons Fract., 161 (2022), 112325. https://doi.org/10.1016/j.chaos.2022.112325 doi: 10.1016/j.chaos.2022.112325

|
| [10] |
S. Kumar, R. P. Chauhan, A. H. Abdel-Aty, M. R. Alharthi, A study on transmission dynamics of HIV/AIDS model through fractional operators, Results Phys., 22 (2021), 103855. https://doi.org/10.1016/j.rinp.2021.103855 doi: 10.1016/j.rinp.2021.103855

|
| [11] |
S. Kumar, R. P. Chauhan, M. S. Osman, S. A. Mohiuddine, A study on fractional HIV-AIDs transmission model with awareness effect, Math. Methods Appl. Sci., 46 (2023), 8334–8348. https://doi.org/10.1002/mma.7838 doi: 10.1002/mma.7838

|
| [12] |
Z. Munawar, F. Ahmad, S. A. Alanazi, K. S. Nisar, M. Khalid, M. Anwar, et al., Predicting the prevalence of lung cancer using feature transformation techniques, Egypt. Inf. J., 23 (2022), 109–120. https://doi.org/10.1016/j.eij.2022.08.002 doi: 10.1016/j.eij.2022.08.002

|
| [13] |
S. T. Thabet, M. S. Abdo, K. Shah, Theoretical and numerical analysis for transmission dynamics of Covid-19 mathematical model involving Caputo-Fabrizio derivative, Adv. Differ. Equations, 1 (2021), 184. https://doi.org/10.1186/s13662-021-03316-w doi: 10.1186/s13662-021-03316-w

|
| [14] |
S. T. Thabet, M. S. Abdo, K. Shah, T. Abdeljawad, Study of transmission dynamics of Covid-19 mathematical model under ABC fractional order derivative, Results Phys., 19 (2020), 103507. https://doi.org/10.1016/j.rinp.2020.103507 doi: 10.1016/j.rinp.2020.103507

|
| [15] |
M. Farman, H. Besbes, K. S. Nisar, M. Omri, Analysis and dynamical transmission of Covid-19 model by using Caputo-Fabrizio derivative, Alex. Eng. J., 66 (2023), 597–606. https://doi.org/10.1016/j.aej.2022.12.026 doi: 10.1016/j.aej.2022.12.026

|
| [16] |
W. Ou, C. Xu, Q. Cui, Z. Liu, Y. Pang, M. Farman, et al., Mathematical study on bifurcation dynamics and control mechanism of tri-neuron BAM neural networks including delay, Math. Methods Appl. Sci., 2023. https://doi.org/10.1002/mma.9347 doi: 10.1002/mma.9347

|
| [17] |
C. Xu, D. Mu, Y. Pan, C. Aouiti, L. Yao, Exploring bifurcation in a fractional-order predator-prey system with mixed delays, J. Appl. Anal. Comput., 13 (2023), 1119–1136. https://doi.org/10.11948/20210313 doi: 10.11948/20210313

|
| [18] |
C. Xu, X. Cui, P. Li, J. Yan, L. Yao, Exploration on dynamics in a discrete predator-prey competitive model involving feedback controls, J. Biol. Dyn., 17 (2023), 2220349. https://doi.org/10.1080/17513758.2023.2220349 doi: 10.1080/17513758.2023.2220349

|
| [19] |
C. Xu, Q. Cui, Z. Liu, Y. Pan, X. Cui, W. Ou, et al., Extended hybrid controller design of bifurcation in a delayed chemostat model, Match Commun. Math. Comput. Chem., 90 (2023), 609–648. https://doi.org/10.46793/match.90-3.609X doi: 10.46793/match.90-3.609X

|
| [20] |
C. Xu, D. Mu, Z. Liu, Y. Pang, C. Aouiti, O. Tunc, et al., Bifurcation dynamics and control mechanism of a fractional-order delayed Brusselator chemical reaction model, Match Commun. Math. Comput. Chem., 89 (2023), 73–106. https://doi.org/10.46793/match.89-1.073x doi: 10.46793/match.89-1.073x

|
| [21] |
D. Mu, C. Xu, Z. Liu, Y. Pang, Further insight into bifurcation and hybrid control tactics of a chlorine dioxide-iodine-malonic acid chemical reaction model incorporating delays, Match Commun. Math. Comput. Chem., 89 (2023), 529–566. https://doi.org/10.46793/match.89-3.529M doi: 10.46793/match.89-3.529M

|
| [22] |
M. I. Ayari, S. T. Thabet, Qualitative properties and approximate solutions of thermostat fractional dynamics system via a nonsingular kernel operator, Arab J. Math. Sci., 2023. https://doi.org/10.1108/AJMS-06-2022-0147 doi: 10.1108/AJMS-06-2022-0147

|
| [23] |
S. Djennadi, N. Shawagfeh, M. Inc, M. S. Osman, J. F. Gómez-Aguilar, O. A. Arqub, The Tikhonov regularization method for the inverse source problem of time fractional heat equation in the view of ABC-fractional technique, Phys. Scr., 96 (2021), 094006. https://doi.org/10.1088/1402-4896/ac0867 doi: 10.1088/1402-4896/ac0867

|
| [24] |
A. Khalid, A. Rehan, K. S. Nisar, M. S. Osman, Splines solutions of boundary value problems that arises in sculpturing electrical process of motors with two rotating mechanism circuit, Phys. Scr., 96 (2021), 104001. https://doi.org/10.1088/1402-4896/ac0bd0 doi: 10.1088/1402-4896/ac0bd0

|
| [25] |
S. W. Yao, O. A. Arqub, S. Tayebi, M. S. Osman, W. Mahmoud, M. Inc, et al., A novel collective algorithm using cubic uniform spline and finite difference approaches to solving fractional diffusion singular wave model through damping-reaction forces, Fractals, 31 (2023), 2340069. https://doi.org/10.1142/S0218348X23400698 doi: 10.1142/S0218348X23400698

|
| [26] |
Z. A. Khan, S. U. Haq, T. S. Khan, I. Khan, K. S. Nisar, Fractional Brinkman type fluid in channel under the effect of MHD with Caputo-Fabrizio fractional derivative, Alex. Eng. J., 59 (2020), 2901–2910. https://doi.org/10.1016/j.aej.2020.01.056 doi: 10.1016/j.aej.2020.01.056

|
| [27] |
J. P. Chauhan, S. R. Khirsariya, G. S. Hathiwala, M. B. Hathiwala, New analytical technique to solve fractional-order Sharma-Tasso-Olver differential equation using Caputo and Atangana-Baleanu derivative operators, J. Appl. Anal. Anal., 2023. https://doi.org/10.1515/jaa-2023-0043 doi: 10.1515/jaa-2023-0043

|
| [28] |
S. T. Thabet, M. Vivas-Cortez, I. Kedim, Analytical study of \mathcal ABC -fractional pantograph implicit differential equation with respect to another function, AIMS Math., 8 (2023), 23635–23654. https://doi.org/10.3934/math.20231202 doi: 10.3934/math.20231202

|
| [29] |
S. W. Yao, S. Behera, M. Inc, H. Rezazadeh, J. P. S. Virdi, W. Mahmoud, et al., Analytical solutions of conformable Drinfel'd-Sokolov-Wilson and Boiti Leon Pempinelli equations via sine-cosine method, Results Phys., 42 (2022), 105990. https://doi.org/10.1016/j.rinp.2022.105990 doi: 10.1016/j.rinp.2022.105990

|
| [30] |
J. P. Chauhan, S. R. Khirsariya, A semi-analytic method to solve nonlinear differential equations with arbitrary order, Results Control Optim., 13 (2023), 100267. https://doi.org/10.1016/j.rico.2023.100267 doi: 10.1016/j.rico.2023.100267

|
| [31] |
S. R. Khirsariya, S. B. Rao, J. P. Chauhan, Semi-analytic solution of time-fractional korteweg-de vries equation using fractional residual power series method, Results Nonlinear Anal., 5 (2022), 222–234. https://doi.org/10.53006/rna.1024308 doi: 10.53006/rna.1024308

|
| [32] |
S. R. Khirsariya, S. B. Rao, J. P. Chauhan, A novel hybrid technique to obtain the solution of generalized fractional-order differential equations, Math. Comput. Simul., 205 (2023), 272–290. https://doi.org/10.1016/j.matcom.2022.10.013 doi: 10.1016/j.matcom.2022.10.013

|
| [33] |
S. R. Khirsariya, S. B. Rao, On the semi-analytic technique to deal with nonlinear fractional differential equations, J. Appl. Math. Comput. Mech., 22 (2023), 17–30. https://doi.org/10.17512/jamcm.2023.1.02 doi: 10.17512/jamcm.2023.1.02

|
| [34] |
S. Rashid, K. T. Kubra, S. Sultana, P. Agarwal, M. S. Osman, An approximate analytical view of physical and biological models in the setting of Caputo operator via Elzaki transform decomposition method, J. Comput. Appl. Math., 413 (2022), 114378. https://doi.org/10.1016/j.cam.2022.114378 doi: 10.1016/j.cam.2022.114378

|
| [35] |
L. Shi, S. Rashid, S. Sultana, A. Khalid, P. Agarwal, M. S. Osman, Semi-analytical view of time-fractional PDES with proportional delays pertaining to index and Mittag-Leffler memory interacting with hybrid transforms, Fractals, 31 (2023), 2340071. https://doi.org/10.1142/S0218348X23400716 doi: 10.1142/S0218348X23400716

|
| [36] |
P. Li, Y. Lu, C. Xu, J. Ren, Insight into Hopf bifurcation and control methods in fractional order BAM neural networks incorporating symmetric structure and delay, Cogn. Comput., 15 (2023), 1825–1867. https://doi.org/10.1007/s12559-023-10155-2 doi: 10.1007/s12559-023-10155-2

|
| [37] |
A. Atangana, K. M. Owolabi, New numerical approach for fractional differential equations, Math. Modell. Natural Phenom., 13 (2018), 3. https://doi.org/10.1051/mmnp/2018010 doi: 10.1051/mmnp/2018010

|
| [38] |
K. K. Ali, M. A. A. E. Salam, E. M. Mohamed, B. Samet, S. Kumar, M. S. Osman, Numerical solution for generalized nonlinear fractional integro-differential equations with linear functional arguments using Chebyshev series, Adv. Differ. Equations, 2020 (2020), 494. https://doi.org/10.1186/s13662-020-02951-z doi: 10.1186/s13662-020-02951-z

|
| [39] |
O. A. Arqub, S. Tayebi, D. Baleanu, M. S. Osman, W. Mahmoud, H. Alsulami, A numerical combined algorithm in cubic B-spline method and finite difference technique for the time-fractional nonlinear diffusion wave equation with reaction and damping terms, Results Phys., 41 (2022), 105912. https://doi.org/10.1016/j.rinp.2022.105912 doi: 10.1016/j.rinp.2022.105912

|
| [40] |
L. Shi, S. Tayebi, O. A. Arqub, M. S. Osman, P. Agarwal, W. Mahamoud, et al., The novel cubic B-spline method for fractional Painleve and Bagley-Trovik equations in the Caputo, Caputo-Fabrizio, and conformable fractional sense, Alex. Eng. J., 65 (2023), 413–426. https://doi.org/10.1016/j.aej.2022.09.039 doi: 10.1016/j.aej.2022.09.039

|
| [41] |
S. Qureshi, M. A. Akanbi, A. A. Shaikh, A. S. Wusu, O. M. Ogunlaran, W. Mahmoud, et al., A new adaptive nonlinear numerical method for singular and stiff differential problems, Alexandria Eng. J., 74 (2023), 585–597. https://doi.org/10.1016/j.aej.2023.05.055 doi: 10.1016/j.aej.2023.05.055

|
| [42] |
S. R. Khirsariya, S. B. Rao, Solution of fractional Sawada-Kotera-Ito equation using Caputo and Atangana-Baleanu derivatives, Math. Methods Appl. Sci., 46 (2023), 16072–16091. https://doi.org/10.1002/mma.9438 doi: 10.1002/mma.9438

|
| [43] |
S. R. Khirsariya, J. P. Chauhan, S. B. Rao, A robust computational analysis of residual power series involving general transform to solve fractional differential equations, Math. Comput. Simul, 216 (2023), 168–186. https://doi.org/10.1016/j.matcom.2023.09.007 doi: 10.1016/j.matcom.2023.09.007

|
| [44] |
T. Abdeljawad, S. T. Thabet, I. Kedim, M. I. Ayari, A. Khan, A higher-order extension of Atangana-Baleanu fractional operators with respect to another function and a Gronwall-type inequality, Bound. Value Probl., 2023 (2023), 49. https://doi.org/10.1186/s13661-023-01736-z doi: 10.1186/s13661-023-01736-z

|
| [45] |
S. T. Thabet, M. M. Matar, M. A. Salman, M. E. Samei, M. Vivas-Cortez, I. Kedim, On coupled snap system with integral boundary conditions in the G-Caputo sense, AIMS Math., 8 (2023), 12576–12605. https://doi.org/10.3934/math.2023632 doi: 10.3934/math.2023632

|
| [46] |
S. Thabet, I. Kedim, Study of nonlocal multiorder implicit differential equation involving Hilfer fractional derivative on unbounded domains, J. Math., 2023 (2023), 8668325. https://doi.org/10.1155/2023/8668325 doi: 10.1155/2023/8668325

|
| [47] |
S.Qureshi, A. Soomro, E. Hincal, J. R. Lee, C. Park, M. S. Osman, An efficient variable stepsize rational method for stiff, singular and singularly perturbed problems, Alex. Eng. J., 61 (2022), 10953–10963. https://doi.org/10.1016/j.aej.2022.03.014 doi: 10.1016/j.aej.2022.03.014

|
| [48] |
O. A. Arqub, M. S. Osman, C. Park, J. R. Lee, H. Alsulami, M. Alhodaly, Development of the reproducing kernel Hilbert space algorithm for numerical pointwise solution of the time-fractional nonlocal reaction-diffusion equation, Alex. Eng. J., 61 (2022), 10539–10550. https://doi.org/10.1016/j.aej.2022.04.008 doi: 10.1016/j.aej.2022.04.008

|
| [49] | M. Caputo, M. Fabrizio, New numerical approach for fractional differential equations, Progr. Fract. Differ. Appl., 1 (2015), 73–85. |
| [50] |
D. Baleanu, A. Jajarmi, H. Mohammad, S. Rezapour, A new study on the mathematical modelling of human liver with Caputo-Fabrizio fractional derivative, Chaos Solitons Fract., 134 (2020), 109705. https://doi.org/10.1016/j.chaos.2020.109705 doi: 10.1016/j.chaos.2020.109705

|
| [51] |
S. Ullah, M. A. Khan, M. Farooq, Z. Hammouch, D. Baleanu, A fractional model for the dynamics of tuberculosis infection using Caputo-Fabrizio derivative, Discrete Contin. Dyn. Syst., 13 (2020), 975–993. https://doi.org/10.3934/dcdss.2020057 doi: 10.3934/dcdss.2020057

|
| [52] |
M. A. Dokuyucu, E. Celik, H. Bulut, H. M. Baskonus, Cancer treatment model with the Caputo-Fabrizio fractional derivative, Eur. Phys. J. Plus, 133 (2018), 92. https://doi.org/10.1140/epjp/i2018-11950-y doi: 10.1140/epjp/i2018-11950-y

|
| [53] |
M. M. El-Dessoky, M. A. Khan, Application of Caputo- Fabrizio derivative to a cancer model with unknown parameters, Discrete Contin. Dyn. Syst., 14 (2021), 3557–3575. https://doi.org/10.3934/dcdss.2020429 doi: 10.3934/dcdss.2020429

|
| [54] |
M. Ngungu, E. Addai, A. Adeniji, U. M. Adam, K. Oshinubi, Mathematical epidemiological modeling and analysis of monkeypox dynamism with non-pharmaceutical intervention using real data from United Kingdom, Front. Public Health, 11 (2023), 1101436 https://doi.org/10.3389/fpubh.2023.1101436 doi: 10.3389/fpubh.2023.1101436

|
| [55] |
A. Yousef, F. Bozkurt, T. Abdeljawad, Mathematical modeling of the immune-chemotherapeutic treatment of breast cancer under some control parameters, Adv. Differ. Equations, 2020 (2020), 696. https://doi.org/10.1186/s13662-020-03151-5 doi: 10.1186/s13662-020-03151-5

|
| [56] |
E. Alzahrani, M. M. El-Dessoky, M. A. Khan, Mathematical model to understand the dynamics of cancer, prevention diagnosis and therapy, Mathematics, 11 (2023), 1975. https://doi.org/10.3390/math11091975 doi: 10.3390/math11091975

|
| [57] |
S. M. Albeshan, Y. I. Alashban, Incidence trends of breast cancer in Saudi Arabia: a joinpoint regression analysis (2004–2016), J. King Saud Univ. Sci., 33 (2021), 101578. https://doi.org/10.1016/j.jksus.2021.101578 doi: 10.1016/j.jksus.2021.101578

|
| [58] | J. Losada, J. J. Nieto, Properties of a new fractional derivative without singular kernel, Progr. Fract. Differ. Appl., 1 (2015), 87–92. https://doi.org/12785/pfda/010202 |
| [59] | S. M. Ulam, Problems in modern mathematics, Dover Publications, 2004. |
| [60] | S. M. Ulam, A collection of mathematical problems, Interscience Publishers, 1960. |
| 1. | Anil Chavada, Nimisha Pathak, Sagar R. Khirsariya, Fractional‐order modeling of Chikungunya virus transmission dynamics, 2024, 0170-4214, 10.1002/mma.10372 | |
| 2. | Parveen Kumar, Sunil Kumar, Badr Saad T Alkahtani, Sara S Alzaid, A mathematical model for simulating the spread of infectious disease using the Caputo-Fabrizio fractional-order operator, 2024, 9, 2473-6988, 30864, 10.3934/math.20241490 | |
| 3. | Twinkle R Singh, A novel analytical iterative approach to time-fractional Vibration equation using Aboodh transform, 2025, 100, 0031-8949, 015296, 10.1088/1402-4896/ad9e4c | |
| 4. | A. M. Alqahtani, Shivani Sharma, Arun Chaudhary, Aditya Sharma, Application of Caputo-Fabrizio derivative in circuit realization, 2025, 10, 2473-6988, 2415, 10.3934/math.2025113 | |
| 5. | Akanksha Singh, Anil Chavada, Nimisha Pathak, Fractional Calculus Approach to Pancreatic Cancer Therapy: Modeling Tumor and Immune Interactions with siRNA Treatment, 2025, 11, 2349-5103, 10.1007/s40819-025-01873-2 |