A double time-delay Holling Ⅱ predation model with weak Allee effect and age-structure

1.   Introduction

This paper considers the following double-time-delay Holling Ⅱ predation model with weak Allee effect and age-structure:

The boundary conditions are

Here, $V\left(t \right)$ and $p\left({t, a} \right)$ represent the number of predator densities at time $t$ and age $a$, $\gamma$ is the rate of prey' intrinsic growth, and $\Lambda = \gamma + \mu$, where $\Lambda$ is the birth and $\mu$ is the mortality rate of the prey. $K$ indicates the maximum environmental load of prey, while $\sigma$ and $\eta$ indicate the predator mortality rate and the conversion coefficient of predator intake to each prey. In addition, ${\tau _1}$ is the time delay effect, and $0 < m < K$ indicates the survival threshold of the food bait in the weak Allee effect. Meanwhile $F\left({V\left(t \right)} \right) = \frac{{\alpha V\left(t \right)}}{{\beta + V\left(t \right)}}$ represents the Holling Ⅱ functional reaction function, where $\alpha$ represents the capture rate and $\beta$ is a semi-saturated constant. In addition, the reproductive generation of species in the ecosystem generally takes some time to mature to have fertility, i.e., "age-dependent fertility". Fertility $\delta \left(a \right) \in L_ + ^\infty \left({\left({0, + \infty } \right), A} \right)$ depends on age, for which it is often assumed that:

Assumption 1.1. Suppose that

where ${\tau _2} > 0, {\delta _*} > 0$, and$\int_0^{ + \infty } {\delta \left(a \right){e^{ - \sigma a}}da} = 1$.

It is well known that there is a long history of mathematical modeling of the interactions between predators and bait, and that different biological properties are considered in classical models, thus developing various types of predation models. Besides, there is growing evidence that functional responses play a crucial role in the interaction between predators and prey. The Gauss predation math model is given as

where, $V(t)$ indicates the species density of the prey at time $t$, and $P(t)$ indicates the species number of predators at time $t$. The normal constants $K$ and $\gamma$ denote the environmental capacity and inherent growth rate, respectively. $d$ and $\eta$ denote the predator mortality and the conversion coefficient of predator intake to each prey, respectively. The functional reaction function $F(x)$ indicates the feeding rate of predators feeding on their prey.

For functional reaction functions, the earliest function form is the Lotka-Volterra type functional response $F(x) = \alpha x$. This was followed by Holling Ⅱ: $F\left(x \right) = \frac{{\alpha x}}{{\beta + x}}$, Holling Ⅲ: $F\left(x \right) = \frac{{\alpha {x^2}}}{{\beta + {x^2}}}$, Holling Ⅳ: $F\left(x \right) = \frac{{\alpha {x^2}}}{{\beta + x}}$, and Ivlev-type: $F\left(x \right) = 1 - {e^{ - \alpha x}}$. For example, a class of Leslie-Gower and Holling Ⅱ predator models are proposed in ^[1], which gives the global stability of the bounds of understanding, the existence of attracting sets, and the equilibrium points of coexistence:

However, in the real biological world, due to food digestion, reproduction, and other reasons, organisms need reaction time, so the time delay effect is a very important factor in many biological systems. In recent years, many researchers have studied the stability of predation models with time delay, and time delay systems, such as ^{[2,3,4,5,6,7]}.

At the same time, recent literature has done extensive analysis of predator-prey models of age structure, see ^[8,9,10]. To study age structure models, a common method is to convert the original model to a time delay differential equation, such as ^[11]. Another critical method is to turn it into an abstract Cauchy problem, thus applying semi-group theory (^[12,13]). In ^[8], Yang proposed a class of age-structure predation models containing the functional response of the Holling Ⅱ with a prey refuge:

and obtained the Hopf bifurcation of the model at the internal equilibrium point, indicating that the model has a special periodic orbit that bifurcations from the internal equilibrium point when the parameter $\tau$ exceeds the bifurcation threshold ${\tau _0}$. The validity of the theoretical analysis is verified by numerical simulation.

In recent years, the Allee effect in predator-prey models has also been widely studied ^{[14,15,16,17]}. The Allee effect is defined as the relationship between population size and fitness. In a predator-prey model, the impact of the Allee effect on logistic growth is expressed by including an $V-m$ form multiplier, where $m$ is the Allee threshold. The Allee effect is broadly divided into two categories: the strong Allee effect and the weak Allee effect ^[18]. The strong Allee effect indicates negative population growth when the population size is below a certain threshold. In contrast, the weak Allee effect indicates a positive population growth trend below a certain threshold. In ^[16], the author considered a kind of generalized Holling Ⅲ-type functional reaction, predation model with weak Allee effect, and explored the existence conditions of model equilibrium and singularity, as well as some properties of equilibrium stability:

Inspired by the above work, in this paper we will study the dynamical behavior of the predation model (1.1) of the double time-delay Holling Ⅱ functional response function with weak Allee effect and age structure.

The organization plan for this article is as follows: In Section 2, the transformation of Cauchy's problem is given, and the system well-posedness is obtained. In Section 3, the equilibrium solution of the system is studied, and the linearized system is obtained. In Section 4, the dynamical behavior of the system is studied. In Section 5, some numerical simulations and discussions are conducted.

2.   Well-posedness

First we normalize ${\tau _{\rm{2}}}$ in the system (1.1), which gives

and we consider the distribution

After the wave is removed, system (1.1) becomes

where

The new function $\delta \left(a \right)$ is

and

i.e., ${\delta _*} = \sigma {e^{ - \sigma {\tau _2}}}, ({\tau _2} > 0)$.

Based on the integral semigroup theory, the suitability of the solution of system (2.1) is discussed below. For this purpose, (2.1) will be rewritten as the abstract cauchy problem(ACP). First, two lemmas about operator semigroups are introduced.

Lemma 2.1. ^[19,20] Let $\left({G, \mathcal{T}\left(G \right)} \right)$ be the $Hille$-$Yosida$ operator on the Banach space Y, $A \in {\cal L}\left(Y \right)$ is the set of all bounded linear operators on Y, and $C = G+A$ are the $Hille$-$Yosida$ operators.

Lemma 2.2. ^[19,20] Let ${G_0}$ be part of the operator $G$ on ${Y_0}: = \overline {\mathcal{T}\left(G \right)}$, defined as: ${G_0}x = Gx$, where $x \in \mathcal{T}\left({{G_0}} \right) = \left\{ {x \in \mathcal{T}\left(G \right):Gx \in {Y_0}} \right\}$. If $\left({G, \mathcal{T}\left(G \right)} \right)$ is the $Hille$-$Yosida$ operator on the Banach space, then $\left({{G_0}, \mathcal{T}\left({{G_0}} \right)} \right)$ generates a ${C_0}$-semigroup on ${Y_0}$.

First, let

and model (2.1) is converted to:

and

where

Further, let

then system (2.1) becomes

where

Here, we introduce the Banach space

We have the following usual product norm

Further, $G:\mathcal{T}\left(G \right) \subset Y \to Y$ is defined as

with domain

and then

Next, we introduce the space

and define the map $H:{I_G} \to Y$ as

where

Let $h\left(t \right) = \left({\begin{array}{*{20}{c}} {{0_{{\mathbb{R}^2}}}} \\ {w \left(t \right)} \end{array}} \right)$, where $w \left(t \right) = w \left(t \right)\left(a \right) = w \left({t, a} \right)$, then system (2.2) becomes

where ${h_t} \in {I_G}, {h_t}\left(\theta \right) = h\left({t + \theta } \right)$, and ${h_0}\left(\theta \right) = \left({\begin{array}{*{20}{c}} 0\\ {{w _0}\left({\theta, \cdot } \right)} \end{array}} \right)$. Obviously this is an abstract time delay differential equation, which is further rewritten (2.3) as the ACP for applying the theory of the integral semigroup. Define $y \in I\left({\left[{0, + \infty } \right] \times \left[{- \frac{{{\tau _1}}}{{{\tau _2}}}, 0} \right]:Y} \right)$, where $y\left({t, \theta } \right) = h\left({t + \theta } \right), t \ge 0$, and $\theta \in \left[{- \frac{{{\tau _1}}}{{{\tau _2}}}, 0} \right]$. Thus, we can get the following equation:

Below we take the product of space $Y$ and space ${{{\rm I}}}$ as the state space $Z$, so

and the usual product norm

Therefore, system (2.4) can be rewritten as the Cauchy problem of an abstract non-dense definition, and the linear operator $\mathcal{T}:\mathcal{T}\left(\mathcal{L} \right) \subset Z \to Z$ is defined as follows:

Since ${Z_0}: = \overline {\mathcal{T}\left(\mathcal{L} \right)} = \left\{ {{0_Y}} \right\} \times {I_G} \ne Z$, we obtain that $\mathcal{L}$ is apparently a non-dense linear operator defined in $Z$. Furthermore, we take the following operator $\mathcal{H}:{Z_0} \to Z$:

Finally, let $z\left(t \right) = \left({\begin{array}{*{20}{c}} 0\\ {y\left(t \right)} \end{array}} \right), y\left(t \right) = y\left(t \right)\left(\theta \right) = y\left({t, \theta } \right).$ Then, (2.4) is the non-dense definition of the Cauchy problem

^[19,21] studied the global existence and uniqueness of solutions containing (2.5).

Let

and then the following conclusion holds:

Theorem 2.1. For $G$ and $\mathcal{L}$, we can get:

($i$) If $\lambda \in \Omega$, then $\lambda \in w \left(G \right)$ and

where $\left({\begin{array}{*{20}{c}} {\tilde \varphi }\\ {\tilde g} \end{array}} \right) \in Y, \left({\begin{array}{*{20}{c}} 0\\ g \end{array}} \right) \in \mathcal{T}\left(G \right);$

($ii$) $w \left(\mathcal{L} \right) = w \left(G \right)$. Also, for the each $\lambda \in w \left(L \right)$, we can obtain the explicit formula of $\mathcal{L}$' resolvent

($iii$) $\mathcal{L}$ and $G$ are $Hille-Yosida$ operators on $Z$ and $Y$, respectively.

Proof. The first two proof methods are shown in ^[22], and here we only need to prove ($iii$). Let $\lambda \in \left({ - \varsigma, + \infty } \right)$, then from ($i$) we can get

the integral for $a$, then

This indicates that $\left({G, \mathcal{T}\left(G \right)} \right)$ is the $Hille$-$Yosida$ operator. By the proof method in ^[21], we get that $\left({\mathcal{L}, \mathcal{T}\left(\mathcal{L} \right)} \right)$ is a $Hille$-$Yosida$ operator.

Finally, let ${Z_{0 + }}: = {Z_0} \cap {Z_ + }$, and

Since both $G$ and $L$ are $Hille-Yosida$ operators, using the theory about the integral semigroup, we can get the well-posedness of model (2.5) as follows:

Theorem 2.2. There exists a unique continuous semigroup ${\left\{ {U\left(t \right)} \right\}_{t \ge 0}}$ on ${Z_{0 + }}$ such that for any $z \in {Z_{0 + }}$, we have that $t \to U\left(t \right)z$ is the unique integral solution for the following problem:

or

3.   Equilibrium points and linearized systems

Now we prove the existence and linearization of the equilibrium points of system (2.5). Suppose $\bar z = \left(\begin{array}{c} {0_Y}\\ {\bar \chi } \end{array} \right) \in \mathcal{T}\left(\mathcal{L} \right)$ is the steady state solution of system (2.5), where

then we have $\mathcal{L}\bar z + \mathcal{H}\left({\bar z} \right) = 0$, that is,

The following conclusions can be obtained from (3.1):

Theorem 3.1. System (2.5) always has equilibrium:

where

In addition, (2.5) has only the positive equilibrium solution

if

where

Therefore, the following theorem holds for system (1.1):

Theorem 3.2. ($i$) System (1.1) always has equilibriums ${E_0}\left({0, 0} \right), {E_1}\left({m, 0} \right), {E_2}\left({K, 0} \right)$;

($ii$) when $\alpha \eta > 1, K\left({\alpha \eta - 1} \right) > \beta$, the positive equilibrium point ${E_*}\left({{V_*}, {p_*}\left(a \right)} \right)$ exists in the system, where

Next, we linearize system (2.5) at the equilibrium point, set $\bar z$ as the steady state of the system (2.5), let $\varpi \left(t \right) = z\left(t \right) - \bar z$, and replace it with (2.5). Then,

Thus, the linearization system around $\bar z$ is as follows:

with

and

where

According to Lemma 2.1 and Theorem 2.1, we get Theorems 3.3 and 3.4:

Theorem 3.3. $\mathcal{L} + \mathcal{T}\mathcal{H}\left({\bar z} \right)$ is a Hille-Yosida operator.

Then, by Lemma 2.2, we can get the following:

Theorem 3.4. $\left({\mathcal{L}, \mathcal{T}\left(\mathcal{L} \right)} \right), \left({\mathcal{L} + \mathcal{T}\mathcal{H}\left({\bar z} \right), \mathcal{T}\left({\mathcal{L} + \mathcal{T}\mathcal{H}\left({\bar z} \right)} \right)} \right)$ generate ${C_0}$-semigroups ${\left({{\cal I}\left(t \right)} \right)_{t \ge 0}}$, ${\left({{\cal J}\left(t \right)} \right)_{t \ge 0}}$ on space ${Z_0}$, respectively.

Based on the proof of Theorem 2.1, the $Hille-Yosida$ estimate domain is $\left\| {{\cal I}\left(t \right)} \right\| \le {e^{ - dt}}$. Moreover, $\mathcal{T}\mathcal{H}\left({\bar z} \right){\cal I}\left(t \right):{Z_0} \to Z$ is clearly compact for any $t > 0$. Then, we have

And then we can get ${\left({{\cal J}\left(t \right)} \right)_{t \ge 0}}$ is quasi-compact. According to ^[18], the quasi-compact related conclusion for strong continuous semigroups, when all eigenvalues of $\mathcal{L} + \mathcal{T}\mathcal{H}\left({\bar z} \right)$ are negative, then for $\bar d > 0$, when $t \to + \infty$, ${e^{\bar dt}}\left\| {{\cal J}\left(t \right)} \right\| \to 0$.

Theorem 3.5. The solution semigroup $T\left(t \right)$ of the system (2.5) satisfies the following: the solution of the steady state $\bar z\left(t \right)$ is locally asymptotically stable (LAS), when all eigenvalues of $\mathcal{L} + \mathcal{T}\mathcal{H}\left({\bar z} \right)$ have strictly negative real parts; the solution of the steady state $\bar z\left(t \right)$ is unstable, when the presence of $\mathcal{L} + \mathcal{T}\mathcal{H}\left({\bar z} \right)$ has a strictly positive real eigenvalue.

4.   Dynamics behavior

Obviously, ${E_0}$ and ${E_1}$ are unstable equilibrium points. Next we consider ${E_2}$'s stability.

4.1.   Stability at point ${E_2}$

4.1.1.   Local stability at point ${E_2}$

Theorem 4.1. When $\frac{{\alpha \eta K}}{{\beta + K}} < 1$, the equilibrium state ${\bar z_1}$ of system (2.5), i.e., the equilibrium point ${E_1}\left({K, 0} \right)$ of system (1.1), is LAS; when $\frac{{\alpha \eta K}}{{\beta + K}} > 1$, ${E_1}\left({K, 0} \right)$ is unstable.

Proof. Let

where

From this, the linearized system ${\bar z_1}$ can be written as

where

which is equivalent to

where $\tilde V\left(t \right) = \int_0^{ + \infty } {\tilde v\left({t, a} \right)da}$.

Let $\tilde V\left(t \right) = {\tilde V_0}{e^{\lambda t}}, \tilde p\left({t, a} \right) = {\tilde p_0}\left(a \right){e^{\lambda t}}$, and substituting this into (4.1), the characteristic equations of (4.1)

Let ${f_0}\left(\lambda \right) = \frac{{{\tau _2}\eta \alpha \beta K}}{{\beta + K}}\int_0^{ + \infty } {\delta \left(a \right){e^{ - \left({\lambda + {\tau _2}\sigma } \right)a}}da} - 1$. Then

Obviously, the root of ${g_0}\left(\lambda \right) = 0$ is negative, and for ${f_0}\left(\lambda \right) = \frac{{{\tau _2}\alpha \eta K}}{{\beta + K}}\int_0^{ + \infty } {\delta \left(a \right){e^{ - \left({\lambda + {\tau _2}\sigma } \right)a}}da} - 1$, we have

Because ${f_0}\left(\lambda \right)$ is strictly decreasing and satisfies continuous real functions, we have:

When $\frac{{\eta \alpha K}}{{\beta + K}} - 1 > 0$, ${f_0}\left(\lambda \right) = 0$ has at least one positive root, and ${E_2}$ is unstable.

When $\frac{{\eta \alpha K}}{{\beta + K}} - 1 < 0$, ${f_0}\left(\lambda \right) = 0$ has no complex solution with real root and no negative, suppose that ${\lambda _0} = \theta + \omega i$ is the solution, so

Clearly, this is contradictory, so the solution of the characteristic equation must have negative real parts, that is, when $\frac{{\eta \alpha K}}{{\beta + K}} - 1 < 0$, ${f_0}\left(\lambda \right) = 0$, and ${E_2}$ is LAS.

4.1.2.   Local stability at point ${E_2}$

This section demonstrates the global stability of ${E_2}$ using asymptotic autonomous semigroup theory.

Theorem 4.2. When $\frac{{\eta \alpha K}}{{\beta + K}} - 1 < 0$, ${E_2}$ is globally asymptotically stable.

Proof. From $\frac{{dV(t)}}{{dt}}$ of system (2.1), we can obtain

and, by the comparison principle, we have:

Therefore, for any $\kappa > 0$, there exists ${t_1}$ such that $V\left({t - \frac{{{\tau _1}}}{{{\tau _2}}}} \right) \le K + \kappa$, when $t \ge {t_1} + \frac{{{\tau _1}}}{{{\tau _2}}}$, and then

Now, we consider the following system:

Using the same method as in Theorem 4.1, the solution of (4.2) exists in the form of $\hat p\left({t, a} \right) = {\hat p_0}\left(a \right){e^{{\lambda _0}t}}$, where ${\hat p_0}\left(a \right)$ is non-negative and ${\lambda _0}$ is the root of the characteristic equation of (4.2), i.e.,

From the second equation of (2.1), we can get

namely $p\left({t, a} \right) \le \hat p\left({t, a} \right)$ for $t \ge {t_1} + \frac{{{\tau _1}}}{{{\tau _2}}}$. So, $p\left({t, a} \right) \le {\hat p_0}\left(a \right){e^{{\lambda _0}t}}.$

From Theorem 4.1, when $\frac{{\eta \alpha K}}{{\beta + K}} < 1$, $\mathop {\lim }\limits_{{\rm{t}} \to \infty } p\left({t, a} \right) = 0$. Thus, when $t \to \infty$, $\frac{{dV}}{{dt}}$ of (2.1) converges to

which illustrates that $\mathop {\lim }\limits_{t \to \infty } \hat V\left(t \right) = K.$

Applying the related theories from ^[23], we can get $\mathop {\lim }\limits_{t \to \infty } V\left(t \right) = K$. Hence, when $\frac{{\eta \alpha K}}{{\beta + K}} < 1$, ${E_2}$ is globally asymptotically stable.

4.2.   Dynamics behavior at ${E_*}$

4.2.1.   Stability at ${E_*}$

First, we need to obtain the characteristic equation of system (3.2). Let ${\mathcal{K}} = \mathcal{T}F\left({\bar z} \right)$, where $\bar z$ represents the equilibrium state of system (2.5).

Now, we note $\bar A = {\lambda I - \left({\mathcal{L} + {\mathcal{K}}} \right)}$, $\bar B = {I - {\mathcal{K}}{{\left({\lambda I - \mathcal{L}} \right)}^{ - 1}}}$, $\bar C = {\lambda I - \mathcal{L}}$. Suppose that $\lambda \in \Omega$. Because $\bar C$ is reversible, then $\bar A$ is equivalent to

From this, we get that

If $\bar B$ is reversible, then

Applying Theorem 2.1 and (3.3), we can get that, for

we have

which is equivalent to

i.e.,

Let

and

then we have

From this, we can derive that

Let

From the first equation of (4.6), we can get $\Delta \left(\lambda \right)\vartheta = {\chi _1} + \bar \Phi \left({\lambda, {\chi _2}} \right)$. That is, when $\Delta \left(\lambda \right)$ is reversible, we have

Thus, $\bar A$ is reversible, i.e.,

So, Theorem 4.3 can be obtained:

Theorem 4.3. The following conclusion holds: $\sigma \left({\mathcal{L} + {\mathcal{K}}} \right) \cap {\rm{\Omega }} = {\sigma _P}\left({\mathcal{L} + {\mathcal{K}}} \right) \cap {\rm{\Omega }} = \left\{ {\lambda \in {\rm{\Omega }}:\det \left({\Delta \left(\lambda \right)} \right) = 0} \right\}$, and if $\lambda \in w \left({\mathcal{L} + {\mathcal{K}}} \right) \cap {\rm{\Omega }}$, then the resolvents formula is

where

Proof. Because $\lambda \in {\rm{\Omega }}$ with $\det \left({\Delta \left(\lambda \right)} \right) \ne 0$, we can get that $\left({I - \mathcal{T}H\left({\bar \chi } \right)\left({{e^{\lambda \theta }}{{\left({\lambda I - G} \right)}^{ - 1}}} \right)} \right)$ is reversible, and then from (4.5) we can get

and

Thus, $\bar B$ is reversible for any $\left(\begin{array}{l} {\tilde x}\\ {\tilde \chi } \end{array} \right) \in Z$,

where $x$ as shown in formula (4.8), $\chi = \tilde \chi$. Therefore, we obtain (4.7) and

Further, take $\lambda \in {\rm{\Omega }}:\det \left({\Delta \left(\lambda \right)} \right) = 0$, and according to (4.3), there exists $\left(\begin{array}{l} {\rm{0}}\\ {\chi _{\rm{0}}} \end{array} \right) \in \mathcal{T}\left(L \right), \left(\begin{array}{l} {\rm{0}}\\ {\chi _{\rm{0}}} \end{array} \right) \ne 0$, so

is established if and only if there exists $\left(\begin{array}{l} {{\mathord{\buildrel{\lower3pt\hbox{ $ \smile$ }} \over x} }_0}\\ {{\mathord{\buildrel{\lower3pt\hbox{ $ \smile$ }} \over \chi } }_0} \end{array} \right) \in Z$, and $\left(\begin{array}{l} {{\mathord{\buildrel{\lower3pt\hbox{ $ \smile$ }} \over x} }_0}\\ {{\mathord{\buildrel{\lower3pt\hbox{ $ \smile$ }} \over \chi } }_0} \end{array} \right) \ne 0$ satisfies

Let the $(\begin{array}{l} {\tilde \xi }\\ {\tilde \chi } \end{array})$ of the Eq (4.4) be equal to 0, and then we can obtain the existence of $\left(\begin{array}{l} {{\mathord{\buildrel{\lower3pt\hbox{ $ \smile$ }} \over x} }_0}\\ {{\mathord{\buildrel{\lower3pt\hbox{ $ \smile$ }} \over \chi } }_0} \end{array} \right) \in Z\backslash \left\{ 0 \right\}$ is equivalent to (4.10), where ${\mathord{\buildrel{\lower3pt\hbox{ $ \smile$ }} \over x} _0}{\rm{ = }}\left(\begin{array}{l} {{\mathord{\buildrel{\lower3pt\hbox{ $ \smile$ }} \over \vartheta } }_{\rm{0}}}\\ {{\mathord{\buildrel{\lower3pt\hbox{ $ \smile$ }} \over f} }_0} \end{array} \right)$ satisfies

Thus, (4.9) has solutions if and only if there exists ${\mathord{\buildrel{\lower3pt\hbox{ $ \smile$ }} \over \vartheta } _{\rm{0}}} \ne 0$, so $\Delta \left(\lambda \right){\mathord{\buildrel{\lower3pt\hbox{ $ \smile$ }} \over \vartheta } _{\rm{0}}} = 0$, and $\lambda \in {\sigma _P}\left({\mathcal{L} + {\mathcal{K}}} \right)$. Therefore, $\left\{ {\lambda \in {\rm{\Omega }}:\det \left({\Delta \left(\lambda \right)} \right) = 0} \right\} \subset {\sigma _P}\left({\mathcal{L} + {\mathcal{K}}} \right)$.

The above analysis shows that $\det \left({\Delta \left(\lambda \right)} \right) = 0$ is the characteristic equation of (3.2) about ${\bar z_*}$.

Below, we analyze the stability at ${E_*}$ and the Hopf bifurcation's existence. Due to the complexity of ${\tau _{\rm{1}}} \ne {\tau _{\rm{2}}}$, only ${\tau _{\rm{1}}}{\rm{ = }}{\tau _{\rm{2}}} = \tau$ is considered below, and then the characteristic equation is:

where

Let $\lambda = \tau \vartheta$, then

Because of ${\rm{g}}\left(\lambda \right) \ne 0$, there is

First, when $\tau = 0$, we have $h\left(\vartheta \right) = {\vartheta ^2} + \left({{p_1} + {q_1}} \right)\vartheta + \left({{p_0} + {q_0}} \right) = 0$, where ${p_0} + {q_0} = \frac{{\sigma \gamma \left[{K\left({\alpha \eta - 1} \right) - \beta } \right]\left[{\beta + m\left({\alpha \eta - 1} \right)} \right]}}{{Km\eta \alpha \left({\alpha \eta - 1} \right)}} > 0$, hence we get the following theorem:

Theorem 4.4. When $\tau = 0$, if ${p_1} + {q_1} > 0$, then ${E_*}$ is locally asymptotically stable; otherwise, it is unstable.

4.2.2.   Hopf bifurcation at ${E_*}$

This section considers the Hopf bifurcation problem when $\tau > 0$. Since the age structure model studied is infinite and the central manifold theory needs to be applied to the abstract non-dense Cauchy problem, we can simplify the system considering the finite-dimensional equation on the central manifold. Thus, the Hopf bifurcation theorem of Hassard remains valid. Therefore, we will use Hassard's theorem directly below to explore the existence of the Hopf bifurcation.

Let $\tau > 0$, so the root of $h\left(\vartheta \right) = 0$ has continuous dependence on ${\tau _{\rm{0}}}$. As $\tau$ increases, the root of $h\left(\vartheta \right) = 0$ can pass through the imaginary axis to the right. Let $\vartheta = i\omega \left({\omega > 0} \right)$ be the purely imaginary roots of $h\left(\vartheta \right) = 0$ and substitute it into $h\left(\vartheta \right) = 0$, which gives

disassociating the real part and imaginary part,

i.e.,

and

which is

Let $\Theta = {\omega ^2}$, then above equation becomes

Due to ${p_0} + {q_0} > 0$,

and, when ${p_0} - {q_0} < 0$, the above equation has the sole positive root, and denote it as ${\Theta _*}$. That means (4.12) has the only positive root ${\omega _*} = \sqrt {{\Theta _*}}$, hence $h\left(\vartheta \right) = 0, \left({\tau = {\tau _k}} \right)$ has a pair of purely imaginary roots, with

and

Lemma 4.5. In the case of Assumption 1.1 holding, when $\alpha \eta > 1$, ${p_1} + {q_1} > 0$ and ${p_0} - {q_0} < 0$, then

and, at this time, $\vartheta = i{\omega _*}$ is the unique root of $h\left(\vartheta \right) = 0$.

Proof. From (4.11), we can get that

Because of $h\left(\vartheta \right) = 0$, we derive that

If ${\left. {\frac{{dh\left(\vartheta \right)}}{{d\vartheta }}} \right|_{\vartheta = i{\omega _*}}} = 0$ is correct, then $i{\omega _*}\left({i{q_1}{\omega _*} + {q_0}} \right){e^{ - i{\omega _*}\tau }} = 0$, i.e., $i{q_1}{\omega _*} + {q_0} = 0$, hence ${q_1} = {q_0} = 0$. Because ${q_1} = - \sigma < 0$, which contradicts the conclusion, ${\left. {\frac{{dh\left(\vartheta \right)}}{{d\vartheta }}} \right|_{\vartheta = i{\omega _*}}} \ne 0$.

Let $\vartheta \left(\tau \right) = \bar \alpha \left(\tau \right) + i\bar \omega \left(\tau \right)$ become the root of $h\left(\vartheta \right) = 0$ where $\bar \alpha \left({{\tau _k}} \right) = 0, \bar \omega \left({{\tau _k}} \right) = {\omega _*}$. Evaluating $\tau$ on both sides of $h\left(\vartheta \right) = 0$, we get that

so

Besides,

Replace $\omega _*^2$ with ${\mathop{\rm Re}\nolimits} \left({{{\left. {{{\left({\frac{{d\vartheta }}{{d\tau }}} \right)}^{ - 1}}} \right|}_{\vartheta = i{\omega _*}}}} \right)$, so

According to the correlation theorem of the Hopf bifurcation in ^[24], we get Theorem 4.6:

Theorem 4.6. In the case of Assumption 1.1 holding, when $\alpha \eta > 1, K\left({\alpha \eta - 1} \right) > \beta$, ${p_1} + {q_1} > 0$, and ${p_0} - {q_0} < 0$, then

$(i)$ when $\tau \in \left[{0, {\tau _0}} \right)$, ${E_*}$ is asymptotically stable, and when $\tau > {\tau _0}$, it is unstable;

$(ii)$ when $\tau = {\tau _k}$, system (1.1) undergoes a Hopf bifurcation at the equilibrium ${E_*}$.

5.   Numerical simulation

This section uses the MATLAB software to simulate the model numerically. First, the parameters are:

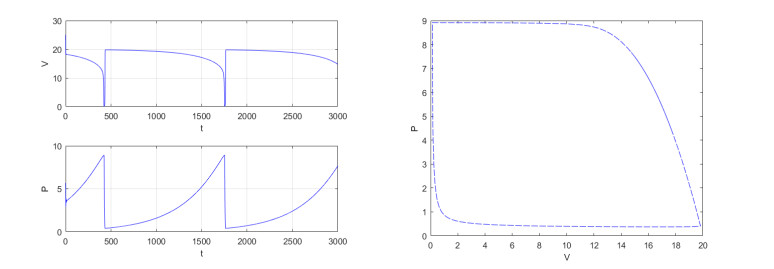
By calculating, we can get $\frac{{\eta \alpha K}}{{b + K}} - 1 = - 0.074 < 0$, which satisfies the condition of Theorem 4.2, that ${E_2}\left({20, 0} \right)$ is globally asymptotically stable at this time.

Let ${\tau _1} = 1, {\tau _2} = 2$. The available time series diagrams and phase diagrams are shown in Figure 1, and ${E_2}$ are globally stable at this time.

Next, let the parameters become

and set $V\left(0 \right) = 14, p\left({0, a} \right) = 16{e^{ - a}}$. By calculating, we have

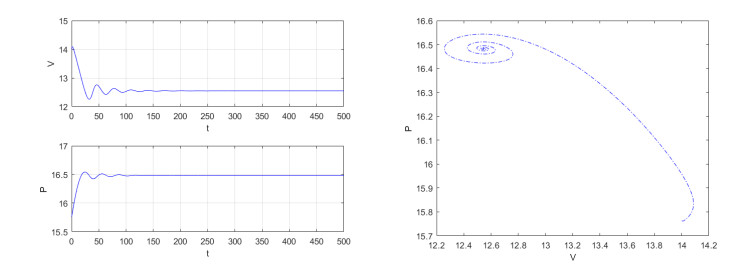
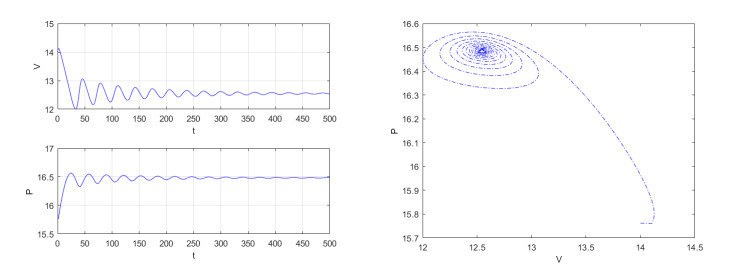
satisfying the condition of Theorem 4.6, and we can get ${\tau _0} = 3.185$. First, let ${\tau _1} = {\tau _2} = 2$. ${E_*}\left({12.548, 6.593{e^{ - 0.4a}}} \right)$ is asymptotically stable at this time, and the available time series diagrams and phase diagrams are shown in Figure 2. Second, let ${\tau _1} = {\tau _2} = 4$, ${E_*}$ pass through a Hopf bifurcation. For aesthetics, we modify the initial value to $V\left(0 \right) = 25, p\left({0, a} \right) = 5.395{e^{ - a}}$. The system has periodic solutions, and the available time series diagrams and phase diagrams are shown in Figure 3.

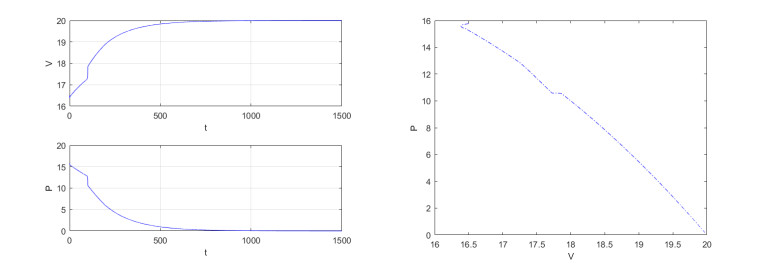
Finally, we observe the dynamics of the system under the current parameter conditions ${\tau _1} \ne {\tau _2}$, and let ${\tau _1} = 1, {\tau _2} = 0$. ${E_*}$ is asymptotically stable at this time, and the available time series diagrams and phase diagrams are shown in Figure 4.

As can be seen from the above analysis, the time delay effects of predation processes, energy conversion, reproductive reproduction, etc., can cause changes in the dynamics behavior of the predation system over a later period of time. At a time when the delay is less than a certain threshold, the final size of the two species is in a state of coexistence and tends to stabilize. When this threshold is exceeded, the two species still coexist, but, because the system undergoes a Hopf bifurcation, the number of the two species is subject to periodic oscillations. We know that the weak Allee effect affects the population size of the predator system by influencing its time delay threshold, which is essential for the study of the predator system.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This work is supported by National Natural Science Foundation of China Grants 12071268 and 11971281, Inner Mongolia Autonomous Region University Science and Technology Research Project NJZY22036 and by Innovation Capability Support Program of Shaanxi Province (Program No. 2023-CX-TD-61).

Conflict of interest

The authors declare there are no conflicts of interest.