1.
Introduction
One of the most researched areas of differential geometry is curve theory, with studies presented in different dimensions and spaces. Generally, the geometric location of the different positions taken by a moving point in space during motion is a curve. In this motion, the parameter range of the curve represents the time elapsed through the motion. In addition, the parameter of the curve has an important place to characterize the curve. For example, the parameter of any given curve has many differences in terms of whether the curve is parameterized with respect to arc length. On the other hand, the characterization of a regular curve is one of the most important problems in curve studies in differential geometry, where curvature and torsion play a major role in solving the problem. The definitions of some special curves can be made by using the curvature and torsion [3,4,5,6,7,8,9,10,11]. One of them is the helices definition given by Lancret in 1806 [18]. Lancret defined the classical definition of helices as "curves whose tangent vector makes a constant angle with a constant direction" [18]. Starting from this definition, the helices drawn on a right circular cylinder were considered, and they were called a circular helix. It is among the first characterizations indicating that curvature and torsion are constants separately in these helices. Later, although these curvatures are not constant, curves with constant ratios were found, which were called the general helices, and the proof of this theory was proved by Venant in 1845 [11]. Helices have an impressive place both in nature and science. Fractal geometry, the arrangement of molecules in the structure of DNA, and its applications in physics and civil and mechanical engineering are some examples. In addition to that, Izumiya and Takeuchi named the curves slant helices, where the angle between the principal normal vector field and a constant direction is constant at every point of the curve, and they obtained that the necessary and sufficient condition for curves to be slant helices is that the geodesic curvature of the principal normals indicator of the given curves is a constant function [14]. Then, some studies about slant helices were conducted [2,24]. Ali and Lopez [1] studied slant helices in Lorenz space and investigated the tangent indicatrix on the binormal indicatrix of a slant helix in Minkowski space. On the other hand, Kula and Yaylı investigated the tangential and binormal indicatrices of slant helices and showed that these spherical indicatrices are spherical helices [17]. Later, Önder et al. introduced B2-slant helices in E4 and determined the properties of these curves [21]. In addition, Yaylı and Zıplar examined the relationship between slant helices and spherical helices in En space [26]. Then, Gök et al. defined Vn-slant helices in the space En [12], K\i z\i ltu\u{g} et al. [16] obtained the characterization of slant helices using a type-2 bishop frame and Lucas and Ortega-Yagües [20] investigated the relationship between helix surfaces and slant helices in a sphere S3. Recently, Uzuno\u{g}lu et al. [25] explained a recent alternative orthogonal frame as {N,C=N′‖N′‖,W} and gave a characterization of C-slant helices. Moreover, they investigated curves of C-constant precession according to an alternative frame [25]. After that, Kaya and Önder et al. [15] defined C-partner curve with respect to the frame {N,C,W}. On the other hand, the modified orthogonal frame has been defined by Sasai [23], and the helices and Bertrand curves for modified orthogonal frames in E3 have been given in [19].
2.
Preliminaries
In this section, we give some basic definitions of curves in Euclidean 3-space. Let α:I⊂R⟶E3 be a regular-unit speed curve with the arc-length parameter s (‖α′(s)‖=1). Therefore, the curve (α) is called a Frenet curve if it has non-zero curvature (α″(s)≠0). Moreover, the derivative formulas of the Frenet frame of a regular-unit speed curve can be given as
where {T,N,B} constitutes the Frenet frame and κ=‖α″‖=⟨T′,N⟩; and, τ=⟨N′,B⟩ are the curvature and torsion of the unit speed curve (α), respectively. In addition to the Frenet frame, Uzunoǧlu et al. [25] explained a new alternative orthogonal frame such that {N,C,W}, where N is the principal normal vector field, C=N′‖N′‖, W=τT+κB√κ2+τ2 and W is the Darboux vector. Therefore, the derivative formulae of this alternative frame {N,C,W} are provided by
where
κ and τ are the curvature and torsion of the curve (α), respectively, and H is the harmonic curvature. Moreover, the relationship between the new alternative frame {N,C,W} and Frenet frame {T,N,B} are given as follows:
where the vector field N is common [15].
Now, for a regular-unit speed curve α=α(s), we can say that, if the vector field T of the curve (α) makes a constant angle with a fixed-unit vector field, α=α(s) is called a general helix [11,18]. Moreover, a helix curve is characterized by κτ=constant, where κ and τ are the curvature and torsion of the curve (α), respectively [11]. Then, Izumiya and Takeuchi described a slant helix as "a curve α whose principal normal vector make a constant angle with such a constant direction, that is
for every s∈I and θ≠π2" [7]. At the same time, they also stated that (α) is a slant helix where the necessary and sufficient condition is that its curvatures satisfy the equation
After that, Uzunoǧlu et al. [25] gave the following definition of a slant helix according to the alternative orthogonal frame {N,C,W}.
Definition 1. Let (α) be a unit speed curve in E3 and {N,C,W} be the alternative frame of the curve (α). In that case, (α) is called a C-slant helix according to the alternative frame if the vector field C makes a constant angle with a constant direction V, that is, if
for all s∈I. Therefore, the ratio
for the adapted curvatures fandg [25].
3.
Main theorems and proofs
3.1. Modified adapted frame and N∗-slant helix and C∗-slant helix with modified adapted frame
In this section, we first define the modified adapted frame; later, we give the definitions of the N∗-slant helix and C∗-slant helix and some of their characterizations using the modified adapted frame in E3.
Let α:I⊂R⟶E3 be a unit speed curve that can be parameterized in terms of the arc length s. Now, we define a new and different frame i.e., a modified adapted frame. The motivation for us to define this new frame in this study is that the frame defined by Uzunoǧlu et al. [25] cannot be created at every position of the curve. If the equation f(s)=‖N′(s)‖=0 holds in the frame {N,C,W} defined by them, then the vector field C=N′f=N′‖N′‖ cannot be defined. Therefore, the frame {N,C,W} cannot be constructed for ∀s∈I. In this case, the alternative frame given by them [25] needs to be modified. In this study, we modified this frame and named this new frame the "modified adapted frame". As a result, we defined this new frame {N∗,C∗,W∗} such that
where C∗(s0)=W∗(s0)=0 if f(s0)=0. Now, we give the derivative formulas of the modified adapted frame {N∗,C∗,W∗}. For this, if we use Eqs (2.1) and (3.1), then we get
where ⟨N∗,N∗⟩=κ2,⟨C∗,C∗⟩=f2,⟨W∗,W∗⟩=f2, f=√κ2+τ2, κ and τ are the Frenet curvature and torsion of the curve (α), respectively, and f and g are the modified adapted curvatures. Moreover, the relationship between the modified adapted frame {N∗,C∗,W∗} and Frenet frame {T,N,B} can be written as
Now, we give some characterizations of the N∗-slant helices and C∗-slant helices with the modified adapted frame {N∗,C∗,W∗}.
Theorem 1. Let (α) be a unit speed curve with the modified adapted apparatus {N∗,C∗,W∗,f,g} in E3. In that case, if the unit speed curve (α) is an N∗-slant helix according to the modified adapted frame, then the axis of the N∗-slant helix (α) is the constant unit vector X, which can be written as
where κ is the Frenet curvature of (α), f=√κ2+τ2 and ζ is the angle between the vector fields N∗ and X.
Proof. Suppose that (α) is an N∗-slant helix with respect to the modified adapted frame {N∗,C∗,W∗} in E3. Then, for the vector fields N∗ and X, we get
where ζ is the constant angle between the vector fields N∗ and X. In that case, differentiating (3.3) according to s with the aid of Eq (3.2), we obtain
Thus, we can write the constant unit vector X as
where λ is a differentiable function. If we apply the differentiation process again to Eq (3.4), we have
and
Finally, considering (3.5) and (3.6), we obtain
Theorem 2. Consider that (α) is a unit speed curve with the modified adapted apparatus {N∗,C∗,W∗,f,g} in E3; then, (α) is a C∗-slant helix such that the constant unit vector Y characterizing this C∗-slant helix is given by
where f=√κ2+τ2, η is the angle between the vector fields C∗ and Y, μ=gκ(f2+g2)g′f−f′g and δ=f2(f2+g2)g′f−f′g.
Proof. Suppose that (α) is a C∗-slant helix with respect to the modified adapted frame {N∗,C∗,W∗}. In that case, with aid of Definition 1, we have
such that η is the constant angle between the vector fields C∗ and Y. Now, we take successive derivatives of Eq (3.7) with respect to the arc-length parameter s of (α); thus, we obtain
and, as a result,
respectively. Consequently, considering μ=gκ(f2+g2)g′f−f′g and δ=f2(f2+g2)g′f−f′g, we can easily get
3.2. C∗-partner curves with modified adapted frame
In this section, we define the C∗-partner curves considering the modified adapted frame {N∗,C∗,W∗} and we give some characterizations of these curves.
Let α:I⊂R⟶E3 and β:J⊂R⟶E3 be considered as two different unit speed curves with arc-length parameters s∈I and s1∈J, respectively. Moreover, we consider that the Frenet frames and curvatures of the curves (α) and (β) are {T,N,B,κ,τ} and {T1,N1,B1,κ1,τ1}, respectively. In that case, the following definitions and theorems can be given.
Definition 2. Consider that α:I⟶E3 and β:J⟶E3 are two regular curves and the modified adapted frames and curvature of the curves (α) and (β) are {N∗,C∗,W∗,f,g} and {N∗1,C∗1,W∗1,f1,g1}, respectively. In that case, if the vector fields C∗ and C∗1 are linear-dependent at the corresponding noncoincident points of these curves, then (α) and (β) are called C∗-partner curves.
Theorem 3. Suppose that (α) and (β) are C∗-partner curves in E3. In that case, the distance between the corresponding noncoincident points of (α) and (β) is not constant.
Proof. Suppose that (α) and (β) are C∗-partner curves in E3. {N∗,C∗,W∗} and {N∗1,C∗1,W∗1} are the modified adapted frames of the curves (α) and (β), respectively. In that case, the relationship between the C∗-partner curves at the corresponding noncoincident points can be written as
where D=D(s) is the distance function and the arc-length parameter of the curve (α) is s∈I. If we take the derivative of Eq (3.8) with respect to the parameter s∈I, we get
where the tangent vectors of the C∗-partner curves (α) and (β) are, respectively, T and T1, and the arc-length parameter of the curve (β) is s1. Now, we use the relationships between the Frenet and modified adapted frames of the C∗-partner curves. Therefore, we have
and
where {κ,τ} and {κ1,τ1} are the Frenet curvatures of C∗-partner curves (α) and (β), respectively. By considering the linear-dependent pair {C∗,C∗1}, the equation
holds. Consequently, we see that the distance function D=D(s) is not constant.
Now, we assume that the vector fields C∗ and C∗1 satisfy the equation C∗=C∗1. In this case, for the adapted curvatures f and f1 of the C∗-partner curves, the equation f2=f21 holds. As a result, the following theorem can be given:
Theorem 4. Suppose that (α) and (β) are C∗-partner curves. In that case, if the angle between N∗ and N∗1 is ϱ, then the relationships between the modified adapted frames {N∗,C∗,W∗} and {N∗1,C∗1,W∗1} of the curves (α) and (β), respectively, are
where κ,κ1 and f,f1 are the Frenet curvatures and adapted curvatures of the C∗-partner curves (α,β), respectively.
Proof. Consider that (α,β) are C∗-partner curves and C∗=C∗1. In that case, if we consider that the angle between the vector fields N∗ and N∗1 is ϱ, we can write
Consequently, considering the basic arrangements in differential geometry, we obtain
Alternatively, we can write
where f=f1.
Theorem 5. Consider that (α) and (β) are C∗-partner curves in E3. Therefore, the angle between N∗ and N∗1 of these curves is constant.
Proof. We know that (α) and (β) are C∗-partner curves, and that there is the relationship
from (3.10), where {N∗,C∗,W∗,f,g} and {N∗1,C∗1,W∗1,f1,g1} are the modified adapted frames and κ and κ1 are the Frenet curvatures of the C∗-partner curves (α,β), respectively. In that case, by differentiating (3.11) with respect to s, we obtain
and by considering Eqs (3.2) and (3.11), we can write
As a result, we get
and
Moreover, we obtain from Eqs (3.12) and (3.13) the equations
and
Consequently, for κ1≠0, we have ϱ′=0, and it is easy to see that the angle ϱ is constant.
Theorem 6. Let the curves (α) and (β) be considered C∗-partner curves and D=D(s) be the distance function between corresponding noncoincident points of these curves. Therefore, the distance D is a constant necessary and sufficient condition, i.e.,
where τ and f and g are the Frenet torsion and adapted curvatures of the curve (α), respectively, and ϱ is the angle between the vector fields N∗ and N∗1.
Proof. If (α) and (β) are C∗-partner curves, then we know that the relationship between these curves is
In that case, considering the derivative of the last equation with respect to s, we get
If we make necessary arrangements using (3.9), then we have
The vector field C∗ and C∗1 are linear-dependent; therefore, the equation
is satisfied. In that case, we obtain
and
Now, we assume that the distance function D(s) is a constant necessary and sufficient condition, where D′(s)=0. As a result, we get
from the last equation. Consequently, we obtain
where ϱ is constant.
Let (α) and (β) be considered C∗-partner curves. Now, we give some applications to show the character of the C∗-partner curve, where any given curve (α) or (β) is helix or slant helix. For this, the following theorems can be given.
Theorem 7. Let (α,β) be C∗-partner curves in E3. In that case, the modified adapted curvatures {f1,g1} of the curve (β) in terms of {f,g} of the curve (α) is given by
where ϱ is the constant angle between N∗ and N∗1.
Proof. Suppose that (α) and (β) are C∗-partner curves. Therefore, if we differentiate W∗1 in (3.10) with respect to s∈I of (α), we obtain
where, by using the derivative formulas given by Eqs (3.2) and (3.10) in (3.15), the equation
holds. We know that C∗=C∗1; therefore, we obtain
consequently, we get
The following corollaries can be given as consequences of Theorem 7.
Corollary 1. Consider that (α,β) are C∗-partner curves in E3. In addition, let (τ,τ1) be the Frenet torsions of the C∗-partner curves (α,β) and {f,g} and {f1,g1} be the modified adapted curvatures of the curves (α,β), respectively. Therefore, the torsions (τ,τ1) can be written by modified adapted curvatures such that
Corollary 2. Let the curves (α,β) be C∗-partner curves. If the curve (α) is a slant helix, then the necessary and sufficient condition is that (β) is a slant helix.
Proof. Consider that (α,β) are C∗-partner curves and the curve (α) is a slant helix. In that case, we know that gf=constant from (2.2). If we consider Eq (3.14), we have g1f1=constant. As a result, (β) is a slant helix. Similarly, if the curve (β) is a slant helix, then g1f1=constant. Therefore, from Eq (3.14), we obtain
Consequently, we have gf=constant and the curve (α) is a slant helix.
Corollary 3. Suppose that the curves (α,β) are C∗-partner curves. If (α) is a helix, then (β) is a slant helix. If (β) is a helix, then (α) is a slant helix.
Proof. We assume that the curve (α) is a helix. The Frenet curvature ratio τκ=constant and g=0; therefore, considering Eq (3.14) we obtain
and the curve (β) is a slant helix. Similarly, if we take that the curve (β) is a helix, then g1=0. Consequently, from Eq (3.17), we see that gf=tanϱ=constant and the curve (α) is a slant helix.
Corollary 4. Consider that the curves (α,β) are the C∗-partner curves. In that case, if the curve (α) (or(β)) is a slant helix, then τ1τ=constant where (τ,τ1) are the Frenet torsions of the C∗-partner curves (α) and (β), respectively.
Proof. Let the curve (α) (or(β)) be a slant helix from the C∗-partner curves (α,β). Therefore, we know that (α) is a slant helix necessary and sufficient condition whereby the curve (β) is a slant helix from Corollary 2. As a result, the ratio gf=constant with the necessary and sufficient condition of g1f1=constant. Consequently, consider Eq (3.16); we obtain τ1τ=constant.
Example 1. Consider a circular helix ω given by the parameterization
Then, let the C∗-partner curves of the curve ω be ψ∗, ψ∗∗ for the distance function D(s);
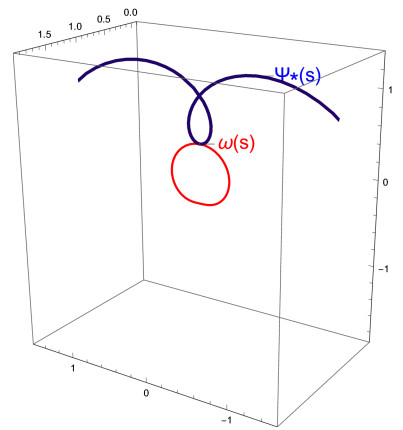
i) for D(ρ)=√3ρ, the C∗-partner curve ψ∗ of ω is obtained as
Figure 1 shows the graph of the curve ω and the C∗-partner curve ψ∗.
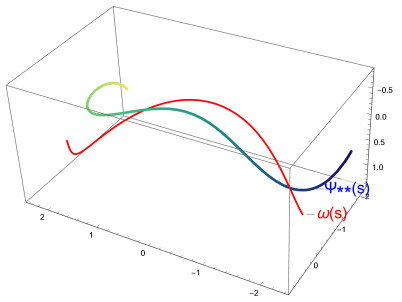
ii) for D(ρ)=√3ρ, the C∗-partner curve ψ∗∗ of ω is obtained as
Figure 2 shows the graph of the curve ω and the C∗-partner curve ψ∗∗.
Example 2. Consider a circular helix ω given by the parameterization
Then, let the C∗-partner curves of the curve ω be ψ∗, ψ∗∗ for the distance function D(s);
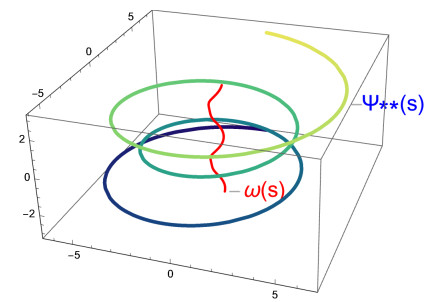
i) for D(ρ)=√32ρ, the C∗-partner curve ψ∗ of ω is obtained as ψ∗(s)=ω(s)+D(s)C∗(s)
Figure 3 shows the graph of the curve ω and the C∗-partner curve ψ∗.
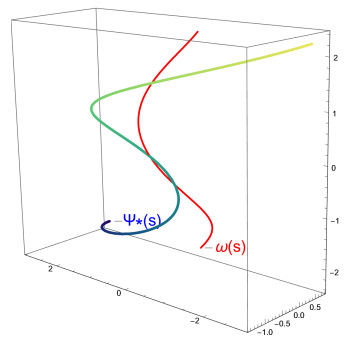
ii) for D(ρ)=8√2+ρ26√2ρ, the C∗-partner curve ψ∗∗ of ω is obtained as
Figure 4 shows the graph of the curve ω and the C∗-partner curve ψ∗∗.
4.
Conclusions
The fundamental theorem of regular curves is that there is a unit speed curve with curvature and torsion κ and τ, respectively, where κ>0 and τ are differentiable functions. In addition, the principal normal and binormal vector fields of the curve are not continuous at the zero points of the curvature. In this case, at a point where the curvature of a generally considered space curve disappears, the Frenet frame for this curve causes uncertainty. To solve this problem, Hord [13] and Sasai [22,23] found a simple but useful way and introduced a new orthogonal frame i.e., a the modified frame. On the other hand, another frame, as an alternative to the Frenet frame i.e., an adapted frame, was defined by Uzunoǧlu et. al [25] with the help of the Darbuox vector and Frenet normal vector of a regular curve. However, if the equation f=0 holds in the adapted frame {N,C,W} defined by them, then the vector field C cannot be defined. Therefore, the frame {N,C,W} cannot be constructed for all points on the curve. In that case, the alternative frame given by them [25] needs to be modified. So, the purpose of our study was to define a new modified adapted frame that removes all singular points in a curve. Moreover, with this new frame we have defined in this study, we believe that the curve theory, which will be studied with this frame in future studies, will be open to many innovations by bringing a different perspective to the curve theory in differential geometry. In addition, with this new frame, curve theory will gain a different perspective in many fields such as engineering and physics. Our theoretical and practical studies on this new frame continue.
Conflict of interest
The authors declare that they have no conflict of interests.









 DownLoad:
DownLoad: