Construction of vectorial moments via direction curves

1.   Introduction

In differential geometry, one of the primary study areas is the curve theory in 3-dimensional Euclidean space. The geometric properties of a curve are described by the Frenet-Serret frame and it plays an important role to do this description. An effective way to classify curves is by giving the relation between Frenet apparatus of curves. For example; a curve that is a helix in $\mathbb{E}^{3}$ is defined via the property that its tangent vector field constitutes a constant angle with a fixed direction. Lancret's theorem proves a helix as the proportion of its torsion and curvature is constant ^[10]. Helix was generalized by Hayden in ^[7]. Then with the help of the Killing vector field through a curve, the general helix was defined in real space form of three dimensions and in this space form Lancret Theorem was given again for general helices by Barros ^[1]. Camcı et al. gave characterizations for a curve that is non-degenerate to be a general helix by using its harmonic curvature in ^[3]. Also, general helices were studied in different spaces. Ciftci defined general helices in three dimensional Lie group via a bi-variant metric, proved Lancret Theorem and gave the generalization of helices ^[4]. Barros et al. presented Lancret-type theorems for general helices in three-dimensional Lorentzian space forms which showed remarkable differences with regard to the same question in Riemannian space forms ^[2].

In addition to the studies mentioned above, there are helix applications in many different fields.The helix is the primary structural pattern found in biological macromolecules like DNA and proteins. It is also the most common structure seen in all of nature, from the microscopic to the macroscopic scales. Yashima et al. noted that helical architectures in synthetic polymers inspired by biological helices and functions will lead to emerging opportunities for applications for chiral materials with specific functions ^[16]. Moreover, in ^[8] authors mentioned that linear chained polymers have a good chance to stabilize as a helix. A series of linear polymers were included into this study.

Another example of the classification of curves is associated curve (direction curve, adjoint curve or conjugate mate) which is defined by taking integral of a vector field created by one of a given curve's Frenet vectors. A particular solution to a differential equation or system of equations describes a curve that is parametrized. This curve is called an integral curve. In the case of $X$ is a vector field and $\alpha (t)$ is a parametric curve, the solution of the differential equation $\alpha ^{\prime }(t) = X(\alpha (t))$ imputes an integral curve of $X$. Despite being investigated for long years, one of the most attractive study field in curve theory is been still the title of associated curves. Several kinds of research can be found in the literature about this subject and some of them are in ^{[5,6,9,11,15]}.

On the other hand in physics, momentum is the product of the mass and velocity of an object and it is a vector quantity that is fully described by both magnitude and direction. Torque affecting any object at point $P$ is defined as

concerning the reference point $O$. By using this definition, in a recent paper, Tunçer took the points $P$ at any time-dependent trajectory and while points $P$ are drawing regular trajectory under affect of any force $\overrightarrow{F}$, torque draws a new time-dependent trajectory with respect to a reference point. He described vectorial moments of any space curve and called them $T$-dual, $N$-dual, $B$-dual curve. By doing so, some physical and geometric properties were connected. Frenet apparatus of these curves were obtained and curve pairs of constant breadth were investigated ^[14].

Immediately after that, Şenyurt et al. introduced the curve plotted by the vectorial moment of unit Darboux vector and they showed that the new curve does not form a constant width curve pairs with the main curve ^[13].

In light of the above literature, we construct some integral curves of a vector field created by vectorial moments of a curve which are new associated curves. We call these new curves dual direction curves. We establish some connections between a Frenet curve and its dual direction curves. Additionally, we obtain necessary and sufficient conditions for these curves to be a general helix.

2.   Basic concepts

In this part, some basic terms are recollected in relation to differential geometry of space curves in Euclidean space $\mathbb{E}^{3}.$

Let $\alpha :I\longrightarrow \mathbb{E}^{3}$ be a regular curve and the Frenet frame of $\alpha$ be $\left\{ T, N, B\right\}$. $\left\Vert \alpha ^{\prime }(s)\right\Vert = 1$ if and only if the curve $\alpha$ is a unit speed curve (or has arc-length parametrization $s$). For a unit speed curve $\alpha$; $T(s) = \alpha ^{\prime }(s)$ is called the unit tangent vector of $\alpha$. $\kappa (s) = \left\Vert \alpha ^{\prime \prime }(s)\right\Vert$ denotes the curvature of $\alpha$ which measures the amount by which the curve deviates from being a straight line. The unit principal normal vector $N(s)$ of $\alpha$ is given by $\alpha ^{\prime \prime }(s) = \kappa (s)N(s)$. The unit binormal vector of $\alpha$ is defined by the unit vector $B(s) = T(s)\times N(s)$. Then, the famous Frenet formula is given as ^[12]:

where $\tau (s)$ is the torsion of $\alpha$ and it measures the amount by which the curve deviates from a plane.

The Frenet vectors of an arc-length parameterized curve $\alpha$ can be calculated as:

The curvature and torsion of $\alpha$ are calculated respectively by

A curve is given the name general helix where the angle between its tangent lines and a fixed direction is constant. This fixed direction is called the axis of the general helix. Lancret expressed the characterization of helix in 1802, that a curve is a general helix, if and only if, the harmonic curvature or the ratio $\dfrac{\tau }{\kappa }$ is constant, with $\tau \neq 0.$ The general helix is called circular helix if both $\kappa \neq 0$ and $\tau \neq 0$ are constants ^[12].

In ^[14], author mentioned:

As a linear combination of Frenet vectors, we can express the position vector of any curve $\alpha \left(s\right)$ in the following way:

where $f,$ $g$ and $h$ are at least $C^{3}$-functions. By differentiating both sides of Eq (2.3) and using Frenet formulas, the following differential equations are obtained:

with nonzero torsion and curvature. Given a unit speed Frenet curve $\alpha \left(s\right)$ with its Frenet vectors $\left\{ T\left(s\right), N\left(s\right), B\left(s\right)\right\}$, the curve

has been defined as vectorial momentum or $\mathbf{X}$-dual curve of $\alpha \left(s\right)$, where $s^{\ast }$ denotes the arc-length parameter of $\beta$ and $\mathbf{X}\left(s\right) \in \left \{ T\left(s\right), N\left(s\right), B\left(s\right) \right \}$.

3.   Dual direction curves of vectorial moments in $\mathbb{E}^{3}$

In this section, based on the above dual curves, we will introduce $T$-dual direction curve, $N$-dual direction curve and $B$-dual direction curve in $E^{3}$ and give some characterizations with the terms $f,$ $g$ and $h$ given in Eq (2.3).

Note that we will use parameter-free demonstrations for some long equations.

Definition 1. Let $\alpha$ be $s$ arc-length parameterized regular curve with nonvanishing curvature and torsion. If the Frenet frame of $\alpha$ is $\left\{ T, N, B\right\},$ then $T$-dual direction curve of $\alpha$ with arc-length parameter $s^{\ast }$ is defined as

Theorem 1. Let $\gamma$ be $T$-dual direction curve of $\alpha$. The Frenet vector fields, curvature and torsion of $\gamma$ are given by

where $\rho = \dfrac{1}{\kappa \sqrt{f^{2}+h^{2}}}$ and $\kappa \neq 0$.

Proof. Let $\alpha$ be $s$ arc-length parameterized curve and $\gamma$ be $s^{\ast }$ arc-length parameterized curve. Also the Frenet apparatus of $\alpha$ is $\{T, N, B, \kappa, \tau \}$ and $\gamma$ is $\{T_{\gamma }, N_{\gamma }, B_{\gamma }, \kappa _{\gamma }, \tau _{\gamma }\}$.

By the definition of $T$-dual direction curve we know that

If we take the derivatives of this equation with respect to $s^{\ast }$ and use the relationship between $\alpha$ and $T$-dual curve of $\alpha$ in ^[14], we get

where $\rho = \dfrac{ds}{ds^{\ast }} = \dfrac{1}{\kappa \sqrt{f^{2}+h^{2}}}.$

Then by making some calculations, we have the following quantities:

Using the above quantities and Eqs (2.1) and (2.2), the expressions mentioned in the theorem can be reached easily.

Theorem 2. Let $\alpha \left(s\right)$ be a regular unit speed curve with $\kappa \neq 0$ and $\tau \neq 0$. The coefficients of the vectors $T,$ $N$ and $B$ of tangent vector of its $T$-dual direction curve are constant, then $T$-dual direction curve is general helix if and only if $\alpha$ is general helix with the position vector

Also in this case, curvature and torsion of $\alpha$ are

and

where $c_{1}, c_{2}\in \mathbb{R} \backslash \left\{ 0\right\}$ and $c_{3}$–$c_{5}\in \mathbb{R}.$

Proof. Let us suppose that $\alpha$ is a general helix and the coefficients of the vectors $T,$ $N$ and $B$ of tangent vector of its $T$-dual direction curve are constant. So, we have from the Theorem 1 and definition of general helix that $\tau \left(s\right) = c_{1}\kappa \left(s\right)$, $h\left(s\right) \tau \left(s\right) = c_{2}$ and $g\left(s\right) \tau \left(s\right) = c_{3}$ where $c_{1}, c_{2}$ and $c_{3}$ are nonzero constants. From Eqs (2.4) and (2.6), we obtain

and from Eq (2.5), we get

By comparing Eqs (3.1) and (3.2), we find the curvature and torsion of $\alpha$ as:

By substituting $\kappa$ and $\tau$ in Eq (2.5) and solving it for $g$, we have

Using equations

and

which come from $h\left(s\right) \tau \left(s\right) = c_{2}$ and $g\left(s\right) \tau \left(s\right) = c_{3}$, final results in theorem are obtained.

Theorem 3. Let $\alpha \left(s\right)$ be a regular unit speed curve with $\kappa \neq 0$ and $\tau \neq 0$. There is no any general helix where the coefficients of the vectors $T,$ $N$ and $B$ of tangent vector of its $T$-dual direction curve (as a general helix) are nonconstant.

Proof. Suppose that the coefficients of $T,$ $N$ and $B$ of $T_{\gamma }$ are nonconstant. If $\alpha \left(s\right)$ is a general helix, then $\tau \left(s\right) = c_{1}\kappa \left(s\right)$ and the angle $\theta \neq 0$ is constant which is formed between $T$ and constant direction $U$ indicated as

Hence, we get $\cot \theta = c_{1}$ and $\cos \theta = c_{1}\sin \theta.$ From Theorem 1 and Eq (3.3), we obtain

If the above expression is arranged as

it will be seen that $\dfrac{h}{g}$ must be constant to make this equation constant. The fact that $\dfrac{h}{g}$ is constant contradicts with the fact that the coefficients of $T,$ $N$ and $B$ of $T_{\gamma }$ are nonconstant. So the result is appear.

Definition 2. Let $\alpha$ be $s$ arc-length parameterized regular curve with nonvanishing curvature and torsion. If the Frenet frame of $\alpha$ is $\left\{ T, N, B\right\},$ then $N$-dual direction curve of $\alpha$ with arc-length parameter $s^{\ast }$, is defined as

Theorem 4. Let $\phi$ be $N$-dual direction curve of $\alpha$. Then Frenet vector fields, curvature and torsion of $\phi$ are given by

where $\rho = \dfrac{1}{\sqrt{\left(1+\kappa g\right) ^{2}+\left(\kappa h+\tau f\right) ^{2}+\tau ^{2}g^{2}}}$ and $\kappa \neq 0$.

Proof. The proof can be made in the same way as Theorem 1.

Theorem 5. Let $\alpha \left(s\right)$ be a regular unit speed curve with $\kappa \neq 0$ and $\tau \neq 0$. Let the coefficients of the vectors $T,$ $N$ and $B$ of tangent vector of its $N$-dual direction curve are constant, then $N$-dual direction curve is general helix if and only if $\alpha$ is general helix with the position vector

Also in this case, curvature and torsion of $\alpha$ are

and

where $c_{2}\in \mathbb{R} \backslash \left\{ 0\right\}$, $c_{1}, c_{3}, c_{4}\in \mathbb{R}$ and $c_{1}c_{2}\neq c_{3}.$

Proof. Let's consider that the main curve $\alpha$ is a general helix and the coefficients of the vectors $T,$ $N$ and $B$ of tangent vector of its $N$-dual direction curve are constant. So, we have from Theorem 4 and definition of general helix that $\tau \left(s\right) = c_{1}\kappa \left(s\right)$, $h\left(s\right) \kappa \left(s\right) = c_{2}$ and $f\left(s\right) \kappa \left(s\right) = c_{3}$ where $c_{1}, c_{2}$ and $c_{3}$ are nonzero constants. From Eq (2.5), we obtain

Since $h\left(s\right) \kappa \left(s\right) = c_{2}$ and $f\left(s\right) \kappa \left(s\right) = c_{3}$, we have $\frac{h}{f} = \frac{c_{2}}{c_{3}}$ and also $c_{3}h^{\prime } = c_{2}f^{\prime }$. In the last equation if we use Eqs (2.4) and (2.6), then we find

By rewriting Eq (3.4) in (3.5) and using $\tau \left(s\right) = c_{1}\kappa \left(s\right),$ we get the curvature and torsion of $\alpha$ as

By substituting $\kappa$ in $h\left(s\right) \kappa \left(s\right) = c_{2}$ and $f\left(s\right) \kappa \left(s\right) = c_{3}$, we have

Theorem 6. Let $\alpha \left(s\right)$ be a regular unit speed curve with $\kappa \neq 0$ and $\tau \neq 0$. Let all the coefficients of the vectors $T,$ $N$ and $B$ of tangent vector of its $N$-dual direction curve are nonconstant, then $N$ -dual direction curve is general helix if and only if $\alpha$ is general helix with the curvature and torsion

and

where $\omega \left(s\right) = e^{\int \dfrac{h^{2}\left(s\right) }{ g^{2}\left(s\right) }ds}, c_{1}\in \mathbb{R} \backslash \left\{ 0\right\}$ and $c_{2}\in \mathbb{R}.$

Proof. Assume that all the coefficients of the vectors $T,$ $N$ and $B$ of $T_{\phi }$ are nonconstant. If $\alpha \left(s\right)$ is a general helix, then $\tau \left(s\right) = c_{1}\kappa \left(s\right)$ and the angle $\theta \neq 0$ is constant which is formed between $T$ and constant direction $U$ indicated as

Therefore, we get $\cot \theta = c_{1}$ and $\cos \theta = c_{1}\sin \theta.$ From Theorem 4 and Eq (3.6), we can obtain

Differentiating this equation according to $s$ and by using Eqs (2.4)–(2.6), we have

There is no any solution for $c_{1}f\left(s\right) +h\left(s\right) = 0.$ Because if $c_{1}f\left(s\right) +h\left(s\right) = 0$, then the coefficients of $T,$ $N$ and $B$ of $T_{\phi }$ are constant. This is a contradiction. So the right term of equation must be zero. Namely

Solving last equation for $c_{1}$, we have

Since $c_{1}$ is constant, then by differentiating Eq (3.7) and by using Eqs (2.4)–(2.6); we have

When we solve this differential equation we find that

where $\omega \left(s\right) = e^{\int \dfrac{h^{2}\left(s\right) }{ g^{2}\left(s\right) }ds}.$ It is easy to see that if $\dfrac{\tau _{\phi }}{ \kappa _{\phi }}$ is constant, by using Theorem 4 and Eqs (2.4)–(2.6), then $\alpha$ is a general helix.

Definition 3. Let $\alpha$ be $s$ arc-length parameterized regular curve with nonvanishing curvature and torsion. If the Frenet frame of $\alpha$ is $\left\{ T, N, B\right\},$ then $B$-dual direction curve of $\alpha$ with arc-length parameter $s^{\ast }$, is defined as

Theorem 7. Let $\sigma$ be $B$-dual direction curve of $\alpha$. Then Frenet vector fields, curvature and torsion of $\sigma$ are given by

where $\rho = \dfrac{1}{\sqrt{\left(f^{2}+h^{2}\right) \tau ^{2}+1}}$ and $\kappa \neq 0$.

Proof. The proof can be made in the same way as the Theorem 1.

Theorem 8. Let $\alpha \left(s\right)$ be a regular unit speed curve with $\kappa \neq 0$ and $\tau \neq 0$. Let the coefficients of the vectors $T,$ $N$ and $B$ of tangent vector of its $B$-dual direction curve be constant, then $B$-dual direction curve is general helix if and only if $\alpha$ is general helix with the position vector

Also in this case, curvature and torsion of $\alpha$ are

and

where $c_{1}, c_{3}\in \mathbb{R} \backslash \left\{ 0\right\}$, $c_{1}$–$c_{6}\in \mathbb{R}$.

Proof. Let us suppose that, $\alpha$ is a general helix and the coefficients of $T,$ $N$ and $B$ vectors of tangent vector of its $B$-dual direction curve are constant. So we have from the Theorem 7 and definition of general helix $\tau \left(s\right) = c_{1}\kappa \left(s\right)$, $g\left(s\right) \kappa \left(s\right) = c_{2}$ and $f\left(s\right) \kappa \left(s\right) = c_{3}$ where $c_{1}$–$c_{3}$ are nonzero constants. From Eqs (2.4) and (2.6), we obtain

and from Eq (2.5), we get

By comparing Eqs (3.8) and (3.9), we obtain the curvature and torsion of $\alpha$ as

By substituting $h\tau$ and $f\kappa$ in Eq (2.5), we have

Using equations

and

which come from $g\left(s\right) \kappa \left(s\right) = c_{2}$ and $f\left(s\right) \kappa \left(s\right) = c_{3}$, we complete the proof.

Theorem 9. Let $\alpha \left(s\right)$ be a regular unit speed curve with $\kappa \neq 0$ and $\tau \neq 0$. There is no any general helix where the coefficients of the vectors $T,$ $N$ and $B$ of tangent vector of its $B$-dual direction curve (as a general helix) are nonconstant.

Proof. Assume that the coefficients of $T,$ $N$ and $B$ of $T_{\sigma }$ are nonconstant. If $\alpha \left(s\right)$ is a general helix, then $\tau \left(s\right) = c_{1}\kappa \left(s\right)$ and the angle $\theta \neq 0$ is constant which is formed between $T$ and constant direction $U$ indicated as

Hence, we get $\cot \theta = c_{1}$ and $\cos \theta = c_{1}\sin \theta.$ From Theorem 7 and Eq (3.10), we obtain

If the above expression is arranged as

it will be seen that $\dfrac{f}{g}$ must be constant to make this equation constant. The fact that $\dfrac{f}{g}$ is constant contradicts with the fact that the coefficients of $T,$ $N$ and $B$ of $T_{\sigma }$ are nonconstant. So the proof is completed.

Example 1. A circular helix is considered as $\alpha :\left(-\pi, \pi \right) \rightarrow E^{3}$ given by

One can calculate its T-dual, N-dual, B-dual direction curves as the following:

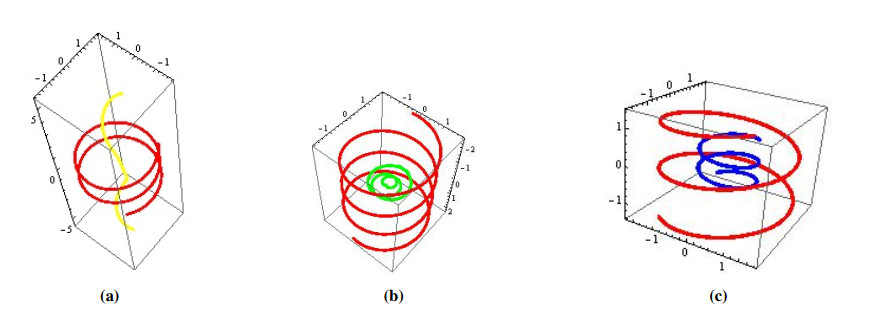
where $c_{1}$–$c_{3}$ are constants. The main curve $\alpha$ and its $T$-dual, $N$-dual, $B$-dual direction curves are shown in the following computer generated graphs. In Figure 2, red curve is $\alpha$ and yellow, green, blue curves are indicated $\gamma, \phi$ and $\sigma$ respectively.

Example 2. A general helix is considered as $\alpha :\left(-\pi, \pi \right) \rightarrow E^{3}$ given by

T-dual, N-dual, B-dual direction curves of general helix can be calculated and represented by the following figures. In Figure 2, red curve is the main curve.

Example 3. A slant helix is considered as $\alpha :\left(-\pi, \pi \right) \rightarrow E^{3}$ given by

$T$-dual, $N$-dual, $B$-dual direction curves of slant helix can be calculated and represented by the following figures. In Figure 3, the red curve is the main curve.

4.   Conclusions

The main point of the study was that generate some new associated curves by constructing some integral curves of a vector field created by vectorial moments of a curve. These new curves are known as dual-direction curves. We establish some links between a Frenet curve and its dual-direction curves.

Further research and applications of dual-direction curves invariably lead to research on different areas. The ways of obtaining helix with the help of dual-direction curves are discussed, and the helix pairs determined by the method here may be helix samples that stabilize linear chain polymers. Research can be made in this direction.

Moreover, for the interest of the readers of our paper, the results presented here have the potential to motivate further researchers of the subject of special ruled surface that can be created using dual-direction curves. This is something that should be looked into further.

Conflict of interest

The authors declare no conflict of interest.