Modeling the role of public health intervention measures in halting the transmission of monkeypox virus

1.   Introduction

The outbreak of the monkeypox virus (mpoxv) across numerous non-endemic countries since May 2022 shows some distint clinical and epidemiological features from previous mpoxv outbreaks, most notably its discerned development and dominance amongst men who have sex with men (MSM) or those who identify as gay or bisexual ^[14]. The majority of recent mpoxv cases have no history of travel to endemic regions or proven contact with infected animals ^[14]. The geographic dispersion and rapid increase in cases indicate substantial person-to-person transmission rather than infection from an animal reservoir ^[14]. Additionally, this is the first significant outbreak of mpoxv that is MSM-dominated and has a significant sexually associated transmission route ^[14,34]. It has also been discovered in Nigeria that mpoxv is likely more predominant in young males and is also linked to genital lesions ^[14,21,35].

By March 2023, more than 86,000 people have been infected with mpoxv worldwide, among which more than 98% of infections have occurred in places that have not experienced transmission of this disease before. Over 100 people have died since the large outbreak of mpoxv in May 2022 ^[7]. In the USA, there have been over 30,000 cases (with 38 death cases), with the largest number of infections since the beginning of the large epidemics in 2022 ^[8]. The majority of those infected are MSM ^[14].

Mpox, a disease caused by mpoxv, spreads from person to person through close contact with respiratory secretions or skin sores from an infected individual ^[47]. Transmission via respiratory droplets requires prolonged face-to-face contact ^[47], which makes healthcare professionals, household members, and other close contacts of active cases especially vulnerable ^[47]. The longest documented chain of transmission has increased from 6 to 9 person-to-person infections. This could be attributed to a general decline in immunity due to the cessation of smallpox vaccination. Transmission can also occur from mother to fetus via the placenta or during close contact during or after birth ^[47]. The extent to which mpox can be transmitted via sexual contact is still unclear. More research is required to understand this risk fully. Mpoxv is a zoonotic virus that spreads to humans by direct contact with infected animals' blood, body fluids, or cutaneous or mucosal lesions ^[47]. The disease has an incubation period of two to four weeks ^[14,21,47].

A considerable number of epidemic models have been developed and employed to understand mpoxv transmission; see, for instance, ^{[4,12,14,21,29,34,35,36,37,38,46,51,52,53]} and the references therein. In particular, Yuan et al. ^[51] analyzed the transmission dynamics of mpoxv in metropolitan municipalities. Vaccination was incorporated into the model to examine its impact on mpoxv transmission at large gatherings ^[52]. In addition, Endo et al. ^[14] fitted a dynamic model to empirical sexual partnership and mpox data and revealed that the heavy-tailed sexual partnership distribution could be used to explain the expansion of current mpoxv outbreaks, especially among MSM. An SIR-based model was used by Peter et al. ^[36] to explore the transmission behavior of mpox. The model was extended by incorporating a fractional order approach ^[37] to gain more detailed insight into mpoxv transmission. Ward et al. ^[46] also used a statistical modelling framework taken advantage of contact tracing data to investigate the mpoxv dynamics in the UK. Their results suggested that the mpoxv epidemic peaked in the UK in early July and began to decline afterward. A similar technique was implemented by Musa et al. ^[29] to investigate the time-varying reproduction number of mpoxv in Nigeria. They found that mpoxv transmission reached an all-time peak in 2022.

Zumla et al. ^[56] investigated the dynamics of mpoxv transmission outside of endemic areas. They emphasized that effective control of mpoxv requires preventing widespread infection among frontline healthcare workers and the most vulnerable populations. Using a multi-group dynamic model, Yang et al. ^[49] examined the potential for mpox viral transmission from high-risk groups to the general population. They calculated the effective reproduction number ($R_{eff}$) to be larger than 3, indicating that mpoxv is highly transmissible in MSM and that exposure to high-risk individuals must be minimized. They indicated that prevention of community transmission is vital to curb the spread of mpoxv. In a cross-sectional study, Hernaez et al. ^[22] discovered high viral loads in the saliva of most mpox patients using quantitative polymerase chain reaction (PCR), and found that they were associated with the severity of skin lesions and symptoms of systemic disease. To remove mpoxv particles from aerosols that can travel a long distance in the air, new nanofiber filters have been developed ^[22]. Following the discovery of highly viable viral loads in saliva in most mpox patients and mpoxv DNA in droplets and aerosols, the authors concluded that additional epidemiological studies are required to determine whether respiratory route of infection is relevant to the mpoxv outbreak in 2022. Americo et al.^[3] studied the virulence variations of mpoxv clades Ⅰ, Ⅱa, and Ⅱb in a small animal model. They discovered that the clades in the order clade Ⅰ $>$ clade Ⅱa $>$ clade IIb in CAST/EiJ mice exhibit highly significant differences compared to the severity of clinical disease in humans.

Due to the sizable mpoxv outbreaks in non-endemic communities, recommendations from researchers and public health professionals are urgently required to help identify the primary factors causing the outbreaks and to formulate policies for effective control.

Epidemiological modeling has been used widely to study the transmission dynamics of reemerging diseases ^{[1,2,13,15,17,19,20,24]}. To better comprehend the factors behind the recent rapid spread of mpoxv, we used a dynamic model in this work to imitate the mpoxv outbreaks and analyze the transmission behaviour. The model extends earlier ones (such as ^[37]) by taking into account several stages of transmission, such as different infection phases, hospitalization, and individuals who do (or do not) adhere to non-pharmaceutical intervention measures (NPIs).

The remainder of this work is organized as follows. In Section 2, an epidemic model is presented. The model is theoretically analyzed in Section 3. We give numerical results in Section 4, and end the paper with a brief discussion and conclusions in Section 5.

2.   Materials and methods

2.1.   Epidemic data

We retrieved the daily epidemiological cases data of the mpoxv epidemic for the USA, as reported by the Centers for Disease Control Prevention (CDC) ^[7,8] from May 10 through December 14, 2022, following laboratory confirmation and case definition of mpoxv. We used the data to calculate the daily cumulative incidence and examined several mpoxv incidence scenarios for the USA.

2.2.   Epidemic model

This study uses a traditional SEIR-based model to examine the transmission dynamics and evaluate control measures for the mpoxv epidemic. It describes the epidemiological dynamics of mpoxv transmission. To more accurately analyze the transmission behavior of mpoxv, the proposed model accounts for both those who adhere to and do not adhere to NPI measures. The model explicitly distinguishes between the various susceptible and infectious stages to assess the overall transmission dynamics of mpoxv outbreaks. The parameter $\rho$ represents the fraction of newly recruited individuals who comply with NPI measures, while $1-\rho$ represents those who do not comply. The model also considers isolation, which is a critical intervention strategy in mpox prevention and control. Several modeling studies have investigated the impact of isolation in suppressing disease transmission (in which infected people are taken into hospitals or isolation centers to prevent large community outbreaks); see, for example, ^[32,40], and the references therein.

Our model has the following notable features: (ⅰ) We only consider direct or human-to-human transmission routes since we aimed to access the mpoxv transmission dynamics in the USA, which has the highest cases since the re-emergence of mpox on May 2022. (ⅱ) Rodent populations are not incorporated into the model since it is believed that the mpoxv infections in the USA are due to human-to-human transmission. However, the situation is different from sub-Saharan Africa, where mpoxv is endemic, and most of the transmission is zoonotic (i.e., animal-to-human transmission). (ⅲ) Our model extends earlier ones (such as ^[37,53]) by taking into account several stages of transmission, such as different infection phases and hospitalization, as well as individuals who adhere (or do not adhere) to basic NPIs (described as high-risk and low-risk populations) to gain a better insight into the overall mpoxv transmission dynamics in the USA and beyond.

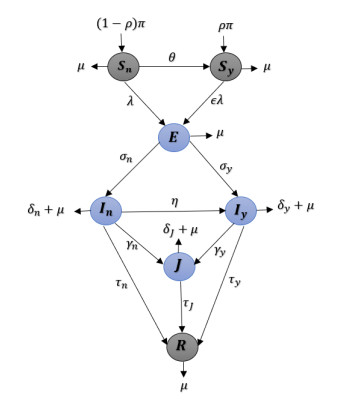
We separate the total population of humans at time $t$, denoted by $N(t)$, into susceptible persons who do not comply with NPIs, $S_n(t)$; susceptible persons who comply with NPIs, $S_y(t)$; exposed persons, $E(t)$; infectious persons who do not comply with NPIs, $I_n(t)$; infectious persons who comply with NPIs, $I_y(t)$; isolated persons, $J(t)$; and recovered persons, $R(t)$, so that $N(t) = S_n(t)+S_y(t)+E(t)+I_n(t)+I_y(t)+J(t)+R(t).$

Figure 1 shows an overview of the mpoxv model and Table 1 lists the state variables and parameters, which satisfy the following system of nonlinear ordinary differential equations:

The model's force of infection is formulated as follows:

Note that $0 < \alpha < 1$ and $0 < \epsilon < 1$ represent alteration parameters for the reduction of infectiousness and efficacy for compliance of NPIs, respectively.

2.3.   Basic epidemiological characteristics of the model

Since the model (1) examines the dynamics of mpoxv infection in humans, all of its state variables and parameters are presumptively positive. To study the fundamental analytic characteristics of model (1), we must first take into account the rate of change of the entire human population, $N$ ($N^{\prime}(t)$, the prime here denotes the derivative with respect to time), which is calculated as follows.

2.3.1.   Positivity of model solutions

For the mpoxv model (1) to be biologically reasonable, all state variables must be positive at time $t > 0$. In other words, solutions of model (1) with positive initial data will remain positive for all time $t > 0$.

Lemma 2.1. Let the initial data $\Theta(0)\geq 0$, where $\Theta(t) = \left(S_n, S_y, E, I_n, I_y, J, R \right)$. Then the solutions $\Upsilon(t)$ of model (1) are positive for all $t > 0$.

Proof. Let $t^1 = sup\left\lbrace t > 0 : \Theta(t) > 0 \in [0, t]\right\rbrace$. Thus, $t^1 > 0$. Since $\pi$ and $1-\rho$ are positive, it follows from the first equation of the model (1) that

Following the comparison theorem in conjunction with the separation of variables method ^[23,39,50], we have

Hence, $S_n(t) > 0$. Similarly, it can be shown that the remaining components of $\Theta(t)$, i.e., $S_y, E, I_n, I_y, J, R$ are all positive for all $t > 0$. Hence, $\Theta(t) > 0$ for all $t > 0$. □

2.3.2.   Invariant region

The following biological feasible region is considered:

Since $N$ is positive, to ensure that any solutions of the system that start in the region $\Omega$ remain in $\Omega$ for all non-negative time $t$, it is sufficient to look at solutions that are limited to $\Omega$, which is positively-invariant. Therefore, the results for a normal existence, uniqueness, and continuity will be satisfied for model (1) per earlier works ^[23,39,50].

3.   Analytical results

3.1.   Disease-free equilibrium

Disease-free equilibrium (DFE) of model (1), denoted by $\Gamma^{0}$, is obtained by setting all the equations of the right-hand side of model (1) to zero, that is $\frac{dS_{n}}{dt} = \frac{dS_{y}}{dt} = \frac{dE}{dt} = \frac{dI_{n}}{dt} = \frac{dI_{y}}{dt} = \frac{dJ}{dt} = \frac{dR}{dt} = 0$. This yields $S^{0}_{n} = \frac{(1-\rho)\pi}{\theta+\mu}$, $S^{0}_{y} = \frac{\rho\pi + \theta S_n^0}{\mu}$, $E^{0} = I^{0}_{n} = I^{0}_{y} = J^{\ast} = R^{0} = 0$. The DFE for model (1) is given by

3.2.   Basic reproduction number

Here, we use the next-generation matrix (NGM) method, which was introduced by van den Driessche & Watmough in ^[45], to calculate model's basic reproduction number ${\mathcal{R}}_{0}$, which is the number of secondary cases that a typical primary case would produce in a fully susceptible population during the infectious period ^{[10,32,44,45]}. Using the NGM technique, the matrices $F$, which stands for the new infection terms, and $V$, which stands for the other transfer terms are calculated and provided below. Note that the linear stability $\Gamma^{0}$ is calculated using (4).

where $A_1 = \sigma_n+\sigma_y + \mu$, $A_2 = \eta+\gamma_n+\tau_n+\delta_n+\mu$, $A_3 = \gamma_y+\tau_y+\delta_y+\mu$, and $A_4 = \tau_J+\delta_J+\mu$. Consequently, the mpoxv infection and transition matrices are computed as follows:

Therefore, the ${\mathcal{R}}_{0}$ is now computed as

with $\rho$ characterising the spectral radius of the NGM, $B_1 = \frac{\beta (S_n^0 +\epsilon S_y^0)}{N^0}$, and $B_2 = \frac{\beta \alpha (S_n^0 +\epsilon S_y^0)}{N^0}$.

Therefore, based on the Theorem in ^[45], we established the following results about local stability of the DFE of model (1).

Theorem 3.1. The DFE of model (1) is locally-asymptotically stable whenever ${\mathcal{R}}_{0} < 1$ and unstable if ${\mathcal{R}}_{0} > 1$.

A value $\mathcal{R}_{0} < 1$ indicates that a small number of mpoxv cases cannot lead to a large outbreak. For mpoxv containment measures in the epidemic model (1), making $\mathcal{R}_{0} < 1$ necessary. Thus, whenever ${\mathcal{R}}_{0} < 1$, mpoxv can be eradicated over time, while mpoxv persistence is continuous for ${\mathcal{R}}_{0} > 1$. Therefore, adequate NPI measures are required to mitigate the disease effectively.

3.3.   Endemic equilibrium

When mpoxv infiltrates a community, at least one infected compartment is not empty. Following some algebraic manuplulation, we obtain an endemic equilibrium (EE) state by setting the vector field of the system (1) to zero. Thus, the EE is now given by

The following equations give the EE points in terms of $\lambda^{*}$.

Epidemiologically, the existence of the EE state indicates that at least one of the infected classes in the model is not empty, which shows that the mpoxv spreads and persists in the community.

3.4.   Stability analysis of the endemic equilibrium

In this section, we examine the model's interior feasible region, which converges to the singular EE, denoted by $\Gamma^*$ (6), whenever ${\mathcal{R}}_{0} > 1$. The mpoxv will spread and remain in a population at $\Gamma*$. By driving a Lyapunov function for a model, we demonstrate the overall stability of the EE. This method has been used extensively in earlier works ^[27,39,50].

Theorem 3.2. The EE $\Gamma^*$ is globally asymptotically stable (GAS) in the region $\Omega$ whenever ${\mathcal{R}}_{0} > 1$ under a specific condition (see Appendix A).

Appendix A contains a proof of the aforementioned Theorem 3.2. In addition, in Appendix B, a bifurcation phenomenon is analyzed to further assess the dynamics of the model with respect to ${\mathcal{R}}_{0}$.

4.   Numerical results

4.1.   Fitting results

We obtained reported mpoxv outbreak data for the USA from the Centers for Disease Prevention and Control (CDC) ^[8] and fitted the mpoxv model(1) to the data using Pearson's Chi-square test and the least-squares framework, implemented in the R statistical software (version 4.1.1) ^[23,54].

In the numerical fitting results, the daily and cumulative numbers of mpoxv cases from May 10, 2022, through December 14, 2022, were used to fit the mpoxv model. As shown in Figure 2, the results revealed that the model (1) fitted the cumulative and the daily number of reported cases of mpoxv well, indicating that the model can be used to explain the transmission behavior of the mpoxv dynamics, since it reproduces the patterns of real data on the mpox situation in the USA. The parameter values used to fit the model are given in Table 2, with $N(0) = 3.35374570 \times 10^8$ million ^[9,48], $S_n(0) = 2.5\times 10^8$, $S_y(0) = 0.8\times 10^8$, $E = 800$, $I_n(0) = 5$, $I_y(0) = 1$, $J(0) = 0$, $R(0) = 0$.

4.2.   Numerical simulations

This section presents various numerical results for the proposed mpoxv model using parameters from Table 2 and different initial conditions for the model's state variables. The model (1) was simulated using the R statistical software to examine its dynamics by varying the values of the transmission rate parameter, which is one of the most crucial parameters in the model and needs to be minimized to control the spread of mpoxv effectively ^{[14,15,17,21,26,33,42,50]}. Figure 3(a)–(d) presents the simulation results. In Figure 3, we used the initial value of $\beta$, whereas, in Figure 3(c) and (d), we simulated the model by decreasing the values of $\beta$ by $25\%$, $50\%$, and $75\%$, respectively, to examine the corresponding dynamics of $I_n$ and $I_y$ in each case.

4.3.   Sensitivity analysis

In epidemiological modeling studies, the basic reproduction number ${\mathcal{R}}_{0}$ is a crucial parameter that determines whether the disease will continue to spread (persist) or die out in a community when an epidemic occurs ^[16]. In the current model, we used ${\mathcal{R}}_{0}$ and the infection attack rate as response functions to determine the partial rank correlation coefficient (PRCC) for sensitivity analysis to find the most sensitive biological parameters in the model that require maximum attention for mitigation and control ^{[16,32,43,55]}. Our sensitivity analysis results show that the parameters $\beta$ (transmission/contact rate), $\alpha_1$, and $\epsilon$ are the most sensitive, followed by $\gamma_n$ and $\tau_y$. The PRCC of the basic reproduction number, ${\mathcal{R}}_{0}$, and the infection attack rate of the model (1) are presented with the estimated parameters in Figure 4.

4.4.   Simulations of the global asymptotic stability of the endemic equilibrium

Following the previous approach ^{[17,33,39,42,50]}, we provide some numerical examples in this section to demonstrate the global asymptotic stability of the analytical results for the model (1) as provided in the appendix A. All the parameters have the same biological meaning as in Table 2. In Figure 5, we consider the case when the transmission rate parameter $\beta = 0.157$, so that $\mathcal{R}_{0}$ = $0.78686606 < 1$, while the other parameters have the same values as given in Table 2, with different initial conditions for the model's state variables. The dynamics of the model (1) with $\mathcal{R}_{0} < 1$ are presented in Figure 5(a)–(d), which show that the system (1) has an EE, which is GAS whenever $\mathcal{R}_{0} < 1$. In Figure 6, we consider the case when the transmission rate parameter $\beta = 0.257$, so that $\mathcal{R}_{0} = 1.28805464 > 1$, while the other parameters have the same values as given in Table 2, with different initial conditions for the model's state variables. The dynamics of the model (1) with $\mathcal{R}_{0} > 1$ are presented in Figure 6(a)–(d) which show that the system (1) has an EE which is unstable whenever $\mathcal{R}_{0} > 1$. These results support the theoretical result stated in Theorem 3.1.

5.   Discussion and conclusions

Mpox is primarily a zoonotic viral disease that has caused recurrent outbreaks in West Africa and is occasionally transmitted to other regions ^[47]. It is transmitted to humans through contact with an infected individual or animal, respiratory droplets, or contaminated materials such as bedding ^[14]. The recent global outbreaks of mpoxv in non-endemic countries have caused substantial public health concern ^[7]. Although the vaccine used for smallpox is currently in use against mpoxv infection, due to inadequate vaccination levels, the public need to follow basic health precautions to protect themselves and others from mpoxv infection ^[47].

In this work, we developed a classical SEIR-based model to assess the transmission dynamics of mpoxv epidemics in the USA. The model was fitted successfully to the reported mpoxv cases and relevant demographic data in the USA. Thus, it can be used to explain the transmission of mpoxv and provide suggestions for optimal control and prevention of the disease. The theoretical and epidemiological outcomes of this work are summarized below.

${\rm{i}})$ Results on the basic reproduction number of the model were determined analytically and were used to assess the impact of mpoxv control strategies. In addition, subsequent mathematical analysis revealed that the DFE of the model is GAS whenever the ${\mathcal{R}}_{0}$ value is below or equal to unity and is unstable when the ${\mathcal{R}}_{0}$ is above unity. Further mathematical analysis showed that the EE is GAS whenever ${\mathcal{R}}_{0}$ is above unity, indicating the potential for mpoxv to spread and persist in a population. Moreover, we analyzed the forward bifurcation property of the model, which occurs under certain conditions (see Appendix B for more detail). Epidemiologically, the existence of forward bifurcation in the model indicates that the stability of the model exchanges between DFE and EE at ${\mathcal{R}}_{0} = 1$.

Hence, the stability behavior of the model changes (from stable to unstable) around the endemic equilibrium when the bifurcation parameter $\beta_{hh}$ changes ^[11,17].

${\rm{ii}})$ The model prediction results provided in Section 4.1 using the daily number of reported mpoxv cases in the USA for the period from May 10 to December 14, 2022, show that the model fitted well to the mpoxv case data, highlighting the applicability of the model to the wave of mpoxv outbreaks.

${\rm{iii}})$ Numerical results were provided in Section 4.2 to examine the dynamics of the model (1) by decreasing the value of the transmission rate parameter $\beta$ by $25\%$, $50\%$, and $75\%$, in turn, for each of the variables $I_n$ and $I_y$. We chose the parameter $\beta$ since it is one the most crucial parameters in the model and needs to be minimized to effectively control the spread of mpoxv. The results show that the transmission of mpoxv can be significantly reduced if the transmission rate parameter can be decreased as much as possible. This could be achieved if most members of the public complied with NPIs and if governments and other relevant organizations provided adequate medical resources, especially to the most vulnerable communities, to respond to epidemics effectively.

${\rm{iv}})$ The basic reproduction number and infection attack rates were used as response functions to perform sensitivity analysis of the model (presented in Section 4.3). Partial rank correlation coefficients (PRCC) were used for the sensitivity analysis, which showed that the top three PRCC ranked parameters are the transmission rate, the parameter representing the efficacy of compliance with NPIs in preventing mpoxv infection, and the modification parameter for the reduction of infectiousness. Other parameters with high PRCCs suggesting high priority (although not as high as the top three) include the isolation rate from $I_n$ and recovery rate from $I_y$. Hence, this study has identified the parameters that should be targeted for effective mpoxv control and prevention.

${\rm{v}})$ Further numerical results were provided in Section 4.4 to investigate the global stability of the EE for the model (1). The results are illustrated in Figures 5 and 6 and support the theoretical results obtained in 3.2, which revealed that the EE is GAS when ${\mathcal{R}}_{0} > 1$.

In summary, this work employed an SEIR-based model to study and theoretivcally analyze the mpoxv transmission dynamics in the US to shed light on the transmission of mpoxv epidemics, taking into account the roles of NPIs on the overall transmission dynamics. We revealed some vital epidemiological parameters that should be emphasized efforts to mitigate and control of mpoxv. Based on our results, we also observed that the transmission rate and other relevant parameters are crucial in controlling the spread of mpoxv outbreaks. The results in this paper could play an essential role in developing a long-term plan for controlling mpoxv epidemics, especially for researchers and policymakers. Moreover, our findings could provide an essential reference for policymakers to contain the virus's spread effectively. The model could be extended in the future by incorporating other control vital factors such as pharmaceuticals, human behavior, and seasonality to gain more insight into the transmission of mpoxv.

Acknowledgments

Part of this research was funded and supported by the Deanship of Scientific Research at Imam Mohammad Ibn Saud Islamic University (IMSIU) through Research Partnership Program with number: RP-21-09-07.

Conflict of interest

The authors declare no conflict of interest.

Appendix A: Proof of global stability analysis

In this section, we prove Theorem 3.2.

Proof. To prove Theorem 3.2, we adopted previous technique ^[39,41,50], and designed a Lyapunov function given below.

Therefore, the derivative of the Lyapunov function (A-1) calculated along solutions of the model (1) is given by

By direct computation from Eq (A-2), we have

and,

and,

and,

similarly,

and,

Substituting $\iota_1 = \iota_2 = \iota_3 = \iota_5 = \iota_6 = 1$, $\iota_4 = \frac{\lambda^* S_n^*+\epsilon\lambda^* S_y*}{\sigma_n E^*}$ and Eqs (A-3)–(A-8) into Eq (A-2), we have

Suppose, a function is define as $u(x) = 1-x+\ln x$, then, if $x > 0$ it leads to $u(x) \leq0$. Also, if $x = 1$, then $u(x) = 0$. Implies that $x-1\geq \ln(x)$ for any $x > 0$ ^[28,50]. By using the above definition, direct calculation from Eq (A-8), and conditions (ⅰ) and (ⅱ), we have

Similarly

Also from Eq (A-7), we have

Similarly,

Hence,

Equations (A-3)–(A-17) and conditions (ⅰ) $(1-\frac{\lambda}{\lambda^*})(1-\frac{I_n \lambda^*}{I_n^*\lambda}) \geq 0$, (ⅱ) $\frac{I_y}{I_y^*}+\frac{E}{E^*} \geq \ln\bigg(\frac{I_y}{I_y^*}\bigg)+\ln\bigg(\frac{E}{E^*}\bigg)$, $\frac{I_y}{I_y^*}+\frac{I_n}{I_n^*} \geq \ln\bigg(\frac{I_y}{I_y^*}\bigg)+\ln\bigg(\frac{I_n}{I_n^*}\bigg)$, $\frac{J}{J^*}+\frac{I_n}{I_n^*} \geq \ln\bigg(\frac{J}{J^*}\bigg)+\ln\bigg(\frac{I_n}{I_n^*}\bigg)$, and $\frac{J}{J^*}+\frac{I_y}{I_y^*} \geq \ln\bigg(\frac{J}{J^*}\bigg)+\ln\bigg(\frac{I_y}{I_y^*}\bigg)$, ensure that $\dot{\gimel(t)}\leq 0$. Further, the equality $\frac{d\gimel}{dt} = 0$ holds only if $S_n = S_n^{*}$, $S_y = S_y^{*}$ $E = E^{*}$, $I_n = I_n^{*}$, $I_y = I_y^{*}$, and $J = J^{*}$. Thus, the EE state (B-1), is the only positive invariant set to the system (1) contained entirely in $\biggl\{(S_n, S_y, E, I_n, I_y, J) \in \Omega : S_n = S_n^{*}, S_y = S_y^{*}, E = E^{*}, I_n = I_n^{*}, I_y = I_y^{*}, J = J^{*} \biggr\}$. Hence, it follows from LaSalle's invariance principle ^[27] that every solution to the Eq (1) with initial conditions in $\Omega$ converge to EE points, $\Gamma ^{*}$, as $t\rightarrow \infty$. Thus, the positive EE is globally asymptotically stable.

Appendix B: Bifurcation analysis

The bifurcation analysis is carried out using center manifold theory (CMT), as presented by Castillo-Chavez and Song ^[6]. The conditions for the parameter values in the model (1) that result in forward or backward bifurcation are investigated. This approach has been widely used in earlier works, for example, ^{[5,6,18,31,45]}. When $\mathcal{R}_0$ crosses unity from below, there is a forward bifurcation, which results in the loss of stability of the DFE and the appearance of a small positive asymptotically stable equilibrium ^[6].

Theorem 5.1. The mpoxv model (1) undergoes forward bifurcation at $\mathcal{R}_0 = 1$ whenever the bifurcation coefficients, $A$ and $B$, are negative and positive, respectively.

Proof. Following ^[5,6,30,45], we employ CMT. First, we let $\dfrac{dx}{dt} = f(x, \Xi)$, where $\Xi$ is the bifurcation parameter, and $f$ is continuously differentiable at least twice with respect to both $x$ and $\Xi$. The DFE ($\Gamma^0$) is the point $(x_0 = 0, \Xi = 0)$ and the local stability of $\Gamma^0$ changes at the point $(x_0, 0)$ ^[45]. We define a nontrivial equilibrium near the bifurcation point $(x_0, \Xi)$.

Suppose that $\beta = \beta^*$ is chosen as a bifurcation parameter and we let $\mathcal{R}_0 = 1$ from (3). Then, by Theorem 5.1, the DFE $\Gamma^0$, is locally stable when $\beta < \beta^*$ and unstable when $\beta > \beta^*$. Here $\beta = \beta^*$ is a bifurcation value.

For convenience, let $S_n = x_1$, $S_y = x_2$, $E = x_3$, $I_n = x_4$, $I_y = x_5$, $J = x_6$ and $R = x_7$, so that $N = x_1+x_2+x_3+x_4+x_5+x_{6}+x_7$. Further, by adopting the same vector notation with $x = (x_1, x_2, ..., x_{7})^T$, the model (1) can be written as $\frac{dx}{dt} = f(x)$ where $f = (f_1, f_2, ..., f_{7})^T$ is as follows:

where the associated forces of infection are respectively given by

The Jacobian matrix of the system (B-2) (computed from the relation $J(\Gamma^0) = F-V$, where $F$ and $V$ are infection and transition matrices, respectively), evaluated at the DFE $(\Gamma^0)$ with $\beta = \beta^*$, is given by

where

$c_1 = {\frac {A_{{5}}\beta\, \mu}{{\mu}^{3}\rho+\theta\, \left(2\, \rho+1 \right) {\mu}^{2}+ \left(\left(\rho+2 \right) {\theta}^{2}+A_{{5}} \right) \mu+{\theta}^{3}}}$, $c_2 = {\frac {\epsilon\, \left(\mu\, \rho+\theta \right) \left(\theta+\mu \right) ^{2}\beta}{{\mu}^{3}\rho+\theta\, \left(2\, \rho+1 \right) { \mu}^{2}+ \left(\left(\rho+2 \right) {\theta}^{2}+A_{{5}} \right) \mu+{\theta}^{3}}}$,

$c_3 = {\beta \left({\frac {\epsilon\, \pi\, \left(\mu\, \rho+\theta \right) \left(\theta+\mu \right) }{\mu}}+{\frac {\pi\, A_{{5}}}{\theta+\mu}} \right) \left({\frac {\pi\, A_{{5}}}{\theta+\mu}}+{\frac {\pi\, \left(\mu\, \rho+\theta \right) \left(\theta+\mu \right) }{\mu}} \right) ^{-1}}$, $c_4 = {\frac {A_{{5}}\beta\, \alpha\, \mu}{{\mu}^{3}\rho+\theta\, \left(2\, \rho+1 \right) {\mu}^{2}+ \left(\left(\rho+2 \right) {\theta}^{2}+A _{{5}} \right) \mu+{\theta}^{3}}}$,

$c_5 = {\frac {\epsilon\, \left(\mu\, \rho+\theta \right) \left(\theta+\mu \right) ^{2}\beta\, \alpha}{{\mu}^{3}\rho+\theta\, \left(2\, \rho+1 \right) {\mu}^{2}+ \left(\left(\rho+2 \right) {\theta}^{2}+A_{{5}} \right) \mu+{\theta}^{3}}}$, and $c_6 = {\beta\, \alpha \left({\frac {\epsilon\, \pi\, \left(\mu\, \rho+\theta \right) \left(\theta+\mu \right) }{\mu}}+{\frac {\pi\, A_{{5}}}{ \theta+\mu}} \right) \left({\frac {\pi\, A_{{5}}}{\theta+\mu}}+{ \frac {\pi\, \left(\mu\, \rho+\theta \right) \left(\theta+\mu \right) }{\mu}} \right) ^{-1}}$.

The Jacobian matrix $J(\Gamma^0)$ of the system (B-2) has a simple zero eigenvalue (other eigenvalues have negative real parts). Hence, the CMT ^[6,45] can be employed to analyse the dynamics of the system (B-2) located at $\beta = \beta^*$ ^[6]. The subsequent computations are carried out using similar notations as in ^[6].

Eigenvectors of $J(\Gamma^0)_{\beta = \beta^*}$: For the case when $\mathcal{R}_0 = 1$, it can be shown that the $J(\Gamma^0)$ has a right eigenvector (corresponding to the zero eigenvalues), given by $\Psi = (\Psi_1, \Psi_2, ..., \Psi_{7})^T$, where

Similarly, the components of the left eigenvector of $J(\Gamma^0)$ (corresponding to the zero eigenvalue), denoted by $\Phi = (\Phi_1, \Phi_2, ..., \Phi_{7})$, are given by

Note that the free components (entry) are chosen to be $\Phi_{3} = 1$ and $\Psi_{3} = \frac{1}{A_1+A_2}$ respectively, where

so that, ${\textbf v}\cdot {\textbf w} = 1$ (in line with ^[6]).

It can be shown, by computing the non-zero partial derivatives of $f_i\; (i = 1, ..., 7)$, that the associated bifurcation coefficients, $A$ and $B$, are given, respectively, by

where $U_1 = (\Psi_1+\Psi_3+\Psi_4+\Psi_5+\Psi_6+\Psi_7)\epsilon - \Psi_1$ and $U_2 = \epsilon \Psi_2-\Psi_2-\Psi_3-\Psi_4-\Psi_5-\Psi_6-\Psi_7$. Now, since $\Phi_3 > 0$, $\Psi_3 > 0$, $\Psi_4 > 0$, and $\Psi_5 > 0$, indicating that $B \geq 0$, therefore, forward bifurcation occurs if and only if $A < 0$ else we have backward bifurcation (i.e. when $A > 0$). To verify the above results numerically, we computed the expression using the parameter values in Table 2 and found that $A$ ($-651.5562000$) and $B$ ($5.585740031$) were negative and positive, respectively. As a result, forward bifurcation is likely for the mpoxv model (1) at $\mathcal{R}_{0} = 1$. Furthermore, an EE will not exist if $\mathcal{R}_0 < 1$, leaving DFE as the only local attractor. However, if $\mathcal{R}_0 > 1$, the EE exists. Therefore, a forward bifurcation likely exists because disease prevalence is an increasing function of $\mathcal{R}_0$ in the vicinity of the bifurcation point.