Figure 1.
Peridynamic horizon and interaction between material points.
In this paper, we investigate Euler–Maruyama approximate solutions of stochastic differential equations (SDEs) with multiple delay functions. Stochastic differential delay equations (SDDEs) are generalizations of SDEs. Solutions of SDDEs are influenced by both the present and past states. Because these solutions may include past information, they are not necessarily Markov processes. This makes representations of solutions complicated; therefore, approximate solutions are practical. We estimate the rate of convergence of approximate solutions of SDDEs to the exact solutions in the Lp-mean for p≥2 and apply the result to obtain confidence interval estimations for the approximate solutions.
Citation: Masataka Hashimoto, Hiroshi Takahashi. On the rate of convergence of Euler–Maruyama approximate solutions of stochastic differential equations with multiple delays and their confidence interval estimations[J]. AIMS Mathematics, 2023, 8(6): 13747-13763. doi: 10.3934/math.2023698
| [1] | Haiming Liu, Xiawei Chen, Jianyun Guan, Peifu Zu . Lorentzian approximations for a Lorentzian α-Sasakian manifold and Gauss-Bonnet theorems. AIMS Mathematics, 2023, 8(1): 501-528. doi: 10.3934/math.2023024 |
| [2] | Haiming Liu, Jiajing Miao . Gauss-Bonnet theorem in Lorentzian Sasakian space forms. AIMS Mathematics, 2021, 6(8): 8772-8791. doi: 10.3934/math.2021509 |
| [3] | B. B. Chaturvedi, Kunj Bihari Kaushik, Prabhawati Bhagat, Mohammad Nazrul Islam Khan . Characterization of solitons in a pseudo-quasi-conformally flat and pseudo- W8 flat Lorentzian Kähler space-time manifolds. AIMS Mathematics, 2024, 9(7): 19515-19528. doi: 10.3934/math.2024951 |
| [4] | Mehmet Gülbahar . Qualar curvatures of pseudo Riemannian manifolds and pseudo Riemannian submanifolds. AIMS Mathematics, 2021, 6(2): 1366-1376. doi: 10.3934/math.2021085 |
| [5] | Süleyman Şenyurt, Filiz Ertem Kaya, Davut Canlı . Pedal curves obtained from Frenet vector of a space curve and Smarandache curves belonging to these curves. AIMS Mathematics, 2024, 9(8): 20136-20162. doi: 10.3934/math.2024981 |
| [6] | Beyhan YILMAZ . Some curve pairs according to types of Bishop frame. AIMS Mathematics, 2021, 6(5): 4463-4473. doi: 10.3934/math.2021264 |
| [7] | Mohd Danish Siddiqi, Fatemah Mofarreh . Schur-type inequality for solitonic hypersurfaces in (k,μ)-contact metric manifolds. AIMS Mathematics, 2024, 9(12): 36069-36081. doi: 10.3934/math.20241711 |
| [8] | Aliya Naaz Siddiqui, Meraj Ali Khan, Amira Ishan . Contact CR δ-invariant: an optimal estimate for Sasakian statistical manifolds. AIMS Mathematics, 2024, 9(10): 29220-29234. doi: 10.3934/math.20241416 |
| [9] | Ayşe Yavuz, Melek Erdoǧdu . Non-lightlike Bertrand W curves: A new approach by system of differential equations for position vector. AIMS Mathematics, 2020, 5(6): 5422-5438. doi: 10.3934/math.2020348 |
| [10] | Sezai Kızıltuǧ, Tülay Erişir, Gökhan Mumcu, Yusuf Yaylı . C∗-partner curves with modified adapted frame and their applications. AIMS Mathematics, 2023, 8(1): 1345-1359. doi: 10.3934/math.2023067 |
In this paper, we investigate Euler–Maruyama approximate solutions of stochastic differential equations (SDEs) with multiple delay functions. Stochastic differential delay equations (SDDEs) are generalizations of SDEs. Solutions of SDDEs are influenced by both the present and past states. Because these solutions may include past information, they are not necessarily Markov processes. This makes representations of solutions complicated; therefore, approximate solutions are practical. We estimate the rate of convergence of approximate solutions of SDDEs to the exact solutions in the Lp-mean for p≥2 and apply the result to obtain confidence interval estimations for the approximate solutions.
Peridynamics (PD) is a new formulation of continuum mechanics that was developed to overcome the limitations of classical continuum mechanics (CCM) [1]. Although CCM has been utilised for the analysis of numerous problems, it is challenged by discontinuities in the displacement field and/or its derivatives, since the governing equations of CCM contain derivatives with respect to space coordinates. On the other hand, equations of motion in PD theory do not have spatial derivatives and, therefore, do not suffer from issues related to discontinuities.
There has been significant progress in PD research, especially in recent years. A general overview of PD can be found in [2]. In this study, recent developments in PD theory are briefly described. Only journal papers published since 2019 were considered since previous ones were reviewed in a former study [3]. The current review is organised under different categories, which are listed in alphabetical
order; relevant studies are discussed. Note that due to the large number of publications available in the literature, only a selected set of publications is presented for each category.
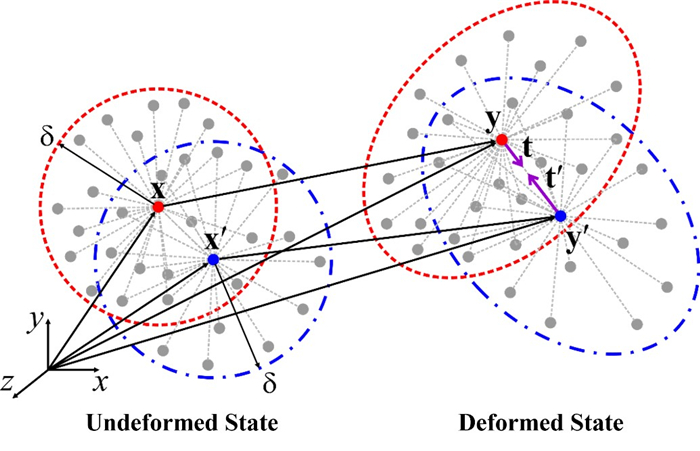
The peridynamic theory is a nonlocal continuum mechanics formulation; its equation of motion can be expressed in Eq 1 as [4]
| ρ(x)¨u(x,t)=∫H(t(u′−u,x′−x,t)−t′(u−u′,x−x′,t))dH+b(x,t) | (1) |
Eq 1 can be rewritten in discrete form in Eq 2 as (see Figure 1):
| ρ(k)¨u(k)=∞∑j=1[t(k)(j)(u(j)−u(k),x(j)−x(k),t)−t(j)(k)(u(k)−u(j),x(k)−x(j),t)]V(j)+b(k) | (2) |
where ρ is the density of a material point, x is the original location of a material point, u represents the displacement of a material point, b is the body load of a material point, t is time, and ".." represents the second derivative with respect to time. Peridynamic force densities between two material points can be defined in Eq 3 as
| t(k)(j)(u(j)−u(k),x(j)−x(k),t)=12Ay(j)−y(k)|y(j)−y(k)| | (3) |
with Eq 4 as
| A=4w(k)(j){ad(y(j)−y(k)|y(j)−y(k)|⋅x(j)−x(k)|x(j)−x(k)|)θ(k)+b(|y(j)−y(k)|−|x(j)−x(k)|)} | (4) |
and in Eq 5
| t(j)(k)(u(k)−u(j),x(k)−x(j),t)=−12By(j)−y(k)|y(j)−y(k)| | (5) |
with Eq 6 as
| B=4w(j)(k){ad(y(k)−y(j)|y(k)−y(j)|⋅x(k)−x(j)|x(k)−x(j)|)θ(j)+b(|y(k)−y(j)|−|x(k)−x(j)|)} | (6) |
Note that y is the current location of a material point. The peridynamic dilatation term can be expressed in Eq 7 as
| θ(k)=d∞∑j=1w(k)(j)s(k)(j)y(j)−y(k)|y(j)−y(k)|⋅(x(j)−x(k))V(j) | (7) |
and the stretch term can be defined in Eq 8 as
| s(k)(j)=(|y(j)−y(k)|−|x(j)−x(k)|)|x(j)−x(k)| | (8) |
The influence function can be chosen in Eq 9 as
| w(k)(j)=δ|x(j)−x(k)| | (9) |
where δ represents the horizon size. The constants, a, b, and d can be expressed in Eqs 10–12, respectively, as
| a=12(κ−5μ3) | (10) |
| b=15μ2πδ5 | (11) |
| d=94πδ4 | (12) |
where κ is the bulk modulus and μ is the shear modulus. For brittle materials, if the stretch between two material points exceeds a critical stretch value, then it can be assumed that the bond (interaction) is broken. The critical stretch for isotropic materials can be obtained in Eq 13 as
| sc=√Gc(3μ+(34)4(κ−5μ3))δ | (13) |
where Gc is the critical energy release rate.
In this section, a large number of journal papers on peridynamics were organised under different categories, which are listed in alphabetical order.
Additive manufacturing is a new and promising manufacturing approach. Hartmann et al. [5] developed a model to simulate the extrusion-based additive manufacturing process of soft polymers using peridynamics. Karpenko et al. [6,7,8] investigated the influence of porosity and residual stresses on fatigue nucleation and crack propagation for additively manufactured titanium alloys based on peridynamic simulations. Kendibilir et al. [9] performed a peridynamic topology optimisation study for additive manufacturing with surface cracks. Zhu et al. [10] worked on a peridynamic buildability analysis of additively manufactured concrete by considering damage, plastic flow, and collapse.
Analytical solutions of peridynamic equations are very limited in the literature. Yang et al. [11] provided the analytical solution for one-dimensional problems. In another study [12], the analytical solution for a two-dimensional membrane was presented. Yang et al. [13,14] also derived analytical solutions for peridynamic beam and plate equations. Mikata [15] presented analytical solutions to linearised peridynamic equations for isotropic and anisotropic materials. Recently, they also provided analytical solutions for three-dimensional isotropic materials under both static and dynamic conditions [16].
Artificial intelligence and machine learning are emerging areas used in many different engineering applications. Kim et al. [17] utilised deep neural networks based on data generated by peridynamic simulations that significantly decreased the computational time for fracture problems. Nguyen et al. [18,19] developed peridynamic-based machine learning models for bond-based and ordinary state-based peridynamics. Bekar and Madenci [20] predicted terms in partial differential equations describing physical phenomena based on measured data and peridynamic differential operators. Xu et al. [21] utilised machine learning to determine a proper peridynamic material model for a particular problem. Ning et al. [22] developed a peridynamic-informed neural network and analysed the displacement field in heterogeneous elastic plates. Babu and Gopalakrishanan [23] presented a peridynamic-based machine learning model for thermal diffusion problems by considering cracks.
In many engineering applications, structures can be simplified by considering them as beams, plates, and shells. These simplifications can significantly reduce the computational time for full three-dimensional models. Peridynamic beam, plate, and shell formulations are also available in the literature. Nguyen et al. [24] presented a peridynamic beam formulation utilised for predicting damage in offshore structures. In another study [25], the authors investigated the thermomechanical behaviour of shell structures. Diyaroglu et al. [26] introduced a new formulation for Euler-Bernoulli beams in an ordinary state-based peridynamic framework. Yang et al. [27] explained how peridynamic beam and plate formulations can be implemented in commercial finite element software packages. They also presented peridynamic formulations for Timoshenko beams [28] and Kirchhoff plates [29]. Vazic et al. [30] investigated the case of a Mindlin plate resting on a Winkler elastic foundation. Oterkus et al. [31] presented a new formulation for peridynamic shell membranes. Yolum and Güler [32] derived a peridynamic formulation for orthotropic Mindlin plates subjected to bending loading. Nguyen and Oterkus [33,34] performed geometrically nonlinear analysis of beams and plates. Shen et al. [35] modelled peridynamic beams and shells by utilising the interpolation method and considering transverse shear effect. Yang et al. [36,37,38] introduced peridynamic formulations for Mindlin plates, higher-order beams, and higher-order plates. Zhang et al. [39] derived the peridynamic Reissner–Mindlin shell theory. Dai et al. [40] performed fracture parameter analysis of flat shells in an ordinary state-based peridynamic framework by considering out-of-plane loading conditions. In another study [41], the authors studied the utilisation of different horizon sizes for the analysis. Moreover, they investigated the fracture behaviour of cracked Mindlin plates under static and dynamic conditions [42]. Naumenko and Eremeyev [43] presented a nonlinear direct peridynamics plate theory. Behzadinasab et al. [44] introduced a new inelastic and rotation-free peridynamic Kirchhoff–Love shell formulation. Yang et al. [45] performed an analysis of peridynamic curved beams. Xia et al. [46] demonstrated the coupling of isogeometric analysis and peridynamics for peridynamic shells.
Buckling and free vibration analyses are important for the durability of structures. Heo et al. [47] utilised peridynamics to determine the natural frequency of cracked plates. Moreover, they also determined critical buckling loads by implementing peridynamics in a commercial finite element framework [48]. Yang et al. [49] performed buckling analysis of beams.
Coatings are widely utilised in many different industrial applications. Their durability is critical to the structure that coatings are attached to. Zhang et al. [50] utilised peridynamics to investigate the fracture behaviour of functionally graded coatings under dynamic conditions. Guski et al. [51] studied the microstructural behaviour of plasma-sprayed ceramic coatings. Vasenkov [52] performed multiphysics analysis to determine damage processes in protective coatings. Wang et al. [53] investigated the fracture behaviour of multilayer thermal barrier coatings. Wen et al. [54] developed a peridynamic model for coupled thermomechanical-oxygenic analysis of carbon/carbon composites with silicon carbide coating.
Composite materials are widely used in different areas due to their superior properties to traditional materials. Analysis of the fracture behaviour of composite materials is complex since various fracture modes can occur, such as delamination, fibre breakage, fibre-matrix splitting, etc. There are many peridynamic studies focused on the analysis of composite materials. Rädel et al. [55] utilised an energy-based damage criterion to investigate fibre-matrix debonding and matrix failure. Gao and Oterkus [56] developed a fully coupled thermomechanical model for composites and investigated the effect of shock loading. Hu et al. [57] introduced a peridynamic model for composite laminates by considering transverse shear deformation and material coupling. Postek and Sadowski [58] investigated the impact behaviour of aluminium oxide/zirconia composite. Basoglu et al. [59] studied how the toughness of unidirectional fibre-reinforced composites can increase by introducing microcracks. Li et al. [60] coupled peridynamics and finite element method to examine the fracture behaviour of composites. Yang et al. [61] developed a peridynamics-based statistical multiscale model to investigate fracture behaviour in composites. Madenci et al. [62] used peridynamics to predict failure in variable angle tow composites. Yang et al. [63] performed out-of-plane damage analysis of composites. Ma et al. [64] analysed interfacial failure in composite materials by using an extended peridynamic model and non-uniform discretization. Wang et al. [65] investigated the fracture mechanics of 2D orthotropic materials based on ordinary state-based peridynamics.
Kamensky et al. [66] developed a peridynamic model of frictional contact. Lu et al. [67] studied fracture due to Hertzian indentation. In another study, they modelled cracks with frictional contact [68]. Wang et al. [69] studied contact fatigue crack initiation and propagation. Zhang et al. [70] examined the sticking and sliding frictional contact by considering fracture. Mohajerani and Wang [71] presented a "touch-aware" frictional contact model suitable for simulating the contact behaviour between irregularly shaped particles. Guan et al. [72] introduced an adaptive contact model including friction. Zhu et al. [73] developed a peridynamic model to investigate stochastic fractures in bolted glass plates. Naumenko et al. [74] examined damage patterns in float glass plates by performing both experiments and peridynamic analysis.
Corrosion is a major challenge for structures subjected to corrosive environments, such as marine structures. There are various corrosion mechanisms, such as uniform corrosion, pitting corrosion, or stress corrosion cracking. Modelling corrosion based on physics and chemistry is complex. However, peridynamics can be a suitable approach to tackle this challenging problem. Rokkam et al. [75] developed a peridynamic model for corrosion damage and crack propagation. Nguyen and Oterkus [76] investigated brittle damage in corroded stiffened structures subjected to static loading conditions. Karpenko et al. [77] studied corrosion fatigue crack growth rates for titanium alloys. Jafarzadeh et al. [78] utilised peridynamics to model crevice corrosion. Tan et al. [79] performed crack analysis of atmospheric stress corrosion. Wang et al. [80] investigated corrosion fatigue crack growth in stainless steel. Zhou et al. [81] developed a peridynamic model suitable for electrochemical and stress chemical corrosion by establishing a coupled chemomechanical framework.
Small-size defects such as microcracks and pores that can occur at the microstructure can have a significant influence on the overall fracture behaviour of the material and structure. Peridynamics is a suitable tool to analyse such defects and their influence on the material and structure. Basoglu et al. [82] demonstrated how to change the direction of crack propagation by using microcracks. Karpenko et al. [83] studied the effect of various kinds of small defects on crack propagation in brittle materials. Rahimi et al. [84] showed how to increase the toughness of brittle materials by drilling stop-holes. Candas et al. [85] presented how macro and microcracks interact with each other under impact-loading conditions. Wang et al. [86] developed a mesoscale model to investigate the influence of micro-void defects on the transverse mechanical properties of composites. Ozdemir et al. [87] performed an in-depth investigation on the macro–microcrack interactions for functionally graded materials.
Peridynamics is a very suitable approach for dynamic fracture analysis of materials and structures. Such conditions can lead to sophisticated fracture patterns such as branching and fragmentation, which can be easily captured by peridynamics demonstrating the superior features of peridynamic methodology. For instance, Cheng et al. [88] performed dynamic fracture analysis of shale. Imachi et al. [89] studied dynamic crack arrest analysis by using ordinary state-based peridynamics. Butt and Meschke [90] investigated the influence of horizon, dimensionality, and specimen size for peridynamic dynamic fracture analysis. Yang et al. [91] coupled the boundary element method and bond-based peridynamics to examine dynamic crack propagation.
Peridynamics has been mainly introduced for failure prediction in materials and structures. To make accurate failure predictions, it is critical to use a suitable failure criterion depending on the material and loading. There are several failure criteria available in the literature for different conditions. Imachi et al. [92] introduced a new failure criterion named "new transition bond" that eliminates oscillations for dynamic stress intensity factors. Jiang et al. [93] utilised energy-based failure criteria to predict the open-hole tensile strength of fibre-reinforced composites. Karpenko et al. [94] did a detailed study to determine the most suitable critical stretch-based failure criterion in an ordinary state-based peridynamic framework. Silling [95] investigated the dynamic behaviour of an elastic material by considering a nonconvex potential and incubation time for the nucleation of a crack. Wang et al. [96] presented fracture predictions in brittle materials using a strength-induced peridynamic model. Kumagai [97] defined a parameter corresponding to stress triaxiality in CCM and used it for a fracture criterion in an ordinary state-based peridynamic framework. Ignatiev et al. [98] presented a peridynamic formulation of the mean stress and incubation time fracture criteria.
Fatigue is one of the most common and dangerous damage mechanisms that structures experience under cyclic loading conditions. Fatigue calculations are mostly done based on traditional S-N curves and Paris law approaches. Although these are useful techniques, they have certain limitations. The peridynamic fatigue model can be a very suitable alternative approach to these traditional techniques. Ma et al. [99] developed a peridynamic model to predict fatigue crack initiation in railheads. Han and Chen [100] presented the fatigue cracking of ferrite and pearlite wheel materials. Nguyen et al. [101] introduced a peridynamic fatigue model suitable for fatigue crack growth prediction subjected to overload and underload. Hong et al. [102] simulated fatigue crack growth in fillet welded joints. Bang et al. [103] provided an analytical solution approach for the peridynamic fatigue model. Zhu et al. [104] performed fatigue analysis of polycrystalline materials by introducing a new crack tip detection algorithm. Nguyen et al. [105] developed an energy-based peridynamic fatigue model. Binchao et al. [106] introduced a cumulative peridynamic fatigue damage model. Li et al. [107] presented a fatigue model for non-ordinary state-based peridynamics suitable for low-cycle cases. Hamarat et al. [108] performed a fatigue damage assessment of complex railway turnout crossings. Zhang and Madenci [109] implemented a coupled peridynamic and finite element fatigue life prediction approach in ANSYS framework by using the kinetic theory of fracture. Cao et al. [110] developed a peridynamic fatigue model for composites for non-ordinary state-based peridynamics. Cruz and Donadon [111] presented a peridynamic mixed-mode energy-based fatigue model by considering elastoplastic material behaviour. Bang and Ince [112] integrated the peridynamic fatigue model with a two-parameter crack driving force. Nguyen et al. [113] investigated fatigue crack growth in ceramic materials and porous media. Wang et al. [114] studied mixed-mode fatigue crack growth in an ordinary state-based framework. Ni et al. [115] introduced a peridynamic fatigue model for composites. Altay et al. [116] presented a peridynamic fatigue model suitable for functionally graded materials. Chen et al. [117] performed fatigue crack growth analysis of hydrogels. Cheng et al. [118] investigated the fatigue behaviour of engineered cementitious composites. Zhang and Chen [119] developed a peridynamic fatigue model suitable for spectrum loadings.
Although peridynamics was originally introduced for structural analysis, it is now used for the analysis of other physical fields including fluid flow modelling. It can also be used for the analysis of fluid-structure interactions, which can be especially important for aerospace and maritime fields. Gao and Oterkus [120] utilised a peridynamic differential operator to simulate low Reynolds number laminar fluid flow. Mikata [121] derived peridynamic equations of fluid mechanics for barotropic flow. Nguyen et al. [122] developed a peridynamic model for incompressible fluids by using the Eulerian approach. Kim et al. [123] introduced a peridynamic model for fluid-structure interaction problems with damage prediction capability. Wang et al. [124] presented a peridynamic model to simulate multiphase flow wetting and thermocapillary flow.
As additive manufacturing methods are advancing, manufacturing materials with varying properties has become a reality. Having such characteristics, functionally graded materials can be a good alternative to composites, mitigating the risk of delamination failure problems. Cheng et al. [125,126] investigated dynamic fracture in functionally graded materials. Dorduncu [127] performed stress analysis of sandwich plates with functionally graded cores by utilising refined zigzag theory. Ozdemir et al. [128] studied the fracture behaviour of functionally graded materials under dynamic loading conditions. Yang et al. [129,130,131,132,133,134] provided formulations for functionally graded Euler–Bernoulli beams, Mindlin plates, Timoshenko beams, Kirchhoff plates, higher-order beams, and higher-order plates. He et al. [135] performed fracture analysis of functionally graded materials subjected to shock loading. Dorduncu et al. [136] developed a peridynamic model for functionally graded plates. Wang et al. [137] determined fracture parameters for functionally graded materials. Candas et al. [138,139] investigated the impact behaviour of functionally graded materials with or without microcracks. Jiang et al. [140] utilised element-based peridynamics to analyse orthotropic functionally graded materials.
One of the main advantages of peridynamics is its capability to be used for modelling materials at a small scale. Its length scale parameter, the horizon, can allow capturing physical phenomena mainly occurring at small scales. Celik et al. [141] determined the elastic moduli of polymer thin films by numerically simulating the nanoindentation process. Liu et al. [142] studied the fracture behaviour of single-layer graphene sheets with preexisting cracks. In another study, Liu et al. [143] developed a peridynamic model depending on chirality for analysing fractures in graphene sheets. Silling and Fermen-Coker [144] introduced a peridynamic model to simulate the microballistic perforation of multilayer graphene. Torkaman-Asadi and Kouchakzadeh [145] used peridynamics for the analysis of pre-cracked graphene layer sheets. Liu et al. [146] examined the fracture behaviour in polycrystalline graphene. Silling et al. [147] developed a peridynamic model for single-layer graphene based on coarse-grained bond forces. Liu et al. [148] utilised peridynamics to determine the mechanical and fracture properties of graphene. Liu et al. [149] investigated fractures in multi-layer graphene sheets.
For materials having periodic microstructures, it is important to determine homogenised properties to reduce computational time. Peridynamics allows the determination of such properties during the existence of microdefects such as micro-voids and microcracks. Xia et al. [150] performed representative volume element homogenisation of a composite material within a bond-based peridynamics framework. Diyaroglu et al. [151] performed peridynamic homogenisation in a finite element framework for microstructures with orthotropic components. Buryachenko [152] presented the computational homogenisation of composites with periodic microstructure by considering linear elasticity and static conditions. Galadima et al. [153] studied the influence of inclusion shapes on homogenised properties. Xia et al. [154] demonstrated a peridynamic model suitable for materials with periodic microstructure. Eriksson and Stenström [155] demonstrated a one-dimensional homogenisation process by considering triangular micromodulus. Xia et al. [156] presented a three-dimensional representative volume element homogenisation for bond-based peridynamics. In another study [157], the authors explained the homogenisation process of periodic microstructure materials in an ordinary state-based peridynamic framework. Buryachenko [158] presented the computational homogenisation of composite materials with periodic microstructure. Li et al. [159] utilised improved bond-based peridynamics for homogenisation based on representative volume elements. Galadima et al. [160,161] performed computational homogenisation for viscoelastic composites to investigate the influence of phase contrast and inclusion shape on homogenised properties. In another study [162], they considered the effect of changing microstructure and damage. They also explained how computational homogenisation can be done in a non-ordinary state-based peridynamic framework [163]. Buryachenko [164] used a generalised Mori-Tanaka methodology for the homogenisation of multilayered composites with random structures. Qi et al. [165] performed peridynamic homogenisation by utilising a peridynamic differential operator to obtain the displacement gradient and stress field.
As mentioned earlier, peridynamics has a length scale parameter, called horizon, which defines the range of interactions between material points. Several studies have investigated different aspects of peridynamics. Oterkus et al. [166] studied the influence of the shape of the horizon in peridynamics by considering circular, irregular, and square shape horizons. Vazic et al. [167] investigated an important aspect of the numerical implementation of peridynamics, which is related to the determination of material points inside the horizon of a material point, i.e., family members. They compared different algorithms to determine the most efficient algorithm for family member search purposes. Wang et al. [168] demonstrated how to determine horizon size in state-based peridynamics.
The study of ice–structure interactions is an important field of engineering. In the Arctic region, ice and structures interact with each other in different forms. One common application is ship and ice interactions. The Arctic can serve as a potential ship route for the transportation of products from the Far East to Europe. Another important application is offshore platforms and their interaction with ice, especially during winter time. The material behaviour of ice is very complex and depends on many factors. During ice–structure interactions, while ice may be fracturing, it can also apply a significant load on the structure, which can cause damage to the structure. The consequences can be significant as in the well-known Titanic accident due to the impact of an iceberg on the ship's hull. Peridynamics can play an important role in representing the ice–structure interaction process. Song et al. [169] studied ice fragmentation due to impact loading by using non-ordinary state-based peridynamics. Ye et al. [170] simulated the submarine surfacing through ice. Vazic et al. [171] utilised peridynamics to investigate the in-plane and out-of-plane failure of an ice sheet. Liu et al. [172] presented an ice–water interaction model by coupling peridynamics and updated Lagrangian particle hydrodynamics. Lu et al. [173] introduced a peridynamic model for the fracture analysis of polycrystalline ice. Liu et al. [174] used micropotential-based peridynamics to study model-scale ice. Chunyu et al. [175] utilised peridynamics to simulate a dynamic ice-milling process. Zhang et al. [176] investigated the effect of rigid ball impact on ice plate fracture. Song [177] developed a thermomechanical peridynamic model for inhomogeneous ice fracture. Xiong et al. [178] simulated the impact process by considering spherical ice and rigid plate. Zhang et al. [179] studied the computational efficiency of peridynamics for ice–structure interaction modelling.
The peridynamic equation is defined to describe the evolution of materials and structures in time due to external loading conditions. Therefore, peridynamics is very suitable for predicting dynamic cases. An important dynamic scenario is impact condition and damage patterns emerging as a result of impact phenomenon. There are numerous studies in the literature focusing on impact analysis by using peridynamics. Rivera et al. [180] investigated the effect of the ballistic impact on glass fracture. Kazemi et al. [181] examined plasticity behaviour occurring during high-velocity impact cases. Ha [182] introduced an extended ghost interlayer model to study high-velocity impact fracture of laminated glass structures. Altenbach et al. [183] compared classical continuum mechanics and peridynamics for an elastic plate subjected to low-velocity impact loading. Zheng et al. [184] predicted failure characteristics of a reinforced concrete T-beam under impact loading. Wu and Huang [185] proposed a new elastoplastic contact model for low and high-speed impact conditions. Jafaraghaei et al. [186] simulated damage in glass plates due to impact loading. Candas et al. [187] analysed the impact behaviour of wire ropes subjected to transverse loading. Xu et al. [188] studied damage evolution in carbon fiber-reinforced plastic (CFRP) due to multiple impacts. Zhang et al. [189] developed an elasto-viscoplastic peridynamic model to investigate brittle and ductile fractures due to high-velocity impact loading. In another study, Lu et al. [190] performed viscoelastic peridynamic fracture analysis for concrete beams with preexisting cracks subjected to impact loading conditions. Cheng et al. [191] examined the impact behaviour of engineering cement-based composite materials.
One of the main advantages of peridynamics is its capability to represent interfaces between two different material systems. This can be done by assigning different properties for the peridynamic interactions (bonds) passing through interfaces. Alebrahim [192] investigated Lamb wave propagation in bimaterial plates. Nguyen et al. [193] examined interface modelling in an ordinary state-based peridynamic framework. Zhang et al. [194] introduced a modified critical energy density criterion to represent the failure of interface bonds. Wu et al. [195] performed a fracture analysis of Ni/Ni3Al bimaterial structure. Wang et al. [196] utilised extended peridynamics to study interfacial and subinterfacial crack propagation. Masoumi et al. [197] developed modified bond-based peridynamics to investigate viscoelastic-elastic interfaces.
In addition to the application of peridynamics for different purposes by considering different loading and material systems, there have also been fundamental developments in peridynamic formulation. Liu et al. [198] introduced element-based peridynamics by defining interactions (bonds) by using elements. Imachi et al. [199] proposed a smoothed variable horizon peridynamic formulation by introducing a smoothing length between different scale particle distributions to eliminate the effect of "ghost" forces. Xia et al. [200] combined isogeometric analysis and peridynamics to utilise the benefits of both approaches. Javili et al. [201] developed a geometrically exact formulation of peridynamics that is suitable for large deformations and variationally consistent. Yang et. al. [202] proposed a double-horizon peridynamic formulation by using two horizons instead of one as in the original peridynamic formulation, which can lead to a computational efficiency of peridynamic simulations with larger horizon sizes. Wang et al. [203] demonstrated that dual horizon state-based peridynamic formulation can be obtained using the Euler–Lagrange equation. Chen et al. [204] introduced a bond-associated correspondence formulation. They derived a bond-associated deformation gradient, eliminating the need for zero-energy-mode stabilisation and allowing for a more straightforward implementation of existing damage models [205]. Jafarzadeh et al. [206] introduced a fast convolution-based method for peridynamics. By using Fourier transforms, they significantly reduced the computational complexity of peridynamics simulations and greatly improved the simulation time and memory consumption.
Peridynamics is not limited to macroscopic analysis. In some cases, microstructural behaviour can have a significant influence on macroscopic behaviour. In such cases, it could be necessary to incorporate microstructural details in the peridynamic model. For certain material systems such as metals, ceramics, ice, etc., crystals should be considered as part of the microstructure. To represent crystals, it is critical to develop a corresponding material model in the peridynamic framework. Gu et al. [207] simulated a fracture of polycrystals under dynamic conditions by using non-ordinary state-based peridynamics. Gur et al. [208] investigated the influence of grain size on the fracture behaviour of polycrystalline silicon carbide. Li et al. [209] studied the effect of porosity on intergranular brittle fractures. In another study, Li et al. [210] performed a thermomechanical analysis of polycrystalline materials. Zhu et al. [211] developed a peridynamic model for fracture analysis of polycrystalline BCC-Fe. Premchander et al. [212] simulated crack propagation in photovoltaic panels by considering a polycrystalline microstructure.
Some materials, such as metals, rocks, or ice, may contain porosity in their microstructure, which should be considered in structural analysis. The effect of porosity should be reflected in the peridynamic model if it is not explicitly modelled. Chen et al. [213] developed a peridynamic model for porous materials suitable to predict brittle fracture. Shen et al. [214] simulated the fracture behaviour of random porous materials. Ni et al. [215] investigated how fracture occurs in dry and saturated porous media. Ozdemir et al. [216] studied the dynamic behaviour of porous media with microcracks. Shangkun et al. [217] performed a fracture simulation of porous material by coupling dual-variable-horizon peridynamics and classical continuum mechanics. Gu et al. [218] predicted the mechanical properties of porous quasi-brittle materials by using peridynamics. Altay et al. [219] examined the dynamic crack behaviour of porous materials based on dual horizon peridynamics.
Peridynamics is also a suitable technique for modelling porous flow. Various studies utilised this new feature of peridynamics. Amongst these, Yan et al. [220] simulated coupled chemical transport and water flow in unsaturated porous media in a peridynamic framework. Katiyar et al. [221] developed a peridynamic model for multiphase transport of non-Newtonian compressible fluids in porous media. Sun and Fish [222] coupled finite element methods and non-ordinary state-based peridynamics to simulate crack propagation in saturated porous media. Ni et al. [223] also introduced a coupled finite element and peridynamic model for saturated porous solids.
Peridynamic simulations can be computationally demanding, especially for three-dimensional models. Therefore, it is important to develop a reduced-order model to accelerate peridynamic simulations, especially for real-time monitoring purposes. Galadima et al. [224] presented a two-dimensional implementation of the coarsening method for linear peridynamics. In another study [225], the authors presented a way to use model order reduction for linear peridynamic systems based on static condensation. They also developed a procedure for static condensation of the peridynamic heat conduction model [226]. Dong et al. [227] introduced an adaptive partitioned reduced-order model of peridynamics. Zhao et al. [228] developed a reduced-order peridynamic model to predict nonlocal heat conduction in nanocomposites.
Stress intensity factor (SIF) is an important parameter in fracture mechanics. It describes the stress field around the crack tip and can be used to determine if the crack has the potential to propagate. There are numerous studies in the literature that provide SIF values for different configurations corresponding to different geometries, loadings, boundary conditions, and material systems. Analytical and numerical approaches such as the finite element method have been widely utilised. SIFs can also be determined by using peridynamics. Dai et al. [229] provided SIFs for mixed-mode conditions for flat shells subjected to in-plane loading conditions. Zhu and Oterkus [230] presented how the displacement extrapolation method can be used to obtain SIFs in the peridynamic framework. Le [231] determined SIFs for mode-I conditions based on tensile stresses and using the virial theorem. Wang et al. [232] calculated SIFs for thermal loading conditions by utilising the domain integral method.
Many structures are operating in harsh conditions, which can cause damage such as fatigue and corrosion. It is critical to take action before any catastrophic situation occurs. Structural health monitoring (SHM) is an effective approach for this purpose, and peridynamics can be used as part of an SHM framework. Kefal et al. [233] demonstrated how to couple peridynamics and inverse finite element method (iFEM) to monitor crack propagation in plate structures.
Deformation behaviour may show non-classical behaviour at small scales due to molecular interactions and surface effects. As a nonlocal approach, peridynamics can be suitable to capture these non-classical behaviours if continuum mechanics can be applied. For instance, Oterkus and Oterkus [234] developed a new peridynamic surface elasticity formulation based on a modified core-shell model.
Although it was originally developed for the mechanical analysis of structures and materials, peridynamics can also be a very effective tool for modelling other fields such as thermal diffusion. A coupled field peridynamic analysis framework can be established by including damage prediction capability. Javili et al. [235] worked on thermomechanical analysis by utilising continuum kinematics–inspired peridynamics. Pathrikar et al. [236] investigated damage occurrence in brittle materials due to the effect of temperature. Wang et al. [237] developed a dual-horizon peridynamic formulation suitable for thermal diffusion analysis. Chen et al. [238] used a fully coupled peridynamic thermomechanical formulation to investigate cracking in concrete. Martowicz et al. [239] investigated phase transformation in shape-memory alloys by performing peridynamic thermomechanical analysis. Wang et al. [240] introduced a thermomechanical phase-change peridynamic model suitable for welding analysis. Liu et al. [241] studied fractures in nuclear fuel pellets based on state-based peridynamic thermomechanical analysis. Zhang et al. [242] applied a fully coupled peridynamic thermomechanical formulation for the analysis of the cracking of frozen rocks. Sun et al. [243] presented a three-dimensional coupled thermomechanical peridynamic model for the fracture analysis of homogeneous and heterogeneous materials. Nikolaev et al. [244] performed peridynamic analysis to investigate the thermal behaviour of phase change material composites for heat storage. Wen et al. [245] developed a peridynamic model for non-Fourier heat transfer in an orthotropic plate with uninsulated cracks. Abdoh [246] introduced a highly efficient algorithm for peridynamic modelling of transient heat conduction in solids.
Computational modelling can be very beneficial in determining the optimum shape of structures under different types of loading conditions. Kefal et al. [247] utilised peridynamics for topology optimisation of structures with cracks. Oh et al. [248] performed shape design optimisation of dynamic crack growth in a peridynamic framework.
Peridynamics is not limited to elastic material behaviour; it can be used for the analysis of other types of material behaviour such as viscoelasticity. Silling [249] investigated the attenuation of waves in a viscoelastic peridynamic medium. Behera et al. [250] studied bonded-lap joints having viscoelastic adhesives by considering finite deformation. Yu and Chen [251] introduced a viscoelastic micropolar peridynamic model suitable for quasi-brittle materials. Ozdemir et al. [252] simulated fracture in viscoelastic membranes. Huang et al. [253] developed a peridynamic model for visco-hyperelastic material behaviour. Tian and Zhou [254] presented a viscoelastic material model in a non-ordinary state-based peridynamic framework. Azizi et al. [255] analysed viscoelastic creep behaviour in a peridynamic framework. Galadima et al. [256] presented a non-ordinary state-based peridynamic formulation suitable for viscoelastic materials.
Due to the nonlocal behaviour of peridynamics, it can represent wave dispersion behaviour differently than classical continuum mechanics. Peridynamic dispersion relationships can be nonlinear as opposed to the linear behaviour of classical continuum mechanics. Zhang et al. [257] presented wave dispersion and propagation in linear peridynamic media. Wang et al. [258] provided analytical wave dispersion relationships for a bond-based peridynamic formulation. Li et al. [259] considered different attenuation functions to investigate wave dispersion in bond-based peridynamics. Oterkus and Oterkus [260] compared wave dispersion relationships obtained from peridynamics and lattice dynamics. Alebrahim et al. [261] compared exact and numerical wave dispersion in peridynamics. Wang et al. [262] presented closed-form wave dispersion relationships in ordinary state-based peridynamics.
In this review study, recent advances in peridynamics research were presented by considering a large number of journal papers. It can be clearly seen that there has been significant progress in peridynamics research during the recent five-year period. In addition to the fundamental developments in peridynamic theory, this formulation has been applied to the analysis of many challenging problems. Some future directions can include artificial intelligence and machine learning, micropolar elasticity, nanomechanics, peridynamic differential operator, soft materials, and surface elasticity.
The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.
This material is based upon work supported by the Air Force Office of Scientific Research under award number FA8655-23-1-7037.
All authors contributed to study conception and design, data collection, analysis and interpretation of results, and manuscript preparation.
Erkan Oterkus and Selda Oterkus are on a special issue editorial board for AIMS Materials Science and were not involved in the editorial review or the decision to publish this article. All authors declare that there are no competing interests.
| [1] | D. Llemit, J. M. Escaner Ⅳ, Value functions in a regime switching jump diffusion with delay market model, AIMS Math., 6 (2021), 11595–11609. http://www.aimspress.com/article/doi/10.3934/math.2021673 |
| [2] |
K. Ito, M. Nisio, On stationary solution of a stochastic differential equation, J. Math. Kyoto Univ., 4 (1964), 1–75. https://doi.org/10.1215/kjm/1250524705 doi: 10.1215/kjm/1250524705
|
| [3] | A. F. Ivanov, Y. I. Kazmerchuk, A. V. Swishchuk, Theory, stochastic stability and applications of stochastic delay differential equations: a survey of recent results, Differ. Equ. Dyn. Syst., 11 (2003), 55–115. |
| [4] | U. Küchler, E. Platen, Strong discrete time approximation of stochastic differential equations with time delay, Math. Comput. Simul., 54 (2000), 189–205. |
| [5] |
X. Mao, S. Sabanis, Numerical solutions of stochastic differential delay equations under local Lipschitz condition, J. Comput. Appl. Math., 151 (2003), 215–227. https://doi.org/10.1016/S0377-0427(02)00750-1 doi: 10.1016/S0377-0427(02)00750-1
|
| [6] |
G. Song, J. Hu, S. Gao, X. Li, The strong convergence and stability of explicit approximations for nonlinear stochastic delay differential equations, Numer. Algorithms, 89 (2022), 855–883. https://doi.org/10.1007/s11075-021-01137-2 doi: 10.1007/s11075-021-01137-2
|
| [7] |
S. You, L. Hu, J. Lu, X. Mao, Stabilization in distribution by delay feedback control for hybrid stochastic differential equations, IEEE Trans. Automat. Contr., 67 (2022), 971–977. https://doi.org/10.1109/TAC.2021.3075177 doi: 10.1109/TAC.2021.3075177
|
| [8] |
W. Zhang, M. H. Song, M. Z. Liu, Almost Sure Exponential Stability of Stochastic Differential Delay Equations, Filomat, 33 (2019), 789–814. https://doi.org/10.2298/FIL1903789Z doi: 10.2298/FIL1903789Z
|
| [9] | S. Kanagawa, S. Ogawa, Numerical solutions of stochastic differential equations and their applications, Sugaku Expositions, 18 (2005), 75–99. |
| [10] |
S. Kanagawa, The rate of convergence for approximate solutions of stochastic differential equation, Tokyo J. Math., 12 (1989), 33–48. https://doi.org/10.3836/tjm/1270133546 doi: 10.3836/tjm/1270133546
|
| [11] | S. Kanagawa, On the rate of convergence for Maruyama's approximate solutions of stochastic differential equations, Yokohama Math. J., 36 (1988), 79–86. http://doi.org/10131/5546 |
| [12] |
H. Takahashi, Confidence intervals for Euler–Maruyama approximate solutions of stochastic delay equations, Theor. Appl. Mech. Japan, 63 (2015), 127–132. https://doi.org/10.11345/nctam.63.127 doi: 10.11345/nctam.63.127
|
| [13] |
M. Hashimoto, H. Takahashi, Interval estimations for Euler–Maruyama approximate solutions of stochastic differential equations with multiple delays, J. Jpn. Soc. Civ. Eng., Ser. A2, 75 (2019), 105–111. https://doi.org/10.2208/jscejam.75.2_I_105 doi: 10.2208/jscejam.75.2_I_105
|
| [14] |
S. Kanagawa, Confidence intervals of discretized Euler–Maruyama approximate solutions of SDE's, Nonlinear Anal. Theory Methods Appl., 30 (1997), 4101–4104. https://doi.org/10.1016/S0362-546X(97)00159-4 doi: 10.1016/S0362-546X(97)00159-4
|
| [15] |
S. Kanagawa, S. Hasegawa, A confidence interval for the Euler–Maruyama approximate solution of SDE with unbounded coefficients, Theor. Appl. Mech. Japan, 62 (2014), 91–98. https://doi.org/10.11345/nctam.62.91 doi: 10.11345/nctam.62.91
|
| [16] | E. Platen, N. Bruti-Liberati, Numerical solution of stochastic differential equations with jumps in finance, Stochastic Modelling and Applied Probability, volume 64, Berlin: Springer-Verlag, 2010. https://doi.org/10.1007/978-3-642-13694-8 |
| [17] |
H. Takahashi, K. Yoshihara, Approximation of solutions of multi-dimensional linear stochastic differential equations defined by weakly dependent random variables, AIMS Math., 2 (2017), 377–384. https://doi.org/10.3934/Math.2017.3.377 doi: 10.3934/Math.2017.3.377
|
| [18] |
Y. A. Alnafisah, A New Approach to Compare the Strong Convergence of the Milstein Scheme with the Approximate Coupling Method, Fractal Fract., 6 (2022), 339. https://doi.org/10.3390/fractalfract6060339 doi: 10.3390/fractalfract6060339
|
| [19] |
M. Milošević, The Euler–Maruyama approximation of solutions to stochastic differential equations with piecewise constant arguments, J. Comput. Appl. Math., 298 (2016), 1–12. https://doi.org/10.1016/j.cam.2015.11.019 doi: 10.1016/j.cam.2015.11.019
|
| 1. | Xiawei Chen, Haiming Liu, Two Special Types of Curves in Lorentzian α-Sasakian 3-Manifolds, 2023, 15, 2073-8994, 1077, 10.3390/sym15051077 |
Masataka Hashimoto, Hiroshi Takahashi. On the rate of convergence of Euler–Maruyama approximate solutions of stochastic differential equations with multiple delays and their confidence interval estimations[J]. AIMS Mathematics, 2023, 8(6): 13747-13763. doi: 10.3934/math.2023698
DownLoad:
