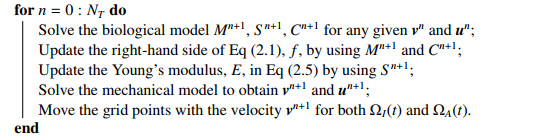An integrative pan-cancer analysis reveals the carcinogenic effects of NCAPH in human cancer

1.   Introduction

Abdominal aortic aneurysm (AAA) is a leading cause of death globally and involves complex and multi-factorial pathogenesis including factors such as hypertension, dyslipidemia, and tobacco use. Half of patients with untreated aneurysms larger than 5.5 cm will die of rupture within five years, and there is currently no recognized treatment for these AAAs. Patients with AAAs frequently have atherosclerosis, and numerous studies show the association of coronary heart disease and peripheral atherosclerosis with AAA ^[1]. Whether this association between AAA and atherosclerosis is causal or simply due to common risk factors is unknown. However, the term "atherosclerotic aneurysms" is commonly used and prevalent today. As one of most common causes of AAA, atherosclerosis originates with an accumulation of blood-borne lipids in the inner-most arterial wall (intima), followed by a detailed immune response and the progressive formation of a lesion in the arterial wall ^[2]. Mature lesions then form atherosclerotic plaques, then arterial walls lose the elasticity via arterial remodeling and develop the AAA. Thus, it is vital to understand the pathophysiology of atherosclerotic aneurysms whose pathology is largely unknown and likely multifactorial ^[3,4]. Though the pathophysiology is hard to study experimentally due to its network complexity, a computational model could integrate this complex network and include all the possible factors in the pathogenesis. Moreover, computational modeling techniques, such as fluid-structure interactions or computational fluid dynamics, has been successfully implemented in the study of CVD and provides many insightful suggestions for clinical practice ^{[5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21]}.

In this paper, we develop a mathematical model that accounts not just for the biological networks associated with the pathophysiology of atherosclerotic aneurysms, but also for the multi-layered structure of the arterial wall. Modeling one or two layers would not be sufficient for capturing the progression of the atherosclerotic aneurysm. Therefore our model accounts for the multi-layered structure of the arterial walls, with attention paid to the distinct physical properties of each layer. Biologically speaking, atherosclerosis silently and slowly hardens, narrows, and blocks the arteries, putting blood flow at risk ^[22]. Then atherosclerotic plaques restrict blood vessels (a process called stenosis) and lead to the destruction of smooth muscle cells (SMCs), depletion of elastin, and disruption of the extracellular matrix (ECM) in the media/adventitia which causes the AAA. Our mathematical model, by including both the mechanism of the arterial wall and the biology of the atherosclerotic aneurysm, can help us to construct the cardiovascular environment virtually and to mimic plaque/aneurysm growth. This is an innovative tool for potential biomarkers' detection, drug efficacy evaluation, and reducing the risk of misdiagnosis due to patient variations. More specifically, we use our model to assess the risk of atherosclerotic aneurysms on a 2D biomarker, the cholesterol ratio and the level of the receptor tyrosine kinase, discoidin domain receptor 1 (DDR1). We further explore the efficacy of three treatments, anti-cholesterol drugs, the anti-DDR1 injection, and the combined therapy. Our simulation results suggest that the dosage of anti-cholesterol drugs is critical for treating atherosclerotic aneurysm patients who can also benefit from additional anti-DDR1 injections.

2.   Mathematical model

In order to model the atherosclerotic aneurysm, we present a hybrid computational model which consists of a mechanical model, including the psychical properties and multi-layer structure of arterial wall, and a biological model, including the molecular mechanism of etiology and pathophysiology of atherosclerotic aneurysm.

2.1.   Mechanical model for the multi-layered structure of arterial wall

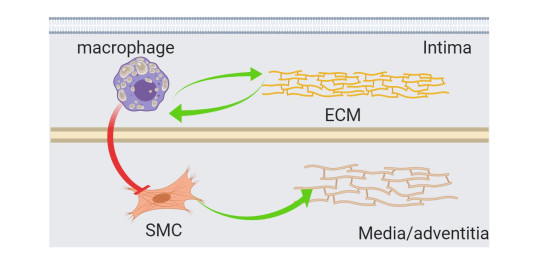
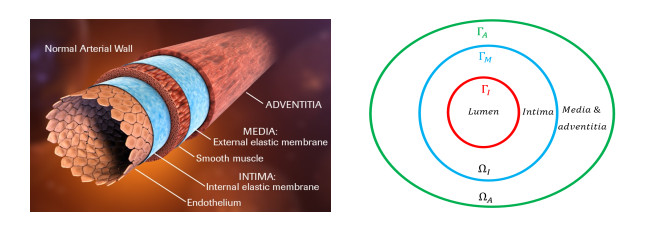
The arterial wall has a multi-layer structure (see Figure 1), comprising intima, media, and adventitia. ^[23]. This multi-layered structure is central to the progression atherosclerotic aneurysm which involves changes in all three arterial layers, including changes to their geometry and composition. Modeling the multi-layered structure makes our model possible to render an accurate virtual cardiovascular environment, even recreating and observing the pathophysiological networks of both atherosclerosis (affecting the intima) and aneurysm formation (affecting the media/adventitia).

Porous medium for intima: In light of the intima's high permeability to white cells and platelets ^[24,25,26], we propose to treat the intima as a porous medium and all the cells in the intima as a low speed flow ^[27,28] moving with a common velocity, $\mathit{\boldsymbol{v}}$, which is the result of the movement of macrophages, T cells and SMCs in the intima. The pressure, $p$, results from the cells' movement and proliferation. This leads to the following Darcy's law and mass conservation equation ^[27,28]:

where

which is derived by the biological model for which variables $M$, $S$, and $C$ refer to macrophages, SMCs, and collagen, respectively. See next section for more details. Here $K$ is the Darcy permeability of the intima layer, $\mu$ is the viscosity of the cell fluid in the intima, $p_B$ is the blood pressure (we treat as a constant since we do not include the blood fluid dynamics), $\gamma$ is a dimensionless surface tension coefficient, $\kappa$ is the mean curvature of the corresponding free boundaries and $\sigma$ is the stress tensor determined by the media/adventitia in $\Omega_A(t)$.

Elasticity for media/adventitia: From the continuum mechanics point of view, mechanical response of the media/adventitia layers of an arterial wall, is a elastic material ^[29,30]. Specifically, the Cauchy stress tensor is given by

where $\mu_s$ and $\lambda$ are material constants, called Lame or elastic moduli coefficients, and ${\boldsymbol \varepsilon}$ is the so-called strain stressor defined as

where ${{\mathit{\boldsymbol{u}}}}$ is the displacement. Therefore,

The coefficients are directly related to Young's modulus, $E$, and Poisson's ratio, $\nu$, namely, $\lambda = \frac{E\nu}{(1-2\nu)(1+\nu)}$ and $\mu_s = \frac{E}{1+\nu}$. In our model, $E = E_0-\beta\Big(\frac{S}{S_0}-1\Big)$ where $S$ is the SMCs density and produces the elastic modulus. Then the momentum equation is given by

where $d$ is the tissue density. Here we impose the stress-free boundary condition on $\Gamma_A$ and the velocity continuous condition on $\Gamma_M(t)$.

2.2.   Biological model

Pathophysiology of atherosclerosis (intima): The atherosclerosis involves a complex series of biological processes with the formation of plaque inside the intima layer. This process begins with a lesion, allowing low-density lipoprotein (LDL), to move from the blood into the intima, where LDL then becomes oxidized (ox-LDL) by free radicals ^[31]. Because ox-LDL is toxic, macrophages are recruited and differentiated in the intima ^[32,28]. The ingestion of large amounts of ox-LDL transforms the fatty macrophages into foam cells, which contribute to plaque formation ^{[33,34,35,36]}. Moreover, The presence of collagen in the intima also causes activation of macrophages via the DDR1, which is a member of the receptor tyrosine kinase family and binds to several collagen(s) as its ligand, including collagen I, III and IV present in the vasculature ^[37]. With regard to vascular diseases, it is important to note that DDR1 is expressed in monocytes and macrophages, endothelial cells, SMCs as well as in adventitial fibroblasts. It can thus have a multifaceted role in regulation of vascular diseases such as atherosclerosis and aneurysms. Studies using vessel wall or bone-marrow specific deletion of DDR1 in mice models have elucidated on how DDR1 expression on macrophages mediates their infiltration into the developing plaque, whereas DDR1 expression in resident vessel wall SMCs limits SMC infiltration and lesion fibrosis ^[38]. The biological network is shown in Figure 2.

Pathophysiology of aneurysm growth (media/adventitia): Aneurysm is due to the destruction of smooth muscle cells (SMCs), depletion of elastin in the media, and disruption of the extracellular matrix (ECM) in the adventitia. Foam cells in the plaque ^[39,40], degrade elastin and ECM to weaken the pressure of the adventitia layer to withstand blood stress ^[41]. Foam cells are also known to cause apoptosis in SMCs, which leads to a reduction in elastin and subsequent overall decline of the media's strength ^[39,40,42].

Equation for Macrophages ($M$): Activated ECs secrete cytokines like MCP-1 to recruit monocytes to the fatty streak area ^[43]. The collagens in the intima also causes activation of macrophages. Then the equation of $M$ is written as

where $\lambda_M M$ is the macrophages proliferation due to the scavenger receptor class A (SR-A) expressed by tissue macrophages ^[44,45], $\lambda_{MC} C$ accounts for the macrophages activation by the DDR1 ^[46], $d_M C$ represents the natural death of macrophages, $\alpha(C) = \alpha_0 + \alpha\frac{C}{K_C+C}$ for which $\alpha_0$ indicates the MCP-1 induced by the oxidized LDL ^[47] and $\alpha\frac{C}{K_C+C}$ describes the production of MCP-1 activated by collagens via the DDR1 ^[48], and $M_0$ is the monocytes density in the blood.

Equation for SMCs ($S$): Foam cells secrete large amounts of cytokines and growth factors which stimulate the migration of SMCs from the medial layer of the artery into the intima ^[49]. Then the equation of $S$ is written as

where $\chi_{\Omega_A} = 1$ in $\Omega_A$, $\chi_{\Omega_A} = 0$ in $\Omega_I$. $S = S_0 = \frac{\lambda_{S}}{d_S}$ represents the SMCs density in health, $\lambda_{SM} \frac{M}{K_M+M}$ describes the SMCs proliferation due to the stimulation from platelet-derived growth factor (PDGF) produced by activated macrophages ^[50], and $\alpha(M) = \alpha\frac{M}{K_M+M}$ accounts for the migration of SMCs due to the foam cells. Since no migration of SMCs occurs on the boundaries $\Gamma_I$ and $\Gamma_A$, nonflux boundary conditions are specified on them.

Equation for collagen ($C$): Foam cells form extracellular deposits of lipid material, known as the lipid or necrotic core in the intima while SMCs produce elastin. Thus we have

where on $\Gamma_M(t)$, since the 'synthetic' SMCs secrete a matrix rich elastin in the initima ^[51], we use $S_0-S$ account for the 'synthetic' SMCs and model the production through a flux boundary condition.

3.   Results and discussion

3.1.   Healthy case

We cover the healthy case in our model by setting $\alpha = 0$ and $\alpha_0 = 0$ in Eq (2.6) which means that there is no inflammation in the arterial wall. Moreover, we assume $\alpha$ is proportional to the ratio of the cholesterol levels, LDL/HDL, and refer $\alpha = 0$ in our model to the cholesterol ratio less than $5$ ^[52,53]. Thus we have the density of macrophages in Eq (2.6) be zero. Therefore, there is no migration of SMCs on the interface between the intima and the media in Eq (2.7) which implies that the density of SMCs achieves the steady-state in health, namely, $S = S_0$. Similarly, the density of collagen in Eq (2.8) has steady states $C = K_C$ in $\Omega_A$ and $C = 0$ in $\Omega_I$. Thus we have ${{\mathit{\boldsymbol{v}}}} = 0$ in Eq (2.1) and ${{\mathit{\boldsymbol{u}}}} = 0$ in Eq (2.5). Therefore, there is no plaque formation and no deformation of the arterial wall for the healthy case.

3.2.   Numerical methods

We simulate the hybrid model in the 2D radially symmetric case with finite difference method and moving mesh method ^[54]. More specifically, for given a function $f$, we have the following formulas in the polar coordinate with radial symmetry:

where $f_r$ is the projection of the function $f$ on $\mathbf{e}_r$. By denoting grid points as $r_0 < r_1 < \cdots\leq r_N$ and the numerical approximation of $f(r_i)$ as $f_i$, we employ the following numerical schemes to approximate the first and second derivatives with respect to $r$:

where $h_{i+1} = r_{i+1}-r_i$ and $h_{i-1} = r_{i-1}-r_i$. If the grid point is uniformly distributed, these numerical schemes recover the central difference schemes with the second order accuracy by setting $h_{i+1} = -h_{i-1}$. Due to the free boundaries, we use the moving mesh method to update the grid points ^[54], namely, $r_i(t+\Delta t) = r_i(t)+{{\mathit{\boldsymbol{v}}}}_r \Delta t$. We outline the algorithm of solving the hybrid system with free boundaries in Algorithm 1.

In order to ensure the numerical stability, we need to satisfy the CFL condition ^[55], namely, $\max|v|\frac{\Delta t}{\Delta h}\le C$, where $C$ is the so-called Courant number between 0 and 1. For simplicity, we used a small fixed $\Delta t$ in the numerical computation to ensure this stability condition. More specifically, we choose the time step $\Delta t = 0.01$ day and the initial grid size $\Delta h = 0.01$ cm, for which the choice has been tested in the simulations to satisfy the CFL condition. The initial conditions have also been specified as:

3.3.   The progression of atherosclerotic aneurysm

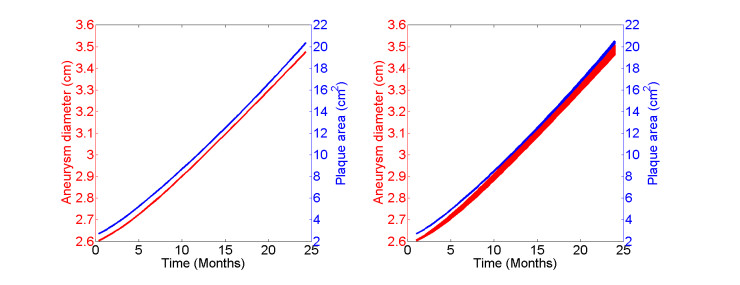
Since the thickness of the abdominal aorta is measured $2.77$ cm $\pm$ $0.20$ cm ^[56], we set the diameter of lumen, the thickness of intima layer, and the thickness of media layer to be $2$ cm, $0.1$ cm, and $0.2$ cm, respectively, and simulate our model by setting $\alpha = 1$ and $\alpha_0 = 0.1$ in Eq (2.6) for 2 years. Figure 3 shows the density distributions of macrophages in the intima and SMCs in the media every three months. The macrophage density starts increasing from the boundary $\Gamma_I$ and then spreads to the boundary $\Gamma_M$ in the first six months. Then SMCs start decreasing from month 9-15 and triggers the expansion of the aneurysm after 1 year while the plaque growth starts after 6 months. This is consistent with the pathology of atherosclerotic aneurysm: the inflammation associated with atherosclerosis first leads to destruction and plaque formation then weakening of vascular wall, specifically the tunica media, which leads to aneurysmal dilation of the vessel ^[57]. In Figure 4 Left, the diameter of the aneurysm grows from $2.60$ to $3.48$ cm, thus the average aneurysm growth rate is $4.4$ mm/year which is in the 95% range of the aneurysm diameter growth rate, $1.0$ to $6.1$ mm/year ^[58]. The plaque area is computed by $\pi (R_M^2-R_I^2)$, where $R_I$ and $R_M$ represents the radius of intima and media, respectively, and grows from $2.72$ to $20.37$ $\rm cm^{2}$, thus the growth rate from Y1 to Y2 is around 100%.

3.4.   The effect of the blood pressure on atherosclerotic aneurysm

Hypertension is a risk factor for the development of atherosclerosis ^[59] and also has long been suspected to increase the growth rate of abdominal aortic aneurysms ^[60], although the mechanisms have not been well elucidated. In our model, we studied the effect of blood pressure on the growth of the atherosclerotic aneurysm. The systolic blood pressure corresponds to $p_B$ in our model via Eq (2.1) which is taken to be $120$ mmHg as the normal blood pressure in Figure 3. We simulate our model for different blood pressure with $p_B$ ranging from $90$ mmHg (hypotension) to $200$ mmHg (hypertensive crisis) ^[61] and show the results in Figure 4 Right. The effect of blood pressure on the aneurysm diameter varies from $3.46$ to $3.51$ cm (1.45%), while the effect on the plaque area varies from $20.30$ to $20.53$ $\rm cm^2$ (1.13%). The effect of blood pressure in our model is not significant due to the early stage of the atherosclerotic aneurysm and also gets larger as the time evolves shown in Figure 4. Moreover, hypertension also induces oxidative stress on the arterial wall ^[59] and the inflammatory cell infiltration ^[60]. However, we do not include these mechanisms in the current model so we might underestimate the effect of blood pressure on atherosclerotic aneurysm.

3.5.   Biomarkers associated with atherosclerotic aneurysm and the risk map

The LDL-cholesterol to HDL-cholesterol (LDL/HDL-cholesterol) ratio is recognized as a good biomarker in atherosclerosis ^[67]. Although there are no effective biomarkers for aneurysm ^[68], the level of DDR1 is highly associated with aneurysm growth in mice experiments ^[69,70]. We will explore the possibility of using the cholesterol ratio and DDR1 as a 2D biomarkers for atherosclerotic aneurysm via our model. As in section 3.1, we refer the cholesterol ratio as the flux rate, $\alpha$, in Eq (2.6).

The DDR1 is deleted exclusively in vessel wall cells, macrophages can colonize and initiate an inflammatory response in the arterial intima of both Ddr1+/+ and Ddr1-/- hosts. However, vessel-wall specific deletion of DDR1 results in (over 3-fold) increase in the size of aortic sinus plaques due to enhanced collagen accumulation. The cellular composition of the lesions in DDR1-/- hosts shifted toward increased numbers of vessel wall-derived SMCs compared to bone marrow-derived macrophages. In vitro studies confirmed that Ddr1(-/-) SMCs expressed more matrix, proliferated more, and migrated farther than Ddr1(+/+) SMCs. ^[38]. One plausible cause is that in the absence of DDR1, N-cadherin mediated cell-cell contacts in vSMCs are mislocalised from cell-cell junctions ^[71], thus facilitating cell invasion. As Ddr1-/- SMCs invade the plaque, their enhanced expression of interstitial matrix genes results in extracellular matrix synthesis and assembly which contributes directly to plaque expansion.

Moreover, DDR1 is also reported to be a negative regulator of collagen(s) in SMCs. The mRNA for collagen type I (and III) was significantly increased in DDR1-/- SMC as compared to DDR1+/+ cells ^[38,70]. Consistent with these results, overexpression by transient transcription of DDR1 in human SMC was found to induce a significant decrease in collagen type I mRNA, which was accompanied by a similar decrease at the protein level ^[72]. Besides decreasing the mRNA levels, expression of DDR1 on the cell surface is also reported to inhibit collagen. These multiple effects of DDR1 in suppressing collagen deposition account for increased collagen deposition observed in the adventitial layer of DDR1 KO mice ^[69]. Therefore we model the level of DDR1 as follows:

● Since DDR1 limits SMC migration ^[38] and regulates the inflammation ^[70], $\alpha(M)$ in Eq (2.7) becomes $\alpha(M) = \alpha_{DDR1}\big(\frac{M}{K_M+M}-d_{DDR1}\big)$, where $\alpha_{DDR1}$ is the SMC migration and $d_{DDR1}$ accounts for the inflammation regulation;

● Since DDR1 increases SMC-mediated collagen and elastin degradation ^[73] and is also a central mediator of SMC migration ^[74], $\alpha$ in Eq (2.8) becomes $\alpha = \alpha_{DDR1}$.

Thus we define the risk of atherosclerotic aneurysm associated with these two biomarkers as

where the LDL/HDL ratio, $L/H$, varies from 5 to 15 ^[67], the level of DDR1 varies from 5 to 15 $\rm \mu m/ml$ ^[70], and the outer/inner diameters of the artery is measured at year 2. The risk, $\mathcal{R}$, combines both the aneurysm growth (the outer diameter) and the plaque size (the inner diameter) and is a good indicator of the progression of the combined disease. The contour plot of the risk map is shown in Figure 5 with two contour curves $1.5$ and $2$. We have a high-risk region (above 2), a medium-risk region (between 1.5 and 2), and a low-risk region (below $1.5$). The DDR1 level contributes significantly to the risk map: if the DDR1 level is low, no matter how large the cholesterol ratio is, the risk remains low; if the DDR1 level is high, even if the cholesterol ratio is low, the risk could be very high. Considering that the DDR1 level remains the same for one patient in the early stage of the aneurysm, thus controlling the cholesterol ratio can still minimize the risk of atherosclerotic aneurysm.

3.6.   Potential intervention strategies

We next test some potential intervention strategies for atherosclerotic aneurysm via our model, e.g. anti-cholesterol drugs, anti-DDR1 injection, and the combined therapy. Statins, only cholesterol-lowering drug class, are recommended for most patients with atherosclerosis to reduce the risk of heart attack or stroke ^[75]. In our study, we tested the efficacy of Statins on the atherosclerotic aneurysm. Although there are some medications for aneurysm patients whose size is less than 5 cm such as beta blockers and calcium channel blockers ^[76], these drugs are to lower your blood pressure and relax your blood vessels not related directly to the pathology of aneurysm ^[77]. Anti-DDR1 has been used in the mice experiments to slow the progression of the aneurysm ^[78,69]. Therefore, we will test the feasibility of the anti-DDR1 as a treatment for the atherosclerotic aneurysm. More specifically, we will test the three potential intervention strategies as follows:

● Anti-cholesterol drugs, statins, help lower LDL/HDL-cholesterol ratio in our model. We take the flux rate, $\alpha$, in Eq (2.6) as a control function

where the initial LDL/HDL-cholesterol ratio is assumed to be $10$. One patient starts taking the medications to achieve the ideal cholesterol ratio, 3.5, by 2 months (60 days);

● The anti-DDR1 injection affects the flux rates, $\alpha$, in Eqs (2.7) and (2.8) and is modeled as follows:

where the DDR1 concentration is assumed to be $10$ $\rm \mu m/ml$ initially and returns back to the initial value after one year since the injection;

● The combined therapy of the first two treatments is modeled by changing the flux rates, $\alpha$, in Eqs (2.6)-(2.8) as the control functions mentioned above.

Figure 6 shows the control functions for both the anti-cholesterol drugs and the anti-DDR1 injection in our study: anti-cholesterol drugs reduces the flux rate consistently after 2 months while the anti-DDR1 injection reduces the flux rate immediately and returns the original flux rate after around 1 year. To explore the three potential treatment strategies, we first let the atherosclerotic aneurysm develop to a certain size, e.g., running our model for 2 years, and then start three treatments for three years. The anit-DDR1 injection is given annually. Figure 7 shows the effects of three different treatments on both the aneurysm diameter and the plaque area. The anti-cholesterol drugs reduce the growth rate of plaque area from 7.19 $\rm cm^2$/year to 2.33 $\rm cm^2$/year and the growth rate of aneurysm diameter from $3.2$ $\rm mm$/year to $1.04$ $\rm mm$/year while the anti-DDR1 injection reduces the growth rates of plaque area and aneurysm diameter to 5.8 $\rm cm^2$/year and $2.56$ $\rm mm$/year, respectively. The combined therapy has the best efficacy by reducing the growth rates of plaque area and aneurysm diameter to 1.42 $\rm cm^2$/year and $0.64$ $\rm mm$/year, respectively. To further explore the efficacy of the combined therapy, we model the dosage of two drugs as follows

where $\gamma_A$ and $\gamma_B$ is the dosage of anti-cholesterol drugs and the anti-DDR1 injection, respectively. Then we define the efficacy effectiveness as

where $d({\gamma_A, \gamma_B})$ and $Area({\gamma_A, \gamma_B})$ are the diameter of aneurysm and the plaque area at Year 5 for given dosage $\gamma_A$ and $\gamma_B$, respectively. Thus $d({0, 0})$ and $Area(0, 0)$ are the control values of no drug treatment. By varying $\gamma_A$ from $0.3$ to $0.9$ with a step size $0.05$ and $\gamma_B$ from $0.1$ to $1$ with a stepsize $0.05$, we have the efficacy maps for both $E_1$ and $E_2$ plotted in Figure 8 and show that the dosage of anti-cholesterol drugs affects significantly both plaque area and aneurysm diameter. Moreover, for any given dosage of anti-cholesterol drugs, the anti-DDR1 injection can also improve the efficacy of the combined therapy.

4.   Conclusions

More than 80% of aortic aneurysms are associated with atherosclerosis which develops firstly when cholesterol and fat build up inside the arteries. Atherosclerosis accelerates the breakdown of collagen and SMCs, structure and elasticity to the arterial wall. Over time, this causes the arterial walls to weaken and become damaged. As the diameter of the vessel grows, the wall tension increases, leading to even more dilation. The end result is an aneurysm. In this paper, we account for both cardiovascular diseases in the model and develop a comprehensive mathematical model to mimic the progression of the atherosclerotic aneurysm. Our model includes both the multi-layer structure of the arterial wall and the pathophysiology of the atherosclerotic aneurysm. More specifically, we model the plaque formed in the intima layer as a porous medium and use the linear elastic model to describe the media layer; we also include the role of macrophage, SMCs migration, and collagen proliferation into our hybrid model. Then our model is used to predict the progression of atherosclerotic aneurysm, the growth rate of the plaque and the aneurysm diameter. A 2D biomarker, the cholesterol ratio and the level of DDR1, is revealed to evaluate the risk of atherosclerotic aneurysm via our model shown in Figure 5. Then the efficacy of three clinical treatments is also illustrated via our model: the anti-cholesterol treatment is better than the anti-DDR1 injection but the combined therapy is optimal. We accordingly explore the efficacy of the combined therapy with different dosages of the anti-cholesterol treatment and the anti-DDR1 injection. Based on our results shown in Figure 8, we suggest that the anti-cholesterol treatment significantly decreases the risk of the atherosclerotic aneurysm while patients can also benefit from the additional anti-DDR1 injection.

In the current study, we use a simplified circular geometry of the arterial wall with the radially symmetric assumption and do not consider the effect of complex arterial shapes. In the future study, we intend to incorporate the CT scan data of atherosclerotic aneurysm patients into our model and give a personalized prediction for each patient. This would also help us to evaluate the personalized efficacy of different treatments. Another limitation of the current work is the effect of blood pressure via the force balance condition in our model. However, we do not take the biological effects of the blood pressure into consideration, e.g. the inflammatory cell infiltration, therefore, might underestimate the effect of hypertension on the atherosclerotic aneurysm. In the future, we will include a more complex biological network to evaluate the effect of blood pressure. Moreover, the parameters in the current model will be calibrated when clinical data become available. Another future direction is to incorporate a better clinical serum biomarker than DDR1 which is not easily obtainable from a biomarker standpoint. One possible serum biomarker is platelet counts or activated platelet counts since platelets play a significant role in atherosclerosis and have been proved the cross-talk with other inflammatory cells. Furthermore, we plan to validate our suggested treatments to aneurysm patients and quantify the progression of atherosclerosis by using clinical data.

Author contributions

GK and WH carried out all simulations and analyzed the data. GK, CH, GA, KO, MG and WH discussed the project and wrote the article.

Data availability statement

Data sharing is not applicable to this article as no new data were created or analyzed in this study.

Acknowledgments

This work is supported by National Institutes of Health (Grant R01HL124155, CH) and by the American Heart Association (Grant 17SDG33660722, WH).

Conflict of interest

The authors declare there is no conflict of interest.