$M-$truncated optical soliton and their characteristics to a nonlinear equation governing the certain instabilities of modulated wave trains

1.   Introduction

It is well-known that in the theory of linear operators there are three different points of view to represent semigroups ^[1,2,3]. One is the classical algebraic approach, i.e., a strongly continuous operator function $T(\cdot; A): \mathbb{R_{+}} \to \mathcal{L}(X)$ is called a $C_{0}$-semigroup if $T(0;A) = I$ and $T(t; A)T(s; A) = T(t+s; A)$ for all $t, s \in \mathbb{R_{+}}$. The second approach involves the abstract Cauchy problem

that is, $A:D(A)\subseteq X \to X$ generates a $C_{0}$-semigroup $T(t; A), t\in \mathbb{R_{+}}$ if and only if there exists a unique mild solution $u$ for every initial value $x\in X$. Furthermore, in this case, the closed-form representation of a mild solution is $u(t) = T(t; A)x$ for all $t\in \mathbb{R_{+}}$ and $x\in X$. And the third approach is related to the Laplace integral transform, i.e., a strongly continuous operator function $T(\cdot; A): \mathbb{R_{+}} \to \mathcal{L}(X)$ is a $C_{0}$-semigroup if and only if there exists an infinitesimal generator $A: D(A)\subseteq X \to X$ and $\omega \in \mathbb{R}$ such that $(\omega, \infty)\in \rho(A)$ and $Re(\lambda) > \omega$,

The same behaviour applies to strongly continuous cosine families ^[4,5,6]. In agreement with the purely algebraic approach, a strongly continuous operator function $C(\cdot:A): \mathbb{R} \to \mathcal{L}(X)$ is called a cosine family if $C(0;A) = I$ and $C(t+s; A)+C(t-s; A) = 2C(t; A)C(s; A)$ for all $t, s \in \mathbb{R}$ and the associated sine family $S(\cdot; A): \mathbb{R} \to \mathcal{L}(X)$ is given by $S(t; A)x = \int_{0}^{t}C(s; A)x\mathrm{d}s$ for each $x\in X$ and $t\in \mathbb{R}$. Based on the second approach, the following abstract initial value problem

has a unique mild solution $u$ for each initial values $x, y \in X$ if and only if $A:D(A)\subseteq X \to X$ is an infinitesimal generator of strongly continuous cosine and sine families $C(t; A), t\in \mathbb{R}$ and $S(t; A), t\in \mathbb{R}$, respectively. Moreover, in this case, the closed-form representation of a mild solution is $u(t) = C(t; A)x+S(t; A)y$ for all $t\in \mathbb{R}$ and $x, y\in X$. According to the last approach strongly continuous operator functions $C(\cdot; A): \mathbb{R_{+}} \to \mathcal{L}(X)$ and $S(\cdot; A): \mathbb{R_{+}} \to \mathcal{L}(X)$ are strongly continuous cosine and sine families if and only if there exists an infinitesimal generator $A: D(A)\subseteq X \to X$ and $\omega \in \mathbb{R}$ such that $(\omega, \infty)\in \rho(A)$ and $Re(\lambda) > \omega,$

Furthermore, we would like to draw the readers' attention to the research work of Vasil'ev, Krein and Piskarev ^[7,8] on operator theory, in particular on semigroup theory and cosine operator families in abstract spaces. These fundamental surveys on operator theory can serve as a fairly complete source of information on abstract differential equations and methods for solving them in recent years.

In recent years there has been a considerable increase in interest to fractional calculus and fractional differential equations, where the order of differentiation is permitted to be any real (or even complex) number, not just a natural number. This is largely due to the applications of fractional differential equations to problems in various fields of physics and engineering, namely electrical circuits ^[9], electrical power systems ^[10,11,12], vibration theory ^[13] and so on.

One of the emerging branches of fractional calculus and fractional-order differential equations are the fractional semigroups and fractional cosine (sine) families and their applications to the theory of fractional evolution equations, i.e., evolution equations in which the integer-order derivatives with respect to time are replaced by the derivatives of fractional-order. In ^[14], Bazhlekova has studied the following abstract Cauchy problem for a fractional evolution equation of Caputo type in a Banach space $X$ and introduced the solution operator for (1.6) as follows:

where $m-1 < \alpha < m$, $m \in \mathbb{N}$.

Definition 1.1. A family $T_{\alpha}(t; A)$, $t\in \mathbb{R_{+}}$ of bounded linear operators on $X$ is called a solution operator for (1.6) if the following three conditions are satisfied:

$(i)$ $T_{\alpha}(t; A)$ is strongly continuous for any $t\in \mathbb{R_{+}}$ and $T_{\alpha}(0;A) = I$;

$(ii)$ $T_{\alpha}(t; A)D(A)\subset D(A)$ and $AT_{\alpha}(t; A)x = T_{\alpha}(t; A)Ax$ for all $x\in D(A)$ and $t\in \mathbb{R_{+}}$;

$(iii)$ $u(t) = T_{\alpha}(t; A)x$ is a strong solution of (1.6) for every $x\in D(A)$.

Note that the solution operator for an abstract Cauchy problem (1.6) was systematically studied in the thesis of Bazhlekova ^[14], and the results obtained generalise some facts of $C_{0}$-semigroups (in case of $0 < \alpha < 1$) and cosine families (in case of $1 < \alpha < 2$). Furthermore, Lizama in ^[15] has reviewed the fundamental theory of solution operators associated to abstract linear evolution equations of fractional-order and provided their basic results concerning generation, analyticity and inversion problems. In ^[16], Jigen and Kexue have developed the notation of fractional semigroup to characterize solution operator for fractional abstract linear systems (1.6) of order $0 < \alpha < 1$ and discussed the well-posedness of the abstract Cauchy problem (1.6). It is shown that in ^[16] the problem (1.6) is well-posed if and only if its coefficient operator $A$ generates a fractional semigroup. The same authors have also investigated similar results in ^[17] for Riemann-Liouville type fractional evolution equations of order $\alpha \in(0, 1)$.

In terms of fractional anologue of strongly continuous cosine families, Kexue and Jigen in ^[18] and Mei et al. in ^[19] have developed an operator theory to study abstract Cauchy problems of order $\alpha \in (1, 2)$ in terms of Caputo and generalized type fractional differentiation operators, respectively and proposed a generation theorem for exponentially bounded fractional solution operators-fractional strongly continuous sine families. Furthermore, in ^[20], Mei et al. have studied a new characteristic property of the Mittag-Leffler function $E_{\alpha}(at^{\alpha})$, $a\in \mathbb{R}$ with $\alpha \in (1, 2)$ and motivated by this property developed a new notion, named $\alpha$-order cosine function. It is interesting to note that in ^[21] Mei et al. have introduced a novel one-parameter algebraic functional equation for fractional resolvent families, and using this functional equation, all fractional resolvent families except $C_{0}$-semigroups can be obtained from this equation.

In addition, a subordination principle can be used to analyse fractional evolution equations, which is a useful tool to connect solution operators in the classical and fractional sense. Using a subordination formula, it is possible to construct new solutions from known solutions, e.g., solutions of fractional-order evolution equations from the solutions of the classical diffusion or wave equations (see ^{[22,23,24,25]}).

A strong inspiration for the study of perturbation theory for strongly continuous operator families, particularly, for cosine families comes from the fact that they have been proven to be useful tools for evolution equations in modeling many physical phenomena. The perturbed wave equation is a typical linear hyperbolic second-order partial differential equation which naturally arises when modeling phenomena of continuum mechanics such as sound, light, water or other kind of waves in acoustics, electro-magnetics, elasticity and fluid dynamics, etc. (see ^[26]).

The perturbation theory of linear operators in a Banach space has been explored to a considerable extent, most notably by Phillips ^[27], Travis & Webb ^[28] and Lutz ^[29]. In ^[27], Phillips intended to perturb the infinitesimal generator by adding to it a linear bounded operator and investigating some perturbation results for infinitesimal generators of strongly continuous $C_{0}$-semigroups. In ^[28], Travis and Webb have proposed sufficient conditions for perturbed cosine operator families. In ^[29], Lutz has first studied the implication for the homogeneous initial value problem associated with the infinitesimal generator of the cosine function generated by bounded time-varying perturbations:

where $B:\mathbb{R_{+}}\to \mathcal{L}(X)$ is a continuously differentiable function on $\mathbb{R_{+}}$.

In her dissertation, Bazhlekova showed that perturbation theory does not work in general for the solution operators of the perturbed abstract Cauchy problem with $0 < \alpha < 1$ (see counterexample in ^[14]). In the special case, a treatment of the perturbation problem from the point of view of the subjacent fractional abstract Cauchy problem in the case of $0 < \alpha < 1$ was given by El-Borai ^[30]. In the general case, however, perturbation properties are true for the fractional analogue of an abstract initial value problem (1.7) with $1 < \alpha < 2$ which has been established by Bazhlekova in ^[31]. She has proposed to uniquely determine a classical solution of the following homogeneous abstract Cauchy problem for the fractional evolution equation with Caputo derivative by time-dependent perturbations:

where $B:\mathbb{R_{+}}\to \mathcal{L}(X)$ is a continuous function on $\mathbb{R_{+}}$.

Furthermore, the fractional analogue of the inhomogeneous abstract problem (1.7) was developed by Ahmadova et al. in ^[32] and the results presented in ^[32] extend those of ^[29,31] in several aspects. The authors in ^[32] have shown that the inhomogeneous abstract Cauchy problem with the infinitesimal generator $A$ of fractional cosine families remains uniformly well-posed under bounded time-varying perturbations:

where $B:\mathbb{R_{+}}\to \mathcal{L}(X)$ and $h:\mathbb{R_{+}}\to X$ are continuously differentiable functions on $\mathbb{R_{+}}$.

While there are several papers on operator theory for fractional evolution equations (for example, see ^{[15,16,17,18,33]}), there are few papers ^[30,31,32] dealing with perturbation theory for fractional abstract Cauchy problems. The lack of perturbation properties of the fractional strongly contionuous operator functions motivates us to develop new results on perturbation theory for evolution equations of fractional-order. The pioneering work on this subject in the classical sense was done by Phillips ^[27], Lutz ^[29] and Travis & Webb ^[28] and our development follows these approaches. Therefore, the main contributions of our work are described in detail below:

$1)$ We propose some new perturbation results for fractional strongly continuous cosine families in a Banach space $X$;

$2)$ We establish sufficient conditions such that $A$ is the infinitesimal generator of a fractional strongly continuous cosine (sine) family in a Banach space $X$, and $B$ is a bounded linear operator in $X$, then $A+B$ is also the infinitesimal generator of a fractional strongly continuous cosine (sine) family in $X$;

$3)$Depending on commutativity condition of linear bounded operators, we obtain the elegant analytical representation formulas for perturbed Mittag-Leffler type functions generated by $A+B$ where $A, B \in \mathcal{L}(X)$ are permutable and nonpermutable linear bounded operators;

$4)$ We present an example in the context of a one-dimensional fractional perturbed wave equation to demonstrate the applicability of our theoretical results and we give some comparisons with the existing literature.

The paper contains significant innovations on the perturbation theory for fractional cosine families and is organized as follows. Section 2 is a preparatory section in which we recall the main definitions and results from functional analysis, fractional calculus, and operator theory of linear operators. In Section 3, we investigate some perturbation properties for fractional strongly continuous cosine families. We intend to perturb the infinitesimal generator by adding to it a linear bounded operator. Furthermore, we propose the elegant representation formulas for perturbed fractional uniformly continuous cosine families in a Banach space $X$. In Section 4, we present an example in the context of one-dimensional perturbed fractional wave equation to demonstrate the applicability of our theoretical results and we give some comparisons with existing ones. In Section 5, we give an overview of our main contributions and point out some open problems in the spirit of this research.

2.   Preliminaries

We start this section by briefly introducing the fundamentals of fractional calculus, the essential structure of an operator theory for strongly continuous cosine families and their fractional analogues. For the more salient details on these subjects, see the textbooks ^[2,34,35].

Let $\mathbb{R_{+}} = [0, \infty)$ and $\mathbb{N}$ denote the set of natural numbers with $\mathbb{N}_{0} = \mathbb{N}\cup\left\lbrace 0\right\rbrace$. Let $X$ be a Banach space equipped with the norm $\left \lVert{\cdot}\right \rVert$. We donote by $\mathcal{L}(X)$ the Banach algebra of all bounded linear operators on $X$ and becomes a Banach space with regard to the norm $\left \lVert{T}\right \rVert = \sup\left\lbrace \left \lVert{Tx}\right \rVert: \left \lVert{x}\right \rVert \leq 1\right\rbrace$, for any $T\in \mathcal{L}(X)$. Let $D(A)$ be the domain of $A$ and $\rho(A)$ be the resolvent set of $A$. The identity and zero operators on $X$ are denoted by $I\in \mathcal{L}(X)$ and $0\in \mathcal{L}(X)$, respectively.

We will use the following functional spaces ^[2] through the paper:

● $\mathbb{C}\left(\mathbb{R_{+}}, X\right)$ denotes the Banach space of continuous $X$-valued functions $g:\mathbb{R_{+}}\to X$ equipped with an infinity norm $\|g\|_{\infty} = \sup\limits_{t\in \mathbb{R_{+}}}\left \lVert{g(t)}\right \rVert$;

● $\mathbb{C}^{n}(\mathbb{R_{+}}, X)$, $n\in \mathbb{N}$ denotes the Banach space of $n$-times continuously differentiable $X$-valued functions defined by

and equipped with an infinity norm $\|g\|_{\infty} = \sum\limits_{k = 0}^{n}\sup\limits_{t\in \mathbb{R_{+}}}\left \lVert{g^{(k)}(t)}\right \rVert$. In addition, $\mathbb{C}^{n}(\mathbb{R_{+}}, X)\subset \mathbb{C}(\mathbb{R_{+}}, X)$, $n\in \mathbb{N}$;

● $\mathbb{L}^{p}(\mathbb{R}_{+}, X)$ denotes the Banach space of all (equivalence classes of) Bochner-measurable $X$-valued functions $g:\mathbb{R}_{+}\to X$ which are integrable and normed by $\left \lVert{g}\right \rVert_{\mathbb{L}_{p}} = \Big(\int_{\mathbb{R}_{+}}\left \lVert{g(s)}\right \rVert^{p}\mathrm{d}s\Big)^{1/p} < \infty$ where $1\leq p < \infty$;

● The Sobolev spaces can be defined in the following way ^[14] for $n\in \mathbb{N}$ and $1\leq p < \infty$:

$\mathbb{W}^{n, p}\left(\mathbb{R}_{+}, X\right):=\Biggl\{\phi: \exists h \in \mathbb{L}^{p}\left(\mathbb{R}_{+}, X\right) : \phi(t) = \sum\limits_{k = 0}^{n-1}c_{k}\frac{t^{k}}{k!}+\frac{t^{n-1}}{(n-1)!}\ast h(t), t\in \mathbb{R}_{+}\Biggr\}$.

Note that $c_{k} = \phi^{(n)}(0)$ and $\phi^{(n)}(t) = h(t)$.

Let $f:\mathbb{R_{+}}\to\mathbb{R}$ be an integrable scalar-valued function and let $g:\mathbb{R_{+}}\to X$ be a continuous $X$-valued function. We denote by

the convolution operator of $f$ and $g$. Furthermore, if $T:\mathbb{R_{+}}\to\mathcal{L}(X)$ is a strongly continuous operator-valued map, we define

Definition 2.1. The Riemann-Liouville fractional integral of order $\alpha > 0$ for a function $f\in \mathbb{L}^{1}\left(\mathbb{R_{+}}, X\right)$ is defined by

By setting $\left(I^{0}_{t}f\right) (t) = f(t)$. For the sake of brevity we use the following notation for $\alpha\geq 0$:

where $\Gamma:\mathbb{R_{+}}\to \mathbb{R}$ is the well-known Euler's gamma function. Note that $g_{0}(t) = 0$, since $\frac{1}{\Gamma(0)} = 0$. These functions satisfy the semigroup property

Moreover, the Riemann-Liouville fractional integral operators $\left\lbrace I^{\alpha}_{t} \right\rbrace_{\alpha \geq 0}$ satisfy the semigroup property

Definition 2.2. The Caputo fractional derivative of a function $f\in \mathbb{C}^{n}\left(\mathbb{R_{+}}, X\right)$ with fractional order $n-1 < \alpha < n$, $n\in\mathbb{N}$ is defined by

In particular, for $\alpha\in(1, 2)$, the definition is given by for $f\in \mathbb{C}^{2}\left(\mathbb{R_{+}}, X\right)$:

Remark 2.1. Since $f$ is an abstract function with values in $X$, the integrals which appear in Definition 2.1 and 2.2 are taken in Bochner's sense.

The Mittag-Leffler function is a natural generalization of the exponential function, first proposed as a single parameter function of one variable by using an infinite series ^[36].

Definition 2.3. ^[36] The classical Mittag-Leffler function is defined by

The two-parameter Mittag-Leffler function is given by

It is important to note that

Strongly continuous cosine and sine families of linear operators

Definition 2.4. See reference^[37] 1) A one parameter family $\left\lbrace C(t; A), t \in \mathbb{R}\right\rbrace \in \mathcal{L}(X)$ into itself is called a strongly continuous cosine family in the Banach space $X$ if and only if

● $C(0;A) = I$;

● $C(s+t; A)+C(s-t; A) = 2C(s; A)C(t; A)$ for all $s, t\in\mathbb{R}$;

● $C(t; A)x$ is continuous in $t$ on $\mathbb{R}$ for each fixed $x \in X$.

2) The corresponding strongly continuous sine family $\left\lbrace S(t; A), t \in \mathbb{R}\right\rbrace \in \mathcal{L}(X)$ is defined by

3) The linear operator $A: D(A)\subseteq X \to X$ defined by

is called the infinitesimal generator of a strongly continuous cosine family $\left\lbrace C(t; A), t \in \mathbb{R}\right\rbrace$ and $D(A)$ is a domain of $A$. It is known that the infinitesimal generator $A$ is closed, densely-defined operator on $X$.

Theorem 2.1 (See reference ^[37]). Let $\{C(t; A):t\in \mathbb{R}\}$ be a strongly continuous cosine family in $X$ satisfying $\left \lVert{C(t; A)}\right \rVert\leq Me^{\omega |t|}$ for all $t\in\mathbb{R}$ and let $A$ be the infinitesimal generator of $\{ C(t; A):t\in \mathbb{R}\}$. Then for $Re(\lambda) > \omega$, $\lambda^{2}$ is in the resolvent set of $A$ and

Definition 2.5. See reference ^[33] Let $\alpha \in (1, 2)$. A family $C_{\alpha}(\cdot; A):\mathbb{R_{+}}\to \mathcal{L}(X)$ of all bounded linear operators on $X$ is called a fractional strongly continuous cosine family if it satisfies the following hypotheses:

● $C_{\alpha}(t; A)$ is strongly continuous for all $t \in \mathbb{R_{+}}$ and $C_{\alpha}(0;A) = I$;

● $C_{\alpha}(s; A)C_{\alpha}(t; A) = C_{\alpha}(t; A)C_{\alpha}(s; A)$ for all $s, t\in \mathbb{R_{+}}$;

● The functional equation

The closed linear operator $A$ is defined by

where $A$ is the infinitesimal generator of the fractional strongly continuous cosine family $\{ C_{\alpha}(t; A):t\in \mathbb{R_{+}}\}$.

Definition 2.6. See reference ^[33] A fractional strongly continuous cosine family $\{ C_{\alpha}(t; A):t\in \mathbb{R_{+}}\}$ is said to be exponentially bounded if there exists constants $M\geq 1$, $\omega \geq 0$ such that

Definition 2.7. See reference ^[33] The fractional strongly continuous sine family $S_{\alpha}(\cdot; A):\mathbb{R_{+}}\to \mathcal{L}(X)$ associated with $C_{\alpha}$ is defined by

This implies that

Definition 2.8. See reference ^[33] The fractional strongly continuous Riemann-Liouville family $T_{\alpha}(\cdot; A):\mathbb{R_{+}}\to \mathcal{L}(X)$ associated with $C_{\alpha}$ is defined by

Theorem 2.2 (See reference ^[33]). Let $\{ C_{\alpha}(t; A):t\in \mathbb{R_{+}}\}$ be a fractional strongly continuous cosine family in $X$ satisfying $(2.13)$ and let $A$ be the infinitesimal generator of $\{ C_{\alpha}(t; A):t\in \mathbb{R_{+}}\}$. Then for $Re(\lambda) > \omega$, $\lambda^{\alpha} \in \rho(A)$, $\alpha \in (1, 2)$, the following relations hold true:

3.   Main results

In many concrete situations, the fractional evolution equation is given as a sum of several terms that have various physical meanings and various mathematical properties. While the mathematical analysis for each term may be straightforward, it is not entirely clear what happens after the summation. In the context of perturbed generators of fractional cosine families, we take this as a starting point. To study some perturbation results for fractional strongly continuous cosine families, we first prove the following lemma which establishes a connection between the resolvents of cosine (sine) families generated by $A$ and $A+B$, respectively.

Note that the following lemma and corollary are true in more general case for closed linear operators and play an important role in the proof of Theorem 3.1.

Lemma 3.1. Let $A$ be a closed linear operator on $X$ to $X$ and suppose $B\in \mathcal{L}(X)$ is such that $\left \lVert{B\mathcal{R}(\lambda^{\alpha}; A)}\right \rVert = \theta < 1$ for some $\lambda^{\alpha}\in \rho(A)$, $\alpha \in (1, 2)$. Then, $A+B$ is a closed linear operator with domain $D(A)$ and $\mathcal{R}(\lambda^{\alpha}; A+B)$ exists and

Furthermore,

Proof. Obviously, $A+B$ is a closed linear operator with domain $D(A)$. Since $\left \lVert{B\mathcal{R}(\lambda^{\alpha}; A)}\right \rVert = \theta < 1$, we note that

and hence that

Moreover, the range of $\mathcal{R}$ is precisely $D(A)$ since the range of $\Big[I-B\mathcal{R}(\lambda^{\alpha}; A)\Big]^{-1}$ is $X$. Therefore, given $x\in D(A)$ there exists a $y$ such that $x = \mathcal{R}y$. Therefore, we attain that

so that $\mathcal{R}$ is both a left and a right inverse of $\Big[\lambda^{\alpha}I-(A+B)\Big]$. The bound $\left \lVert{\mathcal{R}(\lambda^{\alpha}; A+B)-\mathcal{R}(\lambda^{\alpha}; A)}\right \rVert$ comes directly from the expansion (3.1):

The proof is complete.

Corollary 3.1. Let $A$ be a closed linear operator on $X$ to $X$ and suppose $B\in \mathcal{L}(X)$ is such that $\left \lVert{B\mathcal{R}(\lambda^{\alpha}; A)}\right \rVert = \theta < 1$ for some $\lambda^{\alpha}\in \rho(A)$, $\alpha \in (1, 2)$. Then, $A+B$ is a closed linear operator with domain $D(A)$ and $\lambda^{\alpha-1}\mathcal{R}(\lambda^{\alpha}; A+B)$, $\lambda^{\alpha-2}\mathcal{R}(\lambda^{\alpha}; A+B)$ exist and

Furthermore,

In the following theorem, we impose sufficient conditions such that $A$ is the infinitesimal generator of a fractional strongly continuous cosine (sine) family in $X$, and $B$ is a bounded linear operator in $X$, then $A+B$ is also the infinitesimal generator of a fractional strongly continuous cosine (sine) family in $X$.

Theorem 3.1. Let $A$ be the infinitesimal generator of the fractional strongly continuous cosine family $\left\lbrace C_{\alpha}(t; A): t \in \mathbb{R_{+}}\right\rbrace$ with $(2.13)$, and let $\left\lbrace S_{\alpha}(t; A): t \in \mathbb{R_{+}}\right\rbrace$ denote the fractional strongly continuous sine family associated with $C_{\alpha}$ where $\alpha \in (1, 2)$. Furthermore, suppose that $B\in \mathcal{L}(X)$. Then, fractional strongly continuous families of linear bounded operators $C_{\alpha}(\cdot; A+B), S_{\alpha}(\cdot; A+B): \mathbb{R}_{+} \to \mathcal{L}(X)$ generated by $A+B$ (defined on $D(A)$) can be represented by the series expansion:

where for $t\in \mathbb{R_{+}}$, $x\in X$ and $n \in \mathbb{N}$,

Proof. From (2.13), it follows that $\left \lVert{S_{\alpha}(t; A)}\right \rVert\leq Mte^{\omega t}$. This implies that $C_{\alpha}(t; A)$ and $S_{\alpha}(t; A)$ are strongly continuous on $\mathbb{R_{+}}$. Moreover, by using the formula (2.16), we obtain:

Then, we suppose $C_{\alpha, n}(t; A)$ and $S_{\alpha, n}(t; A)$ are strongly continuous on $\mathbb{R_{+}}$ and it is true that for $n \in N_{0}$:

Firstly, we start with the formula (3.12). Then, $T_{\alpha}(t-s; A)BC_{\alpha, n}(s; A)$ will be strongly continuous on $[0, t]$ such that the integral defining $C_{\alpha, n+1}(t; A)$ exists in the strong topology. Moreover, in the case of (3.12), this is true by our remark above for $n = 0$. By mathematical induction principle, we verify ^[32]:

The analogues procedure gives the bound for $S_{\alpha, n}(t; A)$, $t\in \mathbb{R_{+}}$, as follows:

Finally, for $t_1 < t_2$, we have

As $t_1, t_2 \to t_0$, the integrands in the first terms on the right of (3.16), (3.17) to zero boundedly and the integrands of the second terms of (3.16), (3.17) are bounded. Therefore, $C_{\alpha, n+1}(t; A)x$, $S_{\alpha, n+1}(t; A)x$ are strongly continuous on $\mathbb{R_{+}}$ for each fixed $x\in X$. By induction, $C_{\alpha, n}(t; A)x$, $S_{\alpha, n}(t; A)x$ are well-defined, strongly continuous, and satisfying (3.12) and (3.13), respectively, for $n\in \mathbb{N}_{0}$. Hence, the fractional-order families $C_{\alpha}(t; A+B)$, $S_{\alpha}(t; A+B)$ are uniformly convergent on compact subsets of $\mathbb{R_{+}}$ with respect to the operator norm topology. Moreover, the series are majorized by the following series expansions ^[32]:

Next, we claim that for $C_{\alpha, n}(t; A)x$, $n\in \mathbb{N}$ for sufficiently large $Re(\lambda)$ which holds the condition $\left \lVert{B\mathcal{R}(\lambda^{\alpha}; A)}\right \rVert < 1$ (it follows from the asymptotic expansion and continuity of the Mittag-Leffler function, see ^[14], Theorem 2.5, pp. 21):

With the help of the mathematical induction principle, well-known Fubini's theorem for iterated integrals, commutative property of convolution operator (2.1) and relation (2.17), for $n = 1$, we verify that

In a recursive way, for $n = 2$, we obtain that

Therefore, the relation (3.20) is true for arbitrary $n \in \mathbb{N}$. Then, by the formulae (3.12), (3.18) and Corollary 3.1, we derive that for $C_{\alpha}(t; A+B)x$, $t\in \mathbb{R_{+}}$, for chosen sufficiently large $Re(\lambda)$ which holds the condition $\left \lVert{B\mathcal{R}(\lambda^{\alpha}; A)}\right \rVert < 1$,

Therefore, for sufficiently large $Re(\lambda)$, the Laplace transforms of both $C_{\alpha}(t; A+B)$ and $\sum\limits_{n = 0}^{\infty}C_{\alpha, n}(t; A)$ are equal and hence by the uniqueness theorem, these two functions are equal.

In a similar way, by using the following formula (3.22), Corollary 3.1 and relations (2.18), (3.13), (3.19) for $n\in \mathbb{N}$ and sufficiently large $Re(\lambda)$ which holds the condition $\left \lVert{B\mathcal{R}(\lambda^{\alpha}; A)}\right \rVert < 1$:

we can derive the corresponding result for fractional strongly continuous sine family:

The proof is complete.

Remark 3.1. Our results coincide with the classical ones whenever $\alpha = 2$ ^[29]. It should be note that in the case of $\alpha = 2$, $T_{\alpha}(t; A)$ and $S_{\alpha}(t; A)$ coincide with the strongly continuous sine function $S(t; A)$ and correspondingly, $C_{\alpha}(t; A)$ coincide with the strongly continuous cosine function $C(t; A)$. Furthermore, for $\alpha = 2$, two-parameter Mittag-Leffler type functions are converting to the hyperbolic cosine and sine functions, respectively:

Theorem 3.2. Let $A$ be the infinitesimal generator of the strongly continuous cosine family $\left\lbrace C(t; A): t \in \mathbb{R}\right\rbrace$ with $\|C(t; A)\|\leq Me^{\omega |t|}$ for all $t \in \mathbb{R}$, and let $\left\lbrace S(t; A): t \in \mathbb{R}\right\rbrace$ denote the strongly continuous sine family associated with $C$. Furthermore, suppose that $B\in \mathcal{L}(X)$. Then, strongly continuous families of linear bounded operators $C(\cdot; A+B), S(\cdot; A+B)\in \mathcal{L}(X)$ generated by $A+B$ (defined on $D(A)$) can be represented by the series expansion:

where for $t\in \mathbb{R}$, $x\in X$ and $n \in \mathbb{N}$,

Moreover, Travis and Webb have proved anlogues results in ^[28] for the case of $\alpha = 2$. The authors in ^[28] have used instead of (3.24) the following recursion formula:

which can be proven via integrating (formally) by parts formula in (3.24).

We end this chapter by adding some results on fractional analogues of uniformly continuous operator cosine and sine functions which are Mittag-Leffler type operator-valued functions generated by $A+B$ where $A, B$ are linear bounded operators in a Banach space $X$.

It is known that if $C_{\alpha}(\cdot; A): \mathbb{R}_{+} \to \mathcal{L}(X)$ is fractional uniformly continuous cosine function then there is an $A\in \mathcal{L}(X)$ with

Moreover, the corresponding fractional uniformly continuous sine and Riemann-Liouville families $S_{\alpha}(\cdot; A)$, $T_{\alpha}(\cdot; A): \mathbb{R}_{+} \to \mathcal{L}(X)$ are defined by

and

In this case, we have $A = \Gamma(\alpha+1)\lim\limits_{t \to 0_{+}}\frac{C_{\alpha}(t; A)-I}{t^{\alpha}}$ in the uniform operator topology and the domain $D(A)$ coincides with the state space $X$ i.e., $D(A) = X$.

For $t\in \mathbb{R}_{+}$, $x\in X$ and $n\in \mathbb{N}$, we define the following sequence of operator-valued functions via a recursive way:

and

Therefore, in this case, fractional uniformly continuous families of linear bounded operators $C_{\alpha}(\cdot; A+B), S_{\alpha}(\cdot; A+B):\mathbb{R}_{+}\to \mathcal{L}(X)$ become the perturbation of a Mittag-Leffler type operator-valued functions defined on $X$:

It is interesting to note that depending of commutativity condition of linear bounded operators $A, B \in \mathcal{L}(X)$, we can derive the following elegant representation formulas for the perturbation of fractional uniformly continuous cosine and sine families. First, we obtain closed-form representations for perturbation of Mittag-Leffler type functions generated by $A+B$, where $A, B \in \mathcal{L}(X)$ are nonpermutable linear bounded operators in a Banach space $X$.

Theorem 3.3. Let $A, B \in \mathcal{L}(X)$ with non-zero commutator $[A, B]:= AB-BA\neq 0$. Then, the perturbation of Mittag-Leffler type operator-valued functions $C_{\alpha}(\cdot; A+B), S_{\alpha}(\cdot; A+B): \mathbb{R}_{+} \to \mathcal{L}\left(X \right)$ can be represented by

and

where $Q_{k, n}^{A, B} \in \mathcal{L}\left(X\right)$, $k, n\in \mathbb{N}_{0}$ is given by

Proof. By making use of the definition of fractional uniformly continuous cosine function $C_{\alpha}(\cdot; A):\mathbb{R}_{+} \to \mathcal{L}\left(X\right)$ (3.27), we derive the basis case for $n = 0$:

For $n = 1$, by using the well-known Cauchy product formula and interchanging the order of summation and integration which is permissible in accordance with the uniform convergence of the series (3.27) and (3.29), we get:

In a recursive way, for $n = 2$, we derive that

Eventually, for the $n$-th case, it yields that

Therefore, for a perturbation of Mittag-Leffler operator-valued function $C_{\alpha}(\cdot; A+B):\mathbb{R}_{+}\to \mathcal{L}\left(X \right)$, with the help of Cauchy product formula, we attain a desired result:

By making use of the definition of fractional uniformly continuous sine function $S_{\alpha}(\cdot; A):\mathbb{R}_{+} \to \mathcal{L}\left(X\right)$ (3.28), we derive the basis case for $n = 0$:

For $n = 1$, by making use of the above calculations, the well-known Cauchy product formula and interchanging the order of summation and integration which is permissible in accordance with the uniform convergence of the series (3.28) and (3.29), we get:

In a recursive way, for $n = 2$, we attain that

Finally, for the $n$-th case, it follows that

Therefore, for a perturbation of Mittag-Leffler type operator-valued function $S_{\alpha}(\cdot; A+B):\mathbb{R}_{+}\to \mathcal{L}\left(X \right)$, by using the Cauchy product formula, we obtain a desired result:

where we have used that the following relation which is a generalization of binomial theorem for nonpermutable linear bounded operators $A, B\in \mathcal{L}(X)$

where $Q_{k, n}^{A, B} \in \mathcal{L}\left(X\right)$, $k, n\in \mathbb{N}_{0}$ is given by

The proof is complete.

Remark 3.2. Further, it is interesting to note that the operator (matrix) construction $Q_{k, n}^{A, B}$, $k, n\in \mathbb{N}_{0}$ is satisfying the following crucial property which is a generalization of the well-known Pascal rule for nonpermutable linear bounded operators (matrices):

To get more information regarding the properties of $Q_{k, n}^{A, B}\in \mathcal{L}\left(X\right)$, $k, n\in \mathbb{N}_{0}$, we refer to ^[38,39].

Secondly, we attain analytical representation formulas for perturbation of Mittag-Leffler type functions generated by $A+B$, where $A, B \in \mathcal{L}(X)$ are permutable linear bounded operators in a Banach space $X$.

Theorem 3.4. Let $A, B \in \mathcal{L}(X)$ with zero commutator $[A, B]:= AB-BA = 0$. Then, the perturbation of Mittag-Leffler type operator-valued functions $C_{\alpha}(\cdot; A+B), S_{\alpha}(\cdot; A+B): \mathbb{R}_{+} \to \mathcal{L}\left(X \right)$ can be represented by

and

Proof. By making use of the definition of fractional uniformly continuous cosine function $C_{\alpha}(\cdot; A):\mathbb{R}_{+} \to \mathcal{L}\left(X\right)$ (3.27), we derive the basis case for $n = 0$:

For $n = 1$, by using the condition $AB = BA$, well-known Cauchy product formula and interchanging the order of summation and integration which is permissible in accordance with the uniform convergence of the series (3.28) and (3.29), we get:

In a recursive way, for $n = 2$, we derive that

Eventually, for the $n$-th case, it yields that

Therefore, for a perturbation of Mittag-Leffler operator-valued function $C_{\alpha}(\cdot; A+B):\mathbb{R}_{+}\to \mathcal{L}\left(X \right)$, by using well-known Cauchy product formula and binomial theorem, we attain a desired result:

By making use of the definition of fractional uniformly continuous sine function $S_{\alpha}(\cdot; A):\mathbb{R}_{+} \to \mathcal{L}\left(X\right)$ (3.28), we derive the basis case for $n = 0$:

For $n = 1$, by making use of the above calculations, the well-known Cauchy product formula and interchanging the order of summation and integration which is permissible in accordance with the uniform convergence of the series (3.28) and (3.29), we get:

In a recursive way, for $n = 2$, we derive that

Eventually, for the $n$-th case, it yields that

Therefore, for a perturbation of Mittag-Leffler type operator-valued function $S_{\alpha}(\cdot; A+B):\mathbb{R}_{+}\to \mathcal{L}\left(X \right)$, by using the Cauchy product formula for double infinite series, we obtain a desired result:

where we have used the following well-known binomial theorem for permutable linear bounded operators $A, B\in \mathcal{L}(X)$

The proof is complete.

Remark 3.3. This case can also be obtained directly with the help the following property of the construction $Q_{k, n}^{A, B}\in \mathcal{L}(X)$, $k, n \in \mathbb{N}_{0}$ which is valid for permutable linear bounded operators (in particular, matrices) $A, B\in \mathcal{L}(X)$:

To get more information regarding this property of $Q_{k, n}^{A, B}\in \mathcal{L}(X)$, $k, n \in \mathbb{N}_{0}$, we refer to ^[38,39].

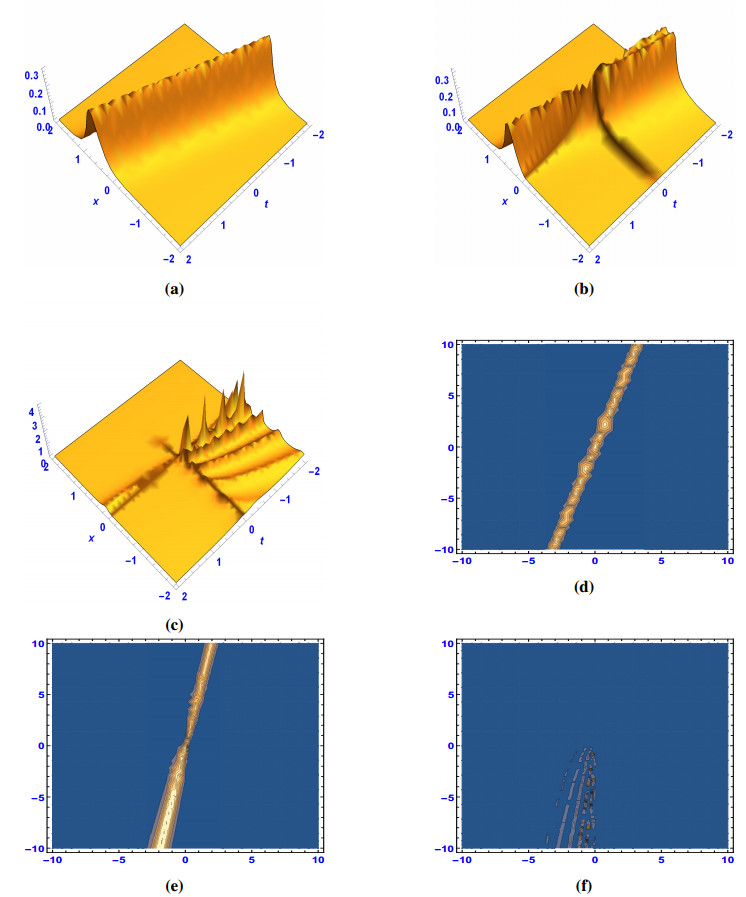
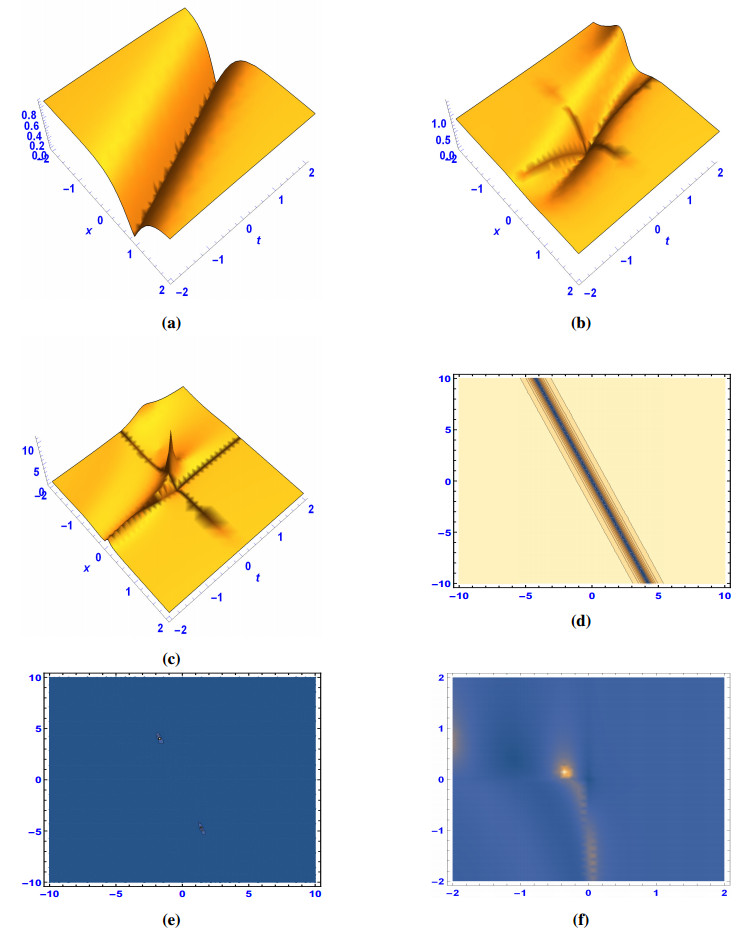
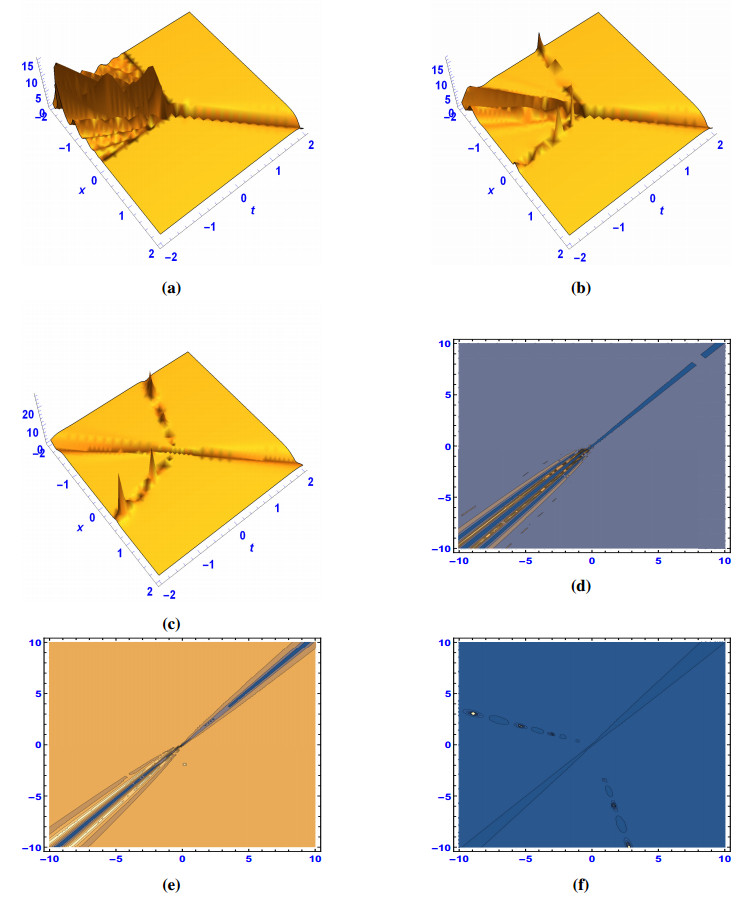
4.   Application: A perturbed fractional wave equation

Let us take $X:= \mathbb{L}^{2}\left(0, 1 \right)$ and $\mathbb{W}^{2, 2}\left(0, 1\right):=\Biggl\{\phi: \exists h \in \mathbb{L}^{2}\left(0, 1 \right) : \phi(t) = ct+t\ast h(t), \quad t\in \left(0, 1\right)\Biggr\}$. Note that $c = \phi^{\prime}(0)$ and $\phi^{\prime \prime}(t) = h(t)$ for any $t \in(0, 1)$. We consider the following abstract initial-boundary value problem with homogeneous Dirichlet boundary conditions for a one-dimensional perturbed fractional wave equation:

where $a, b\in \mathbb{R}$ and $\frac{\partial^{\alpha}}{\partial t^{\alpha}}$ is a fractional partial differentiation operator of order $\alpha\in(1, 2)$ in Caputo's sense which is defined by

We define the following linear operator $A:D(A)\subseteq X\to X$ as follows:

with the domain is given by

Moreover, a linear bounded operator $B: X\to X$ is defined by $Bu = bu$ for all $b\in \mathbb{R}$ and $u\in X$. It is obvious that $A$ has eigenvalues of the form $\lambda_{n}:= -a^{2}n^{2}\pi^{2}$ and the corresponding eigenvectors are given by $u_{n}(x):= \sin(n \pi x)$, $x\in(0, 1)$ for any $n\in \mathbb{N}$.

Therefore, if $f(x) = \sum\limits_{n = 1}^{\infty}c_{n}\sin(n\pi x)$ and $g(x) = \sum\limits_{n = 1}^{\infty}d_{n}\sin(n\pi x)$, then by making use the formulas (3.32) and (3.33), the mild solution of abstract Cauchy problem (4.1) can be expressed with the help of perturbation of Mittag-Leffler type functions as below:

and it follows that $A+B$ is the infinitesimal generator of strongly continuous fractional cosine $C_{\alpha}(t; A+B)$ and sine $S_{\alpha}(t; A+B)$ families, $u(x, t) = C_{\alpha}(t; A+B)f(x)+S_{\alpha}(t; A+B)g(x)$.

It is interesting to note that in the case of $\alpha = 2$, the mild solution of the following classical one-dimensional perturbed wave equation:

can be expressed with the help of perturbed cosine and sine functions as follows:

Remark 4.1. Furthermore, in the case of $b = 0$, by using a method of seperating variables the explicit representation of a mild solution to perturbed fractional and classical wave Eqs (4.1) and (4.3), respectively can be represented with the Fourier coefficients which is studied in ^[40]

and

where $B_{n}(0)$ and $B_{n}^{\prime}(0)$ for $n\in \mathbb{N}$ are Fourier coefficients of $f(x)$ and $g(x)$, respectively, that is

5.   Conclusions and future directions

The goal of this paper is to develop some perturbation results for infinitesimal generators of fractional strongly continuous cosine families. That is, we establish sufficient conditions such that $A$ is the infinitesimal generator of a fractional strongly continuous cosine (sine) family in a Banach space $X$, and $B$ is a bounded linear operator in $X$, then $A+B$ is also the infinitesimal generator of a fractional strongly continuous cosine (sine) family in $X$. Meanwhile, our results coincide with the classical ones whenever $\alpha = 2$. Moreover, depending on commutativity condition of linear bounded operators, we derive the elegant analytical representation formulas for uniformly continuous perturbed fractional operator cosine and sine functions. At last, we present an illustrative example in the context of one-dimensional perturbed fractional wave equation to demonstrate the applicability of our theoretical results and we give some comparisons with the existing literature.

We conclude this paper with some open problems concerning with the perturbation of infinitesimal generators of the fractional strongly continuous cosine families and their applications.

● If $A$ is the infinitesimal generator of a fractional strongly continuous cosine (sine) family and $B$ is a closed (unbounded) linear operator in a Banach space $X$, is $A+B$ the infinitesimal generator of a fractional strongly continuous cosine (sine) family? This problem has been considered in the classical case for $\alpha = 2$ in ^[7,28,41], but for $\alpha \in(1, 2)$ it still remains an unsolved problem. One way of obtaining these desired results is to apply the principle of subordination, which serves to construct new results in the fractional sense on the basis of the classical results.

● The attained perturbation results can be applied to derive the explicit representation in closed-form for solutions of the following fractional functional evolution equation with $\alpha \in (1, 2)$ in a Banach space $X$ based on ^[42]:

where $A:D(A)\subseteq X \to X$ is the infinitesimal generator of a fractional strongly continuous cosine (sine) family and $B\in \mathcal{L}(X)$. Moreover, $\varphi:[-\tau, 0]\to X$ is a continuous function which is describing the prehistory of the system. Note that these ideas are new even for the classical case with $\alpha = 2$.

Therefore, all these questions and more are open for consideration in our future research.