1.
Introduction
Very recently the concept of fractal differentiation and fractional differentiation have been combined to produce new differentiation operators [1,2,3,4]. The new operators were constructed using three different kernels namely, power law, exponential decay and the generalised Mittag-Leffler function. The new operators have two parameters, the first is considered as fractional order and the second as fractal dimension.
The operators were tested to model some real world problems [9,10,11] surprisingly, the new differential and integral operators were found to be powerful mathematical tools able to capture even hidden complexities of nature [5,6,16]. Very detailed attractors could be captured when modelling with such differential and integral operators [8]. One of the great advantage of these new operators is that they can at the same time capture processes following power law, exponential decay law, fading memory, crossover and self-similar processes. This unique and outstanding capacity makes these new operators suitable tools to model many complex real world problems. Additionally when the fractal dimension is one, we recover all the existing fractional differential and integral operators, if the fractional order is one, we recover the so-call fractal differential and integral operators. Finally if the fractal and fractional orders tend to 1 we recover classical differential and integral operators. Therefore, it is believed that these new operators are the future for modeling.
On the other hand, modeling real-life problems have been always of interest of researchers. Mathematicians especially have introduced and developed a variety of well-known and sophisticated tools to model problems arising from other sciences such as biology, finance, epidemiology, and geology. The list is not exhaustive. Moreover, they used these tools to investigate solutions to many important and crucial problems that humans are challenging in their daily life. Among these tools are differential equations and fractal differential equations for instance. Nevertheless, the continuous improvement leads constantly their researches in order to obtain better solutions that aim at reaching the reality. Fractal-fractional differential operators can be seen as an enhanced instrument for modeling important practical problems. One of the main motivations for this article was to introduce methods for solving fractal-fractional problems that have not been considered before. By using the proposed methods, approximate solutions to these problems can be determined more easily and with higher accuracy. In addition, the methods can be applied to real-world problems. In this work, we present applications of such numerical schemes in solving chaotic models that involve the new class of differential operators. We consider some well-known chaotic models with fractal-fractional differential operators, so that we can compare our results with those in the literature. The article is organized as follows: In section 2, we give a brief overview of some basic definitions of fractal-fractional differential calculus. Two efficient and effective numerical methods for determining approximate solutions to fractal-fractional problems are presented in section 3. The first is for the Caputo fractal derivative second is for Caputo-Fabrizio-Caputo fractal-fractional derivative and the thierd is for the Atangana-Baleanu-Caputo fractal-fractional derivative. The kernels used in these two definitions are singular and non-singular, respectively. Several numerical simulations for chaotic systems are described in section 4 we find the numerical analysis for Duffing attractor. Numerical analysis for EL-Niˆno Southern Oscillation is find in section 5. In section 6–9, we analysis numerical analysis for Ikeda system, numerical analysis for Dadras attractor and numerical analysis for Aizawa attractor, numerical analysis for Thomas attractor and numerical analysis for 4 Wings attractor. In section 9 we introduce a new Atangana Sonal attractor and find the solution of this. The results obtained are accurate, interesting, and meaningful. Finally, we present our overall conclusions.
2.
Preliminaries on fractal-fractional calculus
Definition 2.1. [3] The fractal fractional derivative of f(t) with order ϖ−κ in the Riemann-Liouville sense is defined as follows:
where m−1<κ,ϖ≤m∈N and df(s)dsϖ=limt→sf(t)−f(s)tϖ−sϖ.
Definition 2.2. [3] The Caputo-Fabrizio fractal-fractional derivative of f(t) with order ϖ−κ in the Riemann-Liouville sense is defined as follows:
where κ>0,ϖ≥m∈N and M(0)=M(1)=1.
Definition 2.3. [2] The Atangan-Baleanu fractal-fractional derivative of f(t) with order ϖ−κ in the Riemann-Liouville sense is defined as follows:
where 0<κ,ϖ≤1 and AB(κ)=1−κ+κΓ(κ).
Definition 2.4. [3] The fractal-fractional derivative of with order ϖ−κ in the Liouville-Caputo sense is defined as follows:
where m−1<κ,ϖ≤m∈N and df(s)dsϖ=limt→sf(t)−f(s)tϖ−sϖ.
Definition 2.5. [2] The Caputo-Fabrizio fractal-fractional derivative of f(t) with order ϖ−κ in the Liouville-Caputo sense is defined as follows:
where κ>0,ϖ≥m∈N and M(0)=M(1)=1.
Definition 2.6. [4] The Atangana-Baleanu fractal-fractional derivative of f(t) with order ϖ−κ in the Liouville-Caputo sense is defined as follows:
where 0<κ,ϖ≤1 and AB(κ)=1−κ+κΓ(κ).
Definition 2.7. [2] The Liouville-Caputo fractal-fractional integral of f(t) with order κ is defined as follows:
Definition 2.8. [3] The Caputo-Fabrizio fractal-fractional integral of f(t) with order κ is defined as follows:
Definition 2.9. [3] The Atangana-Baleanu fractal-fractional integral of f(t) with order κ is defined as follows:
3.
Numerical approximation of fractal-fractional calculus
In this section, we have given three numerical schemes for Caputo-fractal-fractional, Caputo-Fabrizio-fractal fractional and the Atangana-Baleanu fractal-fractional derivative operators [7].
3.1. Caputo-fractal-fractional derivative
Consider the following differential equations in the fractal-fractional Liouville-Caputo sense
Equation (3.1) can be converted to the Volterra case and the numerical scheme of this system using a Caputo-fractal-fractional approach at tn+1 is given by
We can approximate the above integral to
With in the finite interval [tj,tj+1], we approximate the function sϖ−1,f(t,u,v) using the Lagrangian piecewise interpolation such that
So we obtain
Solving the integral of the right hand side, we obtain the following numerical scheme
3.2. Caputo-Fabrizio-Caputo fractal-fractional derivative
Consider the following differential equations in the Caputo-Fabrizio-fractal-fractional derivative
Applying the Caputo-Fabrizio integral, we obtain
Here we present the detailed derivation of the numerical scheme. Thus, at tn+1 we have
Taking the difference between the consecutive terms, we obtain
Now using the Lagrange polynomial piece-wise interpolation and integrating, we obtain
3.3. Atangana-Baleanu-Caputo fractal-fractional derivative
Consider the following differential equations in the Atangana-Baleanu fractal-fractional derivative in the Liouville-Caputo sense
Applying the Atangana-Baleanu integral, we have
At tn+1, we have the following
the above system can be expressed as
Approximating sϖ−1f(s,u,v) in [tj,tj+1], we have the following numerical scheme
4.
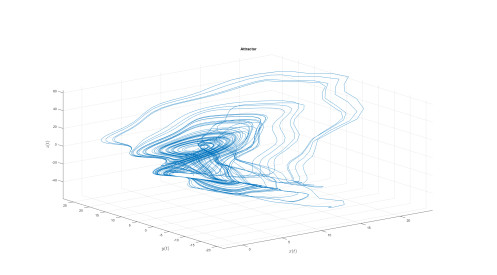
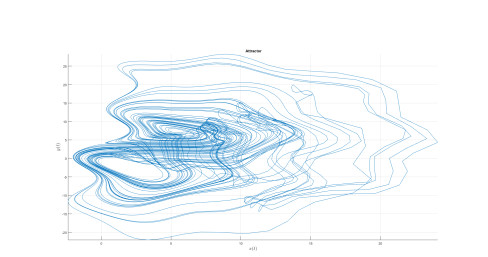
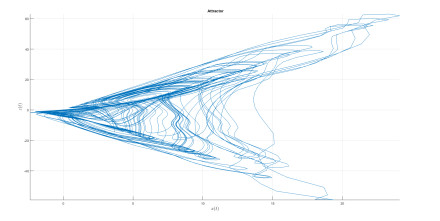
Numerical analysis for Duffing attractor
The Duffing Pendulum is a kind of a forced oscillator with damping, the mathematical model represented in state variable as when we apply Caputo-fractal-fractional derivative is given by
where initial conditions are u1(0)=0.01, u2(0)=0.5 and the constant are κ=0.25, b=0.3, ω=1, h=0.01, and t=100. The numerical scheme is given by
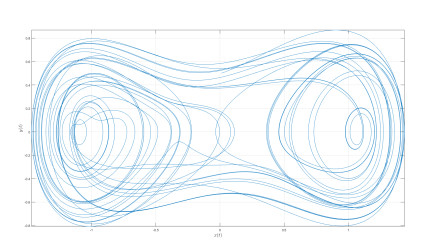
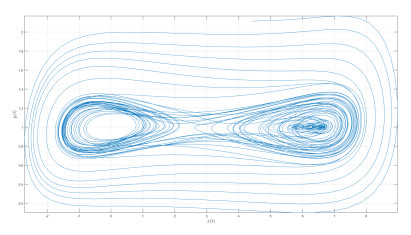
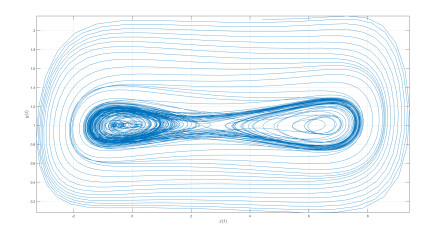
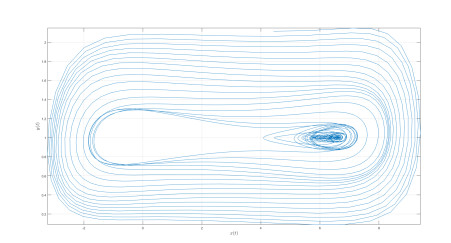
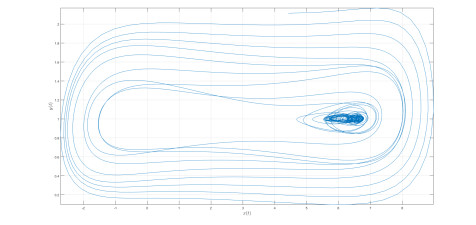
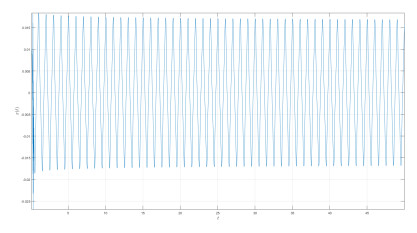
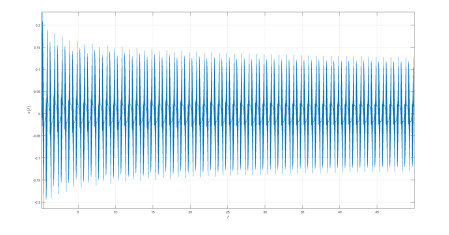
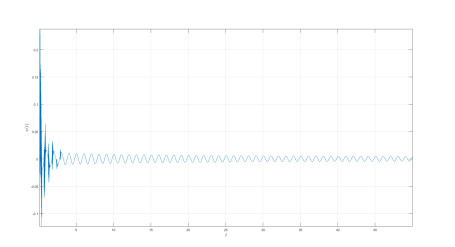
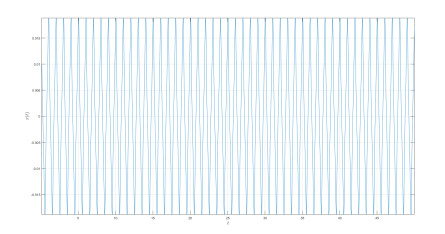
Numerical simulation of the Caputo-power law case are depicted in Figures 1–3 for different values of fractional order κ and fractal dimension ϖ.
Involving the fractal-fractional derivative in the Caputo-Fabrizio-Caputo, we have
The numerical scheme is given by
Involving the fractal-fractional derivative in the Atangana-Baleanu-Caputo sense, we have
The differential and integral operators used in the case of Caputo and Caputo-Fabrizio have kernel with no crossover in waiting time distribution. Therefore to include the effect of crossover in waiting time distribution, we make use of the differential operator whose kernel has crossover behavior, thus the Atangana-Baleanu operators are used here. Also the numerical simulation is presented in Figures 4–8.
Additionally adapting the previously used numerical scheme, we obtain the following:
5.
Numerical analysis for EL-Niˆno Southern Oscillation
The EL-Niˆno Southern Oscillation known as ENSO is an unconventional repetitive variation in sea area temperatures over the tropical eastern Pacific Ocean and winds that affect the climate change of much of the tropics and sub-tropics The natural behavior of this dynamical system can be classified in two phases. The first phase is the warming phase of the sea temperature, this phase was named EL-Niˆno. The second phase known as EL-Niˆno is the cooling phase. The results of some data collection showed that, the Southern Oscillation is following atmospheric component, more importantly the phenomena is coupled with the sea temperature change. On the other hand, the EL-Niˆno is followed by high air surface pressure in the side of tropical western Pacific and La Nina is accompanied with low pressure. In this section, we consider the mathematical model able to replicate such natural occurrence, nevertheless, here we consider the model with different non-local differential and integral operators.
The behavior of this phenomena is described by the following equation as in Caputo-fractal-fractional derivative sense
where κ=100 and b=1.
The numerical scheme is given by
The above numerical solution is depicted in Figures 9–13, for different value of fractional order and fractal dimension. In this exercise, we chose to simulate the case with Caputo derivative. The numerical simulation depend on the fractional order and the fractal dimension. More precisely for the values 0.8 and 0.5, we observed a very strange behavior where the oscillation are vanishing.
Involving the fractal-fractional derivative in the Caputo-Fabrizio-Caputo, we have
The numerical scheme is given by
Involving the fractal-fractional derivative in the Atangana-Baleanu-Caputo sense, we have
The numerical scheme is given by
6.
Numerical analysis for Ikeda system
Consider the ikeda delay system in Caputo-fractal-fractional derivative sense
In [12], the author proposed a second delay parameter. The below given equation is resultant solution
here we consider a = 24, b = 3 and c = 1 and the delays τ1=0.01 and τ2=0.1.
The numerical scheme is given by
Involving the fractal-fractional derivative in the Caputo-Fabrizio-Caputo, we have
The numerical scheme is given by
Involving the fractal-fractional derivative in the Atangana-Baleanu-Caputo sense, we have
The numerical scheme is given by
7.
Numerical analysis for Dadras attractor
Consider the Dadras system described [13] by the following equation as in Caputo-fractal-fractional derivative sense
where A = 3, B = 2.7, C = 1.7, D = 2 and E = 9.
The numerical scheme is given by
Involving the fractal-fractional derivative in the Caputo-Fabrizio-Caputo, we have
The numerical scheme is given by
Involving the fractal-fractional derivative in the Atangana-Baleanu-Caputo sense, we have
The numerical scheme is given by
Numerical simulation are depicted in Figures 14–17 for the value of κ=0.8 and value of ϖ=0.9. The used numerical model is that with the fractal-fractional differential operator. The model with this new differential operator display some important behavior.
8.
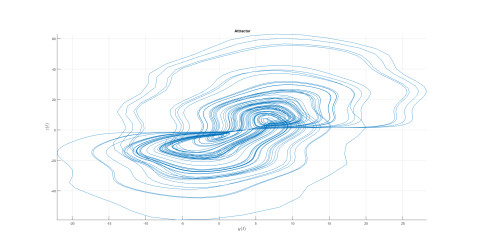
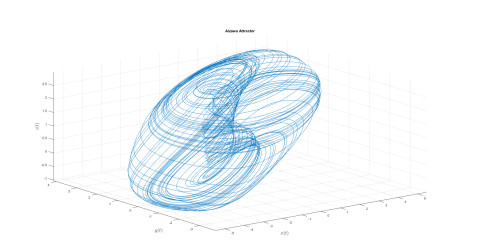
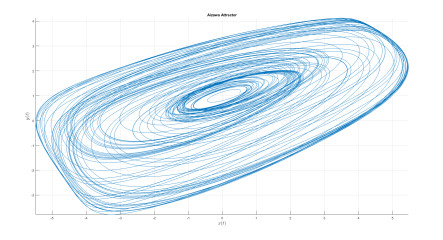
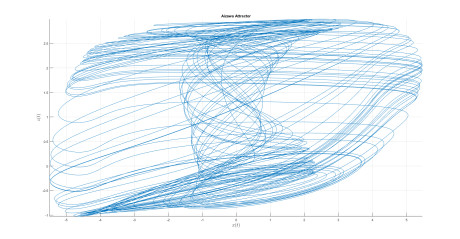
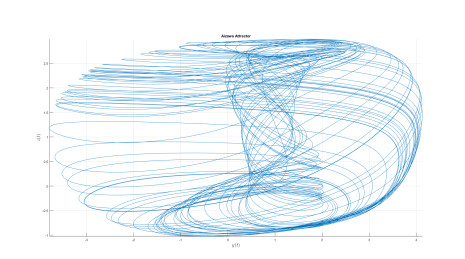
Numerical analysis for Aizawa attractor
A very strange attractor have been studied in the last past years, although such system of equations have not being attracting attention of many researchers, but the attractor is very strange as the system is able to display very interesting attractor in form of sphere. The model under investigation is called Aizawa attractor, this system when applied iteratively on three-dimensional coordinates, it is important to point out that, evolving in such a way as to have the consequential synchronizes map out a three dimensional shape, in this case a sphere with a tube-like structure powerful one of it's axis. In this section, we consider the model using the fractal-fractional with power law, exponential decay law and the generalized Mittag-Leffler function.
Consider the Aizawa system described by the following equation as in Caputo-fractal-fractional derivative sense
where A=0.95, B=0.7, C=0.6, D=3.5, E=0.25, and F=0.1. The numerical scheme is given by
Involving the fractal-fractional derivative in the Caputo-Fabrizio-Caputo, we have
The numerical scheme is given by
Involving the fractal-fractional derivative in the Atangana-Baleanu-Caputo sense, we have
The numerical scheme is given by
Numerical simulation are depicted in Figures 18–21 for the value of κ=0.8 and value of ϖ=0.9. The used numerical model is that with the fractal-fractional differential operator. The model with this new differential operator display some important behavior.
9.
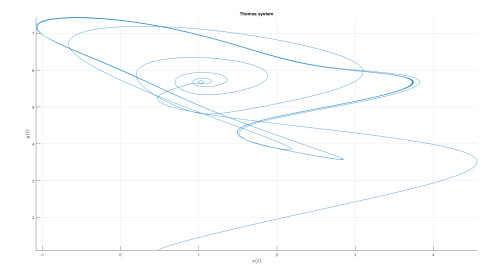
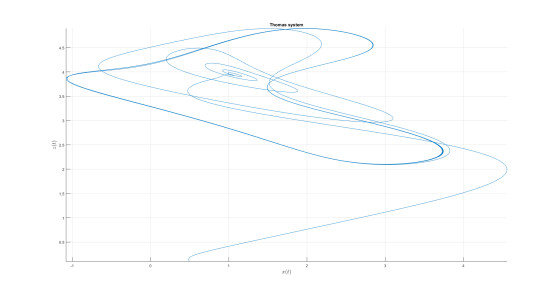
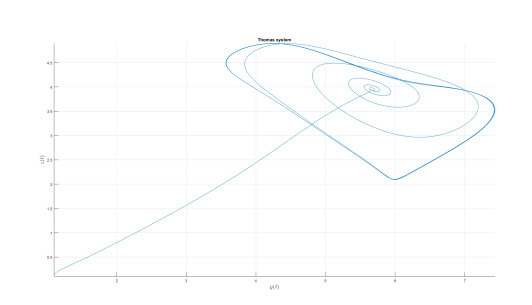
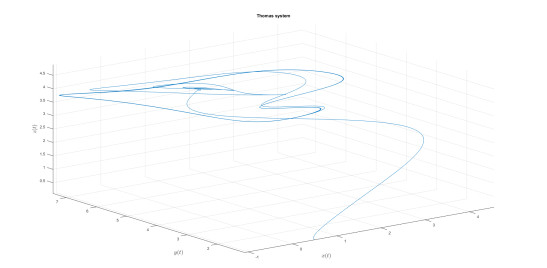
Numerical analysis for Thomas attractor
Consider the Thomas system described by the following equation as in Caputo-fractal-fractional derivative sense
The numerical scheme is given by
Involving the fractal-fractional derivative in the Caputo-Fabrizio-Caputo, we have
The numerical scheme is given by
Involving the fractal-fractional derivative in the Atangana-Baleanu-Caputo sense, we have
where A=0.19.
The numerical scheme is given by
Numerical simulation are depicted in Figures 22–25 for the value of κ=0.9 and value of ϖ=0.9. The used numerical model is that with the fractal-fractional differential operator. The model with this new differential operator display some important behavior.
10.
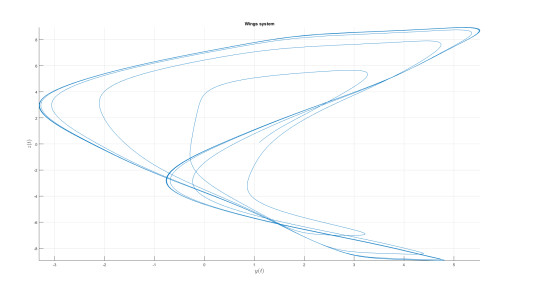
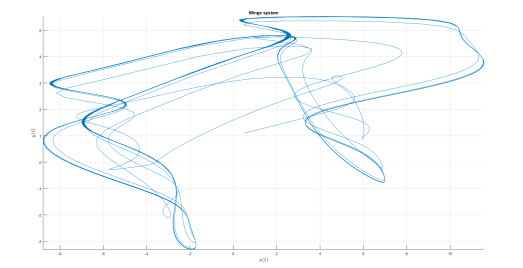
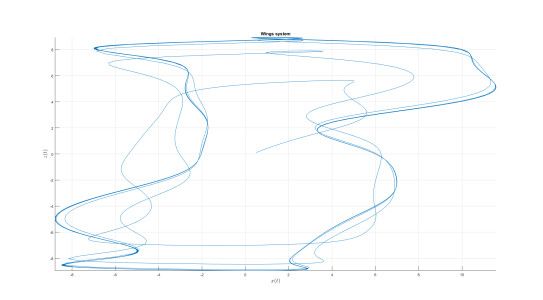
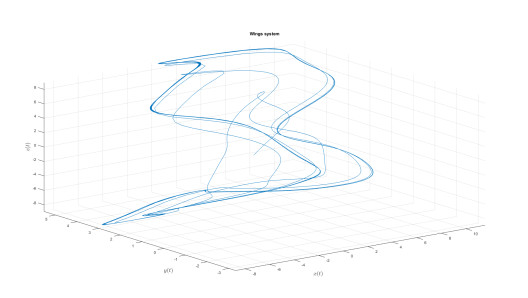
Numerical analysis for 4 Wings attractor
Consider the 4 Wings system proposed in [15] and modifying in [14] is described by the following equation as in Caputo-fractal-fractional derivative sense
where A=4, B=6, C=10, D=5, and E=1.
The numerical scheme is given by
Involving the fractal-fractional derivative in the Caputo-Fabrizio-Caputo, we have
The numerical scheme is given by
Involving the fractal-fractional derivative in the Atangana-Baleanu-Caputo sense, we have
The numerical scheme is given by
Numerical simulation are depicted in Figures 26–29 for the value of κ=0.9 and value of ϖ=0.8. The used numerical model is that with the fractal-fractional differential operator. The model with this new differential operator display some important behavior.
11.
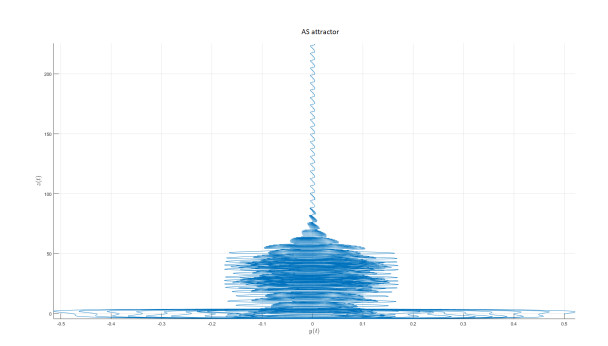
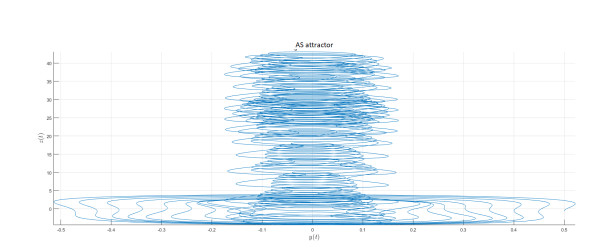
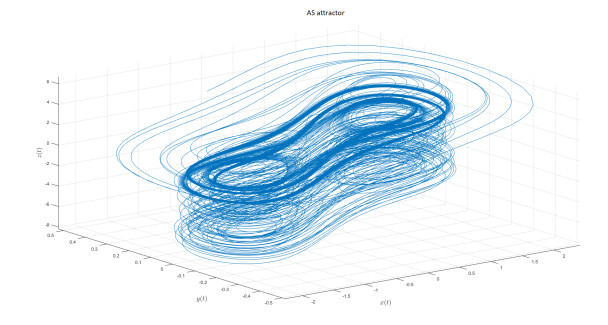
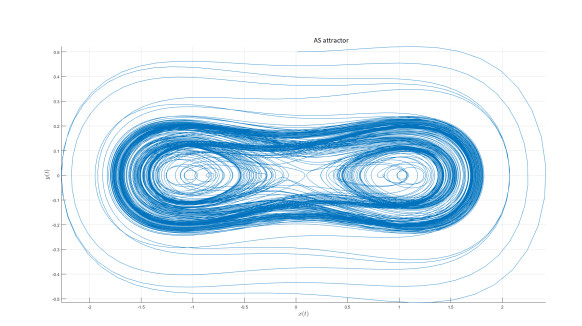
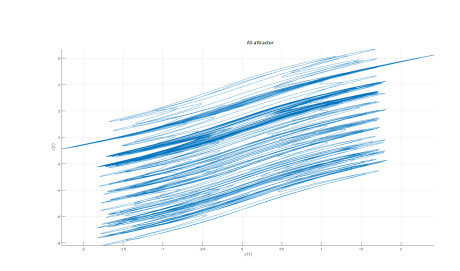
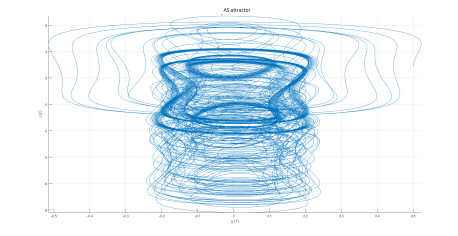
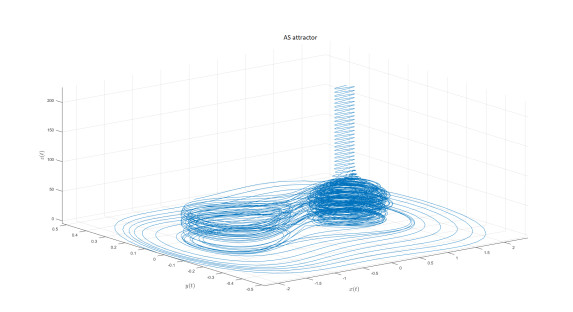
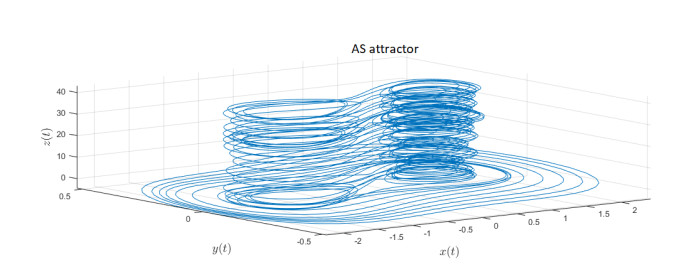
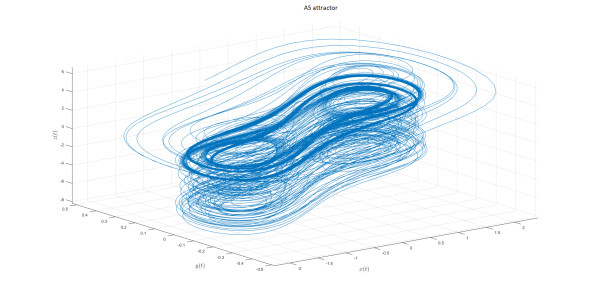
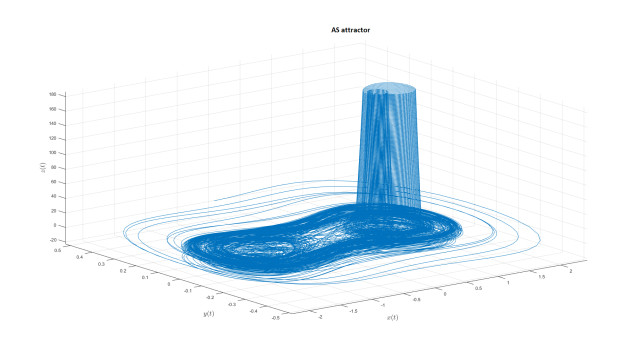
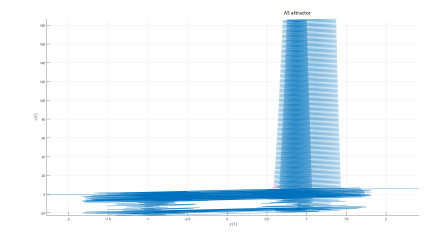
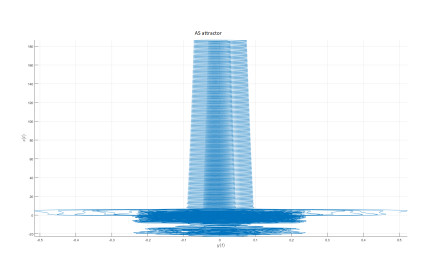
AS attractor
We introduce the following attractor called AS attractor
where the initial conditions
The mathematical model represented in state variable as when we apply Caputo-fractal-fractional derivative is given by
The numerical scheme is given by
Involving the fractal-fractional derivative in the Caputo-Fabrizio-Caputo, we have
Involving the fractal-fractional derivative in the Atangana-Baleanu-Caputo sense, we have
The numerical scheme is given by
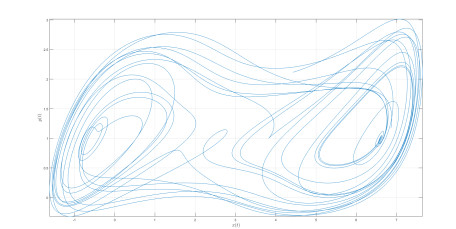
We present the numerical simulation in the following Figures 30–42 for different values of fractional order and fractal dimension.
12.
Conclusions
Fractal-fractional differential operators have been introduced very recently; however, the new concept has not yet attracted attention of many scholars. In fact, few works have being done where such differential and integral operators are used. The advantages if this work is that it considers operators capturing new complexities of nature with great success. Such differential and integral operators are sophisticated tools to model complex real world problems. Moreover, in order to evaluate the efficiency and the capabilities of the new differential and integral operators, we investigate the behavior of some well-known chaotic attractors and see if one will capture more complexities compared to existing differential and integral operators. Additionally, we introduced a new chaotic model with alternative attractors and we showed by numerical simulation that these new differential and integral operators are powerful mathematical operators able to capture heterogeneity. Since any new numerical method should be validated in terms of convergence, stability and consistency of solutions, these are important research directions left to future work.
Acknowledgment
The authors would like to express their sincere appreciation to the United Arab Emirates University for the financial support through UPAR Grant No. 31S369.
Conflict of interest
The authors have declared no conflict of interest.









 DownLoad:
DownLoad: