A systematic synthesis on the context reliant performance of organic farming

1.   Introduction

Topology optimization is an advanced method for structural optimization which has achieved vast progress over the last four decades. Topology optimization is mostly utilized to confirm the material(s) distribution within a prescribed spatial domain during the initial design stage, and it is realized by applying one or several certain conditions (volume constraints, perimeter constraints, mass constraints, etc.) to enhance structural performance. Topology optimization methods are of great significance in studies of the force transmission path and the performance of materials. By topology optimization, an optimal structure with better performance or less material consumption (while the structural performance is retained) can be obtained. So far, various distinctive approaches have become increasingly popular and have, therefore, been widely studied and applied for topology optimization ^[1,2,3], such as the homogenization theory ^[1], the density-based scheme (e.g., solid isotropic microstructure with penalty (SIMP)) ^[2], the evolutionary structural optimization (ESO) concept ^[4], the level-set approach ^[5,6,7,8,9], the parametric level-set method ^{[10,11,12,13,14,15]}, the isogeometric method ^[16,17], the bionic approach ^[18], the meshless method ^[19,20], and so on.

Since Bendsøe and Kikuchi realized the structural topology optimization of porous materials successfully by applying the homogenization theory ^[1], structural topology optimization has garnered much attention for application to computational mechanics, material mechanics, and engineering structures. The research field of topology optimization can be mainly categorized as either continuum topology optimization or discrete structure topology optimization, both of which are closely related to finite element analysis (FEA). However, FEA is closely related to the mesh generation of structural design domains, so the generator of finite element meshes has significant influence on the efficiency of structure optimization. Most computationally oriented papers on topology optimization that rely on FEA apply unified low-order linear triangular meshes ^[21] or quadrilateral meshes ^[22] to discretize a design domain. However, numerical instability phenomena like the checkerboard patterns and the single-node connections often appear in the results of the variable density method ^[22,23]. Usually, a regularization scheme such as filtering ^[23] can be used to suppress such numerical instability phenomena, but regularization measures often involve the related parameters in the heuristic algorithm (for example, the SIMP method ^[23]) that can increase the complexity of topology optimization. A polygonal discretization method has been proposed by Talischi et al. ^[24] to achieve stable topology optimization formulations ^[25] by using lower-order polygonal elements. Jie et al. ^[26] extended the above method, introduced a simulated annealing algorithm into the process of mesh generation for finite element methods on the basis of the Centroidal Voronoi tessellations (CVTs), and solved the problems related to it being difficult to achieve convergence via the MacQueen's method and the Lloyd's algorithm. Recently, Bruggi ^[27] has proposed a topology optimization method that uses mixed finite elements on regular grids. The efficient mixed finite elements furnish accuracy and robustness on regular grids, and the topology optimization problem is solved only in terms of stresses. From the above references, the methods using the Voronoi elements have the ability to discretize the design domain with complex boundaries and solve the topology optimization problems of non-convex domains. Moreover, the methods have good numerical stability. Therefore, a topology optimization approach for multi-material structures is proposed on the basis of Voronoi elements in this paper.

The research on topology optimization currently focuses on solving the problems of stress constraints, nonlinear problems, and dynamic problems. However, it is not difficult to address the problems of single-material topology optimization ^[5,28]. With the development of topology optimization methods and engineering application requirements, research on topology optimization problems of multi-material structures is gradually becoming the mainstream. There are many works that focus on the solution of multi-material topology optimization ^{[29,30,31,32,33,34,35,36]}. In accordance with the concept of material distribution, Bendsøe and Sigmund put forward a SIMP method with a multi-material mixing principle ^[37], which has been successfully put to use for the compliance agencies of multiphysics ^[38]. Another method for optimizing the topology of multiple materials has been derived from the variable density method ^[39]. During the process of designing intelligent and sensitive structures, the multi-material topology optimization models have been used to find the optimal distribution of elastic and piezoelectric materials ^[40,41,42]. Hvejsel and Lund ^[43] proposed a couple of multi-material interpolation methods which summarized the well-known material interpolation schemes based on SIMP and the rational approximation of material properties. For topology optimization involving multiple materials, Tavakoli and Mohseni ^[44] put forward an alternating active-phase algorithm and a 115-line MATLAB implementation, through which a multi-material topology optimization problem is transformed into a range of two-material topology optimization sub-problems. Zhou and Wang ^[45] brought forward a universal method to tackle the multi-phase topology optimization problems on the basis of the Cahn-Hilliard equation. According to the penalization of objective functionals with the Ginzburg-Landau energy functional, Tavakoli ^[46] introduced a new method for multi-material topology optimization. The level-set method has been widely employed to multi-material structural topology optimization since the development of the SIMP method. For example, a "color" level-set approach was proposed by Wang and Wang ^[47] to solve the topology optimization problem involving compliance minimization with multiple materials. Moreover, Wang et al. ^[48] have put forward a level-set approach for multi-material topology optimization, in which M materials are expressed by M level sets with accurate mathematical expressions. By using the method, the redundant regions, as well as the overlaps between different materials, can be avoided. However, the traditional level-set method can only move or merge the existing holes, but not generate a new hole. Hence, it is generally decided by the initial design. The level-set method with moving morphable components (MMC) was proposed by Guo et al. ^[49] to realize topology optimization explicitly and geometrically. By utilizing this method, geometric and mechanical information can be directly combined and integrated with the topology optimization process. The method has greater flexibility in terms of handling topology optimization problems and reducing computational burden. Then, Zhang et al. ^[50] and Guo et al. ^[51] expanded the explicit structural topology optimization. Both of their methods are based on MMC and a level-set approach, which have shown great potential for use in multi-material topology optimization. Besides the SIMP method and the level-set approach, another procedure to address the problem of multi-material topology optimization is the evolutionary topology optimization involving multiple materials. For example, Huang and Xie ^[52] proposed a bi-directional ESO method which can be put to use to handle the binary-phase or multi-material topology optimization problem. In this article, the discretization method using Voronoi elements based on SIMP is considered. Therefore, a multi-material topology optimization method based on the alternating active-phase algorithm ^[44] is adopted as the framework to address the topology optimization problem involving multiple materials. The design variables are improved by using a filtering matrix and mapped to element variables so that the proposed method can be successfully implemented.

In existing methods for topology optimization involving multiple materials, the unified quadrilateral elements are usually utilized to discretize the design domains. However, it is difficult to optimize the structures with complex boundaries by using the unified quadrilateral elements, which confines the application range of the methods. To overcome the limitation, we propose a discretization method that uses the centroidal Voronoi elements to discretize the design domain of structures involving multiple materials. The centroidal Voronoi elements are based on the signed distance functions and the corresponding reflecting functions ^[53,54]. For an arbitrary mesh, the FEA routine can be implemented by using the unstructured and isoparametric polygonal elements. Therefore, the discretization method can deal with the design domains with complex boundaries, obtain good robustness, and avoid the checkerboard patterns ^[55,56].

The rest of this article is organized as follows. The polygonal meshes which can be used to discretize the design domain are introduced in Section 2. The model of topology optimization, combined with the alternating active-phase algorithm, is depicted in Section 3. The modified model of topology optimization is expressed in Section 4. The sensitivity analysis and the update scheme for design variables are described in Section 5. In Section 6, several numerical examples are provided to demonstrate the performance and effectiveness of this method. The conclusions are finally drawn in Section 7.

2.   Polygonal elements

Inspired by References ^{[24,25,57,58]}, we introduce the approximate hexagonal CVT elements to discretize the structural design domain with complex curve boundaries. In this section, we present the signed distance function, the corresponding mapping functions, the formation process for Voronoi elements, as well as the discretization method of the design domain. Finally, we discretize the design domain through the use of CVT elements.

2.1.   Distance function

Here, the signed distance function ^[24] is incorporated and used to implicitly express the design domain. Assuming that $\Omega$ is a subset of the two-dimensional real number space ${{\text{R}}^2}$, then the distance function ${\text{d}}({\mathbf{x}})$ can be described as follows:

where ${\mathbf{x}}$ represents the point set of $\Omega$, $\partial \Omega$ signifies the boundary of $\Omega$, and ${{\mathbf{x}}_b}$ represents the point set of $\partial \Omega$. $|| \bullet ||$ signifies the standard Euclidean norm. Hence, the distance between ${\mathbf{x}}$ and ${{\mathbf{x}}_b}$ can be denoted by $||{\mathbf{x}} - {{\mathbf{x}}_b}||$ here.

In this mesh algorithm, it is necessary to judge whether the point set ${\mathbf{x}}$ lies within the design domain, which is similar to the situation in which a level-set function is used to represent the design domain. Then, by means of Eq (1), the design domain can be represented as follows.

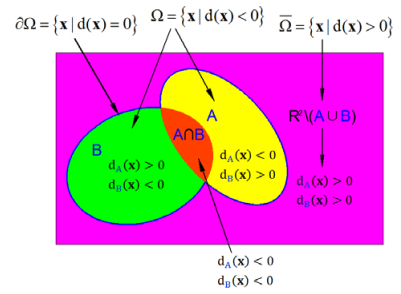
Figure 1 shows a schematic diagram of the relationship between the signed distance functions and the design domain. The green, orange, and yellow parts represent the solid design domain $\Omega$, the magenta part represents ${{\text{R}}^2}\backslash \Omega$, and the indigo curve signifies the boundary of the design domain $\partial \Omega$.

Figure 1.  The relationship between the signed distance functions and the design domain.

DownLoad: Full-Size Img PowerPoint

To describe the distance functions more clearly, the gradient of the signed distance function $\frac{{\nabla {\text{d}}({\mathbf{x}})}}{{|\nabla {\text{d}}({\mathbf{x}})|}}$ is used to display the direction from an arbitrary point ${\mathbf{x}}$ to its nearest boundary point of the design domain. Certainly, it can also be said that $\frac{{\nabla {\text{d}}({\mathbf{x}})}}{{|\nabla {\text{d}}({\mathbf{x}})|}}$ represents the direction closest to the boundary from point ${\mathbf{x}}$. If the boundary of the design domain $\Omega$ is smooth and ${\mathbf{x}}$ is a point located on the boundary $\partial \Omega$, then the length of the gradient vector $\frac{{\nabla {\text{d}}({\mathbf{x}})}}{{|\nabla {\text{d}}({\mathbf{x}})|}}$ is equal to 1 and its direction remains the same as the normal direction of the boundary. In general, for almost all points ${\mathbf{x}} \in {{\text{R}}^2}$, we have

The above-mentioned features of the gradient vector $\frac{{\nabla {\text{d}}({\mathbf{x}})}}{{|\nabla {\text{d}}({\mathbf{x}})|}}$ can be used to determine the mirror reflection (mapping) point ${\text{R}}({\mathbf{x}})$ of the point ${\mathbf{x}}$ about its closest boundary $\partial \Omega$. Correspondingly, the formula for the mirror reflection point ${\text{R}}({\mathbf{x}})$ can be expressed as below.

Figure 2 explains the formation of the reflection ${\text{R}}({\mathbf{x}})$ in the form of a diagram, where the distance of ${\mathbf{x}}$ to ${{\mathbf{x}}_b}$ remains the same as the distance of ${{\mathbf{x}}_b}$ to ${\text{R}}({\mathbf{x}})$.

Figure 2.  The reflection R(x) of x about the design domain boundary $\partial \Omega$.

DownLoad: Full-Size Img PowerPoint

The signed distance functions and their corresponding mapping functions are used to describe the structural design domain in this article. Therefore, it is necessary to construct the signed distance functions about a given domain. For simple geometries, it is easy to confirm the signed distance function. For instance, the distance function of design domain $\Omega$ can be expressed as ${\text{d}}({\mathbf{x}}) = ||{\mathbf{x}} - {{\mathbf{x}}_0}|| - l/2$ in the case that $\Omega$ indicates a quadrate with a side length l centered at point ${{\mathbf{x}}_0}$. The level curves of the signed distance function are a series of quadrates centered at point ${{\mathbf{x}}_0}$ and with a side length less than l. For the design domains with geometric complexity, they should first be discretized into a series of simple geometric configurations. Then, the set operation rules, namely, the union, intersection, difference, and complementarity, are very suitable for the purpose of piecing and connecting different simple geometric configurations. Given two regions A, B and the corresponding distance functions ${{\text{d}}_{\text{A}}}({\mathbf{x}})$ and ${{\text{d}}_{\text{B}}}({\mathbf{x}})$ as an example, the aforementioned set operation rules are described as follows.

where A and B are the different domains of a simple geometry, such as a circle, straight line, rectangle, triangle, etc. The characteristics for the signed distance functions of combined geometric configurations are shown in Figure 1.

For a given design domain with complex curve boundaries, it can be discretized into a series of simple geometric regions (${\Omega_i}$, i = 1, 2, ..., n). The distance function of the ith simple geometric region is defined as ${{\text{d}}_i}({{\mathbf{x}}_i})$. According to Eq (5), the signed distance function can be described by

where ${\text{F}}$ means an appropriate multivariate function for the set operation rules mentioned above.

2.2.   Voronoi meshes and correlation calculations

Define the set of seeds ${\mathbf{P}} = \{ {{\mathbf{p}}_i}\} _{i = 1}^{\text{N}}$ which assembles the x and y coordinates of all N points of meshes into an N-by-2 array in the design domain $\Omega \in {{\text{R}}^2}$. The Voronoi tessellation of ${{\mathbf{p}}_i}$ (${{\mathbf{p}}_i}$ is a seed in the set ${\mathbf{P}}$), denoted by ${{\mathbf{V}}_i}$ (as shown in Figure 3), can be defined by

where $|| \bullet ||$ is the distance function (i.e., the standard Euclidean norm). In other words, the Voronoi tessellation ${{\mathbf{V}}_i}$ consists of the points nearer to the point ${{\mathbf{p}}_i}$ than the others inside ${\mathbf{P}}$. The properties of Voronoi diagrams mainly include the following: 1) Each V-polygon has a generator element inside it; 2) The distance from the inner point of each V-polygon to the generating element is shorter than the distance to other generating elements; 3) The distance between each of the points on the polygon boundary and the generating element that generates this boundary is equal; 4) The Voronoi polygon boundaries of adjacent graphics are subsets of the original adjacent boundaries. It is worth noting that Voronoi diagrams are bounded convex polygons and play an important role in computational geometry due to their ability to partition regions based on point sets with the closest distance to points, making them essential in the FEA.

Figure 3.  Illustration of the Voronoi tessellation ${{\mathbf{V}}_i}$ and the approximate boundary of $\Omega$. (Note that the Voronoi edge shared between each seed ${{\mathbf{p}}_i}$ and its reflection ${\text{R}}({{\mathbf{p}}_i})$ is a segment of the approximate boundary of $\Omega$).

DownLoad: Full-Size Img PowerPoint

If each seed is coincident with the centroid of the corresponding Voronoi element, then the Voronoi tessellation ${{\mathbf{V}}_i}$ will be centroidal. Then, the distribution of discrete seeds is optimal, and Voronoi diagrams have minimal energy ^[59] that promotes the regularization of Voronoi tessellation. Additionally, a discretization method based on CVT elements can be used to prevent such imperfections as grid slivers and crossovers, which is very advantageous for the FEA in the future. Therefore, a multi-material topology optimization method combined with the CVT elements is put forward.

According to References ^[57,58], a minimum distance method of the interior points can eliminate the clustering of randomly generated points and generate the graded meshes. However, many distorted elements may be produced near the complex curve borders and affect the FEA. Taking inspiration from References ^[25] and ^[59], a method is proposed here, in combination with Lloyd's algorithm, to make the obtained Voronoi elements centroidal and consequently ensure the quality of meshes. The edge lengths of each polygonal element are employed as evaluation metrics for the quality of meshes. In addition, all edge lengths corresponding to each CVT element are equal. In terms of the quality of meshes, the CVT elements have clear and significant advantages over the triangular and quadrilateral elements. Lloyd's algorithm, which is used to update the seeds ${\mathbf{P}}$ and gain the CVTs, is expressed as follows.

where ${\mathtt{ρ}}({\mathbf{x}})$ represents a defined density function that exists throughout the entire design domain; k denotes the kth iteration. It can be observed that the seed set ${\mathbf{P}}$ is mapped by ${\mathbf{L}}$ to the seed set corresponding to the centroids of Voronoi elements. From Eqs (8) and (9), it is obvious that the Voronoi elements are CVTs if the seeds satisfy that ${\mathbf{P}} = {\mathbf{L}}({\mathbf{P}})$.

Once the set of discrete points ${\mathbf{P}}$ is determined, the set of reflections will be established by Eq (4), which enables the construction of the Voronoi diagram of ${\mathbf{P}} \cup {\text{R}}({\mathbf{P}})$. With Lloyd's algorithm, the convergence criterion is set to depend upon the motion of the seeds or the energy gradient function during the iterative process; meanwhile, the centroid set $\overline {\mathbf{P}}$ takes the place of the original point set ${\mathbf{P}}$ until the iterative process ultimately reaches convergence. Here, the energy gradient function with the CVT point ${\overline {\mathbf{p}} _i}$ is chosen as the convergence criterion:

A "non-dimensional" error parameter is defined by Eq (11):

The convergence criterion is described as follows:

In this work, the discretization for the interior of design domains is achieved through the relevant calculations corresponding to the discrete point set ${\mathbf{P}}$, while the discretization for the boundary of design domains is achieved by using the Voronoi diagrams corresponding to the seeds ${\mathbf{P}}$ and their reflections ${\text{R}}({\mathbf{P}})$ (i.e., ${\mathbf{P}} \cup {\text{R}}({\mathbf{P}})$). It is assumed that this work involves a bounded convex design domain $\Omega$, and that, consequently, the mapping points are located outside of $\Omega$. As for the design domain boundary, it approximates an edge which is formed by many tangents across the boundary points (as shown in Figure 3). Therefore, the boundary discretization approximation approach can be used to tackle the issue of complex curve boundaries by the Voronoi elements. For the specified set of points ${\mathbf{P}}$, the design domain discretized by Voronoi diagrams is expressed below.

3.   Alternating active-phase algorithm

Due to the fact that the grid discretization method using Voronoi elements is grounded in the variable density concept, this work adopts the use of a topology optimization method combined with the alternating active-phase algorithm ^[44], which decomposes a multi-phase topology optimization problem into a series of two-phase topology optimization problems and solves them step by step. It should be pointed out that we consider the void as a separate phase (or material) when expressing the formulas. The distribution of each material can be determined via the fields of local volume fraction, namely, ${\vartheta _j}$ (note that ${\vartheta _j} = {\vartheta _j}({\mathbf{y}})$) ($j = 1, 2, \ldots, {\text{M}}$), i.e., the local volume fraction of the corresponding material can be defined as the design variable. It is assumed that ${\vartheta _j}$ satisfies that ${\vartheta _j} \in {\text{V}}(\Omega)$ ($j = 1, 2, \ldots, {\text{M}}$), and ${\text{V}}$ represents a function space that is sufficiently regular. Thus, the boundary constraints on each ${\vartheta _j}$ ($j = 1, 2, \ldots, {\text{M}}$) are as follows:

where ${{\mathbf{u}}_j}$ and ${{\mathbf{l}}_j}$ indicate the lower and upper limits of design variables ${\vartheta _j}$, respectively.

One global volume constraint is usually defined as the constraint of topology optimization. Considering the volume fractions for all materials, the global volume constraint can be expressed as below.

where ${\mathbf{y}}$ signifies a point in $\Omega$ (here, ${\mathbf{y}} \in {\mathbf{P}}$ and ${\mathbf{y}} = {{\mathbf{p}}_i} = {\overline {\mathbf{p}} _i}$); ${{\Lambda}_j}$ is a customization parameter; obviously, $0 \leqslant {{\Lambda}_j} \leqslant 1$, and $\sum\limits_{j = 1}^{\text{M}} {{{\Lambda}_j}} = 1$.

In order to facilitate the process of solving the two-dimensional topology optimization problems, all design variables ${\vartheta _j}$ ($j = 1, 2, \ldots, {\text{M}}$) are compressed into one vector field which is marked with ${\mathbf{J}}$, namely, ${\mathbf{J}} = \{ {\vartheta _1}, ..., {\vartheta _j}, ..., {\vartheta _{\text{M}}}\}$. After the discretization for the design domain is finished, the admissible design space ^[44] $\Pi$ can be defined as below.

In this article, the performance parameters of each material are given in advance. Here, $\overline {\text{M}} (\vartheta)$ represents the material performance interpolation functions for the volume fraction. The solutions to the partial differential equation (PDE) constraints are represented by ${\text{U}}(\vartheta ) = \Theta (\vartheta ({\mathbf{y}}))$, where $\Theta$ indicates a function space that is sufficiently regular. The partial differential operator subject to PDE constraints can be represented by the operator $\Gamma(...)$. Accordingly, the discrete form for PDE constraints is expressed below.

Considering the above terminology, the structural minimum compliance is defined as the objective of topology optimization. Generally speaking, the objective function $\Phi$, which is dependent upon $\vartheta$ and ${\text{U}}$, can be expressed as an integral spanning the entire region of $\Omega$. Therefore, the discrete mathematical model for each multi-material topology optimization problem can be abstractly represented as follows.

According to the alternating active-phase topology optimization algorithm, the optimization process can be implemented by the nested inner and outer loops. In the outer loop, it is necessary to solve ${\text{M(M}} - 1)/2$ two-phase topology optimization sub-problems, that is, to solve the 0-1-type single-material topology optimization problem shown in the inner loop.

All topology optimization sub-problems in the inner loop are solved via the modified density method. Therefore, in each topology optimization of the inner loop, ${\text{M}} - 2$ materials are fixed, and the remaining two materials are handled by the binary phase method (as illustrated in Figure 4). The two active materials are represented by subscripts "a" and "b", respectively, and the corresponding volume fractions of the two active materials are represented by ${\vartheta _{\text{a}}}$ and ${\vartheta _{\text{b}}}$. The volume fraction field of the two active materials is represented by ${{\mathbf{r}}_{{\text{ab}}}}$.

Figure 4.  Illustration of alternating active-phase algorithm with four materials (A, B, C, and D).

DownLoad: Full-Size Img PowerPoint

Since $\sum\limits_{j = 1}^{\text{M}} {{\vartheta _j}} = 1$ (i.e., $\sum\limits_{j = 1}^{\text{M}} {{{\text{v}}_j}} = 1$), the volume fraction of material a is required as the design variable for the topology optimization sub-problem of binary phases (material a and material b). After the sub-problem of material a is solved, the volume fraction field of material b can be calculated by solving ${\vartheta _{\text{b}}} = {{\mathbf{r}}_{{\text{ab}}}} - {\vartheta _{\text{a}}}$.

Considering Eqs (14) and (19), in the sub-problem of binary-phase topology optimization, the temporary upper limit of material a, ${{\mathbf{u}}^{{\text{a, temp}}}}$ (which is adopted for updating the design variables), can be calculated as follows:

where ${{\mathbf{u}}_a}$ denotes the upper limit of the volume fraction corresponding to material a (as described by Eq (14)), and the lower bound of material a does not need to change. With the "active phases" a and b, the parameter ${\vartheta _{{\text{ab}}}}$ denotes the design vector of the active materials (a and b) and fixed materials ($j \ne a, b$). Thus, the topology optimization sub-problem corresponding to the inner loop becomes a 0-1-type (binary phase) counterpart, which is formulated as below.

In this work, the objective function of topology optimization is set to minimize the structural compliance, and the material property function $\overline {\text{M}}$ is obtained via analogy by using the elasticity tensor ${\mathbf{E}}({\mathbf{y}}){\text{ = }}{\mathbf{E}}(\vartheta ({\mathbf{y}}))$. Note that ${\mathbf{E}}$ is a fourth-order super-symmetric tensor (symmetric in both the right and the left Cartesian index pair, together with symmetry under the interchange of the pairs). According to References ^[44] and ^[45], the SIMP version, as improved by linear interpolation, can be applied in multi-material interpolation as follows.

where ${{\mathbf{E}}_j}$ indicates the constant elasticity tensor corresponding to material $j$ ($j = 1, 2, \ldots, {\text{M}}$); q signifies a power in the SIMP interpolation; ${\mathbf{E}}(\vartheta)$ represents the structural stiffness to be used for subsequent FEA and sensitivity analyses.

For a given volume fraction vector of each material, the PDE operator can be formulated as below.

where ${\mathbf{u}}$ represents the displacement field corresponding to the PDE constraints; ${\mathbf{f}}$ represents the volumetric body force; ${\mathbf{\hat u}}$ indicates the prescribed displacement of boundaries ${\gamma _u}$; ${\gamma _f}$ indicates the traction-free part of boundaries; ${\mathbf{\hat t}}$ indicates the traction of a structure through the traction boundaries ${\gamma _t}$; the integrated boundary of the design domain is $\partial \Omega = {\gamma _u} \cup {\gamma _f} \cup {\gamma _t}$. Furthermore, ${\text{D}}({\mathbf{u}}): = \frac{1}{2}(\nabla {\mathbf{u}} + {(\nabla {\mathbf{u}})^T})$.

4.   Topology optimization model involving multiple materials

In this work, the design domain with the complex curve boundaries is discretized by using the CVT elements, and the main framework for handling topology optimization involving multiple materials is the alternating active-phase algorithm. To overcome the challenges of applying CVT elements in topology optimization involving multiple materials, the design variables denoted by ${\vartheta _j}$ ($j = 1, 2, \ldots, {\text{M}}$) are improved and regularized by the filtering matrix ${{\mathbf{F}}_t}$ and consequently mapped to the element variables denoted by ${{\mathbf{z}}_j}$ ($j = 1, 2, \ldots, {\text{M}}$). Taking inspiration from References ^{[23,24,25,44]}, we propose a new model which combines the alternating active-phase algorithm with centroidal Voronoi elements.

The improved design variables and the filtering sub-matrix are defined as follows:

where ${\mathbf{z}}$ indicates the improved design variables; ${{\mathbf{F}}_t}$ represents the global filtering matrix which is derived from the classic filtering formulas, corresponding to the linear hat filter ^[23]; ${({{\mathbf{F}}_t})_{lk}}$ indicates the sub-matrix of ${{\mathbf{F}}_t}$; ${\text{R}}$ indicates the filtering radius; $|{{\text{V}}^k}|$ represents the kth Voronoi element.

According to optimization criteria of the SIMP method and the filtered elements, the structural volume fraction is described as follows:

There are obvious similarities between the volume fraction for each material ^[44] and the element density in the SIMP method ^[23,60]. Therefore, the optimal model with the objective function to minimize compliance can be specified as follows:

where ${{\text{V}}^*}$ represents the upper limit of the structural volume fraction.

Figure 5 describes the specific implementation steps in a topology optimization process for the proposed method. In this work, all CVT elements are generated by random seeds, so the optimal structures may be slightly different from each other for the same numerical example. Nevertheless, the very little difference can be neglected. Thus, topology optimization for all of the following numerical examples is addressed by using random seeds.

Figure 5.  The implementation steps in the topology optimization process according to the proposed method.

DownLoad: Full-Size Img PowerPoint

5.   Sensitivity analysis and update scheme

The discrete problems are solved by using the gradient-based optimization algorithm in this article. Therefore, it is necessary to calculate the cost function gradient with respect to the original design variables. Note that the sensitivity analysis only involves its own internal parameters ${\mathbf{E}}$ and ${\mathbf{V}}$, and these two parameters are functions of the design variables. The sensitivity analysis of the cost function is separated along the same line. The sensitivity analysis of the linear separation cost function is usually performed by using the gradient-based algorithms, and it can be described by a chain rule as follows.

In the compliance problem ${\text{C}} = {{\mathbf{F}}^T}{\mathbf{U}}$, according to References ^[23] and ^[25], there are the expressions of sensitivities that are given below.

Thus, the design sensitivities are converted into the following expressions:

According to the methods for updating design variables under the condition of variable density ^[23,60], and combined with Eq (29), the new active-phase design variable $\vartheta _a^{new}$ which satisfies the box constraints is defined as follows:

where m is a constant, ${\text{m}} = 0.2$; ${{\text{z}}_{\min }}$ denotes the minimum value of ${z}$; ${\text{η }}$ denotes the damping coefficient; ${\rm{\rlap{-} \lambda }}$ denotes the Lagrange multiplier, which can be solved via the bisection method.

6.   Demonstrative examples

To demonstrate the effectiveness and feasibility of the proposed method, several typical numerical examples of topology optimization are provided in this section. It should be noted that the maximum number of iterations to discretize the structural design domain was set to 500 so as to ensure the quality of Voronoi elements. In addition, the termination criterion for topology optimization was set such that a change in the volume fraction is less than the user-defined threshold. However, it is hard to achieve the termination criterion at times due to the numerical oscillation, so we set the user-defined maximum iteration number to 800, which serves as an additional termination criterion for topology optimization iterations to save program running time.

6.1.   Semi-MBB beam

Taking a semi-Messerschmitt-Bölkow-Blohm (semi-MBB) beam as this numerical example, Figure 6 shows its design domain and boundary conditions with an aspect ratio of 3:1. The horizontal displacement at the left boundary of the design domain and the vertical displacement at the bottom-right corner of the design domain are both constrained. Moreover, there is an external downward force ${\mathbf{F}} = 1$ at the top-left corner of the design domain. In this section, to explore the impact of different factors on the optimization results from different perspectives, we divided the examples into different cases (i.e., the following cases 1–6). The topology optimization design of a semi-MBB beam involving three different materials (where voids are considered as one material) was first studied (i.e., case 1). In case 1, for materials 1, 2, and 3 (void), their corresponding Young's moduli were set to 3, 1, and 10^-9, respectively. For all the materials involved, a Poisson's ratio of 0.3 was equally set. The filtering radius used here was set to 0.08. In addition, for materials 1, 2, and 3, their corresponding volume fractions were set to 0.3, 0.1, and 0.6, respectively.

Figure 6.  Initial design domain of semi-MBB beam.

DownLoad: Full-Size Img PowerPoint

Figure 7 shows the discretization of the initial design domain, as obtained by utilizing 4000 Voronoi elements. For the polygonal elements and seeds, especially those on the boundaries, their distribution is uniform.

Figure 7.  Discrete structure of semi-MBB beam in the form of polygonal elements.

DownLoad: Full-Size Img PowerPoint

Figure 8 illustrates the topology optimization process corresponding to the semi-MBB beam with three materials in case 1, where red regions denote material 1, indigo blue regions denote material 2, and the light green regions denote material 3 (void). The solutions after 50,100,200,400,600, and 800 iterations are shown in Figure 8(a)–(f), respectively. The minimum compliance of the semi-MBB beam with three materials is ${\text{C}} = {\text{22}}{\text{.8265 }}$ after 800 iterations, which corresponds to the optimal structure in Figure 8(f). The results in Figure 8 indicate that a reasonable distribution of materials can be obtained by using the proposed method under volume constraints. Therefore, the feasibility and effectiveness of the proposed method are verified. Figure 9 illustrates the convergence history for structural compliance in the topology optimization design process for the semi-MBB beam with three materials in case 1. Figure 10 illustrates the changes in volume fraction of the three materials in the topology optimization process for the semi-MBB beam with three materials in case 1. The results in Figures 9 and 10 indicate that the compliance value (i.e., objective function) can be quickly minimized and a reasonable material distribution can be obtained under volume constraints by using the proposed method, with little change in the volume fraction of each material. Therefore, the feasibility and effectiveness of the proposed method are further confirmed.

Figure 8.  Topology optimization design results in case 1 for different iterations. (a) The result corresponding to 50 iterations; (b) The result corresponding to 100 iterations; (c) The result corresponding to 200 iterations; (d) The result corresponding to 400 iterations; (e) The result corresponding to 600 iterations; (f) The optimal design, namely, the result corresponding to 800 iterations.

DownLoad: Full-Size Img PowerPoint

Figure 9.  Convergence history for structural compliance in case 1.

DownLoad: Full-Size Img PowerPoint

Figure 10.  Changes in volume fraction of the three materials in case 1. (a) Volume fraction curve for material 1; (b) Volume fraction curve for material 2; (c) Volume fraction curve for material 3.

DownLoad: Full-Size Img PowerPoint

It is necessary to study the influence of different parameters, such as the number of elements, filtering radius, different stiffness ratios, and different volume fraction ratios of three-material structures. Therefore, other cases of the semi-MBB beam are further provided to investigate the influence of the above-mentioned parameters on the results with the same seeds ${\mathbf{P}}$.

All parameters set in case 2 remained the same as those set in case 1, except that the semi-MBB structure was initially discretized into 2000 and 5000 Voronoi elements, as respectively illustrated in Figure 11(a), (c). The optimal structures obtained in case 2 are illustrated in Figure 11(b), (d), respectively. The results in Figure 11 indicate that, although the structure is discretized into different numbers of Voronoi elements, the material distributions with little difference under volume constraints can still be obtained by using this method. Specifically, in the case of the optimal structure, the distribution of the material with a high elastic modulus (material 1) remains basically unchanged, whereas the distribution of the material with a low elastic modulus (material 2) is slightly different. Therefore, it can be concluded that different numbers of Voronoi elements have little impact on the optimization results obtained via this method.

Figure 11.  Topology optimization design domains and results in case 2. (a) Design domain which is initially discretized into 2000 Voronoi elements; (b) Optimal design, namely, the result corresponding to 669 iterations, with a minimum compliance of ${\text{C}} = {\text{22}}{\text{.7302}}$; (c) Design domain which is initially discretized into 5000 Voronoi elements; (d) Optimal design, namely, the result corresponding to 623 iterations, with a minimum compliance of ${\text{C}} = {\text{22}}{\text{.5797}}$.

DownLoad: Full-Size Img PowerPoint

In case 3, the filtering radius was changed from 0.08 to 0.03 and 0.1, respectively. The initial discretized semi-MBB beam structure is also shown in Figure 7. Figure 12(a), (b) illustrate the optimal structures with the different filter radii (0.03 and 0.1, respectively). The results in Figure 12 indicate that significantly different material distributions in the optimal structure can be obtained by using the proposed method under the condition of setting different filtering radii. Specifically, in the optimal structure, setting a smaller filtering radius leads to a more dispersed distribution of materials, while setting a larger filtering radius leads to a more concentrated distribution of materials. Therefore, it can be concluded that different filtering radii have a significant impact on the optimization results obtained via this method.

Figure 12.  Optimal structures with different filtering radii. (a) Optimal structure with filtering radius of 0.03 and objective function value of ${\text{C}} = {\text{24}}{\text{.3989}}$, corresponding to 62 iterations; (b) Optimal structure with filtering radius of 0.1 and objective function value of ${\text{C}} = {\text{22}}{\text{.9340}}$, corresponding to 800 iterations.

DownLoad: Full-Size Img PowerPoint

In case 4, the stiffness ratios (i.e., Young's modulus ratios) between different materials are changeable. Under the condition that the values of the Young's modulus of material 2 remained the same as that in case 1, the values of the Young's modulus of material 1 were set to 10 and 50, respectively. The optimal structures with different stiffness ratios for material 1 to material 2 are illustrated in Figure 13(a), (b), respectively. The results in Figure 13 indicate that the proposed method can realize significantly different material distributions and structural compliance in the optimal structure by setting different material stiffness ratios. Specifically, in the optimal structure with the unchanged Young's modulus of material 2, setting a smaller Young's modulus of material 1 results in greater structural compliance, while setting a larger Young's modulus of material 1 results in smaller structural compliance. Therefore, it can be concluded that different material stiffness ratios have a significant impact on the optimization results obtained via this method.

Figure 13.  Optimal structures with different stiffness ratios (i.e., Young's modulus ratios). (a) Optimal structure with stiffness ratio of 10, and objective function value of ${\text{C}} = {\text{7}}{\text{.3658}}$ corresponding to 800 iterations; (b) Optimal structure with stiffness ratio of 50, and objective function value of ${\text{C}} = {\text{1}}{\text{.4893}}$ corresponding to 471 iterations.

DownLoad: Full-Size Img PowerPoint

In case 5, the values of volume fraction that were set for the three materials differ from each other, and the corresponding optimal solutions are shown in Figure 14. The optimal structure with values of volume fraction for the three materials equal to 0.2, 0.2 and 0.6 is shown in Figure 14(a). The optimal structure with values of volume fraction for the three materials equal to 0.1, 0.3 and 0.6 is shown in Figure 14(b). The results in Figure 14 indicate that the proposed method can realize significantly different material distributions and structural compliance in the optimal structure by setting different values of volume fractions for the three materials. Specifically, the larger the volume fraction of a strong material (i.e., material 1 with a high Young's modulus) and the smaller the volume fraction of a weak material (i.e., material 2 with a low Young's modulus), the smaller the objective function (structural compliance) of the optimal structure. In other words, the distributions of the strong material (i.e., material 1) and weak material (i.e., material 2) are changed by setting different material volume fractions. Therefore, it can be concluded that different material volume fractions have a significant impact on the optimization results obtained via this method.

Figure 14.  Optimal structures with different volume fractions for the three materials. (a) Optimal structure with volume fractions of three materials equal to 0.2, 0.2, and 0.6, and objective function value of ${\text{C}} = {\text{ 29}}{\text{.3784}}$, corresponding to 800 iterations; (b) Optimal structure with volume fractions of three materials equal to 0.1, 0.3, and 0.6, and objective function value of ${\text{C}} = {\text{35}}{\text{.8576}}$, corresponding to 800 iterations.

DownLoad: Full-Size Img PowerPoint

To investigate the effect of material quantity on the optimization design results, another new numerical case (i.e., case 6) is given here. The parameters in case 6 were set as follows. The quantity of materials involved in this case is 4, and the Young's moduli for the materials were respectively set to 4, 2, 1, and 10^-9. The values of volume fraction for the materials were respectively set to 0.24, 0.08, 0.08, and 0.6. Moreover, the Poisson's ratio, filtering radius, and quantity of polygonal elements were set to the same as those in case 1.

Figure 15 illustrates the topology optimization process for the semi-MBB beam involving four materials in case 6, where the red area represents material 1, the indigo blue area represents material 2, the green area represents material 3, and the black area represents material 4 (void). The solutions after 50,100,200,400,600, and 731 iterations are shown in Figure 15(a)–(f), respectively. The minimum compliance is ${\text{C}} = {\text{18}}{\text{.8914}}$ after 731 iterations. The change in structural compliance for the semi-MBB beam with four materials in the optimization process of case 6 is illustrated in Figure 16. The variation in the volume fraction of each of the four materials in the optimization process of case 6 is illustrated in Figure 17. The results in Figures 15–17 indicate that the structural compliance (i.e., objective function) can be quickly minimized and a reasonable material distribution can be obtained via the proposed method under volume constraints, with little change in the volume fraction of each material. Therefore, the feasibility and effectiveness of the proposed method are further confirmed.

Figure 15.  Topology optimization design process for the semi-MBB beam with four materials in case 6. (a) The result corresponding to 50 iterations; (b) The result corresponding to 100 iterations; (c) The result corresponding to 200 iterations; (d) The result corresponding to 400 iterations; (e) The result corresponding to 600 iterations; (f) The optimal structure, namely, the result corresponding to 731 iterations.

DownLoad: Full-Size Img PowerPoint

Figure 16.  Convergence history for structural compliance in case 6.

DownLoad: Full-Size Img PowerPoint

Figure 17.  Change in volume fractions of four materials in case 6. (a) Volume fraction curve for material 1; (b) Volume fraction curve for material 2; (c) Volume fraction curve for material 3; (d) Volume fraction curve for material 4.

DownLoad: Full-Size Img PowerPoint

Figure 18 shows the different optimal semi-MBB structures for three and four materials with quadrilateral elements, both of which were discretized by using 60×20 quadrilateral elements. In this case, the filtering radius was set to 1.5. Comparing the objective function values, the results were obtained as follows: ${{{C_{3 - q}}} \mathord{\left/ {\vphantom {{{C_{3 - q}}} {{C_{3 - p}}}}} \right. } {{C_{3 - p}}}} \approx 4.6994$, ${{{C_{4 - q}}} \mathord{\left/ {\vphantom {{{C_{4 - q}}} {{C_{4 - p}}}}} \right. } {{C_{4 - p}}}} \approx 4.4113$. Additionally, ${C_{{\text{M}} - el}}$ denotes the objective function value, M signifies the material number, and $e l \quad(e l = q \text { or } e l = p)$ signifies the discretization method (i.e., q signifies the discretization method with quadrilateral elements, or p signifies the discretization method with polygonal elements).

Figure 18.  Optimal structures with the quadrilateral elements. (a) Optimal structure for the semi-MBB beam with three materials, and objective function value of ${\text{C}} = 107.2710$, corresponding to 151 iterations; (b) Optimal structure for the semi-MBB beam with four materials, and objective function value of ${\text{C}} = 83.3352$, corresponding to 234 iterations.

DownLoad: Full-Size Img PowerPoint

From the above numerical cases, the effectiveness and feasibility of this method are verified. Moreover, a reasonable distribution of materials is shown in each optimal structure, where the strong material mainly undertakes the task of power transmission, and the other materials assume auxiliary roles. It certifies that the proposed method can be used for the topology optimization of multi-material structures with linear boundaries.

6.2.   Hook structure

The hook structures with three and four materials were studied as another example. The design domain, constraints, and loads for this example are shown in Figure 19. For the first case, the hook structure involves three different materials (where voids are considered as one material), i.e., M = 3. The Young's moduli for the materials were respectively set to 3, 1 and 10^-9(for voids), respectively. For all materials involved, a Poisson's ratio of 0.3 was equally set. The filtering radius used here was set to 4. In addition, for materials 1, 2 and 3, their corresponding volume fractions were set to 0.3 (for solid material), 0.1 (for solid material), and 0.6 (for voids), respectively. Here, 4000 Voronoi elements were used to discretize the design domain, as shown in Figure 20.

Figure 19.  Initial design domain of hook structures.

DownLoad: Full-Size Img PowerPoint

Figure 20.  The discretization of hook structure using polygonal elements.

DownLoad: Full-Size Img PowerPoint

Figure 21 demonstrates the topology optimization design process for the hook structure with three materials, where the red area represents material 1, the indigo blue area represents material 2, and the green area represents material 3 (void). The solutions after 20,100,200,400,600 and 800 iterations are shown in Figure 21(a)–(f), respectively. For the case of 800 iterations, the optimal solution is shown in Figure 21(f), with the minimum compliance of ${\text{C}} = {\text{311}}{\text{.3395}}$. The change in structural compliance in the optimization process for the three-material hook structure is illustrated in Figure 22. The variation in the volume fraction corresponding to three materials in the optimization process for this case is illustrated in Figure 23. The results in Figures 21–23 indicate that the structural compliance (i.e., objective function) can be quickly minimized and a reasonable material distribution can be obtained via the proposed method under volume constraints, with little change in the volume fraction of each material. Therefore, the feasibility and effectiveness of this method are further confirmed.

Figure 21.  Topology optimization design process for the hook structure with three materials. (a) The result corresponding to 20 iterations; (b) The result corresponding to 100 iterations; (c) The result corresponding to 200 iterations; (d) The result corresponding to 400 iterations; (e) The result corresponding to 600 iterations; (f) The optimal structure, namely, the result corresponding to 800 iterations.

DownLoad: Full-Size Img PowerPoint

Figure 22.  Convergence history for compliance of hook structure with three materials.

DownLoad: Full-Size Img PowerPoint

Figure 23.  Change in volume fraction for the three materials in the hook structure. (a) Volume fraction curve corresponding to material 1; (b) Volume fraction curve corresponding to material 2; (c) Volume fraction curve corresponding to material 3.

DownLoad: Full-Size Img PowerPoint

To further examine the performance of this method, similar to the hook structure with three materials in the first case, a hook structure with four materials (M = 4) was considered as another case. The Young's moduli for the materials were set to 9, 3, 1, and 10^-9, respectively. The volume fractions were set to 0.24, 0.08, 0.08, and 0.6, signifying that the total volume fraction for solid materials was 40%. The Poisson's ratios, filtering radius, and number of polygonal elements were the same as those in the first case.

Figure 24 describes the topology optimization design process for the hook structure with four materials, where the red area represents material 1, the indigo blue area represents material 2, the green area represents material 3, and the gray area represents material 4 (void). The solutions after 20,100,200,400,600 and 800 iterations are shown in Figure 24(a)–(f), respectively. The minimum compliance is ${\text{C}} = {\text{119}}{\text{.0761}}$ after 800 iterations. Moreover, it is clear that a reasonable distribution of material can also be obtained via this method under volume constraints for each material. The change in structural compliance in the optimization process for the four-material hook structure is illustrated in Figure 25. The variation in the volume fraction for the four materials in the optimization process for this case is illustrated in Figure 26. The results in Figures 24–26 indicate that the structural compliance (i.e., objective function) can be quickly minimized and a reasonable material distribution can be obtained via the proposed method under volume constraints, with little change in the volume fraction of each material. Therefore, the feasibility and effectiveness of this method are further confirmed.

Figure 24.  Topology optimization design process for the hook structure with four materials. (a) The result corresponding to 20 iterations; (b) The result corresponding to 100 iterations; (c) The result corresponding to 200 iterations; (d) The result corresponding to 400 iterations; (e) The result corresponding to 600 iterations; (f) The optimal structure, namely, the result corresponding to 800 iterations.

DownLoad: Full-Size Img PowerPoint

Figure 25.  Convergence history for compliance of hook structure with four materials.

DownLoad: Full-Size Img PowerPoint

Figure 26.  Change in volume fraction for the four materials in the hook structure. (a) Volume fraction curve corresponding to material 1; (b) Volume fraction curve corresponding to material 2; (c) Volume fraction curve corresponding to material 3; (d) Volume fraction curve corresponding to material 4.

DownLoad: Full-Size Img PowerPoint

From the above two numerical cases for the hook structure, it is found that this method can effectively address the structural topology optimization problem involving multiple materials with complex curve boundaries, eliminate the checkerboard patterns, and realize a reasonable solution for topology optimization.

6.3.   Serpentine beam

A serpentine beam structure was considered as another example to further confirm the feasibility and effectiveness of this method. The design domain, constraints, and loading situation are shown in Figure 27. Similar to the example above (the hook structure), this example for the serpentine beam structure was also studied by analyzing two cases: one with three materials and the other with four materials. In both cases, the serpentine beam was discretized into 4000 Voronoi elements as shown in Figure 28.

Figure 27.  Initial design domain of serpentine beam.

DownLoad: Full-Size Img PowerPoint

Figure 28.  The discrete structure of serpentine beam using polygonal elements.

DownLoad: Full-Size Img PowerPoint

First, one case of a three-material serpentine beam structure is considered in this example. In this case, several parameters were set as follows: the Young's moduli for the materials were set to 3, 1, and 10^-9, respectively; the filtering radius was set to 0.3; the material volume fractions were set to 0.3, 0.1, and 0.6, respectively; Poisson's ratio was set to 0.3 for all materials.

Figure 29 describes the topology optimization design process for the serpentine beam structure with three materials, where the red regions indicate material 1, the indigo blue regions indicate material 2, and the green regions indicate material 3 (void). The solutions after 20,100,200,400,600, and 800 iterations are shown in Figure 29(a)–(f), respectively. The minimum compliance is ${\text{C}} = {\text{186}}{\text{.0482}}$ after 800 iterations. The change in the structural compliance in the optimization process for the three-material serpentine beam structure is illustrated in Figure 30. The variation in the volume fraction for the three materials in the optimization process for this case is illustrated in Figure 31. The results in Figures 29–31 indicate that the structural compliance (i.e., objective function) can be quickly minimized and a reasonable material distribution can be obtained via the proposed method under volume constraints, with little change in the volume fraction of each material. Therefore, the feasibility and effectiveness of this method are further confirmed.

Figure 29.  Topology optimization design process for the serpentine beam with three materials. (a) The result corresponding to 20 iterations; (b) The result corresponding to 100 iterations; (c) The result corresponding to 200 iterations; (d) The result corresponding to 400 iterations; (e) The result corresponding to 600 iterations; (f) The optimal structure, namely, the result corresponding to 800 iterations.

DownLoad: Full-Size Img PowerPoint

Figure 30.  Change in structural compliance of the serpentine beam with three materials.

DownLoad: Full-Size Img PowerPoint

Figure 31.  Change in volume fraction for the three materials in the serpentine beam structure. (a) Volume fraction curve corresponding to material 1; (b) Volume fraction curve corresponding to material 2; (c) Volume fraction curve corresponding to material 3.

DownLoad: Full-Size Img PowerPoint

Then, we consider the other case of a serpentine beam with four materials in this example. In this case, the Young's moduli for the materials were set to 4, 2, 1, and 10^-9, respectively; the material volume fractions were set to 0.24, 0.08, 0.08, and 0.6, respectively. The Poisson's ratios, filtering radius, and quantity of polygonal elements were the same as those in the case above.

Figure 32 describes the topology optimization design process for the serpentine beam structure with four materials, where the red area indicates material 1, the indigo blue area indicates material 2, the green area indicates material 3, and the gray area indicates material 4 (void). The solutions after 20,100,150,200,300, and 362 iterations are shown in Figure 32(a)–(f), respectively. The optimal result is realized at 362 iterations, with the corresponding structural compliance of ${\text{C}} = {\text{ 149}}{\text{.4421}}$. The change in the structural compliance in the optimization process for the four-material serpentine beam structure is illustrated in Figure 33. The variation in the volume fraction for the four materials in the optimization process for this case is illustrated in Figure 34. The results in Figures 32–34 also indicate that the structural compliance (i.e., objective function) can be quickly minimized and a reasonable material distribution can be obtained via the proposed method under volume constraints, with little change in the volume fraction of each material. Therefore, the feasibility and effectiveness of this method are further confirmed.

Figure 32.  Topology optimization design process for the serpentine beam with four materials. (a) The result corresponding to 20 iterations; (b) The result corresponding to 100 iterations; (c) The result corresponding to 150 iterations; (d) The result corresponding to 200 iterations; (e) The result corresponding to 300 iterations; (f) The optimal structure, namely, the result corresponding to 362 iterations.

DownLoad: Full-Size Img PowerPoint

Figure 33.  Change in structural compliance of the serpentine beam with four materials.

DownLoad: Full-Size Img PowerPoint

Figure 34.  Change in volume fraction for the four materials in the serpentine beam structure. (a) Volume fraction curve corresponding to material 1; (b) Volume fraction curve corresponding to material 2; (c) Volume fraction curve corresponding to material 3; (d) Volume fraction curve corresponding to material 4.

DownLoad: Full-Size Img PowerPoint

From the above numerical cases for the serpentine beam structure, it is also found that this method can effectively solve the structural topology optimization problem involving multiple materials and complex curve boundaries, eliminate the checkerboard patterns, and realize a reasonable distribution of materials.

For all of the above examples, it should be noted that the objective function is pursued in the optimization process and multiple materials contribute to the stiffness of the structure as a whole. Therefore, the volume convergence law for structural materials is related to the type of structure, the number of materials, and the type of load. Therefore, the convergence law for structural material volume during the optimization process varies for different examples due to different structural types, material quantities, and load types.

7.   Conclusions

A topology optimization method for the multi-material problems has been developed in this work, and it combines the polygonal discretization method with the alternating active-phase algorithm. The topology optimization objective function serves to minimize structural compliance, with the volume fraction as the constraint condition. The volume fraction of each material is considered as a design variable, which is mapped to its corresponding element variable through a filtering matrix. The structural design domain for topology optimization involving multiple materials has been discretized by using the CVT elements. The feasibility and effectiveness of the proposed method have been verified and confirmed via topology optimization of semi-MBB beam, hook, and serpentine beam structures, respectively. All numerical examples involve three-material and four-material problems, which were divided into multiple cases to study the impact of various factors on the obtained results. By means of this method, the problems of topology optimization involving structures with complex curve boundaries can be effectively solved. Therefore, the applicability scope of this method for structural topology optimization has been substantively expanded. In addition, with the proposed method using polygonal elements, the results of multi-material topology optimization have better numerical stability and higher calculation accuracy than those obtained via topology optimization methods using quadrilateral elements or triangle elements. Furthermore, the sensitivity filtering is avoidable and a relatively concise optimal structure can be obtained via this method, so this work is innovative and contributes to the development of multi-material structural topology optimization design.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This work was supported by Natural Science Foundation of Shaanxi Province (2020JM-200). The authors would like to express thanks to the reviewers for their useful and constructive suggestions that have improved the manuscript.

Conflict of interest

The authors declare there is no conflict of interest.