Mathematical analysis and simulation of a Hepatitis B model with time delay: A case study for Xinjiang, China

1.   Introduction

Hepatitis B is an infectious disease which is caused by HBV. The virus is transmitted via contacting the blood or body fluids of an infected person. HBV infection can cause acute, chronic illness and cirrhosis or liver cancer eventually provided the effective treatments are not performed. According to World Health Organization(WHO), people living with hepatitis B virus was estimated 257 million, nearly 900, 000 deaths in 2015 ^[1]. Xinjiang locates the northwest of China, which is an autonomous region and the largest Chinese administrative division. Xinjiang has been one of the high incidences areas of hepatitis B for a long time. The incidence rate attained 16.431%, the highest region of China in 2015 ^[2]. Till now, there is still not effectively available treatment for chronic carriers of the virus, but an HBV vaccine is consider to be available to protect general people.In 1992, the the Ministry of Health of China began to carry out the Expanded Program on Immunization (EPI). Hepatitis B vaccination is integrated into the nationwide immunization program with vaccines provided entirely by the government starting from 2002 ^[3]. The prevalence of HBV in China has declined, especially among children 3 to 12 years old. The result of Sampling Survey for HBV Epidemiology in 2006 indicated that the HBsAg prevalence is less than 1% among children under the age of 5 ^[4].

Both horizontal transmission and vertical transmission for HBV are still the most common routes in many people of China. The incubation period within the human is one of Hepatitis B virus propagation characteristics. It is the time from infection to infectiousness. During this period, many patients do not realize who are infected by the virus since the symptom is mild. They may probably contribute to more infection for HBV because of less public awareness of prevention. Therefore, the influence of the incubation period can not be omitted when we study the HBV transmission law. Mathematical models play an important role for better understanding the HBV transmission rules. In generally, there are two types of epidemic models: Mathematical models to investigate HBV dynamic behavior within human (Micro-models), Mathematical Models to investigate Hepatitis B dynamic behavior among population (Macro-models). Nowak et al. designed a mathematical model and quantitatively analyzed the replication dynamics of HBV in vivo and showed the impact on the optimal timing of drug treatment, as well as the immunotherapy of chronic HBV infection^[5]. In ^[6], a dynamic model was proposed to analyze how Hepatitis B virus load changes within human body. The result shows that a cell-mediated immune response is very important to control the virus. In ^[7], Xu and Ma proposed an HBV model with spatial diffusion and saturation of the infection rate and time delay describing the intracellular incubation period. The results show that the delay can postpone the time for virus to reach the infection steady state. In ^[8], Tchinda et al. studied an HBV infection differential model with two concentrated delays by some gamma distribution. It is shown that the model can appear the phenomenon of backward bifurcation. This indicates that the Hepatitis B virus may not be controlled by simply reducing the value of the basic reproduction number below one. Hattaf ^[9] formulated a virus dynamics model with general incidence rate and two delays and obtained the global dynamics of the model. Based on the fact of HBV infection, Wang et al. developed a diffusion model confined to a finite domain, induced by the intracellular time delay between infection of a cell and production of new virus particles^[10]. Considering the cytokine-mediated 'cure', Wang et al. discussed the global dynamics for an improved HBV model with standard incidence^[11]. The global dynamics of the model is obtained. For better understanding Hepatitis B disease spatio-temporal spread tendency among population, mathematical models have been used extensively in researching the transmission dynamics of HBV. Zhao et al. used a partial differential equations model to describe the transmission of HBV infection^[12]. The results show that the most important control measure is vaccination coverage, especially full coverage of infants immunity. In ^[13], Zou et al. established a six compartmental mathematical model to understand the transmission dynamics and prevalence of HBV in mainland China. Zhang and Xu investigated hepatitis B models with age structure. The stability and uniform persistence of the models are concluded ^[14,15]. Pang et al. proposed a hepatitis B model to explore the effect of vaccination and other controlling measures. Theoretical and numerical results indicate that the vaccination is a very effective measure to control the HBV infection^[16]. In ^[17], Zou et al. proposed a mathematical model including under-aged children, male adults, and female adults to understand the effect of sexual transmission on the spread and prevalence of HBV in China. In ^[18], an MSLIR model is constructed to describe the role of vaccination and treatment on HBV transmission. In ^[19], an SEICRS epidemic model with vaccination and treatment is formulated for describing the spread of HBV infection. In ^[20] Mann and Roberts presented an SECIR epidemic model to study the dynamics involved in the transmission of HBV in New Zealand. The results imply that the number of carriers will decrease after vaccination has been introduced, but the carriers will continue to provide a route of infection to those still susceptible. On the basis of the above statements, we will formulate and study a hepatitis B model with time delay in this paper. At the same time, we will use the model to simulate the hepatitis B transmission of Xinjiang.

The paper is organized as follows. The model structure is developed in next section. In Section 3, we present the existence of the equilibria under the threshold conditions. Some of the dynamic behavior of the model are analyzed in Section 4. Numerical simulations of the model including Hepatitis B transmission trends in Xinjiang, sensitivity analysis of parameters, HBV infection control strategy etc. are presented in Section 5. The main conclusions from this study are summarized in the last section.

2.   Model formulation

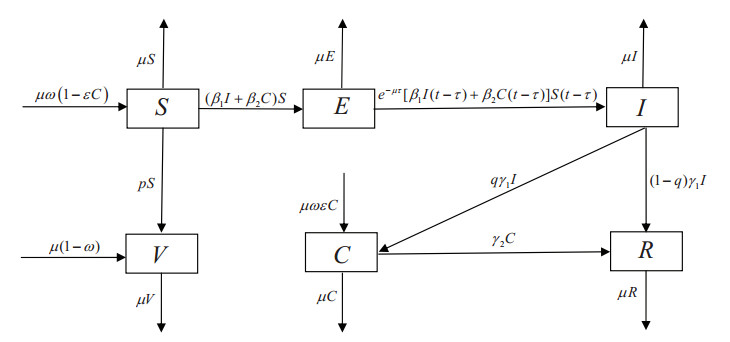
In this section, we will formulate an epidemic model to describe Hepatitis B transmission. At time $t$, the host population is composed of six compartments: susceptible $S(t)$, exposed $E(t)$, acute infection $I(t)$, chronic HBV carriers $C(t)$, recovered $R(t)$ and immunized $V(t)$. Some assumptions are as follows.

1. A susceptible individual is infected by HBV mainly due to contacts with acute and chronic stage patients.

2. For acute HBV infected individuals, the infection duration is about 2–3 months. Furthermore, acute HBV infected patient have obvious symptoms, such as malaise, loss of appetite, nausea, abdominal distension. Few newborn babies come from mothers with acute hepatitis. Therefore, we only consider the vertical transmission from mothers with chronic hepatitis.

3. Incubation period $\tau$ is constant. In general, the incubation period of HBV infections lasts about 1.5~6 months.

4. 80-90% of infants are infected during the first year of life develop chronic infections, and vertical infected infants change directly into the chronic carriers.

5. We omit the rate of waning vaccine-induced immunity of vaccinated individuals, because there is no evidence to support the need for a booster dose of hepatitis B vaccine. Protection lasts at least 20 years, and is possibly life-long ^[21].

Accordingly, we obtain the following HBV model with time delay:

The initial conditions for system (1.1) have the form

Let $N(t) = S(t)+E(t)+I(t)+C(t)+V(t)+R(t)$ be the total population number at time $t$. It is clear that $N'(t) = \mu-\mu N$. Therefore, the total number approaches 1 as $t\to \infty$. From (1.1), it is obvious that in order to determine the dynamics of each class, we only need to study the first, third and fourth equations in model (1.1), thereby lowering the order of the system to be studied, i.e.,

Let us denote by $\Gamma$ the set

By the Comparison Principle and basic mathematical analysis, we may show that $\Gamma$ is a positive invariant set. Hence, we can focus the model (1.2) on the set $\Gamma$.

3.   Basic reproductive number and equilibria

In order to obtain the basic reproductive number of our model, we first give all possible equilibria. The model (1.2) always has a disease-free equilibrium $P_0(S_0, 0, 0)$, where $S_0 = \frac{\mu \omega}{\mu+p}$. The model may have an endemic equilibrium $P^*(S^*, I^*, C^*)$, where

Within (3.1), the parameter ${\mathcal R}_0$ is given by

By Corollary 2.1 of ^[22], the parameter ${\mathcal R}_0$ may be obtained via next generation operator methods when the progression to chronic stage ($q\gamma_1 I$) is not considered to be a new infections. In fact, we give the following system which comes from infectious classes $I$ and $C$ in the lineariation of the model (1.2) at the disease-free equilibrium $P_0$

where

It then follows that the basic reproductive number $\mathrm{r}(\bf{F}\bf{V}^{-1}) = \mathcal{R}_0$. Moreover, if $q\gamma_1 I$ is taken as a new infection, we can get another basic reproductive number as follows

It is easy to check that $\mathcal R_0 < 1( = 1, > 1)$ is equivalent to $\mathcal{ \widehat{R}}_0 < 1( = 1, > 1)$. In fact, when $\mathcal R_0 = 1$, one has

Substituting it into (3.2) yields $\mathcal{ \widehat{R}}_0 = 1$ and the converse is also true. The same conclusion can be drawn for $\mathcal R_0 < 1(>1) \Leftrightarrow \mathcal{ \widehat{R}}_0 < 1(>1)$.

In the following, we take $\mathcal R_0$ as the basic reproductive number of the model (1.2). Regarding the existence of the equilibria $P_0$ and $P^*$, we have the following result.

Theorem 1. For the model (1.2), there always exists a disease-free equilibrium $P_0(S_0, 0, 0)$ and a unique endemic equilibrium $P^*(S^*, I^*, C^*)$ exists only when $\mathcal R_0 > 1$.

4.   Stability of equilibria

In this section, we will discuss the stability of two equilibria. First, we give the following theorem about the stability of the disease-free equilibrium $P_0(S_0, 0, 0)$.

Theorem 2. If $\mathcal R_0 < 1$, then the disease-free equilibrium $P_0(S_0, 0, 0)$ is globally asymptotically stable on $\Gamma$; If $\mathcal R_0 < 1$, then $P_0$ is unstable.

Proof. Linearizing the model (1.2) at the disease-free equilibrium $P_0$, we obtain the system as follows.

The characteristic equation for disease-free equilibrium $P_0$ is

Write

This gives

where

Of course, equation (4.3) has a root $-(\mu+p) < 0$. For this reason, the stability of $P_0$ is deteremined by the following equation

Case 1: $\mathcal R_0 < 1$

When $\tau = 0$, the equation (4.4) becomes

where $c_1 = m_1+m_2-\beta_1S_0$ and $c_2 = m_1m_2-(\beta_1S_0m_2+q\gamma_1\beta_2S_0)$. The inequility $R_0 < 1$ implies that $c_1 > 0$ and $c_2 > 0$. Therefore, all roots of (4.5) have neagtive real parts.

Substituting $\lambda = \mathrm{i}\sigma$ into (4.4) and separating the real and imaginary parts, we have

From (4.6), it follows that

Since

and

we conclude that the equation (4.7) has no real roots. Hence, the equation (4.4) has no pure imaginary roots for all time delays $\tau > 0$. Then the disease-free equilibrium $P_0$ is locally asymptotically stable as $\mathcal R_0 < 1$.

Case 2: $\mathcal R_0 > 1$

Set

It is evident that $f(0) = a_2-b_2 < 0$ by $\mathcal R_0 > 1$ and $f(\lambda)\to\infty$ as $t\to\infty$. Then (4.4) has at least one positive real root. Thus, the disease-free equilibrium $P_0$ is unstable as $\mathcal R_0 > 1$.

Next, using Liapunov functional technique, we discuss the global stability of $P_0$. From $\mathcal R_0 < 1$, it may be concluded that there exist two positive number $\rho_1$ and $\rho_2$ such that

Consider a Liapunov functional:

The derivative of $L$ along solutions of (1.2) is given by

We define $\Omega = \{(S(t), I(t), C(t))\in\Gamma: \dot L = 0 \}$. It is easily seen that $P_0(S_0, 0, 0)$ is the largest invariant set. By the Liapunov-LaSalle type theorem ^[23], $P_0$ is globally asyptotically stable on $\Gamma$. This completes the proof of Theorem 2.

Theorem 3. If $\mathcal R_0 > 1$, then the endemic equilibrium $P^*(S^*, I^*, C^*)$ is locally asymptotically stable.

Proof. Linearizing the system (1.2) at the positive equilibrium $P^*(S^*, I^*, C^*)$, we obtain the following system

The characteristic equation for the system (4.9) is

Let

With above-mentioned notations, the equation (4.10) becomes

where

When $\tau = 0$, now (4.11) becomes

where

We claim that all roots of equation (4.11) admit negative real parts. In fact, we only need to show

A trivial verification shows that (4.12) is valid. By Routh-Huritz criterion, each root of equation (4.11) has negative real part. Therefore, the endemic equilibrium $P^*$ is locally asymptotically stable as $\tau = 0$.

Assuming that the characteristic equation (4.11) has a pure imaginary root $\mathrm{i}\sigma$, one has

Separating the real and imaginary parts of (4.13) yields

Set $z = \sigma^2$, from the above it follows that

where

Since

we conclude that there is no nonnegative real root for the equation (4.15). Hence, the equation (4.11) has no pure imaginary roots for all time delays $\tau > 0$. Then the endemic equilibrium $P^*$ is locally asymptotically stable as $\mathcal R_0 > 1$. This completes the proof of Theorem 3.

Our next concern will be the global stability of the endemic equilibrium. We will use Lyapunov functionals methods to prove it. The technique of proofs is to use an extended Volterra-type functionals developed in ^[24,25].

Theorem 4. If $\varepsilon = 0$, then the endemic equilibrium $P^*(S^*, I^*, C^*)$ is globally asymptotically stable as $\mathcal R_0 > 1$.

Proof. Define a Lyapunov functional for endemic equilibrium $P^*$

where

and

The time derivative of $U_1$ along solutions of (1.2) is given by

The time derivative of $U_2$ along solutions of (1.2) is given by

Similarly, we have

and

By above-mentioned calculation, we obtain the derivative of $L(t)$ along solutions of model (1.2) as follows

Notice that

We are now in position to show $\frac{\mathrm dL}{\mathrm dt}\leq 0$. We denote by $\mathcal M$ the set

We conclude from $C^*I(t)\equiv I^*C(t)$ that $\frac{\mathrm dC}{\mathrm dt} = 0$, hence that $C(t)\equiv \mbox{const}$ and $I(t)\equiv \mbox{const}$, and finally that $S(t) = S^*$ implies $C(t) = C^*$ and $I(t) = I^*$. Thus, it can be verified that the only invariant set in $\mathcal M$ the singleton $\{P^*(S^*, I^*, C^*)\}$. By LaSalle's invariance principle ^[23], the endemic equilibrium is globally asymptotically stable as $\mathcal R_0 > 1$. This completes the proof of Theorem 4.

Remark By the theory of internally chain transitive sets ^[26], we can obtain the permanence of the model (1.2). We only get the global stability of the endemic equilibrium under an extra condition $\varepsilon = 0$. This is because of the restriction of the Lyapunov functional form chosen by us. To obtain a complete global dynamics for the model, we put forward an open problem: the endemic equilibrium is globally asymptotically stable as $\mathcal R_0 > 1$.

5.   Model applications

5.1.   Model fitting

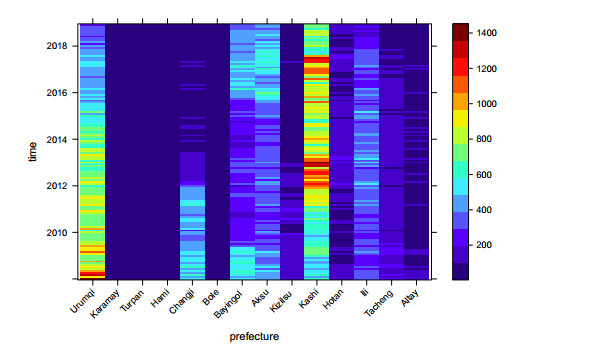
The monthly new reported HBV cases for 14 prefectures of Xinjiang from January 2008 to December 2018 are obtained from infectious disease report information management system of China (see Figure 2.). The values of parameters are listed in Table 2. We explain the parameter values as follows.

● The average life expectancy of people in Xinjiang Uygur Autonomous Region of China was 71.12 years in 2005 ^[27]. We take it as the current average life expectancy. Thus, $\mu = 1/ 71.12 = 0.0141.$

● From ^[28], ^[29], ^[27] and ^[30] we can obtain the parameters $\omega$, $\varepsilon$, $\tau$, $\gamma_1$, $q$ and $\gamma_2$ (see Table 2).

● In order to get a better fitting effect, we choose transmission coefficient for acute infection individuals $\beta_1 = 0$ and vaccination rate of susceptible individuals $p = 0$. Actually, patients in acute period have acute illness with symptoms that last several weeks, including yellowing of the skin and eyes, dark urine, extreme fatigue, nausea, vomiting and abdominal pain. They usually don't have sexual and blood contact with susceptible person. On the contrary, susceptible person also don't have close contact with these patients due to obvious clinical symptoms for these patients. So we think the spread of chronic carriers is the major cause for epidemic of hepatitis b. The similar results were seen in ^[27]. Moreover, we find the formula of $\mathcal{ \widehat{R}}_0$ does not contain $p$. It means that parameter $p$ may has no influence on the effect of HBV transmission.

● We define $M(t)$ as the cumulative number of acute HBV case. Then, we have $M'(t) = e^{-\mu\tau}(\beta_1 I(t-\tau)+\beta_2 C(t-\tau))S(t-\tau)$. The data from public health science data center showed that the new infected HBV case is 49504 in 2008. Hence, we estimate that the initial condition of $M(t)$ is $M(0) = 49504$.

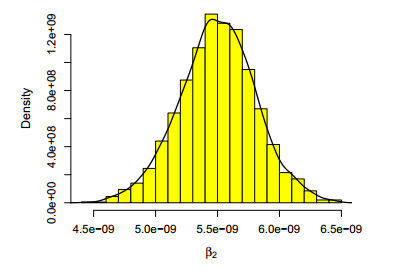
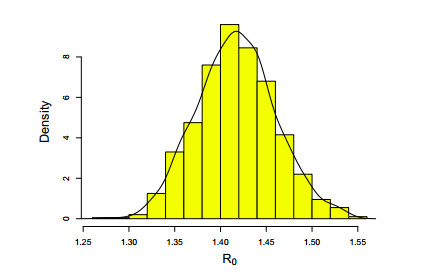
● The parameter $\beta_2$ is obtained by fitting the model to data. By the least-square estimation the transmission coefficient is estimated as $\beta_2 = 5.52\times 10^{-9}$. The results of bootstrap inference are summarized in Figure 3, where we provide the histograms of the 2000 bootstrap replicates of transmission coefficient $\beta_2$. By taking 2.5th and 97.5th percentiles we also derive from those replicates confidence intervals on $\beta_2$ and the 95% bootstrap confidence interval of $\beta_2$ is $(4.77\times 10^{-9}, 6.21\times 10^{-9})$. We apply the least-square method to carry out parameter estimation, which is implemented by the function fminsearch, a part of the optimization toolbox in MATLAB.

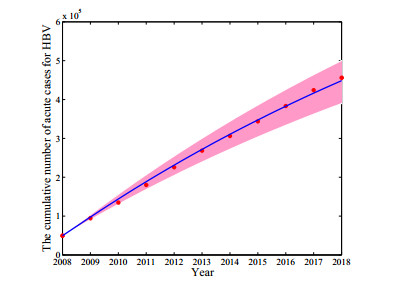
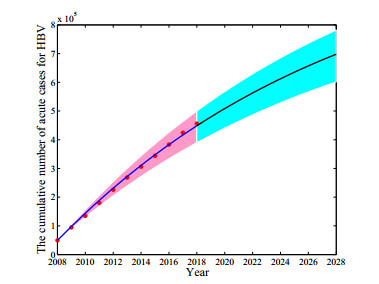
Based on the model and the parameter values in Table 2, the cumulative numbers of newly HBV cases and fitted curve are presented in Figure 4. At the same time, by simulation model (1.1) with bootstrap replicates of transmission coefficient $\beta_2$ with 2.5th and 97.5th percentiles interval we estimated the 95% confidence interval for fitted curves by the bootstrap sampling method with pink areas which are also presented in Figure 4. We can predict the general tendency of the epidemic according to the current situation, which is presented in Figure 5. We can obtain 2000 bootstrap replicates for ${\mathcal R}_0$ by putting the 2000 bootstrap replicates $\beta_2$ and the rest of parameters in Table 2 into the formula of basic reproductive number ${\mathcal R}_0$. Thus, we can estimate basic reproductive number to be ${\mathcal R}_0 = 1.47 (95\% {\rm CI}: 1.34, 1.50)$. According to the bootstrap estimate value for each parameter, we plot the frequency distribution histogram and the probability density curve which are presented in Figure 6. This indicates that the disease is uniform persistence. Therefore, if no further effective prevention and control measures are taken, the disease will not vanish.

5.2.   Sensitivity analysis and disease control

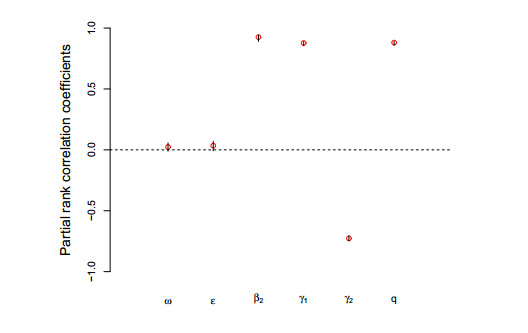
Sensitivity analysis is vital to identify key parameters and find effective control strategies for combatting the spread of the disease. It is well known that the basic reproduction number (${\mathcal R}_0$) is a very important parameter in the infectious disease model, which determines whether the could spread. In our model, we focus on the parameters $\gamma_1$, $\gamma_2$, $\omega$, $\beta_2$, $\varepsilon$, $q$ in ${\mathcal R}_0$. In order to identify the impacts of theses parameters on HBV transmission and prevalence, we used the Latin hypercube sampling method and partial rank correlation coefcient (PRCC)(see ^[31]). Using model (1.1), 2000 samples are randomly generated by assuming a uniform distribution for each parameter based on values from Table 2. We choose parameters of interest as the input variables, and the value of ${\mathcal R}_0$ as the output variable. The PRCC values of six parameters and corresponding $p$-values are computed. The results are illustrated in Table 3 and shown in Figure 7. The larger PRCCs in absolute value, the more important the parameter in responding to the change in $R_0$. Plus sign or minus sign means the influence is positive or negative respectively. Table 3 and Figure 7 show that $\beta_2$, $\gamma_1$ and $q$ have positive impact upon ${\mathcal R}_0$, whilst $\gamma_2$ has negative impact. We also know that ${\mathcal R}_0$ is not sensitive to parameters $\omega$ and $\varepsilon$. Further, Table 3 shows that the transmission coefficient from carriers to susceptible individuals $\beta_2$ has greatest impact on ${\mathcal R}_0$ followed by proportion of acute infection individuals who become chronic infections $q$, then rate leaving the acute infections $\gamma_1$. Hence, from sensitivity we conclude that the most effective approach to reduce the HBV infection is to reduce the parameters $\beta_2$ and $q$.

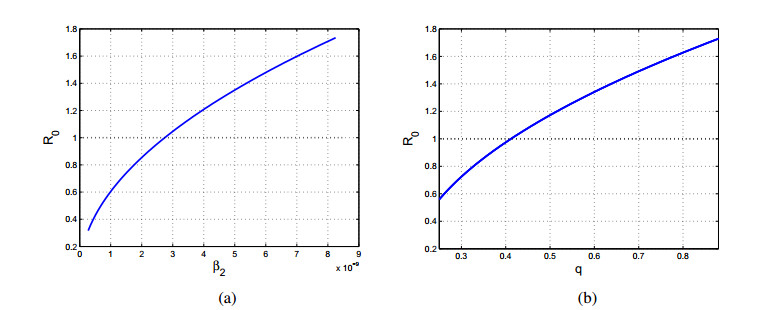
In the following, we focus on parameters $\beta_2$ and $q$. The influence of parameters $\beta_2$ and $q$ on ${\mathcal R}_0$ is shown in Figure 8. We can see from Figure 8(a) that when $\beta_2$ is reduced to $2.8\times 10^{-9}$, which is about 1/2 of current level, the basic reproductive number will drop under 1. Figure 8(b) shows that when $q < 0.4$, that is, the proportion of acute infection individuals who become chronic infections is below 0.4 through improving the therapy.

6.   Conclusion

Hepatitis B virus infection is a public health problem all over the world. The epidemic caused by HBV affects mostly the WHO African Region and the Western Pacific Region. The Global Health Sector Strategy calls for the elimination of viral hepatitis as a public health threat by 2030 ^[32]. Xinjiang is an autonomous region in the northwest of China. It is the largest province-level administrative regions of China. There are 47 ethnic groups in Xinjiang mainly the Uygur, Han, Kazak, Hui Kirgiz, Tatar, Russian and so on. About 60% of the population are ethnic minorities, especially Uyghurs are the majority in southwestern Xinjiang. Economic underdevelopment, inconvenient transportation and language obstacle etc. lead to high incidence rate for HBV infection. These bring a lot of difficulties in medical treatment, publicity and education of HBV-related knowledge and information, high-risk groups intervention, disease monitoring etc. Treatment access is still very low in Xinjiang. Motivated by these reasons, we hope to reveal the propagation rule of the HBV epidemic in Xinjiang from the view point of epidemiological dynamics. In order to explore the HBV epidemic in Xinjiang, we model and analyze a Hepatitis B Model in which the total population is divided into six subetaoup. The time delay is introduced into the model to stand for the incubation period. The basic reproductive number is obtained by the standard next generation operator method ^[22]. By using Lyapunov functional method and LaSalle invariance principle for delay differential equations ^[33,23], we establish the global asymptotic stability of the disease-free and endemic equilibria. The theoretical results show that the HBV infection can be controlled and eliminated eventually provided reducing the value of the basic reproduction number below unity.

Based on the monthly new reported HBV cases data in Xinjiang(see Figure 2), the parameters in the model are estimated by the least-square methods. We can calculate the basic reproductive number of HBV $\mathcal{R}_0 = 1.47$. It is shown that the HBV still need to be prevented and controlled in the long run. If there is no more effective measures, the cumulative HBV cases will arrive at about 700, 000. Sensitivity analysis results (see Figure 7) indicate that the control and treatment to the chronic HBV carriers are the key prevention measures to decline the prevalence of HBV in Xinjiang. The government should further enhance comprehensive campaign on HBV prevention and control such as HBV awareness campaigns, interventions among most-at-risk populations, treatment, care and support to HBV patients, especially HBV chronic patients. From the view of data analysis, Cui, Moriyama and Rahman also think that education, health program and treatment are the key measures for prevention of HBV in Xinjiang ^[2]. Furthermore, from our analysis parameters $\beta_2$ and $q$ are sensitive to $\mathcal R_0$. This implies that reduce the transmission coefficient for chronic infection individuals and proportion of acute infection individuals who become chronic infections are also effective measures to decline the prevalence of HBV. In order to reduce $\beta_2$, we should reduce household and sexual contacts of people with chronic HBV infection and improving the therapy can reduce proportion rate $q$.

Acknowledgements

This work was supported by the Natural Science Basic Research Plan in Shaanxi Province of China [2018JM1011] and the National Natural Science Foundation of China [11961071].