MHD Casson nanofluid boundary layer flow in presence of radiation and non-uniform heat source/sink

Nomenclature

1.   Introduction

The purpose of this work is to explain the flow of non-Newton Casson fluids by mass and heat conduction to elongated surfaces coupled with periodic hydromagnetic effects, along with the effects of thermophoresis and radiation absorption. In this case, the endothermic parameters are also included. A time-dependent set of linear equations was established to describe the fluid flow system, including momentum, energy and concentration (see ^[1]). Siddiqui and Shankar ^[2] aimed to understand the heat transfer and MHD boundary layer flow of non-Newtonian fluids across stretched surfaces in porous media. The behavior of non-Newtonian liquids is described by the Casson liquid model. Two different forms of nanofluids are being investigated, Cu-water and Ag-water. Ali et al. ^[3,4] have investigated the dual Cattaneo-Christov dispersion and activation energies in the unstable magnetohydrodynamic transitions of rotating Maxwellian nanofluid flows across stretched foils. The Arrhenius activation energy was used to assess the dispersion of chemically reactive species. They investigated how rotating water-based silver nanoparticles impact fluid velocity over a continuous stretched film, considering the effects of volume fraction, Coriolis force and Lorentz force. By influencing the fluid motion on the earth's surface, the Coriolis force has a significant impact on fluid dynamics in the study of materials, solar dynamics, ocean and astronomy. The inclusion of nanoparticles is due to certain properties, including improved heat transfer and is important in heat exchangers, advanced nanotechnology, electronics and materials science. Improving heat transport is the main goal of this work.

In Alam et al. ^[5] an incompressible and conductive bio-magnetohydrodynamic flow; specifically, blood flow containing magnetic particles through a cylinder that is stretched in two dimensions under the action of a magnetic dipole was investigated. The relationship between liquid viscosity and thermal conductivity was assumed to be reciprocal and the relationship with temperature was assumed to be linear. Two analytical subfields ferro-hydrodynamics and MHD, were involved in this investigation. They described the basic properties of pure blood and the properties that emerge when magnetic particles are introduced into the blood. The outcome showed that the velocity of the liquid (blood-Fe3O4) declines with increasing values of the other ferromagnetic interaction parameters, while the curvature parameters, axial velocity and temperature increase. Both the heat transfer coefficient and the skin friction coefficient decrease as the value of the thermal conductivity parameter increases. The study also included a stability analysis over time to ensure that the results were physically reliable. Gadicolaei et al. ^[6] investigated and performed numerical analysis of MHD flow-mixing convection in Casson nanofluids across nonlinear permeable stretched sheets. They considered how heat is generated or absorbed by thermal radiation, chemical reactions, viscous dissipation, suction and Joule heating. Nanoparticles were modeled using Brownian motion and thermophoretic phenomena (Buongiorno's model). Gnaneswara et al. ^[7] considered the problem of laminar boundary laminar flow and heat transfer in MHD fluids induced by unstable stretched films with extended heat flow. Thermal conductivity and viscosity are thought to vary with temperature. Alkasasbeh ^[8] used magnetic fields to investigate heat transfer in Casson hybrid nanofluids across vertically stretched foils. Methanol contained copper oxide and graphite oxide, which were considered hybrid nanoparticles.

Ibrah et al. ^[9] investigated the effects of thermally radiating magneto-nano-Casson liquids on fine needles. Under the Navier slip effect, the problem was simulated numerically. MWCNTs, also called multi-walled carbon nanotubes, reduced friction. Compared to parabolic rotation, the surface of the needle transfers heat faster from the liquid. Compared to single-walled carbon nanotubes (SWCNTs), multi-walled carbon nanotubes transport more heat from fluids. SWCNTs are superior to MWCNTs in terms of heat transfer because paraboloids conduct heat more efficiently than cylindrical surfaces. Kamran et al. ^[10] performed a numerical analysis of Casson nanofluids on a horizontally spreading surface under the influence of magnetism. The analysis considered the slip boundary condition and the thermal convection boundary condition. Kouse et al. ^[11] investigated is the heat transfer properties of non-Newtonian Casson nanofluids and their three-dimensional flow across a linearly extending plane in a rotating frame. Buongiorno's nanofluid model, included with their model, involves the thermal transfer and random motion of nanoparticles. Both continuous heat flow and viscous heating mechanisms at the boundary were considered. Liaquat et al. ^[12] used MHD theory to study the flow of Casson nanofluids with thermal radiation across unstable contracting surfaces. For the Navier-Stokes model of a non-Newtonian fluid with symmetric elements in the viscosity term, a momentum equation was obtained.

Mani et al. ^[13] studied the effects of heat generation and coalescence on the boundary-level flow of viscous liquids induced by unevenly stretched sections in the absorbing medium with changes in external heat. Numerical solutions of the same equations were obtained by a shooting procedure to obtain analogous solutions of the modified main equations. A detailed investigation and analysis were carried out on the current and heat transfer characteristics for various values of relevant factors. Meena Kumari et al. ^[14] used gradient magnetic fields, viscous dissipation and radiation as non-uniform heat sources/sinks and chemical reactions. Various types of nanoparticles were examined including silver, copper, aluminum oxide, titanium oxide and magnesium oxide (MgO). Ahmed et al. ^[15] provided a computational analysis of the effects of nonlinear thermal radiation, heat generation/absorption, Joule heating and slips limit conditions on the magnetohydrodynamic flow of Casson nanofluids across stretched sheets through porous materials. The nanofluidic combination was modeled using a two-phase nanofluidic approach. The Darcy model served as a representation of porous materials. Ali et al. ^[16] studied magnetohydrodynamically unstable Sakiadis and Blasius boundary layer flows in nanofluids with leading-edge accretion and explored the combined effects of bioconvection and magnetic fields. In addition, they were able to investigate the effects of Biot number, thermal radiation, chemical reactions and convective boundary conditions. The magnetization was acting transverse to the plate and was constant and convective conditions and radiant heat sources existed at the boundary.

Partha et al. ^[17] studied how two immiscible thin liquid films flow across a linearly expanding foil in the presence of a uniform transverse magnetic field. Radha Madhavi et al. ^[18] studied the effects or consequences of the 'heat source' parameter via a wedge across the porous medium on the conductive fluid flow of magnetohydrodynamic Casson nanofluids with activation energy. For conducting fluids, they also investigated the effect of "second law" analysis on chemical reactions. Rafique et al. ^[19] investigated the results of boundary layer flow with her Casson nanofluids on inclined surfaces are investigated with Soret and Dufour effects by Keller-Box method. His Buo-ngiornopattern of the heat efficiency of liquid flow in the existence of Brownian motion and thermophoretic characteristics served as the basis for the model used in the study. Given the dominant flow properties of the enhanced boundary layer, they modeled Casson nanofluid flow problems along inclined channels to learn more about heat and mass transfer phenomena. Ramudu et al. ^[20] investigated the heat transfer properties of a continuous two-dimensional magnetohydrodynamic shear-thickening Casson fluid across a vertically extending sheet with varying heat sources/sinks. The temperature distribution was improved by increasing the Biot number and thermal radiation parameters. It could be seen that both the distribution velocity and the temperature in the intake and injection situations decrease as the intake/injection parameters increase. Reddy and Reddy ^[21] investigated the effect of radiant energy on the imbalanced 3-dimensional MHD flow of a micropolor fluid along the horizontal plane of a parabola of rotation.

Shiva et al. ^[22] investigated heat and mass transport in unstable two-dimensional Casson nanofluidic flows through porous sheets stretched nonlinearly with respect to chemical reactions, viscous dissipation, heat emission and radiant energy. The equations governing the boundary layer were made dimensionless before being solved using the explicit finite difference method. Effective convergence criteria were determined using stability analysis. This made the numerical method more reliable. To investigate the implications of various flow parameters, profiles of temperature, velocity and nanoparticle concentration were shown. Day and Mukhopaghyay ^[23] investigated the combined effects of suction/injection, external magnetic fields and first-order binding processes on the forced convective motion of nanoliquids over absorbent sheets. Zero nanoparticle flux at the boundary was postulated to push components still on the plate surface to control the flux. As a result, the model can be used in various engineering fields to passively control nanoelement components. Srinivasalu et al. ^[24] numerically investigated the effects of synchronous magnetic fields on Williamson nanofluids on stretched surfaces with convective boundary conditions. Pallavarapu et al. ^[25] with Cattaneo-Christov double diffusion on stretched surfaces, examined the heat and mass transmission of Williamson MHD nanofluids in porous media. Additionally, they investigate the impacts of chemical processes, radiation, heat production and sucking/injecting effects on the current flow. They found that the decrease in the velocity field was due to the increase in the magnetic field, the porosity parameters and the attraction parameter.

Oudina et al. ^[26] numerically investigated the hydrodynamic and thermal properties of titanium nanofluids filling a cylindrical annulus. Base fluids included water, motor oil and ethylene glycol. To take into consideration the implications of the nanoparticle volume fraction distribution on the continuity, momentum and energy equations, the Maxwell model for convective heat transfer in nanofluids was used. Mebarek-Oudina et al. ^[27] quantitatively evaluated a revolving stretchable disc that causes a hydromagnetic flow of magnetite-water nanofluid. The updated Buongiorno model, which takes into account the effective nanofluid characteristics that rely on the volume fraction and the main slip processes, was used to predict the nanofluid flow. Mebarek-Oudina et al. ^[28] reviewed the practical area of nano-fluid applications, covering a wide variety of subjects. The utilization of magnetic fields, porous media and nanofluids in various heat transfer applications was covered in this review study, with a focus on the solar thermal field. Due to its potential for enhanced thermal characteristics that lead to high transfer rates, the idea of a hybrid nanofluid has caught the interest of many researchers. Hybrid nanofluids have uses in biomedical and pharmacological relief as well as heat transfer systems like electrical cooling. Khan et al. ^[29] investigated how Lorentz forces affect the Casson fluid flow of a water-based Fe3O4-MWCNT hybrid nanofluid that is driven by dust particles from a stretched sheet Given the multiple ways non-Newtonian fluids are used in technological advancement and improvement, many engineers and scientists are engaged in several research projects including cosmetics, drugs, chemicals, oil, gas, food and many other topics. Compared to Newtonian fluids, non-Newtonian fluids are more challenging to work with. A numerical analysis of mixed and convective Casson liquid flow through a conduit inside of a permeable material under the Lorentz force effect was conducted by Raza et al. ^[30] due to its extensive applicability. Dharmaiah et al. ^[31] examined the effects of nonlinear thermal radiation, Brownian and thermophoresis through a wedge on an MHD with dissipative effects for Jeffrey fluid. Analysis of heat transmission was also performed. Chabani et al. ^[32] by neglecting the effects of thermal radiation, numerically examined the convective heat transfer supplied by a hybrid nano-fluid moving within a porous annulus between a triangle and a special trapezoidal shape.

Ganesh et al. ^[33] investigated the topic of the combined effects of Joule heating and viscous dissipation on an Oldroyd B nanofluid flow in three dimensions. According to the model, flow is produced by a bi-directionally extending sheet that also exhibits thermophoresis and Brownian motion characteristics. The energy equation additionally includes a radiation factor. Padmavathi et al. ^[34] evaluated the thermophysical characteristics of a stretched sheet-induced 2D flow of a dusty Eyring-Powell fluid in the presence of a magnetic field. Ganesh et al. ^[35] studied the streamline analysis of AA7072-AA7075 alloys due to a sheet. In the presence of a magnetic dipole field that varies radially, the pertinent system of the flow arrangement was taken into consideration by utilizing stretching surface geometry. Ganesh et al. ^[36] examined how a chemical reaction affects the three-dimensional flow, heat and mass transfer of a Casson nano liquid over an exponentially extending surface. Ganesh et al. ^[37] described the heat transmission and non-Newtonian nanofluid flow characteristics over a stretched sheet. Models of energy expression are susceptible to the slip factor phenomena. The mass transfer mechanism was characterized by taking chemical reactions into account. Archana et al. ^[38] studied the incompressible and compressed flow between two parallel plates. The constitutive equations of the Casson nanofluid, which was used as a lubricant, were included in the mathematical formulation. Reddy et al. ^[39] modeled an unsteady MHD flow of nonlinear radiative heat transfer of Casson liquid over a contracted cylinder. Gireesha et al. ^[40], by taking mixed convection into account, examined the effects of viscous dissipation on MHD flow, heat transfer and mass transfer of Casson fluid across a plate.

Abbas et al. ^[41] discussed the flow over an erratic, thin, stretching sheet when second-grade nanofluid with mixed convection was used. Thermophoresis and Brownian diffusion effects were examined in light of the characteristics of non-linear thermal radiation. A non-linear stretching surface with changing thickness induced the flow. Analyzed were key characteristics of coupled zero mass flux and convective situations. According to Katta et al. ^[42] by the use of activation energy, thermal radiation and applied magnetic force, the advanced thermal properties of nanomaterials enable increased heat and mass transfer performance in diverse engineering, industrial and technical processes. Yu-Ming et al. ^[43] mathematically modeled the flow of non-Newtonian nanofluid (second grade) in a two-dimensional magnetohydrodynamic boundary layer towards the surface of a permeable and stretchable Riga plate. The suggested Cattaneo-Christov double diffusions (CCDD) model is intended to evaluate the thermal and solute relaxation properties. Variable mass diffusivity and varied thermal conductivity were also taken into account. The condition of heat transport known as convection was also involved. Khan et al. ^[44] put forth the Ree-Eyring model, a mathematical model for non-Newtonian liquid moving towards a stretched surface. The modeling of flow problems including homogeneous-heterogeneous processes, Brownian motion, Joule heating, thermophoresis diffusion, entropy production, nonlinear thermal radiation and magnetohydrodynamics is done using the Buongiorno model. At the stretched surface, convective boundary conditions were put into practice. They created the governing flow expressions with the use of the Ree-Eyring model's rheological expression. Brownian diffusion, nonlinear thermal radiation, Joule heating and thermophoresis were used to generate the energy equation. For the investigation of mass transfer, two distinct species (homogeneous-heterogeneous processes) were taken into account. A nonlinear stretched surface was the only factor that induces the flow. For the examination of a stretched surface, the electrically conducting and chemically reactive fluid was taken into account. Pei et al. ^[45] modeled Reiner-Philippoff fluid flow across an expanding sheet. The issue of energy expression in the context of thermal radiation, heat creation and dissipation was discussed. The second and first laws of thermodynamics were used to establish the processes of entropy creation and energy transmission. According to the second rule of thermodynamics, irreversibility may be created in any process and cannot be destroyed in any system. The production of entropy was utilized to increase system effectiveness. Ashraf et al. ^[46] investigated the physical behavior of the combined impact of heat generation and absorption from nanoparticle material motion and the influence of various flow model-prescribed parameters. Khan et al. ^[47] examined the new theory of fractal fractional operators with a power-law kernel for heat transfer in a fluid flow. They specifically thought about a Newtonian fluid's free convection heat transfer. Between two parallel static plates, the flow is restrained. One of the plates receives continuous heating. Muhammad et al. ^[48] examined based on the first and second principles of thermodynamics with different geometries, the forced convection of nanofluid flow in a microtube with twisted porous blocks and a uniform magnetic field. Madhukesh et al. ^[49] studied the flow of AA7072-AA7075/water-based hybrid nanofluid across a curved stretched sheet using a non-Fourier heat flux model, which was motivated by applications. Also, the analysis of heat transfer for two distinct boundary conditions, Newtonian heating (NH) and constant wall temperature (CWT) was performed. Ibrahim et al. ^[50] studied a two-dimensional model of the natural convective heat transfer (NCHT) and production of entropy (POF) in a section of a tube was developed. A quarter-tubular enclosure that is filled with water-alumina nanofluid and exposed to a magnetic field was the focus of the investigation.

In the current paper, we provide numerical solutions for the flow and heat transfer caused by a porous stretched sheet in the presence of thermal radiation and an irregular heat source/sink for Casson nanofluids. To convert the nonlinear dimensional partial differential boundary layer equations into a set of ordinary differential equations that can be solved using the Runge-Kutta technique, similarity transformations are used. The fluctuations of the many related parameters are shown on graphs and described in depth.

2.   Problem formulation

In this research, the constant 2D MHD flow of a conducting non-Newtonian Casson nanofluid across a stretched foil at $y = 0$ is considered, along with the effects of heat generation and absorption due to chemical reactions and thermal radiation increase. In the zone where $y > 0$, the flow is contained. Applying two equal and opposite pressures along the x-axis causes the wall to expand while the origin remains stationary. The isotropic incompressible flow of Casson nanofluids is described by the rheological equation of state.

where $\pi = e_{ij} e_{ij}$ and $e_{ij}$ is the $[i, j]^{th}$ component of the deformation rate. In the non-Newtonian model, $n$ is the product of the strain rate with itself, $c$ is the product's critical value, $B$ is the non-Newtonian fluid's elastic dynamic viscosity and $P_y$ is the fluid's yield stress. Such a flow is governed by the momentum, continuity, and energy equations, whereby

In the above equation, $x$ and $y$ direction velocity components are denoted with $u$ and $v$. The Casson fluid density is $\rho_{nf}$ and $\nu_{nf}$ is the kinematic viscosity. $\gamma = \mu_B \sqrt{\frac{2\pi_c}{P_y}}$ is the parameter of Casson, $k_0$ is the permeability of the medium, $T$ is the temperature, $Q_0$ is the dimensional thermal generation/absorption coefficient, $C_p$ is the specific heat and $\alpha_{nf}$ is the thermal diffusivity.

Equation (2.4)'s $q^{'''}$ non-uniform heat source/ heat sink is represented as,

where, $A^*$ and $B^*$ are, respectively, the coefficients of a heat source or sink that is dependent on temperature and space. Here, we remark that the situation relates to the production of internal heat and the absorption of internal heat. Additionally, it is believed that the generated magnetic field is minuscule.

The boundary conditions affect the governing equations.

where $u_w = bx$, with $b > 0$ stretching sheet velocity, Characteristic length is $l$, $A$ is a constant, temperature of the foil is $T_w$, free stream temperature is $T_\infty$ and the temperature of the fluid is $T$.

We present the subsequent similarity variables

where $\psi$ stream function is defined as follows in the standard fashion:

3.   Solution methodology

The ordinary differential equations with the following boundary conditions are eventually produced by substituting equations (2.6) and (2.7) in the PDE (2.3) and (2.4).

Circumstances in Eqn. (2.6) become

The following definitions apply to the dimensionless variables and integers in the equations above: $M$ stands for magnetic parameter, $\gamma$ is Casson nanofluid parameter and porous parameter is $k$.

The nanoparticle volume fraction is the parameter $\phi$ and the Prandtl number is defined as $\frac{\nu_f}{\alpha_f}$.

The physical quantities of interest are the skin friction coefficient $C_f$ and the local Nusselt number $Nu_x$, which are represented as

where $\tau_w$ is the shear stress along the strain plane, $q_w$ is surface heat flux and both are presented as

Equations (3.3) and (3.4) are changed by substituting the transformations from (2.6). The result is,

where, $Re_x = \frac{u_w^2}{\nu}$ is the local Reynolds number.

4.   Results discussion

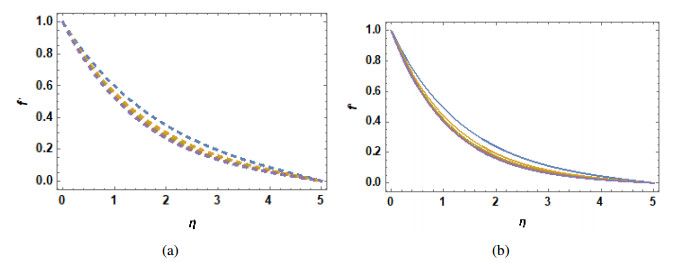
The current work investigates Casson nanofluidic flow with a non-uniform thermal source/sink along with viscous dissipation in the existence of MHD. Numerical calculations were performed to determine the temperature profile, velocity profile, local Nusselt number and skin friction coefficient for different values of the parameters that characterize the flow properties. This section's goal is to look at the physical implications of various implantation settings on the temperature and velocity profiles $[f(\nu), \theta(\nu)]$ displayed in graphs 1 through 15.

Graphs 1 to 3 show the effects of $M, \gamma, K$ and $f'$ on the velocity profile. According to Graph 1, increasing $\gamma$ decreases yield stress, which in turn causes a rise in the Casson parameter, which reduces fluid plasticity. This is because increasing $\gamma$ has an inverse relationship with yield stress, which causes the fluid velocity to decline for larger values of $\gamma$. The effect of $M$ on fluid velocity is shown in Graph 2 and as would be predicted, greater numbers of $M$ result in a decrease in fluid velocity. The cause of this behavior is that the applied magnetic field induces a resistive force in the conducting liquid, known as the Lorentz force, which equates to the resistive force. The fluid flow over the border zone is slowed down by this force. It is shown in Graph 3. As k increases, the fluid velocity decelerates rapidly around stretched sheets. This physically demonstrates that the fluid's velocity next to the foil is lower compared to the velocity of a stretched foil as a whole.

The domination of the Casson parameter $\gamma$ on the temperature profile $\theta(\eta)$ is shown in graph 4. It is clear that when the Casson nanofluid parameter $\gamma$ is increased, the temperature of the nanofluids rises, increasing the thickness of the thermal boundary layer as the elasticity stress parameter rises. It is clear from Graph 5 that as the magnetic parameter M increases, the thickness of the thermal boundary layer increases as well because the presence of the magnetic field increases the temperature of the fluid in the boundary layer. One explanation for this behavior is that when an electric current is passed through a flowing fluid, it cools down and increases the thickness of the thermal boundary layer. From Graph 6, it can be seen that the porous parameter k has an impact on the temperature and that the temperature of the fluid rises as the porosity parameter's value increases.

According to Graph 7, as the volume fraction of nanoparticles $\phi$ increases, the fluid temperature increases. The impact of Pr on the variation of temperature is seen in Graph 8. A drop in temperature profile is produced by an increase in $Pr$. Graph 9 shows that raising Eckert number $Ec$ raises the fluid temperature. Rising values of A* and B* clearly show that the variation of temperature in the border zone is increased. The non-uniform heat source/sink parameter typically has positive values that act as heat generators and negative values that act as heat absorbers from the boundary layer. Graph 12 shows that the skin friction coefficient grows as the volume proportion of nanoparticles volume fraction $\phi$ increases, although the local Nusselt number in graphs 13, 14 does not show similar results for increasing $Pr$ value.

This section elaborates on the physical behavior of the fluid flow and heat transfer in boundary layer difficulties across the various industries. The fluid parameter which defines the efficiency of the heat transfer from one substance to another reflects the quality of the product which is produced in different manufacturing industries. Quenching and liquid cooling are the processes that most of the manufacturing and sheet metal industries practices for better production of quality products. Overall the life and precision of the end products in the manufacturing industry depend on the heating and cooling processes.

5.   Conclusions

We have analyzed the 3-dimensional Casson nanofluid flow behavior of momentum and heat transmission across stretched sheets having non-uniform sources of heat and heat sink. Graphs are used to describe and display several non-dimensional controlling characteristics that affect velocity distribution and heat transfer rate. From the outcomes, we may infer the following. The velocity profiles progressively decrease as the Casson nanofluid parameter increases.

● Local skin friction coefficients in both directions increase numerically when the porosity parameter $k$ increases.

● Temperature increases with increase in the Eckert number.

● The presence of non-uniform heat sources and sinks aids in the establishment of the temperature profile.

● As the thermal radiation parameter Nr rises, the thermal boundary layer and heat thickness rise.

The results show that fluid parameters directly or indirectly impact the velocity and temperature of the fluid over a stretching sheet. In the process of manufacturing like compression, forging, combustion engines and extrusion processes the controlling of temperature loss is a very important aspect. The factor which is directly impacting the loss of heat from one medium to another can be controlled using the type of coolant defined for the different processes in the production industry. These critical parameters vary from compressible to incompressible fluids and the correlation of shear stress and strain rates is also comparatively complex in incompressible fluids.

Conflict of interest

All authors declare that they have no conflicts of interest.

Figure 1.  The effect of Casson fluid parameter $\gamma$ on velocity profile $f'(\nu)$ $M = 1, \phi_1, \phi_2, \phi_3 = 0.005, 0.01, 0.03. k = 0.5, k_f = 0.613, k_{nf} = 1.08, Pr = 6.2, A^* = 1, B^* = 1, Ec = 1$.

DownLoad: Full-Size Img PowerPoint

Figure 2.  Velocity profile $f'(\nu)$ for various values of magnetic parameter $M$ $\gamma = 1, \phi_1, \phi_2, \phi_3 = 0.005, 0.01, 0.03. k = 0.5, k_f = 0.613, k_{nf} = 1.08, Pr = 6.2, A^* = 1, B^* = 1, Ec = 1$.

DownLoad: Full-Size Img PowerPoint

Figure 3.  Velocity profile $f'(\nu)$ for various values of porosity parameter $k$ $\gamma = 1, \phi_1, \phi_2, \phi_3 = 0.005, 0.01, 0.03. M = 1, k_f = 0.613, k_{nf} = 1.08, Pr = 6.2, A^* = 1, B^* = 1, Ec = 1$.

DownLoad: Full-Size Img PowerPoint

Figure 4.  Temperature profile $\theta(\nu)$ for various values of Casson parameter $\gamma$ $M = 1, \phi_1, \phi_2, \phi_3 = 0.005, 0.01, 0.03. k = 0.5, k_f = 0.613, k_{nf} = 1.08, Pr = 6.2, A^* = 1, B^* = 1, Ec = 1, Nr = 1$.

DownLoad: Full-Size Img PowerPoint

Figure 5.  Temperature profile $\theta(\nu)$ for various values of magnetic parameter $M$ $\gamma = 1, \phi_1, \phi_2, \phi_3 = 0.005, 0.01, 0.03. M = 1, k_f = 0.613, k_{nf} = 1.08, Pr = 6.2, A^* = 1, B^* = 1, Ec = 1, Nr = 1$.

DownLoad: Full-Size Img PowerPoint

Figure 6.  Temperature profile $\theta(\nu)$ for various values of porosity parameter $k$ $\gamma = 1, \phi_1, \phi_2, \phi_3 = 0.005, 0.01, 0.03. M = 1, k_f = 0.613, k_{nf} = 1.08, Pr = 6.2, A^* = 1, B^* = 1, Ec = 1, Nr = 1$.

DownLoad: Full-Size Img PowerPoint

Figure 7.  Temperature profile $\theta(\nu)$ for various values of nanoparticle parameter $\phi_1$ $\gamma = 1, M = 1, \phi_1, \phi_2 = 0.005, 0.01, k = 0.5, k_f = 0.613, k_{nf} = 1.08, Pr = 6.2, A^* = 1, B^* = 1, Ec = 1, Nr = 1$.

DownLoad: Full-Size Img PowerPoint

Figure 8.  Temperature profile $\theta(\nu)$ for various values of Prandtl number $Pr$ $\gamma = 1, \phi_1, \phi_2, \phi_3 = 0.005, 0.01, 0.03. k = 0.5, k_f = 0.613, k_{nf} = 1.08, Ec = 1, A^* = 1, B^* = 1, M = 1, Nr = 1$.

DownLoad: Full-Size Img PowerPoint

Figure 9.  Temperature profile $\theta(\nu)$ for various values of Eckert number $Ec$ $\gamma = 1, \phi_1, \phi_2, \phi_3 = 0.005, 0.01, 0.03. k = 0.5, k_f = 0.613, k_{nf} = 1.08, Pr = 6.2, A^* = 1, B^* = 1, M = 1, Nr = 1$.

DownLoad: Full-Size Img PowerPoint

Figure 10.  Velocity profile $\theta(\nu)$ for various values of $A^*$ $\gamma = 1, M = 1, \phi_1, \phi_2, \phi_3 = 0.005, 0.01, 0.03, k = 0.5, k_f = 0.613, k_{nf} = 1.08, Pr = 6.2, A* = 1, Ec = 1, Nr = 1$.

DownLoad: Full-Size Img PowerPoint

Figure 11.  Temperature profile $\theta(\nu)$ for various values of $B^*$ $\gamma = 1, M = 1, \phi_1, \phi_2, \phi_3 = 0.005, 0.01, 0.03, k = 0.5, k_f = 0.613, k_{nf} = 1.08, Pr = 6.2, B^* = 1, Ec = 1, Nr = 1$.

DownLoad: Full-Size Img PowerPoint

Figure 12.  Temperature profile $\theta(\nu)$ for various values of $Nr$ $\gamma = 1, M = 1, \phi_1, \phi_2, \phi_3 = 0.005, 0.01, 0.03, k = 0.5, k_f = 0.613, k_{nf} = 1.08, Pr = 6.2, B^* = 1, Ec = 1$.

DownLoad: Full-Size Img PowerPoint

Figure 13.  For different levels of the porosity parameter $k$, skin friction $-f^{''}(\nu)$ with nanoparticle volume fraction $\phi_3$.

DownLoad: Full-Size Img PowerPoint

Figure 14.  Variations in the Prandtl number $Pr$ and the heat transfer coefficient $–\theta'(0)$ for various values of the porosity parameter $k$.

DownLoad: Full-Size Img PowerPoint

Figure 15.  Variation in the Eckert number $Ec$ and the heat transfer coefficient $–\theta'(0)$ for different values of the porosity parameter $k$.

DownLoad: Full-Size Img PowerPoint