Griffith energies as small strain limit of nonlinear models for nonsimple brittle materials

1.   Introduction

Polycyclic aromatic hydrocarbons (PAHs) are hydrocarbons with two or more benzene cycle structures in their molecules, such as our common naphthalene, anthracene, phenanthrene, etc. They are the most abundant group of carcinogens and are widely distributed in air, soil, water, and plants, in addition to being an important raw material for the chemical industry. At the same time, the chemical and biological activities of thickened aromatic hydrocarbons make them extremely versatile for applications in the petroleum industry, chemical manufacturing, and pharmaceutical industry, and these activities are dependent on their topology, while topological indicators are numerical descriptors of the topology of a molecule, which can be used as direct numerical descriptors to check the physical, chemical or biological activity of a molecule.

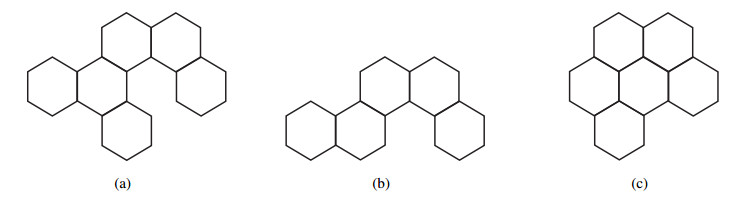
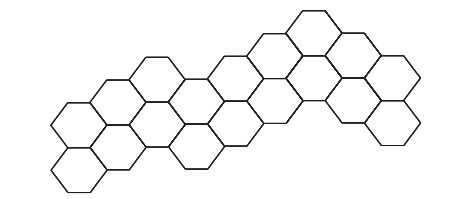
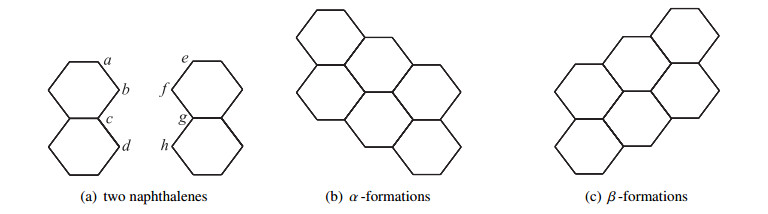
Hexagonal systems are a typical class of PAHs. In graph theory terminology, a hexagonal system (benzene-type hydrocarbons) is a 2-connected planar graph, each of whose internal faces is bounded by a unit regular hexagon with side length 1. The subgraph of a hexagonal system is called a generalized hexagonal system. A hexagonal system $H$ is called a double hexagonal chain if it can be seen as a hexagonal system of naphthalene and naphthalene adhered in a certain way, which is formed by the adhesion of naphthalenes (see Figure 1(a)) in the $\alpha$-formations, where two naphthalenes are adhered in a downward dislocation, i.e., the vertices $b$ and $e$, $c$ and $f$, and $d$ and $g$ are made to coincide, respectively (see Figure 1(b)), or in the $\beta$-formations, where two naphthalenes are adhered in an upward dislocation, i.e., the vertices $a$ and $f$, $b$ and $g$, and $c$ and $h$ are made to coincide, respectively (see Figure 1(c)).

In 1996 ^[1], F. Zhang and H. Zhang first introduced the concept of Clar covering polynomials for the hexagonal system diagram $H$ and denoted it. The Clar covering polynomial for the hexagonal system contains many important topological indicators, such as the Kekulé number, the Clar number, and the first Herndon number. It has been shown that the Clar covering polynomials allow more accurate calculation of the chemical activity of PAHs in terms of resonance energy, which is an important theoretical quantity for predicting the aromatic stability of PAH conjugation systems. Therefore, the study of the Clar covering polynomials for PAHs will help to reduce laboratory work on the topological parameters of PAHs and to maintain the ecological natural balance in terms of pollution control and air pollution reduction. The study of the Clar covering polynomials of PAHs will also provide an effective theoretical basis for the generation of unsynthesized PAHs.

Let $H$ be a generalized hexagonal system. A Kekulé structure in $H$ corresponds to a perfect matching of $H$, that is, the set of mutually disjoint edges in $H$ that cover all the vertices of $H$. Denote by $K(H)$ the number of Kekulé structures of $H$, i.e., the number of perfect matchings of $H$ ^[2]. A hexagonal system is called Kekuléan if and only if it has Kekulé structures. In recent decades, the Kekulé structure has been widely used to describe the local aromaticity of molecules ^[3,4,5] and predict carbon-carbon bond lengths and the stability of molecules ^[6]. If no three hexagons share a common vertex in a hexagonal system, then the hexagonal system is called cata-condensed (see Figure 2(a)), otherwise, it is peri-condensed (see Figure 2(c)). If each hexagon is adjacent to at most two hexagons, the cata-condensed hexagonal system is said to be an unbranched cata-condensed hexagonal system (see Figure 2(b)) ^[6], namely, a hexagonal chain.

Let $Q$ be a set of mutually disjoint hexagons of a generalized hexagonal system $H$, then $H$-$Q$ is denoted by a subgraph of $H$, obtained by deleting all vertices of $Q$ together with their incident edges. $Q$ is said to be a cover of $H$ if $H$-$Q$ has at least one perfect matching or if $H$-$Q$ is empty, following Gutman ^[2]. We add a Kekulé structure of $H$-$Q$ to the cover $Q$ to get a vertex-cover of $H$, which is called a Clar cover of a (generalized) hexagonal system $H$. In other words, a spanning subgraph $C$ of $H$ is said to be a Clar cover of $H$ if each of its components is either a hexagon or an edge.

Let $\mathbb{C}$ be the set of all Clar covers of $H$. For a Clar cover $C\in{\mathbb{C}}$, we denote by $h(C)$ the number of hexagons of $C$. Define the Clar covering polynomial of $H$ as follows ^[1]:

In particular, the Clar covering polynomial of a graph $H$ without any Kekulé structure is satisfied with $P(H, w) = 0$; and the Clar covering polynomial of a null graph $H$ is $P(H, w) = 1$ ^[1].

In the papers ^[1,7,8], F. Zhang and H. Zhang gave a series of recursive formulas for Clar covering polynomials and specific expressions for Clar covering polynomials for some special hexagonal chains. Early research on Clar covering polynomials mainly focused on the calculation of several related topological indices associated with them ^[9,10,11]. Gutman and colleagues ^{[12,13,14,15,16,17,18]} demonstrated the relevance between Clar covering polynomials of benzene hydrocarbons and their resonance energy. In 2005 ^[14], it was proven that when $w \approx 1$, $\ln {P(H, w)}$ shows the best correlation with resonance energy, suggesting that $P(H, 1)$ can be considered a new structural descriptor, similar to the role of Kekulé structure numbers based on Kekulé structure theory. In the same year ^[15], Gutman showed that in the case of benzene molecules, the Dewar resonance energy (DRE) and topological resonance energy (TRE) are linearly related to $\ln{P(H, 0)}$ and $\ln{P(H, 1)}$, respectively. Subsequently, Clar covering polynomials were further investigated and many results were obtained ^{[19,20,21,22,23,24,25,26,27,28,29,30]}. For example, in 2006 ^[20], Gutman and Borovicanin obtained explicit combined expressions for Clar covering polynomials of multiple linear hexagonal chains $M_{n, m}$. In 2009 ^[21], Q. Guo provided explicit recursive formulas for Clar covering polynomials of cyclo-polyphenacenes and determined their Clar numbers, Kekulé structure numbers, and first Herndon numbers. Chien-Pin Chou and others ^{[23,24,25,26]} developed an automatic computer program for calculating Clar covering polynomials of small to medium-sized benzene systems and determined specific expressions for Clar covering polynomials of a series of benzene compounds using a self-developed calculation program.

In conjugate circuits, resonance energies are determined using conjugate rings of different lengths ^[31], not just hexagonal cycles. However, only hexagonal and decagon rings have uniquely determined structures. Therefore, in 2016 ^[32], Zigert Pleteršek introduced the concept of generalized Clar covering polynomials containing both six- and ten-membered cycles in the literature. In 2022 ^[33], Boris Furtula and his team, based on the definition of generalized Clar covering polynomials, researched a series of recursive formulas of generalized Clar covering polynomials and provided an algorithm to compute the generalized Clar covering polynomials of any hexagonal chain. They demonstrated that generalized Clar covering polynomials can more accurately estimate and compute the resonance energy of PAHs and other chemical activities, thus being used to predict the aromatic stability of PAH conjugated systems. In the same year ^[34], Radenković demonstrated that the vibrational energy of a molecule is related to parameters based on the Clair structure by using the generalized Clar covering polynomial.

In addition, the Clar covering polynomials are also associated with various mathematical and chemical concepts. This includes the connection between the Clar covering polynomial and the sextet polynomial ^[8], the chromatic polynomial ^[35], as well as the relationship between the Clar covering polynomial and the cube polynomial of their resonance graph ^[36], and the relationship between the generalized Clar covering polynomial and the generalized cube polynomial of its resonance graph ^[32]. However, there is not much research on the double hexagonal chain, mainly because the double hexagonal chain belongs to the peri-condensed hexagonal system, and its structure is complex and difficult. Gutman ^[37] studied the partition of the $\pi$-electrons in the rings of linear double hexagonal chains. In 2020, M. Alishahi and S.H. Shalmaee ^[38] gave the exact formulae for the edge eccentric connectivity index and modified edge eccentric connectivity index of linear double hexagonal chains. In Ref ^{[39,40,41,42]}, H. Ren and F. Zhang characterized a series of extreme double hexagonal chains, such as the double hexagonal chains with maximal Hosoya index and minimal Merrifield-Simmons index.

In this paper, we first obtained some recursive formulae for the Clar covering polynomials of double hexagonal chains and proposed a Matlab algorithm to compute the Clar covering polynomial of any double hexagonal chain. Moreover, we presented the characterization of extremal double hexagonal chains with maximum and minimum Clar covering polynomials in all double hexagonal chains. For other concepts not described in the text, one can refer to the book ^[43].

2.   Preliminaries

In this section, we will introduce some relevant conclusions for the Clar covering polynomial of the hexagonal system. F. Zhang and H. Zhang have obtained some properties and recurrence relations for the Clar covering polynomial of a hexagonal system and have derived some formulae for calculating the Clar covering polynomials of some special classes of hexagonal systems.

Theorem 2.1. ^[1] Let $H$ be a generalized hexagonal system, the components of which are $H_1$, $H_2$, $H_3$, $\cdots$, $H_s$, then

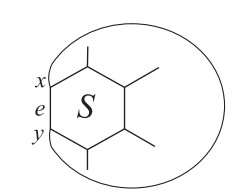
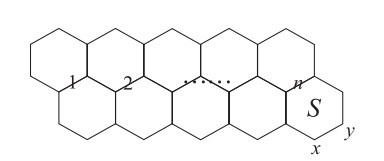
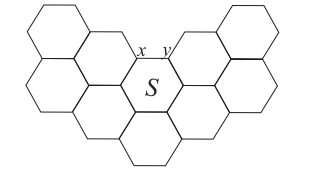
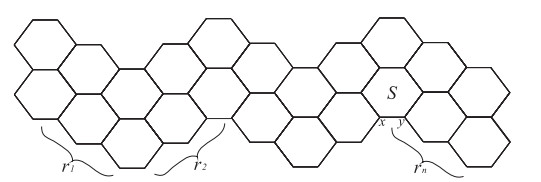
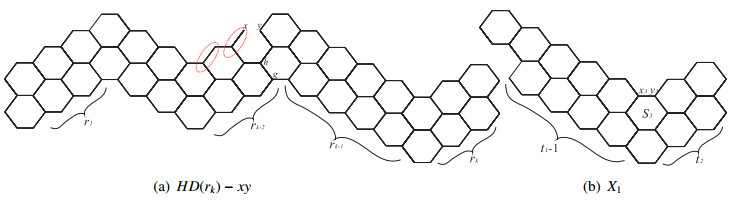
Theorem 2.2. ^[1] Let $H$ be a generalized hexagonal system. Assuming that $e = xy$ is an edge of a hexagon $S$ of $H$, which lies on the periphery of $H$ (see Figure 3), then

Theorem 2.3. ^[20] Let $H$ be a generalized hexagonal system. Assuming $xy$ is an edge not belonging to any hexagons of $H$ and the vertex $x$ is of degree 1 (see Figure 4), then

Let $H$ be an any generalized hexagonal system containing the vertex $x$ is degree 1. According to the result of the Theorem 2.3, the Clar covering polynomial of $H$ can be calculated in the following simple way:

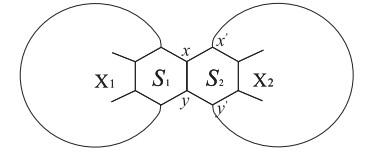
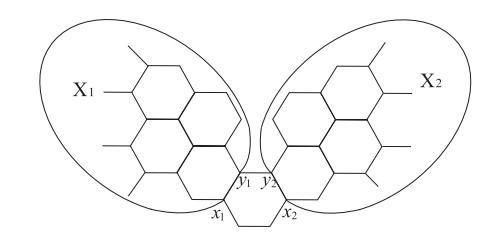
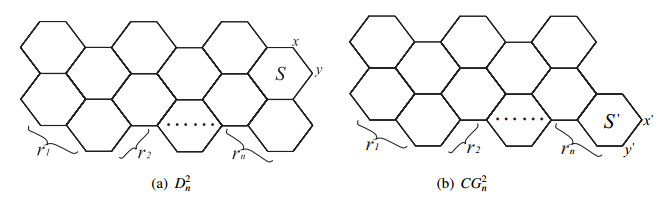
Let $X_1$, and $X_2$ be two Kekuléan hexagonal systems. We get a hexagonal system, which identifies an edge on the periphery of $X_1$ with an edge on the periphery of $X_2$, denoted by $X_1\cdot X_2$ (see Figure 5).

Theorem 2.4. ^[1] Let $X_1$ and $X_2$ be two Kekuléan hexagonal systems, which contain hexagons $S_1$ and $S_2$, respectively, as indicated in Figure 5 (or let one of them be $K_2$). The Clar covering polynomial of hexagonal system $X_1\cdot X_2$ is

where $X_{i}^{'} = X_i-x-y$ for $i = 1$ or 2.

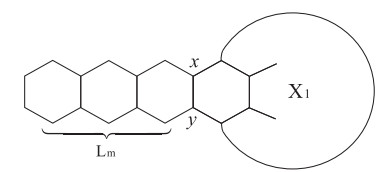
Without danger of confusion, we use $L_m$ to denote a linear hexagon chain, and denote $l_m$ by the Clar covering polynomial of a linear hexagonal chain with $m$ hexagons.

Corollary 2.1. ^[1] Let $L_m\cdot X_1$ be a hexagonal system (see Figure 6), then $P(L_m\cdot X_1, w) = m(w+1)P(X_{1}^{'}, w)+P(X_1, w)$.

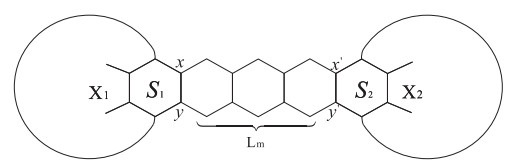
Theorem 2.5. ^[1] Let $X_1$ and $X_2$ be two Kekuléan hexagonal systems or $K_2$, and $G = (X_1\cdot L_m)\cdot X_2$ (see Figure 7), then

where $X_{1}^{'} = X_1-x-y$, and $X_{2}^{'} = X_2-x^{'}-y^{'}$.

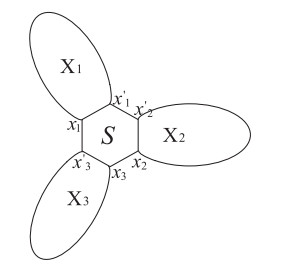
Let $X_1$, $X_2$, and $X_3$ be three Kekuléan hexagonal systems. Identifying each of a triple of pairwise disjoint edges of an additional hexagon with a peripheral edge of $X_1$, $X_2$, $X_3$, denote by $X_1\cdot X_2\cdot X_3$ (see Figure 8).

Theorem 2.6. ^[1] Let $X_1$, $X_2$, and $X_3$ be three Kekuléan hexagonal systems or $K_2$, and let $G = X_1\cdot X_2\cdot X_3$ (see Figure 8), then

where $X_{i}^{'} = X_i-x_i-x_{i}^{'}$, for $i = 1, 2, 3$.

3.   Main results

In the above, some properties and recurrence relations for the Clar covering polynomial of a hexagonal chain have been obtained. In this section, we will deduce the relevant conclusions for the Clar covering polynomial of a double hexagonal chain, and we will consider the sequence relation of the polynomial in the hexagonal chains by quasi-order, which denote $\preceq$ and $\prec$. Let $f(x) = \sum_{k = 0}^{n}a_kx^k$ and $g(x) = \sum_{k = 0}^{n}b_kx^k$ be polynomials in $x$. We write $f(x)\preceq g(x)$ if $a_k\leq b_k$ for all integers $k$, and $f(x)\prec g(x)$ if the polynomials are not equal. In the following, we denote by $L_{n}^{\alpha}$ and $L_{n}^{\beta}$ the linear double hexagonal chains containing $n$ naphthalene in the $\alpha$-formations and $\beta$-formations, and $l_{n}^{\alpha}$ and $l_{n}^{\beta}$ by their corresponding Clar covering polynomials, respectively. Moreover, in this section we will use square brackets $\left[a, b\right]$ to denote all real numbers in the closed interval $a$ to $b$.

Theorem 3.1. Let $L_{n}^{\alpha}$ be a linear double hexagonal chain containing $n$ naphthalenes (see Figure 9), in which the adhesion of naphthalenes are the $\alpha$-formations, then

Proof. Obviously, the Clar covering polynomial of naphthalene is $l_{1}^{\alpha} = l_2 = 2w+3$. Applying Theorem 2.4 to the edge $xy$, we have

According Theorem 2.3, we have $P(L_{n}^{\alpha}-S, w) = l_{n-1}$, $P(L_{n}^{\alpha}-x-y, w) = P(L_{n-1}^{\alpha}, w) = l_{n-1}^{\alpha}$, $P(L_{n}^{\alpha}-xy, w) = l_{n}$, and $l_n = l_{n-1}+w+1.$

Therefore,

Similar to the proof of Theorem 3.1, or simply following by symmetry, we have

Corollary 3.1. Let $L_{n}^{\beta}$ be a linear double hexagonal chain containing $n$ naphthalenes, in which the adhesion of naphthalenes are the $\beta$-formations, then $l_{n}^{\beta} = (w+1)l_{\frac{n(n-1)}{2}}+l_{2n-1}.$

According to Theorems 2.1 and 2.6, we have the following result:

Theorem 3.2. Let $X_1$ and $X_2$ be two double hexagonal chains or linear hexagonal chains, and $G$ be a hexagonal system as shown in Figure 10, then

where $X_{1}^{'} = X_1-x_1-y_1$, and $X_{2}^{'} = X_2-x_2-y_2$.

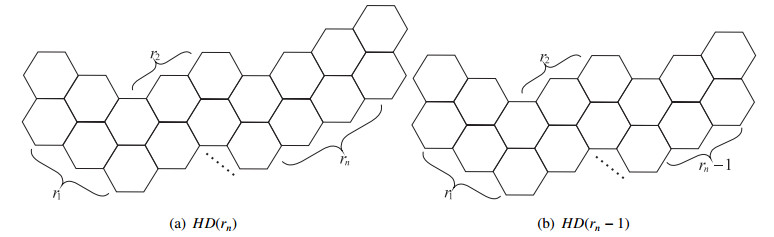
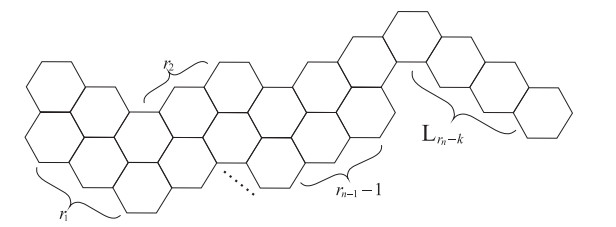
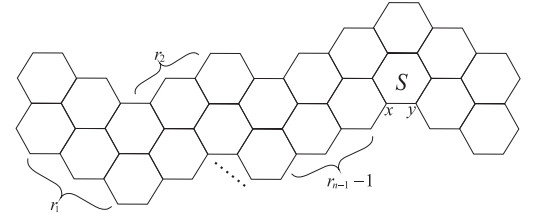
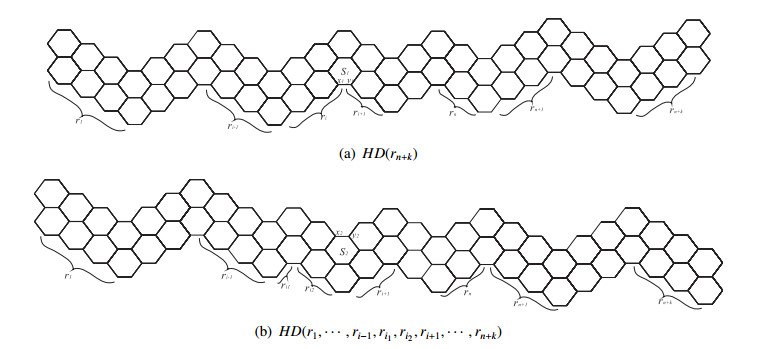
Let $H$ be a double hexagonal chain, in which has $n$ maximal linear double hexagonal chains with more than two naphthalenes. We in turn denote the number of naphthalenes in these maximal linear double hexagonal chains by $r_1, r_2, \cdots, r_n$ ($r_i\geq2$, $i = 1, 2, \cdots, n$), respectively, which is also said to be a related sequence of $H$. Thus, we can use $HD(r_1, r_2, \cdots, r_n)$ (without danger of confusion, abbreviated as $HD(r_n)$, see Figure 11(a)) to denote by a double hexagonal chain $H$ with related sequence $r_1, r_2, \cdots, r_n$. We also denote by $HD(r_n-1)$ an auxiliary double hexagonal chain from $HD(r_n)$ by removing the terminal naphthalene of the last maximal linear double hexagonal chain (see Figure 11(b)), and denote by $Hd(r_n)$ and $Hd(r_n-1)$ the Clar covering polynomials of $HD(r_n)$ and $HD(r_n-1)$, respectively. Furthermore, we use $Cg(r_n-k)$ to denote the Clar covering polynomial of the following combination graph $CG(r_n-k)$ (see Figure 12), where $CG(r_n-k) = HD(r_{n-1}-1)\cdot L_{r_n-k}$, $k = 0, 1, \cdots, r_{n}-1$.

Apply Theorem 3.2 to graph $CG(r_n-k)$ and we can obtain the following result:

Proposition 3.1. Let $n (\geq2)$ be a positive integer, then the Clar covering polynomial of $CG(r_n-k)$ is

Obviously, we have $Cg(r_1-1) = l_{r_1-1} = r_1(w+1)+1$, and $HD(r_1)$ is exactly the linear double hexagonal chain $L_{r_1}^{\alpha}$. By Theorem 3.1, the Clar covering polynomial of $HD(r_1)$ equals to

Therefore, we know that the coefficient of each term in the Clar covering polynomial of $Cg(r_n-k)$ is a nonnegative integer.

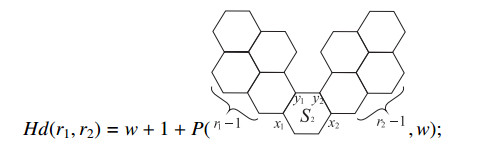
In the next proposition, we will calculate the Clar covering polynomial of $HD(r_1, r_2)$ (see Figure 13), and also denote by $Hd(r_1, r_2)$ the Clar covering polynomial of $HD(r_1, r_2)$.

Proposition 3.2. The Clar covering polynomial of $HD(r_1, r_2)$ can be computed as

Proof. To begin, we can apply Theorem 2.2 to the graph $HD(r_1, r_2)$, then the Clar covering polynomial of $HD(r_1, r_2)$ can be computed as the following:

and then we apply Theorem 3.2 to $L_{r_1-1}^{\alpha}$ and $L_{r_2-1}^{\beta}$, which are joined by the hexagon $S_2$. We can obtain

Finally, based on Eq (3.1) and some of the elementary calculations, we can obtain the result.

Proposition 3.3. Let $n (\geq3)$ be a positive integer, then the Clar covering polynomial of $HD(r_n)$ can be computed as

Proof. According to the Theorems 2.2 and 2.6, suppose that $S$ is a hexagon and $xy$ is an edge of $HD(r_n)$ as shown in Figure 14, and we have

Thus, Theorems 3.2 and 2.6 enable us to calculate $P(HD(r_n)-xy, w)$, and the result is obtained.

Corollary 3.2. Let $n (\geq3)$ be a positive integer, then the Clar covering polynomial of $HD(r_n-1)$ can be computed as

Proof. According to Proposition 3.3, where $l_{r_n-1}^{\alpha}$ and $l_{r_n-1}$ are replaced by $l_{r_n-2}^{\alpha}$ and $l_{r_n-2}$, respectively.

By Propositions 3.1 and 3.2, we know that each coefficient of each term in $Hd(r_1-1)$, $Hd(r_2-1)$, and $Cg(r_n-k)$ is a nonnegative integer, where $r_1$ and $r_2$ are all larger than 2. Hence, we can obtain that the coefficient of each term in Clar covering polynomials $Hd(r_n)$ and $Hd(r_n-1)$ are nonnegative integers by Proposition 3.3 and Corollary 3.2.

Due to Propositions 3.1 and 3.3, and Corollary 3.2, we can recursively calculate the Clar covering polynomial of an arbitrary double hexagonal chain. Now we will present a Matlab algorithm (see Table 1) to compute the Clar covering polynomial of an arbitrary double hexagonal chain in the following. In the algorithm, we denote by $h_i$, $d_i$ and $p_i$ by $Hd(r_i)$, $Hd(r_i-1)$ and $Cg(r_i-1)$, respectively. First, in lines 1–3 of the Matlab algorithm, we define the independent variable $w$, the number of related sequences of $HD(r_n)$, and the value of each relevant sequence, respectively. Second, in lines 6–8 of the algorithm, we compute $Hd(r_1)$, $Hd(r_1-1)$, and $Cg(r_1-1)$, respectively, according to Eq (3.1) and Proposition 3.1. Note that when using this algorithm to compute the Clar covering polynomial of an arbitrary linear double hexagonal chain, we need replace line 2 with $n = 1$ and delete line 5. Of course, if we use the algorithm to compute the Clar covering polynomial of an arbitrary double hexagonal chain, we only need to replace lines 2 and 3.

According to the above Matlab algorithm, we can easily compute the Clar covering polynomial of a double hexagonal chain $HD(3, 2, 4, 3)$, as shown in Figure 15, and obtain the following result:

Meanwhile, by the Matlab algorithm, we know that if any two double hexagonal chains have the same related sequence, then their Clar covering polynomials are also the same. We present the exact formulae of the Clar covering polynomials of some double hexagonal chains in the Appendix (see Table 2).

Next, we will calculate the Clar covering polynomial of any arbitrary double hexagonal chain $HD(r_n)$ with related sequences $r_1 = r_2 = \cdots = r_n = p$, and its Kekulé number and the first Herndon number. For simplicity, we denoted by $D_{n}^{p}$ an arbitrary double hexagonal chain with related sequences $r_1 = r_2 = \cdots = r_n = p$, its Clar covering polynomial by $d_{n}^{p}$, and denoted the Clar covering polynomial of $D_n^{p'}$ (which is obtained by removing the terminal naphthalene of the last maximal linear double hexagonal chain from $D_{n}^{p}$) by $d_n^{p'}$. In particular, if $r_1 = r_2 = \cdots = r_n = 2$, we also denoted it and its Clar covering polynomial by $D_n^{2}$, $d_{n}^2$, respectively. Meanwhile, denoted by $CG_n^{p}$ an auxiliary graph $CG(r_n-1) = D_{n-1}^{p'}\cdot L_{p-1}$, and its Clar covering polynomial by $Cg_n^{p}$. In particular, when $r_1 = r_2 = \cdots = r_n = 2$, we use $Cg_n^{2}$ to denote the Clar covering polynomial of graph $CG_n^{2}$ with related sequences $r_1 = r_2 = \cdots = r_{n-1} = r_n = 2$ (see Figure 16(b)), where $Cg_n^{2} = D_{n-1}^2\cdot L_{1}$.

Proposition 3.4. Let $D_{n}^2$ $(n\geq4)$ be a double hexagonal chain with related sequences $r_1 = r_2 = \cdots = r_n = 2$ (see Figure 16(a)), then

where $d_1^2 = w^2+6w+6$, $d_2^2 = w^3+9w^2+21w+14$, and $d_3^2 = w^4+10w^3+39w^2+60w+31$.

Proof. Applying Theorem 2.4 to the edge $xy$ and $x^{'}y^{'}$, respectively, we have that

According to Eqs (3.2) and (3.3), we have that $Cg_n^{2} = d_{n}^2-(w+1)d_{n-2}^2$, $Cg_{n-1}^{2} = d_{n-1}^2-(w+1)d_{n-3}^2$, and

where $d_1^2 = w^2+6w+6$, $d_2^2 = w^3+9w^2+21w+14$ and $d_3^2 = w^4+10w^3+39w^2+60w+31$.

Due to the coefficients of the lowest degree term and the primary term of the Clar covering polynomial equal to the Kelulé number and the first Herndon number, respectively, we can obtain the recurrence relations for the number of perfect matchings and the first Herndon number of $D_{n}^2$ by taking $w = 0$ in the Clar covering polynomial and taking $w = 0$ in the first derivative of the Clar covering polynomial in Proposition 3.4, respectively.

The recurrence relations for the number of perfect matchings of $D_{n}^2$ $(n\geq4)$ are as following:

where $K(D_{1}^2) = 6$, $K(D_{2}^2) = 14$ and $K(D_{3}^2) = 31$.

The recurrence relations for the first Herndon number of $D_{n}^2$ $(n\geq4)$ are as following:

where $h_1(D_{1}^2) = 6$, $h_1(D_{2}^2) = 21$ and $h_1(D_{3}^2) = 60$.

According to Eqs (3.4) and (3.5) and relevant properties, we give two Matlab algorithms to compute the Kekulé number (or the number of perfect matchings) and the first Herndon number of $D_{n}^2$ (see Tables 3 and 4, respectively). Meanwhile, according to the two Matlab algorithms, we can compute the number of perfect matchings and the first Herndon number of some double hexagonal chains (see Table 5).

Now, we will give a more general result for the Clar covering polynomial of a double hexagonal chain with $r_1 = r_2 = \cdots = r_n = p$.

Proposition 3.5. Let $D_n^p$ be a double hexagonal chain with related sequences $r_1 = r_2 = \cdots = r_n = p$ (see Figure 17), then

Proof. Apply Theorems 2.2 and 3.2 to the hexagon $S$ and edge $xy$ in $D_n^p$, we have

then from Proposition 3.1, we have that

According to Eq (3.6), we have that

According to Eqs (3.7) and (3.8) and $r_1 = r_2 = \cdots = r_n = p$, we can obtain the following recurrence relations for the Clar covering polynomials of $d^{p'}_n$ and $Cg^{p}_{n}$:

for $n\geq4$, where $d^{p'}_1 = l_{p-1}^\alpha$, $d^{p'}_2 = Hd(m, m-1)$, $d^{p'}_3 = Hd(m, m, m-1)$;

for $n\geq4$, where $Cg^{p}_{1} = l_{p-1}$, $Cg^{p}_{2} = d^{p'}_1l_{p-2}+(w+1)l_{p-1}$, $Cg^{p}_{3} = d^{p'}_2l_{p-2}+(w+1)Cg^{p}_{2}$.

By dealing with $d^{p'}_n$ and $Cg^{p}_{n}$ in the same way as Proposition 3.4, we can directly obtain recurrence relations for the Clar covering polynomial of $d^{p'}_n$ and $Cg^{p}_{n}$, and the recurrence relations for the Kekulé numbers and the first Herndon number for $D^{p'}_n$ and $CG^{p}_{n}$ will be obtained. The recurrence relations for the Kekulé numbers and the first Herndon number for $D^{p}_n$ are also obtained.

Next, we will consider the extreme of Clar covering polynomials of double hexagonal chains with the fixed number of naphthalenes. Without loss of generality, we only consider double hexagonal chains represented in Figure 11, being of the reason that any two double hexagonal chains have the same Clar covering polynomials if they have the same related sequence $r_1, r_2, \cdots, r_n$. Let $\mathcal{H}D(r_1, r_2, \cdots, r_n)$ be the set of double hexagonal chains with a fixed number of naphthalenes, and its related sequences are $r_1, r_2, \cdots, r_n$, then we have the following result.

Theorem 3.3. Let $HD(r_1, r_2, \cdots, r_n)$ (abbreviated by $HD(r_n)$) be a double hexagonal chain in $\mathcal{H}D(r_1, r_2, \cdots, r_n)$, then $P(HD(r_n), w)\preceq d^{p}_n$, for any fixed positive integer $n$.

Proof. We prove it by induction on $n$. It is clearly true that for $n = 1$. For $n = 2$, the result is true for $r_1 = r_2 = p$. In fact, we can obtain the Clar covering polynomial of $HD(r_1, r_2)$ by Proposition 3.2. Therefore, $d^{p}_2$ is the largest Clar covering polynomial of $HD(r_1, r_2)$.

Next, assuming that it is true for $r_1 = r_2 = \cdots = r_{k-1}$, namely, the Clar covering polynomial of $HD(r_1, r_2, \cdots, r_{k-1})$, for $r_1 = r_2 = \cdots = r_{k-1} = p$, is the largest one. Now, we will prove that the theorem is true for $HD(r_1, r_2, \cdots, r_{k})$, $r_1 = r_2 = \cdots = r_k$.

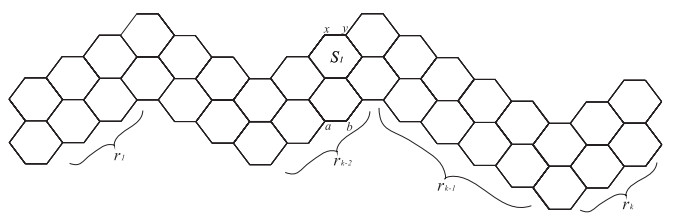
Suppose that $r_1 = r_2 = \cdots = r_{k-2} = p$, $r_{k-1} = t_1$, $r_{k} = t_2$, and $t_1+t_2 = 2p$ (see Figure 18). According to the induction hypothesis, $d^{p}_{k-2}$ is the largest Clar covering polynomial of $HD(r_{k-2})$, for $r_1 = r_2 = \cdots = r_{k-2} = p$.

By Theorem 2.4, we have

First, for $P(HD(r_k)-S_1, w)$, due to the lack of kekulé structure in graphs with odd vertices, then $ab$ does not belong to any kekulé structure of $HD(r_k)-S_1$. Hence, according to Theorem 2.1, we have $P(HD(r_k)-S_1, w) = Cg(r_{k-2}-2)\cdot Hd(r_{k-1}-1, r_k)$.

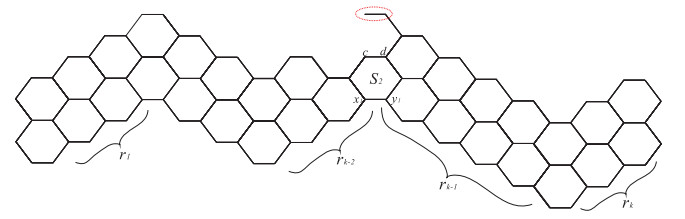
Second, for $P(HD(r_k)-x-y, w)$ (see Figure 19), applying Theorem 2.2 to the edge $x_1y_1$ and hexagon $S_2$, we can obtain $P(HD(r_k)-x-y, w) = wP(HD(r_k)-x-y-S_2, w)+P(HD(r_k)-x-y-x_1-y_1, w)+P(HD(r_k)-x-y-x_1y_1, w)$. Since the Clar covering polynomial of a graph with odd vertices is equal to 0, and we know that the edge $cd$ does not belong to any kekulé structure of $HD(r_k)-x-y-x_1y_1$, we have $P(HD(r_k)-x-y, w) = w\cdot 0+0+Hd(r_{k-2}-2)\cdot Hd(r_{k-1}-1, r_k)$.

Finally, for $P(HD(r_k)-xy, w)$ (see Figure 20), applying Theorem 2.4 to the edge $hg$, we can obtain $P(HD(r_k)-xy, w) = d_{k-3}^{p^{\prime}} \cdot H d\left(r_{k-1}, r_k\right)+(w+1) \cdot(p-2) \cdot d_{k-3}^{p^{\prime}} \cdot P\left(X_1, w\right)+(w+1) \cdot G g_{k-2}^p \cdot P\left(X_1, w\right)$.

Hence,

Similarly, applying Theorem 2.2 to the edge $x_3y_3$, and by Theorem 3.2 and Eq (3.1), we have

obviously, $P(X_1, w)$ is maximum when $t_1 = t_2$.

Meanwhile, according to the induction hypothesis, $Cg^{p}_{k-2}$, $Cg(r_{k-2}-2)$, $d^{p'}_{k-2}$, and $d^{p'}_{k-3}$ are fixed, respectively. By Proposition 3.2, we know that $Hd(t_1-1, t_2)$ is a maximum when $t_1 = t_2$, so we can immediately obtain that $d^{p}_n$ is the maximum Clar covering polynomial ranging over all Clar covering polynomials of double hexagonal chains in $\mathcal{H}D(r_1, r_2, \cdots, r_n)$.

Theorem 3.4. Let $HD(r_{n+k})$ be a double hexagonal chain containing $s$ naphthalenes, with related sequence $r_1, r_2, \cdots, r_{i-1}, r_{i}, r_{i+1}, \cdots, r_n, r_{n+1}, \cdots, r_{n+k}$, therein $r_i = p$, and $p$, $r_1$, $\cdots$, $r_{n+k}$ are nonnegative integers. Thus,

where $r_i = p$, $r_{i_1}+r_{i_2} = p+1$.

Proof. Apply Theorems 2.2 and 3.2 to the $x_1y_1$ (see Figure 21(a)) and $x_2y_2$ (see Figure 21(b)), respectively. We can immediately obtain

where $P_{\Delta} = l_{r_{i+1}-2}Hd^{'}(r_{n+k}, r_{n+k-1}, \cdots, r_{i+2})+(w+1)Cg(r_{n+k}, r_{n+k-1}, \cdots, r_{i+2}-1)$. Obviously, the coefficient of each term in $P_{\Delta}$ is a nonnegative integer.

Hence,

Due to the coefficients of each term in $Hd(r_n)$, $Hd^{'}(r_n)$ and $P_{\Delta}$ are nonnegative integers. We will only consider the coefficients of each term in $Hd^{'}(r_{i1})-Hd^{'}(r_{i-1})$, $Hd^{'}(r_{i2})-Hd^{'}(r_{i})$, $Cg(r_{i2}-1)-Cg(r_i-1)$. For the convenience of calculation, set $w+1 = x$ in the following, then

(ⅰ) First, consider $Hd^{'}(r_{i1})-Hd^{'}(r_{i-1})$. According to Corollary 3.2, we have

(ⅱ) Next, consider $Hd^{'}(r_{i2})-Hd^{'}(r_{i})$. According to Theorems 2.4 and 3.2, Proposition 3.2 and Corollary 3.2, we have

where $A = x+l_{r_{i1-2}}^\alpha l_{r_{i2-2}}^\alpha+xl_{r_{i1}-2}l_{r_{i2}-2}.$

Hence,

Obviously, through simple calculations, we know that the coefficients of each term in $l_{r_{i1}-2}l_{r_{i2}-2}^\alpha-l_{p-2}$ and $l_{r_{i1-2}}^\alpha l_{r_{i2-2}}^\alpha-l_{p-2}^\alpha$ are nonnegative integers, so we have that the coefficient of each term in $Hd^{'}(r_{i2})-Hd^{'}(r_{i})$ is a nonnegative integer.

(ⅲ) Eventually, consider $Cg(r_{i2}-1)-Cg(r_i-1)$. By Proposition 3.1, Corollary 3.2 and $r_{i_1}+r_{i_2} = p+1$, we can obtain

when $r_1 = 2$ or $r_1 = r_2 = 2$, $l_{r_{i2}-2}l_{r_{i1-2}}^\alpha+xl_{r_{i1-2}}-l_{p-2} = 0$. If $r_2 = 2$ and $r_1\neq2$, we have $l_{r_{i2}-2}l_{r_{i1-2}}^\alpha+xl_{r_{i1-2}}-l_{p-2} = \frac{(r_{i1}-2)(r_{i1}-1)}{2}x^2+(r_{i1}-2)x$. Hence, we also know that the coefficient of each term in $Cg(r_{i2}-1)-Cg(r_i-1)$ is a nonnegative integer.

To sum up, the proof is completed.

Corollary 3.3. Let $HD(r_{n+k})$ be a double hexagonal chain containing $s$ naphthalenes, with related sequence $r_1, r_2, \cdots, r_n, r_{n+1}, \cdots, r_{n+k}$, therein $r_1 = r_2 = \cdots = r_i = p$, $r_{i+1} = r_{i+2} = \cdots = r_n = t$, $r_{n+1} = r_{n+2} = \cdots = r_{n+k} = r$, $i\in\left[1, n\right]$, and $p$, $t$, $r$, $i$ are nonnegative integers. Thus,

where $r_1 = r_2 = \cdots = r_{i-1} = p$, $r_{i_1}+r_{i_2} = p+1$ and $r_{i+1} = r_{i+2} = \cdots = r_n = t$, $r_{n+1} = r_{n+2} = \cdots = r_{n+k} = r$.

Corollary 3.4. Let $HD(r_{n})$ be a double hexagonal chain containing $s$ naphthalenes, with related sequence $r_1, r_2, \cdots, r_n$, therein $r_1 = r_2 = \cdots = r_i = p$, $r_{i+1} = r_{i+2} = \cdots = r_n = t$, $i\in\left[1, n\right]$, and $p$, $t$, $i$ are nonnegative integers. Thus,

where $r_1 = r_2 = \cdots = r_{i-1} = p$, $r_{i_1}+r_{i_2} = p+1$, and $r_{i+1} = r_{i+2} = \cdots = r_n = t$.

Corollary 3.5. Let $HD(r_{n})$ be a double hexagonal chain containing $s$ naphthalenes, with related sequence $r_1, r_2, \cdots, r_n$, therein $r_1 = r_2 = \cdots = r_n = p$, $p\geq3$, and $p$ is a nonnegative integer, then

where $r_1 = r_2 = \cdots = r_{n-1} = p$, $r_{n_1}+r_{n_2} = p+1$.

Theorem 3.5. Let $HD(r_{n})$ be a double hexagonal chain containing $s$ naphthalenes, then $d_{s-1}^2$ is the maximum Clar covering polynomial of $HD(r_{n})$.

Proof. For any double hexagonal chain containing $s$ naphthalenes, according to Theorem 3.4, we can split it into

where $u$, $v$ are nonnegative integers, and $u$, $v$ represent the number of maximal linear double hexagonal chains containing exactly 3 naphthalenes and the number of maximal linear double hexagonal chains containing exactly 2 naphthalenes, respectively.

Hence, we know that $u$, $v$ must exist and $v = 0, 2, 4, \cdots, s-1$ (if $2\nmid s$) or $v = 1, 3, 5, \cdots, s-1$ (if $2|s$). Obviously, we only need to consider the case of $v = 0\; or\; 1$, since the case of $v > 1$ can be obtained simply by splitting some maximal linear double hexagonal chains of $v = 0\; or\; 1$ according to Theorem 3.4, i.e., the case $v > 1$ is covered in the process of splitting $v = 0\; or\; 1$. The following discussion of $v = 0\; or\; 1$: When $v = 0\; or\; 1$, we know that any related sequence of a double hexagonal chain containing $s$ naphthalenes can be written as either $r_1 = r_2 = \cdots = r_u = 3$ or $r_1 = \cdots = r_{i-1} = r_{i+1} = \cdots = r_{u+1} = 3, r_i = 2, i\in[1, u+1]$, then

(ⅰ) For $r_1 = r_2 = \cdots = r_u = 3$, according to Corollaries 3.4 and 3.5, we split $r_u, \; r_{u-1}, \; \cdots r_1$ one by one into $r_{u1} = r_{u2} = 2, \; r_{(u-1)1} = r_{(u-1)2} = 2, \cdots$. Obviously, the Clar covering polynomials get bigger and bigger as we keep splitting them;

(ⅱ) For $r_1 = r_2 = \cdots = r_u = 3, \; r_{u+1} = 2$, it is similar to (ⅰ);

(ⅲ) For $r_i = 2, r_1 = \cdots = r_{i-1} = r_{i+1} = \cdots = r_{u+1}$($i\in\left[2, u\right]$), according to Corollary 3.3, we split $r_{i-1}, \; r_{i-2}, \; \cdots r_1$ one by one into $r_{(i-1)1} = r_{(i-1)2} = 2, \; r_{(i-2)1} = r_{(i-2)2} = 2, \cdots$, then according to Corollary 3.4, we split $r_{i+1}, \; r_{i+2}, \; \cdots r_{u+1}$ one by one into $r_{(i+1)1} = r_{(i+1)2} = 2, \; r_{(i+2)1} = r_{(i+2)2} = 2, \cdots$. Obviously, the Clar covering polynomials get bigger and bigger as we keep splitting them.

To sum up, we can obtain the fact that if the number of naphthalenes in any double hexagonal chain is fixed as $s$, the Clar covering polynomial of the double hexagonal chain $D_{s-1}^2$ is maximum.

According to the analysis as described above, for any double hexagonal chain $HD(r_{n})$ containing $s$ naphthalenes, with related sequences $r_1, r_2, ..., r_n$, splitting any one of the maximal linear chains in $HD(r_{n})$, which makes the Clar covering polynomial of $HD(r_{n})$ larger, the Clar covering polynomial of a double hexagonal chain containing only one maximal linear chain is minimum. Thus, we have the following result:

Theorem 3.6. Let $HD(r_{n})$ be a double hexagonal chain containing $s$ naphthalenes, then $l_s^\alpha$ is the minimum Clar covering polynomial in $HD(r_{n})$.

4.   Conclusions

Hexagonal systems are a typical class of PAHs. The Clar covering polynomial of a hexagonal system, which is also called a Zhang-Zhang polynomial, unifies several important topological indices used in chemistry. Furthermore, the Clar covering polynomial of a hexagonal system can be used to produce a good approximation to the resonance energy of a hexagonal system. In previous research work, we present extreme hexagonal chains with the maximum and minimum values of the Clar covering polynomials. The double hexagonal chain is a special kind of substructure of the peri-condensed hexagonal system. In this paper, we first obtained some recursive formulae for the Clar covering polynomials of double hexagonal chains and proposed a Matlab algorithm to compute the Clar covering polynomial of any double hexagonal chain. Moreover, we presented the characterization of extremal double hexagonal chains with maximum and minimum Clar covering polynomials in all double hexagonal chains with fixed $s$ naphthalenes.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

We are grateful to anonymous referees for a careful reading of the manuscript and many helpful suggestions. This work was supported in part by National Natural Science Foundation of China Grant 12361072 and 11971406; 2023 Xinjiang Uygur Autonomous Region National Natural Science Foundation General Project (2023D01A36); 2023 Xinjiang Uygur Autonomous Region National Natural Science Foundation For Youths (2023D01B48); 2021 Xinjiang Uygur Autonomous Region National Natural Science Foundation Joint Research Fund (2021D01C078); 2022 Special Foundation for Innovation Team Xinjiang Normal University (2022XJNU).

Conflict of interest

The authors declare no conflicts of interest in this paper.