Stochastic assessment of temperature–CO₂ causal relationship in climate from the Phanerozoic through modern times

1.   Introduction

While causality is a fundamental notion in science and life, there also exist fundamental problems on philosophical, scientific and practical grounds, in its essence and its identification ^[1]. These problems are manifested in controversies, which are not only theoretical but have important social, political, and economic implications. Some of the most controversial issues of our time are related to Earth's climate, not excluding the causal relationship between atmospheric temperature (T) and carbon dioxide (CO₂) concentration ([CO₂]). Notice that I denote carbon dioxide as CO₂ and its concentration in the atmosphere, expressed as mole fraction and measured in parts per million (ppm), as [CO₂].

Earth's climate has varied in all times and on all time scales. Its variability should not be regarded a puzzle, given the huge complexity and the connections of the climatic system with numerous agents of change, internal, such as atmospheric composition, hydrological processes, and biosphere evolution, or external, such as geologic activity and tectonic changes, solar activity, galactic cosmic ray flux, and orbital changes. Rather, the puzzling issue is the relative stability (small variation) of Earth's climate. Specifically, geological evidence presented by Veizer ^[2,3,4] suggests the presence of running water as far back as we have a record, up to 3.8 or even 4.2 billion years, while it was thought that Earth would be in an ice ball state up to about 1 billion years ago because of the much smaller solar irradiance. This is known as the faint young sun puzzle. In addition, the carbon isotope record suggests that the fundamentals of the planetary carbon cycle and life may have been established as early as 3.5 billion years ago, which would necessitate the presence of oceans on Earth in turbulent motion.

However, the reconstructed climate information of the long distant past, before the geologic period known as the Phanerozoic eon (541 million years), is unclear. As strange as it may seem, at a time horizon of the order of 100 million years and beyond, even the location and orbit of the Earth become uncertain as the solar system becomes chaotic and unpredictable in such long horizons ^[5,6,7,8,9]. Certain orbital aspects influence climate. The exploration of the latter was pioneered, during the Hellenistic period, by Hipparchus (Ἵππαρχος ὁ Νικαεύς; c. 190–c. 120 BC), who discovered and calculated the precession of the equinoxes (μετάπτωσις ἰσημεριών) by studying measurements on several stars. In the 20th century, this precession would be found to be related to the climate, constituting one of the so-called Milanković cycles, after the Serbian civil engineer Milutin Milanković (1879–1958) ^[10,11,12]. These cycles, i.e., oscillations of the Earth's eccentricity, axial tilt, and precession, are important drivers of climate.

The influence of orbital cycles on climate for the late Quaternary period, namely the last half million years, has been substantial. The relevant research has been pioneered by Hays et al. ^[13], who used three indices of global climate and found agreement of these records with dominant periods of the Earth's solar orbit, namely 23, 42 and approximately 100 thousand years. He concluded that changes in the Earth's orbital geometry are the fundamental cause of the succession of Quaternary ice ages. More recently, Roe ^[14] demonstrated that it is the effect of the Milanković cycles that explains the glaciation process in the Quaternary. To this aim, he effectively used reconstructions of global ice volume during the last 750 thousand years, which relied on measurements of oxygen isotopes incorporated into the shells of foraminifera recovered from deep-sea sediment cores.

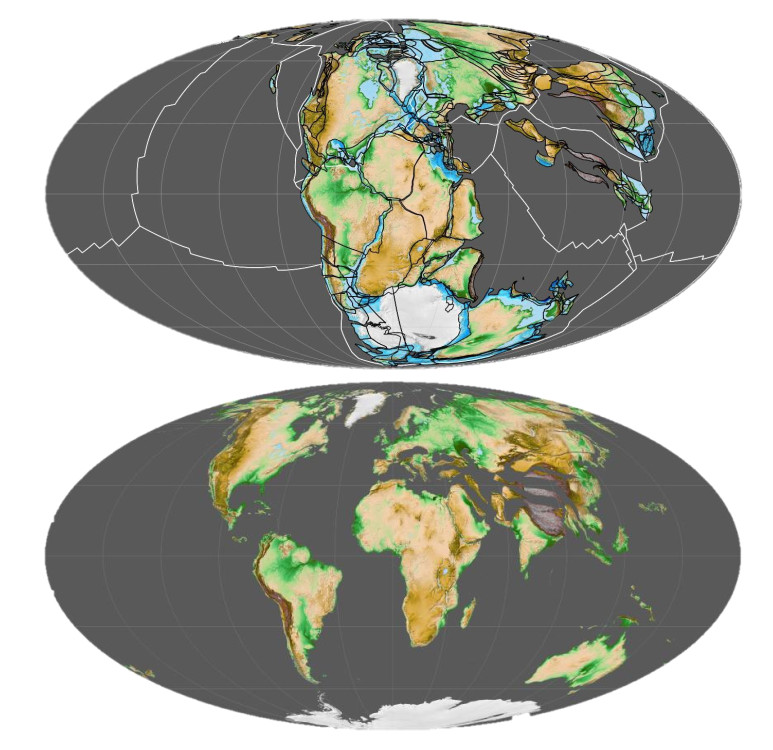
However, if we go further back to the past, to cover the entire Phanerozoic eon, for which reliable reconstructions exist, or merely the Cenozoic era (the last 66 million years), in which the reconstructions have superior resolution and reliability, other climate drivers may become more important. In such a long period, the tectonics play important role, as the Earth's continents and oceans are moving (see Figure 1 for a couple of examples) and clearly the distribution of land and sea on the globe affects climate. In addition, the solar radiation was not constant but rose consistently, with a total 5% increase over the Phanerozoic ^[15]. It is also asserted that the cosmic ray flux has a large effect on the climate and this flux had variations, including a cycle with a period of about 145 million years, corresponding to the passage of the solar system through one of the two sets of spiral arms of the Milky Way ^[15]. Furthermore, life on Earth has evolved and this influenced climate substantially, as the biosphere processes control the chemical synthesis on the atmosphere and the water solvents in the oceans.

Figure 1.  Reconstruction of Earth's continents and oceans in the Phanerozoic eon, (upper) during the Mesozoic era, about 200 million years ago (Pangaea) and (lower) during the Cenozoic era (Eocene epoch), about 40 million years ago (images retrieved, respectively, from https://en.wikipedia.org/wiki/Pangaea#/media/File:Pangaea_200Ma.jpg and https://upload.wikimedia.org/wikipedia/commons/archive/c/c6/20230814125217%2140_Ma_paleoglobe.png, both licensed under the Creative Commons Attribution-Share Alike 4.0 International license).

DownLoad: Full-Size Img PowerPoint

A particular substance in the chemical synthesis of the atmosphere that has been regarded as an essential climate driver is CO₂. It has been generally thought that it is a strong greenhouse gas and its concentration in the atmosphere determines temperature. In the last decades, the observed atmospheric [CO₂] increase was presented as the cause of the (also observed) temperature rise. In addition, the [CO₂] increase in the last century was blamed on human actions, namely the burning of fossil fuels. According to this narrative, which is simplistic and negligent of the huge complexity of the climatic system, humans emit CO₂ by burning fossil fuels, and the emissions accumulate into the atmosphere and increase the greenhouse effect causing increase in temperature. However, it is healthy to question whether these premises and the narrative are valid. Is CO₂ a climate driver or an internal state variable of the climatic system? Does CO₂, with a share of about 5% in the greenhouse effect ^[16], have a decisive role in it? Has the intensity of the greenhouse effect increased in the last century? Have humans become a climate driver by pumping CO₂ into the atmosphere through burning fossil fuels? In particular, is the human share in CO₂ emissions, i.e. 4% of the total, decisive in determining [CO₂]? Or are the biosphere processes, with a share of 96% in emissions, more important than human actions? Does [CO₂] change cause temperature change ($\left[\mathrm{C}{\mathrm{O}}_{2}\right]\to T$), or is the causality direction the exact opposite ($T\to \left[\mathrm{C}{\mathrm{O}}_{2}\right]$) or bidirectional (also known as Hen-Or-Egg; HOE; $T\leftrightarrow \left[\mathrm{C}{\mathrm{O}}_{2}\right]$)?

These questions have been investigated in a number of recent publications ^{[1, 17,18,19,20,21,22,23,24]} and the answers given mostly contradict conventional wisdom. Here I study the last question using proxy data from the Phanerozoic and modern instrumental data, and a stochastic methodology. This question has already been studied in a similar (stochastic) framework ^[1,19,21,22] but here I use a richer data set and I propose some improvements of the methodology.

The question is crucial for the dominant climate narrative and thus, not surprisingly, several works tried to verify the $\left[\mathrm{C}{\mathrm{O}}_{2}\right]\to T$ direction using paleoclimatic reconstructions and with methodologies different from the stochastic framework, but without success. Yet, a study by Shakun et al. ^[25] claimed to have shown "that temperature is correlated with and generally lags CO₂ during the last (that is, the most recent) deglaciation". However, even this claim was for a short period and only for the north hemisphere as the lead-lag relationships were found different for the two hemispheres. Given the unsuccessful attempts to support the $\left[\mathrm{C}{\mathrm{O}}_{2}\right]\to T$ case, other studies sought a synchrony claim, on the basis that the estimated positive lags of $\left[\mathrm{C}{\mathrm{O}}_{2}\right]$ from $T$ are often within the 95% uncertainty range ^[26], that the asynchrony is not significant ^[27], or that a "short lead of CO₂ over temperature cannot be excluded" ^[28].

In a more neutral approach, Berner and Kothavala ^[29] studied the entire Phanerozoic (the last 530 million years) asserting that "over the long term there is indeed a correlation between CO₂ and paleotemperature", and emphasized the "importance of considering ALL factors affecting CO₂ when modelling the long term carbon cycle and not concentrating [on] only one cause". On the other hand, Veizer et al. ^[30] presented evidence for decoupling of atmospheric CO₂ and global climate during the Phanerozoic, questioning the role of the CO₂ as the main driving force of past global (long-term) climate changes, at least during two of the four main cool climate modes of the Phanerozoic. Later, referring to the Cenozoic, Veizer ^[4] asserted that "the temperature signal appears to precede carbon signal, arguing for climate being the cause of variability in the carbon cycle". Referring to the latest one million years, he asserted that "while ice cores demonstrate conclusively that on multimillennial time scales climate and greenhouse gases correlate, they again show that the shifts in climate precede the trends in gas concentrations." For the last 750 thousand years, Roe ^[14] found that "variations in atmospheric CO₂ appear to lag the rate of change of global ice volume. This implies only a secondary role for CO₂ […] in driving changes in global ice volume." For the most recent ~400 thousand years, several studies, based on paleoclimatic reconstructions and mostly the Vostok ice cores (see Section 2.3), have also identified the precedence of temperature change over that in [CO₂], with estimates of the time lag varying from 50 to 1000 years, depending on the time period and the particular study [19, 21, ^[31,32]. Finally, for the recent period covered by instrumental data with monthly time step, the most recent studies by Koutsoyiannis et al. ^[21,22] found a unidirectional, potentially causal link between temperature as the cause and [CO₂] as the effect with time lags of the order of 0.5 to 1 year for time scales from 1 to 16 years, thus corroborating earlier studies with similar findings using different methods ^[33].

Here, as described in Section 2, I use temperature and [CO₂] data series for all these time frames, namely proxy data for the Phanerozoic, the Cenozoic, the late Quaternary and the Common Era, and instrumental data for the last seven decades. In Section 3, I explain the inappropriateness of deterministic methodologies for detecting causality and I adapt the stochastic methodology proposed in ^[1,21] to be used with the above data series. In Section 4, I present in detail the results of the methodology application to each of the data series, which I summarize and further discuss in Section 5. As will be seen in Section 6, these results allow drawing sound conclusions.

2.   Data

2.1.   Phanerozoic

As evident by its name, Phanerozoic (from the Greek φανερός and ζωή, visible life) started with the emergence of complex life forms, followed by the emergence of animals on land, and later was characterized by the rise of flowering plants (angiosperms), and diversification of species, as indicated in Figure 2. Several aspects of life fossils (stomata in leaves, soils) enable broad estimates of temperature and atmospheric carbon dioxide levels. Several reconstructions of T and [CO₂] over the Phanerozoic eon have been recently published. For such very long period, temperature reconstructions are of three types ^[15]: (a) based on lithological indicators of climate, such as coals, evaporites, bauxites, and tillites, which provide information about Earth's past climatic zones (Köppen belts) and the pole-to-equator temperature gradient; (b) geochemical reconstructions that use oxygen isotope measurements of paleotemperature; and (c) combinations of the two. Here, I retrieved four series constructed in the last 5 years, two of category (c), namely those by Scotese et al. ^[34] and Shaviv et al. ^[15] (who also reproduced the series by Scotese et al. ^[34]), as well two of category (b), those by a Grossman & Joachimski ^[35], and Song et al. ^[36]. These four series are depicted in Figure 2, where a general agreement is seen for the last 350 million years, but, earlier than that, the series of isotopic origin show much higher paleotemperatures than the combined ones, almost reaching 50 ℃ at about 500 million years before present (BP). Such high temperatures may not be implausible, as additional evidence shows huge climatic shifts, even for periods more recent than that. For example, for the Cretaceous Period (144–66 million years ago) it was estimated that the average annual low-latitude sea surface temperatures probably reached ~35 ℃, that the global sea level was ~170 m higher than at present and that Antarctica was covered in rainforest ^[37]. Greenland was nearly ice-free for extended periods even in more recent periods, i.e. during the Pleistocene ^[38,39].

Figure 2.  Recent reconstructions of atmospheric temperature and carbon dioxide concentrations over the Phanerozoic eon (541 million years). Sources of temperature series: Scotese et al. ^[34] (after digitization of their figure 17, Global Average Temperature); Shaviv et al. ^[15] (table in Supporting Information and their figure 2); Grossman & Joachimski ^[35] (their figure 4 and supplementary material, table S3, after offsetting by ΔT = –5 ℃ to make it consistent with the other time series, as it originally refers to low latitude); and Song et al. ^[36] (their figure 3 and supplementary material, table S1). Sources of [CO₂] series: Royer ^[43] / Davis ^[44] (figure 5 in Davis ^[44], after digitization); Foster et al. ^[42] / Song et al. ^[36] (figure 1 and supplementary data 2 in ^[42]); Berner ^[45] (their figure 1B, after digitization). For completeness, the divisions of the Phanerozoic into three geological eras and 12 geological periods are shown, along with information on creation events (first appearance of the indicated taxa) and extinction events, with percentages of mean genus loss, taken from references ^[48,49].

DownLoad: Full-Size Img PowerPoint

Atmospheric CO₂ concentrations are most often reconstructed from the GEOCARB model, pioneered by Berner and Kothavala ^[29] and later expanded in the GEOCARB-SULF model to describe the carbon, sulfur, and oxygen cycles, which integrates various proxy measurements of CO₂ ^[40,41]. A compilation of about 1500 discrete estimates of atmospheric CO₂ from 112 published studies covering the last 420 million years, was presented by Foster et al. ^[42]. Here, as shown in Figure 2, I retrieved three different time series published in the last 16 years, namely by Royer ^[43] (also contained in Davis ^[44]), Foster et al. ^[42] (also reproduced by Song et al. ^[36]) and Berner ^[45]. Most of the time series are available at a time step of 1 million years. Thus, for the application in causality assessment, I use this time step for all time series, after converting to that fixed time step those series which are given at different time step using linear interpolation.

The reconstructions of both temperature and [CO₂], depicted in Figure 2, show large variations, while the disagreements among them suggest high uncertainty. Apparently, the uncertainty is not limited to the magnitude of each quantity, but extends also to the dating of each data point. This creates even higher uncertainty in assessing the causality direction, which is the subject of this paper.

The large variations reflect the cosmogonic changes that occurred during the Phanerozoic, both in geology and in the evolution in the biosphere. The former are exemplified in Figure 1, which shows two likely instances of Earth's continents and oceans, indicative of the huge tectonic changes that occurred in the Phanerozoic. Figure 2 also includes the divisions of the Phanerozoic into geological eras and periods. The evolution in the biosphere is epigrammatically noted in Figure 2 in terms of creation and extinction events. New fauna and flora (creation and expansion events) are associated to increase in diversity, which seems to align with an approximately exponential decline of the previously dominant fauna and flora, suggesting possible displacement of each evolutionary species by its successor ^[46].

2.2.   Cenozoic

As seen in Figure 2, Cenozoic is the latest geological era, which began about 66 million years ago. It has been a dynamic period marked by the dominance of mammals and birds, changes in vegetation and shifts in ecosystems. Some of these changes are marked in Figure 3. On the other hand, the continents assumed their modern configuration (see Figure 1, lower). These conditions have allowed reconstruction of climate records with superior resolution and reliability.

Figure 3.  Recent reconstructions of the isotopic ratio δ¹⁸O, which is a temperature proxy with the indicated temperature scale, and [CO₂] over the Cenozoic era (66 million years). Data for temperature are from Westerhold et al. ^[47] (available online in their Supplementary Material https://www.science.org/doi/suppl/10.1126/science.aba6853/suppl_file/aba6853_tables_s8_s34.xlsx; Table S34; column "ISOBENd18oLOESSsmooth"), and for [CO₂] from Rae et al. ^[50] (available online in their Supplemental Material, https://www.annualreviews.org/deliver/fulltext/earth/49/1/ea49_rae_suppl_data1.xlsx; columns "xco2_84pc" and "co2" for alkenones and boron isotopes, respectively, after merging). For completeness, the divisions of the Cenozoic era into three geological periods and seven geological epochs are shown, along with information on creation events (first appearance of certain families or species) and extinction events, with percentages of mean genus loss, taken from references ^[48,49].

DownLoad: Full-Size Img PowerPoint

Continuous composite astronomically dated climate reconstructions have been presented by Westerhold et al. ^[47] based on oxygen and carbon isotope variations in deep-sea benthic foraminifera (single-celled amoeba-like organisms, producing calcite shells, widely used in environmental reconstruction). The reconstructions are available online; here, I retrieved the oxygen-18 (δ¹⁸O) time series, which is a temperature proxy.

For [CO₂], Rae et al. ^[50] compiled paleo reconstructions from marine archives based on carbon isotopes in alkenones (long-chain unsaturated ethyl and methyl ketones, commonly used as biomarkers in sediments) and boron isotopes in foraminifera. Both sources of information, as shown in figure 6c in ^[50], are retrieved and used here.

Both δ¹⁸O and [CO₂] reconstructions are depicted in Figure 3. For better understanding, a temperature scale has also been drawn, by transforming δ¹⁸O to temperature based on the Epstein et al. ^[51] formula. It is noted that Rae et al. ^[50], who also used the Westerhold et al. ^[47] reconstructions, converted δ¹⁸O to temperature (their figure 6a) using a different algorithm and found somewhat lower temperatures than those inferred from the temperature scale of Figure 3. However, here I use the δ¹⁸O time series per se (multiplying it by –1) without conversion.

It is noted that in the [CO₂] time series, the time distance between consecutive samples is highly variable, with an average of 73 thousand years, while this is much lower for the δ¹⁸O time series. Based on this, for the application to assessment of causality I chose a fixed time step of 100 thousand years and I performed linear interpolation to convert the two time series from irregular to regular time step.

2.3.   Late Quaternary

As seen in Figure 3, Quaternary is the most recent of the three geologic periods of the Cenozoic era, which spans from 2.58 million years ago to the present. Due to the relatively lower temperatures during it, also seen in Figure 3, ice has been permanent at least in Antarctica for the latest part of it. This enabled better climatic reconstructions from ice cores in Antarctica. Here, I use the Vostok ice core data, which include both temperature and [CO₂] ^[52,53] and whose dating studies have been most extensive.

The two time series go back to about 420 000 years before present (more precisely, before 1950) and, as seen in Figure 4, are strongly correlated to each other. They are originally given at an irregular time step, which needs to be regularized for causality assessment. The time steps are quite different for the two series. Namely, the average time step for the T and [CO₂] time series are ~128 and ~1150 years, respectively. It must be noted that the age of the gas (air bubbles) at a certain ice layer differs from the ice age. Specifically, the air extracted from the ice is younger than the surrounding ice. Extensive studies to date the air with respect to ice by Barnola et al. ^[54] concluded that "the age difference between air and ice is about 6000 years during the coldest periods instead of about 4000 years, as previously assumed". Indeed, in the data provided online, the difference between the ice and air age is about 6000 years for the coldest periods, decreasing to about 2000 years for the hottest periods and averaging at a difference of ~4070 years. Naturally, in the calculations for the CO₂ time series the air age is used, as given in the publicly available data series.

Figure 4.  Time series of temperature and CO₂ concentration from the Vostok ice core, retrieved, respectively, from http://cdiac.ess-dive.lbl.gov/ftp/trends/temp/vostok/vostok.1999.temp.dat and from http://cdiac.ess-dive.lbl.gov/ftp/trends/co2/vostok.icecore.co2.

DownLoad: Full-Size Img PowerPoint

The regularized time step was initially chosen at 1000 years, i.e., close to the average time step of the original [CO₂] time series. After a detailed investigation, it was seen that in the period from 100 to 300 thousand years BP, the data are denser in time, with an average time step of about 800 years which goes down to 500 years for some subperiods. Therefore, I also constructed a second couple of time series with time step of 500 years spanning the period 100 to 300 thousand years BP.

2.4.   Common Era

The climate variations in the last two millennia (a period known as "Common Era") have been intensively studied and, at the same time, have been one of the most controversial issues of the last decades. Here, I include this period in the analyses for its wide interest, albeit expecting high uncertainty in the results due to the controversy and the reasons behind it.

In their recent review paper, Christiansen and Ljungqvist ^[55], reproduced 18 reconstructions covering the last two millennia in part or completely (their figure 1). Of those, here I used the three reconstructed series that are (almost) complete for the entire Common Era. Specifically, these are those by Moberg et al. ^[56], who combined low-resolution proxies with tree-ring data, Loehle and McCulloch ^[57], who used non-tree-ring data that had been previously calibrated and converted to temperature by other authors, and Christiansen and Ljungqvist ^[58], who used different types of proxies and of different resolutions, from annual to decadal. As seen in Figure 5 (upper), the three series differ substantially from each other, in magnitude, resolution and smoothing.

Figure 5.  (upper) Temperature reconstructions of the last two millennia from the indicated studies. All series are available online in tabulated form and were retrieved from the following sources: Moberg et al. from ^[56] (Supplementary Information); Loehle and McCulloch ^[57] from https://www.asc.ohio-state.edu/mcculloch.2/AGW/Loehle/LoehleMcC.txt, and Christiansen and Ljungqvist ^[58], from ^[74]. (lower) Reconstruction of paleo-atmospheric CO₂ levels based on stomatal frequency analysis and ice cores. The stomata-based data by Kouwenberg ^[63] (thick blue line) are extracted by digitizing figure 6.3 of that study and are checked to be in agreement (with small differences in dating after 1500 AD) with Figure 3 of Kouwenberg et al. ^[64]; the standard errors (shaded orange area) are extracted by digitizing figure 5.4 of ^[63]. The stomata-based data by van Hoof et al. were taken from Table S1 of ^[65]. The ice core data of Indermühle et al. ^[59] and Etheridge et al. ^[60] were digitized from figure 5.4 of ^[63]. The ice core data by Francey et al. (post 1976, not contained in ^[63]) are taken form ^[61] (table 2). The ice core data were also cross-checked with figure 4 of Böhm et al. ^[62].

DownLoad: Full-Size Img PowerPoint

Reconstructions of paleo-atmospheric CO₂ levels based on ice core data from Antarctica (Indermühle et al. ^[59] and Etheridge et al. ^[60]; Francey et al. ^[61]; Böhm et al. ^[62]), show a rather stable [CO₂] except after 1800 AD, when it started to increase. However, a [CO₂] reconstruction based on stomatal frequency analysis (namely, of buried Tsuga heterophylla needles) by Kouwenberg ^[63] reveals significant centennial-scale atmospheric CO₂ fluctuations. Some of the data from ^[63] are also reproduced in Kouwenberg et al. ^[64], namely the data post 800 AD, even though in the original figure in ^[63] they start at 200 AD; the reasons are not explained but perhaps can be guessed by viewing Figure 5 (lower), which reproduces them. An additional stomata-based reconstruction for the period 1000–1500 AD presented by van Hoof et al. ^[65] also shows fluctuation (albeit smaller than Kouwenberg's) and disagreement with the ice core data. The agreements and disagreements of all these data series are shown in Figure 5. Additional ice core data but from Greenland ^[66,67], not contained in Figure 5, show much higher variation with respect to the Antarctica data. For completeness, it is noted that stomata-based reconstructions, presented for other periods of the Holocene prior to the last two millennia ^{[68,69,70,71,72,73]} (not shown in Figure 5) also present high variation.

2.5.   Modern Period of instrumental data

Systematic instrumental observations of hydrometeorological processes, which apparently provide the highest quality data, start from the 19^th century. Based on them, several series of globally averaged temperature from instrumental measurements have been compiled. However, systematic measurements of [CO₂] are available only from the late 1950s. Therefore causality analysis based on those data cannot start before that time.

Several temperature time series, from ground stations, reanalyses, and satellites have been used in predecessor related studies ^[19,21,22]. Here, I use gridded reanalysis data, namely those of the ERA5 reanalysis ^[75]. This is the fifth-generation atmospheric reanalysis of the European Centre for Medium-Range Weather Forecasts (ECMWF), where the name ERA refers to ECMWF ReAnalysis. The observation period spans from 1940 onward, with daily updates continuing forward in time. The fields are available at a horizontal resolution of 31 km on 139 levels, from the surface up to 0.01 hPa (around 80 km). It has been produced as an operational service and its fields compare well with the ECMWF operational analyses. ERA5 provides hourly estimates of a large number of atmospheric, land and oceanic climate variables. ERA5 combines vast amounts of historical observations into global estimates using advanced modelling and data assimilation systems. The data are available for the period 1950-now at a spatial resolution of 0.5° globally.

For CO₂ concentration, here I use monthly data for two stations, compiled by the US National Oceanic and Atmospheric Administration (NOAA) and the Scripps CO₂ Program of the Scripps Institution of Oceanography, University of California ^[76]. These are the Mauna Loa Observatory, Hawaii (19.5° N, 155.6° W, 3397 m a.s.l.) and South Pole (90.0° S, 2810 m a.s.l.). The former I pair with the globally averaged temperature and the latter with averaged temperature both over the globe and over the southern hemisphere. The time series used in the analyses are depicted in Figure 6.

Figure 6.  (upper) Temperature and [CO₂] time series based on instrumental observation for the indicated cases. The temperature data from the ERA5 reanalysis were retrieved and spatially aggregated through the ClimExp platform (the Climate Explorer of the Dutch Royal Netherlands Meteorological Institute—KNMI; ^[86]). The [CO₂] data were retrieved from the Scripps CO₂ Program, which made them available online ^[87].

DownLoad: Full-Size Img PowerPoint

2.6.   A note on varying time scales

It has been a (misleading) common practice to merge data of different time resolutions, without considering the essential differences among them, which prohibit merging. For instance, we see graphs merging instrumental data at annual or monthly time scale with paleoclimatic data at a timescale of hundreds or thousands of years. This has been practiced by most political organizations (e.g. the Word Economic Forum ^[77]), by news portals (e.g. The Conversation ^[78]), by scientific organizations (e.g. NASA ^[79]), and is also sometimes reproduced in scientific literature (e.g. ^[80]).

To illustrate how problematic the mixing of different time scales is, we need a very large time series of measurements. Such time series are available from laboratory experiments of turbulent velocity, measured at a high frequency, so that very large samples be formed. Here, I use grid data of nearly isotropic turbulence from the Corrsin Wind Tunnel at a high-Reynolds-number ^[81], which were made available on the Internet by the Johns Hopkins University ^[82]. This rich dataset consists of 40 time series with 36 × 10⁶ data points of wind velocity along the flow direction and an equal number of time series of cross-stream velocity, all measured at a frequency of 40 kHz (sampling time interval D = 25 µs). Here I use part of the data, namely 1.2 × 10⁶ data values at a single point (the first of the probes) along the flow direction, averaged at D = 1 ms, so that each value be the average of 40 original consecutive measurements and the length of the time series be 30 000. Like the temperature and [CO₂] time series, the turbulent velocity time series exhibits long range dependence, else known as Hurst-Kolmogorov (stochastic) dynamics ^[83,84,85]. The latter term describes the tendency of high or low values of natural events to group. This behavior is more commonly perceived as "trends" or "shifts" in a process, but a more scientific perception is offered by stochastics, through the notions of the long-range dependence and clustering of similar events.

The illustration is seen in Figure 7, where six time scales have been used, from 1 to 1024 ms, along with two methods of scale aggregation, sampling (i.e., taking the original series value at the time instance corresponding to the coarser scale) and averaging (i.e. taking the average of original series values at the coarser scale). As seen in the figure, the coarser scale series do not correspond to the one at the smallest scale. Even in the case of sampling, the variability of the original series is lost, as the highest (and less frequent) values are more likely to disappear due to coarse scale sampling. This worsens in the case of averaging, in which the shape of the coarse-scale series tends to be flat. Some small variability continues to appear at the coarse scale, but this is purely due to the Hurst-Kolmogorov dynamics.

Figure 7.  A long turbulent velocity time series, plotted for varying time scales, from 1 to 1024 ms, with each increased one being a quadruple of the immediate smaller time scale; (upper) the first 1500 terms; (lower) 30 000 terms. The information in red, followed by the arrows, is the scale of data aggregation.

DownLoad: Full-Size Img PowerPoint

The situation in climate proxies resembles the case of averaging, because of the diffusion that occurs, particularly when the proxies originate from ice cores ^[88]. In this case, the situation can be even worse than seen in Figure 7, as the diffusion time scale could be even coarser than the nominal time averaging time scale. For these reasons, in the analyses that follow I do not merge time series of different scales originating from different construction methods.

3.   Methodology

3.1.   The inappropriateness of deterministic methodologies

Commonly, the methods to identify time precedence between two related processes, and thus infer the causality direction, are deterministic. As an example, Shakun et al. ^[25] and Humlum et al. ^[33] use the terms "phase" or "phasing" as if the two processes (T and [CO₂]) were harmonic oscillators, while clearly their evolution is irregular, only describable as stochastic processes with complex structure, including Hurst-Kolmogorov dynamics. Using Monte Carlo simulation (as Shakun et al. did), e.g., for testing statistical significance of lags, does not make the methodology non-deterministic, once its fundamental characteristic in identifying these lags is based on peaks, troughs, or trends in time series.

To show the inappropriateness of the deterministic setting, two independent synthetic time series are used, ${x}_{\tau }\;\mathrm{a}\mathrm{n}\mathrm{d}\;{v}_{\tau }$ of 1000 terms each (plus some necessary redundant terms), generated from the Hurst-Kolmogorov model ^[85] with Hurst coefficient $H = 0.95$. Then, a third time series ${y}_{\tau }$ is calculated as follows:

where

Clearly, the system (${x}_{\tau }, {y}_{\tau })$ is causal with causality direction $x\to y$, as ${y}_{\tau }$ depends only on past terms of ${x}_{\tau }$. This will be explained better in Section 3.2, while a graphical depiction of ${g}_{j}$ will also be given in that section (Figure 9).

However, by merely inspecting the time series following a deterministic approach that looks for "phasing" in time series through trends, peaks and troughs, is misleading and inappropriate. This is illustrated in Figure 8. It is more likely to see sequences like the ones shown in the left column of Figure 8, which correctly reflect the true causality. However, sequences like the ones shown in the right column, which indicate reverse causality, are possible. This does not mean that the causality was indeed reversed: All terms of the time series were generated by the same causal system ${x}_{\tau }\to {y}_{\tau }$. It just means that irregular time series cannot be treated deterministically. Furthermore, the example shows that with a proper choice of a particular time frame, such as that in the right panel of Figure 8, and with deterministic thinking helped by good imagination, one can draw conclusions opposite to reality.

Figure 8.  Two groups of consecutive values of time series from a causal system ${x}_{\tau }\to {y}_{\tau }$, each consisting of 30 items, for illustrating the inappropriateness of a deterministic approach that looks for "phasing" in time series through (upper) trends, visualized as dashed double-line arrows with same color as the time series they refer to, and (lower) peaks and troughs, with successions visualized by red and green arrows, respectively. (left column) A group of 30 terms preserving the correct time precedence of ${x}_{\tau }$ over ${y}_{\tau }$; (right column) a group of 30 terms incorrectly suggesting the reverse time precedence.

DownLoad: Full-Size Img PowerPoint

3.2.   Stochastic methodology

The stochastic methodology used here for identifying potential causal links was developed in ^[1,21,22] and is based on the impulse response function (IRF) between two stochastic processes $\underline{x}\left(t\right), \underline{y}\left(t\right)$, denoted as $g\left(h\right)$ where $h$ denotes time lag, based on the convolution:

where $\underline{v}\left(t\right)$ is another stochastic process representing the part that is not explained by the causal link. Notice that the Dutch notational convention is used, in which stochastic variables and processes are underlined, while common variables and functions are not.

To see that the function $g\left(h\right)$ is the impulse response function (IRF) of the system ($\underline{x}\left(t\right), \underline{y}\left(t\right)$), we set $\underline{v}\left(t\right)\equiv 0$ and $\underline{x}\left(t\right) = \mathrm{\delta }\left(t\right)$ (the Dirac delta function, representing an impulse of infinite amplitude at $t = 0$ and attaining the value 0 for $t\ne 0$), and we readily get $\underline{y}\left(t\right) = g\left(t\right)$. On the other hand, if we set $g\left(h\right) = b\mathrm{\delta }(h-{h}_{0})$ (with constant $b$ and ${h}_{0}$), which means that the IRF is zero for every lag except for the specific lag ${h}_{0}$, then equation (1) becomes $\underline{y}\left(t\right) = b\underline{x}\left(t-{h}_{0}\right)+\underline{v}\left(t\right)$. This special case is equivalent to simply correlating $\underline{y}\left(t\right)$ with $\underline{x}\left(t-{h}_{0}\right)$ at any time instance $t$. It is easy to find (cf. linear regression) that in this case the multiplicative constant $b$ is the correlation coefficient of $\underline{y}\left(t\right)$ and $\underline{x}\left(t-{h}_{0}\right)$ multiplied by the ratio of the standard deviations of the two processes. In general, however, we expect that the actual $g\left(h\right)$ is not a Dirac delta function but a continuous one over some domain. Thus, the IRF is a much more powerful tool than correlation, as it integrates the correlations in the entire spectrum of lags.

In applications, the continuous time representation is replaced by a discrete time one, with a time step Δ, the IRF becomes a sequence of values ${g}_{j}$, where $j$ denotes the time lag, the infinite range of the time lag $h$ becomes a finite window of time lag $j$, specified in the interval $[L, U]$ (the lower and upper computational lag, respectively), the integrals are replaced by sums, and the true values of statistics are replaced by estimates. Specifically, the discrete time version is

and the conversion from continuous to discrete time is described in ^[1].

For any two processes ${\underline{x}}_{\tau }$ and ${\underline{y}}_{\tau }$, Equation (4) has infinitely many solutions in terms of the sequence ${g}_{j}$, and the process ${\underline{v}}_{\tau }$. An obvious and trivial one is ${g}_{j}\equiv 0, {\underline{y}}_{\tau }\equiv {\underline{v}}_{\tau }$. The sought solution is the one that corresponds to the minimum variance of ${\underline{v}}_{\tau }$ called the least-squares solution. Equivalently, this solution maximizes the explained variance ratio:

where ${\gamma }_{\upsilon }$ and ${\gamma }_{y}$ denote the variances of the processes ${\underline{v}}_{\tau }$ and ${\underline{y}}_{\tau }$, respectively. (This is similar as in correlation at a single time lag.) If the attained maximum $e$ is close to zero, this will mean that the two processes are uncorrelated and thus no causality condition can exist between them (non-causal system). Otherwise, we may assume, without loss of generality, that processes ${\underline{x}}_{\tau }$ and ${\underline{y}}_{\tau }$ are positively correlated, i.e., an increase in ${\underline{x}}_{\tau }$ would result in an increase in ${\underline{y}}_{\tau }$. In the opposite case (if the processes are negatively correlated) we multiply one of the two by $-1$. Therefore, we impose a nonnegativity constraint for the sought IRF,

In the estimation of IRF, we may also impose a roughness constraint,

where E is the roughness of the IRF determined in terms of the second difference of ${g}_{j}$, ${\mathrm{\Delta }}^{2}{g}_{j}$:

Further justification for the two constraints is provided in ^[1]. The roughness $E$ can be standardized as

where ε ranges in (0, 1) for nonnegative ${g}_{j}$. The determination of the IRF ordinates ${g}_{j}$ is thus formulated as a constrained optimization problem, whose numerical solution is always possible, simple and fast, and can be attained even by commonly available solvers, e.g., in commercial or open-source spreadsheet software. By choosing a proper multiplier $\lambda > 0$ (which can be adjusted in a trial-and-error fashion, until an acceptable smoothness is attained), we can simplify the optimization problem to:

The total number of unknowns ${g}_{j}$ is $N≔U-L+1$, where we assume that $L\le 0\le U$. Depending on the results of the estimation procedure, if $e$ is non-negligible, the system is deemed:

● potentially HOE causal if we have ${g}_{j} > 0$ for both some positive and some negative lags j,

● potentially causal if ${g}_{j} = 0$ for all $j < 0$, and

● potentially anticausal if ${g}_{j} = 0$ for all $j > 0$.

These three cases are graphically illustrated in Figure 9. The adverb "potentially" in the above characterizations highlights the fact that the conditions tested provide necessary but not sufficient conditions for causality.

Figure 9.  Explanatory sketch for the definition of the different potential causality types. For each IRF curve, the mean ${\mu }_{h}$ is also plotted with dashed line. (Reproduced from ^[22] licensed under Creative Commons Attribution).

DownLoad: Full-Size Img PowerPoint

In a potentially causal (or anticausal) system, the time order is explicitly reflected in the above characterizations. In a potentially HOE causal system the time order needs to be clarified by defining the principal direction. The most natural indices for this are:

1. The time lag $h = {h}_{\mathrm{c}}$ maximizing the (absolute value of) cross-covariance ${c}_{yx}\left(j\right)$.

2. The mean (time average) of the sequence ${g}_{j}$, defined as:

3. The median ${h}_{1/2}$ of the sequence ${g}_{j}$, implicitly defined by:

where linear interpolation between consecutive $j$ may be required to specify ${h}_{1/2}$.

It is noted that ${h}_{\mathrm{c}}$, is fully independent from ${g}_{j}.\;\mathrm{T}\mathrm{h}\mathrm{e}\;\mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\;\mathrm{t}\mathrm{w}\mathrm{o}, {\mu }_{h}$ and ${h}_{1/2}$, depend on the sequence ${g}_{j}$ that is determined. However, extensive analyses in ^[1] showed that their estimation is quite robust; for example, the use of the roughness constraint, while affecting the resulting sequence ${g}_{j},$ has little impact on the values of ${\mu }_{h}$ and ${h}_{1/2}$. Usually, the characteristic lags ${\mu }_{h}$ and ${h}_{1/2}$ do not differ substantially from each other and any of them could be chosen for further use. Here I prefer to note both, as well as ${h}_{\mathrm{c}}$, as they all provide useful information about the relationship of the two processes (like in the case of using mean, median and mode, in the characterization of the probability distribution of a single stochastic variable).

In estimating the sequence ${g}_{j}$, parsimony requires that the number of unknowns N be as small as possible. On the other hand, a small N may not be appropriate to properly reconstruct the IRF. To resolve this conflict, we may keep using a small N and extend the time length of the IRF using an integer multiplier $m\ge 1$. In this case we modify Equation (4) as follows:

with values ${g}_{j}^{{'}}$ determined from ${g}_{j}$ as specified in Appendix A. The multiplier m should not be large, otherwise the number of values of ${\underline{y}}_{\tau }$ and ${\underline{v}}_{\tau }$ remaining to estimate their variances becomes too low (for example, it can be verified from Equation (13) that if $m > n/U$, where n is the length of the available time series, then no item ${y}_{\tau }$ can be estimated).

Furthermore, the time scale of analysis, k, should not necessarily be identical to the computational time step, Δ. The ratio $l≔\varDelta /k$ is thus another multiplier referred to the time series, instead of the IRF. For example, if the data values are given on a monthly time step, but the analysis is made for the annual scale, then $l = 1/12$.

In all applications here, I use $N = 21, L = -20, \dots 0, m\in \left\{\mathrm{1, 4}\right\}, l\le 1,$ where the exact value of $l$ depends on time scale of analysis and the discretization step of the data. When $L = 0$, we have a potentially causal system as all ${g}_{i}$ for $i < 0$ are zero. In contrast, when $L = -20$, we have a potentially anticausal system. In all other values of L we have a potentially HOE causal system. By sliding the window of length $N = 21$ with the lower computational lag L moving from –20 to 0, we determine the explained variance in each of the cases and finally we keep as final L that which yields the highest explained variance. If that is $L = 0$, the system is deemed potentially causal, if $L = -20$, it is deemed potentially anticausal, and in all other cases it is deemed potentially HOE causal.

It is further noted that, given the two processes, each of the directions $x\to y$ and $y\to x$ can be investigated separately as there is no symmetry (or antisymmetry) in the produced IRFs in the two directions. When we refer to direction $y\to x$ we mean that we interchange the time series $x$ and $y$ and estimate the IRF in the same way, as described in the above equations in which the direction $x\to y$ is assumed. As stated, the method is linear, but nonlinear extensions are possible and will be discussed later (see also ^[21,22]).

As detailed in ^[21,22], there exist a variety of other methods for estimating IRF and for inferring causality but our method differs conceptually and computationally from them, including from the so-called "Granger causality" ^[89,90] and the framework proposed by Pearl and collaborators ^[91,92,93].

3.3.   A synthetic example for assessing the behavior of the method

As an illustration of the method, we may use the synthetic example already introduced in Section 3.1, but now using the stochastic method instead of the inconsistent deterministic approach. The true system is causal and the true IRF function extends to lags up to 30, but here it is attempted to recover it with only 21 time lags, with $L$ varying from –20 to 0 and $U = L+20$ varying from 0 to 20. The results of the method are shown in Figure 10, for both directions $x\to y$ (the correct one, with the true IRF of a triangular shape shown in the upper left panel of Figure 10) and $y\to x$ (the incorrect one).

Figure 10.  An example of the application of the methodology with a couple of related time series exhibiting Hurst-Kolmogorov dynamics, generated from a causal system $x\to y$ with true IRF of a triangular shape shown in the upper left panel. (upper row) Reconstruction from the data of the system $x\to y$; (lower row) application of the method for the reverse system $y\to x$. (left column) Estimated IRFs for the indicated lower computational lag, L (marked at the high end of each curve); (right column) explained variance and characteristic time lags (mean, median and cross-correlation maximizing) as functions of the lower computational lag, L; the true characteristic time lags are also plotted in the upper-left panel.

DownLoad: Full-Size Img PowerPoint

For the system $x\to y$ and lower computational lag $L = 0$ (the true one), the method produces a good approximation of the true IRF, but the exact recovering is impossible as the time coverage (20 time steps) is smaller than the true one (30 time steps). The higher estimated ${g}_{j}$ ordinates, in comparison to the true ones, are due to the reduction of the true time coverage. As seen in the upper right panel, for $L = 0$ the method approximates well the true characteristic lags, mean (${\mu }_{h}$) and median (${h}_{1/2}$). The cross-correlation maximizing lag and is not well reproduced, but this is independent of the produced IRF and is related to the high Hurst parameter, which creates high statistical uncertainty. The explained variance for $L = 0$ is very high, about 0.7.

As we decrease the lower computational lag $L$, the shape of the IRF no longer corresponds to the true one but assumes a high value at the rightmost end. This is expected, because it has to substitute the limited information due to the decrease of the time coverage. Expectedly, the explained variance is reduced, and so are the characteristic time lags. At the lowest computational lag $L = -20$, the performance becomes bad in all aspects, as it should. As a result of the application, we correctly recover the fact that the system we deal with is causal and we keep as final IRF that of the causal system, with $L = 0$.

Figure 10 also shows the case where we incorrectly assumed that the causality direction was opposite, $y\to x$. In this case, all evidence depicted in the lower row of Figure 10, whose behavior is opposite to that of the upper row, is convincing that that system ($y\to x$) is anticausal, as actually is.

One may wonder why even for bad choices, e.g. for $L = -20$ in the direction $x\to y$ or in any L in the direction $y\to x$, we have some positive explained variance. The answer to this question is not difficult. It is the high autocorrelation, which results in some explained variance, as any value in a time series contains some information about its close neighbors due to time dependence.

A further behavior of IRFs seen in Figure 10, which needs to be discussed, is the appearance of high tails on the left or the right end of IRFs. Such tails are inconsistent with the (a priori known in this case) true shape of the IRF. Their appearance is an indication that the assumed time frame of the IRF is narrower than required for its faithful representation. Another factor that we should consider in the explanation of the high tails is the fact that the second derivative is not defined in the end points of the IRF and hence these do not contribute to the roughness, which in the other points is constrained.

Overall, the example illustrates the fact that the method has excellent performance and a reasonable behavior, as it provides information on how successful the potential causality identification is and what the potential caveats can be.

4.   Results

4.1.   General notes for the real-world applications

Section 4 presents the application of the method to the real-world cases for identifying causality between temperature and [CO₂] using the data described in Section 2. In cases where the time series were given in an irregular time step, this had to be regularized before the application, which was done by linear interpolation. The appropriate time steps have already been discussed in Section 2. In all cases, the time series after interpolation were visually checked against the original series and no visual differences appeared. In addition, an alternative approach was also tried, the closest time estimation. In the latter, we estimate the unknown value at a specific time using the value of the given time series at the date closest to this specific time (without doing any calculation). We applied the same algorithm with these alternative time series and the results were virtually indistinguishable, which means that they are practically indifferent to the type of interpolation.

As explained in earlier studies ^[19,21,22], before the application, the [CO₂] time series has to be transformed by taking the logarithms. This is justified by the old rule by Arrhenius ^[94], who stated that "if the quantity of carbonic acid increases in geometric progression, the augmentation of the temperature will increase nearly in arithmetic progression" and, more recently, by showing that the changes in longwave radiation in the atmosphere are almost linearly correlated with the logarithm of [CO₂] ^[16]. In several initial applications both directions, $T\to \left[{\mathrm{C}\mathrm{O}}_{2}\right]$ and $\left[{\mathrm{C}\mathrm{O}}_{2}\right]\to T$ were tried but only the former is presented, as the latter did not provide useful results. As an exception, just for illustration, in one of the cases the application for the latter direction is also presented (namely, in Figure 22). Results in which the maximum achieved explained variance is higher than 0.1 are presented, as those with lower than this are deemed insignificant. Applications in which the cross-correlations between $T$ and $\left[{\mathrm{C}\mathrm{O}}_{2}\right]$ are negative, even for small lags, are omitted. Negative cross-correlations are interpreted as suspected errors in the data, or suggesting time series inconsistent with each other, possibly due to errors in dating. Yet in all families of data presented in Section 2, at least one pair of time series was found which yielded positive cross-correlations and allowed application of the method.

The results are presented graphically for the causality direction $T\to \left[{\mathrm{C}\mathrm{O}}_{2}\right]$ and occasionally those of the direction $\left[{\mathrm{C}\mathrm{O}}_{2}\right]\to T$ are referred to. In all cases, the method with gradually increasing lower computational lag L from –20 to 0 is applied and the particular value that yields the highest explained variance, e, is located. For a fair comparison the same time frame for all values of L must be used. This means that, if the time spans from 1 to n, the comparison is made for the data points in a time frame spanning $20m$ to $n+1– 20m$, where m is the time step multiplier (1 or 4 in our case).

One important issue that should be kept in mind is related to the very high autocorrelations, which appear, particularly in the $\left[{\mathrm{C}\mathrm{O}}_{2}\right]$ series. As high autocorrelation increases uncertainty in the long term, this is a major case leading to false identification of potential causality. This problem was discussed in ^[19,21] and illustrated in the electronic supplementary material of ^[21], along with the technique to handle such situations and avoid false conclusions. Specifically, the appropriate technique is to difference the time series, so as to investigate the changes of the related processes, rather than the processes per se. Differencing reduces the autocorrelations substantially and thus avoids spurious results but has the disadvantage of reducing the explained variance.

Figure 11 shows the empirical autocorrelation functions of the $\left[{\mathrm{C}\mathrm{O}}_{2}\right]$ series, original and differenced. In the instrumental series, the autocorrelations are almost 1, even for lags as high as 100. This prohibits any inference from the original series. However, their differenced series have reasonable positive autocorrelations, which make inference possible. The proxy series have high autocorrelations at small lags, but reasonable ones at large lags. For those, both the original and the differenced series are examined, provided that the latter are positive.

Figure 11.  Autocorrelation functions of [CO₂] series: (left) original; (right) differenced. The differenced series autocorrelation for Cenozoic is not plotted as it is mostly negative. The time lag is in discrete time j, i.e. dimensionless, and, to make it dimensional, we should multiply by the time step Δ of each series ($h = j\varDelta$).

DownLoad: Full-Size Img PowerPoint

4.2.   Proxy data

For the Phanerozoic series, the pair that gives positive cross-correlations for both the original and the differenced versions consists of the Grossman & Joachimski ^[35] temperature series and Berner ^[45] [CO₂] series. The application of the method to these data in the direction $T\to \left[{\mathrm{C}\mathrm{O}}_{2}\right]$, both with the original and the differenced time series, is shown in Figure 12. The original series, while yielding a high explained variance (~0.62), it does not help to discern causality as this explained variance is almost independent of the lower lag L. However, the differenced series clearly suggests that we have a potentially causal system, as the explained variance is maximized for $L = 0$, even though it is lower (0.27), as expected. In addition, the more physically consistent shape of the IRF in the case $L = 0$, supports the conclusion of a potentially causal system. Additional support is provided by the results of the reverse system, $\left[{\mathrm{C}\mathrm{O}}_{2}\right]\to T$, not shown in the figure. In this, the explained variance for the system with the original series is maximized for $L = -20$ with an attained value of 0.55, suggesting an anticausal system. The differenced process results in virtually zero explained variance for all values of L for the system $\left[{\mathrm{C}\mathrm{O}}_{2}\right]\to T$.

Figure 12.  Application of the methodology to the Phanerozoic data (Grossman & Joachimski ^[35] series for temperature and Berner ^[45] for [CO₂]). (upper row) Original series; (lower row) differenced series. (left column) Estimated IRFs for the indicated lower computational lag, L (marked at the high end of each curve); (right column) explained variance and characteristic time lags (mean, median and cross-correlation maximizing) as functions of the lower computational lag, L.

DownLoad: Full-Size Img PowerPoint

It is relevant to note that Davis ^[44], analyzing different time series, namely those of Prokoph et al. ^[95] for temperature and Royer ^[43] for [CO₂], and different methodology, i.e., "detrending" the time series and examining transitions, found different results. Specifically, he found that [CO₂] is correlated weakly but negatively with linearly-detrended T proxies over the last 425 million years. He stated that of 68 correlation coefficients between CO₂ and T proxies encompassing all known major Phanerozoic climate transitions, 77.9% are non-discernible (in terms of their statistical significance, i.e., $p > 0.05$) and 60.0% of discernible ($p < 0.05$) correlations are negative. In a later publication, Davis ^[49] also reported discernible and negative correlation (r = −0.76) between the same CO₂ and T proxies, but for a small segment of the record, namely the Cretaceous-Paleogene mass extinction period.

The results for the Cenozoic are shown in Figure 13, which refers to the analysis of the original series in the direction $T\to \left[{\mathrm{C}\mathrm{O}}_{2}\right]$, where the values of –δ¹⁸O were used as a proxy of T. The maximum explained variance (~0.80) is attained for the causal system ($L = 0$), which also gives the most physically plausible shape of IRF. The differenced series lead to practically zero explained variance for all L and thus it does not provide any infor­mation. In the reverse system, $\left[{\mathrm{C}\mathrm{O}}_{2}\right]\to T$, not shown in the figure, the explained variance is maxim­ized for $L = -20$ with an attained value of 0.88, while for $L = 0$ the explained variance takes the minimum value. This again suggests an anticausal system $\left[{\mathrm{C}\mathrm{O}}_{2}\right]\to T$ or a causal system $T\to \left[{\mathrm{C}\mathrm{O}}_{2}\right]$.

Figure 13.  Application of the methodology to the Cenozoic data (original series). (left) Estimated IRFs for the indicated lower computational lag, L (marked at the high end of each curve); (right) explained variance and characteristic time lags (mean, median and cross-correlation maximizing) as functions of the lower computational lag, L.

DownLoad: Full-Size Img PowerPoint

As explained in Section 2.3, for the late Quaternary data, I produced two time series of constant time step, one with time step of 1000 years extending over 416 000 years and one with time step of 500 years extending over 200 000 years. The results for the first case are shown in Figure 14.

Figure 14.  Application of the methodology to the late Quaternary (Vostok) data, namely the original series of 416 000 years with time step of 1000 years; (left) Estimated IRFs for the indicated lower computational lag, L (marked at the high end of each curve); (right) explained variance and characteristic time lags as functions of the lower computational lag, L.

DownLoad: Full-Size Img PowerPoint

The explained variance for $L = 0$ is high, 0.84, and lower for $L = -20$, 0.72. However, the value of 0.84 remains the same for $L = -10$ to 0, which does not provide a clear answer whether the system is potentially causal or potentially HOE causal. Nonetheless, in either case the characteristic lags are positive, supporting a principal direction $T\to \left[{\mathrm{C}\mathrm{O}}_{2}\right]$ whether this is exclusive (potentially causal system) or not (potentially HOE causal system).

The results for the time series with time step of 500 years are shown in Figure 15, both for the original and the differenced series. The former clearly suggests a potentially causal system, with maximum explained variance at $L = 0$ of $e = 0.89$.

Figure 15.  Application of the methodology to the late Quaternary (Vostok) data. (upper row) Original series of 200 000 years with time step of 500 years; (lower row) differenced series of 200 000 years with time step of 500 years. (left column) Estimated IRFs for the indicated lower computational lag, L (marked at the high end of each curve); (right column) explained variance and characteristic time lags as functions of the lower computational lag, L.

DownLoad: Full-Size Img PowerPoint

The differenced series suggest a nearly causal system, as the lower computational lag maximizing the explained variance is not zero but $L = -1$. However, given the uncertainty in dating, as discussed in Section 2.3, and the fact that uncertainty is magnified by differencing, we may regard this small displacement from $L = 0$ to $L = -1$ as a statistical error and remain with the conclusion of a potentially causal system.

For the Common Era, preliminary analysis showed that there is one pair of temperature and [CO₂] series that yields cross-correlations sufficient for further analysis. This consists of the Loehle and McCulloch ^[57] series for temperature, and the ice core data of Indermühle et al. ^[59], Etheridge et al. ^[60] and Francey et al. ^[61] for [CO₂]. However, even this pair gives cross-correlations close to zero or negative (and explained variance zero), after differencing at a differencing time step equal to one. Therefore, only the original series was analyzed and a multiplier of $m = 4$ was used to expand the time frame of the IRF to 80 years. The results of this analysis, for time scale of 1 year, are shown in Figure 16 and support the case of a potentially causal system at the direction $T\to \left[{\mathrm{C}\mathrm{O}}_{2}\right]$, with an explained variance of 0.49 at $L = 0$.

Figure 16.  Application of the methodology to the Common Era data, namely the Loehle and McCulloch ^[57] for temperature and ice core data for [CO₂] (original series at time scale of 1 year with a multiplier $m = 4$). (left) Estimated IRFs for the indicated lower computational lag, L (marked at the high end of each curve); (right) explained variance and characteristic time lags as functions of the lower computational lag, L.

DownLoad: Full-Size Img PowerPoint

These data were also analyzed on a decadal time scale, by replacing the original series with moving averages of ten years. Now, the differenced time series also provides information as the cross-correlations are not zero. The results of the application of the method for both the original and differenced series are shown in Figure 17 and again support the case of a potentially causal system at the direction $T\to \left[{\mathrm{C}\mathrm{O}}_{2}\right]$, with an explained variance at $L = 0$ equal to 0.49 for the original series but only 0.11 for the differenced series.

Figure 17.  Application of the methodology to the Common Era data, namely the Loehle and McCulloch ^[57] for temperature and ice core data for [CO₂]; time scale of 10 years, multiplier $m = 4$. (upper row) Original series; (lower row) differenced series. (left column) Estimated IRFs for the indicated lower computational lag, L (marked at the high end of each curve); (right column) explained variance and characteristic time lags as functions of the lower computational lag, L.

DownLoad: Full-Size Img PowerPoint

4.3.   Instrumental data

As already discussed in Section 4.1, for the instrumental data only differenced series are used. The time step in the instrumental data is monthly, but the analyses are made on annual scale, i.e., with multiplier $l = 1/12$. To this aim, the differencing time step is taken as one year. In the earlier studies ^[19,21,22] from the original time series, ${x}_{i}$, the differenced time series was constructed as:

This has the additional advantage of limiting the influence of seasonality. To completely remove this influence, here we follow a different tactic. First, we take a moving average at a sliding window of one year, forming the time series:

and then we difference with a step of 12 months, forming the time series:

The same transformation is applied to the time series ${y}_{i}$.

The results of the analyses of (${\widetilde{x}}_{i}^{{{'}}}\to {\widetilde{y}}_{i}^{{{'}}}$) are seen in Figure 18 for Mauna Loa and in Figure 19 for the South Pole. In the latter case, two temperature series have been used (even though one is shown in the figure), southern hemisphere and global, and the latter resulted in higher explained variance, 0.30 against 0.21 of the former for $L = 0$. As in the earlier studies, each of the two figures clearly suggests a potentially causal system at the direction $T\to \left[{\mathrm{C}\mathrm{O}}_{2}\right]$. It is further noted that the case (${\widetilde{x}}_{i}\to {\widetilde{y}}_{i}$), i.e., without averaging, was also tested and the results were very similar, with a slightly smaller explained variance.

Figure 18.  Application of the methodology to the Mauna Loa [CO₂] data with global ERA5 temperature data (differenced series at annual scale). (left) Estimated IRFs for the indicated lower computational lag, L (marked at the high end of each curve); (right) explained variance and characteristic time lags as functions of the lower computational lag, L.

DownLoad: Full-Size Img PowerPoint

Figure 19.  Application of the methodology for differenced series at annual scale to the South Pole [CO₂] data with global ERA5 temperature data. (left) Estimated IRFs for the indicated lower computational lag, L (marked at the high end of each curve); (right) explained variance and characteristic time lags as functions of the lower computational lag, L.

DownLoad: Full-Size Img PowerPoint

As the instrumental series cover a period of nearly 70 years, it is possible to investigate the causality at time scales larger than the annual. As in the case of the Common Era data, the system is also analyzed at a time scale an order of magnitude larger, i.e. 10 years. It is first noted that the averaged differenced series for a moving window of 10 years is

Hence, to assess causality at the decadal scale it suffices to analyze the differenced series:

i.e., to change the differencing time step from one year (as in ${\widetilde{x}}_{i}^{{'}}$) to ten years (as in ${\widetilde{x}}_{i}^{{'}{'}}$).

The results are shown graphically in Figure 20 for Mauna Loa and Figure 21 for South Pole. In both cases, the IRFs for multiplier m = 1 do not seem reasonable (in their convex shape) and suggest that an IRF time frame of 20 months does not suffice to properly recover the IRF. Therefore, in both cases an IRF for multiplier m = 4 was also constructed, corresponding to an IRF time frame of 80 months (6.7 years). Inspection of all cases shows no ambiguity that we have a potentially causal system at the decadal scale as the explained variance, particularly for m = 4, is high at $L = 0$ and clearly lower at all other L values. It can be said that the results are even clearer at the decadal scale, compared to those at annual scale.

Figure 20.  Application of the methodology to differenced series at decadal time scale to the Mauna Loa [CO₂] data with global ERA5 temperature data and monthly time step with (upper row) multiplier m = 1; (lower row) multiplier m = 4. (left column) Estimated IRFs for the indicated lower computational lag, L (marked at the high end of each curve); (right column) explained variance and characteristic time lags as functions of the lower computational lag, L.

DownLoad: Full-Size Img PowerPoint

Figure 21.  Application of the methodology to differenced series at decadal time scale to the South Pole [CO₂] data with global ERA5 temperature data and monthly time step with (upper row) multiplier m = 1; (lower row) multiplier m = 4. (left column) Estimated IRFs for the indicated lower computational lag, L (marked at the high end of each curve); (right column) explained variance and characteristic time lags as functions of the lower computational lag, L.

DownLoad: Full-Size Img PowerPoint

For illustration, for the case shown in Figure 21 (lower), i.e. South Pole with an IRF with multiplier m = 4 (corresponding to an IRF time frame of 80 months or 6.7 years), the results of the investigation of the reverse system, $\left[\mathrm{C}{\mathrm{O}}_{2}\right]\to T$, are also presented in Figure 22. The graphs in Figure 22 clearly suggest: (a) an anticausal system with a narrow IRF around a time lag of minus one year; (b) a low explained variance of about 0.10, against 0.54 of the causal system $T\to \left[\mathrm{C}{\mathrm{O}}_{2}\right]$ (for $L = 0$ and even 0.17 for the anticausal system, $L = -20$, but at the direction $T\to \left[{\mathrm{C}\mathrm{O}}_{2}\right]$); (c) almost constant explained variance of about 0.10 for all $L$, except for $-1$ and 0, for which it becomes even lower; and (d) almost constant median and mean IRF lag of about $-1$ year.

Figure 22.  Application of the methodology to differenced series at decadal time scale to the South Pole [CO₂] data with global ERA5 temperature data and monthly time step with multiplier m = 4, as in Figure 21 (lower), but for the reverse system $\left[\mathrm{C}{\mathrm{O}}_{2}\right]\to T$. (left) Estimated IRFs for the indicated lower computational lag, L (marked at the low end of each curve); (right) explained variance and characteristic time lags as functions of the lower computational lag, L.

DownLoad: Full-Size Img PowerPoint

This additional investigation increases the confidence to the important result that the system $T\to \left[\mathrm{C}{\mathrm{O}}_{2}\right]$ is potentially causal at the decadal scale, while the reverse causality direction, $\left[\mathrm{C}{\mathrm{O}}_{2}\right]\to T$, should be excluded. The importance of this result for the decadal scale, which agrees with the results for the decadal scale of the proxy series of the Common Era, should be highlighted for the additional reason that it is based on instrumental data of the modern period. While it had already been recognized that the short-term [CO₂] fluctuations are caused by fluctuations of global temperature (e.g. Park ^[96]), the conventional wisdom is that this is not extended to larger scales, at which it was thought that the causality direction is reversed (e.g. Åsbrink ^[97]) and eventually determined by human emissions. However, this is a speculation, supported by climate models that reproduce their assumptions and algorithms. No real-world, data-based, evidence has ever been provided in support of that popular speculation. Here evidence of the opposite is provided. It is further noted that Koutsoyiannis et al. ^[22] found that the causality direction in climate models, identified by the same methodology, is opposite to that identified from real-world data.

5.   Summary and discussion

The extensive analyses made can easily be summarized as their results converge to the single inference that change in temperature leads and that in carbon dioxide concertation lags. This is supported both by proxy and instrumental data in all time scales and time spans. In quantified terms these results are summarized in Table 1. The causal system at the direction $T\to \left[\mathrm{C}{\mathrm{O}}_{2}\right]$ is always superior, in terms of explained variance, to the anticausal system, which would imply a causality direction $\left[\mathrm{C}{\mathrm{O}}_{2}\right]\to T$. The fact that in an anticausal system the explained variance is mostly nonzero is expected, because of the high autocorrelation values appearing in both processes (particularly in [CO₂]) as discussed in Sections 3.3 and 4.1.

Table 1.  Summary of results of all causality analyses for direction $T\to \left[\mathrm{C}{\mathrm{O}}_{2}\right]$ and for the causal ($L = 0$) and the anticausal ($L = -20$) systems; the time unit is in years.

Case	O/D*	Time span	Time scale	Multipliers $\boldsymbol{l}, \boldsymbol{m}$	Explained variance		Time lags†
					Causal	Anticausal	${\boldsymbol{h}}_{\mathbf{c}}$	${\boldsymbol{h}}_{{\bf{1/2}}}$	${\boldsymbol{\mu }}_{\boldsymbol{h}}$
Phanerozoic	O	491×106	106	1, 1	0.62	0.61	3×106	1.2×106	4.0×106
	D	490×106	106	1, 1	0.27	0.19	2×106	2.3×106	6.4×106
Cenozoic	O	66.8×106	105	1, 1	0.80	0.78	4×105	7.6×105	9.1×105
Late Quaternary	O	416 000	1000	1, 1	0.84	0.71	1000	1160	4540
	O	200 500	500	1, 1	0.89	0.72	1500	1220	3290
	D	200 000	500	1, 1	0.22	0.15	0	1210	2410
Common Era	O	1711	1	1, 4	0.49	0.41	35	25	33
	O	1701	10	1/10, 4	0.49	0.40	35	26	33
	D	1700	10	1/10, 4	0.11	0.05	35	21	30
Modern/Mauna Loa	D	63	1	1/12, 1	0.43	0.07	0.58	0.55	0.65
	D	54	10	1/120, 1	0.49	0.38	0.58	0.44	0.80
	D	54	10	1/120, 4	0.50	0.08	0.67	3.15	3.17
Modern/South Pole	D	65	1	1/12, 1	0.30	0.03	0.58	0.64	0.74
	D	56	10	1/120, 1	0.54	0.43	0.83	1.16	0.86
	D	56	10	1/120, 4	0.54	0.17	0.83	3.31	3.28
* O: original, D: differenced. † The time lags of the causal system are noted, which generally yield the highest explained variance. There are two exceptions, in which a HOE system maximizes the explained variance. These are: (a) Phanerozoic/ Original, with lower computational lag L = –14, in which ${h}_{1/2}=3.7\times {10}^{6}, {\mu }_{h}=0$ (years); (b) Late Quaternary, Differenced, with lower computational lag L = –1, in which ${h}_{1/2}=850, {\mu }_{h}=1970$ (years).

---

 | Show Table

DownLoad: CSV

The direction $\left[\mathrm{C}{\mathrm{O}}_{2}\right]\to T$ was also directly investigated, even though no detailed graphs are provided (except in one case, Figure 22), and the results are consistent with the above, i.e., in this case the explained variance for the anticausal system is greater than that of the causal system. Even a HOE causality is generally excluded, with a couple of exceptions noted in the Table, where again the time lags are positive. This means that, even if the exceptions are not statistical errors, temperature change leads and change in carbon dioxide concertation lags.

A remarkable result is that, as the time scale increases, so do the characteristic time lags. This sounds paradoxical, as one would expect an IRF independent of the data resolution and time span. However, this could be explained both on physical and mathematical grounds. On physical grounds, one may think that several mechanisms exist, which act on different time scales, that produce increase of atmospheric [CO₂] when temperature rises. Usually Henry's law is invoked, according to which increase of water temperature results in decreasing solubility of CO₂ in water and hence CO₂ degassing from the oceans ^[98]. However, this may not be responsible for changes on a multitude of time scales. As explained in ^[22], the biosphere processes offer the key mechanisms to this causal relationship. CO₂ is produced during degradation of biological matter, by bacterial and thermophilic processes. During cool periods, degradation slows more than photosynthesis, and this traps CO₂ into soil. During warm periods, carbon trapped in soils is released faster than photosynthesis can absorb it, and atmospheric CO₂ increases. Respiration of all aerobic organisms also emits CO₂ and hence changes in the species occurring at creation and extinction events, which enter the scene as time scales increase, affect the T – [CO₂] relationship. Thus, as time span increases, more mechanisms of this relationship manifest themselves in the data.

On mathematical grounds, it is explained in Appendix B that the increase of time span may result in increasing characteristic lags. This is particularly the case for the mean, which may diverge to infinity if the IRF has a heavy tail with tail index higher than 1. The median is finite, but again its convergence to its true value can be very slow. Thus, even the median lag could increase as the time span of the data increases.

6.   Conclusions

The premise of this study is that the climatic system is very complex and subject to perpetual change due to numerous processes, either internal or external to it. The fact that one of them, namely the relationship of climate with atmospheric CO₂, is highlighted in the last decades does not correspond to its actual importance as a climate driver. The promoted importance is a non-scientific issue, related to the narrative that humans, through their emissions by fossil fuel burning, are responsible for the changes we see in climate.

However, changes occurred in the history of Earth and the data sets used here, going back to the entire Phanerozoic eon (the last 541 million years), clearly show the perpetual nature of change. Furthermore, the consistent stochastic methodology for causality identification further developed in this study, as opposite to inconsistent deterministic methods, clearly supports a single conclusion: While there is a close relationship between temperature and atmospheric carbon dioxide concertation, it is temperature that leads, while [CO₂] lags. That is, the causality direction is $T\to \left[\mathrm{C}{\mathrm{O}}_{2}\right]$ and not the opposite, as emphatically promoted in the last decades. This is the case not only in the distant past and on large time scales, but also in the recent period covered by reliable instrumental records. This happens not only at the monthly or annual time scale, but also at the decadal time scale, which can be resolved by the existing data sets. Notably, the results of the method application on the decadal time scale with instrumental data are even more conclusive than those on the annual time scale. This is similar to what the proxy data for the Common Era suggest.

In conclusion, both the paleoclimatic and the instrumental data confirm the same causality direction $T\to \left[\mathrm{C}{\mathrm{O}}_{2}\right]$ for all time scales, from very large to very short, and all periods. The mechanisms responsible to this causality direction are physical, related to the interaction of oceans and atmosphere, but mostly are related to the biosphere processes. Did human actions, such as fossil fuel combustion and other presumed 'unnatural' actions, reverse directionality, as the popular claim is? Perhaps, but no analysis based on observational data has shown that. Rather, such claims are based on imagination and climatic models full of assumptions. However, as shown in ^[22] the causality direction in time series produced by climatic models is opposite to that of the real-world data.

Use of AI tools declaration

The author declares he has not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This research received no funding but was conducted out of scientific curiosity. I would like to thank Judith Curry and the discussers in her blog (https://judithcurry.com/2023/09/26/causality-and-climate/) on an earlier paper ^[22] coauthored by me. I particularly thank Robert Cutler for providing independent confirmation of the findings of that paper, using a spectral method, and for his comments on an initial draft of this paper. In addition, I thank an anonymous blogger nicknamed "Agnostic" for providing rich information, which also supported our results. I also thank John A Marcou (Jakarta, Indonesia) for the encouragement to make the present research and Richard Cina (St. Louis, Missouri, USA) for his constructive suggestions on a first draft of the paper. I am grateful to the editor and three anonymous reviewers of the original submission of the paper for the positive reception of the paper and the constructive comments which helped me to make substantial improvements. Two additional reviewers, invited after the submission of the revision, focused their reviews on my earlier works and forced me to produce a 50-page report to rebut their comments, clarifying several issues related to my earlier works, which these two reviewers were not aware of or had not understood.

Conflict of interest

The author declares no conflict of interest.

Data availability

This research uses no new data. The data sets used have been retrieved from the sources described in detail in the paper.