The occurrence of pests and diseases during agricultural production affects the quality and quantity of agricultural products. It is important to evaluate the impact of various factors on pests to achieve optimal results of integrated pest management (IPM) during its implementation. In this paper, we considered the transient and non-transient effects of chemical control on pests and the effects on natural enemies at different times, and developed a corresponding pest control model. Detailed studies and comparisons were conducted for spraying pesticides either more or less frequently as compared to strategies for releasing natural enemies. The threshold conditions for global asymptotic stabilization of the pest extinction period solution was obtained. Using two-parameter and sensitivity analysis techniques, the parameters affecting the variation of the threshold were discussed. By comparing these two pest control strategies, we found the existence of optimal application and release frequencies. Finally, in order to control pests below the economic threshold level, the state-dependent pest model was numerically investigated. The results show that the presence or absence of chemical control of pests can depend on the values taken for the parameters in the model. Based on this information, pest control experts can make decisions about the best spraying time and the best release rate.
Citation: Liping Wu, Zhongyi Xiang. A study of integrated pest management models with instantaneous and non-instantaneous impulse effects[J]. Mathematical Biosciences and Engineering, 2024, 21(2): 3063-3094. doi: 10.3934/mbe.2024136
| [1] | Bing Liu, Gang Hu, Baolin Kang, Xin Huang . Analysis of a hybrid pest management model incorporating pest resistance and different control strategies. Mathematical Biosciences and Engineering, 2020, 17(5): 4364-4383. doi: 10.3934/mbe.2020241 |
| [2] | Yuan Tian, Sanyi Tang . Dynamics of a density-dependent predator-prey biological system with nonlinear impulsive control. Mathematical Biosciences and Engineering, 2021, 18(6): 7318-7343. doi: 10.3934/mbe.2021362 |
| [3] | Yi Yang, Lirong Liu, Changcheng Xiang, Wenjie Qin . Switching dynamics analysis of forest-pest model describing effects of external periodic disturbance. Mathematical Biosciences and Engineering, 2020, 17(4): 4328-4347. doi: 10.3934/mbe.2020239 |
| [4] | Xinli Hu, Wenjie Qin, Marco Tosato . Complexity dynamics and simulations in a discrete switching ecosystem induced by an intermittent threshold control strategy. Mathematical Biosciences and Engineering, 2020, 17(3): 2164-2178. doi: 10.3934/mbe.2020115 |
| [5] | Wenjie Qin, Yue Xia, Yi Yang . An eco-epidemic model for assessing the application of integrated pest management strategies. Mathematical Biosciences and Engineering, 2023, 20(9): 16506-16527. doi: 10.3934/mbe.2023736 |
| [6] | Luis F. Gordillo . Optimal sterile insect release for area-wide integrated pest management in a density regulated pest population. Mathematical Biosciences and Engineering, 2014, 11(3): 511-521. doi: 10.3934/mbe.2014.11.511 |
| [7] | Yanyun Li, Juhua Liang . Models for determining the optimal switching time in chemical control of pest with pesticide resistance. Mathematical Biosciences and Engineering, 2021, 18(1): 471-494. doi: 10.3934/mbe.2021026 |
| [8] | Zhenzhen Shi, Huidong Cheng, Yu Liu, Yanhui Wang . Optimization of an integrated feedback control for a pest management predator-prey model. Mathematical Biosciences and Engineering, 2019, 16(6): 7963-7981. doi: 10.3934/mbe.2019401 |
| [9] | Aniket Banerjee, Urvashi Verma, Margaret T. Lewis, Rana D. Parshad . Two species competition with a "non-smooth" Allee mechanism: applications to soybean aphid population dynamics under climate change. Mathematical Biosciences and Engineering, 2025, 22(3): 604-651. doi: 10.3934/mbe.2025023 |
| [10] | Baolin Kang, Xiang Hou, Bing Liu . Threshold control strategy for a Filippov model with group defense of pests and a constant-rate release of natural enemies. Mathematical Biosciences and Engineering, 2023, 20(7): 12076-12092. doi: 10.3934/mbe.2023537 |
The occurrence of pests and diseases during agricultural production affects the quality and quantity of agricultural products. It is important to evaluate the impact of various factors on pests to achieve optimal results of integrated pest management (IPM) during its implementation. In this paper, we considered the transient and non-transient effects of chemical control on pests and the effects on natural enemies at different times, and developed a corresponding pest control model. Detailed studies and comparisons were conducted for spraying pesticides either more or less frequently as compared to strategies for releasing natural enemies. The threshold conditions for global asymptotic stabilization of the pest extinction period solution was obtained. Using two-parameter and sensitivity analysis techniques, the parameters affecting the variation of the threshold were discussed. By comparing these two pest control strategies, we found the existence of optimal application and release frequencies. Finally, in order to control pests below the economic threshold level, the state-dependent pest model was numerically investigated. The results show that the presence or absence of chemical control of pests can depend on the values taken for the parameters in the model. Based on this information, pest control experts can make decisions about the best spraying time and the best release rate.
Crop pests have many characteristics, a great influence, and a strong explosiveness. In China, there are more than 1000 types of pests recorded on important crops. When pests erupt, they can affect crop yields and, in severe cases, even extinction, thus resulting in economic losses and being the biggest barrier to agricultural production [1,2,3]. For example, an outbreak of the grass-craving nightshade moth in 2019 caused considerable economic losses in many parts of southern China [3]. Therefore, the management of pests to achieve the most favorable conditions for humans is an important research topic.
Chemical and biological control are the most popular approaches of pest management. Chemical control involves the use of pesticides and other chemicals to deal with pests, which has the advantages of convenience and a high efficiency. The effect on pests can be observed in a brief term; however, when pesticides are applied for a prolonged term, the pests will be resistant to the chemicals and cause pollution to the environment, thus affecting the health of the human body [4,5,6]. Biological control is the use of artificially released natural enemies and host natural enemies to control pests. It not only controls pests but also minimizes environmental pollution. However, natural enemies often require artificial cultivation and the expense is high [7,8,9,10].
Therefore, chemical and biological control are often combined (i.e., integrated pest management (IPM) is employed), which is a prolonged control strategy. Considering the population dynamics of pests and their environment, the pest population is controlled below the level of economic harm by using all appropriate methods and techniques [8,11,12,13,14]. Economic threshold (ET) and economic injury level (EIL) are two essential concepts in the IPM process. EIL is defined as the lowest pest density that can cause economic losses, and the ET is determined as the pest density at which control measures should be applied to prevent the pest from reaching the EIL [12,15]. In 2015, Xiang et al. [14] studied the application of comprehensive intervention strategies of pest control in the pest-natural enemy model, and discussed the situation where the frequency of pesticide application is greater than the frequency of natural enemy release. This information can help pest control experts come up with new ideas.
Spraying pesticides or releasing natural enemies during pest control can be described as a split-second act. To model this process, we can build either continuous or discrete impulse differential equations. Scholars have studied the transient effects of pesticides on pests using periodic pulse differential equations [16,17,18] and state-dependent pulse differential equations [19,20,21]. However, the impacts produced by pesticides on both pests and natural enemies occur not only in a single moment, but also on both organisms over the following timescale, which can be characterized by either a continuous or segmented continuous periodic function of time [22,23,24]. For example, Tang et al. [24] incorporated the non-transient effects of chemical control on pests and natural enemies in an integrated pest management model. Threshold conditions for the pest extinction period solutions were acquired, and the impacts of factors such as application frequency, killing efficiency, and the application period on the threshold conditions were analyzed.
Holling II predator-prey systems are thought to play an important role in characterizing the relationship between pest and natural enemy populations. Therefore, it is of a great biological importance to study models of Holling II [14,25,26,27]. For instance, in 2018, Yang and Tan [25] investigated the effect of pesticide dosage on a predation model with a Holling II predation and showed complex dynamics in the proposed model. In 2018, Páez Chávez et al. [26] conducted a comparative study on integrated pest management strategies based on impulsive control. Compared with other functions, the modeling with the Holling II function was more effective in controlling pest populations. Additionally, Wei et al. [27] examined the classical Holling II predation model with the addition of multiple factors.
Because pesticide spraying affects natural enemies, their predation and conversion rates on pests can differ before and after pesticide spraying. Switching systems (or the Filippov system) can represent this process very well. Recently, the switching system has been extensively studied by scholars [28,29,30,31,32,33]. For instance, Gao et al. [33] established a corresponding Huanglong disease switching model which took the different removal and susceptibility rates of citrus trees with seasonal changes into account; additionally they investigated the effect of the switching control scheme on the model dynamics. In 2023, Liu et al. [32] investigated a pest control switching model with a transient and non-transient pulse impact and discussed the impact of applying a switching control scheme on the model dynamics when the pesticide spraying frequency was higher than the release frequency of natural enemies. Moreover, numerical studies of pest control switching models with state-dependent switching were performed. We all know that spraying pesticides has an impact on pests and natural enemies, and the conversion and predation rate of natural enemies to pests before and after spraying pesticides will also be different. However, none of the models studied so far simultaneously considered them in a predator-prey switching system of the Holling II. Therefore, in this paper, we establish the corresponding switching model while taking these factors into account.
In this paper, based on the above discussion and [21,32], we study a model with the Holling II using IPM intervention as a pulse control strategy, to study the impact of different control strategies on pest management and population changes. We construct the corresponding model in Section 2. In Section 3, we study the situation where the frequency of pesticide spraying is higher than the frequency of natural enemy release, and analyze threshold conditions for pest extinction. The estimation of the partial correlation coefficient (PRCC) is carried out using the Latin hypercube sampling (LHS) method to give the effect of each parameter on the threshold. Moreover, in Section 4, we examine the situation where the frequency of natural enemy release is higher than the frequency of pesticide sprays, thereby comparing the effect of the parameters on the pest extinction thresholds in the two cases. In view of the fact that the ideal goal of the IPM is to control the density of pests below the ET, we establish a pest model with state-dependent modeling in Section 5, and analyze the number of pesticide sprays required when the parameters are varied. Finally, we analyze the biological significance they represent.
Many studies have been conducted in the previous literature for the Holling II pest management model, though the effects of pesticide residues have rarely been considered. Therefore, we consider the effects of pesticide residues on pests and natural enemies in this paper, thus leading to a better IPM. From reference [21], we have the following:
| {dx(t)dt=rx(t)(1−x(t)K)−ax(t)y(t)1+dx(t),dy(t)dt=kax(t)y(t)1+dx(t)−cy(t), | (2.1) |
where x(t) and y(t) denote the pest and natural enemy densities, respectively, K is its carrying capacity, r is the intrinsic growth rate of the pest population, (ax(t))/(1+dx(t)) is the Holling II function response, which is a saturating function of the number of pests present, and c is the mortality rate of the predator population.
Referring to references [24] and [32], the following exponential function is introduced to represent the impact of pesticide residues on pests and natural enemies:
| bi(t)=mie−δi(t−nT),nT≤t<(n+1)T, |
where mi≥0(i=1,2) denotes the non-instantaneous kill rate of the pesticide on pests and natural enemies, respectively, T represents for pulse period, and δi>0(i=1,2) denotes the positive decay rate of the pesticide on pests and natural enemies, respectively.
In the following third and fourth parts, we will study the frequency of spraying pests higher and lower than the frequency of releasing natural enemies. We have established the following two systems.
Case 1: Applying pesticides more frequently than releasing natural enemies.
Considering the differences in capture and transformation rates of pests by natural enemies during the time of pesticide action and inaction, alongside the instantaneous and non-instantaneous impacts of insecticide spraying on pest and natural enemy populations, the following switching model for integrated pest control is established:
| {dx(t)dt=rx(t)(1−x(t)K)−a1x(t)y(t)1+dx(t),dy(t)dt=k1a1x(t)y(t)1+dx(t)−cy(t),}t∈(hTN,(h+l)TN],x(t+)=(1−p1)x(t),y(t+)=(1−p2)y(t),}t=(h+l)TN+nTk,n=0,1,2,...k−1,dx(t)dt=rx(t)(1−x(t)K)−a2x(t)y(t)1+dx(t)−b1(t)x(t),dy(t)dt=k2a2x(t)y(t)1+dx(t)−cy(t)−b2(t)y(t),}t∈((h+l)TN,(h+1)TN],t≠(h+l)TN+nTk,x(t+)=x(t),y(t+)=y(t)+τ,}t=(h+1)TN,h∈N, | (2.2) |
bi(t)=mie−δi(t−(h+l)TN−nTk),(h+l)TN+nTk≤t<(h+l)TN+(n+1)Tk, where TN is the pulse period, 0<l<1 denotes the starting time of pesticide spraying, 0<a1,a2<1 and 0<k1,k2<1 represent the predation rate and transformation rate of the natural enemies on the pests in the corresponding time period, respectively, τ>0 is the release of the natural enemies at the moment t=hTN, and 0≤p1,p2<0 denote the momentary killing efficiency of the pesticide on pests and natural enemies at the moment t=(h+l)TN, respectively. During the time TN of releasing the natural enemy, the pesticide is periodically sprayed k times, t=(h+l)TN+nTk,(n=0,1,2,...k−1), and the period of the number of pesticide sprays is set to Tk, which is (1−l)TN=kTk. The other parameters are the same as in model (2.1).
For system (2.2), we have the following interpretation. In a large pulse period TN, pests and natural enemies undergo several processes of change. At time t∈(hTN,(h+l)TN), the density changes of pests and natural enemies follow their own development rules, which are expressed by the first two equations of system (2.2). When the time is t=(h+l)TN, we spray pesticides. During this moment, pesticides have instantaneous effects on pests and natural enemies at the same time, and the action equations are the third and fourth equations of system (2.2). At time t∈((h+l)TN,(h+l)TN+Tk), followed by time t=(h+l)TN, (i.e., after spraying pesticides), we consider the residual effects of pesticides on pests and natural enemies, (i.e., on the fifth and sixth equations). At time t∈((h+l)TN,(h+1)TN) in the middle of the large pulse TN, the pesticides are sprayed k times, indicating that the instantaneous and non-instantaneous effects of pesticides on pests and natural enemies are also carried out k times. At time t=(h+1)TN, the natural enemies are released, as expressed by the seventh and eighth equations. This is a complete cycle. The detailed process is given in the third section.
Case 2: Natural enemies are released more frequently than pesticide applications.
In a period where pesticide spraying is followed by the release of natural enemies, we have the following:
| {dx(t)dt=rx(t)(1−x(t)K)−a2x(t)y(t)1+dx(t)−b1(t)x(t),dy(t)dt=k2a2x(t)y(t)1+dx(t)−cy(t)−b2(t)y(t),}t≠hTz,t≠(h+l)Tz+kTp,k=0,1,2,...,p−1,x(t+)=x(t),y(t+)=y(t)+τ,}t=(h+l)Tz+kTp,k=0,1,2,...,p−1,x(t+)=(1−p1)x(t),y(t+)=(1−p2)y(t),}t=(h+1)Tz,h∈N,bi(t)=mie−δi(t−hTz),hTz≤t<(h+1)Tz,i=1,2, | (2.3) |
parameter meaning reference system (2.2). For system (2.3), when the frequency of releasing natural enemies is greater than that of spraying pesticides, we assume that the pesticides are sprayed first (i.e., pesticides are sprayed on pests at each large pulse period point t=hTZ). At time t∈(hTZ,(h+l)TZ], pests and natural enemies will be affected by pesticides, as expressed as the first two equations of system (2.3). At time t=(h+l)TZ, we release natural enemies, and the action equations are the third and fourth equations of system (2.3). Similar to system (2.2), in system (2.3), we assume that the natural enemy is released p times within the time t∈((h+l)TZ,(h+1)TZ) in the middle of the large pulse TZ. At time t=(h+1)TZ, it is sprayed with pesticides, as expressed as the fifth and sixth equations of system (2.3). Thus, a pulse period TZ is formed. The detailed process is given in Section 4.
To begin with, we study the following subsystems of system (2.2):
| {dy(t)dt=−cy(t),t∈(hTN,(h+l)TN],y(t+)=(1−p2)y(t),t=(h+l)TN+nTk,n=0,1,2,...k−1,dy(t)dt=−cy(t)−b2(t)y(t),t∈((h+l)TN,(h+1)TN],t≠(h+l)TN+nTk,y(t+)=y(t)+τ,t=(h+1)TN,h∈N. | (3.1) |
Theorem 3.1. The system (3.1) has a unique, globally asymptotically stable, positive periodic solution y*(t) and limt→∞|y(t)−yN∗(t)|=0, where
| yN∗(t)={yN∗1(t),t∈(hTN,(h+l)TN],yN∗j(t),t∈((h+l)TN+(j−2)Tk,(h+l)TN+(j−1)Tk],j=2,3,⋯,k+1, | (3.2) |
| yN∗1(t)=yN∗exp(−c(t−hTN)), |
| yN∗j(t)=yN∗(1−p2)j−1exp(−c(t−hTN)−(j−2)m2δ2(1−e−δ2Tk)−m2δ2(1−e−δ2(t−(h+l)TN−(j−2)Tk))), |
| yN∗=τ1−(1−p2)kexp(−cTN−km2δ2(1−e−δ2Tk). | (3.3) |
Proof. Solving the equation of system (3.1) on interval [hTN,(h+l)TN) yields the following:
| yN(t)=yN(hT+N)exp(−c(t−hTN)). |
At the first spraying of pesticides in a period TN, there are
| yN((h+l)T+N)=(1−p2)yN(hT+N)exp(−clTN). |
In one period TN, after the first spraying of pesticides, i.e., t∈((h+l)TN,(h+l)TN+Tk), then
| yN(t)=(1−p2)yN(hT+N)exp(−c(t−hTN)−m2δ2(1−e−δ2(t−(h+l)TN))). |
On the second spraying of pesticides during the cycle, there are
| yN(((h+l)TN+Tk)+)=(1−p2)2yN(hT+N)exp(−c(lTN+Tk)−m2δ2(1−e−δ2Tk)). |
After the second spraying of pesticides during the period, i.e., at t∈((h+l)TN+Tk,(h+l)TN+2Tk), there are
| yN(t)=(1−p2)2yN(hT+N)exp(−c(t−hTN)−m2δ2(1−e−δ2Tk)−m2δ2(1−e−δ2(t−(h+l)TN−Tk))). |
Repeating the previous process, after the kth spraying of pesticides in a period TN, i.e., t∈((h+l)TN+(k−1)Tk,(h+1)TN], we have the following:
| yN(t)=(1−p2)kyN(hT+N)exp(−c(t−hTN)−(k−1)m2δ2(1−e−δ2Tk)−m2δ2(1−e−δ2(t−(h+l)TN−(k−1)Tk))). |
When t=(h+1)TN, for which the first natural enemy is dropped, there are
| yN((h+1)T+N)=(1−p2)kyN(hT+N)exp(−c(lTN+kTk)−km2δ2(1−e−δ2Tk))+τ. |
Let yNh=yN(hT+N); then, we have the following equation:
| yNh+1=(1−p2)kyNhexp(−c(lTN+kTk)−Pm2δ2(1−e−δ2Tk))+τΔ=G(yNh). | (3.4) |
From the above equation, the only possible immovable point is the following:
| yN∗=τ1−(1−p2)kexp(−cTN−km2δ2(1−e−δ2Tk)). |
Because (3.4) is a linear system and |dG(yNh)yNh|=1−(1−p2)kexp(−cTN−km2δ2(1−e−δ2Tk))<1, it follows from the theory of differential equations that it is a positive equilibrium point of global asymptotic stability of the differential equations. Thus, system (2.2) exists as a single globally asymptotically stable periodic solution yN∗(t). An arbitrary solution y(t) of system (2.2) converges to yN∗(t), as denoted by (3.2) when t→∞. The proof is accomplished.
Thus, system (2.2) has a pest extinction period solution (0,yN∗(t)).
Theorem 3.2. If RTN0<1 is established, the pest extinction period solution (0,yN∗(t)) of system (2.2) is globally asymptotically stable.
Proof. In the first step, we show that the extermination period solution (0,yN∗(t)) of system (2.2) is locally asymptotically stable, which is determined by considering a small amplitude perturbation (u(t),v(t)) of the solution. Defining x(t)=u(t),y(t)=yN∗(t)+v(t), where (u(t),v(t)) is a small perturbation and can be written as follows:
| (u(t)v(t))=Φ(t)(u(0)v(0)),t∈(0,TN], |
where Φ(t)=∏k+1j=1Φj(t), and Φj(t) fulfill
| dΦ1(t)dt=(r−a1yN∗1(t)0k1a1yN∗1(t)−c)Φ1(t),t∈(0,lTN], |
| dΦj(t)dt=(r−b1(t)−a2yN∗j(t)k2a2yN∗j(t)0−c−b2(t))Φj(t), |
where
| t∈(lTN+(j−2)Tk,lTN+(j−1)Tk],j=2,3,…,k+1. |
Hence,
| Φ1(t)=(exp(∫t0(r−a1yN∗1(s))ds)∗0exp(−ct)), |
| Φj(t)=(V1∗0V2), |
where
| V1=exp(∫tlTN+(j−2)Tk(r−b1(s)−a2yN∗j(s))ds), |
| V2=exp(−c(t−lTN−(j−2)Tk−m2δ2(1−e−δ2(t−lTN−(j−2)Tk))). |
It is not necessary to compute the precise form of (∗) because it is not needed in the following theories. By the Floquet theory, if the modes of the two eigenvalues of a single-valued matrix
| U=Φ1(lTN)k+1∏j=2(1−p1001−p2)(1001)Φj(lTN+(j−1)Tk), |
are less than 1, the pest extinction period solution is locally asymptotically stable. Indeed, the eigenvalues are as follows:
| λN1=(1−p1)kexp(∫lTN0(r−a1yN∗1(s))ds+k+1∑n=2∫lTN+(n−1)TklTN+(n−2)Tk(r−b1(s)−a2yN∗n(s))ds), |
| λN2=(1−p2)kexp(−cTN−km2δ2(1−e−δ2Tk))<1. |
Thus, when |λN1|<1, i.e., rTNln(1(1−p1)k)+A+B+k+1∑n=2lTN+(n−1)Tk∫lTN+(n−2)Tk(a2yN∗k(s))ds<1, where
| A=a1cyN∗(1−e−clTN),B=km1δ1(1−e−δ1Tk). |
Let
| RTN0=rTNln(1(1−p1)k)+A+B+k+1∑n=2lTN+(n−1)Tk∫lTN+(n−2)Tk(a2yN∗k(s))ds, |
that is, when RTN0<1, the periodic solution of system (2.2) for pest extinction is locally asymptotically stable. The first step of the proof is complete.
In the second step, we prove that the pest extinction period solution (0,yN∗(t)) of the system (2.2) is globally attractive. Choose a ε(ε>0) such that
| γΔ=(1−p1)k⋅exp((h+l)TN∫hTN(r−a1(yN∗1(s)−ε)1+d(K+ξ))ds)⋅exp(k+1∑n=2(h+l)TN+(n−1)Tk∫(h+l)TN+(n−2)Tk(r−b1(s)−a2(yN∗n(s)−ε)1+d(K+ξ))ds)<1. |
Based on the second and sixth formulas of model (2.2), it follows that
| dy(t)dt>−cy(t),t∈(hTN,(h+l)TN], |
| dy(t)dt>−cy(t)−b2(t)y(t),t∈((h+l)TN,(h+1)TN]. |
Consider the following comparison equation:
| {dz(t)dt=−cz(t),t∈(hTN,(h+l)TN],z(t+)=(1−p2)z(t),t=(h+l)TN+nTk,n=0,1,2,…,k−1,dz(t)dt=−cz(t)−b2(t)z(t),t∈((h+l)TN,(h+1)TN],t≠(h+1)TN+nTk,z(t+)=z(t)+τ,t=(h+1)TN, |
where y(t)≥z(t), and z(t)→yN∗(t) as t→∞. Thus, this gives us y(t)≥z(t)>yN∗(t)−ε for a sufficiently large t and a sufficiently small ε. For the sake of simplicity, it can be assumed that y(t)≥z(t)>yN∗(t)−ε for all t≥0.
By the first equation of model (2.2), we obtain the following:
| dx(t)dt≤rx(t)(1−x(t)K). |
Consider the following comparison equation:
| dN(t)dt=rN(t)(1−N(t)K), |
where x(t)≤N(t) and N(t)→K as t→∞. Thus, there exists a ξ>0 making x(t)≤K+ξ for a large enough t. We assume x(t)≤K+ξ for all t>0 without a loss of generality. By system (2.2), it follows that
| {dx(t)dt≤x(t)(r−a1(yN∗1(s)−ε)1+d(K+ξ)),t∈(hTN,(h+l)TN],x(t+)=(1−p1)x(t),t=(h+l)TN+nTk,n=0,1,2,…,k−1,dx(t)dt≤x(t)(r−b1(s)−a2(yN∗j(s)−ε)1+d(K+ξ)),t∈((h+l)TN,(h+1)TN],t≠(h+1)TN+nTk,x(t+)=x(t),t=(h+1)TN. |
According to the comparison theorem for impulse differential equations, for t∈(hTN,(h+1)TN], then
| x((h+l)TN)≤x(hT+N)exp(∫(h+l)TNhTN(r−a1(yN∗1(s)−ε)1+d(K+ξ))ds), |
| x((h+l)TN+Tk)≤(1−p1)x(hT+N)⋅exp(∫(h+l)TNhTN(r−a1(yN∗1(s)−ε)1+d(K+ξ))ds)⋅exp(∫(h+l)TN+Tk(h+l)TN(r−b1(s)−a2(yN∗2(s)−ε)1+d(K+ξ))ds), |
| ⋮ |
| x((h+1)TN)≤(1−p1)kx(hT+N)⋅exp(∫(h+l)TNhTN(r−a1(yN∗1(s)−ε)1+d(K+ξ))ds)⋅exp(k+1∑n=2∫(h+l)TN+(n−1)Tk(h+l)TN+(n−2)Tk(r−a2(yN∗n(s)−ε)1+d(K+ξ)−b1(s))ds)Δ=x(hT+N)γ. |
Since γ<1, we obtain x(hT+N)≤x(0+)γh and x(hT+N)→0 as t→∞. Thus x(t)→0 as t→∞.
Since limt→∞x(t)→0, for a small enough ε1>0, there exists a t1>0 such that 0<x(t)<ε1 for t>t1. Clearly, for a sufficiently small ε2>0, there exists a t2>t1, making a1x(t)y(t)1+dx(t)<ε2 for t>t2.
In the following discussion, we will show that y(t)→yN∗(t) as t→∞. From system (2.2), we obtain the following:
| −cy(t)≤dy(t)dt≤ε2−cy(t),t∈(hTN,(h+l)TN],−cy(t)≤dy(t)dt≤ε2−cy(t)−b2(t)y(t),t∈((h+l)TN,(h+1)TN]. |
We get y(t)≥z(t) and z(t)→yN∗(t) as t→∞ by the left side of the two inequalities listed above. With respect to the right side of the two inequalities mentioned above, we study the following equation:
| {dω(t)dt=ε2−cω(t),t∈(hTN,(h+l)TN],ω(t+)=(1−p2)ω(t),t=(h+l)TN+nTk,n=0,1,2,…,k−1,dω(t)dt=ε2−cω(t)−b2(t)ω(t),t∈((h+l)TN,(h+1)TN],t≠(h+1)TN+nTk,ω(t+)=ω(t)+τ,t=(h+1)TN. |
From Theorem 3.1, the details of which can be found in Appendix, we obtain the following
| ω∗(t)={ω∗1(t),t∈(hTN,(h+l)TN],ω∗j(t),t∈((h+l)TN+(j−2)Tk,(h+l)TN+(j−1)Tk],j=2,3,…,k+1, |
| ω∗1(t)=ω∗exp(−c(t−hTN))+ε2c(1−exp(−c(t−hTN))), |
| ω∗j(t)=(1−p2)j−1ω∗exp(−c(t−hTN)−Aj−2−Bj−2)+ε2(1−p2)j−1c⋅(1−exp(−clTN))⋅exp(−C0−Aj−2−Bj−2)+ε2(1−p2)c+m2exp(−δ2Tk)⋅j−2∑i=1(1−p2)i−1⋅exp(−Cj−1−i−Ai−1−Bj−2)−ε2c+m2⋅j−2∑i=0(1−p2)i⋅exp(−Cj−2−i−Ai−Bj−2)+ε2c+m2exp(−δ2(t−(h+l)TN−(j−2)Tk)), |
| ω∗=E(1−(1−p2)kexp(−cTN−Ak)), |
where
| E=ε2(1−p2)kc⋅(1−exp(−clTN))⋅exp(−ckTk−Ak)+ε2c+m2exp(−δ2Tk)⋅k∑i=1[(1−p2)i−1exp(−c(i−1)Tk−Ai−1)]−ε2c+m2⋅k−1∑i=0[(1−p2)iexp(−c(i+1)Tk−Ai+1)]+τ |
with
| Ai=im2δ2(1−e−δ2Tk),A0=0,Bi=m2δ2(1−e−δ2(t−(h+l)TN−iTk)),B0=m2δ2(1−e−δ2(t−(h+l)TN)),Ci=c(t−(h+l)TN−iTk),C0=c(t−(h+l)TN),i=0,1,⋯,k. |
Thus, for any ε3>0, there exists a t3>0 such that
| yN∗(t)−ε3<y(t)<ω∗(t)+ε3. |
Let ε,ε1,ε2→0; we obtain yN∗(t)−ε3<y(t)<yN∗(t)+ε3 for a sufficiently large t, which this means that y(t)→yN∗(t) as t→∞.
As a consequence, then the pest extinction cycle solution of model (2.2) is globally asymptotically stable if RTN0<1 stands. The proof ends here.
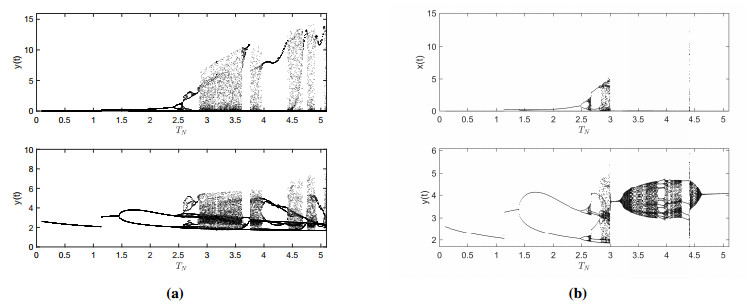
Up to now, we have only theoretically analyzed system (2.2). By theoretical studies, sufficient conditions are obtained for the global asymptotic stability of the pest extinction period solution (0,yN∗(t)). Below, we investigate the complexity of the dynamics of system (2.2) by numerical modeling. We take r=8,K=20,a1=2.1,c=0.5,k1=0.82,p1=0.4,p2=0.2,d=0.15,a2=2,k2=0.4,l=0.2,δ1=0.3,δ2=0.1,m1=0.4,m2=0.13,τ=1.6, and (x(0),y(0))=(2,2.5). By fixing these parameters, we simulate the bifurcation diagram of system (2.2) with respect to the impulse period TN in Figure 1. Figure 1(a) shows the complex dynamic behavior of system (2.2) as TN increases from 0.1 to 5.1. The results show that the pest extinction period solution (0,yN∗(t)) of system (2.2) has global asymptotic stability when the parameter a is increased from 0.1 to 1.1. With an increase of the impulse period TN, system (2.2) exhibits a variety of complex dynamic behaviors, such as periodic, multiperiodic bifurcation, and chaotic phenomena. In Figure 1(b), we let a1=1.9, and d=0.12; as the parameter a increases from 3.1 to 4.7, we observe that the natural enemy population undergoes a complex dynamic behavior. Moreover, there is a coexistence of multiple attractors, which finally stabilizes.
Chaos refers to the unpredictable and random motion of a deterministic dynamic system because of its sensitivity to initial values [34,35]. In Figure 2(a), letting r=8,K=8,a1=1.9,c=0.5,k1=0.82,p1=0.4,p2=0.2,d=0.12,a2=2,k2=0.4,l=0.2,δ1=0.3,δ2=0.1,m1=0.3,m2=0.13,TN=2.7, and (x(0),y(0))=(2,2.5), and fixing these parameters, we simulate a bifurcation diagram of system (2.2) with respect to the number of natural enemy releases τ, this showing the complex dynamic behavior of system (2.2) as τ increases from 0.1 to 7.1. The system (2.2) undergoes period → doubling bifurcation → chaos → half-period bifurcation → chaos → inverse multiplicative cycle bifurcation → stabilization as the parameter τ increases from 0.1 to 7.1. Letting (x(0),y(0))=(2,2.3), we obtain the complex dynamic behavior of system (2.2), including switching transients and chaotic phenomena, as shown in Figure 2(b).
Next, we study the influence of the key parameters in system (2.2) on the threshold condition (RTN0<1). For this reason, we first chose the instantaneous killing efficiency p2 of pesticides on natural enemies, the non-transient death efficiency m1 of pesticides on pests, and the frequency k of pesticide spraying as the bifurcation parameters while the others were fixed, as shown in Figure 3. The results show that the spraying frequency k affects RTN0 differently when parameters p2 and m1 are varied, and that an increased frequency is not necessarily better for pest control. In Figure 3(a), (c), (e), we investigate the effects of the instantaneous killing efficiency p2 of pesticides on natural enemies and the frequency k of pesticide spraying on the threshold RTN0. The findings show that if the pesticide kills natural enemies at a lower killing rate p2 (i.e., p2 = 0.02), then the threshold RTN0 is a monotonically decreasing function of k (as shown in Figure 3(a)). If the instantaneous killing efficiency p2 of the pesticide on natural enemies increases, then the threshold RTN0 is not monotonic with the number of applications k, as shown in Figure 3(c), in which case there is an optimal number of applications during the period TN. If the killing rate p2 for natural enemies increases from 0.04 to 0.6, then the value of the threshold RTN0 initially increases and then decreases with an increase of application times, that is, there is a maximum point, as shown in Figure 3(e). This suggests that fewer applications should be made if insecticides have a significant impact on natural enemies. Similar effects of the non-transient death efficiency m1 of pesticides against pests and the number of pesticide applications k on the threshold RTN0 are shown in Figure 3(b), (d), (f). The larger the non-transient death efficiency m1 of pesticides against pests, the smaller the threshold. The above findings suggest that the frequency of pesticide spraying during the release of natural enemies must be carefully considered, and that an increased frequency of spraying is not better for pest control.
In addition, we can perform a two-parameter bifurcation analysis on the threshold RTN0, as shown in Figure 4, where we observe that the parameter m1 has a significant effect on the threshold RTN0 relative to the other parameters. Increasing the number of natural enemies released τ, increasing the instantaneous kill rate p1 and the non-instantaneous kill rate m1 of the pesticide against the pests are favorable for pest control, and neither the release period TN nor the increase in the decay rate δ1 of the pests are favorable for pest control. Moreover, we note that RTN0 is not a monotonic function with respect to l. Therefore, we should be careful in choosing the timing of pesticide spraying.
In this subsection, we assess the PRCC of various input parameters by evaluating them against the threshold condition RTN0 and then identifying the most important parameters that affect the threshold. PRCC enables the measurement of the effect of uncertainty in the estimated input parameter values on the imprecision of the predicted output variable values, and investigates the sensitivity of the parameters to thresholds. In our analysis, we used the LHS method to perform uncertainty and sensitivity analyses of all parameters in system (2.2) on 5000 samples. For the PRCC values in Figure 5, a parameter is positively correlated with the threshold if the sign of the PRCC for that parameter is positive, (i.e., RTN0 will increase as the parameter increases and the reverse is also true). Conversely, they are negatively correlated if the sign of the parameter is negative, (i.e., RTN0 decreases as the parameter increases and the reverse is also true). If the absolute value of its PRCC is larger than 0.4, then it means that the parameter has a strong correlation with RTN0 and has a large influence on RTN0. If the absolute value of its PRCC is between 0.2 and 0.4, then it demonstrates that the parameter has a moderate influence on RTN0. If the absolute value of its PRCC is less than 0.2, then it indicates that the parameter is weakly correlated with RTN0 and has little influence on RTN0.
As seen in Figure 5, the absolute values of the PRCC for the parameters r,a1,a2,p1,p2,τ, and TN are greater than or close to 0.4, thus demonstrating that these parameters have a large influence on RTN0 and are important control parameters. By increasing the values of the parameters r,p2,m2, and TN, the value of RTN0 also increases; thus, an increase in all of these parameters may lead to pest explosion. Besides, a1,p1,a2, and τ will decrease the value of RTN0; thus, an increase in all these parameters will favor pest control.
To start, we study the following subsystems of system (2.3):
| {dy(t)dt=−cy(t)−b2(t)y(t),t≠hTz,t≠(h+l)Tz+kTp,k=0,1,2,...,p−1,y(t+)=y(t)+τ,t=(h+l)Tz+kTp,k=0,1,2,...,p−1,y(t+)=(1−p2)y(t),t=(h+1)Tz,b2=m2e−δ2(t−hTz),hTz≤t<(h+1)Tz. | (4.1) |
Theorem 4.1. System (4.1) has a unique, globally asymptotically stable, positive, periodic solution y*(t) and limt→∞|y(t)−yZ∗(t)|=0, where
| yz∗(t)={yz∗1(t),t∈(hTz,(h+l)Tz],yz∗i(t),t∈((h+l)Tz+(i−2)Tp,(h+l)Tz+(i−1)Tp],j=2,3,⋯,p+1, | (4.2) |
| yz∗1(t)=yz∗exp(−c(t−hTz)−m2δ2(1−exp(−δ2(t−hTz)))), |
| yz∗j(t)=yz∗exp(−c(t−hTz)−m2δ2(1−e−δ2lTz)−Mj−2−Nj−2)+τj−2∑i=0exp(−Qi−Mj−2−i−Nj−2), |
| yZ∗=(1−p2)⋅τ⋅p∑i=1exp(−ciTp−Mi)1−(1−p2)exp(−cTZ−m2δ2(1−e−δ2lTZ))−Mp). |
Note
| Qi=c(t−(h+l)TZ−iTp),C0=c(t−(h+l)TZ),Mi=im2δ2(1−e−δ2Tp),M0=0,Ni=m2δ2(1−e−δ2(t−(h+l)TZ−iTp)),N0=m2δ2(1−e−δ2(t−(h+l)TZ)),i=0,1,⋯,p. |
Proof. Solving the equations of system (4.1) on the interval [hTZ,(h+l)TZ) yields the following:
| {y^Z}(t) = {y^Z}(hT_{_Z}^ + )\exp \left( { - c(t - h{T_Z}) - \frac{{{m_2}}}{{{\delta _2}}}(1 - {e^{ - {\delta _2}(t - h{T_Z})}})} \right). |
When t = (h + l){T_N} , we have the following:
| {y^Z}\left( {(h + l)T_{_Z}^ + } \right) = {y^Z}(hT_{_Z}^ + )\exp \left( { - cl{T_Z} - \frac{{{m_2}}}{{{\delta _2}}}(1 - {e^{ - {\delta _2}l{T_Z})}})} \right) + \tau . |
When t \in \left({(h + l){T_z}, (h + l){T_z} + {T_p}} \right) , we have the following:
| {y^Z}(t) = {y^Z}(hT_{_Z}^ + )\exp \left( { - c(t - h{T_Z}) - \frac{{{m_2}}}{{{\delta _2}}}(1 - {e^{ - {\delta _2}l{T_Z})}}) - {N_0}} \right) + \tau \cdot \exp \left( { - {Q_0} - {N_0}} \right). |
At the second release of natural enemies during cycle {T_z} , we have the following:
| \begin{aligned} {y^Z}\left( {{{\left( {(h + l){T_Z} + {T_p}} \right)}^ + }} \right) & = {y^Z}(hT_Z^ + )\exp \left( { - c(l{T_Z} + {T_p}) - \frac{{{m_2}}}{{{\delta _2}}}(1 - {e^{ - {\delta _2}l{T_Z})}}) - {M_1}} \right)\\ & + \tau \cdot \exp \left( { - c{T_p} - {M_1}} \right) + \tau . \end{aligned} |
In t \in ((h + l){T_Z} + {T_p}, (h + l){T_Z} + 2{T_p}) , we have the following:
| \begin{aligned} {y^Z}(t) = &{y^Z}(hT_Z^ + )\exp \left( { - c(t - h{T_Z}) - \frac{{{m_2}}}{{{\delta _2}}}(1 - {e^{ - {\delta _2}l{T_Z})}}) - {M_1} - {N_1}} \right)\\ &+ \tau \cdot \exp \left( { - {Q_0} - {M_1} - {N_1}} \right) + \tau \cdot \exp \left( { - {Q_1} - {N_1}} \right). \end{aligned} |
Repeating the previous process, after the pth release of the natural enemy in a cycle {T_Z} , i.e., t \in ((h + l){T_Z} + (k - 1){T_p}, (h + 1){T_Z}] , we have the following:
| \begin{aligned} {y^Z}(t) & = {y^Z}(hT_Z^ + )\exp \left( { - c(t - h{T_Z}) - \frac{{{m_2}}}{{{\delta _2}}}(1 - {e^{ - {\delta _2}l{T_Z})}}) - {M_{p - 1}} - {N_{p - 1}}} \right)\\ & + \tau \cdot \sum\limits_{i = 0}^{p - 1} {\exp \left( { - {Q_i} - {M_{p - 1 - i}} - {N_{p - 1}}} \right)} . \end{aligned} |
When t = (h + 1){T_Z} , and pesticides are sprayed, then we have the following:
| {y^Z}((h + 1)T_Z^ + ) = (1 - {p_2}){y^Z}(hT_{_Z}^ + )\exp \left( { - c{T_Z} - \frac{{{m_2}}}{{{\delta _2}}}(1 - {e^{ - {\delta _2}l{T_Z})}}) - {M_p}} \right) + (1 - {p_2}) \cdot \tau \cdot \sum\limits_{i = 1}^p {\exp \left( { - ci{T_p} - {M_i}} \right)} . |
Let y_h^Z = {y^Z}(hT_{_Z}^ +) ; thus, we have the following:
| y_{h + 1}^Z = (1 - {p_2})y_h^Z\exp \left( { - c{T_Z} - \frac{{{m_2}}}{{{\delta _2}}}(1 - {e^{ - {\delta _2}l{T_Z})}}) - {M_p}} \right) + (1 - {p_2}) \cdot \tau \cdot \sum\limits_{i = 1}^p {\exp \left( { - ci{T_p} - {M_i}} \right)} \buildrel \Delta \over = F(y_h^N). |
From the above equation, the only possible immovable point is as follows:
| {y^{Z*}} = \frac{{(1 - {p_2}) \cdot \tau \cdot \sum\limits_{i = 1}^p {\exp \left( { - ci{T_p} - {M_i}} \right)} }}{{1 - (1 - {p_2})\exp \left( { - c{T_Z} - \frac{{{m_2}}}{{{\delta _2}}}(1 - {e^{ - {\delta _2}l{T_Z})}}) - {M_p}} \right)}}. |
Because (3.4) is a linear system and \left| \frac{{dF(y_h^N)}}{{y_h^N}}\right| = 1 - (1 - {p_2})\exp \left({ - c{T_Z} - \frac{{{m_2}}}{{{\delta _2}}}(1 - {e^{ - {\delta _2}l{T_Z})}}) - {M_p}} \right) < 1, it follows from the theory of differential equations that it is a positive equilibrium point of global asymptotic stability of the differential equations. Thus, system (2.3) exists as a single globally asymptotically stable periodic solution {y^{Z*}}(t) . An arbitrary solution y(t) of system (2.3) converges to {y^{Z*}}(t) , as denoted by (4.2) when t \to \infty . The proof is accomplished.
Thus, system (2.3) exists as a pest extinction period solution (0, {y^{Z*}}(t)).
Theorem 4.2. If R_0^{{T_z}} < 1 stands, then the pest extinction period solution for system (2.3) is globally asymptotically stable.
Proof. In the first step, we show that the extermination period solution (0, {y^{Z*}}(t)) of system (2.3) is locally asymptotically stable, which is determined by considering a small amplitude perturbation (\alpha (t), \beta (t)) of the solution. Defining x(t) = \alpha (t), y(t) = {y^{Z*}}(t) + \beta (t), where \alpha (t), \beta (t) is a small perturbation, which can be written as follows:
| \left( \begin{array}{l} \alpha (t)\\ \beta (t) \end{array} \right) = \varphi (t)\left( \begin{array}{l} \alpha (0)\\ \beta (0) \end{array} \right),{\rm{ }}t \in (0,{T_Z}], |
where \varphi (t) = \prod\limits_{j = 1}^{p + 1}{\varphi _j}(t) , and {\varphi _j}(t) fulfill
| \frac{{d{\varphi _1}(t)}}{{dt}} = \left( {\begin{array}{*{20}{c}} {r - {b_1}(t) - {a_2}y_1^{Z*}(t)}&0\\ {\begin{array}{*{20}{c}} {{k_2}{a_2}y_1^{Z*}(t)}&{ - c} \end{array}}&{ - c - {b_2}(t)} \end{array}} \right){\varphi _1}(t),{\rm{ }}t \in (0,l{T_Z}], |
| \frac{{d{\varphi _j}(t)}}{{dt}} = \left( {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {r - {b_1}(t) - {a_2}y_j^{Z*}(t)}\\ {{k_2}{a_2}y_j^{Z*}(t)} \end{array}}&{\begin{array}{*{20}{c}} 0\\ { - c - {b_2}(t)} \end{array}} \end{array}} \right){\varphi _j}(t), |
where
| t \in (l{T_Z} + (j - 2){T_p},l{T_Z} + (j - 1){T_p}],j = 2,3, \ldots ,p + 1. |
Hence,
| {\varphi _1}(t) = \left( {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} { \exp (\int_0^t {(r - {b_1}(t) - {a_2}y_1^{Z*}(t))ds)} }\\ * \end{array}}&{\begin{array}{*{20}{c}} 0\\ {\exp ( - ct - \frac{{{m_2}}}{{{\delta _2}}}(1 - {e^{ - {\delta _2}t}})} \end{array}} \end{array}} \right), |
| {\varphi _j}(t) = \left( {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {V_3 }\\ * \end{array}}&{\begin{array}{*{20}{c}} 0\\ {V_4} \end{array}} \end{array}} \right), |
where
| V_3 = \exp (\int_{l{T_Z} + (j - 2){T_p}}^t {(r - {b_1}(s) - {a_2}y_j^{Z*}(s))ds)}, |
| V_4 = \exp ( - c(t - l{T_Z} - (j - 2){T_p} - \frac{{{m_2}}}{{{\delta _2}}}(1 - {e^{ - {\delta _2}(t - l{T_Z} - (j - 2){T_p})}})). |
It is not necessary to compute the precise form of \left(* \right) because it is not needed in the following theories. By the Floquet theory, if the modes of the two eigenvalues of a single-valued matrix
| V = \left( {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {1 - {p_1}}\\ 0 \end{array}}&{\begin{array}{*{20}{c}} 0\\ {1 - {p_2}} \end{array}} \end{array}} \right){\varphi _1}(l{T_Z})\prod\limits_{j = 2}^{p + 1} {\left( {\begin{array}{*{20}{c}} 1&0\\ 0&1 \end{array}} \right){\varphi _j}(l{T_Z} + (j - 1){T_p})} , |
are less than 1, then the pest extinction period solution is locally asymptotically stable. Indeed, the eigenvalues are as follows:
| \lambda _1^Z = (1 - {p_1})\exp (\int_0^{l{T_Z}} ( r - {b_1}(s) - {a_2}y_1^{Z*}(s))ds + \sum\limits_{j = 2}^{p + 1} {\int_{l{T_Z} + (j - 2){T_p}}^{l{T_Z} + (j - 1){T_p}} {(r - {b_1}(s) - {a_2}y_j^{Z*}(s))ds)} } , |
| \lambda _2^Z = (1 - {p_2})\exp \left( { - c{T_Z} - (p + 1)\frac{{{m_2}}}{{{\delta _2}}}(1 - {e^{ - {\delta _2}{T_p}}})} \right) < 1. |
Thus, when \left| {\lambda _1^Z} \right| < 1 , i.e., \frac{{r{T_z}}}{{\ln (\frac{1}{{1 - {p_1}}}) + C + D + \sum\limits_{k = 2}^{p + 1} {\int_{l{T_z} + (k - 2){T_p}}^{l{T_z} + (k - 1){T_p}} {(ay_k^{z*}(s))ds} } }} < 1 , where
| \begin{aligned} &C = \frac{{{m_1}}}{{{\delta _1}}}(1 - {e^{ - {\delta _1}l{T_Z}}}) + \frac{{a{y^{{Z^*}}}}}{{c + {m_2}}} - \frac{{a{y^{{Z^*}}}\exp ( - cl{T_Z} - \frac{{{m_2}}}{{{\delta _2}}}(1 - {e^{ - {\delta _2}l{T_Z}}}))}}{{c + {m_2}{e^{ - {\delta _2}l{T_Z}}}}},\\ &D = p\frac{{{m_1}}}{{{\delta _1}}}{e^{ - {\delta _1}l{T_Z}}}(1 - {e^{ - {\delta _1}{T_p}}}). \end{aligned} |
Let
| R_0^{{T_z}} = \frac{{r{T_z}}}{{\ln ( \frac{1}{{1 - {p_1}}}) + C + D + \sum\limits_{k = 2}^{p + 1} {\int_{l{T_z} + (k - 2){T_p}}^{l{T_z} + (k - 1){T_p}} {(ay_k^{z*}(s))ds} } }}, |
that is, when R_0^{{T_Z}} < 1 , the periodic solution of system (2.3) for pest extinction is locally asymptotically stable.
Similar to the global attractiveness proof of Theorem 3.2, we can also conclude that the periodic solution (0, {y^{Z*}}(t)) of system (2.3) is globally attractive.
For the case where the frequency of natural enemy releases is higher than the frequency of pesticide spraying, we consider a bifurcation diagram of system (2.3) with respect to the pulse period and the number of natural enemy releases.
In Figure 6(a), we take r = 6, K = 7, c = 0.4, {{p_1}} = 0.6, {{p_2}} = 0.3, d = 0.5, {{a_2}} = 0.35, {{k_2}} = 1.8, l = 0.8, {\delta _1} = 0.4, {\delta _2} = 0.2, {{m_1}} = 0.3, {{m_2}} = 0.1, \tau = 0.2 , and (x(0), y(0)) = (2, 2.5) ; fixing these parameters, we simulate the bifurcation diagram of system (2.3) with respect to the impulse period {T_Z} . Observing Figure 6(a), as {T_Z} increases from 0.1 to 8.1, system (2.3) undergoes complex dynamical behaviors, including cycles, tangent bifurcations (from cycles directly into chaos), chaos, multiplicative bifurcations, half-cycle bifurcations, and stabilization. The value of the parameter c is varied so that it is c = 0.45 , as shown in Figure 6(b), which is known as the mouse diagram.
In Figure 7, we model the bifurcation diagram of system (2.3) with respect to the number of releases \tau by natural enemies. Let r = 6, K = 7, c = 0.4, {{p_1}} = 0.6, {{p_2}} = 0.3, d = 0.5, {{a_2}} = 0.35, {{k_2}} = 1.8, l = 0.8, {\delta _1} = 0.3, {\delta _2} = 0.1, {{m_1}} = 0.3, {{m_2}} = 0.13, {T_Z} = 2.7 , and (x(0), y(0)) = (2, 2.5) to obtain Figure 7(a). The dynamic behavior consists of a series of periodically doubled chaotic direct, reverse cascade, and non-unique dynamics as \tau increases from 0.1 to 5.1. We can vary the value of the parameter c so that c = 0.42 , to obtain Figure 7(b), where there is a clear coexistence of multiple attractors.
Here, we fix all other parameters and make k (p) change; for various periods {T_N} = {T_Z} , R_0^{{T_N}} is compared with R_0^{{T_Z}} , as shown in Figure 8. First, we observe that the threshold R_0^{{T_N}} is a monotonically increasing function with regard to the number of sprays k in the shorter period {T_N} , which indicates that the control measures are not ideal (as shown in Figure 8(a)). If the period {T_N} increases, then the relationship between the threshold and the number of sprays k is not monotonic, and the threshold R_0^{{T_N}} has minimal values between the number of sprays (4-5). If the period {T_N} increases from 9 to 14, then the threshold R_0^{{T_N}} is monotonically decreasing as a function of the number of sprays k , at which point more sprays are better. However, we must note that the value of the threshold R_0^{{T_N}} in the short period {T_N} is always smaller than the value of the threshold in the long period {T_N} , thus we should choose the number of sprays carefully in a given period.

Observing Figure 8, under the same period, the threshold R_0^{{T_Z}} is always a monotonic decreasing function with respect to the parameter p , thus indicating that the frequent release of natural enemies is beneficial to the prevention of pests, regardless of the length of the period. Comparing the variation of the thresholds R_0^{{T_N}} and R_0^{{T_Z}} , we also conclude that the thresholds R_0^{{T_N}} and R_0^{{T_Z}} intersect at a point within each given period {T_N} = {T_Z} . Before this intersection point, the value of the threshold R_0^{{T_Z}} is greater than the value of the threshold R_0^{{T_N}} . This indicates that when we have a low release frequency or spraying frequency, applying a spraying pesticide frequency greater than the release of natural enemies frequency measure is better for controlling pests. The above findings indicate that the long-term use of chemical or biological controls is not ideal, and that we should combine these two measures to design the best pest control strategy.
The more prominent control parameters affecting the threshold R_0^{{T_Z}} when the frequency of release of natural enemies is higher than the frequency of pesticide application are the instantaneous killing efficiency of pesticides against pests {p_1} , the non-instantaneous killing efficiencies of pesticides against both pests and natural enemies {m_1} and {m_2} , and the period of time to implement a pest control strategy {{T_Z}} (shown in Figure 9).
Here, we study system (2.2) in more depth. In Parts III and IV, we are more interested in adopting effective measures to eliminate pests. However, from an ecological and economic point of view, the strategy of pest extermination is not ideal. This is because frequent spraying of pesticides causes severe environmental pollution, the cost of captive breeding of natural enemies is high, and more importantly, the right amount of pests is conducive to maintaining the balance of natural ecosystems. Therefore, we only need to take control measures when the pest density reaches the ET to prevent the pest density from increasing to the EIL.
In this section, it is hypothesized that the IPM is employed when the pest density reaches ET; if the appropriate time series are {\lambda _1}, {\lambda _2}, \ldots, and {\lambda _1} < {\lambda _2} < \cdots < {\lambda _j} < {\lambda _{j + 1}} < \cdots, then x({\lambda _j}) = ET for j = 1, 2, \ldots . Following these assumptions, the following state-dependent IPM model with an ET is established.
| \begin{equation} \left\{ \begin{array}{l} \left. \begin{array}{l} \frac{{dx(t)}}{{dt}} = rx(t)(1 - \frac{{x(t)}}{K}) - \frac{{{a_1}x(t)y(t)}}{{1 + dx(t)}},\\ \frac{{dy(t)}}{{dt}} = \frac{{{k_1}{a_1}x(t)y(t)}}{{1 + dx(t)}} - cy(t), \end{array} \right\}t \in (0,{\lambda _1}],\\ \left. \begin{array}{l} x({t^ + }) = (1 - {p_1})x(t),\\ y({t^ + }) = (1 - {p_2})y(t), \end{array} \right\}t = {\lambda _j},\\ \left. \begin{array}{l} \frac{{dx(t)}}{{dt}} = rx(t)(1 - \frac{{x(t)}}{K}) - \frac{{{a_2}x(t)y(t)}}{{1 + dx(t)}} - {b_1}(t)x(t),\\ \frac{{dy(t)}}{{dt}} = \frac{{{k_2}{a_2}x(t)y(t)}}{{1 + dx(t)}} - cy(t) - {b_2}(t)y(t), \end{array} \right\}t \ne {\lambda _j},t > {\lambda _j},\\ \left. \begin{array}{l} x({t^ + }) = x(t),\\ y({t^ + }) = y(t) + \tau , \end{array} \right\}t = h{T_N},h \in N, \end{array} \right. \end{equation} | (5.1) |
where {b_i}(t) = {m_i}{e^{ - {\delta _i}(t - {\lambda _j})}}, i = 1, 2, {\lambda _j} \le t < {\lambda _{j + 1}}, j \in {N^ + }. The starting values are x(0) = {x_0} < ET, y(0) = {y_0}, and the other parameters have the same meaning as in model (2.2).
It is very difficult to theoretically study system (5.1). This is because we are unable to determine the exact time and frequency of insecticide spraying. In the following, we investigated the effect of the starting values (x(0), y(0)) , the intrinsic growth rate r, the non-instantaneous kill rate of pesticides on pests {{m_1}} , the natural enemy release \tau , and the impulse release period {T_N} on the number of pesticide applications for controlling pests up to the ET in a given time by numerical simulations.
We take r = 2.45, K = 2.2, {{a_1}} = 1.5, {{a_2}} = 1.2, c = 0.45, {{k_1}} = 0.6, {{k_2}} = 0.4, {{p_1}} = 0.5, {{p_2}} = 0.08, d = 0.5, l = 0.8, {{m_1}} = 0.2, {{m_2}} = 0.1, {\delta _1} = 0.2, {\delta _2} = 0.4 , and ET = 1.7. We fix {T_N} = 2.7 and \tau = 0.35 for a fixed time t \in [0,140] . We fix the values of other parameters and change the initial values in Figure 10. In Figure 10(a), let (x(0), y(0)) = (0.2, 0.4) be the original densities of the pest and natural enemy populations, and the density of the pests reaches the ET only once, so we only need to apply insecticides to them once.

If its initial density is changed, then the number of times chemical control is required changes. In Figure 10(b)–(d), we set the original densities as (0.4, 0.3) , (0.2, 0.1) , and (0.3, 0.1) , respectively. We observe that two, four, and five pesticide sprays are required to control the pests below the ET. Setting the same initial value as Figure 10(d), increasing the release of natural enemy \tau to 0.5, as compared with \tau = 0.35, the need for chemical control will be reduced. What would have required five sprays of pesticide to bring the density of its pests below ET now requires only two sprays (see Figure 11(a)).

In Figure 11(b), we change the value of {T_N} to reduce it from 2.7 to 0.8, and the other parameters are the same as in Figure 11(a). From Figure 11(b), we can see that the density of the pests never got to 1.7, which is the value of the threshold ET. This indicates that with the appropriate parameter values, the density of the pests can be controlled under the ET in the absence of insecticide spraying. When we reduce the parameter r from 2.45 to 1.8, then chemical control only needs to be implemented once compared to Figure 11(a), see Figure 11(c). Similarly, with other parameters similar to those in Figure 11(a), the number of pesticide sprays changed from five to three when {{m_1}} = 0.6 (see Figure 11(d)). The upper results indicate that the intrinsic growth rate, initial density, number of released natural enemies, non-instantaneous kill rate of pesticides on pests, and the pulse release period influence the frequency of pesticide application. Importantly, appropriate values of the parameters (i.e., adjusting the control strategy) can eliminate the need for chemical control for a given time or maintain the density of the pest population below the ET after a finite insecticide application.
The use of pesticides has an impact not only on pests, but also on natural enemies. In addition, the effects of pesticide spraying on organisms not only occur instantaneously, but are present for the following period of time. Therefore, in this article, we take these factors into account and propose a model that is more consistent with the interrelationship between pests and natural enemies. In this model, the interaction between predator and prey is determined by the nutritional function of Holling II, which can control the pest population more effectively and is more in line with the law of biological development in nature.
First, we considered two scenarios with different frequencies of pest control: pesticide application at a higher or lower frequency than the release of natural enemies. Bifurcation analyses were performed for models (2.2) and (2.3), and the system was found to have complex dynamical behaviors, such as a period-doubling bifurcation, a half-period bifurcation, chaos, the coexistence of multiple attractors, and non-unique dynamics. For the bifurcation diagrams of models (2.2) and (2.3), we can observe that with an increase in pulse period and the number of released natural enemies, the pest and natural enemy populations show almost the same change trend, which is in line with the natural biological development trend. For both cases, we also discuss conditions for local stability, global attractiveness, and global stability of pest extinction period solutions. For the threshold of global asymptotic stability, we investigate the effect of parameters on the threshold conditions. For the case where the frequency of pesticide spraying is higher than the release of natural enemies, as based on the analysis, we can formulate the optimal number of insecticide applications to minimize the threshold. For the case where the frequency of release of natural enemies is higher than the frequency of pesticide spraying, the optimal number of applications of natural enemies can be formulated.
Second, we compared the effect of the spraying frequency on the thresholds in both cases as the impulse period varied, and concluded that there was an intersection of the two thresholds as the frequency increased. It is better to apply a more frequent strategy of natural enemy release before that intersection point is better for controlling pests and to apply pesticide spraying more frequently after the intersection point. By using two-parameter and LHS/PRCC uncertainty and sensitivity analysis techniques to determine the most important parameters of the threshold conditions, we obtained that the key parameters affecting the threshold are the intrinsic growth rate r , the natural enemy release \tau , the attenuation rate {\delta _1} , the instantaneous kill rates {{p_1}} and {{p_2}} , the impulse control period {T_N} and {T_Z} , and the non-instantaneous kill rates {{m_1}} and {{m_2}} . Additionally, we found that applying pesticides too early or too late is not conducive to preventing pests, there is an optimal application time, and increasing the release of natural enemies is conducive to controlling the number of pests. All of these results can help us design appropriate control strategies.
Third, according to the definition of the IPM, the ideal control goal is to maintain its pest population density below the ET rather than eradicating it. Therefore, based on system (2.2), we studied the pest control model with a state-dependent correlation in Section 4. It has been observed that pests and their natural enemies coexist in ecosystems and that an appropriate number of pests is conducive to maintaining the balance of natural ecosystems. You can change the value of each parameter and observe its effect on pest control. Through numerical simulations, we found that varying the values of the initial density, the intrinsic growth rate, the number of natural enemies released, the non-instantaneous kill rate, and the impulse release period all affect the number of pesticides that need to be sprayed in order to control pest densities below the ET. Moreover, it can be seen that at appropriate parameter values, we do not need to chemically control them because pest densities are consistently below the ET. In addition, the effectiveness of increasing the release of natural enemies to control pests was also obtained, which follows the laws of biological change in nature.
Finally, in this paper, we only considered the effects of pesticides on pests and natural enemies and the effects of different application frequencies and measures to control pests. We did not consider the effects of pest resistance following repeated applications of pesticides. In future research, we will set out to investigate how to integrate pesticide resistance with the transient and non-transient effects found in this paper.
The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.
The authors would like to thank the editor and anonymous referees for their valuable comments and suggestions which have led an improvement of the paper. Funding will be provided by The National Natural Science Foundation of China (Grant Nos. 12261033, 12201196) for the publication of this paper.
The authors declare that they have no conflicts of interest.
The data used to support the findings of this study are included within the article.
| \left\{ \begin{array}{l} \frac{{d\omega (t)}}{{dt}} = {\varepsilon _2} - c\omega (t),t \in (h{T_N},(h + l){T_N}],\\ \omega ({t^ + }) = (1 - {p_1})\omega (t),t = (h + l){T_N} + n{T_k},n = 0,1,2, \ldots ,k - 1,\\ \frac{{d\omega (t)}}{{dt}} = {\varepsilon _2} - c\omega (t) - {b_2}(t)\omega (t),t \in ((h + l){T_N},(h + 1){T_N}],t \ne (h + 1){T_N} + n{T_k}\\ \omega ({t^ + }) = \omega (t),t = (h + 1){T_N}. \end{array} \right. |
When t \in [h{T_N}, (h + l){T_N}) , we have the following:
| \omega (t) = \omega (hT_N^ + )\exp ( - c(t - h{T_N})) + \frac{{{\varepsilon _2}}}{c}(1 - \exp ( - c(t - h{T_N}))). |
With t = (h + l){T_N} , there is the following:
| \omega ((h + l)T_N^ + ) = (1 - {p_2})\omega (hT_N^ + )\exp ( - cl{T_N}) + \frac{{{\varepsilon _2}(1 - {p_2})}}{c}(1 - \exp ( - cl{T_N})). |
When t \in ((h + l){T_N}, (h + l){T_N} + {T_k}) , we have the following:
| \begin{array}{l} \omega (t) = (1 - {p_2})\omega (hT_N^ + )\exp \left( { - c(t - h{T_N}) - {B_0}} \right) + \frac{{{\varepsilon _2}(1 - {p_2})}}{c} \cdot \left( {1 - \exp ( - cl{T_N})} \right) \cdot \exp ( - {C_0} - {B_0})\\ \; \; \; \; \; \; \; {\rm{ }} - \frac{{{\varepsilon _2}}}{{c + {m_2}}}\exp ( - {C_0} - {B_0}) {\rm{ + }}\frac{{{\varepsilon _2}}}{{c + {m_2}\exp ( - {\delta _2}\left( {t - (h + l){T_N})} \right)}}. \end{array} |
When t = (h + l){T_N} + {T_k} , we have the following:
| \begin{array}{l} \omega \left( {{{\left( {(h + l){T_N} + {T_k}} \right)}^ + }} \right) = {(1 - {p_2})^2}\omega (hT_N^ + )\exp \left( { - c(l{T_N} + {T_k}) - {A_1}} \right) \\ \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; {\rm{ + }}\frac{{{\varepsilon _2}{{(1 - {p_2})}^2}}}{c} \cdot \left( {1 - \exp ( - cl{T_N})} \right) \cdot \exp ( - c{T_k} - {A_1})\\ \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; {\rm{ + }}\frac{{{\varepsilon _2}(1 - {p_2})}}{{c + {m_2}\exp ( - {\delta _2}{T_k})}} - \frac{{{\varepsilon _2}(1 - {p_2})}}{{c + {m_2}}}\exp ( - c{T_k} - {A_1}), \end{array} |
With t \in ((h + l){T_N} + {T_k}, (h + l){T_N} + 2{T_k}) , there is the following:
| \begin{aligned} \omega (t) = &{(1 - {p_2})^2}\omega (hT_N^ + )\exp \left( { - c(t - h{T_N}) - {A_1} - {B_1}} \right) + \frac{{{\varepsilon _2}{{(1 - {p_2})}^2}}}{c} \cdot (1 - \exp ( - cl{T_N})) \\ &\cdot \exp ( - {C_0} - {A_1} - {B_1}) {\rm{ + }}\frac{{{\varepsilon _2}(1 - {p_2})}}{{c + {m_2}\exp ( - {\delta _2}{T_k})}} \cdot \exp ( - {C_1} - {B_1}) \\ &- \frac{{{\varepsilon _2}}}{{c + {m_2}}}\left[ {(1 - {p_2}) \cdot \exp ( - {C_0} - {A_1} - {B_1}) + \exp ( - {A_1} - {B_1})} \right]\\ & {\rm{ }} + \frac{{{\varepsilon _2}}}{{c + {m_2}\exp ( - {\delta _2}(t - (h + l){T_N} - {T_k}))}}, \end{aligned} |
At t = (h + l){T_N} + 2{T_k} , there is the following:
| \begin{aligned} \omega \left( {{{\left( {(h + l){T_N} + 2{T_k}} \right)}^ + }} \right) & = {(1 - {p_2})^3}\omega (hT_N^ + )\exp \left( { - c(l{T_N} + 2{T_k}) - {A_2}} \right) \\ & {\rm{ + }}\frac{{{\varepsilon _2}{{(1 - {p_2})}^3}}}{c} \cdot (1 - \exp ( - cl{T_N})) \cdot \exp ( - 2c{T_k} - {A_2})\\ & {\rm{ + }}\frac{{{\varepsilon _2}(1 - {p_2})}}{{c + {m_2}\exp ( - {\delta _2}{T_k})}} \cdot \left[ {(1 - {p_2})\exp ( - c{T_k} - {A_1}) + 1} \right]\\ & {\rm{ + }}\frac{{{\varepsilon _2}(1 - {p_2})}}{{c + {m_2}}} \cdot \left[ {(1 - {p_2}) \cdot \exp ( - 2c{T_k} - {A_2}) + \exp ( - c{T_k} - {A_1})} \right]. \end{aligned} |
When t \in ((h + l){T_N} + 2{T_k}, (h + l){T_N} + 3{T_k}) , we have the following:
| \begin{aligned}{l} \omega (t) & = {(1 - {p_2})^3}\omega (hT_N^ + )\exp \left( { - c(t - h{T_N}) - {A_2} - {B_2}} \right) + \frac{{{\varepsilon _2}{{(1 - {p_2})}^3}}}{c} \cdot \left( {1 - \exp ( - cl{T_N})} \right)\\ &\cdot \exp ( - {C_0} - {A_2} - {B_2}) {\rm{ + }}\frac{{{\varepsilon _2}(1 - {p_2})}}{{c + {m_2}\exp ( - {\delta _2}{T_k})}} \cdot \left[ {(1 - {p_2}) \cdot \exp ( - {C_1} - {A_1} - {B_2}) + \exp ( - {C_2} - {B_2})} \right]\\ & {\rm{ }} - \frac{{{\varepsilon _2}}}{{c + {m_2}}} \cdot \left[ {{{(1 - {p_2})}^2} \cdot \exp ( - {C_0} - {A_2} - {B_2}) + (1 - {p_2})\exp ( - {C_1} - {A_1} - {B_2}) + \exp ( - {C_2} - {B_2})} \right]\\ & {\rm{ }} + \frac{{{\varepsilon _2}}}{{c + {m_2}\exp ( - {\delta _2}(t - (h + l){T_N} - 2{T_k}))}}. \end{aligned} |
When t = (h + l){T_N} + 3{T_k} , we have the following:
| \begin{aligned} \omega \left( {{{\left( {(h + l){T_N} + 3{T_k}} \right)}^ + }} \right) & = {{(1 - {p_2})}^4}\omega (hT_N^ + )\exp \left( { - c(l{T_N} + 3{T_k}) - {A_3}} \right)\\ &+ \frac{{{\varepsilon _2}{{(1 - {p_2})}^4}}}{c} \cdot \left( {1 - \exp ( - cl{T_N})} \right) \cdot \exp ( - 3c{T_k} - {A_3}){\rm{ + }}\frac{{{\varepsilon _2}}}{{c + {m_2}\exp ( - {\delta _2}{T_k})}}\\ &\cdot \left[ {{{(1 - {p_2})}^3}\exp ( - 2c{T_k} - {A_2}) + {{(1 - {p_2})}^2}\exp ( - c{T_k} - {A_1}) + (1 - {p_2})} \right]\\ &- \frac{{{\varepsilon _2}}}{{c + {m_2}}} \cdot \left( {{{(1 - {p_2})}^3} \cdot \exp ( - 3c{T_k} - {A_3}) + {{(1 - {p_2})}^2}} \right.\\ & \left. {\cdot \exp ( - 2c{T_k} - {A_2}) + (1 - {p_2}) \cdot \exp ( - c{T_k} - {A_1})} \right). \end{aligned} |
Therefore, when t \in ((h + l){T_N} + (k - 1){T_k}, (h + 1){T_N}) , we have the following:
| \begin{array}{l} \omega (t) = {(1 - {p_2})^k}\omega (hT_N^ + )\exp \left( { - c(t - h{T_N}) - {A_{k - 1}} - {B_{k - 1}}} \right) \\ \; \; \; \; \; \; \; {\rm{ + }}\frac{{{\varepsilon _2}{{(1 - {p_2})}^k}}}{c} \cdot \left( {1 - \exp ( - cl{T_N})} \right) \cdot \exp ( - {C_0} - {A_{k - 1}} - {B_{k - 1}})\\ \; \; \; \; \; \; \; {\rm{ + }}\frac{{{\varepsilon _2}(1 - {p_2})}}{{c + {m_2}\exp ( - {\delta _2}{T_k})}} \cdot \sum\limits_{i = 1}^{k - 1} {{{(1 - {p_2})}^{i - 1}} \cdot \exp ( - {C_{k - i}} - {A_{i - 1}} - {B_{k - 1}})} \\ \; \; \; \; \; \; \; {\rm{ - }}\frac{{{\varepsilon _2}}}{{c + {m_2}}} \cdot \sum\limits_{i = 0}^{k - 1} {{{(1 - {p_2})}^i} \cdot \exp ( - {C_{k - 1 - i}} - {A_i} - {B_{k - 1}})} \\ \; \; \; \; \; \; {\rm{ }} + \frac{{{\varepsilon _2}}}{{c + {m_2}\exp ( - {\delta _2}(t - (h + l){T_N} - (k - 1){T_k}))}}. \end{array} |
When t = (h + 1){T_N} , we have the following:
| \begin{aligned} \omega \left( {{{\left( {(h + 1){T_N}} \right)}^ + }} \right) = & {(1 - {p_2})^k}\omega (hT_N^ + )\exp \left( { - c{T_N} - {A_k}} \right) + \frac{{{\varepsilon _2}{{(1 - {p_2})}^k}}}{c} \\ &\cdot \left( {1 - \exp ( - cl{T_N})} \right) \cdot \exp ( - kc{T_k} - {A_k})\\ & {\rm{ + }}\frac{{{\varepsilon _2}}}{{c + {m_2}\exp ( - {\delta _2}{T_k})}}{\rm{ }} \cdot \sum\limits_{i = 1}^k {\left[ {{{(1 - {p_2})}^{i - 1}}\exp \left( { - c(i - 1){T_k} - {A_{i - 1}}} \right)} \right]} \\ & {\rm{ }} - \frac{{{\varepsilon _2}}}{{c + {m_2}}} \cdot \sum\limits_{i = 0}^{k - 1} {\left[ {{{(1 - {p_2})}^i}\exp \left( { - c(i + 1){T_k} - {A_{i + 1}}} \right)} \right]} + \tau . \end{aligned} |
Let {\omega _h} = \omega (hT_{_N}^ +), we have the following equation:
| \begin{array}{l} {\omega _{h + 1}} = {(1 - {p_2})^k}{\omega _h}\exp \left( { - c{T_N} - {A_k}} \right) + \frac{{{\varepsilon _2}{{(1 - {p_2})}^k}}}{c} \cdot \left( {1 - \exp ( - cl{T_N})} \right) \cdot \exp ( - ck{T_k} - {A_k})\\ \; \; \; \; \; \; \; \; \; {\rm{ + }}\frac{{{\varepsilon _2}}}{{c + {m_2}\exp ( - {\delta _2}{T_k})}}{\rm{ }} \cdot \sum\limits_{i = 1}^k {\left[ {{{(1 - {p_2})}^{i - 1}}\exp \left( { - c(i - 1){T_k} - {A_{i - 1}}} \right)} \right]} \\ \; \; \; \; \; \; \; \; {\rm{ }} - \frac{{{\varepsilon _2}}}{{c + {m_2}}} \cdot \sum\limits_{i = 0}^{k - 1} {\left[ {{{(1 - {p_2})}^i}\exp \left( { - c(i + 1){T_k} - {A_{i + 1}}} \right)} \right]} + \tau \buildrel \Delta \over = G({\omega _h}). \end{array} |
By investigating the above equation, we get that the equation has a unique immovable point
| {\omega ^*} = \frac{E}{{\left( {1 - {{(1 - {p_2})}^k}\exp ( - c{T_N} - {A_k})} \right)}}, |
where
| \begin{array}{l} E = \frac{{{\varepsilon _2}{{(1 - {p_2})}^k}}}{c} \cdot \left( {1 - \exp ( - cl{T_N})} \right) \cdot \exp ( - ck{T_k} - {A_k}) {\rm{ + }}\frac{{{\varepsilon _2}}}{{c + {m_2}\exp ( - {\delta _2}{T_k})}}{\rm{ }}\\ \; \; {\rm{ }} \cdot \sum\limits_{i = 1}^k {\left[ {{{(1 - {p_2})}^{i - 1}}\exp \left( { - c(i - 1){T_k} - {A_{i - 1}}} \right)} \right]} - \frac{{{\varepsilon _2}}}{{c + {m_2}}} \cdot \sum\limits_{i = 0}^{k - 1} {\left[ {{{(1 - {p_2})}^i}\exp \left( { - c(i + 1){T_k} - {A_{i + 1}}} \right)} \right]} + \tau , \end{array}\; \; \; \; \; |
| \begin{array}{l} {A_i} = \frac{{i{m_2}}}{{{\delta _2}}}(1 - {e^{ - {\delta _2}{T_k}}}),{A_0} = 0,\\ {B_i} = \frac{{{m_2}}}{{{\delta _2}}}(1 - {e^{ - {\delta _2}(t - (h + l){T_N} - i{T_k})}}), {B_0} = \frac{{{m_2}}}{{{\delta _2}}}(1 - {e^{ - {\delta _2}(t - (h + l){T_N})}}),\\ {C_i} = c(t - (h + l){T_N} - i{T_k}),{C_0} = c(t - (h + l){T_N}),i = 0,1, \cdots ,k. \end{array} |
Therefore, we have the following:
| \begin{array}{l} {\omega ^{\rm{*}}}(t){\rm{ = }}\left\{ {\begin{array}{*{20}{l}} {\omega _1^{\rm{*}}(t),t \in (h{T_N},(h + l){T_N}],}\\ {\omega _j^{\rm{*}}(t),t \in ((h + l){T_N} + (j - 2){T_k},(h + l){T_N} + (j - 1){T_k}],}\\ {j = 2,3, \ldots ,k + 1.} \end{array}} \right.\\ \omega _1^{\rm{*}}(t) = {\omega ^{\rm{*}}}\exp ( - c(t - h{T_N})) + \frac{{{\varepsilon _2}}}{c}(1 - \exp ( - c(t - h{T_N}))), \end{array} |
| \begin{array}{l} \omega _j^*(t) = {(1 - {p_2})^{j - 1}}{\omega ^{\rm{*}}}\exp \left( { - c(t - h{T_N}) - {A_{j - 2}} - {B_{j - 2}}} \right) \\ \; \; \; \; \; \; \; \; {\rm{ + }}\frac{{{\varepsilon _2}{{(1 - {p_2})}^{j - 1}}}}{c} \cdot \left( {1 - \exp ( - cl{T_N})} \right) \cdot \exp ( - {C_0} - {A_{j - 2}} - {B_{j - 2}})\\ \; \; \; \; \; \; \; \; {\rm{ + }}\frac{{{\varepsilon _2}(1 - {p_2})}}{{c + {m_2}\exp ( - {\delta _2}{T_k})}} \cdot \sum\limits_{i = 1}^{j - 2} {{{(1 - {p_2})}^{i - 1}} \cdot \exp ( - {C_{j - 1 - i}} - {A_{i - 1}} - {B_{j - 2}})} \\ \; \; \; \; \; \; \; \; {\rm{ - }}\frac{{{\varepsilon _2}}}{{c + {m_2}}} \cdot \sum\limits_{i = 0}^{j - 2} {{{(1 - {p_2})}^i} \cdot \exp ( - {C_{j - 2 - i}} - {A_i} - {B_{j - 2}})} \\ \; \; \; \; \; \; \; \; {\rm{ }} + \frac{{{\varepsilon _2}}}{{c + {m_2}\exp ( - {\delta _2}(t - (h + l){T_N} - (j - 2){T_k}))}},\\ {\omega ^*} = \frac{E}{{\left( {1 - {{(1 - {p_2})}^k}\exp ( - c{T_N} - {A_k})} \right)}}. \end{array} |
| [1] |
C. Z. Wang, X. H. Wang, Z. N. Jin, C. Müller, T. A. M. Pugh, A. P. Chen, et al., Occurrence of crop pests and diseases has largely increased in China since 1970, Nat. Food, 3 (2021), 57–65. https://doi.org/10.1038/s43016-021-00428-0 doi: 10.1038/s43016-021-00428-0

|
| [2] | P. Deepika, S. Kaliraj, A survey on pest and disease monitoring of crops, in 2021 3rd International Conference on Signal Processing and Communication (ICPSC), (2021), 156–160. https://doi.org/10.1109/ICSPC51351.2021.9451787 |
| [3] |
X. X. Sun, C. X. Hu, H. R. Jia, Q. L. Wu, X. J. Shen, S. Y. Zhao, et al., Case study on the first immigration of fall armyworm, Spodoptera frugiperda invading into China, J. Integr. Agric., 20 (2021), 664–672. https://doi.org/10.1016/S2095-3119(19)62839-X doi: 10.1016/S2095-3119(19)62839-X

|
| [4] |
J. H. Liang, S. Y. Tang, J. J. Nieto, R. A. Cheke, Analytical methods for detecting pesticide switches with evolution of pesticide resistance, Math. Biosci., 245 (2013), 249–257. https://doi.org/10.1016/j.mbs.2013.07.008 doi: 10.1016/j.mbs.2013.07.008

|
| [5] |
D. Suandi, K. P. Wijaya, M. Apri, K. A. Sidarto, D. Syafruddin, T. GÖtz, A one-locus model describing the evolutionary dynamics of resistance against insecticide in Anopheles mosquitoes, Appl. Math. Comput., 359 (2019), 90–106. https://doi.org/10.1016/j.amc.2019.03.031 doi: 10.1016/j.amc.2019.03.031

|
| [6] |
R. Lahlali, S. Ezrari, N. Radouane, J. Kenfaoui, Q. Esmaeel, H. E. Hamss, et al., Biological control of plant pathogens: A global perspective, Microorganisms, 10 (2022), 596. https://doi.org/10.3390/microorganisms10030596 doi: 10.3390/microorganisms10030596

|
| [7] |
J. C. V. Lenteren, H. J. W. V. Roermund, S. Susanne, Biological control of greenhouse whitefly (Trialeurodes vaporariorum) with the parasitoid Encarsia formosa: How does it work, Biol. Control, 6 (1996), 1–10. https://doi.org/10.1006/bcon.1996.0001 doi: 10.1006/bcon.1996.0001

|
| [8] |
J. C. V. Lenteren, J. Woets, Biological and integrated pest control in greenhouses, Annu. Rev. Entomol., 33 (1988), 239–269. https://doi.org/10.1146/annurev.en.33.010188.001323 doi: 10.1146/annurev.en.33.010188.001323

|
| [9] |
H. H. Liang, S. Y. Tang, R. A. Cheke, Beverton-Holt discrete pest management models with pulsed chemical control and evolution of pesticide resistance, Commun. Nonlinear Sci. Numer. Simul., 36 (2016), 327–341. https://doi.org/10.1016/j.cnsns.2915.12.014 doi: 10.1016/j.cnsns.2915.12.014

|
| [10] |
S. J. Gao, J. Guo, Y. Xu, H. P. Zhu, Modeling and dynamics of physiological and behavioral resistance of Asian citrus psyllid, Math. Biosci., 340 (2021), 108674. https://doi.org/10.1016/j.mbs.2021.108674 doi: 10.1016/j.mbs.2021.108674

|
| [11] | S. Y. Tang, Y. N. Xiao, Biodynamic System of A Single Population, 1st edition, Science Press, China, 2008. |
| [12] |
S. Y. Tang, Y. N. Xiao, L. S. Chen, R. A. Cheke, Integrated pest management models and their dynamical behaviour, Bull. Math. Biol., 67 (2005), 115–135. https://doi.org/10.1016/j.bulm.2004.06.005 doi: 10.1016/j.bulm.2004.06.005

|
| [13] |
B. Liu, G. Hu, B. L. Kan, X. Huang, Analysis of a hybrid pest management model incorporating pest resistance and different control strategies, Math. Biosci. Eng., 17 (2020), 4364–4383. https://doi.org/10.3934/mbe.2020241 doi: 10.3934/mbe.2020241

|
| [14] |
Z. Y. Xiang, S. Y. Tang, C. C. Xiang, J. H. Wu, On impulsive pest control using integrated intervention strategies, Appl. Math. Comput., 269 (2015), 930–946. https://doi.org/10.1016/j.amc.2015.07.076 doi: 10.1016/j.amc.2015.07.076

|
| [15] |
B. Liu, W. B. Liu, F. M. Tao, J. G. Cong, A dynamical analysis of a piecewise smooth pest control SI model, Int. J. Bifurcation Chaos, 25 (2015), 1550068. https://doi.org/10.1142/S0218127415500686 doi: 10.1142/S0218127415500686

|
| [16] | G. J. Lan, F. J. Fu, C. J. Wei, S. W. Zhang, A research of pest management SI stochastic model concerning spraying pesticide and releasing natural enemies, Commun. Math. Biol. Neurosci., 2018 (2018). https://doi.org/10.28919/CMBN/3648 |
| [17] |
S. Y. Tang, G. Y. Tang, R. A. Cheke, Optimum timing for integrated pest management: modelling rates of pesticide application and natural enemy releases, J. Theor. Biol., 264 (2010), 623–638. https://doi.org/10.1016/j.jtbi.2010.02.034 doi: 10.1016/j.jtbi.2010.02.034

|
| [18] |
W. J. Qin, Y. Xia, Y, Yang, An eco-epidemic model for assessing the application of integrated pest management strategies, Math. Biosci. Eng., 209 (2023), 16506–16527. https://doi.org/10.3934/mbe.2023736 doi: 10.3934/mbe.2023736

|
| [19] |
Y. Tian, S. Y. Tang, R. A. Cheke, Dynamic complexity of a predator-prey model for IPM with nonlinear impulsive control incorporating a regulatory factor for predator releases, Math. Model. Anal., 24 (2019), 134–154. https://doi.org/10.3846/mma.2019.010 doi: 10.3846/mma.2019.010

|
| [20] |
Q. Q. Zhang, B. Tang, T. Y. Cheng, S. Y. Tang, Bifurcation analysis of a generalized impulsive Kolmogorov model with applications to pest and disease control, SIAM J. Appl. Math., 80 (2020), 1796–1819. https://doi.org/10.1137/19M1279320 doi: 10.1137/19M1279320

|
| [21] |
S. Y. Tang, B. Tang, A. L. Wang, Y. N. Xiao, Holling II predator-prey impulsive semi-dynamic model with complex Poincaré map, Nonlinear Dyn., 81 (2015), 1575–1596. https://doi.org/10.1007/s11071-015-2092-3 doi: 10.1007/s11071-015-2092-3

|
| [22] |
B. L. Kang, B. Liu, F. G. Tao, An integrated pest management model with dose-response effect of pesticides, J. Biol. Syst., 26 (2018), 59–86. https://doi.org/10.1142/S0218339018500043 doi: 10.1142/S0218339018500043

|
| [23] |
J. H. Liang, S. Y. Tang, R. A. Cheke, An integrated pest management model with delayed responses to pesticide applications and its threshold dynamics, Nonlinear Anal. Real World Appl., 13 (2012), 2352–2374. https://doi.org/10.1016/J.NONRWA.2012.02.003 doi: 10.1016/J.NONRWA.2012.02.003

|
| [24] |
S. Y. Tang, J. H. Liang, Y. S. Tan, R. A. Cheke, Threshold conditions for integrated pest management models with pesticides that have residual effects, J. Math. Biol., 66 (2013), 1–35. https://doi.org/10.1007/s00285-011-0501-x doi: 10.1007/s00285-011-0501-x

|
| [25] |
J. Yang, Y. S. Tan, Effects of pesticide dose on Holling II predator-prey model with feedback control, J. Biol. Dyn., 12 (2018), 527–550. https://doi.org/10.1080/17513758.2018.1479457 doi: 10.1080/17513758.2018.1479457

|
| [26] |
J. Páez Chávez, D. Jungmann, S. Siegmund, A comparative study of integrated pest management strategies based on impulsive control, J. Biol. Dyn., 12 (2018), 318–341. https://doi.org/10.1080/17513758.2018.1446551 doi: 10.1080/17513758.2018.1446551

|
| [27] |
Z. Wei, Y. H. Xia, T. H. Zhang, Dynamic analysis of multi-factor influence on a Holling type II predator-prey model, Qual. Theory Dyn. Syst., 21 (2022), 1–30. https://doi.org/10.1007/s12346-022-00653-3 doi: 10.1007/s12346-022-00653-3

|
| [28] |
X. L. Hu, W. J. Qin, M. C. Tosato, Complexity dynamics and simulations in a discrete switching ecosystem induced by an intermittent threshold control strategy, Math. Biosci. Eng., 17 (2020), 2164–2179. https://doi.org/10.3934/mbe.2020115 doi: 10.3934/mbe.2020115

|
| [29] |
W. J. Qin, J. M. Zhang, Z. J. Dong, Media impact research: a discrete SIR epidemic model with threshold switching and nonlinear infection forces, Math. Biosci. Eng., 20 (2023), 17783–17802. https://doi.org/10.3934/mbe.2023790 doi: 10.3934/mbe.2023790

|
| [30] | M. Q. He, S. Y. Tang, R. A. Cheke, A Holling type II discrete switching host-parasitoid system with a nonlinear threshold policy for integrated pest management, Discrete Dyn. Nat. Soc., 2020 (2020). https://doi.org/10.1155/2020/9425285 |
| [31] |
W. J. Qin, X. W. Tan, X. T. Shi, C. C. Xiang, IPM strategies to a discrete switching predator-prey model induced by a mate-finding Allee effect, J. Biol. Dyn., 13 (2019), 586–605. https://doi.org/10.1080/17513758.2019.1682200 doi: 10.1080/17513758.2019.1682200

|
| [32] |
J. N. Liu, Q. Qi, B. Liu, S. J. Gao, Pest control switching models with instantaneous and non-instantaneous impulsive effects, Math. Comput. Simul., 205 (2022), 926–938. https://doi.org/10.1016/j.matcom.2022.10.027 doi: 10.1016/j.matcom.2022.10.027

|
| [33] |
S. J. Gao, L. Luo, S. X. Yan, X. Z. Meng, Dynamical behavior of a novel impulsive switching model for HLB with seasonal fluctuations, Complexity, 2018 (2018), 1–11. https://doi.org/10.1155/2018/2953623 doi: 10.1155/2018/2953623

|
| [34] |
R. M. May, Simple mathematical models with very complicated dynamics, Nature, 261 (1976), 459–467. https://doi.org/10.1038/261459A0 doi: 10.1038/261459A0

|
| [35] |
J. P. Eckmann, D. Ruelle, Ergodic theory of chaos and strange attractors, Rev. Mod. Phys., 57 (1985), 617–656. https://doi.org/10.1103/REVMODPHYS.57.617 doi: 10.1103/REVMODPHYS.57.617

|