The influence of immune cells on the existence of virus quasi-species

1.   Introduction

Progression of viral infections, both at the individual and population levels, can be influenced by virus mutations and genetic evolution ^{[1,2,3,4,5,6,7]}. However, predicting virus evolution is a difficult task due to the complex interaction between viral infection and the host organism ^[8,9,10,11]. Virus evolution can be described in terms of fitness and its relationship with genotypes and selection of advantageous mutations ^[12]. However, quantitative description of fitness landscapes involves multiple factors that are difficult to quantify ^[13]. To address this issue, mathematical modeling and experimental investigation are used to specify fitness landscapes ^[13,14,15]. This approach considers various factors, such as the binding affinity of viral antigens to T cells ^[9], antibody binding affinity, RNA virus capsid folding stability ^[13], among others. Corresponding mathematical models include deterministic and stochastic ODEs, systems of integro-difference equations, algebraic equations.

The concept of quasi-species represents an appropriate framework to describe virus evolution ^[16,17]. Several models were developed to describe the evolution of a discrete set of virus variants in terms of systems of differential equations ^[18]. Virus evolution in a continuous genotype space was studied in ^[7,19,20,21]. This work continues the investigation of virus density evolution in the space of genotypes in its interaction with the immune response. This approach allows the analysis of key factors affecting viral infection dynamics, such as the presence of wild type virus versus mutants, genotype branching, mutant extinction, and the mechanisms used by viruses to evade the immune system.

We consider the virus density distribution $U(x, t)$ in the space of genotypes $x$ and the concentration of immune cells $C(x, t)$ described by the equations

For mathematical convenience, the genotype variable $x$ is considered on the whole axis. The diffusion terms in both equations characterize small random mutations of viruses and cells. The second term in Eq (1.1) describes virus replication in host cells. It is proportional to the virus density $U$ and to the dimensionless quantity of uninfected cells $(K-k_1H(U))$. Here, $K = 1$ corresponds to the dimensionless total number of cells, and the quantity of infected cells is proportional to the total quantity of virus $H(U)$ competing for host cells. This assumption is justified if we assume that host cells do not die being infected. We will consider two different cases. In the first case, virus compete for the host cells independently of its genotype (global competition), $H(U) = \int_{-\infty}^{\infty}U(x, t)dx ( = I(U))$; in the second case, this competition depends on the distance between the genotypes $H(U) = \int_{-\infty}^{\infty} \phi(x-y) U(x, t)dx ( = J(U))$, where the kernel $\phi(x-y)$ characterizes the efficiency of this competition. It will be convenient in what follows to use different notation for these integrals. The last two terms in this equation describe virus elimination by the immune cells and the virus mortality rate independent of the immune response, which can be dependent on the virus genotype, with the rate $\sigma(x)$.

The second term in the right-hand side of Eq (1.2) describes clonal expansion of immune cells due to the presence of antigen (virus). The function $p(U)$ is positive for $U > 0$. It can be linear, growing with saturation, or growing for small $U$ and decaying for large $U$. Mortality rate $q(U)$ of immune cells can depend on the virus density or be independent of it (positive constant). We assume that $p(0) < q(0)$. This condition means that in the absence of viral load, the cell birth rate is less than its mortality rate and, therefore, the cell concentration decays. We do not consider here memory cells which remain in the organism after infection elimination. If the viral load $U$ is large enough, then $p(U)$ becomes larger than $q(U)$ providing the initiation of the immune response by the pathogenes. Otherwise, the concentration of immune cells vanishes, and the immune response does not influence infection progression in the organism. Let us also note that large virus concentration can down-regulate the proliferation rate of immune cells but we do not consider this effect here (see ^[22,23]).

We will study the existence of positive stationary solutions of system (1.1) and (1.2) decaying at infinity (Section 2). Such solutions correspond to virus quasi-species. Existence of such solutions is determined by the viability intervals in the space of genotypes where their birth rate exceeds the death rate. Previously, it was studied for a single equation obtained as approximation of system (1.1) and (1.2) ^[7,21]. Another mechanism of the emergence of virus quasi-species is related to their competition and to bifurcation of spatial structures from the homogeneous in space solution. It will be considered in Sections 3 and 4.

2.   Existence of positive stationary solution

In this section, we focus on the investigation of positive stationary solutions of system (1.1) and (1.2) under the condition that the virus mortality rate $\sigma(x)$ is lower than the virus replication rate within a specific range of genotypes. Our analysis shows that this genotype-dependent virus mortality rate can lead to the persistence of virus quasi-species.

2.1.   Global competition

The system of equations satisfied by the stationary solutions of system (1.1) and (1.2) on the whole axis is as follows:

where we assume that $D_1 = D_2 = k_1 = k = a = b = 1$, for simplicity of notation. We consider here the case of global competition of virus for host cells, that is, $H(U) = I(U)$. Our objective is to find positive solutions of this system of equations that approach zero as $x \to \pm \infty$. The existence of these solutions depends on the function $\sigma(x)$, which determines virus mortality. A typical example is given by the function $\sigma(x) = 0$ for $|x| \leq x_0$ and $\sigma(x) = \sigma_0 > 1$ for $|x| \geq x_1$ with some $x_0$ and $x_1 > x_0$. Functions $\sigma(x)$, $p(U)$ and $q(U)$ are supposed to be non-negative and sufficiently smooth. Some additional conditions will be formulated below. We will prove the existence of a solution using the topological degree method. To start, we will establish some preliminary estimates of solutions of this problem.

Lemma 1. Let $(U(x), C(x))$ be a positive solution of (2.1) and (2.2), $U(\pm\infty) = 0, C(\pm\infty) = 0$. Then $I(U) < 1$.

Proof. Suppose that the statement of the lemma does not hold, and $I(U)\geq 1$. As a consequence, $U(x)$ is a solution of the equation $U''+ q(x)U = 0$, where $q(x) = (1-I(U))-C(x)-\sigma(x)$. Since $q(x)\leq 0$ and $q(x)\not\equiv 0$, the maximum principle implies that $U(x)$ cannot attain a positive maximum or a negative minimum. Therefore, $U(x)\equiv 0$, which contradicts the hypothesis $U(x) > 0$.

□

Let $(U(x), C(x))$ be a positive solution of (2.1) and (2.2). The lemma below summarizes some properties of this solution.

Lemma 2. 1) There is a positive constant $K$ such that $0 < U(x) < K$ for all $x\in\mathbb{R}$.

2) If $\frac{p(U)}{q(U)}$ is bounded for all $U\geq 0$, then there exists a constant $M > 0$ such that $0 < C(x) < M$ for all $x\in\mathbb{R}$.

Proof. Assume that there exists a point $x_0$ such that $U(x_0)$ is the global maximum of $U(x)$ over the entire domain. One can infer from Eq (2.1) that

By utilizing Taylor's expansion around $x_0$, we can derive the subsequent lower bound for $U(x)$:

with some $\chi$ between $x$ and $x_0$ and where $g(x) = 1-\frac{1}{2}(x-x_0)^2$. Let $\Omega$ denote the interval where this function is positive. Thus, we have $\int_{\Omega}g(x)dx \geq \kappa > 0$. It follows from Lemma 1 that $1 > I(U) > \kappa U(x_0).$ Therefore, the first part of the lemma can be concluded.

We proceed to the second part of the lemma. If $C$ is a solution of (2.2) that attains a positive maximum at some point $y_0$, then $C''(y_0) < 0$. This implies that

and, thus,

which proves the lemma.

□

To prove the existence of solutions, we will employ the topological degree theory, as described in ^[24,25]. Lemma 2 presented above provides preliminary estimates of solutions. Denote $v: = (U, C)$ and consider the operator

The operator $A_\tau(v)$ acts from the weighted Holder space $(C_\mu^{2+\alpha} (\mathbb{R}))^2$ into the space $(C_\mu^\alpha (\mathbb{R}))^2$, where $0 < \alpha < 1$ and $\tau \in [0, 1]$ is a parameter. The space $C_\mu^\alpha (\mathbb{R})$ is defined as the set of functions $u(x)$ such that $u(x)\mu(x) \in C_\mu^{2+\alpha} (\mathbb{R})$, with $\mu(x) = 1+x^2$. This weight function increases at infinity with a polynomial rate. The introduction of weighted spaces allows the definition of topological degree for elliptic operators in unbounded domains (see ^[24,25]). Besides, the integral $I(U)$ is well-defined due to the weighted space, and it does not impact the essential spectrum.

We will suppose for simplicity that $\sigma_\tau(x)$ is an infinitely differentiable function with respect to $x$ and $\tau$. Other conditions will be specified later. Denote by $L_\tau$ the operator obtained by the linearization of the operator $A_\tau$ about $v = 0$:

Let us recall the assumption

Lemma 3. If the principal eigenvalue of the operator

is positive for $\tau_0 \leq \tau\leq \tau_1$ for some fixed $\tau_0, \tau_1$, then there exists a positive constant $\epsilon$ such that for any positive solution of the equation $A_\tau(v) = 0$ with $\tau_0 \leq \tau\leq \tau_1$, we have

Proof. It can be deduced from condition (2.7) that the unique solution of the equation

is zero. Suppose that the statement of the lemma does not hold. This implies the existence of a sequence of solutions $v_k(x)$ for $\tau = \tau_k$ such that $v_{m_k} \to 0$. Without loss of generality, we can assume that $\tau_k \to \tau_*$ for some $\tau_*\in [\tau_0, \tau_1]$. Then, we have:

Set $w_k = v_k/\|v_k\|$. Then $L_{\tau_k} w_k = o(1)$.

Using the fact that operators $L_{\tau_k}$ are proper with respect to $w$ and $\tau$ (see ^[24]), we can conclude that the sequence $w_k$ is compact. Therefore, there exists a subsequence, which we also denote as $w_k$, that converges to some function $w_0$. Hence, $L_{\tau_*}w_0 = 0$. Since the functions $w_k(x)$ are positive, the limit function $w_0(x)$ is also non-negative. Therefore, $w_0(x)\geq 0$ for all $x$. This implies that $L_{\tau_*}$ has a zero eigenvalue with a positive eigenfunction. However, the only positive eigenfunction of $L_{\tau_*}$ corresponds to the principal eigenvalue ^[26]. This leads to a contradiction. Therefore, the assertion of the lemma holds. □

The following theorem presents the main result of this section.

Theorem 1. Suppose that $p(U), q(U), \sigma(x)$ are non-negative infinitely differentiable functions, $p(U)/q(U)$ is bounded for $U \geq 0$, $\sigma(x) = \sigma > 1$ for $|x|\geq x_1$ with some positives $\sigma, \ x_1$, Condition (2.7) is satisfied and the principal eigenvalue of the problem

is positive. Then the system (2.1) and (2.2) has a positive solution converging to $0$ at infinity.

Proof. To prove the theorem, we start by defining $\sigma_\tau(x) = (1-\tau)\sigma(x)+\tau \sigma$, and let $v = (U, C)$ be the solution of problem (2.1) and (2.2). Since $\sigma > 1$, the spectrum of the operator $L_1$ is located in the left half-plane. It is worth mentioning that the essential spectrum $S_e(L_\tau)$ of the operator $L_\tau$ remains unchanged for all values of $\tau$, Re $(L_\tau)\leq -\delta < 0$ for some positive $\delta$. Let $\lambda_0(\tau)$ denote the principal eigenvalue of $L_\tau$. By the assumption of the lemma, we have $\lambda_0(0) > 0$. The principal eigenvalue $\lambda_0(\tau)$ is a decreasing function with respect to $\tau \in [0, 1]$. There exists a value $\tau_0 \in [0, 1]$ such that $\lambda_0(\tau_0) = 0$, $\lambda_0(\tau) > 0$ for $0 < \tau < \tau_0$, and $\lambda_0(\tau) < 0$ for $\tau_0 < \tau < \tau_1$, where $\tau_1$ is a value in the interval $(\tau_0, 1]$. It is not possible to guarantee the existence of the eigenvalue for all values of $\tau$ in the interval $[0, 1]$ due to the possibility of it approaching the essential spectrum. Let us consider the equation $A_\tau(v) = 0$ in a small neighborhood of the bifurcation point $\tau = \tau_0$. As the parameter approaches this value, the trivial solution $v = 0$ loses its stability, resulting in the appearance of another solution $v_\tau(x)$. This new solution is positive since the principal eigenfunction $w_0(x)$ is positive, as stated in Lemma 3. Moreover, the degree of this solution with respect to a small ball containing it is equal to $1$. This can be seen from the homotopy invariance of the degree. Indeed, from the homotopy invariance of the degree, it follows that

for all $\tau > \tau_0$ and sufficiently close to $\tau_0$. Here $\tilde v_\tau$ is a negative solution emerges from the trivial solution and converges to $-v_0(x)$. As $ind(0) = -1$, which is equal to $(-1)^\nu$, where $\nu = 1$ represents the number of positive eigenvalues of the linearized operator, we can conclude that $ind(u_\tau) = ind(\tilde u_\tau) = 1$.

Lemma 2 implies that there exists a positive constant $M_0$ such that $|u|{E_1} < M_0$ for any positive solution $u$ of the equation $A_\tau(u) = 0$. Furthermore, applying Lemma 3, we can deduce that there exists a positive value $\delta(\tau)$ such that $|u|_{E_1} > \delta(\tau)$ for $\tau < \tau_0$.

Let us consider the domain

for some $\delta_0 > 0$ sufficiently small. Choose $\tau_2 < \tau_0$ such that $\delta(\tau) > \delta_0$ for $0\leq \tau\leq \tau_2.$.

Since $A_\tau(v)\neq 0$ for $v\in \partial \Omega$, it follows that the degree $\gamma(A_\tau, \Omega)$ does not depend on $\tau \in [0, \tau_2]$. Therefore, we can conclude that $\gamma(A_0, \Omega) = \gamma(A_{\tau_2}, \Omega) = ind(v_{\tau_2}) = 1$. This means that the equation $A_0(v) = 0$ has a solution in $\Omega$. This conclusion proves the theorem.

□

2.2.   Nonlocal competition

In the case of nonlocal competition, we consider the integral $J(U)$ instead of $I(U)$:

We assume that the kernel $\phi(x)$ is a bounded and integrable function. Some specific examples will be considered below. The proof of the existence of solutions is similar to the previous case. Some difference is related to a priori estimates of solutions given in the following lemma.

Lemma 4. Let $(U(x), C(x))$ be a positive solution of (2.9) and (2.10), then:

1] There is a positive constant $K_1$ such that $0 < U(x) < K_1$.

2] If $\frac{p(U)}{q(U)}$ is bounded for all $U\geq 0$, then there exists a constant $M_1$ such that $0 < C(x) < M_1$.

Proof. We will split the proof of the lemma into two cases: $J(U) < 1$ and $J(U) \geq 1$. In the first case, we can infer that $U''(x) \geq -aU(x)$ for all $x \in \mathbb{R}$. In the second case, we have $U''(x) > 0 > -aU(x)$ for all $x \in \mathbb{R}$, since $U(x) \geq 0$. Let $x_0$ denote the global maximum of $U(x)$, which is guaranteed to exist as the function is positive and decays at infinity. We aim to prove that $J(U(x_0)) < 1$. Suppose otherwise, namely that $J(U(x_0)) \geq 1$. This would lead to a contradiction in signs in (2.9) at $x = x_0$.

The following lower bound for $U(x)$ can be deduced by expanding $U(x)$ in Taylor series about $x_0$:

where $a_2 = U''(\chi)/2$ and $g(x) = 1-a(x-x_0)^2/2$. Note that the function $g(x)$ is positive in the interval $x_0-\sqrt{\frac{2}{a}} < x < x_0+\sqrt{\frac{2}{a}}$ and equals zero at its boundary. Then we can find $x_1$ in this interval such that $g(x)\geq k > 0$ and $\phi(x) > 1/2$ for all $x\in [x_0, x_1]$. Hence

This estimate proves the first part of the lemma. The proof of the second part follows a similar approach to that of Lemma 4.

□ The remaining part of the proof of the existence of solution is similar to the proof in the case of global competition.

3.   Instability of homogeneous in space stationary solutions

3.1.   ODE model

We begin stability analysis with the corresponding ODE model without spatial variable:

where we set $p(U) = pU$ and $q(U) = qU+\sigma_2$, assuming that $a > \sigma_1, p > q$. This model possesses three stationary solutions, $E_0(0, 0)$, $E_1(1-\frac{\sigma_1}{a}, 0)$, and the coexistence (positive) equilibrium $E_*(U^*, C^*)$, where

and $U^*$ is a positive root of the following quadratic equation:

Let us note that $C^*$ is positive if the following inequality holds:

To determine the number of equilibrium points of system (3.1) and (3.2), one needs to count the number of positive real roots of Eq (3.4) that lie in the interval $(0, 1)$

Since $F(0) = -\sigma_2(a-\sigma_1+k) < 0$, and

then there exists a unique $U^*$ in $(0, 1)$ solution of Eq (3.4). Taking into account (3.5), the nontrivial equilibrium exists if

The trivial equilibrium point $E_0$ is a saddle point regardless of the parameter values. On the other hand, the virus-only equilibrium $E_1$ is stable if $\sigma_2 > (p-q)(1-\frac{\sigma_1}{a})$, and unstable otherwise.

Linearizing system (3.1) and (3.2) around $E_*$, we obtain the associated characteristic equation.

where

Hence, $E_*$ is locally asymptotically stable whenever it exists.

3.2.   Spatial perturbations for the local model

Replacing the function $\phi(z)$ with a Dirac delta-function in the system (1.1) and (1.2) where $H(U) = J(U)$, we obtain a reduced reaction-diffusion system:

The following inequalities define the conditions of the Turing instability ^[27]:

where

Two conditions (3.10) and (3.12) can not be satisfied simultaneously since $a_{11} < 0$ and $a_{22} < 0$. Therefore, the local spatiotemporal model does not meet the conditions of the Turing instability.

3.3.   Nonlocal model

Next, we will derive the instability conditions for the positive homogeneous steady-state $(U, C)$ of system (1.1) and (1.2), where $H(U) = J(U)$. The corresponding eigenvalue problem has the form:

where $z(x)$, and $w(x)$ are spatial perturbations and

Applying the Fourier transform to Eqs (3.13) and (3.14), we get

Here, $\bar{z}$, $\bar{w}$, and $\bar{\phi}$ denote the Fourier transforms of the functions $z(x)$, $w(x)$ and $\phi(z)$, respectively. The characteristic equation associated for the system (3.15) and (3.16) can be expressed as follows:

The conditions for the stability of the homogeneous steady-state $(U, C)$ under spatial perturbations are given by the inequalities:

The characteristic equation of the local reaction-diffusion system (3.8) and (3.9) can be derived from (3.17) by setting $\bar{\phi} = 1$. As previously mentioned, if $\bar{\phi} = 1$, then it is not feasible to violate the inequalities stated in (3.18) and (3.19). In numerical simulations below we will consider the kernel function

In this case,

The instability may occur due to the variable sign of this function. As the bifurcation of spatial stationary structures occurs, a single real eigenvalue passes through the origin, while a pair of complex conjugate eigenvalues cross the imaginary axis at the Hopf bifurcation threshold. We consider these two cases below.

3.3.1.   Stationary patterns

To obtain the condition of spatial instability, we begin by solving the system of equations:

Differentiating $\Delta(\xi, M)$ with respect to $M$, we get:

Substituting $\xi M = z$ into the previous equation, we obtain:

Solving this equation yields a countable number of positive roots, $0 < z_1 < z_2 < z_3 < \dots$. Set $\mu_i = \sin z_j/z_j$, $j = 1, 2, 3, \dots$. The equation $\Delta(\xi, M) = 0$ yields:

The corresponding values of $M_j$ can be obtained from the equation:

where $z_j$ are the positive roots of $\Delta(\xi, M) = 0$. Calculating the threshold values of $\xi_j$ and $M_j$ for different parameter values, we can determine the conditions under which spatial instability occurs.

3.3.2.   Time oscillations

To obtain the spatial Hopf bifurcation threshold, we find positive values of $\xi$ and $M$ that satisfy the condition $\Gamma(\xi, M) = 0$. To do so, we differentiate $\Gamma(\xi, M) = 0$ with respect to $M$, which yields

and, accordingly, we can define $\mu_j, j = 1, 2, 3, \dots$, as above. Hence $\xi_j$ and $M_j$ are defined by the equalities:

4.   Instability and pattern formation

We will analyze in this section the instability conditions presented above and will determine the parameter regions with stable and unstable solutions. We will illustrate the emerging patterns with direct numerical simulations.

4.1.   Spatial patterns for the nonlocal model

We begin with the bifurcation of spatial structures and assume that $\lim _{M \rightarrow 0+} \Gamma(\xi, M) < 0$ and $\lim _{M \rightarrow 0+} \Delta(\xi, M) > 0$. These conditions ensure stability of the homogeneous steady-state under space-independent perturbations. To determine the critical wavenumber and corresponding bifurcation threshold in terms of $d_2$, we need to solve the following two equations:

From $\Delta(k, M) = 0$, we get

When we substitute this expression into the second equation in (4.1), we get:

We assume that all parameter values are fixed except for $M$ and $d_2$, and note that this equation can have multiple positive roots. If a chosen value of $M$ results in a finite number of positive roots, denoted as $\xi_1, \xi_2, \cdots, \xi_m$ in (4.3), the corresponding values of $d_2\left(\xi_i\right)$ in (4.2) may not all be positive. To determine the bifurcation threshold $d_{2 T}$ and the corresponding value of $\xi_T$, we take the minimum positive value of $d_2\left(\xi_i\right)$ and the corresponding value of $\xi_i$ for which the minimum is achieved.

Consider, as example, the following values of parameters:

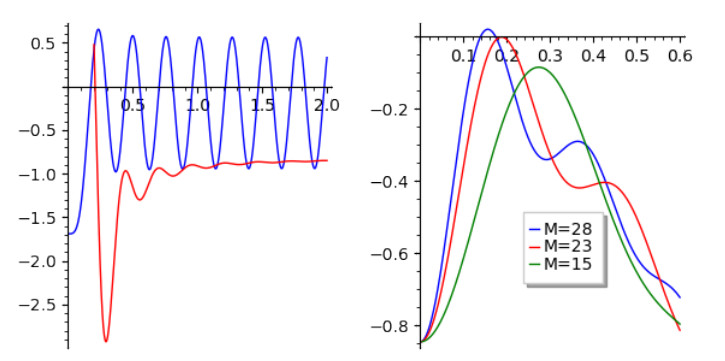
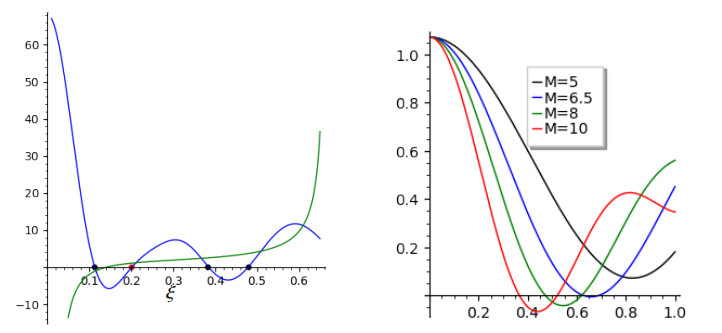
Then $U^* = 0.7, C^* = 0.95$. For $M = 22.2$, Remark that $d_2$ is an increasing function of $\xi$ in $[0, \infty[$. We find $\xi_T = 0.2$ and the bifurcation threshold $d_{2T} = 1.16$ (Figure 1, left).

After that, we calculate the critical value of $M$ that corresponds to the instability boundary, using a specific value for $d_2$. We set $a = 4.9, k = 1.2, \sigma_1 = 0.5, \sigma_2 = 0.2, p = 1.5, q = 0.8, d_1 = 1.73, d_2 = 0.06$. Given these parameters, the spatio-temporal model represented by Eqs (3.8) and (3.9) and with only local interactions ($M = 0$) does not generate any spatial patterns. It is worth noting that the values $U = 0.79$ and $C = 0.42$ correspond to the homogeneous steady-state of the model defined by Eqs (3.8) and (3.9) with the specified parameters. We find

and

Note that here we have employed the value $\bar{\phi} = 1$ to evaluate $\Gamma(\xi, 0)$ and $\Delta(\xi, 0)$. Hence both roots of the associated characteristic equation, i.e., Eq (3.17) with $\bar\phi = 1$ have negative real parts. This leads to both roots of the associated characteristic equation, i.e., Eq (3.17) with $\bar{\phi} = 1$, having negative real parts. As a result, for system (3.8) and (3.9) with local interaction, the homogeneous steady-state $(0.79, 0.42)$ is stable under small heterogeneous perturbations.

To reach a bifurcation point in the models (3.1) and (3.2), the condition (3.19) must be violated, and the bifurcation occurs if the function $\Delta(\xi, M)$, given by

intersects the $\xi$-axis. For the given parameter set, the value of the bifurcation threshold is $M_T = 6.5$. Clearly, $\Delta(\xi, M) > 0$ for all values of $\xi$ if $M < M_T$, while $\Delta(\xi, M_T) = 0$ only at $\xi = 0.62$. Furthermore, if $M > M_T$, there exists a range of values of $\xi$ for which $\Delta(\xi, M) < 0$. The plot of $\Delta(\xi, M)$ versus $\xi$ for various values of $M$ is shown in Figure 1 (right), which clearly illustrates the change in sign of the function $\Delta(\xi, M)$ with respect to $M$.

4.2.   Spatial Hopf bifurcation

To obtain the critical wavenumber for the spatial Hopf bifurcation, we begin with the expression for the bifurcation threshold in terms of the parameter $d_2$. Assuming that $(U, C)$ is locally asymptotically stable for the temporal model (3.1) and (3.2), we note that $\Gamma(\xi, M) < 0$ and $\Delta(\xi, M) > 0$ as $M\to 0+$. Furthermore, we have $\lim_{M \to 0+}\Gamma(\xi, M) = a_{11}$ and $\lim_{M \to 0+} \Delta(\xi, M) = -a_{12}a_{21}$.

If we find a unique value $\xi\equiv \xi_H$ such that $\Gamma(\xi, M) = 0$ for some suitable $M$, then $\xi_H$ is the critical wavenumber for the spatial Hopf bifurcation. This critical wavenumber can be obtained by solving the following two equations simultaneously:

The equation $\Gamma(\xi, M) = 0$ allows us to determine the value of $d_2$ as follows:

Substituting the expression for $d_2(\xi)$ from Eq (4.6) into the second equation in (4.5), we obtain:

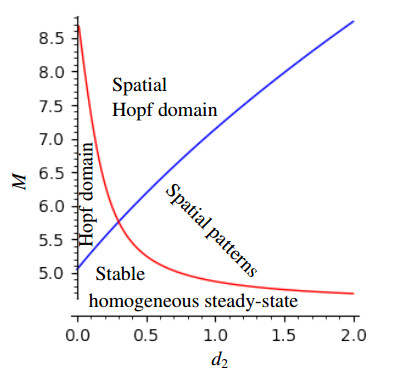
Figure 2 demonstrates that Eq (4.7) can have multiple positive real roots depending on the parameter values. We need to verify that the corresponding values of $d_2(\xi)$ are positive. Among all the positive real roots, we choose $\xi_H$ to be the one for which $d_2(\xi_H)$ is the smallest positive value and $\Delta(\xi_H, M) > 0$.

For the purpose of illustration, let us take the following set of parameter values: $a = 2.3, k = 3.3, \sigma_1 = 0.5, \sigma_2 = 0.2, p = 1.6, q = 0.6, d_1 = 0.83$. Then, $U^* = 0.32, C^* = 0.31$, and Eq (4.7) possesses only one positive root $\xi = 0.19$ for $M = 23$. From (4.6), we find $d_2 = 1$. Since $\Gamma(0.19, 21.5) = 0.19 > 0$, these values of $\xi$ and $d_2$ correspond to the desired spatial Hopf bifurcation thresholds, $\xi_H = 0.19$, $d_{2H} = 1$. The change of sign of the function $\Gamma(\xi, M)$ depending on $M$ is illustrated in Figure 2 (right).

Furthermore, for $d_2 < d_{2H}$, we have $\Gamma(\xi, 21.5) > 0$. Therefore, the spatial Hopf bifurcation occurs as $d_{2H}$ crosses the critical threshold $d_{2H}$ from higher to lower values, i.e., for $d_2 > d_{2H}$.

To determine the critical value of $M$ for Hopf bifurcation with a specific choice of $d_2$, we first show that the spatiotemporal model (3.8) and (3.9) with the local interaction $(M = 0)$ does not have a Hopf instability for the above set of parameter values and $d_2 = 1$. We note that $U^* = 0.32$ and $C^* = 0.31$ is the homogeneous steady state for (3.8) and (3.9) with the chosen parameter values. By substituting $M = 0$ into (4.5), we find

and

for all values of $\xi$. It should be noted that in this case, we use the value $\bar{\phi} = 1$ to compute $\Gamma(\xi, 0)$ and $\Delta(\xi, 0)$. As a result, both roots of the corresponding characteristic equation, i.e., Eq (3.17) with $\bar{\phi} = 1$, possess negative real parts. This implies that the homogeneous steady-state $(U, C) = (0.4, 0.8)$ is stable under small heterogeneous perturbations in the case of model (3.8) and (3.9) with local interaction. The onset of Hopf bifurcation in model (3.1) and (3.2) necessitates the violation of the inequality (3.18), and the Hopf bifurcation threshold is obtained by determining the value of $M$ for which the function

intersects with the $\xi$-axis. For the selected parameter set, the Hopf bifurcation threshold is $M_T = 23$. It is evident that if $M > M_T$, $\Gamma(\xi, M) > 0$ for all $\xi$, if $M < M_T$, $\Gamma(\xi, M) < 0$ for a range of $\xi$ values, and if $M = M_T$, $\Gamma(\xi, M_T) = 0$ only at $\xi = 0.19$.

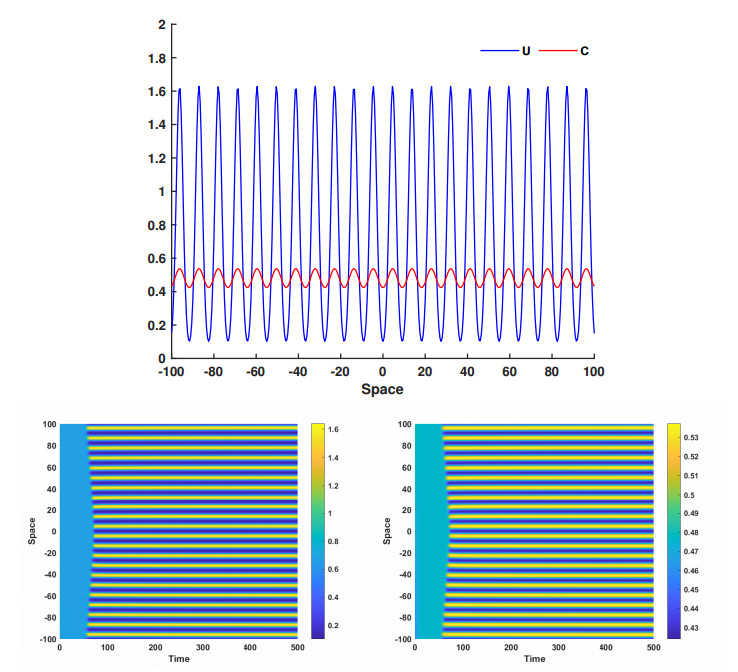
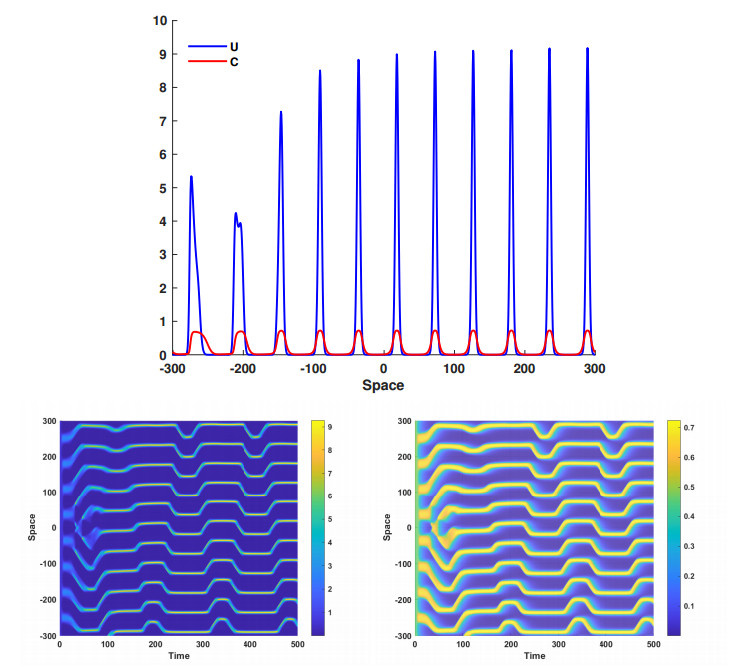
The results of the linear stability analysis are shown in Figure 3. There exists a region in the parameter plane where stationary solutions that are homogeneous in space are stable. These solutions can lose their stability via two primary mechanisms. In the first case, a real eigenvalue passes through the origin, resulting in the appearance of stable stationary solutions that are periodic in space (as illustrated in Figure 4). In the second case, a pair of complex conjugate eigenvalues intersects with the imaginary axis, leading to time-periodic oscillations of a solution that is constant in space (not shown).

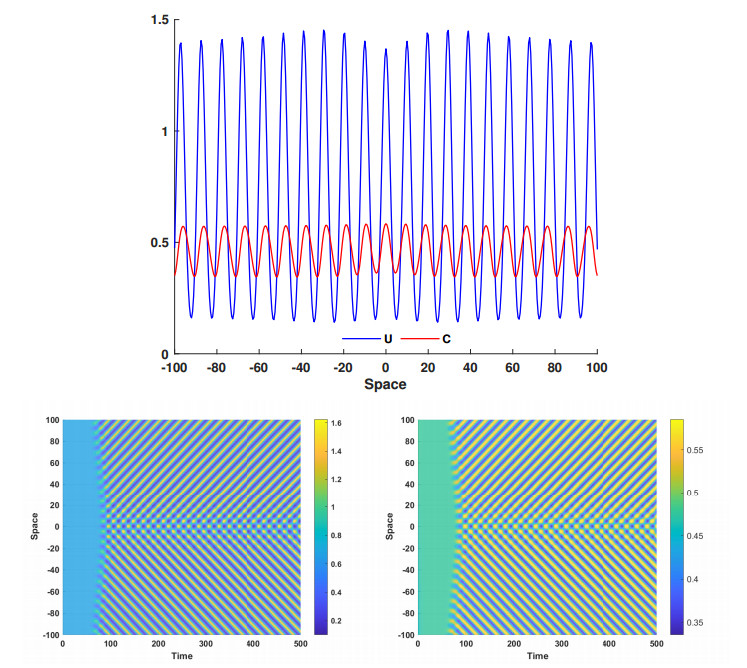
Further in the instability region, both instabilities can occur simultaneously resulting in complex spatiotemporal dynamics. As such, Figure 5 depicts periodic time oscillations of the spatial structure, wherein amplitude waves propagate from the center of the interval towards its boundaries. Meanwhile, Figure 6 displays another type of amplitude waves.

5.   Discussion

Virus in the host organism undergoes frequent mutations leading to the emergence of new variants competing with each other, persisting or disappearing during this competition. This virus population with close genotypes is considered as virus quasi-species. From modelling point of view, they can be interpreted as a virus density distribution in the genotype space localized around some average genotype. Existence of such solutions is determined by the interaction of virus replication in the host cells with the immune response and its natural (independent of the immune response) genotype-dependent death.

The interval of genotypes for which virus replication rate exceeds its death rate (viability interval) determines the emergence of virus quasi-species. A simplified model describing the existence of virus quasi-species without explicit introduction of the immune cells was introduced in ^[7,21]. In this work, we analyze the influence of immune cells on the existence of quasi-species. The conditions of the existence of solutions is formulated in terms of the eigenvalues of the corresponding operator. Let us note that quasi-species can exist in both cases, for nonlocal or global virus competition for the host cells.

The evolution of virus quasi-species is determined by the fitness landscape which depends on the infection interaction with the immune response. As such, genotype-dependent immune response leads to the evolutionary drift of virus quasi-species in the genotype space ^[28]. In the case of competition of two strains, their dynamics depends not only on the fitness landscape but also on their initial distribution. If one of the strains fills initially the whole "ecological niche", the second one cannot appear even if it would have evolutionary advantage otherwise. In the case of antiviral treatment eliminating the first strain, the second one can emerge ^[28]. This is the mechanism of the emergence of resistant strains due to treatment.

Another mechanism of the emergence of virus quasi-species can be realized without the assumption of fitness advantage for some of them. From modelling point of view, it is to some extent similar to the emergence of biological species due to intra-specific competition and natural selection (sympatric speciation) ^[29,30].

Nonlocal competition for the host cells and the interaction with the immune response leads to the emergence of genotype-dependent virus distribution without a priori advantage of some genotypes. The results of numerical simulations presented above show that such distributions can be stationary or time-dependent with the variation of the sizes of virus sub-populations and the emergence of new ones. Contrary to the previous case, the emergence of virus quasi-species can occur only in the case of nonlocal competition, but not in the case of global competition or the case without competition where $H(u) = u$. Let us also note that small virus mutation rate (diffusion coefficient) stimulates the emergence of virus quasi-species, while large mutation rate can lead to their disappearance. It is also interesting to remark that only stationary patterns were found in the previous work ^[31], while here we we observe also temporal dynamics (for a different model).

Thus, we have studied two mechanisms of the emergence of virus quasi-species with simplified but biologically realistic models of virus replication and immune response. More detailed models of the immune response can elucidate the influence of its two main components, the innate and adaptive immune responses, and of other factors involved in viral infections.

It is worth noting that in this study, specific reasonable parameter values are used to verify our analytical results. However, to effectively apply these findings to real-world data, obtaining currently unknown realistic parameter values is of utmost importance. Prioritizing the resolution of this limitation in future research efforts is essential to enhance the overall understanding and practical applicability of the study's outcomes.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This study was supported by PHC-Maghreb 22MAG22 and DGRSDT-Algeria. The second author was supported by the Ministry of Science and Higher Education of the Russian Federation (Megagrant agreement no. 075-15-2022-1115).

Conflict of interest

The authors declare there is no conflict of interest.