Loading [Contrib]/a11y/accessibility-menu.js
Search Advanced

Mathematical Biosciences and Engineering

2023, Volume 20, Issue 7: 12211-12239. doi: 10.3934/mbe.2023544
Previous Article Next Article
Research article Special Issues

An improved immune algorithm with parallel mutation and its application

  • College of Information Engineering, Shanghai Maritime University, Shanghai 201306, China

  • Academic Editor: Shangce Gao

  • The objective of this paper is to design a fast and efficient immune algorithm for solving various optimization problems. The immune algorithm (IA), which simulates the principle of the biological immune system, is one of the nature-inspired algorithms and its many advantages have been revealed. Although IA has shown its superiority over the traditional algorithms in many fields, it still suffers from the drawbacks of slow convergence and local minima trapping problems due to its inherent stochastic search property. Many efforts have been done to improve the search performance of immune algorithms, such as adaptive parameter setting and population diversity maintenance. In this paper, an improved immune algorithm (IIA) which utilizes a parallel mutation mechanism (PM) is proposed to solve the Lennard-Jones potential problem (LJPP). In IIA, three distinct mutation operators involving cauchy mutation (CM), gaussian mutation (GM) and lateral mutation (LM) are conditionally selected to be implemented. It is expected that IIA can effectively balance the exploration and exploitation of the search and thus speed up the convergence. To illustrate its validity, IIA is tested on a two-dimension function and some benchmark functions. Then IIA is applied to solve the LJPP to exhibit its applicability to the real-world problems. Experimental results demonstrate the effectiveness of IIA in terms of the convergence speed and the solution quality.

    Citation: Lulu Liu, Shuaiqun Wang. An improved immune algorithm with parallel mutation and its application[J]. Mathematical Biosciences and Engineering, 2023, 20(7): 12211-12239. doi: 10.3934/mbe.2023544

    Related Papers:

    [1] Lili Jiang, Sirong Chen, Yuanhui Wu, Da Zhou, Lihua Duan . Prediction of coronary heart disease in gout patients using machine learning models. Mathematical Biosciences and Engineering, 2023, 20(3): 4574-4591. doi: 10.3934/mbe.2023212
    [2] Natalya Shakhovska, Vitaliy Yakovyna, Valentyna Chopyak . A new hybrid ensemble machine-learning model for severity risk assessment and post-COVID prediction system. Mathematical Biosciences and Engineering, 2022, 19(6): 6102-6123. doi: 10.3934/mbe.2022285
    [3] Hangle Hu, Chunlei Cheng, Qing Ye, Lin Peng, Youzhi Shen . Enhancing traditional Chinese medicine diagnostics: Integrating ontological knowledge for multi-label symptom entity classification. Mathematical Biosciences and Engineering, 2024, 21(1): 369-391. doi: 10.3934/mbe.2024017
    [4] Faisal Mehmood Butt, Lal Hussain, Anzar Mahmood, Kashif Javed Lone . Artificial Intelligence based accurately load forecasting system to forecast short and medium-term load demands. Mathematical Biosciences and Engineering, 2021, 18(1): 400-425. doi: 10.3934/mbe.2021022
    [5] Xin Jing, Jungang Luo, Shangyao Zhang, Na Wei . Runoff forecasting model based on variational mode decomposition and artificial neural networks. Mathematical Biosciences and Engineering, 2022, 19(2): 1633-1648. doi: 10.3934/mbe.2022076
    [6] Pinpin Qin, Xing Li, Shenglin Bin, Fumao Wu, Yanzhi Pang . Research on transformer and long short-term memory neural network car-following model considering data loss. Mathematical Biosciences and Engineering, 2023, 20(11): 19617-19635. doi: 10.3934/mbe.2023869
    [7] Wajid Aziz, Lal Hussain, Ishtiaq Rasool Khan, Jalal S. Alowibdi, Monagi H. Alkinani . Machine learning based classification of normal, slow and fast walking by extracting multimodal features from stride interval time series. Mathematical Biosciences and Engineering, 2021, 18(1): 495-517. doi: 10.3934/mbe.2021027
    [8] Peng Lu, Ao Sun, Mingyu Xu, Zhenhua Wang, Zongsheng Zheng, Yating Xie, Wenjuan Wang . A time series image prediction method combining a CNN and LSTM and its application in typhoon track prediction. Mathematical Biosciences and Engineering, 2022, 19(12): 12260-12278. doi: 10.3934/mbe.2022571
    [9] Feng Wang, Shan Chang, Dashun Wei . Prediction of conotoxin type based on long short-term memory network. Mathematical Biosciences and Engineering, 2021, 18(5): 6700-6708. doi: 10.3934/mbe.2021332
    [10] Yu-Mei Han, Hui Yang, Qin-Lai Huang, Zi-Jie Sun, Ming-Liang Li, Jing-Bo Zhang, Ke-Jun Deng, Shuo Chen, Hao Lin . Risk prediction of diabetes and pre-diabetes based on physical examination data. Mathematical Biosciences and Engineering, 2022, 19(4): 3597-3608. doi: 10.3934/mbe.2022166

  • The objective of this paper is to design a fast and efficient immune algorithm for solving various optimization problems. The immune algorithm (IA), which simulates the principle of the biological immune system, is one of the nature-inspired algorithms and its many advantages have been revealed. Although IA has shown its superiority over the traditional algorithms in many fields, it still suffers from the drawbacks of slow convergence and local minima trapping problems due to its inherent stochastic search property. Many efforts have been done to improve the search performance of immune algorithms, such as adaptive parameter setting and population diversity maintenance. In this paper, an improved immune algorithm (IIA) which utilizes a parallel mutation mechanism (PM) is proposed to solve the Lennard-Jones potential problem (LJPP). In IIA, three distinct mutation operators involving cauchy mutation (CM), gaussian mutation (GM) and lateral mutation (LM) are conditionally selected to be implemented. It is expected that IIA can effectively balance the exploration and exploitation of the search and thus speed up the convergence. To illustrate its validity, IIA is tested on a two-dimension function and some benchmark functions. Then IIA is applied to solve the LJPP to exhibit its applicability to the real-world problems. Experimental results demonstrate the effectiveness of IIA in terms of the convergence speed and the solution quality.


    1.   Introduction

    Rainfall has played an important role in the development and maintenance of human civilizations. Rain is one of the most important sources of pure water on which humans depend for life. Rain replenishes groundwater, which is the main source of drinking water. Since more than 50% of Australia's land mass is used for agriculture, an accurate rainfall forecasting system can help farmers plan cropping operations, i.e., when to sow seeds, apply fertilizers, and harvest crops. Rainfall prediction [1] can also help farmers decide which crops to plant for maximum harvests and profits. In addition, precipitation plays an important role in the planning and maintenance of water reservoirs, such as dams that generate electricity from hydropower. About half of the renewable energy generated by more than 120 hydropower plants in Australia comes from precipitation. With accurate rainfall forecasts, operators are well informed about when to store water and when to release it to avoid flooding or drought conditions in places with low rainfall. Precipitation forecasts also play a critical role in the aviation industry, from the moment an aircraft starts its engine. An accurate precipitation forecast helps plan flight routes and suggests the right time to take off and land a flight to ensure physical and economic safety. After all, aircraft operations can be seriously affected by lightning, icing, turbulence, thunderstorm activity and more. According to [2], climate is a major factor in aviation accidents, accounting for 23% of accidents worldwide.

    Numerous studies have shown that the duration and intensity of rainfall can cause major weather-related disasters such as floods and droughts. AON's annual weather report shows that seasonal flooding in China from June to September 2020 resulted in an estimated economic loss of 35 billion and a large number of deaths [3]. In addition, rainfall also has a negative impact on the mining industry, as heavy and unpredictable rainfall can affect mining activities. For example, the Bowen Basin in Queensland hosts some of Australia's largest coal reserves. The summer rains of 2010–2011 severely impacted mining operations. An estimated 85% of coal mines in Queensland had their operations disrupted as a result (Queensland Flood Commission, 2012) [4,5]. As of May 2011, the Queensland coal mining sector had recovered only 75% of its pre-flood production and lost $ 5.7 $ billion. As a result, rainfall forecasts are becoming increasingly important in developing preventive measures to minimize the impact of such disasters.

    Predicting rainfall is challenging because it involves the study of various natural phenomena such as temperature, humidity, wind speed, wind direction, cloud cover, sunlight, and more. Therefore, accurate rainfall forecasts are critical in areas such as energy and agriculture. A report produced by Australia's National Climate Change Adaptation Research Facility examined the impacts of extreme weather events. It states that currently available weather forecasts for industry are inadequate. It lacks location information and other details that enable risk management and targeted planning. Traditional weather forecasts use various hardware parameters to predict parameters and use mathematical calculations to predict heavy rainfall, which are sometimes inaccurate and therefore cannot work effectively. The Australian Bureau of Meteorology currently uses the Australian Predictive Ocean Atmosphere Model (POAMA) forecasts to predict rainfall patterns [6]. POAMA is a standard distribution model used for many weeks to specific seasons to look at weather throughout the year. It uses surveys of ocean, atmospheric, ice, and Earth data to develop ideas for up to nine months. In this work, we use machine learning and deep learning methods [7,8] based on the analysis of complex patterns based on historical data to effectively and accurately predict the occurrence of rainfall. The application of this method requires accurate historical data, the presence of patterns that can be detected, and their continuation into the future where predictions are sought.

    Several divisive algorithms such as Random Forest [9], Naive Bayes [10], Logistic Regression [11], Decision Tree [12], XGBoost [13], and others have been studied for rainfall prediction. However, the effectiveness of these algorithms varies depending on a combination of preprocessing and data cleaning techniques, feature scaling, data normalization, training parameters, and segmentation testing, leaving room for improvement. The goal of this paper is to provide a customized set of these techniques to train machine learning [14] and deep learning [15] models that provide the most accurate results for rainfall prediction. The models are trained and tested on the Australian rainfall database using the proposed approach. The database contains records from 49 metropolitan areas over a 10-year period starting December 1, 2008. The research contributions of the proposed work are as follows:

    $ 1) $ To remove outliers using Inter Quartile Range (IQR).

    $ 2) $ To balance the data using Synthetic Minority Oversampling Technique (SMOTE) technique.

    $ 3) $ To apply both classification and regression models which at first predict whether it rain or not and if there is rain then find the amount of rain.

    $ 4) $ To apply XGBoost, Random Forest, Kernel SVM, and Long-Short Term Memory (LSTM) for the classification task.

    $ 5) $ To apply Multiple Linear Regressors, XGBoost, Polynomial Regressor, Random Forest Regressor, and LSTM for the regression task.

    2.   Literature review

    Luk et al. [16] addressed watershed management and flood control. The goal was to accurately predict the temporal and local distribution of rainfall and the amount of water and quality management. The dataset used to train the ML models was collected from the Upper Parramatta River Catchment Trust (UPRCT), Sydney. Three methods were used for modeling features related to rainfall prediction, namely MultiLayer FeedForward Network (MLFN), Partial Recurrent Neural Network (PRNN) and Time Delay Neural Network (TDNN). The main parameters for the above methods were lag, window size and number of hidden nodes.

    Abhishek et al. [17] worked on developing ANN -based effective and nonlinear models for accurate prediction of maximum temperature 365 days a year. The data used were from the Toronto Lester B. Pearson Int'l A station, Ontario, Canada from 1999–2009. They proposed two models and trained them using the Levenberg-Marquardt algorithm with 5 hidden layers and a model with 10 hidden layers. Factors that affected the results were the number of neurons, sampling, hidden layers, transfer function, and overfitting.

    Abhishek et al. [18] performed a regression task to predict average rainfall using a feed forward network trained with the back propagation algorithm, the layer recurrent network, and the feed forward network trained with the cascaded back propagation algorithm for a large number of neurons. The data were collected from www.Indiastat.com and the IMD website. The dataset contains records for the months of April to November from 1960 to 2010 in Udupi district of Karnataka.

    Saba et al. [19] worked on accurate weather predictions using a hybrid neural network model combining MultiLayer Perceptron (MLP) and Radial Basis Function (RBF). The dataset used was from the weather station in Saudi Arabia. They proposed an extended hybrid neural network approach and compared the results of individual neural networks with those of hybrid neural networks. The results showed that hybrid neural network models have greater learning ability and better generalization ability for certain sets of inputs and nodes.

    Biswas et al. [20] focused on the prediction of weather conditions (good or bad) using the classification method. Naive Bayes and chi-square algorithm were used for classification. The main objective was to show that data mining approaches are sufficient for weather prediction. Data was obtained in real time from users and stored in a database. The decision tree generated from the training features is used for classification.

    Basha et al. [21] introduced a Machine and Deep Learning-based rain prediction model. This model utilizes the Kaggle dataset to train various models, including the Support Vector Regressor, Autoregressive Integrated Moving Average (ARIMA), and Neural Network. The authors claim that the performance of the model, as measured by the Root Mean Squared Error (RSME), is 72%.

    Doroshenko et al. [22] worked on refining numerical weather forecasts using a neural network by error to increase the accuracy of the additional 2m weather forecasts of the regional model COSMO. The dataset was obtained from the Kiev weather station in Ukraine. The authors chose the gated recurrent unit (GRU) approach because the error in the weather forecast is a time series and it also has fewer parameters than LSTM. When a lower error history is chosen, better fitting and refinement of the model is possible.

    Appiah-Badu et al. [23] conducted a study to predict the occurrence of rainfall through classification. They employed several classification algorithms, including Decision Tree (DT), Random Forest (RF), Multilayer Perceptron (MLP), Extreme Gradient Boosting (XGB), and K-Nearest Neighbor (KNN). The data for the study was collected from the Ghana Meteorological Agency from 1980 to 2019 and was divided into four ecological zones: Coastal, Forest, Transitional, and Savannah.

    Raval et al. [24] worked on a classification task to predict tomorrow's rain using logistic regression, LDA, KNN, and many other models and compared their metrics. They used a dataset containing daily 10-year weather forecasts from most Australian weather stations. It was found that deep learning models produced the best results.

    Ridwan et al. [25] proposed a rainfall prediction model for Malaysia. The model was trained using a dataset of ten stations and employs both a Neural Network Regressor and Decision Forest Regression (DFR). The authors claim that the R2 score ranges from 0.5 to 0.9. This approach only predicts rainfall and does not perform any classification tasks.

    Adaryani et al. [26] conducted an analysis of short-term rainfall forecasting for applications in hydrologic modeling and flood warning. They compared the performance of PSO Support Vector Regression (PSO-SVR), Long Short-Term Memory (LSTM), and Convolutional Neural Network (CNN). The study considered 5-minute and 15-minute ahead forecast models of rainfall depth based on data from the Niavaran station in Tehran, Iran.

    Fahad et al. [27] conducted a study on forecasting rainfall through the use of a deep forecasting model based on Gated Recurrent Unit (GRU) Neural Network. The study analyzed 30 years of climatic data (1991–2020) in Pakistan, considering both positive and negative impacts of temperature and gas emissions on rainfall. The findings of the study have potential implications for disaster management institutions.

    Tables 1 and 2 compare various state-of-the-art approaches for classification as well as regression tasks respectively.

    Table 1.  Literature review for classification.
    Authors Dataset Approach used Best performance
    Raval et al. (2021) [24] Daily weather observations from several Australian weather stations for 10 years Logistic regression, Linear discriminant analysis, Quadratic discriminant analysis, K-Nearest neighbor, Decision tree, Gradient boosting, Random forest, Bernoulli Naïve Bayes, Deep learning model Precision = 98.26 F1-Score = 88.61
    Appiah-Badu et al. (2021) [23] Data from the 22 synoptic stations across the four ecological zones of Ghana from 1980 – 2019 Decision tree, Multilayer perceptron, Random forest, Extreme gradient boosting, K-Nearest neighbor Precision = 100 Recall = 96.03 F1-Score = 97.98
     | Show Table
    DownLoad: CSV
    Table 2.  Literature review for regression.
    Authors Dataset Approach used Limitations Best performance
    Luk et al. (2001) [16] Dataset is collected from the Upper Parramatta River Catchment Trust (UPRCT), Sydney Multi-Layer Feedforward Network (MLFN), Partial Recurrent Neural Network (PRNN), Time Delay Neural Network Only used the regression model to predict the amount of rainfall NMSE = 0.63
    Abhishek et al. (2012) [17] Data available for the station Toronto Lester B. Pearson Int'l A, Ontario, Canada, 1999-2009 Single layer model, 5 hidden layer model, 10 hidden layer model Not used any sequential model to capture the time series nature of data. MSE = 2.75
    Saba et al. (2017) [19] Data used from Saudia Arabian Weather Forecasting Station Hybrid Model (MLP+RBF) Not used any time series model, only regression model to predict the amount of rainfall Correlation coefficient = 0.95, RMSE = 146, Scatter Index = 0.61
    Basha et al. (2020) [21] Dataset chosen is the Kaggle dataset for the rainfall prediction Support vector regressor, AutoRegressive Integrated Moving Average (ARIMA), and Neural Network Trained on a small dataset, no oversampling techniques are used to increase the size of dataset RSME = 0.72
     | Show Table
    DownLoad: CSV

    Here, NMSE stands for Normalized Mean Square Error, which allows us to compare the error across sets with different value ranges. Using simple Mean Squared Error (MSE) can result in higher variance for sets with larger values, even if the variance for sets with smaller values is actually greater. For example, if set 1 contains elements with values ranging from 1–100 and set 2 contains elements with values ranging from 1000–10,000, the variance for set 2 will be higher if MSE is used, even if the variance for set 1 is actually greater. NMSE is used to compare the error across sets by dividing the entire set by the maximum value in the range, resulting in a conversion of both sets' ranges to 0-ik -1 for better comparison.

    3.   Data description

    The Dataset we used for our study contains data from daily observations over a tenure of 10 years starting from 1/12/2008 up till 26/04/2017 from 49 different locations over Australia [28]. The dataset contains 23 features which are Date, Location, MinTemp, MaxTemp, Rainfall, Evaporation, Sunshine, WindGustDir, WindGustSpeed, WindDir9am, WindDir3pm, WindSpeed9am, WindSpeed3pm, Humidity9am, Humidity3pm, Pressure9am, Pressure3pm, Cloud9am, Cloud3pm, Temp9am, Temp3pm, RainToday and RainTomorrow. The dataset contains around 145 thousand entries.

    For the classification task, RainTomorrow is the target variable that predicts the occurrence of rainfall on the next day. Here, 0 indicates no rain, and 1 indicates chance of rainfall. For the regression task, Rainfall is the target variable that forecasts the amount of precipitation in millimeters. We performed exploratory data analysis on the dataset, which is the key to machine learning problems in order to gain maximum confidence in the validity of future results. This analysis helps us to look for anomalies in the data, figure out correlations between features and check for missing values to enhance the outcomes of the machine learning models. Table 3 presents the analysis of null values in the raw dataset. Here, it is visible that most of the attributes contain null values which need to be addressed carefully before passing the data to train the model, otherwise the model will not give accurate predictions.

    Table 3.  Null values of attributes in the dataset.
    Attribute Null Value Attribute Null value Attribute Null value
    Date 0.0% missing values WindGustSpeed 7.06% missing values Pressure3pm 10.33% missing values
    Location 0.0% missing values WindDir9am 7.26% missing values Cloud9am 38.42% missing values
    MinTemp 1.02% missing values WindDir3pm 2.91% missing values Cloud3pm 40.81% missing values
    MaxTemp 0.87% missing values WindSpeed9am 1.21% missing values Temp9am 1.21% missing values
    Rainfall 2.24% missing values WindSpeed3pm 2.11% missing values Temp3pm 2.48% missing values
    Evaporation 43.17% missing values Humidity9am 1.82% missing values RainToday 2.24% missing values
    Sunshine 48.01% missing values Humidity3pm 3.1% missing values RainTomorrow 2.25% missing values
    WindGustDir 7.1% missing values Pressure9am 10.36% missing values
     | Show Table
    DownLoad: CSV

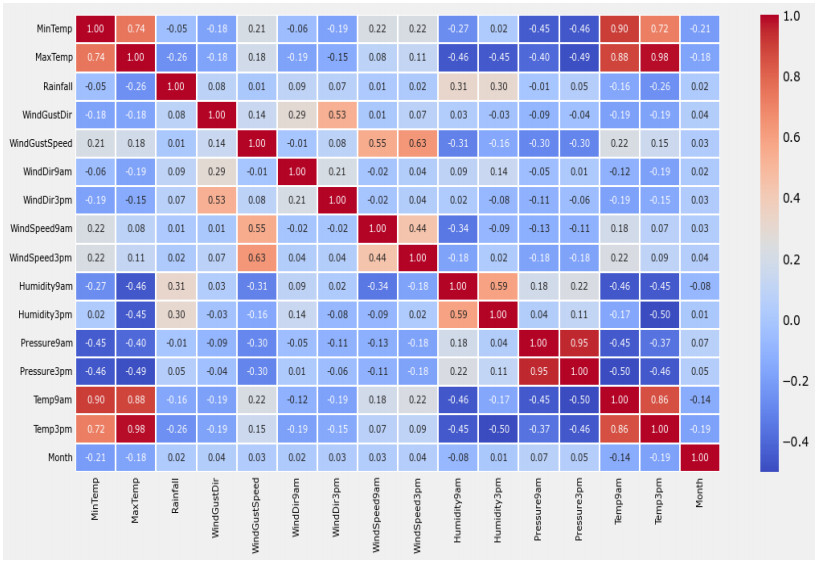
    Figure 1 presents a correlation matrix that states the correlation coefficient between two features, i.e., how much the features are correlated to each other. The scale of the correlation matrix is from –1 to 1, where 1 represents the perfect positive relationship between the two factors and –1 represents the total negative relationship between the two factors. A correlation coefficient of 0 represents an absence of a relation between the two variables.

    Figure 1.  Correlation matrix for various features in the dataset.
    DownLoad: Full-Size Img PowerPoint

    From the analysis of the null values, it appears that the attributes Evaporation, Sunshine, Cloud9am, and Cloud3pm contain almost 50% NaN values. Therefore, we have discarded these 4 columns and did not use them for training our model. This is because even if we use one of the available techniques to populate the data, it might differ from the performance of the model. The actual weather data may not match the padded data, which could affect the learning process of the model. Figure 1 presents a correlation matrix that shows the correlation coefficient between two features. As we removed four features from our dataset, they will not be included in our correlation matrix calculation. The Date feature is categorized into its respective months, and the month feature is taken into consideration for better season-wise categorization of data and the study of correlation. The reason for ignoring the Location feature is that the dataset is already classified into various locations. Therefore, finding a correlation between Location and Date is not beneficial in the data analysis. Additionally, the feature RainToday is ignored because the Rainfall feature, which attributes RainToday, is already included in the study of correlation.

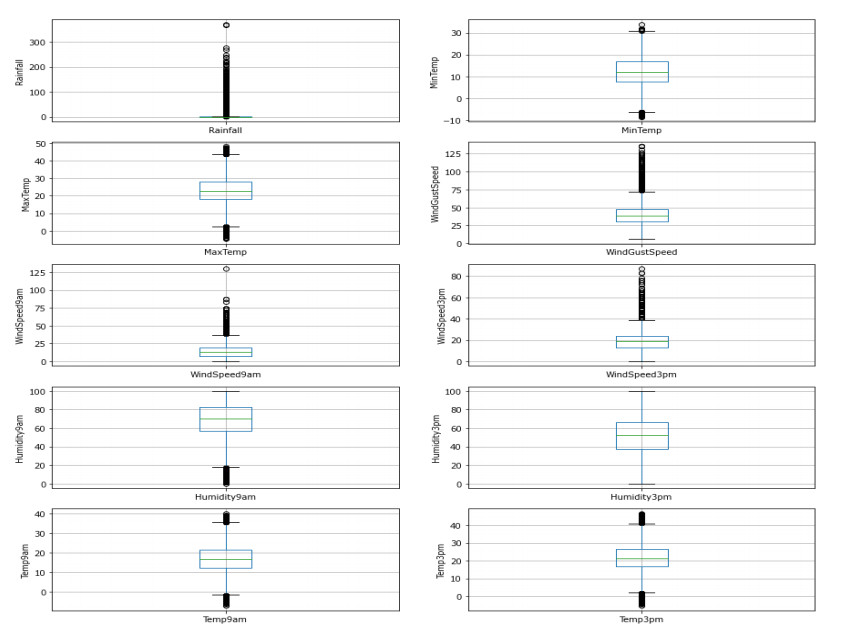
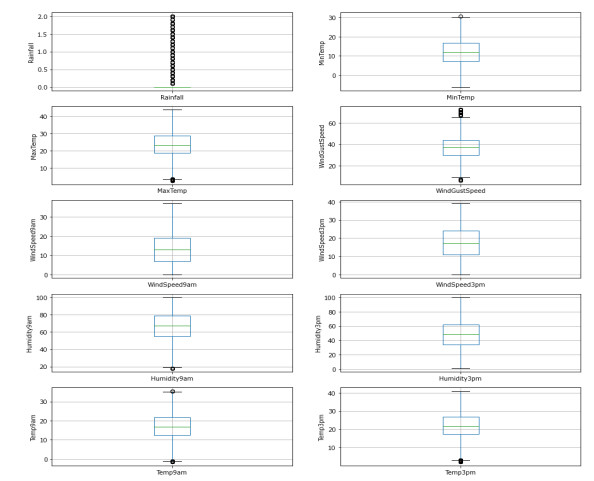
    Figure 2 displays the distribution of numerical data based on the 0th percentile, 25th percentile (1st quartile), 50th percentile (2nd quartile), 75th percentile (3rd quartile), and 100th percentile. This distribution provides insight into the presence of outliers, which must be eliminated prior to training our predictive model to achieve accurate results. In order to analyze the distribution of data with regards to various quartiles, the data must be continuous. Features such as Location, RainTomorrow, WindDir3pm, WindDir9am, WindGustDir, etc. are categorical features, therefore using a boxplot to remove outliers is only feasible with the use of continuous features for data analysis. As a result, we have used only 10 features that are continuous and have the potential for having outliers.

    Figure 2.  Distribution of data points w.r.t. quartile.
    DownLoad: Full-Size Img PowerPoint

    4.   Proposed approach

    Due to various factors such as global warming, deforestation, etc., affecting seasonal variables during the year, uncertainty in rainfall has become one of the most discussed topics among researchers. Therefore, the main objective of this work is to apply different techniques of data preprocessing, machine learning and deep learning models: 1) Data pre-processing to remove uncertainties and anomalies in the provided dataset. 2) Forecasting the occurrence of rainfall. 3) Projecting the amount of rainfall in millimeters. 4) Comparing the results of various models used for classification and regression purposes.

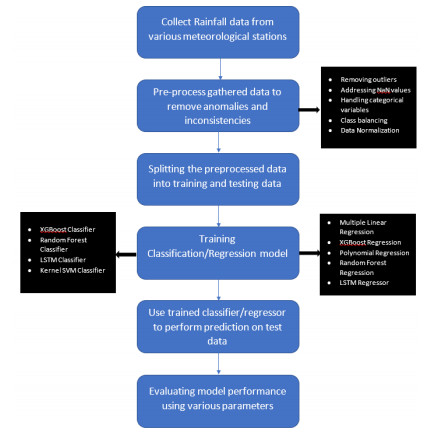
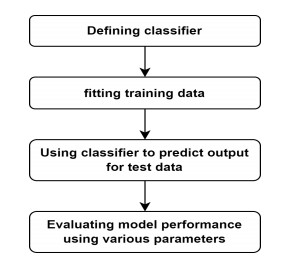
    The comparison of various algorithms for the same task gives us more insights into the problem statement and helps us make decisions regarding the best model to be used for rainfall forecasting. Figure 3 illustrates the flow diagram of the proposed methodology.

    Figure 3.  Flow diagram of the proposed approach.
    DownLoad: Full-Size Img PowerPoint

    4.1.   Data pre-processing

    Data processing is a method of data mining that refers to the cleaning and modification of raw data collected from various sources that are suitable for the work and provide more favorable results.

    4.1.1.   Removing outliers

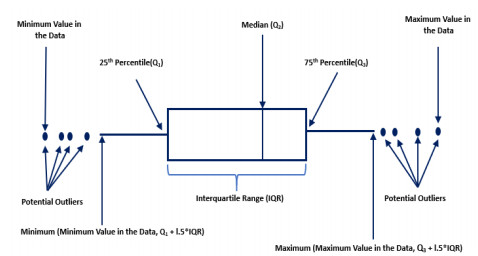
    As it is evident from Figure 4 that our data contains several outliers. Thus, we employed the Inter Quartile Range (IQR) approach to remove the outliers. IQR is basically the range between the 1st and the 3rd quartile, i.e., the 25th and 75th percentile. In this approach, the data point which falls below (Q1 – 1.5 * IQR) and above (Q1 + 1.5 * IQR) are considered outliers. After removing all the outliers approximately 30 thousand rows were removed. Figure 4 represents the IQR approach employed for removing the outliers [29].

    Figure 4.  IQR approach for data cleaning.
    DownLoad: Full-Size Img PowerPoint

    Figures 5 and 6 show the distribution of normalized values and IQR range plot after removing the outliers from the dataset.

    Figure 5.  Distribution of normalized cleaned data points w.r.t. quartiles.
    DownLoad: Full-Size Img PowerPoint
    Figure 6.  Distribution of cleaned data points w.r.t. quartiles.
    DownLoad: Full-Size Img PowerPoint
    4.1.2.   Addressing NaN values

    From the analysis of the null values, it appears that the attributes evaporation, sunshine, cloud9am and cloud3pm contain almost 50% NaN values. Therefore, we discarded these columns and did not use them for training our model. This is because even if we use one of the available techniques to populate the data, it might differ from the performance of the model. The actual weather data may not match that of the padded data, which could affect the learning process of the model.

    For the remaining attributes, we filled the numeric features with the mean value of the attribute and the categorical values with the mode of each feature. However, because location and seasons also play an important role in measuring the attributes, we divided the data set into 4 seasons, namely summer (January to March), fall (March to June), winter (June to September), and spring (September to December). We then averaged the values using the month and location attributes to group the data by season and location and populated the NaN values using a similar pairwise approach. Similarly, for categorical data, the maximum occurrence of the location-season pair value is used to populate the NaN values.

    For the Rainfall, RainToday, and RainTomorrow attributes, we took a different approach to handling NaN values. For the Rainfall attribute, we replaced the NaN values with 0. If NaN values were filled with mean values, the model could not generalize better. For the RainToday and RainTomorrow features, we omitted the rows with NaN values because if we fill them with the most common class values, it could affect classification precision.

    4.1.3.   Handling categorical variables

    To train the model containing categorical features, it needs to be converted into a numerical format. For features RainToday and RainTomorrow, we used LabelEncoder that replaced the values Yes and No with 1 and 0 respectively. We could use LabelEncoder to convert directional features into numerical format but for better generalization, we replaced direction with their respective degree value.

    'N': 0, 'NNE': 22.5, 'NE': 45.0, 'ENE': 67.5, 'E': 90.0, 'ESE': 112.5, 'SE': 135.0, 'SSE': 157.5, 'S': 180.0, 'SSW': 202.5, 'SW': 225.0, 'WSW': 247.5, 'W': 270.0, 'WNW': 292.5, 'NW': 315.0, 'NNW': 337.5

    4.1.4.   Class balancing

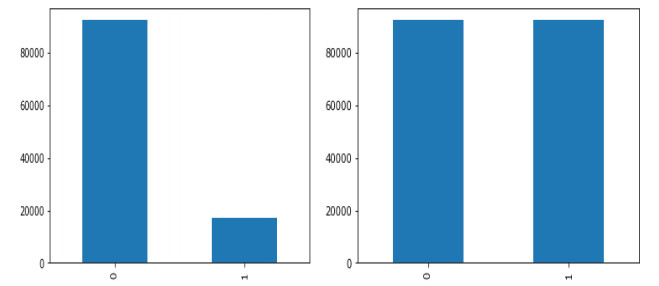
    An important factor affecting the performance of the model is the imbalance of the output classes. If the ratio of the values of the two classes is not close to 1, the model will be biased in favor of the class whose values matter more than those of the others. One of the simplest and most effective solutions is to oversample for class imbalance using SMOTE (Synthetic Minority Oversampling Technique) [30]. Originally, the ratio of class 0 to class 1 frequencies was about 5:1. Because of this, the performance of the model was not better with unseen data. Figure 7(a), (b) show the bar graph of the number of values of both classes before and after balancing the classes. Class equalization is performed only for training classification models.

    Figure 7.  Target variable distribution (a) Before class balancing (b) After class balancing.
    DownLoad: Full-Size Img PowerPoint
    4.1.5.   Data normalization

    Scaling the data is very important in performing a regression task. By scaling our variables, we can compare different variables with the same calibration. We used a standard scaler to normalize our characteristics. The standard scaler converts the feature values to a range of –3 to 3. Equation (1) represents the equation that the standard scaler uses to scale the values.

    $ \begin{equation} z = \frac{(xi - \mu)} {\sigma} \end{equation} $ (1)
    4.1.6.   Dataset capacity

    After conducting exploratory data analysis and data cleaning, the dataset comprises 110 k rows and 19 features. The approach is divided into two parts: 1) forecasting the occurrence of rainfall and 2) estimating the amount of rainfall. For forecasting the occurrence of rainfall, which is a classification task, the training data consists of approximately 147 k rows and the testing data consists of 36 k rows. The number of rows is higher than the actual dataset because the SMOTE technique was applied to oversample the data and balance both classes for classification tasks. For predicting the amount of rainfall, which is a regression task, the training data consists of 87 k rows and the testing data consists of 22 k rows. In this approach, we did not use any oversampling technique for regression.

    4.2.   Forecasting occurrence of rainfall

    The task here is to predict the occurrence of precipitation in two classes, i.e., whether it will rain tomorrow or not. The above task is to implement a classification approach using various features and their corresponding target values from a given dataset. The classification approach is divided into three parts as: 1) Preparing data for classification. 2) Fitting the training data to train a classification model, and 3) Evaluating the model performance. Figures 8 and 9 show flow of the overall implementation of the classification approach. The flow of the overall implementation of the classification approach.

    Figure 8.  Preparing data for classification.
    DownLoad: Full-Size Img PowerPoint
    Figure 9.  Fitting data for classification.
    DownLoad: Full-Size Img PowerPoint

    For forecasting the occurrence of rainfall, we have implemented four classification models as follows:

    XGBoost Classifier: XGBoost [31] stands for eXtreme Gradient Boosting which is a fast and effective boosting algorithm based on gradient boosted decision tree algorithm. XGBoost uses a finer regularization technique, Shrinkage, and Subsampling column to prevent over-submerging, and this is one of the differences in gradient development. The XGBoost classifier takes a 2-dimensional array of training features and target variables as input for training the classification model.

    Random Forest Classifier: Random forest or random decision forest [32] is an integrated learning method for classification, regression, and other activities that work by building a pile of decision trees during training. It basically creates a set of decision trees from a randomly selected small set of the training set and then collects votes from different decision trees to determine the final forecast. For classification tasks, random forest clearing is a class selected by many trees. Random Forest classifier also takes a 2-dimensional array of training features and target variables as input for training the classification model.

    Kernel SVM Classifier: Support Vector Machines [33] are supervised learning models with associated learning algorithms that analyze data for classification and regression analysis. The main motivation of SVM is to create the best decision-making limit that can divide two or more classes so that we can accurately place data points in the correct class for which various kernels are used. We have chosen the Gaussian Radial Basis Function (RBF) as the kernel for training our SVM model as rainfall data is non-linear data. Equation (2) represents the gaussian radial basis function used by the support vector machine.

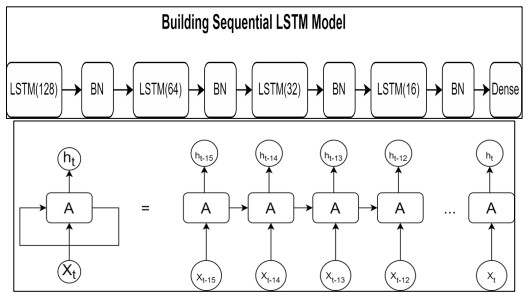
    $ \begin{equation} F(x, x_j) = exp(-y * ||x - x_j||^2 \end{equation} $ (2)

    LSTM Classifier: An LSTM or Long-Short-Term-Memory classifier [34] is an artificial recurrent neural network that has both feedforward communication and feedback, and is often used to classify and make predictions over time-series data. For training the LSTM classifiers a different data format needs to be supplied in which the data must first be converted to a 3-D array according to the provided format: (number of samples, time steps, number of features). To prevent overfitting and visualize the training progress, callbacks are passed as parameters while training the prediction model. In our approach we have used two callbacks that are:

    ● ReduceLRonPlateau: It reduces the learning rate by 'factor' times passed as an argument if the metric has stopped improving for the 'patience' number of epochs. Reducing the learning rate often benefits the model.

    ● EarlyStopping: This will stop training if the monitored metric has stopped improving for the 'patience' number of epochs.

    Figure 10(a), (b) show the layout of the LSTM neural network trained and unrolled RNN for a timestamp of 15 days respectively.

    Figure 10.  The layout of the LSTM neural network trained and unrolled RNN for a timestamp. (a) Sequential LSTM model, and (b) Unrolled RNN for the timestamp of 15 days.
    DownLoad: Full-Size Img PowerPoint

    To predict the occurrence of rainfall tomorrow, the designed algorithm is then shown in Algorithm 1.

     

    Algorithm 1: Algorithm for Classification
    Input: Rainfall Forecasting Dataset
    I = ['MinTemp', 'MaxTemp', 'Rainfall', 'WindGustDir', 'WindGustSpeed', 'WindDir9am', 'WindDir3pm', 'WindSpeed9am', 'WindSpeed3pm', 'Humidity9am, Humidity3pm', 'Pressure9am', 'Pressure3pm', 'Temp9am', 'Temp3pm', 'RainToday', 'RainTomorrow']
    Output: Yes, No
    1 Preprocess the input data and divide it into features and targets.
    2 Balance output classes using SMOTE.
    3 Scale the data using Standard Scaler.
    4 Define classification model.
    5 Train the classifier according to the defined parameters.

    4.3.   Projecting the amount of rainfall in millimeters

    Classification is one of the steps in precipitation forecasting. It tells you whether it will be a sunny day or whether you will need an umbrella throughout the day, since the forecast only says that it will rain at any time. However, another important aspect is that predicting the amount of rainfall based on features of the flow is a good prediction because it helps us make decisions such as whether to leave the station or stay home because it will rain heavily, whether to hold back the water stored in the reservoir or release some water from the reservoir because heavy rain is predicted in the watershed, and more. Therefore, this part deals with different regression techniques that are used to forecast the amount of rainfall in millimeters.

    The regression task is also divided into three parts:

    1) Preparing data for the regression model.

    2) Training a regression model.

    3) Evaluating the regression model.

    For projecting the amount of rainfall, we have implemented various regression algorithms including:

    ● Multiple Linear Regression

    ● XGBoostRegressor

    ● Polynomial Regression

    ● Random Forest Regression

    ● LSTM-based Deep Learning Model

    Multiple Linear Regression: Linear Regression [35] is a supervised learning to perform a regression task. This regression method detects the linear relationship between the input features and the target variable.

    $ \begin{equation} \hat{y} = b_0 + b_1 x_1 + b_2 x_2 + ... + b_k x_k \end{equation} $ (3)

    Equation (3) is the statistical equation used for prediction by the Multiple Linear regression algorithm. In order to achieve the best fit line the model aims to predict ŷ so that the difference in error between the predicted value and the real value is as small as shown in Eq (4).

    $ \begin{equation} mininmize \frac{1}{n}\sum\limits_{i = 1}^n(pred_i - y_i)^2 \end{equation} $ (4)

    XGBoostRegressor: XGBoost [36] stands for eXtreme Gradient Boosting which is a fast and effective boosting algorithm based on gradient boosted decision tree algorithm. XGBoost's objective function consists of a loss function and a regularization term. It tells us about the difference between real values and predicted values, i.e, how far the model results are from the real values. We used reg: linear as the XGBoost loss functions to perform the regression task.

    Polynomial Regression: Polynomial regression [37] is a special case of linear regression in which the correlation between the independent variable x and the target variable y is modeled as an nth polynomial degree of x. This regression technique is used to identify a curvilinear relationship between independent and dependent variables.

    $ \begin{equation} \hat{y} = b_0 + b_1 x_1 + b_2 x_1^2 + b_3 x_1^3 + ... + b_n x_1^n \end{equation} $ (5)

    Equation (5) represents the statistical equation used for prediction by the Polynomial regression algorithm. In order to achieve the best fit line, the model aims to predict ŷ so that the difference in error between the predicted value and the real value is as small as shown in Eq (4).

    Random Forest Regression: Random Forest or random decision forest [38] is an integrated learning method for classification, regression and other activities that work by building a pile of decision trees during training. Random Forest has many decision trees as base learning models. The end results of the random forest is the mean of all the results of decision trees.

    LSTM based Deep Learning Model: An LSTM or Long-Short-Term-Memory classifier [39] is an artificial recurrent neural network that has both feedforward communication and feedback. LSTM for regression is typically a time series problem. For training the LSTM regression model data must first be converted to 3-D array according to the provided format: (number of samples, time steps, number of features). To prevent overfitting and visualize [40] the training progress, callbacks are passed as parameters while training the prediction model. In our approach we have used two callback that are:

    ● ReduceLRonPlateau: It reduces learning rate by "factor" times passed as argument if metric has stopped improving for "patience" number of epochs. Reducing learning rate oftens benefits the model.

    ● EarlyStopping: This will stop training if the monitored metric has stopped improving for "patience" number of epochs.

    Algorithm 2 is used for forecasting the amount of precipitation, as is given here.

     

    Algorithm 2: Algorithm for Regression
    Input: Rainfall Amount Prediction Dataset
    I = ['MinTemp', 'MaxTemp', 'Rainfall', 'WindGustDir', 'WindGustSpeed', 'WindDir9am', 'WindDir3pm', 'WindSpeed9am', 'WindSpeed3pm', 'Humidity9am, Humidity3pm', 'Pressure9am', 'Pressure3pm', 'Temp9am', 'Temp3pm', 'RainToday']
    Output: Amount of precipitation in millimeters
    1 Preprocess the input data and divide into features and target.
    2 Scale the data using Standard Scaler.
    3 Scale the data using Standard Scaler.
    4 Define regression model.
    5 Train regressor according to defined parameters.

    5.   Evaluation results

    There are numerous evaluation metrics that can be used for measuring model performance. In our paper we have evaluated our machine learning and deep learning models on confusion matrix, accuracy, precision, recall and F1-score for classification models and mean absolute error, mean squared error and r2 score for regression models.

    ● For Classification

    Confusion Matrix: Confusion matrix yields the output of a classification model in a matrix format. The matrix is defined as shown in Table 4.

    Table 4.  Confusion matrix.
    Predicted Values
    Positive Negative
    Actual Values Positive TP FN
    Negative FP TN
     | Show Table
    DownLoad: CSV

    A list of evaluation metrics used for evaluating trained classifiers is stated in Eqs (6)–(9).

    $ \begin{equation} Accuracy = \frac{No. of correct predictions}{Total no. of predictions} \end{equation} $ (6)
    $ \begin{equation} Precision = \frac{True Positive}{True Positive + False Positive} \end{equation} $ (7)
    $ \begin{equation} Recall = \frac{True Positive}{True Positive + False Negative} \end{equation} $ (8)
    $ \begin{equation} F1 = \frac{2 * (Precision * Recall)}{(Precision + Recall)} \end{equation} $ (9)

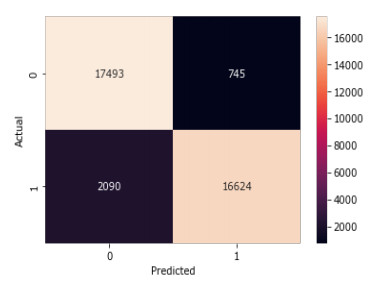
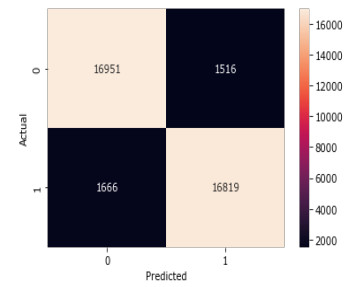
    XGBoost Classifier: Figure 11 and Table 5 represent the confusion matrix and the classification report for the XGBoost classifier. The classification report shows that the precision, recall, and f1-score for both the classes, i.e., rain and no rain are 96, 89, 92%, and 89, 96, 93% respectively.

    Figure 11.  Confusion matrix for XGBoost Classifier.
    DownLoad: Full-Size Img PowerPoint
    Table 5.  Classification report for XGBoost Classifier.
    Precision Recall F1-Score Support
    0 89% 96% 93% 18238
    1 96% 89% 92% 18714
    Accuracy 92% 36952
    Macro Avg 93% 92% 92% 36952
    Weighted Avg 93% 92% 92% 36952
     | Show Table
    DownLoad: CSV

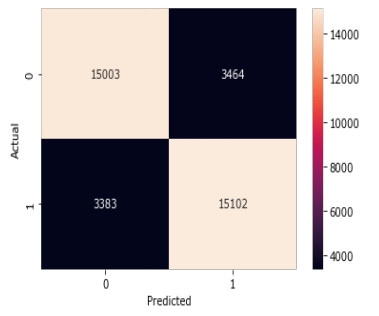
    Kernel SVM: Figure 12 and Table 6 represent the confusion matrix and the classification report for the Support Vector Machine Classifier with a radial basis kernel function. The classification report shows that the precision, recall, and f1-score for both the classes, i.e., rain and no rain are 81, 82, 92%, and 82, 81, 81% respectively.

    Figure 12.  Confusion matrix for SVM Classifier.
    DownLoad: Full-Size Img PowerPoint
    Table 6.  Classification report for SVM Classifier.
    Precision Recall F1-Score Support
    0 82% 81% 81% 18467
    1 81% 82% 82% 18485
    Accuracy 81% 36952
    Macro Avg 81% 81% 81% 36952
    Weighted Avg 81% 81% 81% 36952
     | Show Table
    DownLoad: CSV

    LSTM Classifier: Figure 13 and Table 7 represent the confusion matrix and the classification report for the LSTM classifier. The classification report shows that the precision, recall, and f1-score for both the classes, i.e., rain and no rain are 86, 87, 86%, and 87, 85, 86% respectively.

    Figure 13.  Confusion matrix for LSTM Classifier.
    DownLoad: Full-Size Img PowerPoint
    Table 7.  Classification report for LSTM Classifier.
    Precision Recall F1-Score Support
    0 87% 85% 86% 18531
    1 86% 87% 86% 18531
    Accuracy 86% 37062
    Macro Avg 86% 86% 86% 37062
    Weighted Avg 86% 86% 86% 37062
     | Show Table
    DownLoad: CSV

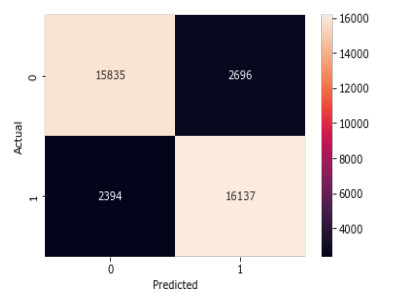
    Random Forest Classifier: Figure 14 and Table 8 represent the confusion matrix and the classification report for the Random Forest classifier. The classification report shows that the precision, recall, and f1-score for both the classes, i.e., rain and no rain are 92, 91, 91%, and 91, 92, 91% respectively.

    Figure 14.  Confusion matrix for Random Forest Classifier.
    DownLoad: Full-Size Img PowerPoint
    Table 8.  Classification report for Random Forest Classifier.
    Precision Recall F1-Score Support
    0 91% 92% 91% 18467
    1 92% 91% 91% 18485
    Accuracy 91% 36952
    Macro Avg 91% 91% 91% 36952
    Weighted Avg 91% 91% 91% 36952
     | Show Table
    DownLoad: CSV

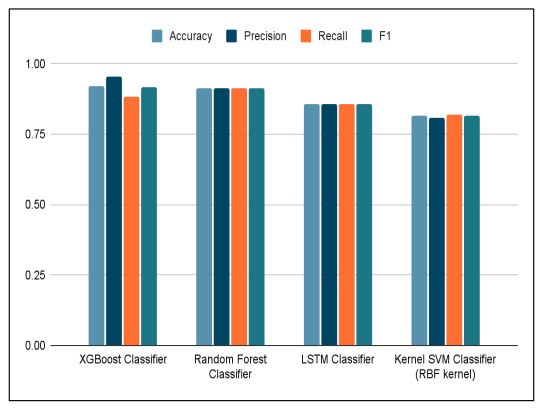
    Table 9 and Figure 15 represent the comparison of the evaluation results of the employed classification models. It is visible that the XGBoost classifier surpasses all the other classifiers with an accuracy (92.2%), precision (95.6%), and F1-Score (91.9%). However, Random Forest Classifier provided the best recall (91.2%) over the other classifiers. On the other hand, Kernel SVM with Radial Basis Function performed the worst among the four classifiers with an accuracy (81.4%), precision (80.9%), recall (82.1%), and F1-Score (81.5%), respectively.

    Table 9.  Evaluation results for Classification.
    Approach Accuracy Precision Recall F1-Score
    XGBoost Classifier 92.2% 95.61% 88.4% 91.87%
    Random Forest Classifier 91.3% 91.42% 91.16% 91.29%
    LSTM Classifier 85.84% 85.81% 85.88% 85.85%
    Kernel SVM Classifier (rbf kernel) 81.44% 80.86% 82.06% 81.45%
     | Show Table
    DownLoad: CSV
    Figure 15.  Comparing Evaluation Results for Classification.
    DownLoad: Full-Size Img PowerPoint

    From Table 10, we can confirm that our classification method is significantly superior to the various modern methods that use the Australian Kaggle rain dataset in terms of accuracy.

    Table 10.  State-of-the-art Results.
    State-of-the-Art Approach Best Accuracy
    Oswal (2019) [41] 84%
    He (2021) [42] 82%
     | Show Table
    DownLoad: CSV

    After undergoing several data processing techniques, a cleaned dataset with approximately 110 thousand rows is utilized for the classification task. Upon analyzing the class imbalance in the "RainTomorrow" feature, it was found to be highly skewed towards the "No" rainfall class, with a 9:1 ratio of "No" to "Yes" rainfall values. Models trained on this highly skewed data produced precision and accuracy values between 0.80 to 0.85. To address this imbalance, we used the SMOTE (Synthetic Minority Oversampling Technique) to balance both classes. This increased the data from 110 k rows to 183 k rows. The data was then divided into training and testing sets accordingly. The precision was improved to 95% and accuracy increased to 92% after using a balanced data set. This improvement in accuracy is attributed to the use of optimized data preprocessing and cleaning techniques, feature scaling techniques, data normalization techniques, training parameters, and train-test split ratios.

    ● For Regression

    The evaluation metrics employed for evaluating the trained regression models are Mean Absolute Error (MAE), Mean Squared Error (MSE), and R2 Score (R$ ^2 $) as stated in Eqs (10)–(12).

    $ \begin{equation} MAE = (\frac{1}{n})\sum\limits_{i = 1}^{n}| y_{i} - \hat{y}_{i} | \end{equation} $ (10)
    $ \begin{equation} MSE = (\frac{1}{n})\sum\limits_{i = 1}^{n}(y_i-\hat{y}_i)^2 \end{equation} $ (11)
    $ \begin{equation} R^2 = 1 - \frac{SS_{Res}}{SS_{TOT}} \end{equation} $ (12)

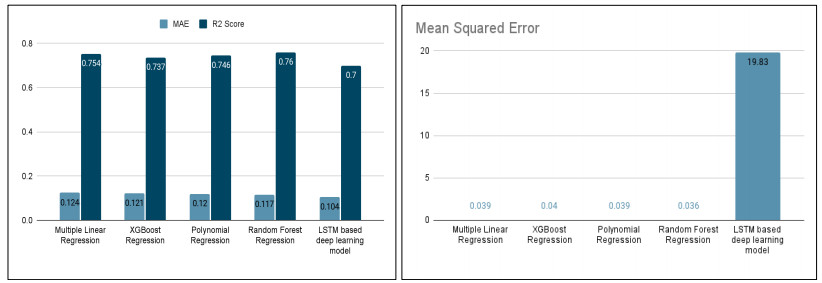
    Table 11 and Figure 16(a), (b) present the evaluation results of Multiple Linear regression, XGBoostRegressor, Polynomial regression, Random Forest regression, and LSTM-based deep learning model.

    Table 11.  Evaluation Results for Regression.
    Approach MAE MSE R2 Score
    Multiple Linear Regression 0.124 0.039 0.754
    XGBoost Regression 0.121 0.04 0.737
    Polynomial Regression 0.120 0.039 0.746
    Random Forest Regression 0.117 0.036 0.760
    LSTM based deep learning model 0.104 19.83 0.70
     | Show Table
    DownLoad: CSV
    Figure 16.  Comparing (a) MAE, R2 Score (b) MSE for Regression.
    DownLoad: Full-Size Img PowerPoint

    Here, it is observed that the Random Forest regressor outperformed all the other regression models with a mean absolute error of 0.117, mean squared error of 0.036, and R2 score of 0.76. On the other hand, the LSTM based deep learning model performed the worst among the five regression models with a mean absolute error of 0.104, mean squared error of 19.83, and R2 score of 0.70.

    ● Novelty and discussions: Data processing is a critical aspect of building a machine learning or deep learning model. Instead of filling missing values with the mean or mode of the entire dataset, the proposed solution uses seasonal and location-based data filling to fill numeric values with the mean and categorical values with the mode. LSTM-based models are often considered to be the best for modeling relationships in time series data. However, in the proposed method, the ensemble learning-based random forest model outperforms the LSTM model in both the classification and regression tasks. Random forest leverages class votes from each decision tree it grows, making it less susceptible to the impact of an inconsistent dataset and less prone to overfitting. In contrast, neural network models require more consistent data to make accurate predictions and may not perform well with inconsistent datasets.

    ● Limitations: Data collection is a major obstacle to accurate rainfall forecasting. Real-time weather data is hard to obtain and must be gathered from multiple meteorological stations, resulting in inconsistent and abnormal data due to incompatible data types and measurements. Therefore, we dropped the "Evaporation", "Sunshine", "Cloud9am", and "Cloud3pm" columns while handling NaN values as they each had 50% NaN values. Although these features can have a strong correlation with the rainfall value.

    6.   Conclusions and future works

    In this work, we implemented different machine learning and deep learning models for predicting the occurrence of rainfall the next day and for predicting the amount of rainfall in millimeters. We used the Australian rainfall dataset in this work. The dataset contains weather data from 49 locations on the Australian continent. In this work, we managed to obtain more accurate results than various state-of-the-art approaches. We achieved an accuracy of 92.2%, precision of 95.6%, F1 score of 91.9%, and recall of 91.1% for next day rainfall prediction. For the prediction of the amount of precipitation in millimeters, we obtained a mean absolute error of 0.117, a mean square error of 0.036, and an R2 value of 0.76. To obtain the above results, we applied several data preprocessing techniques, such as. analyzing null values, populating null values with seasonal and location-specific values, removing outliers using the interquartile range approach, selecting features by analyzing the correlation matrix, converting categorical values to numerical values to use the data for training the predictive model, balancing the class of target variables for the classification task, and normalizing the data using standard scalars for the regression task. We also compared different statistical machine learning and deep learning models for both the classification and regression tasks. This work uses publicly available datasets for training classification and regression models. Satellite and radar data can be used for training models and predicting rainfall in real time.

    In the future, further robustness can be achieved with the use of more recent and accurate data collected from meteorological departments. Incorporating additional features, such as "time of rainfall", "time of strongest wind gusts", "relative humidity at two points of time in a day" and "atmospheric pressure at sea level", could greatly enhance the model. These additional features are highly correlated with the "RainTomorrow" and "Rainfall" features. If the proposed model is trained with more features, it could lead to an increase in model performance. We would also like to work on transfer learning models to get better results.

    Acknowledgments

    This work is partially supported by Western Norway University of Applied Sciences, Bergen, Norway.

    Conflict of interest

    The authors declare there is no conflict of interest.



    [1] A. Kumar, M. Nadeem, H. Banka, Nature inspired optimization algorithms: a comprehensive overview, Evol. Syst., 14 (2023), 141–156. https://doi.org/10.1007/s12530-022-09432-6 doi: 10.1007/s12530-022-09432-6
    [2] K. Worden, W. J. Staszewski, J. J. Hensman, Natural computing for mechanical systems research: A tutorial overview, Mech. Syst. Signal Process., 25 (2011), 4–111. https://doi.org/10.1016/j.ymssp.2010.07.013 doi: 10.1016/j.ymssp.2010.07.013
    [3] S. C. Gao, Z. Tang, H. W. Dai, J. Zhang, An improved clonal algorithm and its application to traveling salesman problems, IEICE Trans. Fundam., E90-A (2007), 2930–2938. https://doi.org/10.1093/ietfec/e90-a.12.2930 doi: 10.1093/ietfec/e90-a.12.2930
    [4] Y. Yang, H. Dai, S. C. Gao, Y. R. Wang, D. B. Jia, Z. Tang, Complete receptor editing operation based on quantum clonal selection algorithm for optimization problems, IEEJ Trans. Electr. Electron. Eng., 14 (2018), 411–421. https://doi.org/10.1002/tee.22822 doi: 10.1002/tee.22822
    [5] A. S. Muhamad, S. Deris, An artificial immune system for solving production scheduling problems: a review, Artif. Intell. Rev., 39 (2013), 1–12. https://doi.org/10.1007/s10462-011-9259-1 doi: 10.1007/s10462-011-9259-1
    [6] F. M. Burnet, The Clonal Selection Theory of Acquired Immunity, Cambridge Press, 1959.
    [7] G. J. V. Nossal, Negative selection of lymphocytes, Cell, 76 (1994), 229–239. https://doi.org/10.1007/978-1-4020-6754-9-11239 doi: 10.1007/978-1-4020-6754-9-11239
    [8] A. Perelson, Immune network theory, Immunol. Rev., 110 (1989), 5–36. https://doi.org/10.1111/j.1600-065X.1989.tb00025.x doi: 10.1111/j.1600-065X.1989.tb00025.x
    [9] P. Matzinger, The danger model: a renewed sense of self, Science, 296 (2002), 301–305. https://doi.org/10.1126/science.1071059 doi: 10.1126/science.1071059
    [10] F. Gu, J. Greensmith, U. Aickelin, Theoretical formulation and analysis of the deterministic dendritic cell algorithm, Biosystems, 111 (2013), 127–135. https://doi.org/10.1016/j.biosystems.2013.01.001 doi: 10.1016/j.biosystems.2013.01.001
    [11] S. C. Gao, H. W. Dai, G. Yang, Z. Tang, A novel clonal selection algorithm and its application to traveling salesman problems, IEICE Trans. Fundam., E90A (2007), 2318–2325. https://doi.org/10.1093/ietfec/e90-a.10.2318 doi: 10.1093/ietfec/e90-a.10.2318
    [12] B. H. Ulutas, S. Kulturel-Konak, A review of clonal selection algorithm and its applications, Artif. Intell. Rev., 36 (2011), 117–138.
    [13] L. N. De Castro, F. J. Von Zuben, Learning and optimization using the clonal selection principle, IEEE Trans. Evol. Comput., 6 (2002), 239–251. https://doi.org/10.1109/TEVC.2002.1011539 doi: 10.1109/TEVC.2002.1011539
    [14] R. Shang, L. Jiao, F. Liu, W. Ma, A novel immune clonal algorithm for mo problems, IEEE Trans. Evol. Comput., 16 (2012), 35–50. https://doi.org/10.1109/TEVC.2010.2046328 doi: 10.1109/TEVC.2010.2046328
    [15] Y. Ding, Z. Wang, H. Ye, Optimal control of a fractional-order HIV-immune system with memory, IEEE Trans. Control Syst. Technol., 3 (2012), 763–769. https://doi.org/10.1109/TCST.2011.2153203 doi: 10.1109/TCST.2011.2153203
    [16] P. A. D. Castro, F. J. Von Zuben, Learning ensembles of neural networks by means of a bayesian artificial immune system, IEEE Trans. Neural Networks, 22 (2011), 304–316. https://doi.org/10.1109/TNN.2010.2096823 doi: 10.1109/TNN.2010.2096823
    [17] G. Dudek, An artificial immune system for classification with local feature selection, IEEE Trans. Evol. Comput., 6 (2012), 847–860. https://doi.org/10.1109/TEVC.2011.2173580 doi: 10.1109/TEVC.2011.2173580
    [18] M. Hunjan, G. K. Venayagamoorthy, Adaptive power system stabilizers using artificial immune system, IEEE Symp. Artif. Life, 2007 (2007), 440–447.
    [19] M. Gui, A. Pahwa, S. Das, Analysis of animal-related outages in overhead distribution systems with Wavelet decomposition and immune systems-based neural networks, IEEE Trans. Power Syst., 24 (2009), 1765–1771. https://doi.org/10.1109/TPWRS.2009.2030382 doi: 10.1109/TPWRS.2009.2030382
    [20] V. Cutello, G. Nicosia, M. Pavone, J. Timmis, An immune algorithm for protein structure prediction on lattice models, IEEE Trans. Evol. Comput., 11 (2007), 101–117. https://doi.org/10.1109/TEVC.2006.880328 doi: 10.1109/TEVC.2006.880328
    [21] V. Cutello, G. Morelli, G. Nicosia, M. Pavone, G. Scollo, On discrete models and immunological algorithms for protein structure prediction, Nat. Comput., 10 (2011), 91–102. https://doi.org/10.1007/s11047-010-9196-y doi: 10.1007/s11047-010-9196-y
    [22] C. Vincenzo, N. Giuseppe, P. Mario, P. Igor, Protein multiple sequence alignment by hybrid bio-inspired algorithms, Nucleic Acids Res., 39 (2011), 1980–1992. https://doi.org/10.1093/nar/gkq1052 doi: 10.1093/nar/gkq1052
    [23] S. C. Gao, R. L. Wang, M. Ishii, Z. Tang, An artificial immune system with feedback mechanisms for effective handling of populationsize, IEICE Trans. Fundam. Electron. Commun. Comput. Sci., E93A (2010), 532–541. https://doi.org/10.1587/transfun.E93.A.532 doi: 10.1587/transfun.E93.A.532
    [24] T. Luo, A clonal selection algorithm for dynamic multimodal function optimization, Swarm Evol. Comput., 50 (2019), 1980–1992.
    [25] W. W. Zhang, W. Zhang, G. G. Yen, H. L. Jing, A cluster-based clonal selection algorithm for optimization in dynamic environment, Swarm Evol. Comput., 50 (2019), 1–13. https://doi.org/10.1016/j.swevo.2018.10.005 doi: 10.1016/j.swevo.2018.10.005
    [26] H. Zhang, J. Sun, T. Liu, K. Zhang, Q. Zhang, Balancing exploration and exploitation in multiobjective evolutionary optimization, Inf. Sci., 497 (2019). https://doi.org/10.1016/j.ins.2019.05.046 doi: 10.1016/j.ins.2019.05.046
    [27] N. Khilwani, A. Prakash, R. Shankar, M. K. Tiwari, Fast clonal algorithm, Eng. Appl. Artif. Intell., 21 (2008), 106–128. https://doi.org/10.1016/j.engappai.2007.01.004 doi: 10.1016/j.engappai.2007.01.004
    [28] X. Yao, Y. Liu, G. Lin, Evolutionary programming made faster, IEEE Trans. Evol. Comput., 3 (1999), 82–102. https://doi.org/10.1109/4235.771163 doi: 10.1109/4235.771163
    [29] C. Y. Lee, X. Yao, Evolutionary programming using mutations based on the levy probability distribution, IEEE Trans. Evol. Comput., 8 (2004), 1–13. https://doi.org/10.1109/TEVC.2003.816583 doi: 10.1109/TEVC.2003.816583
    [30] M. Gong, L. Jiao, L. Zhang, Baldwinian learning in clonal selection algorithm for optimization, Inf. Sci., 180 (2010), 1218–1236. https://doi.org/10.1016/j.ins.2009.12.007 doi: 10.1016/j.ins.2009.12.007
    [31] A. M. Whitbrook, U. Aickelin, J. M. Garibaldi, Idiotypic immune networks in mobile-robot control, IEEE Trans. Syst. Man Cybern. Part B Cybern., 37 (2007), 1581–1598. https://doi.org/10.1016/j.ins.2009.12.007 doi: 10.1016/j.ins.2009.12.007
    [32] S. Gao, H. W. Dai, J. C. Zhang, Z. Tang, An expanded lateral interactive clonal selection algorithm and its application, IEICE Trans. Fundam. Electron. Commun. Comput. Sci., E91A (2008), 2223–2231. https://doi.org/10.1093/ietfec/e91-a.8.2223 doi: 10.1093/ietfec/e91-a.8.2223
    [33] V. Stanovov, S. Akhmedova, E. Semenkin, Selective pressure strategy in differential evolution: Exploitation improvement in solving global optimization problems, Swarm Evol. Comput., 50 2018, 1–14. https://doi.org/10.1016/j.swevo.2018.10.014 doi: 10.1016/j.swevo.2018.10.014
    [34] R. M. Hoare, Structure and Dynamics of Simple Microclusters, John Wiley Sons, Inc., 2007.
    [35] K. Deep, M. Arya, Minimization of Lennard-Jones Potential Using Parallel Particle Swarm Optimization Algorithm, Springer Berlin Heidelberg, 2010.
    [36] M. R. Hoare, Structure and dynamics of simple microclusters, Adv. Chem. Phys., (1979), 49–135.
    [37] J. A. Northby, Structure and binding of lennard-jones clusters, J. Chem. Phys., 87 (1987), 6166–6177. https://doi.org/10.1063/1.453492 doi: 10.1063/1.453492
    [38] G. Xue, Improvement on the northby algorithm for molecular conformation: Better solutions, J. Global Optim., 4 (1994), 425–440.
    [39] D. J. Wales, J. P. K. Doye, Global optimization by basin-hopping and the lowest energy structures of lennard-jones clusters containing up to 110 atoms, J. Phys. Chem. A, 101 (1998), 5111–5116. https://doi.org/10.1021/jp970984n doi: 10.1021/jp970984n
    [40] R. H. Leary, Global optima of lennard-jones clusters, J. Global Optim., 11 (1997), 35–53. https://doi.org/10.1021/jp970984n doi: 10.1021/jp970984n
    [41] R. H. Leary, Global optimization on funneling landscapes, J. Global Optim., 18 (2000), 367–383. https://doi.org/10.1023/A:1026500301312 doi: 10.1023/A:1026500301312
    [42] D. Daven, N. Tit, J. Morris, K. Ho, Structural optimization of lennard-jones clusters by a genetic algorithm, Chem. Phys. Lett., 256 (1996), 195–200. https://doi.org/10.1016/0009-2614(96)00406-X doi: 10.1016/0009-2614(96)00406-X
    [43] B. Hartke, Efficient global geometry optimization of atomic and molecular clusters, Eur. Phys. J. D, 2006 (2006). https://doi.org/10.1007/0-387-30927-6-6 doi: 10.1007/0-387-30927-6-6
    [44] K. Deep, Shashi, V. K. Katiyar, Global optimization of lennard jones potential using newly developed real coded genetic algorithms, in International Conference on Communication Systems and Network Technologies, (2011), 614–618.
    [45] N. P. Moloi, M. M. Ali, An iterative global optimization algorithm for potential energy minimization, Comput. Optim. Appl., 30 (2005), 119–132. https://doi.org/10.1007/s10589-005-4555-9 doi: 10.1007/s10589-005-4555-9
    [46] D. M. Deaven, K. M. Ho, Molecular geometry optimization with a genetic algorithm, Phys. Rev. Lett., 75 (1995), 288–291. https://doi.org/10.1103/PhysRevLett.75.288 doi: 10.1103/PhysRevLett.75.288
    [47] S. Darby, T. V. Mortimer-Jones, R. L. Johnston, C. Roberts, Theoretical study of cu-au nanoalloy clusters using a genetic algorithm, J. Chem. Phys., 116 (2002), 1536–1550.
    [48] M. R. Hoare, Structure and dynamics of simple microclusters, Adv. Chem. Phys., 40 (1979), 49–135. https://doi.org/10.1002/9780470142592.ch2 doi: 10.1002/9780470142592.ch2
    [49] G. Xue, R. S. Maier, J. B. Rosen, Minimizing the lennard-jones potential function on a massively parallel computer, in Proceedings of the 6th International Conference on Supercomputing, ACM, (1992), 409–416.
    [50] D. Dasgupta, S. Yu, F. Nino, Recent advances in artificial immune systems: models and applications, Appl. Soft Comput., 11 (2011), 1547–1587. https://doi.org/10.1016/j.asoc.2010.08.024 doi: 10.1016/j.asoc.2010.08.024
    [51] E. Hart, J. Timmis, Application areas of ais: The past, the present and the future, Appl. Soft Comput., 8 (2008), 191–201. https://doi.org/10.1016/j.asoc.2006.12.004 doi: 10.1016/j.asoc.2006.12.004
    [52] V. Cutello, G. Nicosia, M. Pavone, Exploring the capability of immune algorithms: A characterization of hypermutation operators, in Third International Conference on Artificial Immune Systems, (2004), 263–276. https://doi.org/10.1007/978-3-540-30220-9-22
    [53] T. Jansen, C. Zarges, Analyzing different variants of immune inspired somatic contiguous hypermutations, Theor. Comput. Sci., 412 (2011), 517–533. https://doi.org/10.1016/j.tcs.2010.09.027 doi: 10.1016/j.tcs.2010.09.027
    [54] X. Xu, J. Zhang, An improved immune evolutionary algorithm for multimodal function optimization, in Third International Conference on Natural Computation, (2007), 641–646.
    [55] X. Yao, Y. Liu, G. Lin, Evolutionary programming made faster, IEEE Trans. Evol. Comput., 3 (1999), 82–102. https://doi.org/10.1109/4235.771163 doi: 10.1109/4235.771163
    [56] V. Cutello, G. Nicosia, M. Pavone, Real coded clonal selection algorithm for unconstrained global optimization using a hybrid inversely proportional hypermutation operator, in Proceedings of the 2006 ACM symposium on Applied computing, (2006), 950–954.
    [57] M. Crepinsek, S. H. Liu, M. Mernik, Exploration and exploitation in evolutionary algorithms: a survey, ACM Comput. Surv., 45 (2013), 1–35. https://doi.org/10.1145/2480741.2480752 doi: 10.1145/2480741.2480752
    [58] L. Jiao, Y. Li, M. Gong, X. Zhang, Quantum-inspired immune clonal algorithm for global optimization, IEEE Trans. Syst. Man Cybern. Part B Cybern., 38 (2008), 1234–1253. https://doi.org/10.1109/TSMCB.2008.927271 doi: 10.1109/TSMCB.2008.927271
    [59] E. Atashpaz-Gargari, C. Lucas, Imperialist competitive algorithm: An algorithm for optimization inspired by imperialistic competition, IEEE Congr. Evol. Comput., 2007 (2007), 4661–4667. https://doi.org/10.1109/4235.771163 doi: 10.1109/4235.771163

  • This article has been cited by:

    1. Tumusiime Andrew Gahwera, Odongo Steven Eyobu, Mugume Isaac, Analysis of Machine Learning Algorithms for Prediction of Short-Term Rainfall Amounts Using Uganda’s Lake Victoria Basin Weather Dataset, 2024, 12, 2169-3536, 63361, 10.1109/ACCESS.2024.3396695
    2. Arti Jain, Rajeev Kumar Gupta, Mohit Kumar, 2024, chapter 16, 9798369323519, 324, 10.4018/979-8-3693-2351-9.ch016
    3. Babita Pathik, Rajeev Kumar Gupta, Nikhlesh Pathik, 2024, Chapter 4, 978-3-031-62216-8, 45, 10.1007/978-3-031-62217-5_4
    4. Nan Yao, Jinyin Ye, Shuai Wang, Shuai Yang, Yang Lu, Hongliang Zhang, Xiaoying Yang, Bias correction of the hourly satellite precipitation product using machine learning methods enhanced with high-resolution WRF meteorological simulations, 2024, 310, 01698095, 107637, 10.1016/j.atmosres.2024.107637
    5. Dhvanil Bhagat, Shrey Shah, Rajeev Kumar Gupta, 2024, Chapter 6, 978-3-031-62216-8, 63, 10.1007/978-3-031-62217-5_6
    6. Tumusiime Andrew Gahwera, Odongo Steven Eyobu, Mugume Isaac, 2024, Transfer Learning Approach for Rainfall Class Amount Prediction Using Uganda's Lake Victoria Basin Weather Dataset, 979-8-3503-9174-9, 101, 10.1109/IBDAP62940.2024.10689700
    7. Abhishek Thoke, Sakshi Rai, 2024, Exploring Faster R-CNN Algorithms for Object Detection, 979-8-3503-5293-1, 1, 10.1109/SSITCON62437.2024.10796389
    8. S. P. Siddique Ibrahim, N.Venkata Harika, N.Mohitha Reddy, K. Srija, P.Shiva Sahithi, A. Kohima, 2024, Application of Machine Learning and Data Mining Techniques for Accurate Cloud Burst Prediction, 979-8-3315-1809-7, 1117, 10.1109/ICICNIS64247.2024.10823388
    9. Hiresh Singh Sengar, Sakshi Rai, 2024, A Comparative Analysis of Different Machine Learning Approaches for Crop Yield Prediction, 979-8-3315-0496-0, 1, 10.1109/ICIICS63763.2024.10859455
    10. C. Vijayalakshmi, M. Pushpa, Optimizing non-linear autoregressive networks with Bird Sea Lion algorithms for effective rainfall forecasting, 2025, 18, 1865-0473, 10.1007/s12145-025-01768-2
    11. Tumusiime Andrew Gahwera, Odongo Steven Eyobu, Mugume Isaac, Samuel Kakuba, Dong Seog Han, Transfer Learning-Based Ensemble Approach for Rainfall Class Amount Prediction, 2025, 13, 2169-3536, 48318, 10.1109/ACCESS.2025.3551737
  • Reader Comments
  • © 2023 the Author(s), licensee AIMS Press. This is an open access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0)
通讯作者: 陈斌, bchen63@163.com
  • 1. 

    沈阳化工大学材料科学与工程学院 沈阳 110142

  1. 本站搜索
  2. 百度学术搜索
  3. 万方数据库搜索
  4. CNKI搜索
Mathematical Biosciences and Engineering
3.9

Metrics

Article views(1623) PDF downloads(71) Cited by(0)

Preview PDF
Download XML
Export Citation
Article outline
Abstract
   Introduction
   Literature review
   Data description
   Proposed approach
   Evaluation results
   Conclusions and future works
Acknowledgments
Conflict of interest
References

Other Articles By Authors

Related pages

Tools

Copyright © AIMS Press

/

DownLoad:  Full-Size Img  PowerPoint
Return
Return

Catalog