Healthcare is the method of keeping or enhancing physical and mental well-being with its aid of illness and injury prevention, diagnosis, and treatment. The majority of conventional healthcare practices involve manual management and upkeep of client demographic information, case histories, diagnoses, medications, invoicing, and drug stock upkeep, which can result in human errors that have an impact on clients. By linking all the essential parameter monitoring equipment through a network with a decision-support system, digital health management based on Internet of Things (IoT) eliminates human errors and aids the doctor in making more accurate and timely diagnoses. The term "Internet of Medical Things" (IoMT) refers to medical devices that have the ability to communicate data over a network without requiring human-to-human or human-to-computer interaction. Meanwhile, more effective monitoring gadgets have been made due to the technology advancements, and these devices can typically record a few physiological signals simultaneously, including the electrocardiogram (ECG) signal, the electroglottography (EGG) signal, the electroencephalogram (EEG) signal, and the electrooculogram (EOG) signal. Yet, there has not been much research on the connection between digital health management and multi-modal signal monitoring. To bridge the gap, this article reviews the latest advancements in digital health management using multi-modal signal monitoring. Specifically, three digital health processes, namely, lower-limb data collection, statistical analysis of lower-limb data, and lower-limb rehabilitation via digital health management, are covered in this article, with the aim to fully review the current application of digital health technology in lower-limb symptom recovery.
Citation: Jiayu Fu, Haiyan Wang, Risu Na, A JISAIHAN, Zhixiong Wang, Yuko OHNO. Recent advancements in digital health management using multi-modal signal monitoring[J]. Mathematical Biosciences and Engineering, 2023, 20(3): 5194-5222. doi: 10.3934/mbe.2023241
Healthcare is the method of keeping or enhancing physical and mental well-being with its aid of illness and injury prevention, diagnosis, and treatment. The majority of conventional healthcare practices involve manual management and upkeep of client demographic information, case histories, diagnoses, medications, invoicing, and drug stock upkeep, which can result in human errors that have an impact on clients. By linking all the essential parameter monitoring equipment through a network with a decision-support system, digital health management based on Internet of Things (IoT) eliminates human errors and aids the doctor in making more accurate and timely diagnoses. The term "Internet of Medical Things" (IoMT) refers to medical devices that have the ability to communicate data over a network without requiring human-to-human or human-to-computer interaction. Meanwhile, more effective monitoring gadgets have been made due to the technology advancements, and these devices can typically record a few physiological signals simultaneously, including the electrocardiogram (ECG) signal, the electroglottography (EGG) signal, the electroencephalogram (EEG) signal, and the electrooculogram (EOG) signal. Yet, there has not been much research on the connection between digital health management and multi-modal signal monitoring. To bridge the gap, this article reviews the latest advancements in digital health management using multi-modal signal monitoring. Specifically, three digital health processes, namely, lower-limb data collection, statistical analysis of lower-limb data, and lower-limb rehabilitation via digital health management, are covered in this article, with the aim to fully review the current application of digital health technology in lower-limb symptom recovery.
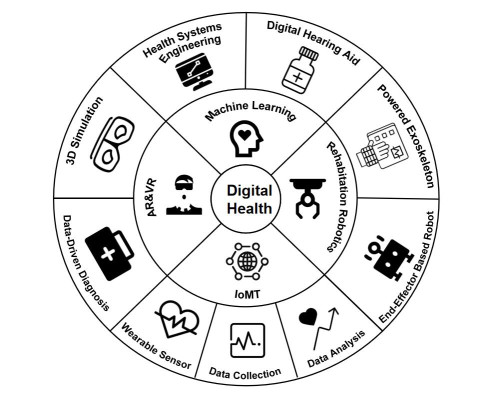
| [1] | M. Entov, L. Polterovich, F. Zapolsky, Quasi-morphisms and the poisson bracket, preprint, arXiv: math/0605406. https://doi.org/10.48550/arXiv.math/0605406 |
| [2] |
K. P. Fadahunsi, S. O'Connor, J. T. Akinlua, P. A. Wark, J. Gallagher, C. Carroll, et al., Information quality frameworks for digital health technologies: systematic review, J. Med. Internet Res., 23 (2021), e23479. https://doi.org/10.2196/23479 doi: 10.2196/23479
|
| [3] |
S. P. Bhavnani, J. Narula, P. P. Sengupta, Mobile technology and the digitization of healthcare, Eur. Heart J., 37 (2016), 1428–1438. https://doi.org/10.1093/eurheartj/ehv770 doi: 10.1093/eurheartj/ehv770
|
| [4] | World Health Organization, Global diffusion of eHealth: making universal health coverage achievable: report of the third global survey on eHealth, 2017. |
| [5] |
W. Qi, S. E. Ovur, Z. Li, A. Marzullo, R. Song, Multi-sensor guided hand gesture recognition for a teleoperated robot using a recurrent neural network, IEEE Robot. Autom. Lett., 6 (2021), 6039–6045. https://doi.org/10.1109/LRA.2021.3089999 doi: 10.1109/LRA.2021.3089999
|
| [6] |
H. Su, W. Qi, C. Yang, J. Sandoval, G. Ferrigno, E. De Momi, Deep neural network approach in robot tool dynamics identification for bilateral teleoperation, IEEE Robot. Autom. Lett., 5 (2020), 2943–2949. https://doi.org/10.1109/LRA.2020.2974445 doi: 10.1109/LRA.2020.2974445
|
| [7] |
Y. El-Miedany, Telehealth and telemedicine: how the digital era is changing standard health care, Smart Homecare Technol. Telehealth, 4 (2017), 43–51. https://doi.org/10.2147/SHTT.S116009 doi: 10.2147/SHTT.S116009
|
| [8] |
J. Byaruhanga, P. Atorkey, M. McLaughlin, A. Brown, E. Byrnes, C. Paul, et al., Effectiveness of individual real-time video counseling on smoking, nutrition, alcohol, physical activity, and obesity health risks: systematic review, J. Med. Internet Res., 22 (2020), e18621. https://doi.org/10.2196/18621 doi: 10.2196/18621
|
| [9] |
H. Su, W. Qi, Y. Hu, H. R. Karimi, G. Ferrigno, E. D. Momi, An incremental learning framework for human-like redundancy optimization of anthropomorphic manipulators, IEEE Trans. Ind. Inf., 18 (2020), 1864–1872. https://doi.org/10.1109/TII.2020.3036693 doi: 10.1109/TII.2020.3036693
|
| [10] |
L. Moreira, J. Figueiredo, P. Fonseca, J. P. Vilas-Boas, C. P. Santos, Lower limb kinematic, kinetic, and emg data from young healthy humans during walking at controlled speeds, Sci. Data, 8 (2021), 1–11. https://doi.org/10.6084/m9.figshare.13169348 doi: 10.6084/m9.figshare.13169348
|
| [11] |
E. Rich, A. Miah, Mobile, wearable and ingestible health technologies: towards a critical research agenda, Health Sociol. Rev., 26 (2017), 84–97. https://doi.org/10.1080/14461242.2016.1211486 doi: 10.1080/14461242.2016.1211486
|
| [12] |
O. Amft, How wearable computing is shaping digital health, IEEE Pervasive Comput., 17 (2018), 92–98. https://doi.org/10.1109/MPRV.2018.011591067 doi: 10.1109/MPRV.2018.011591067
|
| [13] |
K. Klinker, M. Wiesche, H. Krcmar, Digital transformation in health care: Augmented reality for hands-free service innovation, Inf. Syst. Front., 22 (2020), 1419–1431. https://doi.org/10.1007/s10796-019-09937-7 doi: 10.1007/s10796-019-09937-7
|
| [14] |
A. S. Merians, D. Jack, R. Boian, M. Tremaine, G. C. Burdea, S. V. Adamovich, et al., Virtual reality–augmented rehabilitation for patients following stroke, Phys. Ther., 82 (2002), 898–915. https://doi.org/10.1093/ptj/82.9.898 doi: 10.1093/ptj/82.9.898
|
| [15] |
H. Su, A. Mariani, S. E. Ovur, A. Menciassi, G. Ferrigno, E. D. Momi, Toward teaching by demonstration for robot-assisted minimally invasive surgery, IEEE Trans. Autom. Sci. Eng., 18 (2021), 484–494. https://doi.org/10.1109/TASE.2020.3045655 doi: 10.1109/TASE.2020.3045655
|
| [16] |
H. Su, W. Qi, J. Chen, D. Zhang, Fuzzy approximation-based task-space control of robot manipulators with remote center of motion constraint, IEEE Trans. Fuzzy Syst., 30 (2022), 1564–1573. https://doi.org/10.1109/TFUZZ.2022.3157075 doi: 10.1109/TFUZZ.2022.3157075
|
| [17] |
H. Su, Y. Hu, H. R. Karimi, A. Knoll, G. Ferrigno, E. De Momi, Improved recurrent neural network-based manipulator control with remote center of motion constraints: Experimental results, Neural Networks, 131 (2020), 291–299. https://doi.org/10.1016/j.neunet.2020.07.033 doi: 10.1016/j.neunet.2020.07.033
|
| [18] |
B. R. Brewer, S. K. McDowell, L. C. Worthen-Chaudhari, Poststroke upper extremity rehabilitation: a review of robotic systems and clinical results, Top Stroke Rehabil., 14 (2007), 22–44. https://doi.org/10.1310/tsr1406-22 doi: 10.1310/tsr1406-22
|
| [19] |
S. Balasubramanian, J. Klein, E. Burdet, Robot-assisted rehabilitation of hand function, Curr. Opin. Neurol., 23 (2010), 661–670. https://doi.org/10.1097/WCO.0b013e32833e99a4 doi: 10.1097/WCO.0b013e32833e99a4
|
| [20] | Y. Kang, D. Jeon, Rehabilitation robot control using the VSD method, in 2012 IEEE/SICE International Symposium on System Integration (SII), IEEE, (2012), 192–197. https://doi.org/10.1109/SII.2012.6427313 |
| [21] |
K. P. Michmizos, S. Rossi, E. Castelli, P. Cappa, H. I. Krebs, Robot-aided neurorehabilitation: a pediatric robot for ankle rehabilitation, IEEE Trans. Neural Syst. Rehab. Eng., 23 (2015), 1056–1067. https://doi.org/10.1109/TNSRE.2015.2410773 doi: 10.1109/TNSRE.2015.2410773
|
| [22] |
L. Marchal-Crespo, D. J. Reinkensmeyer, Review of control strategies for robotic movement training after neurologic injury, J. NeuroEng. Rehabil., 6 (2009), 1–15. https://doi.org/10.1186/1743-0003-6-20 doi: 10.1186/1743-0003-6-20
|
| [23] |
S. Balasubramanian, R. Colombo, I. Sterpi, V. Sanguineti, E. Burdet, Robotic assessment of upper limb motor function after stroke, Am. J. Phys. Med. Rehabil., 91 (2012), S255–S269. https://doi.org/10.1097/PHM.0b013e31826bcdc1 doi: 10.1097/PHM.0b013e31826bcdc1
|
| [24] |
M. Haghshenas-Jaryani, R. M. Patterson, N. Bugnariu, M. B. Wijesundara, A pilot study on the design and validation of a hybrid exoskeleton robotic device for hand rehabilitation, J. Hand Ther., 33 (2020), 198–208. https://doi.org/10.1016/j.jht.2020.03.024 doi: 10.1016/j.jht.2020.03.024
|
| [25] |
L. Wang, J. Tian, J. Du, S. Zheng, J. Niu, Z. Zhang, et al., A hybrid mechanism-based robot for end-traction lower limb rehabilitation: Design, analysis and experimental evaluation, Machines, 10 (2022), 99. https://doi.org/10.3390/machines10020099 doi: 10.3390/machines10020099
|
| [26] |
J. Wang, Y. Kan, T. Zhang, Z. Zhang, M. Xu, Model analysis and experimental study of lower limb rehabilitation training device based on gravity balance, Machines, 10 (2022), 514. https://doi.org/10.3390/machines10070514 doi: 10.3390/machines10070514
|
| [27] | V. der Loos, H. Machiel, D. J. Reinkensmeyer, E. Guglielmelli, Rehabilitation and health care robotics, in Springer handbook of robotics, Springer, (2016), 1685–1728. https://doi.org/10.1007/978-3-319-32552-1_64 |
| [28] | C. Tefertiller, B. Pharo, N. Evans, P. Winchester, Efficacy of rehabilitation robotics for walking training in neurological disorders: a review, J. Rehabil. Res. Dev., 48 (2011). https://doi.org/10.1682/JRRD.2010.04.0055 |
| [29] |
J. Kim, Y. Kim, S. Kang, S. J. Kim, Biomechanical analysis suggests myosuit reduces knee extensor demand during level and incline gait, Sensors, 22 (2022), 6127. https://doi.org/10.3390/s22166127 doi: 10.3390/s22166127
|
| [30] |
K. Y. Chung, K. Song, K. Shin, J. Sohn, S. H. Cho, J. H. Chang, Noncontact sleep study by multi-modal sensor fusion, Sensors, 17 (2017), 1685. https://doi.org/10.3390/s17071685 doi: 10.3390/s17071685
|
| [31] |
W. Qi, H. Su, A. Aliverti, A smartphone-based adaptive recognition and real-time monitoring system for human activities, IEEE Trans. Hum. Mach. Syst., 50 (2020), 414–423. https://doi.org/10.1109/THMS.2020.2984181 doi: 10.1109/THMS.2020.2984181
|
| [32] | H. Su, W. Qi, Y. Schmirander, S. E. Ovur, S. Cai, X. Xiong, A human activity-aware shared control solution for medical human-robot interaction, Assem. Autom., 2022. https://doi.org/10.1108/AA-12-2021-0174 |
| [33] |
W. Qi, A. Aliverti, A multimodal wearable system for continuous and real-time breathing pattern monitoring during daily activity, IEEE J. Biomed. Health, 24 (2019), 2199–2207. https://doi.org/10.1109/JBHI.2019.2963048 doi: 10.1109/JBHI.2019.2963048
|
| [34] | W. Qi, H. Su, A cybertwin based multimodal network for ecg patterns monitoring using deep learning, IEEE Trans. Ind. Inf., 2022. https://doi.org/10.1109/TII.2022.3159583 |
| [35] |
T. He, C. Lee, Evolving flexible sensors, wearable and implantable technologies towards bodynet for advanced healthcare and reinforced life quality, IEEE Open J. Circuits Syst., 2 (2021), 702–720. https://doi.org/10.1109/OJCAS.2021.3123272 doi: 10.1109/OJCAS.2021.3123272
|
| [36] |
C. T. Li, T. Y. Wu, C. L. Chen, C. C. Lee, C. M. Chen, An efficient user authentication and user anonymity scheme with provably security for iot-based medical care system, Sensors, 17 (2017), 1482. https://doi.org/10.3390/s17071482 doi: 10.3390/s17071482
|
| [37] |
W. Qi, N. Wang, H. Su, A. Aliverti, DCNN based human activity recognition framework with depth vision guiding, Neurocomputing, 486 (2022), 261–271. https://doi.org/10.1016/j.neucom.2021.11.044 doi: 10.1016/j.neucom.2021.11.044
|
| [38] |
J. Y. Oh, Z. Bao, Second skin enabled by advanced electronics, Adv. Sci., 6 (2019), 1900186. https://doi.org/10.1002/advs.201900186 doi: 10.1002/advs.201900186
|
| [39] | Y. Ling, T. An, L. W. Yap, B. Zhu, S. Gong, W. Cheng, Disruptive, soft, wearable sensors, Adv. Mater., 32 (2020), 1904664. https://doi.org/10.1002/adma.201904664 |
| [40] |
Z. Liu, W. Zhou, C. Qi, T. Kong, Interface engineering in multiphase systems toward synthetic cells and organelles: From soft matter fundamentals to biomedical applications, Adv. Mater., 32 (2020), 2002932. https://doi.org/10.1002/adma.202002932 doi: 10.1002/adma.202002932
|
| [41] |
X. Xi, D. Wu, W. Ji, S. Zhang, W. Tang, Y. Su, et al., Manipulating the sensitivity and selectivity of oect-based biosensors via the surface engineering of carbon cloth gate electrodes, Adv. Funct. Mater., 30 (2020), 1905361. https://doi.org/10.1002/adfm.201905361 doi: 10.1002/adfm.201905361
|
| [42] |
S. Bellani, E. Petroni, A. E. D. Rio Castillo, N. Curreli, B. Martín-García, R. Oropesa-Nuñez, et al., Scalable production of graphene inks via wet-jet milling exfoliation for screen-printed micro-supercapacitors, Adv. Funct. Mater., 29 (2019), 1807659. https://doi.org/10.1002/adfm.201807659 doi: 10.1002/adfm.201807659
|
| [43] |
W. Zhang, Y. Xiao, Y. Duan, N. Li, L. Wu, Y. Lou, et al., A high-performance flexible pressure sensor realized by overhanging cobweb-like structure on a micropost array, ACS Appl. Mater. Interfaces, 12 (2020), 48938–48947. https://doi.org/10.1021/acsami.0c12369 doi: 10.1021/acsami.0c12369
|
| [44] |
Y. Hu, Y. He, Z. Peng, Y. Li, A ratiometric electrochemiluminescence sensing platform for robust ascorbic acid analysis based on a molecularly imprinted polymer modified bipolar electrode, Biosens. Bioelectron., 167 (2020), 112490. https://doi.org/10.1016/j.bios.2020.112490 doi: 10.1016/j.bios.2020.112490
|
| [45] |
C. Wang, X. Li, H. Hu, L. Zhang, Z. Huang, M. Lin, et al., Monitoring of the central blood pressure waveform via a conformal ultrasonic device, Nat. Biomed. Eng., 2 (2018), 687–695. https://doi.org/10.1038/s41551-018-0287-x doi: 10.1038/s41551-018-0287-x
|
| [46] |
L. Lu, C. Jiang, G. Hu, J. Liu, B. Yang, Flexible noncontact sensing for human–machine interaction, Adv. Mater., 33 (2021), 2100218. https://doi.org/10.1002/adma.202100218 doi: 10.1002/adma.202100218
|
| [47] |
D. Dias, J. P. S. Cunha, Wearable health devices–vital sign monitoring, systems and technologies, Sensors, 18 (2018), 2414. https://doi.org/10.3390/s18082414 doi: 10.3390/s18082414
|
| [48] |
Y. M. Chi, T. P. Jung, G. Cauwenberghs, Dry-contact and noncontact biopotential electrodes: Methodological review, IEEE Rev. Biomed. Eng., 3 (2010), 106–119. https://doi.org/10.1109/RBME.2010.2084078 doi: 10.1109/RBME.2010.2084078
|
| [49] |
L. Tian, B. Zimmerman, A. Akhtar, K. J. Yu, M. Moore, J. Wu, et al., Large-area mri-compatible epidermal electronic interfaces for prosthetic control and cognitive monitoring, Nat. Biomed. Eng., 3 (2019), 194–205. https://doi.org/10.1038/s41551-019-0347-x doi: 10.1038/s41551-019-0347-x
|
| [50] |
C. M. Boutry, Y. Kaizawa, B. C. Schroeder, A. Chortos, A. Legrand, Z. Wang, et al., A stretchable and biodegradable strain and pressure sensor for orthopaedic application, Nat. Electron., 1 (2018), 314–321. https://doi.org/10.1038/s41928-018-0071-7 doi: 10.1038/s41928-018-0071-7
|
| [51] |
Z. Zhou, K. Chen, X. Li, S. Zhang, Y. Wu, Y. Zhou, et al., Sign-to-speech translation using machine-learning-assisted stretchable sensor arrays, Nat. Electron., 3 (2020), 571–578. https://doi.org/10.1038/s41928-020-0428-6 doi: 10.1038/s41928-020-0428-6
|
| [52] |
A. M. Nightingale, C. L. Leong, R. A. Burnish, S. U. Hassan, Y. Zhang, G. F. Clough, et al., Monitoring biomolecule concentrations in tissue using a wearable droplet microfluidic-based sensor, Nat. Commun., 10 (2019), 1–12. https://doi.org/10.1038/s41467-019-10401-y doi: 10.1038/s41467-019-10401-y
|
| [53] |
M. Bariya, H. Y. Y. Nyein, A. Javey, Wearable sweat sensors, Nat. Electron., 1 (2018), 160–171. https://doi.org/10.1038/s41928-018-0043-y doi: 10.1038/s41928-018-0043-y
|
| [54] |
A. Villoslada, A. Flores, D. Copaci, D. Blanco, L. Moreno, High-displacement flexible shape memory alloy actuator for soft wearable robots, Robot. Auton. Syst., 73 (2015), 91–101. https://doi.org/10.1016/j.robot.2014.09.026 doi: 10.1016/j.robot.2014.09.026
|
| [55] |
J. C. Yeo, H. K. Yap, W. Xi, Z. Wang, C. H. Yeow, C. T. Lim, Flexible and stretchable strain sensing actuator for wearable soft robotic applications, Adv. Mater. Technol., 1 (2016), 1600018. https://doi.org/10.1002/admt.201600018 doi: 10.1002/admt.201600018
|
| [56] |
J. F. Zhang, C. J. Yang, Y. Chen, Y. Zhang, Y. M. Dong, Modeling and control of a curved pneumatic muscle actuator for wearable elbow exoskeleton, Mechatronics, 18 (2008), 448–457. https://doi.org/10.1016/j.mechatronics.2008.02.006 doi: 10.1016/j.mechatronics.2008.02.006
|
| [57] |
K. A. Witte, P. Fiers, A. L. Sheets-Singer, S. H. Collins, Improving the energy economy of human running with powered and unpowered ankle exoskeleton assistance, Sci. Robot., 5 (2020), eaay9108. https://doi.org/10.1126/scirobotics.aay9108 doi: 10.1126/scirobotics.aay9108
|
| [58] |
J. Mendez, S. Hood, A. Gunnel, T. Lenzi, Powered knee and ankle prosthesis with indirect volitional swing control enables level-ground walking and crossing over obstacles, Sci. Robot., 5 (2020), eaba6635. https://doi.org/10.1126/scirobotics.aba6635 doi: 10.1126/scirobotics.aba6635
|
| [59] |
B. Dellon, Y. Matsuoka, Prosthetics, exoskeletons, and rehabilitation [grand challenges of robotics], IEEE Robot. Automat. Mag., 14 (2007), 30–34. https://doi.org/10.1109/MRA.2007.339622 doi: 10.1109/MRA.2007.339622
|
| [60] |
B. Hu, E. Rouse, L. Hargrove, Fusion of bilateral lower-limb neuromechanical signals improves prediction of locomotor activities, Front. Robot. AI, 5 (2018), 78. https://doi.org/10.3389/frobt.2018.00078 doi: 10.3389/frobt.2018.00078
|
| [61] |
S. Wang, R. M. Summers, Machine learning and radiology, Med. Image Anal., 16 (2012), 933–951. https://doi.org/10.1016/j.media.2012.02.005 doi: 10.1016/j.media.2012.02.005
|
| [62] |
Y. Kassahun, B. Yu, A. T. Tibebu, D. Stoyanov, S. Giannarou, J. H. Metzen, et al., Surgical robotics beyond enhanced dexterity instrumentation: a survey of machine learning techniques and their role in intelligent and autonomous surgical actions, Int. J. Comput. Assist. Radiol. Surg., 11 (2016), 553–568. https://doi.org/10.1007/s11548-015-1305-z doi: 10.1007/s11548-015-1305-z
|
| [63] |
L. Jones, D. Golan, S. Hanna, M. Ramachandran, Artificial intelligence, machine learning and the evolution of healthcare: A bright future or cause for concern?, Bone Jt. Res., 7 (2018), 223–225. https://doi.org/10.1302/2046-3758.73.BJR-2017-0147.R1 doi: 10.1302/2046-3758.73.BJR-2017-0147.R1
|
| [64] |
N. Kozic, S. Weber, P. Büchler, C. Lutz, N. Reimers, M. Á. G. Ballester, et al., Optimisation of orthopaedic implant design using statistical shape space analysis based on level sets, Med. Image Anal., 14 (2010), 265–275. https://doi.org/10.1016/j.media.2010.02.008 doi: 10.1016/j.media.2010.02.008
|
| [65] |
H. Cho, Y. Park, S. Gupta, C. Yoon, I. Han, H. Kim, et al., Augmented reality in bone tumour resection: an experimental study, Bone Jt. Res., 6 (2017), 137–143. https://doi.org/10.1302/2046-3758.63.BJR-2016-0289.R1 doi: 10.1302/2046-3758.63.BJR-2016-0289.R1
|
| [66] |
E. van IJsseldijk, E. Valstar, B. Stoel, R. Nelissen, N. Baka, R. Van't Klooster, et al., Three dimensional measurement of minimum joint space width in the knee from stereo radiographs using statistical shape models, Bone Jt. Res., 5 (2016), 320–327. https://doi.org/10.1302/2046-3758.58.2000626 doi: 10.1302/2046-3758.58.2000626
|
| [67] |
K. Karthik, T. Colegate-Stone, P. Dasgupta, A. Tavakkolizadeh, J. Sinha, Robotic surgery in trauma and orthopaedics: a systematic review, Bone Jt. J., 97 (2015), 292–299. https://doi.org/10.1302/0301-620X.97B3.35107 doi: 10.1302/0301-620X.97B3.35107
|
| [68] |
R. Agricola, K. M. Leyland, S. M. Bierma-Zeinstra, G. E. Thomas, P. J. Emans, T. D. Spector, et al., Validation of statistical shape modelling to predict hip osteoarthritis in females: data from two prospective cohort studies (cohort hip and cohort knee and chingford), Rheumatology, 54 (2015), 2033–2041. https://doi.org/10.1093/rheumatology/kev232 doi: 10.1093/rheumatology/kev232
|
| [69] |
T. Yao, F. Gao, Q. Zhang, Y. Ma, Multi-feature gait recognition with dnn based on semg signals, Math. Biosci. Eng, 18 (2021), 3521–3542. https://doi.org/10.3934/mbe.2021177 doi: 10.3934/mbe.2021177
|
| [70] |
X. Chen, Y. Ma, X. Liu, W. Kong, X. Xi, Analysis of corticomuscular connectivity during walking using vine copula, Math. Biosci. Eng, 18 (2021), 4341–4357. https://doi.org/10.3934/mbe.2021218 doi: 10.3934/mbe.2021218
|
| [71] |
M. Zhong, F. Li, W. Chen, Automatic arrhythmia detection with multi-lead ecg signals based on heterogeneous graph attention networks, Math. Biosci. Eng., 19 (2022), 12448–12471. https://doi.org/10.3934/mbe.2022581 doi: 10.3934/mbe.2022581
|
| [72] |
N. Long, Y. Lei, L. Peng, P. Xu, P. Mao, A scoping review on monitoring mental health using smart wearable devices, Math. Biosci. Eng., 19 (2022), 7899–7919. https://doi.org/10.3934/mbe.2022369 doi: 10.3934/mbe.2022369
|
| [73] |
X. Liu, M. Chen, T. Liang, C. Lou, H. Wang, X. Liu, A lightweight double-channel depthwise separable convolutional neural network for multimodal fusion gait recognition, Math. Biosci. Eng, 19 (2022), 1195–1212. https://doi.org/10.3934/mbe.2022055 doi: 10.3934/mbe.2022055
|
| [74] |
A. Meffen, C. J. Pepper, R. D. Sayers, L. J. Gray, Epidemiology of major lower limb amputation using routinely collected electronic health data in the uk: a systematic review protocol, BMJ Open, 10 (2020), e037053. http://dx.doi.org/10.1136/bmjopen-2020-037053 doi: 10.1136/bmjopen-2020-037053
|
| [75] | H. K. Kim, L. S. Chou, Use of musculoskeletal modeling to examine lower limb muscle contribution to gait balance control: Effects of overweight, in 2021 IEEE International Conference on Digital Health (ICDH), IEEE, (2021), 315–317. https://doi.org/10.1109/ICDH52753.2021.00056 |
| [76] |
A. R. Anwary, H. Yu, M. Vassallo, Gait quantification and visualization for digital healthcare, Health Policy Technol., 9 (2020), 204–212. https://doi.org/10.1016/j.hlpt.2019.12.004 doi: 10.1016/j.hlpt.2019.12.004
|
| [77] |
J. W. Kwak, M. Han, Z. Xie, H. U. Chung, J. Y. Lee, R. Avila, et al., Wireless sensors for continuous, multimodal measurements at the skin interface with lower limb prostheses, Sci. Transl. Med., 12 (2020), eabc4327. https://doi.org/10.1126/scitranslmed.abc432 doi: 10.1126/scitranslmed.abc432
|
| [78] |
J. Calle-Siguencia, M. Callejas-Cuervo, S. García-Reino, Integration of inertial sensors in a lower limb robotic exoskeleton, Sensors, 22 (2022), 4559. https://doi.org/10.3390/s22124559 doi: 10.3390/s22124559
|
| [79] |
C. F. Pană, L. F. Manta, I. C. Vladu, I. Cismaru, F. L. Petcu, D. Cojocaru, et al., The design of a smart lower-limb prosthesis supporting people with transtibial amputation–data acquisition system, Appl. Sci., 12 (2022), 6722. https://doi.org/10.3390/app12136722 doi: 10.3390/app12136722
|
| [80] | Y. Nabiyev, K. Tezekbayev, Z. Baubekov, M. Khalkhojayev, M. Aubakirov, S. Aubakirova, et al., Epidemiology evaluation of lower limb injuries in Kazakhstan, Biostat Epidemiol., (2022), 1–20. https://doi.org/10.1080/24709360.2022.2084238 |
| [81] | H. K. Dy, C. Yeh, Assessing lower limb strength using internet-of-things enabled chair and processing of time-series data in google gpu tensorflow colab, preprint, arXiv: 2209.04042. https://doi.org/10.48550/arXiv.2209.04042 |
| [82] | K. Zhao, J. Guo, S. Guo, Q. Fu, Design of fatigue grade classification system based on human lower limb surface emg signal, in 2022 IEEE International Conference on Mechatronics and Automation (ICMA), IEEE, (2022), 1015–1020. https://doi.org/10.1109/ICMA54519.2022.9855927 |
| [83] |
T. M. Doering, J. L. M. Thompson, B. P. Budiono, K. L. MacKenzie-Shalders, T. Zaw, K. J. Ashton, et al., The muscle proteome reflects changes in mitochondrial function, cellular stress and proteolysis after 14 days of unilateral lower limb immobilization in active young men, Plos One, 17 (2022), e0273925. https://doi.org/10.1371/journal.pone.0273925 doi: 10.1371/journal.pone.0273925
|
| [84] |
S. Sadler, J. Gerrard, M. West, S. Lanting, J. Charles, A. Searle, et al., Aboriginal and torres strait islander peoples' perceptions of foot and lower limb health: a systematic review, J. Foot Ankle Res., 15 (2022), 1–11. https://doi.org/10.1186/s13047-022-00557-0 doi: 10.1186/s13047-022-00557-0
|
| [85] |
T. Ikeda, M. Takano, S. Oka, A. Suzuki, K. Matsuda, Changes in postural sway during upright stance after short-term lower limb physical inactivity: A prospective study, Plos One, 17 (2022), e0272969. https://doi.org/10.1371/journal.pone.0272969 doi: 10.1371/journal.pone.0272969
|
| [86] |
L. R. Souto, P. R. M. d. S. Serrão, G. K. Pisani, B. M. Tessarin, H. F. da Silva, E. d. M. Machado, et al., Immediate effects of hip strap and foot orthoses on self-reported measures and lower limb kinematics during functional tasks in individuals with patellofemoral osteoarthritis: protocol for a randomised crossover clinical trial, Trials, 23 (2022), 1–10. https://doi.org/10.1186/s13063-022-06676-0 doi: 10.1186/s13063-022-06676-0
|
| [87] |
M. Moznuzzaman, T. I. Khan, B. Neher, K. Teramoto, S. Ide, Ageing effect of lower limb muscle activity for correlating healthy and osteoarthritic knees by surface electromyogram analysis, Sens. Bio-Sens. Res., 36 (2022), 100488. https://doi.org/10.1016/j.sbsr.2022.100488 doi: 10.1016/j.sbsr.2022.100488
|
| [88] |
F. N. A. Sahabuddin, N. I. Jamaludin, N. A. Hamzah, C. L. Chok, S. Shaharudin, The effects of hip-and ankle-focused exercise intervention on lower limb mechanics during single leg squat among physically active females, Phys. Ther. Sport, 55 (2022), 70–79. https://doi.org/10.1016/j.ptsp.2022.03.001 doi: 10.1016/j.ptsp.2022.03.001
|
| [89] |
A. Kotsifaki, R. Whiteley, S. Van Rossom, V. Korakakis, R. Bahr, V. Sideris, et al., Single leg hop for distance symmetry masks lower limb biomechanics: time to discuss hop distance as decision criterion for return to sport after acl reconstruction?, Br. J. Sports Med., 56 (2022), 249–256. http://dx.doi.org/10.1136/bjsports-2020-103677 doi: 10.1136/bjsports-2020-103677
|
| [90] |
Y. Zhang, L. Wang, Application of microsensors and support vector machines in the assessment of lower limb posture correction in adolescents, Concurr. Comput., 2022 (2022), e7234. https://doi.org/10.1002/cpe.7234 doi: 10.1002/cpe.7234
|
| [91] |
L. T. Duan, M. Lawo, Z. G. Wang, H. Y. Wang, Human lower limb motion capture and recognition based on smartphones, Sensors, 22 (2022), 5273. https://doi.org/10.3390/s22145273 doi: 10.3390/s22145273
|
| [92] |
F. Dong, L. Wu, Y. Feng, D. Liang, Research on movement intentions of human's left and right legs based on electro-encephalogram signals, J. Med. Devices, 16 (2022), 041012. https://doi.org/10.1115/1.4055435 doi: 10.1115/1.4055435
|
| [93] | H. Zhang, L. Meng, D. Chen, Research of dynamic comfort maintaining based on the measurement of low limb edema and compression during seated sleep in flight, preprint, http://dx.doi.org/10.2139/ssrn.4226861 |
| [94] |
J. Chen, H. Qiao, Motor-cortex-like recurrent neural network and multi-tasks learning for the control of musculoskeletal systems, IEEE Trans. Cogn. Develop. Syst., 14 (2020), 424–436. https://doi.org/10.1109/TCDS.2020.3045574 doi: 10.1109/TCDS.2020.3045574
|
| [95] |
J. Chen, H. Qiao, Muscle-synergies-based neuromuscular control for motion learning and generalization of a musculoskeletal system, IEEE Trans. Syst. Man Cybern. Syst., 51 (2020), 3993–4006. https://doi.org/10.1109/TSMC.2020.2966818 doi: 10.1109/TSMC.2020.2966818
|
| [96] |
B. Wang, C. Ou, N. Xie, L. Wang, T. Yu, G. Fan, et al., Lower limb motion recognition based on surface electromyography signals and its experimental verification on a novel multi-posture lower limb rehabilitation robots, Comput. Electr. Eng., 101 (2022), 108067. https://doi.org/10.1016/j.compeleceng.2022.108067 doi: 10.1016/j.compeleceng.2022.108067
|
| [97] |
A. Vijayvargiya, B. Singh, R. Kumar, J. M. R. Tavares, Human lower limb activity recognition techniques, databases, challenges and its applications using semg signal: an overview, Biomed. Eng. Lett., 12 (2022), 343–358. https://doi.org/10.1007/s13534-022-00236-w doi: 10.1007/s13534-022-00236-w
|
| [98] |
S. Lobet, C. Detrembleur, F. Massaad, C. Hermans, Three-dimensional gait analysis can shed new light on walking in patients with haemophilia, Sci. World J., 2013 (2013), 284358. https://doi.org/10.1155/2013/284358 doi: 10.1155/2013/284358
|
| [99] | C. Wang, B. He, W. Wei, Z. Yi, P. Li, S. Duan, et al., Prediction of contralateral lower-limb joint angles using vibroarthrography and surface electromyography signals in time-series network, IEEE Trans. Autom. Sci. Eng., 2022 (2022). https://doi.org/10.1109/TASE.2022.3185706 |
| [100] |
P. B. Júnior, D. P. Campos, A. E. Lazzaretti, P. Nohama, A. A. Carvalho, E. Krueger, et al., Influence of eeg channel reduction on lower limb motor imagery during electrical stimulation in healthy and paraplegic subjects, Res. Biomed. Eng., 38 (2022), 689–699. https://doi.org/10.1007/s42600-021-00189-6 doi: 10.1007/s42600-021-00189-6
|
| [101] |
Y. Zhang, Real-time detection of lower limb training stability function based on smart wearable sensors, J. Sens., 2022 (2022), 7503668. https://doi.org/10.1155/2022/7503668 doi: 10.1155/2022/7503668
|
| [102] | C. M. Kanzler, M. G. Catalano, C. Piazza, A. Bicchi, R. Gassert, O. Lambercy, An objective functional evaluation of myoelectrically-controlled hand prostheses: a pilot study using the virtual peg insertion test, in 2019 IEEE 16th International Conference on Rehabilitation Robotics (ICORR), IEEE, (2019), 392–397. https://doi.org/10.1109/ICORR.2019.8779550 |
| [103] |
A. R. Zangene, A. Abbasi, K. Nazarpour, Estimation of lower limb kinematics during squat task in different loading using semg activity and deep recurrent neural networks, Sensors, 21 (2021), 7773. https://doi.org/10.3390/s21237773 doi: 10.3390/s21237773
|
| [104] | S. Issa, A. R. Khaled, Lower limb movement recognition using EMG signals, in International Conference on Intelligent Systems Design and Applications, Springer, 418 (2022), 336–345. https://doi.org/10.1007/978-3-030-96308-8_31 |
| [105] |
A. Meigal, D. Ivanov, N. Senatorova, U. Monakhova, E. Fomina, Passive-mode treadmill test effectively reveals neuromuscular modification of a lower limb muscle: semg-based study from experiments on iss, Acta Astronaut., 199 (2022), 471–479. https://doi.org/10.1016/j.actaastro.2022.07.045 doi: 10.1016/j.actaastro.2022.07.045
|
| [106] |
P. Zandiyeh, L. R. Parola, B. C. Fleming, J. E. Beveridge, Wavelet analysis reveals differential lower limb muscle activity patterns long after anterior cruciate ligament reconstruction, J. Biomech., 133 (2022), 110957. https://doi.org/10.1016/j.jbiomech.2022.110957 doi: 10.1016/j.jbiomech.2022.110957
|
| [107] | T. Hwang, A. Effenberg, Gait analysis: Head vertical movement leads to lower limb joint angle movements, in 2022 IEEE International Conference on Consumer Electronics (ICCE), IEEE, (2022), 1–5. https://doi.org/10.1109/ICCE53296.2022.9730350 |
| [108] |
C. Wei, H. Wang, F. Hu, B. Zhou, N. Feng, Y. Lu, et al., Single-channel surface electromyography signal classification with variational mode decomposition and entropy feature for lower limb movements recognition, Biomed. Signal Process. Control, 74 (2022), 103487. https://doi.org/10.1016/j.bspc.2022.103487 doi: 10.1016/j.bspc.2022.103487
|
| [109] |
Y. Wang, X. Cheng, L. Jabban, X. Sui, D. Zhang, Motion intention prediction and joint trajectories generation towards lower limb prostheses using emg and imu signals, IEEE Sensors J., 22 (2022), 10719–10729. https://doi.org/10.1109/JSEN.2022.3167686 doi: 10.1109/JSEN.2022.3167686
|
| [110] |
K. Hung, H. Y. Cheung, N. Wan, E. Lee, C. N. Lai, K. Pan, et al., Design, development, and evaluation of upper and lower limb orthoses with intelligent control for rehabilitation, IET Sci. Meas. Technol., 15 (2021), 738–748. https://doi.org/10.1049/smt2.12074 doi: 10.1049/smt2.12074
|
| [111] | J. C. Alcaraz, S. Moghaddamnia, M. Penner, J. Peissig, Monitoring the rehabilitation progress using a dcnn and kinematic data for digital healthcare, in 2020 28th European Signal Processing Conference (EUSIPCO), IEEE, (2021), 1333–1337. https://doi.org/10.23919/Eusipco47968.2020.9287324 |
| [112] |
R. Yan, W. Zhao, Q. Sun, Research on a physical activity tracking system based upon three-axis accelerometer for patients with leg ulcers, Healthc. Technol. Lett., 6 (2019), 147–152. https://doi.org/10.1049/htl.2019.0008 doi: 10.1049/htl.2019.0008
|
| [113] |
S. Y. Gordleeva, S. A. Lobov, N. A. Grigorev, A. O. Savosenkov, M. O. Shamshin, M. V. Lukoyanov, et al., Real time EEG–EMG human machine interface-based control system for a lower-limb exoskeleton, IEEE Access, 8 (2020), 84070–84081. https://doi.org/10.1109/ACCESS.2020.2991812 doi: 10.1109/ACCESS.2020.2991812
|
| [114] |
P. Juneau, E. D. Lemaire, A. Bavec, H. Burger, N. Baddour, Automated step detection with 6-minute walk test smartphone sensors signals for fall risk classification in lower limb amputees, PLOS Digit. Health, 1 (2022), e0000088. https://doi.org/10.1371/journal.pdig.0000088 doi: 10.1371/journal.pdig.0000088
|
| [115] |
D. Camargo-Vargas, M. Callejas-Cuervo, S. Mazzoleni, Brain-computer interfaces systems for upper and lower limb rehabilitation: A systematic review, Sensors, 21 (2021), 4312. https://doi.org/10.3390/s21134312 doi: 10.3390/s21134312
|
| [116] | M. N. A. Ab Patar, A. F. Said, J. Mahmud, A. P. A. Majeed, M. A. Razman, System integration and control of dynamic ankle foot orthosis for lower limb rehabilitation, in 2014 International Symposium on Technology Management and Emerging Technologies, IEEE, (2014), 82–85. https://doi.org/10.1109/ISTMET.2014.6936482 |
| [117] |
N. Mathur, G. Paul, J. Irvine, M. Abuhelala, A. Buis, I. Glesk, A practical design and implementation of a low cost platform for remote monitoring of lower limb health of amputees in the developing world, IEEE Access, 4 (2016), 7440–7451. https://doi.org/10.1109/ACCESS.2016.2622163 doi: 10.1109/ACCESS.2016.2622163
|
| [118] |
W. Huo, S. Mohammed, J. C. Moreno, Y. Amirat, Lower limb wearable robots for assistance and rehabilitation: A state of the art, IEEE Syst. J., 10 (2014), 1068–1081. https://doi.org/10.1109/JSYST.2014.2351491 doi: 10.1109/JSYST.2014.2351491
|
| [119] |
A. Gautam, M. Panwar, D. Biswas, A. Acharyya, Myonet: A transfer-learning-based lrcn for lower limb movement recognition and knee joint angle prediction for remote monitoring of rehabilitation progress from semg, IEEE J. Transl. Eng. Health Med., 8 (2020), 2100310. https://doi.org/10.1109/JTEHM.2020.2972523 doi: 10.1109/JTEHM.2020.2972523
|
| [120] |
J. Li, Z. Wang, S. Qiu, H. Zhao, Q. Wang, D. Plettemeier, et al., Using body sensor network to measure the effect of rehabilitation therapy on improvement of lower limb motor function in children with spastic diplegia, IEEE Trans. Instrum. Meas., 69 (2020), 9215–9227. https://doi.org/10.1109/TIM.2020.2997545 doi: 10.1109/TIM.2020.2997545
|
| [121] | J. A. Saglia, A. D. Luca, V. Squeri, L. Ciaccia, C. Sanfilippo, S. Ungaro, et al., Design and development of a novel core, balance and lower limb rehabilitation robot: Hunova®, in 2019 IEEE 16th International Conference on Rehabilitation Robotics (ICORR), IEEE, (2019), 417–422. https://doi.org/10.1109/ICORR.2019.8779531 |
| [122] |
Q. Zhang, T. Jin, J. Cai, L. Xu, T. He, T. Wang, et al., Wearable triboelectric sensors enabled gait analysis and waist motion capture for iot-based smart healthcare applications, Adv. Sci., 9 (2022), 2103694. https://doi.org/10.1002/advs.202103694 doi: 10.1002/advs.202103694
|
| [123] |
T. Eiammanussakul, V. Sangveraphunsiri, A lower limb rehabilitation robot in sitting position with a review of training activities, J. Healthcare Eng., 2018 (2018), 1927807. https://doi.org/10.1155/2018/1927807 doi: 10.1155/2018/1927807
|
| [124] |
M. Miao, X. Gao, W. Zhu, A construction method of lower limb rehabilitation robot with remote control system, Appl. Sci., 11 (2021), 867. https://doi.org/10.3390/app11020867 doi: 10.3390/app11020867
|
| [125] | N. Nazmi, M. A. A. Rahman, S. A. Mazlan, H. Zamzuri, M. Mizukawa, Electromyography (EMG) based signal analysis for physiological device application in lower limb rehabilitation, in 2015 2nd International Conference on Biomedical Engineering (ICoBE), IEEE, (2015), 1–6. https://doi.org/10.1109/ICoBE.2015.7235878 |
| [126] |
D. Llorente-Vidrio, R. Pérez-San Lázaro, M. Ballesteros, I. Salgado, D. Cruz-Ortiz, I. Chairez, Event driven sliding mode control of a lower limb exoskeleton based on a continuous neural network electromyographic signal classifier, Mechatronics, 72 (2020), 102451. https://doi.org/10.1016/j.mechatronics.2020.102451 doi: 10.1016/j.mechatronics.2020.102451
|
| [127] |
M. Florindo, S. L. Nuno, L. M. Rodrigues, Lower limb dynamic activity significantly reduces foot skin perfusion: Exploring data with different optical sensors in age-grouped healthy adults, Skin Pharmacol. Physiol., 35 (2022), 13–22. https://doi.org/10.1159/000517906 doi: 10.1159/000517906
|
| [128] |
H. Qiao, S. Zhong, Z. Chen, H. Wang, Improving performance of robots using human-inspired approaches: a survey, Sci. China Inf. Sci., 65 (2022), 1–31. https://doi.org/10.1007/s11432-022-3606-1 doi: 10.1007/s11432-022-3606-1
|
| [129] |
A. Kline, H. Wang, Y. Li, S. Dennis, M. Hutch, Z. Xu, et al., Multimodal machine learning in precision health: A scoping review, NPJ Digit. Med., 5 (2022), 1–14. https://doi.org/10.1038/s41746-022-00712-8 doi: 10.1038/s41746-022-00712-8
|
| [130] |
E. Garcia-Ceja, M. Riegler, T. Nordgreen, P. Jakobsen, K. J. Oedegaard, J. Tørresen, Mental health monitoring with multimodal sensing and machine learning: A survey, Pervasive Mob. Comput., 51 (2018), 1–26. https://doi.org/10.1016/j.pmcj.2018.09.003 doi: 10.1016/j.pmcj.2018.09.003
|
| [131] |
H. Qiao, J. Chen, X. Huang, A survey of brain-inspired intelligent robots: Integration of vision, decision, motion control, and musculoskeletal systems, IEEE Trans. Cybern., 52 (2022), 11267–11280. https://doi.org/10.1109/TCYB.2021.3071312 doi: 10.1109/TCYB.2021.3071312
|
Figures(13)
Jiayu Fu, Haiyan Wang, Risu Na, A JISAIHAN, Zhixiong Wang, Yuko OHNO. Recent advancements in digital health management using multi-modal signal monitoring[J]. Mathematical Biosciences and Engineering, 2023, 20(3): 5194-5222. doi: 10.3934/mbe.2023241
DownLoad: