A retrospective study comparing creatinine clearance estimation using different equations on a population-based cohort

Abigail Ferreira; Rui Lapa; Nuno Vale; Abigail Ferreira; Rui Lapa; Nuno Vale

doi:10.3934/mbe.2021287

Mathematical Biosciences and Engineering

2021, Volume 18, Issue 5: 5680-5691. doi: 10.3934/mbe.2021287

Previous Article Next Article

Research article Special Issues

A retrospective study comparing creatinine clearance estimation using different equations on a population-based cohort

1.
OncoPharma Research Group, Center for Health Technology and Services Research (CINTESIS), Rua Dr. Plácido da Costa, Porto 4200-450, Portugal
2.
LAQV/REQUIMTE, Laboratory of Applied Chemistry, Department of Chemical Sciences, Faculty of Pharmacy, University of Porto, Rua de Jorge Viterbo Ferreira, 228, Porto 4050-313, Portugal
3.
Department of Community Medicine, Health Information and Decision (MEDCIDS), Faculty of Medicine, University of Porto, Al. Prof. Hernani Monteiro, Porto 4200-319, Portugal

Received: 21 April 2021 Accepted: 17 June 2021 Published: 23 June 2021

Renal elimination is an important part of drugs' excretion. At the same time, renal function can be impaired as a side effect of medication, particularly during prolonged treatments. Thus, the assessment of patients' renal function is of major consequence, especially in cases where the therapeutic regimen is adjusted taking into consideration renal clearance. Serum creatinine concentration is the most common indicator of renal clearance, since the most accurate indicator, glomerular filtration rate (GFR), is not easily measured. Using equations developed over the last decades, creatinine clearance (CL_Cr) is readily estimated taking into account patients' biological sex, age, body composition, and sometimes race. In this work, differences in estimated CL_Cr between different equations were studied and the influence of some patients' characteristics evaluated. Data collected from 82 inpatients receiving antibiotic therapy was analyzed and CL_Cr was estimated using a total of 12 equations. Patients were stratified according to their sex, age, and body composition to shed some light on the impact of these parameters in the estimations of renal function. More variability between estimation methods was highlighted (a) in patients between 51 and 60 years old, (b) within the normal body mass index group, and (c) in patients with serum creatinine levels below normal criteria. Furthermore, the Cockcroft-Gault equation considering lean body weight produced lower estimated CL_Cr in almost all groups.

Keywords:

Citation: Abigail Ferreira, Rui Lapa, Nuno Vale. A retrospective study comparing creatinine clearance estimation using different equations on a population-based cohort[J]. Mathematical Biosciences and Engineering, 2021, 18(5): 5680-5691. doi: 10.3934/mbe.2021287

Related Papers:

[1]	Hannah Schuster, Bernhard Haller, Sengül Sancak, Johanna Erber, Roland M. Schmid, Tobias Lahmer, Sebastian Rasch . Transpulmonary thermodilution: A revised correction formula for global end-diastolic volume index derived after femoral indicator injection. Mathematical Biosciences and Engineering, 2023, 20(6): 9876-9890. doi: 10.3934/mbe.2023433
[2]	Hans F. Weinberger, Xiao-Qiang Zhao . An extension of the formula for spreading speeds. Mathematical Biosciences and Engineering, 2010, 7(1): 187-194. doi: 10.3934/mbe.2010.7.187
[3]	Suleyman Aydinyuz, Mustafa Asci . Error detection and correction for coding theory on k-order Gaussian Fibonacci matrices. Mathematical Biosciences and Engineering, 2023, 20(2): 1993-2010. doi: 10.3934/mbe.2023092
[4]	Zemin Luan, Zhaoxia Yu, Ting Zeng, Rui Wang, Maozai Tian, Kai Wang . A study on the factors influencing the transfer of COVID-19 severe illness patients out of the ICU based on generalized linear mixed effect model. Mathematical Biosciences and Engineering, 2022, 19(10): 10602-10617. doi: 10.3934/mbe.2022495
[5]	Atsushi Kawaguchi . Network-based diagnostic probability estimation from resting-state functional magnetic resonance imaging. Mathematical Biosciences and Engineering, 2023, 20(10): 17702-17725. doi: 10.3934/mbe.2023787
[6]	Kamil Rajdl, Petr Lansky . Fano factor estimation. Mathematical Biosciences and Engineering, 2014, 11(1): 105-123. doi: 10.3934/mbe.2014.11.105
[7]	Damilola Olabode, Libin Rong, Xueying Wang . Stochastic investigation of HIV infection and the emergence of drug resistance. Mathematical Biosciences and Engineering, 2022, 19(2): 1174-1194. doi: 10.3934/mbe.2022054
[8]	Tuoi Vo, William Lee, Adam Peddle, Martin Meere . Modelling chemistry and biology after implantation of a drug-eluting stent. Part Ⅰ: Drug transport. Mathematical Biosciences and Engineering, 2017, 14(2): 491-509. doi: 10.3934/mbe.2017030
[9]	Ming-Chun Lai, Jiang-Shan Lian, Wen-Jin Zhang, Jun Xu, Lin Zhou, Shu-Sen Zheng . Compare with safety and efficacy of entecavir and adefovir dipivoxil combination therapy and tenofovir disoproxil fumarate monotherapy for chronic hepatitis B patient with adefovir-resistant. Mathematical Biosciences and Engineering, 2020, 17(1): 627-635. doi: 10.3934/mbe.2020032
[10]	Durhasan Turgut Tollu, İbrahim Yalçınkaya, Hijaz Ahmad, Shao-Wen Yao . A detailed study on a solvable system related to the linear fractional difference equation. Mathematical Biosciences and Engineering, 2021, 18(5): 5392-5408. doi: 10.3934/mbe.2021273

Abstract

1. Introduction

Kidneys play an important role in the elimination of many drugs, including antibiotics. Renal function varies according to age, sex, body size, and race, is influenced by strenuous physical activity, diet, and consumption of red meat, certain herbs, and supplements, and is altered during pregnancy. Most importantly, it can be impaired as a collateral effect of medication, which is particularly significant during prolonged treatments. As such, evaluating patients' renal function is a key component of therapeutic drug monitoring (TDM), along with examining peak and trough plasma levels of the drug. Glomerular filtration rate (GFR) is regarded as a crucial indicator of kidney function. Generally, a GFR above 90 mL/min indicates a normal kidney function ^[1]. Unfortunately, GFR is not easily determined in a clinical setting; instead, renal function is often estimated from serum creatinine concentration (SCr), using numerous equations developed over the last decades and demographic parameters as sex, body size, age, and race ^[2,3]. SCr is rapidly determined, and these estimations can be readily calculated. However, these equations were derived from data collected from very diverse study populations, and there is neither a universal nor subpopulation-specific standard equation. As such, clinicians must decide how to calculate this estimation (what equation to use) or most frequently, follow what the institution has established. Since each equation results in dissimilar estimated clearance for the same individual, therapeutic adjustment can be significantly different according to the chosen method.

Antibiotics are one of the most prescribed drugs. Monitoring patients and appropriately adjusting the dose of the antibiotic or the treatment regimen is important to optimize the clinical outcome, reduce the risk of toxic side effects and avoid serious deterioration of renal function associated with increased plasmatic levels and drug accumulation while aiming at improving efficacy, and also due to great inter-individual variability. This can also help limit antibiotic resistance.

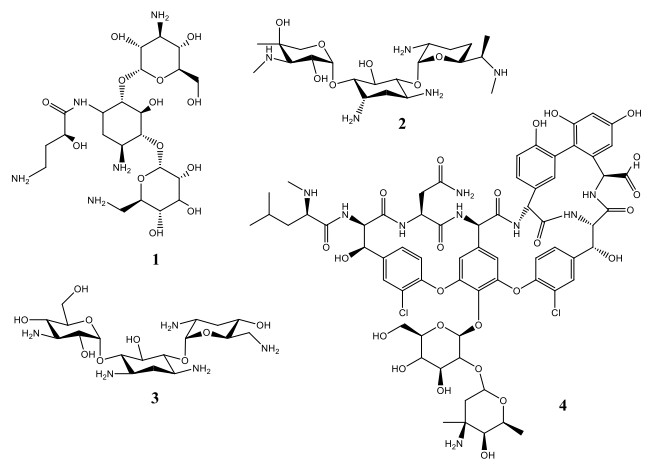
In this work, data was collected from inpatients receiving intravenous antibiotic therapy with amikacin, gentamicin, tobramycin, or vancomycin (chemical structures are presented in Figure 1 and some properties are summarized in Table 1), and their creatine clearance was estimated using five equations plus seven variations of the Cockcroft-Gault formula (total of 12 different estimations). A direct measurement of GFR was not available, a limitation that prevented the comparison between observed and estimated clearance. The aim of this study was to evaluate the differences in estimated creatinine clearance produced by different equations and the influence of some patients' characteristics in these estimations, to better understand the impact of the choice of estimation method.

Figure 1. Chemical structure of amikacin (1), gentamicin (2), tobramycin (3) and vancomycin (4).

DownLoad: Full-Size Img PowerPoint

Table 1. Pharmacokinetic (PK) properties of antibiotics amikacin, gentamicin, tobramycin, and vancomycin ^{[4,5,6,7,8,9,10]}.

PK	Amikacin	Gentamicin	Tobramycin	Vancomycin
Hydrophilicity	Hydrophilic
Metabolism	Eliminated unchanged in urine
F_up	> 90%	> 70%	> 70%	50–90%
T_1/2	2–3 h	2–3 h	2–3 h	~6 h (4–11 h)
V_c	~0.34 L/kg	0.2–0.3 L/kg	0.2–0.3 L/kg	0.4–1 L/kg
Clearance	100 mL/min	57 mL/min	141 mL/min	67.7 mL/min
Typical dosing for susceptible infections	7.5 mg/kg 12/12 h	1 mg/kg 8/8 h	1 mg/kg 8/8 h	1000 mg 12/12 h
F_up: fraction unbound in plasma; T_1/2: half-life; V_c: central volume of distribution.

| Show Table

DownLoad: CSV

2. Materials and methods

2.1. Patients and methods

Data was gathered from 82 inpatients receiving antibiotic therapy for the treatment of serious infections of different etiologies with intravenous amikacin, gentamicin, tobramycin, or vancomycin in CHUP (Centro Hospitalar Universitário do Porto). This information included demographics, such as biological sex, age, total body weight, and height, as well as creatinine (enzymatic method) and drug plasma concentrations determined in multiple days throughout the treatment. All the collected creatinine concentrations were included in this study, in a total of 374 measurements. A summary of all collected data is presented in Table 2.

Table 2. Summary of collected clinical data, with the indication of lower and upper limits and calculation of average value for each parameter.

	Full database	Amikacin	Gentamicin	Tobramycin	Vancomycin
Biological sex	F: 34 (41.5%) M: 48 (58.5%)	F: 1; M: 7	F: 8; M: 14	F: 4; M: 1	F: 21; M: 26
Age (years)	7–93 (avg 58)	14–87 (avg 57)	7–88 (avg 58)	13–19 (avg 15)	19–93 (avg 63)
Weight (kg)	15.5–140 (avg 66.2)	50.0–92.5 (avg 66.0)	15.5–85.0 (avg 66.0)	25.8–44.5 (avg 33.0)	44.5–121.0 (avg 70)
Height (cm)	108–185 (avg 164.7)	163–180 (avg 169)	108–185 (avg 165)	130–158 (avg 146)	147–180 (avg 166)
[Cr] (mg/dL)	0.63–4.78 (avg 0.93)	0.47–1.58 (avg 0.93)	0.29–1.89 (avg 0.83)	0.35–0.64 (avg 0.49)	0.27–4.78 (avg 1.02)
C_min (mg/L)	---	0.30–16.40 (avg 3.70)	0.20–4.80 (avg 1.05)	0.06–0.23 (avg 0.17)	4.50–45.60 (avg 16.45)
C_max (mg/L)	---	19.70–87.80 (avg 38.97)	2.90–19.50 (avg 9.22)	16.32–36.12 (avg 27.05)	11.20–60.10 (avg 25.99)
F: females; M: males; avg: average value; [Cr]: serum creatinine concentration; C_min: antibiotic concentration measured right before a dose; C_max: antibiotic concentration measured 1 h (aminoglycosides amikacin, gentamicin and tobramycin) or 3 h (vancomycin) after the beginning of an infusion.

| Show Table

DownLoad: CSV

Creatinine clearance (CL_Cr) was estimated, in mL/min, according to Eqs (2) through (7). Seven adaptations of the Cockcroft-Gault (CG) equation were included, incorporating body weight as actual (TBW), ideal (IBW), adjusted (AdjBW), modified-adjusted (mAdjBW), and lean body weight (LBW), as described in Eqs (8) through (12). Additionally, variations of ideal plus a fixed percentage of 30, 40, or 50% were calculated. In these equations, body weight is in kg, H is height in m, age is in years, and SCr is the measured serum creatinine in mg/dL. BSA is the body surface area in m², calculated according to the DuBois formula (1) ^[11] (height in cm).

$\mathrm{B}\mathrm{S}\mathrm{A} = 0.007184\times {TBW}^{0.425}\times {H}^{0.725}$

(1)

Cockcroft-Gault (CG) Eq (2) must be multiplied by 0.85 for female individuals ^[12].

${\mathrm{C}\mathrm{L}}_{\mathrm{C}\mathrm{r}} = \frac{(140-\mathrm{A}\mathrm{g}\mathrm{e})\times \mathrm{B}\mathrm{W}}{\mathrm{S}\mathrm{C}\mathrm{r}\times 72}$

(2)

Jelliffe ^[13] developed Eq (3), that can be normalized considering BSA Eq (4). Both equations should be multiplied by 0.9 for female individuals.

${\mathrm{C}\mathrm{L}}_{\mathrm{C}\mathrm{r}} = \frac{98-\left[0.8\times \left(\mathrm{A}\mathrm{g}\mathrm{e}-20\right)\right]}{\mathrm{S}\mathrm{C}\mathrm{r}}$

(3)

${\mathrm{C}\mathrm{L}}_{\mathrm{C}\mathrm{r}} = \frac{(98-[0.8\times (\mathrm{A}\mathrm{g}\mathrm{e}-20)\left]\right)\times \left(\frac{\mathrm{B}\mathrm{S}\mathrm{A}}{1.73}\right)}{\mathrm{S}\mathrm{C}\mathrm{r}}$

(4)

Wright equation (5) ^[14] is likewise multiplied by 0.77 for female individuals:

${\mathrm{C}\mathrm{L}}_{\mathrm{C}\mathrm{r}} = \frac{(6230-32.8\times \mathrm{A}\mathrm{g}\mathrm{e})\times \mathrm{B}\mathrm{S}\mathrm{A}}{\mathrm{S}\mathrm{C}\mathrm{r}\times 88.42}$

(5)

Corcoran–Salazar (CS) ^[15] also developed equations to estimate clearance. For male individuals, Eq (6) should be used, while for female individuals, Eq (7) is applied:

${\mathrm{C}\mathrm{L}}_{\mathrm{C}\mathrm{r}} = \frac{(137-\mathrm{A}\mathrm{g}\mathrm{e})\times (0.285\times \mathrm{T}\mathrm{B}\mathrm{W}+12.1\times {\mathrm{H}}^{2})}{\mathrm{S}\mathrm{C}\mathrm{r}\times 51}$

(6)

${\mathrm{C}\mathrm{L}}_{\mathrm{C}\mathrm{r}} = \frac{(146-\mathrm{A}\mathrm{g}\mathrm{e})\times (0.287\times \mathrm{T}\mathrm{B}\mathrm{W}+9.74\times {\mathrm{H}}^{2})}{\mathrm{S}\mathrm{C}\mathrm{r}\times 60}$

(7)

Ideal body weight was calculated using the Devine equation (8) ^[16]:

$\mathrm{I}\mathrm{B}\mathrm{W} = 50+2.3\times \left(\frac{\mathrm{H}}{2.54}-60\right)$

(8)

where height (H) is in centimeters and the factor 50 is replaced by 45.5 in female individuals. The adjusted body weight was calculated as Eq (9) ^[18] and modified adjusted body weight as Eq (10) ^[17]:

$\mathrm{A}\mathrm{d}\mathrm{j}\mathrm{B}\mathrm{W} = \mathrm{I}\mathrm{D}\mathrm{W}+0.4\times \left(\mathrm{T}\mathrm{B}\mathrm{W}-\mathrm{I}\mathrm{B}\mathrm{W}\right)$

(9)

$\mathrm{m}\mathrm{A}\mathrm{d}\mathrm{j}\mathrm{B}\mathrm{W} = \mathrm{m}\mathrm{I}\mathrm{B}\mathrm{W}+0.4\times (\mathrm{T}\mathrm{B}\mathrm{W}-\mathrm{m}\mathrm{I}\mathrm{B}\mathrm{W})$

(10)

Lean body weight for male individuals was calculated as Eq (11) for males and as Eq (12) for females ^[19]:

$\mathrm{L}\mathrm{B}\mathrm{W} = \frac{9270\times \mathrm{T}\mathrm{B}\mathrm{W}}{6680+216\times \mathrm{B}\mathrm{M}\mathrm{I}}$

(11)

$\mathrm{L}\mathrm{B}\mathrm{W} = \frac{9270\times \mathrm{T}\mathrm{B}\mathrm{W}}{8780+244\times \mathrm{B}\mathrm{M}\mathrm{I}}$

(12)

2.2. Data analysis

Patients were stratified into four groups according to body composition, using body mass index (BMI) as an indicator: underweight (BMI < 17.9 kg/m²), normal weight (BMI = 18–24.9 kg/m²), overweight (BMI = 25–29.9 kg/m²), and obese (BMI ≥ 30 kg/m²). Data was also analyzed according to the sex and age of the patients, as well as to their measured serum creatinine concentration.

BMI was calculated as Eq (13), where TBW is total body weight in kg and H is height in m:

$\mathrm{B}\mathrm{M}\mathrm{I} = \frac{\mathrm{T}\mathrm{B}\mathrm{W}}{{\mathrm{H}}^{2}}$

(13)

Calculations of estimated CL_Cr values were performed in Microsoft Excel 365. Plots were also generated in Excel. The number of records of creatinine concentration of each group is indicated in every plot (as n).

3. Results and discussion

All the serum creatinine concentrations collected from the patients in the study population were included in this study. The distribution of this data is presented in Figure 2.

Figure 2. Distribution of measured creatinine serum concentrations in different groups (biological sex, body composition and age) and of all measures included in this study (overall).

DownLoad: Full-Size Img PowerPoint

Analyzing the distribution of creatinine serum concentrations (SCr), it is noticeable that men of the population studied in this work had higher SCr, as expected. Patients with normal BMI reached more extreme values (mainly elevated) of SCr comparing to the other body composition groups. With increasing age, SCr was also increased, predominantly in patients older than 70 years old.

Patients were then grouped according to their body composition based on BMI. The estimations of CL_Cr based on this stratification are presented in Figure 3. In the studied population, there was more variability in the estimated CL_Cr within the normal weight group. Furthermore, data from this group, followed by the underweight group, resulted in higher estimated CL_Cr. However, it is important to note that only patients under 20 years old and older than 71 years old were part of the underweight group. Overweight and obese patients had lower and less varying estimated CLCr.

Figure 3. Distribution of clearance estimations according to body type (based on BMI).

DownLoad: Full-Size Img PowerPoint

Regarding biological sex, the data from male individuals on populations analyzed in this study resulted in higher estimated CL_Cr (Figure 4), in agreement with expected.

Figure 4. Distribution of clearance estimations according to biological sex.

DownLoad: Full-Size Img PowerPoint

Figure 5 presents the distribution of results considering the age group of the patients. In the age group 1–10, there are only 2 data entries, corresponding to the same patient, an underweight 7-year-old female (TBW = 15.5 kg, H = 108 cm). Since the nonadjusted Jelliffe equation only takes into consideration age and does not include any body composition parameters, this data significantly deviates from the remaining estimations. The estimated CL_Cr decreased with age. The most considerable variations were observed in patients between 51 and 60 years old and were less perceptible above 80 years old.

Figure 5. Distribution of clearance estimations according to age.

DownLoad: Full-Size Img PowerPoint

Next, each body composition group was stratified for age groups. Results are presented in Figures 6–9. Consistently throughout every BMI group, there was less variability in patients older than 61 years. The estimation using the Cockcroft-Gault equation considering lean body weight (CG LBW) results in lower estimated CL_Cr.

Figure 6. Distribution of clearance estimations according to age for underweight patients.

DownLoad: Full-Size Img PowerPoint

Figure 7. Distribution of clearance estimations according to age for patients with normal BMI.

DownLoad: Full-Size Img PowerPoint

Figure 8. Distribution of clearance estimations according to age for overweight patients.

DownLoad: Full-Size Img PowerPoint

Figure 9. Distribution of clearance estimations according to age for obese patients.

DownLoad: Full-Size Img PowerPoint

The measured serum creatinine concentration was also analyzed, and this data is presented in Figure 10. Patients with serum creatinine concentration below reference criteria had an ampler range of estimated CLCr.

Figure 10. Distribution of clearance estimations according to measured serum creatinine concentration (CHUP reference: normal range of [Cr] is 0.7–1.2 mg/dL for male patients and 0.5–0.9 mg/dL for female patients).

DownLoad: Full-Size Img PowerPoint

4. Conclusions

Renal function can be a crucial factor to consider when adjusting therapeutic regimens of inpatients (whose kidneys can suffer significant deterioration throughout treatment duration). Since the most accurate indicator GFR is not as easily determined, creatinine serum concentration is more often used to estimate renal clearance, using various equations. As there is no standard estimation method, estimated creatinine clearance can be significantly disparate, which will influence therapeutic regimens adjustment.

Analyzing the influence of the different clearance estimation equations, the estimation using the Cockcroft-Gault equation considering lean body weight (CG LBW) produced lower estimated CL_Cr in almost all groups. Since creatinine is a product of natural muscle breakdown, this observation can indicate an overestimation of CL_Cr when using other components of body composition.

With this retrospective study, the differences between creatinine clearance estimation equations and the impact of the variables entered in these calculations were highlighted. These results supplement the knowledge about creatinine clearance estimation and provide insight on the disparities of the available estimation methods, that can help clinicians make a better informed and tailored decision when choosing how to evaluate a patient's renal function.

Acknowledgments

This work was financed by FEDER–Fundo Europeu de Desenvolvimento Regional through the COMPETE 2020–Operational Programme for Competitiveness and Internationalization (POCI), Portugal 2020, and by Portuguese funds through FCT–Fundação para a Ciência e a Tecnologia, in a framework of CINTESIS, R & D Unit (reference UIDB/4255/2020). N.V. also thanks support from FCT and FEDER (European Union), award number IF/00092/2014/CP1255/CT0004. RL thanks FCT for support of UID/QUI/50006/2019 (LAQV-REQUIMTE). AF thanks FCT for a doctoral fellowship (PD/BD/135120/2017). The authors also thank Serviço de Química Clínica from CHUP for technical support in obtaining clinical data. The contents of this article are solely the responsibility of the authors and do not necessarily represent the official view of the FCT.

Conflict of interest

On behalf of all authors, the corresponding author states that there is no conflict of interest.

References

[1]	National Kidney Foundation, Estimated Glomerular Filtration Rate (eGFR), Available from: https://www.kidney.org/atoz/content/gfr.
[2]	A. S. Levey, J. Coresh, K. Bolton, B. Culleton, K. S. Harvey, T. A. Ikizler, et al., K/DOQI clinical practice guidelines for chronic kidney disease: evaluation, classification, and stratification, Am. J. Kidney Dis. 39 (2002), S1-266.
[3]	L. A. Stevens, J. Coresh, T. Greene, A. S. Levey, Assessing kidney function-measured and estimated glomerular filtration rate, New Engl. J. Med., 354 (2006), 2473-2483. doi: 10.1056/NEJMra054415
[4]	Amikacin, DrugBank, 2021. Available from: https://go.drugbank.com/drugs/DB00479.
[5]	A. Aminimanizani, P. Beringer, J. Kang, L. Tsang, R. W. Jelliffe, B. J. Shapiro, Distribution and elimination of tobramycin administered in single or multiple daily doses in adult patients with cystic fibrosis, J. Antimicrob. Chemother., 50 (2002), 553-559. doi: 10.1093/jac/dkf168
[6]	Gentamicin, DrugBank, 2021. Available from: https://go.drugbank.com/drugs/DB00798.
[7]	J. Gonçalves-Pereira, A. Martins, P. Póvoa, Pharmacokinetics of gentamicin in critically ill patients: pilot study evaluating the first dose, Clin. Microbiol. Infect., 16 (2010), 1258-1263. doi: 10.1111/j.1469-0691.2009.03074.x
[8]	Tobramycin, DrugBank, 2021. Available from: https://go.drugbank.com/drugs/DB00684.
[9]	Tobramycin for injection, Medscape, 2021. Available from: https://reference.medscape.com/drug/nebcin-injection-tobramycin-342521#10.
[10]	Vancomycin, DrugBank, 2021. Available from: https://go.drugbank.com/drugs/DB00512.
[11]	D. D. Bois, A formula to estimate the approximate surface area if height and weight be known, Nutrition, 5 (1989), 303-313.
[12]	D. W. Cockcroft, M. H. Gault, Prediction of creatinine clearance from serum creatinine, Nephron, 16 (1976), 31-41. doi: 10.1159/000180580
[13]	R. W. Jelliffe, Creatinine clearance: bedside estimate, Ann. Intern. Med., 79 (1973), 604-605.
[14]	J. G. Wright, A. V. Boddy, M. Highley, J. Fenwick, A. McGill, A. H. Calvert, Estimation of glomerular filtration rate in cancer patients, Br. J. Cancer, 84 (2001), 452-459. doi: 10.1054/bjoc.2000.1643
[15]	D. E. Salazar, G. B. Corcoran, Predicting creatinine clearance and renal drug clearance in obese patients from estimated fat-free body mass, Am. J. Med., 84 (1988), 1053-1060. doi: 10.1016/0002-9343(88)90310-5
[16]	B. Devine, Gentamicin therapy, Drug Intell. Clin. Pharm., 8 (1974), 650-655.
[17]	J. Chambers, W. Cleveland, B. Kleiner, P. A. Tukey, Graphical Methods for Data Analysis, Monterey, CA: Boston, 1983.
[18]	M. P. Pai, F. P. Paloucek, The origin of the "ideal" body weight equations, Ann. Pharmacother., 34 (2000), 1066-1069. doi: 10.1345/aph.19381
[19]	S. Janmahasatian, S. B. Duffull, S. Ash, L. C. Ward, N. M. Byrne, B. Green, Quantification of lean bodyweight, Clin. Pharmacokinet., 44 (2005), 1051-1065.

This article has been cited by:

1.	Xuebin Wang, Zhengyue Liu, Jingxia Chen, Yuhui Chai, Xueqing Shao, Wenmin Xie, Kaile Zheng, Jia You, Zhuo Wang, Meiqing Feng, Impact of intra-patient variability of tacrolimus on allograft function and CD4 + /CD8 + ratio in kidney transplant recipients: a retrospective single-center study, 2024, 46, 2210-7703, 918, 10.1007/s11096-024-01726-w
2.	Yusuke Shima, Hironori Yoshida, Keiichiro Suminaga, Hiroshi Yoshida, Kentaro Hashimoto, Tatsuya Ogimoto, Kazutaka Hosoya, Hitomi Ajimizu, Tomoko Funazo, Takashi Nomizo, Hiroaki Ozasa, Toyohiro Hirai, Safety and efficacy of pemetrexed for patients with non-small cell lung cancer in the setting of renal impairment: a retrospective study, 2025, 25, 1471-2407, 10.1186/s12885-025-13785-x

Reader Comments

Your name:*

Email:*
© 2021 the Author(s), licensee AIMS Press. This is an open access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0)

通讯作者: 陈斌, bchen63@163.com

1.
沈阳化工大学材料科学与工程学院沈阳 110142

Mathematical Biosciences and Engineering

3.9

Metrics

Article views(3630) PDF downloads(121) Cited by(2)

Preview PDF

Download XML

Export Citation

Article outline

Show full outline

Figures and Tables

Figures(10) / Tables(2)

Mathematical Biosciences and Engineering

A retrospective study comparing creatinine clearance estimation using different equations on a population-based cohort

Related Papers:

Abstract

1. Introduction

2. Materials and methods

2.1. Patients and methods

2.2. Data analysis

3. Results and discussion

4. Conclusions

Acknowledgments

Conflict of interest

References

This article has been cited by:

Reader Comments

通讯作者: 陈斌, bchen63@163.com

Metrics

Figures and Tables

Other Articles By Authors

Catalog

Abstract

1. Introduction

2. Materials and methods

2.1. Patients and methods

2.2. Data analysis

3. Results and discussion

4. Conclusions

Acknowledgments

Conflict of interest

References

Mathematical Biosciences and Engineering

A retrospective study comparing creatinine clearance estimation using different equations on a population-based cohort

Related Papers:

Abstract

1. Introduction

2. Materials and methods

2.1. Patients and methods

2.2. Data analysis

3. Results and discussion

4. Conclusions

Acknowledgments

Conflict of interest

References

This article has been cited by:

Reader Comments

通讯作者: 陈斌, bchen63@163.com

Metrics

Figures and Tables

Other Articles By Authors

Related pages

Tools

Export File

Citation

Format

Content

Catalog

Abstract

1. Introduction

2. Materials and methods

2.1. Patients and methods

2.2. Data analysis

3. Results and discussion

4. Conclusions

Acknowledgments

Conflict of interest

References