A type of block withholding delay attack and the countermeasure based on type-2 fuzzy inference

Liang Liu; Wen Chen; Lei Zhang; JiaYong Liu; Jian Qin; Liang Liu; Wen Chen; Lei Zhang; JiaYong Liu; Jian Qin

doi:10.3934/mbe.2020017

Mathematical Biosciences and Engineering

2020, Volume 17, Issue 1: 309-327. doi: 10.3934/mbe.2020017

Previous Article Next Article

Research article Special Issues

A type of block withholding delay attack and the countermeasure based on type-2 fuzzy inference

1.
College of Cybersecurity, Sichuan University, Chengdu, China
2.
College of Electronics and Information Engineering, Sichuan University, Chengdu, China
3.
Chengdu No.7 high school, Chengdu, China

Received: 19 August 2019 Accepted: 25 September 2019 Published: 09 October 2019

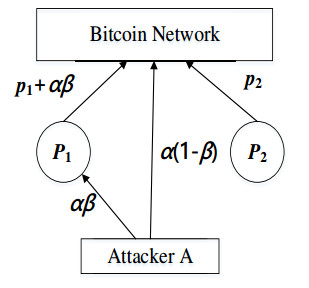
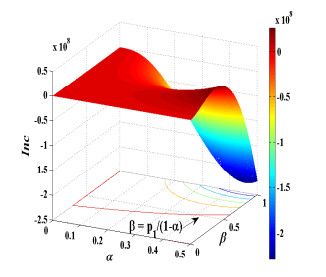
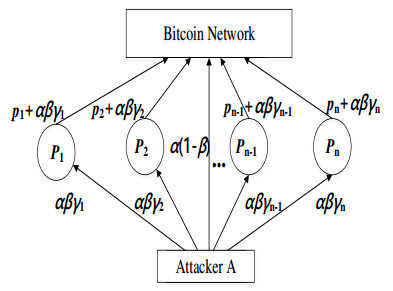
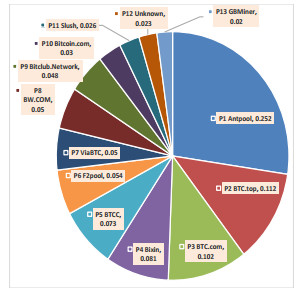
We proposed a new type of bitcoin withholding attack named block withholding delay (BWD). It is different from the traditional withholding attacks which always drop valid blocks. BWD attackers never discard blocks but they delay the submissions of blocks to the pool managers, resulting the pool failed in the mining competitions and loss of rewards. We analyzed the optimum strategy of a BWD attacker who split its computing power into two parts, one was utilized to launch BWD attacks on the victim pools, while the other part was used for solo mining. We present detailed quantitative analysis of the maximum incentive that an attacker can earn by carefully splitting its computing power, and demonstrated that the attacker can obtain higher incentives than its contribution to the network in different conditions. Furthermore, we proposed a countermeasure against BWD based on the interval type-2 Takagi-Sugeno-Kang fuzzy inference system (IT2-TSK-FIS). The principle is to modify the private payoff scheme of pools to increase the risk of losing revenues of the rogue miners who deliberately delay block submissions. The scheme dealing the uncertain cause of block delay using fuzzy inference, and it is so designed that it does not require modifications of public mining protocols or data structures of the bitcoin network, which makes it applicable in practical pools.

Keywords:

Citation: Liang Liu, Wen Chen, Lei Zhang, JiaYong Liu, Jian Qin. A type of block withholding delay attack and the countermeasure based on type-2 fuzzy inference[J]. Mathematical Biosciences and Engineering, 2020, 17(1): 309-327. doi: 10.3934/mbe.2020017

Related Papers:

[1]	Jiafan Zhang . On the distribution of primitive roots and Lehmer numbers. Electronic Research Archive, 2023, 31(11): 6913-6927. doi: 10.3934/era.2023350
[2]	Yang Gao, Qingzhong Ji . On the inverse stability of $z^n+c$ . Electronic Research Archive, 2025, 33(3): 1414-1428. doi: 10.3934/era.2025066
[3]	J. Bravo-Olivares, E. Fernández-Cara, E. Notte-Cuello, M.A. Rojas-Medar . Regularity criteria for 3D MHD flows in terms of spectral components. Electronic Research Archive, 2022, 30(9): 3238-3248. doi: 10.3934/era.2022164
[4]	Zhefeng Xu, Xiaoying Liu, Luyao Chen . Hybrid mean value involving some two-term exponential sums and fourth Gauss sums. Electronic Research Archive, 2025, 33(3): 1510-1522. doi: 10.3934/era.2025071
[5]	Jorge Garcia Villeda . A computable formula for the class number of the imaginary quadratic field $\mathbb Q(\sqrt{-p}), \ p = 4n-1$ . Electronic Research Archive, 2021, 29(6): 3853-3865. doi: 10.3934/era.2021065
[6]	Li Wang, Yuanyuan Meng . Generalized polynomial exponential sums and their fourth power mean. Electronic Research Archive, 2023, 31(7): 4313-4323. doi: 10.3934/era.2023220
[7]	Qingjie Chai, Hanyu Wei . The binomial sums for four types of polynomials involving floor and ceiling functions. Electronic Research Archive, 2025, 33(3): 1384-1397. doi: 10.3934/era.2025064
[8]	Hai-Liang Wu, Li-Yuan Wang . Permutations involving squares in finite fields. Electronic Research Archive, 2022, 30(6): 2109-2120. doi: 10.3934/era.2022106
[9]	Li Rui, Nilanjan Bag . Fourth power mean values of one kind special Kloosterman's sum. Electronic Research Archive, 2023, 31(10): 6445-6453. doi: 10.3934/era.2023326
[10]	Hongliang Chang, Yin Chen, Runxuan Zhang . A generalization on derivations of Lie algebras. Electronic Research Archive, 2021, 29(3): 2457-2473. doi: 10.3934/era.2020124

Abstract

1. Introduction

Let $\mathbb{F}_{q}$ be the finite field of $q$ elements with characteristic $p$ , where $q = p^r$ , $p$ is a prime number. Let $\mathbb{F}_{q}^* = \mathbb{F}_{q}\backslash \{0\}$ and $\mathbb{Z}^+$ denote the set of positive integers. Let $s\in \mathbb{Z}^+$ and $b\in \mathbb{F}_{q}$ . Let $f(x_1, \ldots, x_s)$ be a diagonal polynomial over $\mathbb{F}_{q}$ of the following form

$\begin{equation*} f(x_1,\ldots,x_s) = a_{1}x_{1}^{m_{1}}+a_{2}x_{2}^{m_{2}}+\dots+a_{s}x_{s}^{m_{s}}, \end{equation*}$

where $a_{i}\in \mathbb{F}_{q}^*,$ $m_{i}\in \mathbb{Z}^{+},$ $i = 1, \ldots, s.$ Denote by $N_{q}(f = b)$ the number of $\mathbb{F}_{q}$ -rational points on the affine hypersurface $f = b$ , namely,

$\begin{equation*} N_{q}(f = b) = \#\{\left(x_{1}, \ldots, x_{s}\right) \in \mathbb{A}^{s}(\mathbb{F}_{q}) \mid f\left(x_{1}, \ldots, x_{s}\right) = b\}. \end{equation*}$

In 1949, Hua and Vandiver ^[1] and Weil ^[2] independently obtained the formula of $N_{q}(f = b)$ in terms of character sum as follows

$\begin{equation} N_q( f = b ) = q^{s-1}+\sum{\psi}_1\left( a_{1}^{-1} \right) \cdots \psi _s\left( a_{s}^{-s}\right) J_q^0\left( \psi _1,\dots ,\psi _s \right), \end{equation}$

(1.1)

where the sum is taken over all $s$ multiplicative characters of $\mathbb{F}_{q}$ that satisfy $\psi_{i}^{m_{i}} = \varepsilon,$ $\psi_{i}\ne \varepsilon,$ $i = 1, \dots, s$ and $\psi_{1}\cdots \psi_{s} = \varepsilon$ . Here $\varepsilon$ is the trivial multiplicative character of $\mathbb{F}_{q}$ , and $J_q^{0}(\psi _1, \dots, \psi _s)$ is the Jacobi sum over $\mathbb{F}_{q}$ defined by

$\begin{equation*} J_q^0\left( \psi _1,\dots ,\psi _s \right) = \sum\limits_{c_1+\cdots +c_s = 0,c_i\in \mathbb{F}_{q}}{\psi _1\left( c_1 \right) \cdots \psi _s\left( c_s \right)}. \end{equation*}$

Though the explicit formula for $N_q(f = b)$ are difficult to obtain in general, it has been studied extensively because of their theoretical importance as well as their applications in cryptology and coding theory; see^{[3,4,5,6,7,8,9]}. In this paper, we use the Jacobi sums, Gauss sums and the results of quadratic form to deduce the formula of the number of $\mathbb{F}_{q^2}$ -rational points on a class of hypersurfaces over $\mathbb{F}_{q^2}$ under certain conditions. The main result of this paper can be stated as

Theorem 1.1. Let $q = 2^r$ with $r\in \mathbb{Z}^+$ and $\mathbb{F}_{q^2}$ be the finite field of $q^2$ elements. Let $f(X) = a_{1}x_{1}^{m_{1}}+a_{2}x_{2}^{m_{2}}+\dots+a_{s}x_{s}^{m_{s}},$ $g(Y) = y_{1}y_{2}+y_{3}y_{4}+\dots+y_{n-1}y_{n}+y_{n-2t-1}^{2}+\dots$ $+y_{n-3}^2+y_{n-1}^{2}+b_{t}y_{n-2t}^{2}+\dots +b_{1}y_{n-2}^{2}+b_{0}y_{n}^{2}$ , and $l(X, Y) = f(X)+g(Y)$ , where $a_{i}, b_j\in \mathbb{F}_{q^{2}}^{*},$ $m_i\ne 1,$ $(m_{i}, m_{k}) = 1,$ $i\ne k,$ $m_{i}|(q+1),$ $m_{i}\in \mathbb{Z}^{+},$ $2|n$ , $n > 2$ , $0\leq t\leq \frac{n}{2}-2$ , ${\mathrm{Tr}}_{\mathbb{F}_{q^2}/\mathbb{F}_{2}}(b_{j}) = 1$ for $i, k = 1, \dots, s$ and $j = 0, 1, \dots, t$ . For $h\in \mathbb{F}_{q^2}$ , we have

(1) If $h = 0$ , then

$\begin{equation*} \begin{aligned} N_{q^2}(l(X,Y) = 0) = q^{2(s+n-1)}+ \\\sum\limits_{\gamma\in \mathbb{F}_{q^2}^*}{\left( \prod\limits_{i = 1}^s{\left( \left( \frac{\gamma}{a_i} \right) _{m_i}m_i-1 \right) \left( q^{s+2n-3}+(-1)^{t}q^{s+n-3} \right)} \right)}. \end{aligned} \end{equation*}$

(2) If $h\in \mathbb{F}_{q^2}^{*}$ , then

$\begin{equation*} \begin{aligned} &N_{q^2}(l(X,Y) = h)\\ = &q^{2\left( s+n-1 \right)}+\left( q^{s+2n-3}+\left( -1 \right) ^{t+1}\left( q^2-1 \right) q^{s+n-3} \right) \prod\limits_{i = 1}^s{\left( \left( \frac{h}{a_i} \right)_{m_i} m_i-1 \right) }\\ &+\sum\limits_{\substack{ \gamma \in \mathbb{F}_{q^2}^{*}\backslash \{h\}}}{\left[ \prod\limits_{i = 1}^s{\left( \left( \frac{\gamma}{a_i} \right)_{m_i} m_i-1 \right)}\left( q^{2n+s-3}+\left( -1 \right) ^{t}q^{n+s-3} \right) \right]}. \end{aligned} \end{equation*}$

Here,

$\left(\frac{\gamma}{a_{i}}\right)_{m_{i}} = \left\{\begin{array}{ll} 1, & if\; \frac{\gamma}{a_{i}}\; is \;a\; residue\; of\; order\; m_{i}, \\ 0, & otherwise. \end{array}\right.$

2. Prerequisites

To prove Theorem 1.1, we need the lemmas and theorems below which are related to the Jacobi sums and Gauss sums.

Definition 2.1. Let $\chi$ be an additive character and $\psi$ a multiplicative character of $\mathbb{F}_{q}$ . The Gauss sum $G_q(\psi, \chi)$ in $\mathbb{F}_{q}$ is defined by

$G_q(\psi, \chi) = \sum\limits_{x \in \mathbb{F}_{q}^{*}} \psi(x) \chi(x).$

In particular, if $\chi$ is the canonical additive character, i.e., $\chi(x) = e^{2 \pi i {\mathrm{Tr}}_{\mathbb{F}_{q}/ \mathbb{F}_{p}}(x)/p}$ where ${\mathrm{Tr}}_{\mathbb{F}_{q}/ \mathbb{F}_{p}}(y) = y + y^{p} + \dots + y^{p^{r - 1}}$ is the absolute trace of $y$ from $\mathbb{F}_{q}$ to $\mathbb{F}_{p}$ , we simply write $G_q(\psi): = G_q(\psi, \chi)$ .

Let $\psi$ be a multiplicative character of $\mathbb{F}_{q}$ which is defined for all nonzero elements of $\mathbb{F}_{q}$ . We extend the definition of $\psi$ by setting $\psi(0) = 0$ if $\psi\neq \varepsilon$ and $\varepsilon(0) = 1$ .

Definition 2.2. Let $\psi_1, \ldots, \psi_s$ be $s$ multiplicative characters of $\mathbb{F}_{q}$ . Then, $J_q(\psi _1, \dots, \psi _s)$ is the Jacobi sum over $\mathbb{F}_{q}$ defined by

$\begin{equation*} J_q\left( \psi _1,\dots ,\psi _s \right) = \sum\limits_{c_1+\cdots +c_s = 1,c_i\in \mathbb{F}_{q}}{\psi _1\left( c_1 \right) \cdots \psi _s\left( c_s \right)}. \end{equation*}$

The Jacobi sums $J_q(\psi_1, \ldots, \psi_s)$ as well as the sums $J_q^0(\psi_1, \ldots, \psi_s)$ can be evaluated easily in case some of the multiplicative characters $\psi_i$ are trivial.

Lemma 2.3. ([,Theorem $5.19$ ,p. 206]) If the multiplicative characters $\psi_1, \ldots, \psi_s$ of $\mathbb{F}_{q}$ are trivial, then

$\begin{equation*} J_q(\psi_1,\ldots,\psi_s) = J_q^0(\psi_1,\ldots,\psi_s) = q^{s-1}. \end{equation*}$

If some, but not all, of the $\psi_i$ are trivial, then

$\begin{equation*} J_q(\psi_1,\ldots,\psi_s) = J_q^0(\psi_1,\ldots,\psi_s) = 0. \end{equation*}$

Lemma 2.4. ([,Theorem $5.20$ ,p. 206]) If $\psi_1, \ldots, \psi_s$ are multiplicative characters of $\mathbb{F}_{q}$ with $\psi_s$ nontrivial, then

$\begin{equation*} J_q^0(\psi_1,\ldots,\psi_s) = 0 \end{equation*}$

if $\psi_1\cdots\psi_s$ is nontrivial and

$\begin{equation*} J_q^0(\psi_1,\ldots,\psi_s) = \psi_s(-1)(q-1)J_q(\psi_1,\ldots,\psi_{s-1}) \end{equation*}$

if $\psi_1\cdots\psi_s$ is trivial.

If all $\psi_i$ are nontrivial, there exists an important connection between Jacobi sums and Gauss sums.

Lemma 2.5. ([,Theorem $5.21$ ,p. 207]) If $\psi_1, \ldots, \psi_s$ are nontrivial multiplicative characters of $\mathbb{F}_{q}$ and $\chi$ is a nontrivial additive character of $\mathbb{F}_{q}$ , then

$\begin{equation*} J_q(\psi_1,\ldots,\psi_s) = \frac{G_q(\psi_1,\chi)\cdots G_q(\psi_s,\chi)}{G_q(\psi_1\cdots \psi_s,\chi)} \end{equation*}$

if $\psi_1\cdots \psi_s$ is nontrivial and

$\begin{equation*} \begin{aligned} J_q(\psi_1,\ldots,\psi_s)& = -\psi_s(-1)J_q(\psi_1,\ldots,\psi_{s-1})\\ & = -\frac{1}{q}G_q(\psi_1,\chi)\cdots G_q(\psi_s,\chi) \end{aligned} \end{equation*}$

if $\psi_1\cdots \psi_s$ is trivial.

We turn to another special formula for Gauss sums which applies to a wider range of multiplicative characters but needs a restriction on the underlying field.

Lemma 2.6. ([,Theorem $5.16$ ,p. 202]) Let q be a prime power, let $\psi$ be a nontrivial multiplicative character of $\mathbb{F}_{q^2}$ of order m dividing $q+1$ . Then

$\begin{equation*} G_{q^2}\left(\psi\right) = \left\{\begin{array}{ll} q, & if\; m\; odd \;or\; \frac{q+1}{m}\; even, \\ -q, & if\; m\; even \;and\; \frac{q+1}{m}\; odd. \end{array}\right. \end{equation*}$

For $h\in \mathbb{F}_{q^2}$ , define $v(h) = -1$ if $h\in \mathbb{F}_{q^2}^{*}$ and $v(0) = q^2-1$ . The property of the function $v(h)$ will be used in the later proofs.

Lemma 2.7. ([,Lemma $6.23$ ,p. 281]) For any finite field $\mathbb{F}_{q}$ , we have

$\sum\limits_{c\in \mathbb{F}_{q}}v(c) = 0,$

for any $b\in \mathbb{F}_{q}$ ,

$\begin{equation*} \sum\limits_{c_1+\cdots +c_m = b}{v( c_1 )} \cdots v( c_k ) = \begin{cases} 0,& 1\leqslant k < m,\\ v\left( b \right) q^{m-1},& k = m,\\ \end{cases} \end{equation*}$

where the sum is over all $c_1, \ldots, c_m\in \mathbb{F}_{q}$ with $c_1+\dots+c_m = b.$

The quadratic forms have been studied intensively. A quadratic form $f$ in $n$ indeterminates is called nondegenerate if $f$ is not equivalent to a quadratic form in fewer than $n$ indeterminates. For any finite field $\mathbb{F}_q$ , two quadratic forms $f$ and $g$ over $\mathbb{F}_q$ are called equivalent if $f$ can be transformed into $g$ by means of a nonsingular linear substitution of indeterminates.

Lemma 2.8. ([,Theorem $6.30$ ,p. 287]) Let $f\in \mathbb{F}_{q}[x_1, \ldots, x_n]$ , $q$ even, be a nondegenerate quadratic form. If $n$ is even, then $f$ is either equivalent to

$x_1x_2+x_3x_4+\dots+x_{n-1}x_n$

or to a quadratic form of the type

$x_1x_2+x_3x_4+\dots+x_{n-1}x_n+x_{n-1}^{2}+ax_{n}^2,$

where $a\in \mathbb{F}_{q}$ satisfies ${\mathrm{Tr}}_{\mathbb{F}_{q}/\mathbb{F}_{p}}(a) = 1.$

Lemma 2.9. ([,Corollary $3.79$ ,p. 127]) Let $a\in \mathbb{F}_{q}$ and let $p$ be the characteristic of $\mathbb{F}_{q}$ , the trinomial $x^p-x-a$ is irreducible in $\mathbb{F}_{q}$ if and only if ${\mathrm{Tr}}_{\mathbb{F}_{q}/\mathbb{F}_{p}}(a)\ne 0.$

Lemma 2.10. ([,Lemma $6.31$ ,p. 288]) For even $q$ , let $a\in \mathbb{F}_{q}$ with ${\mathrm{Tr}}_{\mathbb{F}_{q}/\mathbb{F}_{p}}(a) = 1$ and $b\in \mathbb{F}_{q}.$ Then

$\begin{equation*} N_q(x_{1}^{2}+x_{1}x_{2}+ax_{2}^{2} = b) = q-v(b). \end{equation*}$

Lemma 2.11. ([,Theorem $6.32$ ,p. 288]) Let $\mathbb{F}_{q}$ be a finite field with $q$ even and let $b\in \mathbb{F}_{q}$ . Then for even $n$ , the number of solutions of the equation

$x_1x_2+x_3x_4+\cdots+x_{n-1}x_n = b$

in $\mathbb{F}_{q}^n$ is $q^{n-1}+v(b)q^{(n-2)/2}$ . For even $n$ and $a\in \mathbb{F}_{q}$ with ${\mathrm{Tr}}_{\mathbb{F}_{q}/\mathbb{F}_{p}}(a) = 1$ , the number of solutions of the equation

$x_1x_2+x_3x_4+\cdots+x_{n-1}x_n+x_{n-1}^2+ax_n^2 = b$

in $\mathbb{F}_{q}^n$ is $q^{n-1}-v(b)q^{(n-2)/2}$ .

Lemma 2.12. Let $q = 2^r$ and $h\in \mathbb{F}_{q^2}$ . Let $g(Y)\in \mathbb{F}_{q^2}[y_{1}, y_2, \dots, y_n]$ be a polynomial of the form

$g(Y) = y_{1}y_{2}+y_{3}y_{4}+\dots+y_{n-1}y_{n}+y_{n-2t-1}^{2}+\dots +y_{n-3}^2+y_{n-1}^{2}+\\b_{t}y_{n-2t}^{2}+\dots +b_{1}y_{n-2}^{2}+b_{0}y_{n}^{2},$

where $b_j\in \mathbb{F}_{q^{2}}^{*},$ $2|n$ , $n > 2$ , $0\leq t\leq \frac{n}{2}-2$ , ${\mathrm{Tr}}_{\mathbb{F}_{q^2}/\mathbb{F}_{2}}(b_{j}) = 1,$ $j = 0, 1, \dots, t.$ Then

$\begin{equation} N_{q^2}(g(Y) = h) = q^{2(n-1)}+(-1)^{t+1}q^{n-2}v(h). \end{equation}$

(2.1)

Proof. We provide two proofs here. The first proof is as follows. Let $q_{1} = q^2$ . Then by Lemmas 2.7 and 2.10, the number of solutions of $g(Y) = h$ in $\mathbb{F}_{q^2}$ can be deduced as

$\begin{array}{l} N_{q^2}(g(Y) = h)\\ = \sum\limits_{c_{1}+c_{2}+\dots+c_{t+2} = h} N_{q^2}\left(y_{1} y_{2}+y_{3} y_{4}+\cdots +y_{n-2t-3} y_{n-2t-2} = c_{1}\right)\\ \cdot N_{q^2}\left(y_{n-2t-1} y_{n-2t}+y_{n-2t-1}^{2}+b_{t}y_{n-2t}^{2} = c_{2}\right)\cdots N_{q^2}\left(y_{n-1} y_{n}+y_{n-1}^{2}+b_{0} y_{n}^{2} = c_{t+2}\right) \\ = \sum\limits_{c_{1}+c_{2}+\dots+c_{t+2} = h}\left(q_{1}^{n-2t-3}+v\left(c_{1}\right) q_{1}^{\left(n-2t-4\right) / 2}\right)\left(q_{1}-v\left(c_{2}\right)\right)\cdots\left(q_{1}-v\left(c_{t+2}\right)\right) \\ = \sum\limits_{c_{1}+c_{2}+\dots+c_{t+2} = h}\left(q_{1}^{n-2t-2}+v\left(c_{1}\right) q_{1}^{\left(n-2t-2\right) / 2}-v\left(c_{2}\right) q_{1}^{n-2t-3}-v\left(c_{1}\right) v\left(c_{2}\right) q_{1}^{\left(n-2t-4\right) / 2}\right)\\ \cdot\left(q_{1}-v\left(c_{3}\right)\right) \cdots\left(q_{1}-v\left(c_{t+2}\right)\right) \\ = \sum\limits_{c_{1}+c_{2}+\dots+c_{t+2} = h}\\\left(q_{1}^{n-t-2}+v\left(c_{1}\right) q_{1}^{\left(n-2\right) / 2}-v\left(c_{2}\right) q_{1}^{n-t-3}+\cdots+(-1)^{t+1}v\left(c_{1}\right) v\left(c_{2}\right) \cdots v\left(c_{t+2}\right) q_{1}^{\left(n-2 t-4\right) / 2}\right) \\ = q_{1}^{n-1}+q_{1}^{\left(n-2\right) / 2} \sum\limits_{c_{1} \in \mathbb{F}_{q^2}} v\left(c_{1}\right)+\cdots +(-1)^{t+1}\sum\limits_{c_{1}+c_{2}+\dots+c_{t+2} = h}v\left(c_{1}\right) v\left(c_{2}\right) \cdots v\left(c_{t+2}\right) q_{1}^{\left(n-2t-4\right)/2}. \end{array}$

(2.2)

By Lamma 2.7 and (2.2), we have

$N_{q^2}(g(Y) = h) = q_{1}^{n-1}+(-1)^{t+1}v(h) q_{1}^{\left(n-2\right) / 2} = q^{2\left(n-1\right)}+(-1)^{t+1}v(h) q^{n-2}.$

Next we give the second proof. Note that if $f$ and $g$ are equivalent, then for any $b\in \mathbb{F}_{q^2}$ the equation $f(x_1, \ldots, x_n) = b$ and $g(x_1, \ldots, x_n) = b$ have the same number of solutions in $\mathbb{F}_{q^2}.$ So we can get the number of solutions of $g(Y) = h$ for $h\in \mathbb{F}_{q^2}$ by means of a nonsingular linear substitution of indeterminates.

Let $k(X)\in \mathbb{F}_{q^2}[x_1, x_2, x_3, x_4]$ and $k(X) = x_1x_2+x_1^2+Ax_2^2+x_3x_4+x_3^2+Bx_4^2$ , where ${\mathrm{Tr}}_{\mathbb{F}_{q^2}/\mathbb{F}_{2}}(A) = {\mathrm{Tr}}_{\mathbb{F}_{q^2}/\mathbb{F}_{2}}(B) = 1.$ We first show that $k(x)$ is equivalent to $x_1x_2 + x_3x_4$ .

Let $x_3 = y_1+y_3$ and $x_i = y_i$ for $i\neq 3$ , then $k(X)$ is equivalent to $y_1y_2+y_1y_4+y_3y_4+Ay_2^2+y_3^2+By_4^2$ .

Let $y_2 = z_2+z_4$ and $y_i = z_i$ for $i\ne 2$ , then $k(X)$ is equivalent to $z_1z_2+z_3z_4+Az_2^2+z_3^2+Az_4^2+Bz_4^2.$

Let $z_1 = \alpha_1+A\alpha_2$ and $z_i = \alpha_i$ for $i\ne 1$ , then $k(X)$ is equivalent to $\alpha_1\alpha_2+\alpha_3^2+\alpha_3\alpha_4+(A+B)\alpha_4^2.$

Since ${\mathrm{Tr}}_{\mathbb{F}_{q^2}/\mathbb{F}_{2}}(A+B) = 0$ , we have $\alpha_3^2+\alpha_3\alpha_4+(A+B)\alpha_4^2$ is reducible by Lemma 2.9. Then $k(X)$ is equivalent to $x_1x_2+x_3x_4$ . It follows that if $t$ is odd, then $g(Y)$ is equivalent to $x_{1}x_{2}+x_{3}x_{4}+\cdots+x_{n-1}x_{n}$ , and if $t$ is even, then $g(Y)$ is equivalent to $x_{1}x_{2}+x_{3}x_{4}+\cdots+x_{n-1}x_{n}+x_{n-1}^{2}+ax_{n}^{2}$ with ${\mathrm{Tr}}_{\mathbb{F}_{q^2}/\mathbb{F}_{2}}(a) = 1.$ By Lemma 2.11, we get the desired result. □

3. Proof of Theorem 1.1

From (1.1), we know that the formula for the number of solutions of $f(X) = 0$ over $\mathbb{F}_{q^2}$ is

$N_{q^2}(f(X) = 0) = q^{2(s-1)}+\sum\limits_{j_1 = 1}^{d_1-1}{\cdots}\sum\limits_{j_s = 1}^{d_s-1}{\overline{\psi _{1}^{j_1}}}\left( a_1 \right) \cdots \overline{\psi _{s}^{j_s}}\left( a_s \right) J_{q^2}^0\left( \psi _{1}^{j_1},\dots ,\psi _{s}^{j_s} \right),$

where $d_{i} = (m_{i}, q^{2}-1)$ and $\psi_i$ is a multiplicative character of $\mathbb{F}_{q^2}$ of order $d_i$ . Since $m_{i}|q+1,$ we have $d_i = m_i.$ Let $H = \{(j_{1}, \dots, j_{s}) \mid 1 \leq j_{i} < m_{i},$ $1 \leq i \leq s\}$ . It follows that $\psi_{1}^{j_{1}} \cdots \psi_{s}^{j_{s}}$ is nontrivial for any $\left(j_{1}, \dots, j_{s}\right) \in H$ as $(m_{i}, m_{j}) = 1$ . By Lemma 2, we have $J_{q^2}^0\left(\psi _{1}^{j_1}, \dots, \psi _{s}^{j_s} \right) = 0$ and hence $N_{q^2}(f(X) = 0) = q^{2(s-1)}.$

Let $N_{q^2}(f(X) = c)$ denote the number of solutions of the equation $f(X) = c$ over $\mathbb{F}_{q^2}$ with $c\in\mathbb{F}_{q^2}^*$ . Let $V = \{(j_1, \ldots, j_s)|0\leq j_i < m_i, \; 1\leq i\leq s\}$ . Then

$\begin{equation*} \begin{aligned} N_{q^2}(f(X) = c)& = \sum\limits_{\gamma_{1}+\cdots+\gamma_{s} = c} N_{q^2}\left(a_{1} x_{1}^{m_{1}} = \gamma_{1}\right) \cdots N_{q^2}\left(a_{s} x_{s}^{m_{s}} = \gamma_{s}\right) \\ & = \sum\limits_{\gamma_{1}+\cdots+\gamma_{s} = c} \sum\limits_{j_{1} = 0}^{m_{1}-1} \psi_{1}^{j_{1}}\left(\frac{\gamma_{1}}{a_{1}}\right) \cdots \sum\limits_{j_{s} = 0}^{m_{s}-1} \psi_{s}^{j_{s}}\left(\frac{\gamma_{s}}{a_{s}}\right). \end{aligned} \end{equation*}$

Since $\psi_i$ is a multiplicative character of $\mathbb{F}_{q^2}$ of order $m_i$ , we have

$\begin{equation*} \begin{aligned} N_{q^2}(f(X) = c) = &\sum\limits_{\frac{\gamma_{1}}{c}+\cdots+\frac{\gamma_{s}}{c} = 1} \sum\limits_{\left(j_{1}, \dots, j_{s}\right) \in V} \psi_{1}^{j_{1}}\left(\frac{\gamma_{1}}{c}\right) \psi_{1}^{j_{1}}\left(\frac{c}{a_{1}}\right) \cdots \psi_{s}^{j_{s}}\left(\frac{\gamma_{s}}{c}\right) \psi_{s}^{j_{s}}\left(\frac{c}{a_{s}}\right) \\ = & \sum\limits_{\left(j_{1}, \dots, j_{s}\right) \in V} \psi_{1}^{j_{1}}\left(\frac{c}{a_{1}}\right) \cdots \psi_{s}^{j_{s}}\left(\frac{c}{a_{s}}\right) \sum\limits_{\frac{\gamma_{1}}{c}+\cdots+\frac{\gamma_{s}}{c} = 1} \psi_{1}^{j_{1}}\left(\frac{\gamma_{1}}{c}\right) \cdots \psi_{s}^{j_{s}}\left(\frac{\gamma_{s}}{c}\right) \\ = & \sum\limits_{\left(j_{1}, \dots, j_{s}\right) \in V} \psi_{1}^{j_{1}}\left(\frac{c}{a_{1}}\right) \cdots \psi_{s}^{j_{s}}\left(\frac{c}{a_{s}}\right) J_{q^2}\left(\psi_{1}^{j_{1}}, \dots, \psi_{s}^{j_{s}}\right) . \end{aligned} \end{equation*}$

By Lemma 2.3,

$\begin{equation*} N_{q^2}(f(X) = c) = q^{2(s-1)}+\sum\limits_{\left(j_{1}, \dots, j_{s}\right) \in H} \psi_{1}^{j_{1}}\left(\frac{c}{a_{1}}\right) \cdots \psi_{s}^{j_{s}}\left(\frac{c}{a_{s}}\right) J_{q^2}\left(\psi_{1}^{j_{1}}, \dots, \psi_{s}^{j_{s}}\right). \end{equation*}$

By Lemma 2.5,

$\begin{equation*} J_{q^2}\left(\psi_{1}^{j_{1}}, \dots, \psi_{s}^{j_{s}}\right) = \frac{G_{q^2}(\psi_{1}^{j_{1}})\cdots G_{q^2}(\psi_{s}^{j_{s}})}{G_{q^2}(\psi_{1}^{j_{1}}\cdots \psi_{s}^{j_{s}})}. \end{equation*}$

Since $m_i|q+1$ and $2\nmid m_i$ , by Lemma 2.6, we have

$G_{q^2}(\psi_{1}^{j_{1}}) = \cdots = G_{q^2}(\psi_{s}^{j_{s}}) = G_{q^2}(\psi_{1}^{j_{1}}\cdots \psi_{s}^{j_{s}}) = q.$

Then

$\begin{align*} &N_{q^2}(f(X) = c)\nonumber \\ = &q^{2(s-1)}+q^{s-1}\sum\limits_{j_1 = 1}^{m_1-1}\psi_{1}^{j_{1}}\left(\frac{c}{a_1}\right)\dots \sum\limits_{j_s = 1}^{m_s-1}\psi_{s}^{j_{s}}\left(\frac{c}{a_s}\right)\nonumber\\ = &q^{2(s-1)}+q^{s-1}\left(\sum\limits_{j_1 = 0}^{m_1-1}\psi_{1}^{j_{1}}\left(\frac{c}{a_1}\right)-1\right)\cdots \left(\sum\limits_{j_s = 0}^{m_s-1}\psi_{s}^{j_{s}}\left(\frac{c}{a_s}\right)-1\right). \end{align*}$

It follows that

$\begin{equation} N_{q^2}(f(X) = c) = q^{2(s-1)}+q^{s-1} \prod\limits_{i = 1}^{s}\left(\left(\frac{c}{a_{i}}\right)_{m_{i}} m_{i}-1\right), \end{equation}$

(3.1)

where

$\left(\frac{c}{a_{i}}\right)_{m_{i}} = \left\{\begin{array}{ll} 1, & {\text{if}}\; \frac{c}{a_{i}} {\text{ is a residue of order}}\; m_{i}, \\ 0, & {\text{otherwise.}} \end{array}\right.$

For a given $h\in \mathbb{F}_{q^2}$ . We discuss the two cases according to whether $h$ is zero or not.

Case 1: $h = 0$ . If $f(X) = 0$ , then $g(Y) = 0$ ; if $f(X)\ne 0$ , then $g(Y)\ne 0$ . Then

$\begin{align} &N_{q^2}(l(X,Y) = 0) \nonumber \\ = &\sum\limits_{c_{1}+c_{2} = 0} N_{q^2}\left(f(X) = c_{1}\right) N_{q^2}\left(g(Y) = c_{2}\right) \\ = &q^{2(s-1)} \left(q^{2\left(n-1\right)}+(-1)^{t+1}(q^{2}-1) q^{n-2}\right)+\sum\limits_{\substack{c_{1}+c_{2} = 0 \\ c_{1}, c_{2} \in \mathbb{F}_{q^2}^{*}}} N_{q^2}\left(f(X) = c_{1}\right) N_{q^2}\left(g(Y) = c_{2}\right). \end{align}$

(3.2)

By Lemma 2.12, (3.1) and (3.2), we have

$\begin{align} &N_{q^2}(l(X,Y) = 0) \\ = &q^{2\left(s+n-2\right)}+(-1)^{t+1}q^{2(s-1)+h_{n}}-(-1)^{t+1}q^{2(s-2)+n}+\sum\limits_{\substack{c_{1} \in \mathbb{F}_{q^2}^{*}}}\left[q^{2\left(s+n-2\right)}-(-1)^{t+1}q^{2(s-2)+n} \right. \\ &\left.+\prod\limits_{\substack{i = 1}}^{s}\left(\left(\frac{c_{1}}{a_{i}}\right)_{m_{i}} m_{i}-1\right)\left(q^{2 n+s-3}-(-1)^{t+1}q^{n+s-3}\right)\right] \\ = &q^{2\left(s+n-2\right)}+(-1)^{t+1}q^{2(s-1)+n}-(-1)^{t+1}q^{2(s-2)+n}+q^{2(s+n-1)}-(-1)^{t+1}q^{2(s-1)+n}-q^{2(s+n-2)} \\ &+(-1)^{t+1}q^{2(s-2)+n}+ \sum\limits_{\substack{c_{1} \in \mathbb{F}_{q^2}^{*}}}\left[\prod\limits_{i = 1}^{s}\left(\left(\frac{c_{1}}{a_{i}}\right)_{m_{i}} m_{i}-1\right)\left(q^{2 n+s-3}-(-1)^{t+1}q^{n+s-3}\right)\right] \\ = &q^{2\left(s+n-1\right)}+\sum\limits_{c_{1} \in \mathbb{F}_{q^2}^{*}}\left[\prod\limits_{i = 1}^{s}\left(\left(\frac{c_{1}}{a_{i}}\right)_{m_{i}}m_{i}-1\right)\left(q^{2 n+s-3}-(-1)^{t+1}q^{n+s-3}\right)\right]. \end{align}$

(3.3)

Case 2: $h\in \mathbb{F}_{q^2}^{*}$ . If $f(X) = h$ , then $g(Y) = 0$ ; if $f(X) = 0$ , then $g(Y) = h$ ; if $f(X)\notin \{0, h\}$ , then $g(Y)\notin \{0, h\}$ . So we have

$\begin{align} &N_{q^2}( l(X,Y)) = h) \\ = &\sum\limits_{c_1+c_2 = h}{N_{q^2}\left( f\left( X \right) = c_1 \right) N_{q^2}\left( g\left( Y \right) = c_2 \right)} \\ = &N_{q^2}(f(X) = 0)N_{q^2}(g(Y) = h)+N_{q^2}(f(X) = h)N_{q^2}(g(Y) = 0) \\ &+\sum\limits_{\substack{c_{1}+c_{2} = h \\ c_{1}, c_{2} \in \mathbb{F}_{q^2}^{*}\backslash \{h\}}}{N_{q^2}\left( f\left( X \right) = c_1 \right) N_{q^2}\left( g\left( Y \right) = c_2 \right)}. \end{align}$

(3.4)

By Lemma 2.12, (3.1) and (3.4),

$\begin{array}{l} N_{q^2}(l(X,Y) = h)\nonumber\\ = 2q^{2\left( s+n-2 \right)}+\left( -1 \right) ^{t+1}q^{2s+n-2}-\left( -1 \right) ^{t+1}2q^{2s+n-4}+ \\\left( q^{s+2n-3}+\left( -1 \right) ^{t+1}\left( q^2-1 \right) q^{s+n-3} \right) \prod\limits_{i = 1}^{s}\left(\left(\frac{h}{a_{i}}\right)_{m_{i}}m_{i}-1\right) \nonumber\\ +\sum\limits_{\substack{c_{1} \in \mathbb{F}_{q^2}^{*}\backslash \{h\}}}\\\left[ q^{2\left( s+n-2 \right)}-\left( -1 \right) ^{t+1}q^{2s+n-4}+\prod\limits_{i = 1}^{s}\left(\left(\frac{c_{1}}{a_{i}}\right)_{m_{i}}m_{i}-1\right)\left( q^{2n+s-3}-\left( -1 \right) ^{t+1}q^{n+s-3} \right) \right]. \end{array}$

It follows that

$\begin{aligned} &N_{q^2}(l(X,Y) = h)\\ = &2q^{2\left( s+n-2 \right)}+\left( -1 \right) ^{t+1}q^{2s+n-2}-\left( -1 \right) ^{t+1}2q^{2s+n-4}+\left( q^{s+2n-3}+\left( -1 \right) ^{t+1}\left( q^2-1 \right) q^{s+n-3} \right) \prod\limits_{i = 1}^{s}\left(\left(\frac{h}{a_{i}}\right)_{m_{i}}m_{i}-1\right) \\ &+\sum\limits_{\substack{ c_{1} \in \mathbb{F}_{q^2}^{*}\backslash \{h\}}}\left[ q^{2\left( s+n-2 \right)}-\left( -1 \right) ^{t+1}q^{2s+n-4}+\prod\limits_{i = 1}^{s}\left(\left(\frac{c_{1}}{a_{i}}\right)_{m_{i}}m_{i}-1\right)( q^{2n+s-3}-( -1 ) ^{t+1}q^{n+s-3} ) \right]\\ = &q^{2\left( s+n-1 \right)}+\left( q^{s+2n-3}+\left( -1 \right) ^{t+1}\left( q^2-1 \right) q^{s+n-3} \right) \prod\limits_{i = 1}^{s}\left(\left(\frac{h}{a_{i}}\right)_{m_{i}}m_{i}-1\right) +\sum\limits_{\substack{ c_{1} \in \mathbb{F}_{q^2}^{*}\backslash \{h\}}}\left[ \prod\limits_{i = 1}^{s}\left(\left(\frac{c_{1}}{a_{i}}\right)_{m_{i}}m_{i}-1\right)\right.\\&\cdot\left.( q^{2n+s-3}+( -1 ) ^{t}q^{n+s-3} ) \right]. \end{aligned}$

(3.5)

By (3.3) and (3.5), we get the desired result. The proof of Theorem 1.1 is complete.□

4. Corollary and examples

There is a direct corollary of Theorem 1.1 and we omit its proof.

Corollary 4.1. Under the conditions of Theorem 1.1, if $a_1 = \cdots = a_s = h\in \mathbb{F}_{q^2}^*$ , then we have

$\begin{equation*} \begin{aligned} &N_{q^2}(l(X,Y) = h)\\ = &q^{2\left( s+n-1 \right)}+\left( q^{s+2n-3}+\left( -1 \right) ^{t+1}\left( q^2-1 \right) q^{s+n-3} \right) \prod\limits_{i = 1}^s{\left( m_i-1 \right) }\\ &+\sum\limits_{\substack{ \gamma \in \mathbb{F}_{q^2}^{*}\backslash \{h\}}}{\left[ \prod\limits_{i = 1}^s{\left( \left( \frac{\gamma}{h} \right)_{m_i} m_i-1 \right)}\left( q^{2n+s-3}+\left( -1 \right) ^{t}q^{n+s-3} \right) \right]}, \end{aligned} \end{equation*}$

where

$\left(\frac{\gamma}{h}\right)_{m_{i}} = \left\{\begin{array}{ll} 1, & if\; \frac{\gamma}{h}\; is\; a \;residue\; of\; order\; m_{i}, \\ 0, & otherwise. \end{array}\right.$

Finally, we give two examples to conclude the paper.

Example 4.2. Let $\mathbb{F}_{2^{10}} = \left < \alpha \right > = \mathbb{F}_2[x]/{(x^{10}+x^3+1)}$ where $\alpha$ is a root of $x^{10}+x^3+1.$ Suppose $l(X, Y) = \alpha^{33}x_{1}^{3}+x_{2}^{11}+y_{3}^{2}+\alpha^{10} y_{4}^{2}+y_{1}y_{2}+y_{3}y_{4}$ . Clearly, ${\mathrm{Tr}}_{\mathbb{F}_{2^{10}}/\mathbb{F}_{2}}(\alpha^{10}) = 1$ , $m_{1} = 3,$ $m_2 = 11$ , $s = 2,$ $n = 4$ , $t = 0,$ $a_{2} = 1$ . By Theorem 1.1, we have

$N_{2^{10}}(l(X,Y) = 0) = 1024^{5}+(32^7+32^3)\times20 = 1126587102265344.$

Example 4.3. Let $\mathbb{F}_{2^{12}} = \left < \beta \right > = \mathbb{F}_2[x]/{(x^{12}+x^6+x^4+x+1)}$ where $\beta$ is a root of $x^{12}+x^6+x^4+x+1.$ Suppose $l(X, Y) = x_{1}^{5}+x_{2}^{13}+y_{3}^{2}+\beta^{10} y_{4}^{2}+y_{1}y_{2}+y_{3}y_{4}$ . Clearly, ${\mathrm{Tr}}_{\mathbb{F}_{2^{12}}/\mathbb{F}_{2}}(\beta^{10}) = 1$ , $m_{1} = 5,$ $m_2 = 13$ , $s = 2,$ $n = 4$ , $t = 0,$ $a_{1} = a_{2} = 1$ . By Corollary 1, we have

$N_{2^{12}}(l(X,Y) = 1) = 2^{5\times12}+(64^7-64^3\times4095)\times48 = 1153132559312355328.$

Acknowledgments

This work was jointly supported by the Natural Science Foundation of Fujian Province, China under Grant No. 2022J02046, Fujian Key Laboratory of Granular Computing and Applications (Minnan Normal University), Institute of Meteorological Big Data-Digital Fujian and Fujian Key Laboratory of Data Science and Statistics.

Conflict of interest

The authors declare there is no conflicts of interest.

References

[1]	S. Nakamoto, bitcoin: A peer-to-peer electronic cash systemTech, 2008(2008). Available from: https://bitcoin.org/bitcoin.pdf.
[2]	M. K. M. Ly, Coining bitcoin's Legal-Bits: Examining the regulatory framework for bitcoin and virtual Currencies, Harv. J. L. Tech., 27 (2014), 587-608.
[3]	A. Zohar, bitcoin: Under the Hood, Communicat. ACM, 58 (2015), 104-113.
[4]	V. Savvas, P. Perikles, R. Maria, bitcoin value analysis based on cross-correlations, J. Int. Bank. Commerce, 22 (2017), 1-12.
[5]	S. Higgins. $300 Billion: Bitcoin price boosts crypto market value to record high, 2018. Available from: https://www.coindesk.com/.
[6]	M. A. Khan and K. Salah, IoT security: Review, blockchain solutions, and open challenges, Future Generat. Comput. Syst., 82 (2018), 395-411.
[7]	A. Suliman, Z. Husain, M. Abououf, et al., Monetization of IoT Data using Smart Contracts, IET Networks, 8 (2019), 32-37.
[8]	M. Conti, C. Lal and S. Ruj, A Survey on Security and Privacy Issues of bitcoin., 2017. Available from: https://arxiv.org/abs/1706.00916.
[9]	Y. X. WANG and J. T. Gao, A Regulation Scheme Based on the CiphertextPolicy Hierarchical Attribute-Based Encryption in Bitcoin System, IEEE Access, 6 (2018), 16267-16278.
[10]	A. Miller, A. Kosba, J. Katz, et al., Nonoutsourceable Scratch-Off Puzzles to Discourage bitcoin Mining Coalitions, Proc. 22nd ACM SIGSAC Conf. Comput. Comm. Secur. (CCS), Denver, Colorado, USA, October, 2015 (2015), 680-691.
[11]	G. O. Karame, E. Androulaki, M. Roeschlin, et al., Misbehavior in bitcoin: A study of doublespending and accountability, ACM T. Ioform. Syst. SE., 18 (2015), 1-32.
[12]	G. O. Karame, E. Androulaki, M. Roeschlin, et al., Misbehavior in Bitcoin: A Study of DoubleSpending and Accountability ACM Transact. Inform. Syst. Secur., 18 (2015), 1-32.
[13]	Khaled Salah, M. H. U. Rehman, N. Nizamuddin, Blockchain for AI: Review and open research challenges, IEEE Access, 7 (2019), 10127-10148.
[14]	I. Eyal and E. G. Sirer, Majority is not enough: Bitcoin mining is vulnerable, Proc. Int. Conf. Fina. Cryptol. Secur., Christ Church, Barbados, March, 2014 (2014), 436- 454.
[15]	H. R. HASAN and K. Salah, Combating deepfake videos using blockchain and smart contracts, IEEE Access, 7 (2019), 41596-41606.
[16]	B. Johnson, A. Laszka, J. Grossklags, et al., Game-Theoretic analysis of DDoS attacks against bitcoin mining pools, Proc. Int. Conf. Fina. Cryptol. Secur., Christ Church, Barbados, March, 2014 (2014), 72-86.
[17]	E. Heilman, A. Kendler, A. Zohar, et al., Eclipse attacks on bitcoin's peer-to-peer network, Porc. 24th USENIX Symp. Secur., Washington, D.C., USA, 2015 (2015), 129-144.
[18]	K. Nayak, S. Kumar, A. Miller, et al., Stubborn mining: Generalizing selfish mining and combining with an eclipse attack, Proc. IEEE Euro. Symp. Secur Privacy (Euro S&P), Saarbrucken, Germany, March, 2016 (2016), 1-16.
[19]	N. T. Courtois and L. Bahack, On subversive miner strategies and block withholding attack in bitcoin digital currency, 2014. Available from: https://arxiv.org/abs/1402.1718.
[20]	M. Rosenfeld, Analysis of bitcoin pooled mining reward systems. Accessed: Nov.30, 2018, 2011. Available from: https://arxiv.org/abs/1112.4980.
[21]	D. Wu, X. D. Liu, X. B. Yan, et al., Equilibrium analysis of bitcoin block withholding attack: A generalized model, Reliabil. Eng. Syst. Safety, 5 (2019), 1-32.
[22]	L. Luu, R. Saha, I. Parameshwaran, et al., On power splitting games in distributed computation: The case of bitcoin pooled mining, Proc. IEEE Symp. 28th Comput. Secur. Found (CSF), Verona, Italy, July, 2015 (2015), 1-18.
[23]	I. Eyal, The miner's dilemma, Proc. IEEE Symp. Secur. Privacy (SP), San Jose, CA, USA, July, 2015 (2015), 89-103.
[24]	S. Bag, S. Ruj and K. Sakurai, Bitcoin block withholding attack: Analysis and mitigation, IEEE Trans. Inf. Forensic Secur., 12 (2017), 1967-1978.
[25]	N. T. Courtois and L. Bahack, On subversive miner strategies and block withholding attack in bitcoin digital currency, 2014. Available from: Available:https://arxiv.org/abs/1402.1718.
[26]	A. Laszka, B. Johnson and J. Grossklags, When bitcoin mining pools run dry, Proc. Int. Conf. Fina. Cryptol Secur., San Juan, Puerto Rico, January, 2015 (2015), 63-77.
[27]	S. Shen, H. Li, R. Han, et al., Differential game-based strategies for preventing malware propagation in wireless sensor networks, IEEE Trans. Inf. Forensic Secur., 9 (2014), 1962-1973.
[28]	J. Tuwiner, Bitcoin Mining Pools, 2018. Available from: https://www.buybitcoinworldwide.com.
[29]	O. Schrijvers, J. Bonneau, D. Boneh, et al., Incentive compatibility of bitcoin mining pool reward functions, Proc. Int. Conf. Fina. Cryptol.Secur., Christ Church, Barbados, 2016 (2016), 477- 498.
[30]	S. Bag and K. Sakurai, Yet another note on block withholding attack on bitcoin mining pools, Proc. Int. Conf. Inf. Secur.(ISC), Honolulu, HI, USA, 2016 (2016), 167-180.
[31]	J. S. R. Jangn and C. T. Sun, Neuro-fuzzy and soft computing: A computational approach to learning and machine intelligence, Prentice-Hall Inc., Upper Saddle River, NJ, 1996 (1996).
[32]	M. Mizumoto and K. Tanaka, Some properties of fuzzy sets of type-2, Inform. Control, 31 (1976), 312-340.

Reader Comments

Your name:*

Email:*
© 2020 the Author(s), licensee AIMS Press. This is an open access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0)