1. Introduction

In ecological systems, the interactions between different species can generate rich phenomena. Many models are derived to illustrate the predator-prey system from the view of both mathematics and biology [2,22,28,32]. Meanwhile, it is well known that the spatial structure may further affect the population dynamics of the species [7,8,15]. The spatially homogeneous reaction-diffusion predator-prey model with classical Lotka-Volterra interaction and no flux boundary conditions has been studied by many scholars, and the unique positive steady state solution is globally asymptotically stable in that case [21]. Our work is based on the important contribution of Yi, Wei and Shi [35] in the bifurcation analysis from the constant coexistence equilibrium solution of the following Rosenzweig-MacArthur model with Holling type-Ⅱ functional response [14,27]:

$(BP) \begin{cases} U_{t}-d_{1}\Delta U = r_{1}U\left(1-\cfrac{U}{K}\right)-\cfrac{m_{1}UV}{\gamma+U},& x\in\Omega, ~t>0,\\ V_{t}-d_{2}\Delta U = -r_{2}V+\cfrac{m_{2}UV}{\gamma+U},& x\in\Omega, ~t>0,\\ \partial_{\nu}U=\partial_{\nu}V=0,& x\in\partial{\Omega}, ~t>0.\\ U(x,0)=U_{0}(x)\geq 0,~~~V(x,0)=V_{0}(x)\geq 0,& x\in\Omega. \end{cases}$

Here $U=U(x,t)$, ~$V=V(x,t)$ stand for the densities of the prey and predator at time $t>0$, and a spatial position $x\in\Omega$, respectively; $\Omega$ is a bounded domain in $\mathbb{R}^n$ with a smooth boundary $\partial{\Omega}$; $\nu$ is the outward unit normal vector on $\partial{\Omega}$, and no flux boundary condition is imposed, so the system is a closed one. $d_{1},d_{2}>0$ are the diffusion coefficients of the species, and $r_{1},~r_{2},~m_{1},~m_{2},~K$ are positive real constants; the prey population follows a logistic growth, $r_{1}$ is the intrinsic growth rate of $U$, and $K$ is the carrying capacity; $r_{2}$ is the mortality rate of the predator in the absence of prey; $m_{1}$ is the search efficiency of $V$ for $U$ and $m_{2}$ represent the conversion rate of prey to predator; the function $\frac{U}{\gamma+K}$ denotes the functional response of the predator to the prey density changes. The parameter $\gamma(>0)$ is the half saturation constant which measures the "saturation" effect: the consumption of prey by a unit number of predators cannot continue to grow linearly with the number of prey available but must saturate at the value $\frac{1}{\gamma}$ [12,14]. After Yi et al., the method of Hopf bifurcation analysis has been extensively applied in reaction-diffusion equation, see [3,36].

It is worth noting that the functional responses in two species are the same in the model $(BP)$ since the principle of energy conversion, and the only difference is that the coefficients are different. In fact, it is not always true in real ecological environment: energy can be converted or wasted. Motivated by this idea, we consider an interesting but serious interaction between the prey and predator from the view of wastage of energy. Biologists call this interaction "surplus killing"[20,31]. It is a common behavior exhibited by predators, in which they kill more prey than they can immediately eat and then cache or abandon the remainder [19].

The term was invented by Dutch biologist Hans Kruuk [16] after studying spotted hyenas in Africa and red foxes in England. Other than humans, surplus killing has been observed among zooplankton, weasels, honey badgers, wolves, red foxes, leopards, lions, spotted hyenas, spiders[1,5,9,11,17,19,20,31]. The emergence of these phenomena refers to the fact that animals may only partially consume or abandon intact prey they have captured. There are many documented examples of predators exhibiting surplus killing. For example, Samu and Bíró [30] have found that the wandering spider, Pardosa hortensis (Lycosidae), exhibited significant levels of both partial feeding and prey abandonment at high rates of encounter with prey. In Canada's Northwest Territories, the researchers once found the bodies of 34 neonatal caribou calves that had been killed by wolves and scattered-some half-eaten and some completely untouched-over 3 square kilometres. In surplus killing, predators eat only the most-preferred animals and animal parts. Bears engaging in surplus killing of salmon are likelier to eat unspawned fish because of their higher muscle quality, and high-energy parts such as brains and eggs [16]. Surplus killing can deplete the overall food supply, waste predator energy and risk them being injured. Nonetheless, researchers say animals surplus kill whenever they can, in order to procure food for offspring and others, to gain valuable killing experience, and to create the opportunity to eat the carcass later when they are hungry again.

Inspired by their work, in this article, we would like to study the following predator-prey system with the predator exhibiting a "surplus killing" behaviour which can be demonstrated by different functional responses in the equations.

$\begin{cases} \cfrac{\partial u}{\partial t}-d_1\Delta u = r_1 u(1-\cfrac{u}{K_1})-m_1uv,~~x\in\Omega, ~t>0,\\ \cfrac{\partial v}{\partial t}-d_2\Delta v = r_2 v(1-\cfrac{v}{K_2})+\cfrac{ m_2 uv}{\gamma+u},~~x\in\Omega, ~t>0,\\ \cfrac{\partial u}{\partial \nu} ~= \cfrac{\partial u}{\partial \nu} ~= 0,~~x\in\partial\Omega, ~t>0,\\ u(x,0)= u_0(x)\geq 0(\not\equiv 0),~~v(x,0)= v_0(x)\geq 0(\not\equiv 0), ~~~~~~~x\in\Omega. \end{cases}$

(1)

Here $r_{1},r_{2}$ is the intrinsic growth rate of $u,v$, respectively; $K_1,K_2$ is the corresponding carrying capacity of $u,v$; $m_{1}$ is the predation rate, and $m_2$ is the consumption rate with $m_2=\alpha m_1$ where $\alpha$ is a positive constant; the Holling Ⅰ type functional response $m_1u$ and the Holling Ⅱ type functional response $\frac{ m_2 u}{\gamma+u}$ show the " surplus killing" effect: the predators keep hunting whenever they find a potential targets, but the conversion is limited since most of the prey they have captured are abandoned.

With a dimensionless change of variables:

$\tilde{u}=\cfrac{u}{\gamma},~~\tilde{v}=\cfrac{v}{K_2},~~\tilde{t}=r_1 t,~~\tilde{d_1}=\cfrac{d_1}{r_1},~~\tilde{d_2}=\cfrac{d_2}{r_1},\\ $

$~~\theta=\cfrac{r_2}{r_1},~\widetilde{\gamma}=\cfrac{\gamma}{K_1},~~\widetilde{m}_1=\cfrac{m_1K_2}{r_1},~~\widetilde{m}_2=\cfrac{ m_2}{r_1},$

still denote $\tilde{u}$, $\tilde{v}$, $\tilde{t}$, $\widetilde{d}_1$, $\widetilde{d}_2$, $\widetilde{\gamma}$, $\widetilde{m}_1$, $\widetilde{m}_2$ by $u$, $v$, $t$, $d_1$, $d_2$, $\gamma$, $m_1$, $m_2$, then we obtain

$\begin{cases} \cfrac{\partial u}{\partial t}-d_{1}\Delta u = u(1-\gamma u)-m_1 uv,& x\in\Omega, ~t>0,\\ \cfrac{\partial v}{\partial t}-d_{2}\Delta v = \theta v(1-v)+\cfrac{m_2 uv}{1+u},& x\in\Omega, ~t>0,\\ \cfrac{\partial u}{\partial \nu} ~= ~\cfrac{\partial u}{\partial \nu} ~= 0,& x\in\partial\Omega, ~t>0.\\ u(x,0)= u_{0}(x)\geq 0(\not\equiv 0),~~~v(x,0)= v_{0}(x)\geq 0(\not\equiv 0),& x\in\Omega. \end{cases}$

(2)

Considering that the biomass that predator consumed cannot convert into the new production for an instant, we add time delay into the functional response of the second equation of (2), and make it conform with natural situation:

$\begin{cases} \cfrac{\partial u(x,t)}{\partial t}-d_1\Delta u(x,t) = u(x,t)(1-\gamma u(x,t))-m_1u(x,t)v(x,t),~~x\in\Omega, ~t>0,\\ \cfrac{\partial v(x,t)}{\partial t}-d_2\Delta v(x,t) = \theta v(x,t)(1-v(x,t))+\cfrac{m_2u(x,t-\tau)v(x,t)}{1+u(x,t-\tau)},~~x\in\Omega, ~t>0,\\ \cfrac{\partial u}{\partial\nu} = \cfrac{\partial u}{\partial\nu} ~= 0,~~~~x\in\partial\Omega, ~t>0,\\ u(x,t)= u_0(x,t)\geq 0(\not\equiv 0),~v(x,t)= v_0(x,t)\geq 0(\not\equiv 0),~~x\in\Omega,~-\tau\leq t\leq 0. \end{cases}$

(3)

Here, $d_1$, $d_2$, $\theta$, $\gamma$, $m_1$ and $m_2$ are all positive constants, and given that the predators in nature don't usually just eat one species, mostly they have other choices. Based on this, we turn the growth of $v$ into a logistic form which means $u$ is not the only hunting target for the predators, they can still live even though the prey $u$ became extinct.

Define the real-valued Sobolev space

$X:=\{(u,v)\in H^{2}(0,l\pi)\times H^{2}(0,l\pi)|u_{x}=v_{x}=0,x=0,l\pi\},$

with inner product $\langle\cdot,\cdot\rangle$.

For sake of discussion, we make the following assumption:

$\left( {H1} \right){m_1} ＜ 1.$

The system (3) always has three non-negative constant equilibrium solutions: $E_0(0,0)$, $E_1(0,1)$, $E_2(1/\gamma,0)$, meanwhile, under the condition $(H1)$, the system also has a positive equilibrium $E_*(u_*,v_*)$, where

$\begin{array}{ll} u_*=\cfrac{1}{2\gamma\theta}\left[-\Gamma+\sqrt{\Gamma^2-4\gamma\theta^2(m_1-1)}\right],\\ v_*=\cfrac{1}{m_1}(1-\gamma u_*). \end{array}$

with $\Gamma=\theta\gamma-\theta+\theta m_1+m_1 m_2$.

Our main contribution for this article is a detailed and rigorous analysis about the global dynamics of the positive equilibrium of the diffusive predator-prey system (2). Keeping other parameters constant, we use the predation rate $m_1$ as a variable, and find that different values of $m_1$ result in distinct tendencies of the two species. Because of the effect of "surplus killing", the prey must raise their fertility rate or reduce the chances of encountering a predator to avoid extinction. For system (3), we shall be employing $\tau$ as our bifurcation parameter in our stability analyses to follow. When the spatial domain $\Omega$ is one-dimensional, and the parameters satisfy $\gamma\theta-\cfrac{m_2 m_1 }{(1+u_*)^2}<0$, we show the existence of Hopf bifurcation. We derive an explicit formula of the bifurcation point $\tau_{n,j}$ where $n, j$ are integers with $n$ has an upper bound. From the Proposition 2.3 of [4], we get that the smallest value of $\tau_{n,j}$ is $\tau_{0,0}$, which indicates that the periodic solutions bifurcated from the constant steady state solutions at $\tau=\tau_{0,0}$ are homogeneous. We have also studied the direction of Hopf bifurcation and stability of bifurcating periodic solution, one can see the details in Section 4.

The rest of the paper is organized as follows. In Section 2, the existence and priori bound of a positive solution for the reaction diffusion system are given, and the global asymptotically stability of positive equilibrium is proved. In Section 3, the stability of the positive constant steady state is considered, and the existence of the related Hopf bifurcation at the critical points is investigated with delay as the bifurcation parameter. In Section 4, by applying the normal form theory and center manifold reduction of partial functional differential equations, some detailed results of Hopf bifurcation are derived. Some numerical simulations are presented in Section 5. Throughout the paper, we denote $\mathbb{N}$ as the set of positive integers.

---

2. Analysis of solution for model without delay

---

2.1. Existence and priori bound of solution

In this section, we shall investigate the existence of a positive solution for system (3) with delay $\tau=0$, and give a priori bound of the solution.

Clearly, the system (3) with $\tau=0$ is

$\begin{cases} \cfrac{\partial u(x,t)}{\partial t}-d_1\Delta u(x,t) = u(x,t)(1-\gamma u(x,t))-m_1u(x,t)v(x,t),& x\in\Omega, ~t>0,\\ \cfrac{\partial v(x,t)}{\partial t}-d_2\Delta v(x,t) = \theta v(x,t)(1-v(x,t))+\cfrac{m_2u(x,t)v(x,t)}{1+u(x,t)},& x\in\Omega, ~t>0,\\ \cfrac{\partial u}{\partial \nu} ~= ~\cfrac{\partial u}{\partial \nu} ~= 0,& x\in\partial\Omega, ~t>0,\\ u(x,0)= u_0(x)\geq 0(\not\equiv 0),~v(x,0)= v_0(x)\geq 0(\not\equiv 0),& x\in\Omega, \end{cases}$

(4)

where $u_0(x)=u_0(x,0),~v_0(x)=v_0(x,0)$.

Theorem 2.1. Suppose that $d_1,~d_2,~\theta,~\gamma,~m_1,~m_2$ are all positive, $\Omega\subset\mathbb{R}^n$ is a bounded domain with smooth boundary. Then

$(a)$ the system (4) has a unique solution $(u(x,t),~v(x,t))$ satisfying

$0＜u(x,t)\leq u^*(t),~0＜v(x,t)\leq v^*(t),~for~t>0~and~x\in\Omega,$

where $(u^*(t),~v^*(t))$ is the unique solution of

$\left\{ {\begin{array}{*{20}{l}} {\frac{{du}}{{dt}} = u\left( {1 - \gamma u} \right)}\\ {\frac{{dv}}{{dt}} = \theta v(1 - v) + \frac{{{m_2}uv}}{{1 + u}},}\\ {u(0) = {u_0},v(0) = {v_0},} \end{array}} \right.$

(5)

and

$u_0=\sup\limits_{x\in\overline{\Omega}}u_0(x), ~~~~v_0=\sup\limits_{x\in\overline{\Omega}}v_0(x);$

$(b)$ for any solution $(u(x,t),~v(x,t))$ of system (4),

$\limsup\limits_{t\to\infty} u(x,t)\leq \cfrac{1}{\gamma} ,~~~~\limsup\limits_{t\to\infty} v(x,t)\leq 1+\cfrac{m_2}{\theta}.$

Proof. Define

$f(u,v)=u(1-\gamma u)-m_1 uv,~~~~~~g(u,v)=\theta v(1-v)+\cfrac{m_2 uv}{1+u}.$

Obviously, for any $(u,v)\in{\mathbb{R}}^2_+=\{(u,v)|u\geq 0,~v\geq 0\}$, one can see that

$\text{D}f_v=-m_1 u\leq 0 ,~~~~ \text{D}g_u=\cfrac{m_2 v}{(1+u)^2}\geq 0,$

thus system (4) is a mixed quasi-monotone system(see[23]). Let

$(\underline{u}(x,t),~\underline{v}(x,t))=(0,~0)~~ \mbox{and} ~~(\bar{u}(x,t),~\bar{v}(x,t))=(u^*(t),~v^*(t)).$

Substitute $(\underline{u},~\underline{v})$, $(\bar{u},~\bar{v})$ into system (4) gives

$\cfrac{\partial \bar{u}}{\partial t}-d_1\Delta\bar{u}-f(\bar{u},\underline{v})=0\geq 0=\cfrac{\partial\underline{u}}{\partial t}-d_1\Delta \underline{u}-f(\underline{u},\bar{v}),$

$\cfrac{\partial \bar{v}}{\partial t}-d_2\Delta\bar{v}-g(\bar{u},\bar{v})=0\geq 0=\cfrac{\partial\underline{v}}{\partial t}-d_2\Delta \underline{v}-g(\underline{u},\underline{v}),$

and

$0\leq\ u_0(x)\leq u_0,~~~~0\leq v_0(x)\leq v_0.$

Then $(\underline{u}(x,t),\underline{v}(x,t))=(0,~0)$ and $(\bar{u}(x,t),~\bar{v}(x,t))=(u^*(t),~v^*(t))$ are the lower-solution and upper-solution of system (4), respectively. From Theorem 5.3.3 in [34], we know that system (4) has a unique solution $(u(x,t),v(x,t))$ which satisfies

$0\leq u(x,t)\leq u^*(t),~~0\leq v(x,t)\leq v^*(t),~t\geq0.$

Since $u_0(x)\not\equiv 0$, $v_0(x)\not\equiv 0$, from the strong maximum principe, we have $u(x,t),v(x, t)>0$ when $t>0$ for all $x\in\Omega$. This completes the proof of part (a).

Let $u^1(t)$ be the unique solution of

$\begin{cases} \cfrac{\text{d}u}{\text{d}t}=u\left(1-\gamma u\right), \\ u(0)=u_0>0. \end{cases}$

One can see that $u^1(t)\to 1/\gamma$ as $t\to\infty$, then for any $\varepsilon>0$, there exists a $T_0>0$ such that

$u(x,t)\leq 1/\gamma+\varepsilon ,~~~~ \mbox{for}~~t\geq T_0~~\mbox{and}~~x\in\overline{\Omega},$

which implies that

$\limsup\limits_{t\to\infty}u(x,t)\leq 1/\gamma.$

Let $v^1(t)$ be the unique solution of

$\begin{cases} \cfrac{\text{d} v}{\text{d}t}=\theta v(1-v)+m_2 v, \\ v(0)=v_0. \end{cases}$

Then we have $v^1(t)\to 1+\cfrac{m_2}{\theta}$ as $t\to\infty$. From

$\theta v(1-v)+\cfrac{m_2 uv}{1+u}\leq\theta v(1-v)+m_2 v,$

it follows that $v(x,t)\leq v^*(t)\leq v^1(t)$. Hence, for any $\varepsilon'>0$, there exists a $T_0'>0$ such that

$v(x,t)\leq 1+\cfrac{m_2}{\theta}+\varepsilon'~~ \mbox{for}~~t\geq T_0'~~\mbox{and}~~x\in\overline{\Omega},$

which implies that

$\limsup\limits_{t\to\infty}v(x,t)\leq 1+\cfrac{m_2}{\theta}.$

The proof is complete.

---

2.2. Global stability of positive equilibrium

In this section, we shall give the conditions to ensure that the positive constant equilibrium $E_*(u_*,v_*)$ is globally asymptotically stable by utilizing the upper-lower solution method introduced by Pao [24].

Theorem 2.2. Suppose that $d_1,~d_2,~\theta,~\gamma,~m_1$ and $m_2$ are all positive, and $(H1)$ and

$(H2)m_1\left(1+\cfrac{m_2}{\theta(1+\gamma)}\right)＜1$

are satisfied. Then the positive equilibrium $E_*(u_*,v_*)$ of (4) is globally asymptotically stable, that is $E_*(u_*,v_*)$ is stable, and for any initial values $u_0(x)\geq 0(~\not\equiv 0),~v_0(x)\geq 0(~\not\equiv 0)$,

$\lim\limits_{t\to\infty}u(x,t)=u_*,~\lim\limits_{t\to\infty}v(x,t)=v_*,~~ \mbox{for}~~ x\in\overline{\Omega}.$

Proof. In Section 2.1, we get that

$u(x,t)\leq 1/\gamma+\varepsilon, ~~~ \mbox{for}~~ t>T_0,~~x\in\overline{\Omega}.$

From $(H2)$, we can choose an $\varepsilon_0>0$ satisfying

$m_1+(1+m_1)\varepsilon_0+\cfrac{m_1 m_2(1+\gamma \varepsilon_0)}{\theta(1+\gamma+\gamma \varepsilon_0)}＜1.$

(6)

Let $\bar{c}_1=1/\gamma+\varepsilon_0$, without loss of generality, there exists a $T_1>0$, such that $u(x,t)\leq 1/\gamma+\varepsilon_0$ for any $t>T_1$, and this in turn implies

$\cfrac{\partial v}{\partial t}=d_2 \Delta v+\theta v(1-v)+\cfrac{m_2u v}{1+u}\leq d_2 \Delta v+\theta v(1-v)+\cfrac{m_2 \bar{c}_1 v}{1+\bar{c}_1},$

for $t>T_1$. Hence there exists a $T_2>T_1$, such that $v(x,t)\leq \bar{c}_2$ for any $t>T_2$, where

$\bar{c}_2=1+\cfrac{m_2 \bar{c}_1 }{\theta(1+\bar{c}_1)}+\varepsilon_0.$

Again we have

$\cfrac{\partial u}{\partial t}=d_1 \Delta u+u(1-\gamma u)-m_1 uv\geq d_1 \Delta u+u(1-\gamma u)-m_1 u\bar{c}_2,$

for $t>T_2$. Since $m_1＜1$ and $\varepsilon_0$ satisfies (6), then

$1-m_1 \bar{c}_2>0, ~~ \mbox{and}~~~ 1-m_1 \bar{c}_2-\varepsilon_0>0.$

Hence, there exists a $T_3>T_2$, such that $u(x,t)\geq\underline{c}_1>0$ for any $t>T_3$, where

$\underline{c}_1=\cfrac{1}{\gamma}(1-m_1 \bar{c}_2-\varepsilon_0).$

Finally, using the similar method shown above, we have

$\cfrac{\partial v}{\partial t}=d_2 \Delta v+\theta v(1-v)+\cfrac{m_2u v}{1+u}\geq d_2 \Delta v+\theta v(1-v)+\cfrac{m_2 \underline{c}_1 v}{1+\underline{c}_1},$

for $t>T_3$, and we can ensure the following inequalities hold since $\varepsilon_0$ chosen as in (6),

$1+\cfrac{m_2 \underline{c}_1}{\theta(1+\underline{c}_1)}>1,~~\mbox{and}~~1+\cfrac{m_2 \underline{c}_1}{\theta(1+\underline{c}_1)}-\varepsilon_0>1.$

Then there exists a $T_4>T_3$ such that $v(x,t)\geq\underline{c}_2>0$ for any $t>T_4$, where

$\underline{c}_2=1+\cfrac{m_2 \underline{c}_1}{\theta(1+\underline{c}_1)}-\varepsilon_0.$

Therefor for $t>T_4$, we obtain that

$\underline{c}_1\leq u(x,t)\leq \bar{c}_1,~~~~\underline{c}_2\leq v(x,t)\leq \bar{c}_2,$

and $\underline{c}_1$, $\bar{c}_1$, $\underline{c}_2$, $\bar{c}_2$ satisfy

$1-\gamma \bar{c}_1-m_1 \underline{c}_2\leq 0,~~ 1-\bar{c}_2+\cfrac{m_2 \bar{c}_1}{\theta(1+\bar{c}_1)}\leq 0,$

$1-\gamma \underline{c}_1-m_1 \bar{c}_2\geq 0,~~ 1-\underline{c}_2+\cfrac{m_2 \underline{c}_1}{\theta(1+\underline{c}_1)}\geq 0.$

Then $(\bar{c}_1,~\bar{c}_2)$ and $(\underline{c}_1,~\underline{c}_2)$ are a pair of coupled upper and lower solutions of system (4), and when $\underline{c}_1\leq u\leq \bar{c}_1$, $\underline{c}_2\leq v\leq \bar{c}_2$, from the boundedness of the partial derivative of $f_i(i=1,2)$ with respect to $u,~v$, we know that $f_i$ satisfies the Lipschitz condition. Here we denote the Lipschitz constants by $L_i,~i=1,2$.

To investigate the asymptotic behavior of the positive equilibrium, we define two sequences of constant vectors $({\bar{u}^{(m)},~\bar{v}^{(m)}})$, $({\underline{u}^{(m)},~\underline{v}^{(m)}})$ from the recursion

$\begin{cases} \bar{u}^{(m)}=\bar{u}^{(m-1)}+\cfrac{1}{L_{1}}[\bar{u}^{(m-1)}(1-\gamma\bar{u}^{(m-1)})-m_{1}\bar{u}^{(m-1)}\underline{v}^{(m-1)}],\\ \underline{u}^{(m)}=\underline{u}^{(m-1)}+\cfrac{1}{L_{1}}[\underline{u}^{(m-1)}(1-\gamma\underline{u}^{(m-1)})-m_{1}\underline{u}^{(m-1)}\bar{v}^{(m-1)}],\\ \bar{v}^{(m)}=\bar{v}^{(m-1)}+\cfrac{1}{L_{2}}[\theta\bar{v}^{(m-1)}(1-\bar{v}^{(m-1)})+m_{2}\cfrac{\bar{u}^{(m-1)}\bar{v}^{(m-1)}}{1+\bar{u}^{(m-1)}}],\\ \underline{v}^{(m)}=\underline{v}^{(m-1)}+\cfrac{1}{L_{2}}[\theta\underline{v}^{(m-1)}(1-\underline{v}^{(m-1)}) +m_{2}\cfrac{\underline{u}^{(m-1)}\underline{v}^{(m-1)}}{1+\underline{u}^{(m-1)}}],\\ \end{cases}$

(7)

where $(\bar{u}^{(0)},~\bar{v}^{(0)})$ = $(\bar{c}_{1},\bar{c}_{2})$, $(\underline{u}^{(0)},~\underline{v}^ {(0)})$ = $(\underline{c}_{1},\underline{c}_{2})$, $L_{i}$ is the Lipschitz constant, $i=1,2$, and $m=1,2,3,\cdots$.

Then for $m\geq 1$, we know that

$\begin{align*} (\underline{u}^{(0)},\underline{v}^{(0)})&\leq (\underline{u}^{(m)},\underline{v}^{(m)})\leq (\underline{u}^{(m+1)},\underline{v}^{(m+1)})\\&\leq (\bar{u}^{(m+1)},~\bar{v}^{(m+1)})\leq (\bar{u}^{(m)},~\bar{v}^{(m)})\leq (\bar{u}^{(0)},~\bar{v}^{(0)}), \end{align*}$

and

$(\bar{u}^{(m)},~\bar{v}^{(m)})\rightarrow(\bar{u},\bar{v}), ~(\underline{u}^{(m)},~\underline{v}^{(m)})\rightarrow(\underline{u},\underline{v}),~~\mbox{as}~~m\rightarrow\infty.$

From the recursion (7), we can obtain that $\bar{u}, \underline{u}, \bar{v}, \underline{v}$ satisfy

$\begin{array}{ll} \bar{u}(1-\gamma\bar{u})-m_{1}\bar{u}\underline{v}=0,~~\theta\bar{v}(1-\bar{v})+\cfrac{m_{2}\bar{u}\bar{v}}{1+\bar{u}}=0,\\ \underline{u}(1-\gamma\underline{u})-m_{1}\underline{u}\bar{v}=0,~~\theta\underline{v}(1-\underline{v})+\cfrac{m_{2}\underline{u}~\underline{v}}{1+\underline{u}}=0. \end{array}$

(8)

Simplify the equations, we get

$\gamma (\bar{u}-\underline{u})=m_1(\bar{v}-\underline{v}),~m_2(\bar{u}-\underline{u})=\theta(1+\bar{u})(1+\underline{u})(\bar{v}-\underline{v}).$

Then we obtain

$\cfrac{\gamma}{m_1}(\bar{u}-\underline{u})=\cfrac{m_2(\bar{u}-\underline{u})}{\theta(1+\bar{u})(1+\underline{u})}.$

(9)

If we assume that $\bar{u}\neq\underline{u}$, then we can get the following relation from Eq.(9)

$\cfrac{\underline{u}}{1+\underline{u}}=1-\cfrac{\theta \gamma(1+\bar{u})}{m_1 m_2}.$

(10)

From Eq.(8), we can also have

$\underline{v}=\frac{1}{m_1}(1-\gamma \bar{u}) ~~ \mbox{and}~~ 1-\underline{v}+\frac{m_2 \underline{u}}{\theta (1+\underline{u})}=0.$

(11)

Substituting the first equation of Eq.(11) and Eq.(10) into the second equation of Eq.(11), it follows that

$1-\cfrac{1}{m_1}(1-\gamma \bar{u})+\cfrac{m_2}{\theta}\left(1-\cfrac{\theta \gamma(1+\bar{u})}{m_1 m_2}\right)=0,$

that is

$\cfrac{1}{m_1}=\cfrac{m_2}{\theta(1+\gamma)}+\cfrac{1}{1+\gamma}.$

(12)

This is a contraction to the condition $(H2)$. Hence $\bar{u}=\underline{u}$, and consequently $\bar{v}=\underline{v}$. Then from the Theorem 3.3 in [25] and Corollary 2.1 in [24], we can get the asymptotic behavior of the positive solution.

Now we investigate the local stability of positive equilibrium $E_*(u_*,v_*)$. Recall that by writing the vector $(u(x,t),v(x,t))^T$ as

$U(t):=(u(t),v(t))^T.$

Then the system (4) can be rewritten as

$\dot{U}(t)=D\Delta U(t)+F(U),$

(13)

where

$D=\text{diag}\{d_1,d_2\},~~\mbox{and}~~F:X\to \mathbb{R}^2,$

is defined by

$F(U)=\left(\begin{array}{l} u(t)\left(1-\gamma u(t)\right)-m_1 u(t)v(t)\\ \theta v(t)(1-v(t))-\cfrac{m_2 u(t)v(t)}{1+u_(t)} \end{array}\right).$

We consider the linearization at $E_*(u_*,v_*)$ for

$\dot{U}(t)=D\Delta U(t)+L_{E_*}(U),$

(14)

where

$L_{E_*}=\left(\begin{array}{cc} -\gamma u_*&-m_1 u_*\\ \cfrac{m_2 v_*}{(1+u_*)^2}&-\theta v_*\end{array}\right),\\ $

and its characteristic equation satisfies

$\lambda\xi-D\Delta \xi-L_{E_*}\xi=0.$

(15)

It is well known that the eigenvalue problem

$-\Delta \varphi = \mu \varphi, \quad x\in (0,l\pi), \quad \quad \varphi_x|_{x=0, l\pi}=0,$

has eigenvalues

$\mu_n=n^2/l^2, n\in\mathbb{N}_0=\mathbb{N}\cup\{0\},$

with corresponding eigenfunctions $\varphi_n(x)=\cos(nx/l), n\in\mathbb{N}_0$. Let

$\left(\begin{array}{c} \phi\\ \psi\end{array}\right)=\sum\limits_{n=0}^\infty\left(\begin{array}{c} a_n \\ b_n \end{array}\right)\cos(nx/l),~~a_n,~b_n\in \mathbb{C},$

be an eigenfunction for (15). Then from a straightforward computation, we obtain that the eigenvalues of (15) can be given by the following equations

$\text{det}(\lambda I+D\cfrac{n^2}{l^2}-L_{E_1})=0,~~~~~~~~~n\in\mathbb{N}_0,$

where $I$ is $2\times2$ unit matrix. That is

$\lambda^2-T_n\lambda+D_n+B_*=0, ~~n\in\mathbb{N}_0.$

(16)

For all $n\in\mathbb{N}_0$ we have

$\begin{array}{l} T_n=-(d_1+d_2)\cfrac{n^2}{l^2}-(\gamma u_*+\theta v_*)＜0,\\ D_n+B_*=\left(d_1\cfrac{n^2}{l^2}+\gamma u_*\right)\left(d_2\cfrac{n^2}{l^2}+\theta v_*\right)+\cfrac{m_1 m_2 u_* v_*}{(1+u_*)^2}>0. \end{array}$

Then all the roots of Eq.(16) have negative real parts. This implies that the positive equilibrium $E_*(u_*,v_*)$ of (4) is locally asymptotically stable when $m_1＜1$. Combining with the global attractivity proved before, we know that the constant positive equilibrium $E_*(u_*,v_*)$ is globally asymptotically stable.

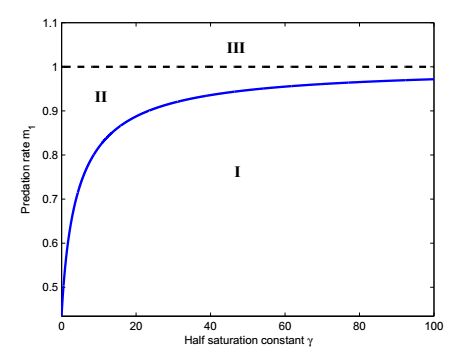
The above result indicates that $E_*(u_*,v_*)$ attracts all feasible solutions under the condition $(H1)$ and $(H2)$. If $(H2)$ doesn't work but $(H1)$ still holds, then $E_*(u_*,v_*)$ is local asymptotically stable. However, if $m_1>1$, then $E_*(u_*,v_*)$ disappears while $E_1(0,1)$ is global asymptotically stable. The critical curve can be drawn on the $(m_1,\gamma)$ plane (see Fig. 1).

Remark 1. According to the relationship between the original equation (1) and the dimensionless equation (2), we can illustrate the effect of "surplus killing". There are two different functional responses in equation (1), in order to be consistent with the assumptions, let the consumption rate $m_2$ be fixed. If the predation rate $m_1$ is sufficiently small(keeping the other parameters constant), then $(H1)$ and $(H2)$ can be satisfied, biologically, the two species can coexist and keep in a certain density. But if $m_1$ is not small enough such that $(H2)$ holds, this coexistence will be shaken, and only near the equilibrium point, they can maintain this balance. As the parameters continue to change, $(H1)$ is not satisfied, the balance will be completely broken: the population of prey will collapse to zero, and then predator population will grow into its carrying capacity. This's reasonable, because the predator population follows a logistic growth, they will never die out in this case, but the prey doesn't seem to be so fortunate: the predator exhibit a "surplus killing" behaviour, they will keep hunting whenever they can. So, the prey must enhance its fertility rate or reduce the chance of encountering a predator to avoid extinction.

Remark 2. If $m_1>1$, the boundary equilibrium $E_1(0,1)$ is global asymptotically stable for system (4). In fact, from the equation of predator in system Eq.(4), we have

$\cfrac{\partial v}{\partial t}=d_2 \Delta v+\theta v(1-v)+\cfrac{m_2u v}{1+u}\geq d_2 \Delta v+\theta v(1-v).$

It is well known that the positive solution of latter equation uniformly approach to $1$ as $t\rightarrow \infty$ under the same initial and boundary conditions. Since $m_1>1$, and the unique solution $(u(x,t),v(x,t))$ satisfies the conclusions of Theorem 2.1, then we can choose a sufficient small $\varepsilon>0$ and $T_0>0$ such that $1-\gamma u-m_1(1-\varepsilon)<0$ and $v(x,t)\geq 1-\varepsilon$ for any $t>T_0$. Now, consider the equation of prey in system Eq.(4),

$\cfrac{\partial u}{\partial t}=d_1 \Delta u+u(1-\gamma v)-m_1 uv \leq d_2 \Delta u+u(1-\gamma u-m_1(1-\varepsilon)),$

for $t>T_0$. Hence we have $u(x,t)\rightarrow 0$ as $t\rightarrow \infty$, and this result in turn implies $v(x,t)\rightarrow 0$ as $t\rightarrow \infty$.

---

3. Stability of the positive equilibrium and Hopf bifurcation

In this section, we shall study the stability of the positive constant steady state $E_*(u_*,v_*)$ and the existence of Hopf bifurcation for (3) with $\tau\geq 0$ by analyzing the distribution of the eigenvalues. Here, we restrict ourselves to the case of one dimensional spatial domain $\Omega=(0,~l\pi)$, for which the structure of the eigenvalues is clear, and let the phase space $\mathscr{C}:=C([-\tau,0],X)$.

The linearization of system (13) at $E_*(u_*,v_*)$ is given by

$\dot{U}(t)=D\Delta U(t)+L_*(U_t),$

(17)

where $L_*:\mathscr{C}\to X$ is defined by

$L_*(\phi_t)=L_1\phi(0)+L_2\phi(-\tau),$

and

$\begin{array}{l} L_1=\left( \begin{array}{cc} -\gamma u_*&-m_1 u_*\\ 0 &-\theta v_* \end{array}\right),~~ L_2=\left( \begin{array}{cc} 0&0\\ \cfrac{m_2 v_*}{(1+u_*)^2}&0 \end{array}\right), \end{array}$

$\phi(t)=(\phi_1(t),~\phi_2(t))^T,~~\phi_t(\cdot)=(\phi_1(t+\cdot),~\phi_2(t+\cdot))^T.$

The corresponding characteristic equation satisfies

$\lambda \xi-D\Delta \xi-L(e^{\lambda\,\cdot}\xi)=0,$

(18)

where $\xi\in\text{dom}(\Delta)\setminus\{0\}$. Similar analysis to section 2, we can equivalently transform (18) into the following equations.

$\det\left(\lambda I+D\cfrac{n^2}{l^2}-L_1-L_2 e^{-\lambda\tau}\right)=0,~~n\in\mathbb{N}_0.$

That is, each characteristic value $\lambda$ is a root of the equation

$\lambda^2-T_n\lambda+D_n+B_*e^{-\lambda\tau}=0, ~~n\in\mathbb{N}_0,$

(19)

where

$\begin{array}{l} T_n=-(d_1+d_2)\cfrac{n^2}{l^2}-\gamma u_*-\theta v_*, \\ D_n=\left(d_1\cfrac{n^2}{l^2}+\gamma u_*\right)\left(d_2\cfrac{n^2}{l^2}+\theta v_*\right),\\ B_*=\cfrac{m_1 m_2 u_* v_*}{(1+u_*)^2}. \end{array}$

Clearly, $\lambda=0$ is not the root of Eq.(19), from the result of Ruan and Wei [29], as parameter $\tau$ varies, the sum of the orders of the zeros of Eq.(19) in the open right half plane can change only if a pair of conjugate complex roots appears on or crosses the imaginary axis. Now we would like to seek critical values of $\tau$ such that there exists a pair of simple purely imaginary eigenvalues.

Let $\pm i\omega(\omega>0)$ be solutions of the $(n+1)$th equation (19). Then we have

$-\omega^2-T_n i\omega+D_n+B_*e^{-i\omega\tau}=0.$

Separating the real and imaginary parts, it follows that

$\begin{cases} B_*\cos\omega\tau = \omega^2-D_n,\\ B_*\sin\omega\tau =-T_n\omega . \\ \end{cases}$

(20)

Then we have

$\omega^4-(2D_n-T_n^2)\omega^2+D_n^2-B^2_*=0.$

(21)

Denote $z=\omega^2$. Then (21) can be rewritten in the following form

$z^2-(2D_n-T_n^2)z+D_n^2-B_*^2=0,$

(22)

where

$2D_n-T_n^2=-(d_1^2+d_2^2)\cfrac{n^4}{l^4}-2(d_1\gamma u_*+d_2\theta v_*)-(\gamma^2u_*^2+\theta^2 v_*^2)＜0.$

Hence Eq.(22) has a unique positive root

$z_n=\cfrac{2D_n-T_n^2+\sqrt{(2D_n-T_n^2)^2-4(D_n^2-B_*^2)}}{2},$

only if $D_n$ and $B_*$ satisfy $D_n^2-B_*^2<0$.

From the explicit formula of $D_n$ and $B_*$, we know that $D_n+B_*>0$, for all $n\in\mathbb{N}_0$. Since

$D_n-B_*=d_1d_2\cfrac{n^4}{l^4}+(d_1\theta v_*+d_2\gamma u_*)\cfrac{n^4}{l^4}+D_0-B_* \to\infty,~\text{as}~n\to\infty,$

where

$D_0-B_*=\gamma\theta u_*v_*-\cfrac{m_2m_1 u_*v_*}{(1+u_*)^2},$

and if

$D_0-B_*= u_*v_*\left(\gamma\theta-\cfrac{m_2 m_1 }{(1+u_*)^2}\right)＜0,$

we find a constant $n_*\in\mathbb{N}$ such that for $\forall{n}\in\mathbb{N}_0$

$D_n-B_*＜0,~~\mbox{for}~~0\leq n＜ n_*.$

and

$D_n-B_*\geq0,~~\mbox{for}~~n\geq n_*.$

Here we denote the set

$\mathcal{S}=\{n\in\mathbb{N}_0|~D_n-B_*<0\}.$

By Eq.(20), we have $\sin\omega_n\tau>0$, then

$\tau_{n,j}=\cfrac{1}{\omega_n}\left(\arccos\cfrac{\omega_n^{2}-D_n}{B_*}+2j\pi\right),~j\in\mathbb{N}_0,~n\in\mathcal{S}.$

(23)

Following the work of Cooke and Grassman[6], we have

Lemma 3.1. Suppose that $(H1)$ and $D_0-B_*<0$ are satisfied. Then

$\text{sign}~\alpha'(\tau_{n,j})=1,~~for~j\in\mathbb{N}_0,~n\in\mathcal{S},$

where

$\alpha(\tau)= ~\textrm{Re}\lambda(\tau).$

Proof. Substituting $\lambda(\tau)$ into Eq.(19) and taking the derivative with respect to $\tau$, we obtain that

$(2\lambda-T_n-\tau B_*e^{-\lambda\tau})\cfrac{\text{d}\lambda}{\text{d}\tau}-\lambda B_*e^{-\lambda\tau}=0.$

Thus

$\left(\cfrac{\text{d}\lambda}{\text{d}\tau}\right)^{-1}=\cfrac{2\lambda-T_n-\tau B_*e^{-\lambda\tau}}{\lambda B_*e^{-\lambda\tau}}.$

By Eq.(20), we have

$\begin{array}{ll} \text{Re}\left.\left(\frac{\text{d}\lambda}{\text{d}\tau}\right)^{-1}\right|_{\tau =\tau_{n,j}} &=\cfrac{2\omega_n\cos\omega_n\tau_{n,j}-T_n\sin\omega_n\tau_{n,j}}{B_*\omega_n}\\ &=\cfrac{2\omega_n^2-2D_n+T_n^2}{B_*^2}\\ &=\cfrac{\sqrt{T_n^4-4T_n^2D_n+4B_*^2}}{B_*^2}. \end{array}$

Since the sign of $\text{Re}\left(\frac{\text{d}\lambda}{\text{d}\tau}\right)$ is same as that of $\text{Re}\left(\frac{\text{d}\lambda}{\text{d}\tau}\right)^{-1}$, the lemma follows immediately.

From the Proposition 2.3 of [4], we have that

$\tau_{n,j}\leq\tau_{n,j+1},~~\mbox{for all}~~~j\in\mathbb{N}_0,n\in\mathcal{S},$

and

$\tau_{n,j}\leq\tau_{n+1,j},~~\mbox{for all}~~~j\in\mathbb{N}_0,n\in\mathcal{S}.$

Then $\tau_{0,0}$ is the smallest $\tau_{n,j}$. Denote $\tau_{0,0}$ as $\tau^*$ so that the stability will change when $\tau$ crosses $\tau^*$. Summarizing the above analysis and indicated by Corollary 2.4 of Ruan and Wei [29], we have the following lemma.

Lemma 3.2. Assume that $(H1)$ is satisfied.

$(a)$ If either

$T_n^4-4T_n^2D_n+4B_*^2＜0,$

or

$T_n^4-4T_n^2D_n+4B_*^2\geq0~~and~~\gamma\theta -\cfrac{m_2 m_1}{(1+u_*)^2}>0,$

for all $n\in\mathbb{N}_0$, then all the roots of (19) have negative real parts for $\tau\geq0$.

$(b)$ If

$\gamma\theta -\cfrac{m_2 m_1}{(1+u_*)^2}＜0,$

then for

$\tau=\tau_{n,j}~~,~~j\in\mathbb{N}_0,~n\in\mathcal{S},$

the $(n+1)$th equation of (19) has a pair of simple pure imaginary roots $\pm i\omega_n$, and all other roots have non-zero real parts. Moreover, all the roots of Eq.(19) have negative real parts for $\tau\in[0,\tau^*)$, and for $\tau>\tau^*$, Eq.(19) has at least one pair of conjugate complex roots with positive real parts.

From Lemmas 3.1 and 3.2, we have the following theorem.

Theorem 3.3. Assume that $(H1)$ is satisfied.

$(a)$ If

$T_n^4-4T_n^2D_n+4B_*^2＜0,$

or

$T_n^4-4T_n^2D_n+4B_*^2\geq0~~and~~\gamma\theta -\cfrac{m_2 m_1}{(1+u_*)^2}>0,$

for all $n\in\mathbb{N}_0$, then the equilibrium point $E_*(u_*,v_*)$ of system (3) is locally asymptotically stable for $\tau\geq0$.

$(b)$ If

$\gamma\theta-\cfrac{m_2 m_1 }{(1+u_*)^2}＜0,$

then system (3) undergoes a Hopf bifurcation at the equilibrium $E_*(u_*,v_*)$ when $\tau=\tau_{n,j}$, for $j\in\mathbb{N}_0,~n\in\mathcal{S}$. Furthermore, the positive equilibrium $E_*(u_*,v_*)$ of system (3) is asymptotically stable for $\tau\in[0,\tau^*)$, and unstable for $\tau>\tau^*$.

---

4. Direction of Hopf bifurcation and stability of bifurcating periodic solution

In section 3, we obtained some conditions under which the system (3) undergoes a Hopf bifurcation. In this section, we shall study the direction of Hopf bifurcation near the positive equilibrium and stability of the bifurcating periodic solutions. We are able to show more detailed information of Hopf bifurcation by using the normal form theory and center manifold reduction due to [10,13,33].

Rescaling the time $t\mapsto t/\tau$, and let $\tilde{u}(x,t)=u(x,t)-u_*$, $\tilde{v}(x,t)=v(x,t)-v_*$, then we have

$\begin{cases} \cfrac{\partial \tilde{u}}{\partial t}=\tau[d_1\Delta\tilde{u}-\gamma u_*\tilde{u}-m_1u_*\tilde{v}-f_1(u_t,v_t)],&x\in\Omega,~t>0,\\ \cfrac{\partial \tilde{v}}{\partial t}=\tau[d_2\Delta \tilde{v}-\theta v_*\tilde{v}+\cfrac{m_2v_*}{(1+u_*)^2}u_t(-1)+f_2(u_t,v_t)],&x\in\Omega,~t>0,\\ \cfrac{\partial \tilde{u}}{\partial \nu}=0,~\cfrac{\partial \tilde{v}}{\partial \nu}=0,&x\in\partial \Omega,~t>0,\\ \tilde{u}(x,t)=\tilde{u}_0(x,t),~ \tilde{v}(x,t)=\tilde{v}_0(x,t),&x\in\Omega,-1\leq t\leq 0, \end{cases}$

(24)

where

$u_t=u(x,t+\theta),~v_t=v(x,t+\theta),~~\theta\in [-1,0],$

$\tilde{u}_0(x,t)=u_0(x,t)-u_*,~~\tilde{v}_0(x,t)=v_0(x,t)-v_*,$

and for $(\phi_1, \phi_2)\in \mathcal{C}:=C([-1,0],X)$

$f_1(\phi_1,\phi_2)=-\gamma\phi_1(0)^2-m_1 \phi_1(0)\phi_2(0),$

(25)

$\begin{array}{ll} f_2(\phi_1,\phi_2)&=-\theta\phi_2(0)^2+\cfrac{m_2}{(1+u_*)^2}\phi_1(-1)\phi_2(0)-\cfrac{m_2 v_*}{(1+u_*)^3}\phi_1(-1)^2\\ &-\cfrac{m_2}{(1+u_*)^3}\phi_1(-1)^2\phi_2(0)+\cfrac{m_2 v_*}{(1+u_*)^4}\phi_1(-1)^3+\mathcal{O}(4). \end{array}$

(26)

Let $\tau=\tau^*+\epsilon$, from the discussion in section 4, we know that when $\epsilon=0$ system (24) undergoes a Hopf bifurcation at the equilibrium $(0,0)$. Then we can rewrite system (24) in a abstract form in the space $\mathcal{C}$ as

$\dot{U}(t)=\tilde{D}\Delta U(t)+L_\epsilon(U_t)+F(\epsilon,U_t),$

(27)

where

$\widetilde{D}=(\tau^*+\epsilon)D~~\mbox{and}~~L_\epsilon:\mathcal{C}\to X,~F:\mathcal{C}\to X$

are defined, respectively, by

$L_\epsilon(\phi(\theta))=(\tau^*+\epsilon)L_1\phi(0)+(\tau^*+\epsilon)L_2\phi(-1),$

$F(\epsilon,\phi(\theta))=(F_1(\epsilon,\phi(\theta)),~F_2(\epsilon,\phi(\theta)))^T,$

with

$(F_1(\epsilon,\phi(\theta)),~F_2(\epsilon,\phi(\theta)))=(\tau^*+\epsilon)(f_1(\phi_1(\theta),\phi_2(\theta)),~f_2(\phi_1(\theta),\phi_2(\theta))),$

where $f_1$ and $f_2$ are defined by (25) and (26) respectively.

The linearized equation at the origin $(0,0)$ has the form

$\dot{U}(t)=\widetilde{D}\Delta U(t)+L_\epsilon(U_t).$

(28)

According to the theory of semigroup of linear operator [26], we have the solution operator of (28) is a $C_0$-semigroup, and the infinitesimal generator $\mathcal{A}_{\epsilon}$ is given by

$\mathcal{A}_{\epsilon}\phi=\begin{cases} \dot{\phi}(\theta), &\theta\in[-1,0), \\ \widetilde{D}\Delta\phi(0)+L_{\epsilon}(\phi), &\theta=0, \end{cases}$

(29)

with

$\text{dom}(\mathcal{A}_\epsilon):=\{\phi\in\mathcal{C}: \dot{\phi}\in\mathcal{C}, \phi(0)\in\text{dom}(\Delta), \dot{\phi}(0)=\widetilde{D}\Delta\phi(0)+L_{\epsilon}(\phi)\}.$

When $\tau=0$, we denote the infinitesimal generator as $\mathcal{A}_0$.

Hence, equation (27) can be rewritten as the abstract ODE in $\mathcal{C}$:

$\dot{U}_t=\mathcal{A}_\epsilon U_t+X_0 F(\epsilon,U_t),$

(30)

where

$X_0(\theta)=\begin{cases} 0 , &\theta\in[-1, 0),\\ I, &\theta=0. \end{cases}$

We denote

$b_n=\cfrac{\cos (nx/l)}{\|\cos(nx/l)\|},~ ~\beta_n=\{(b_n, 0)^{T}, (0, b_n)^{T}\},$

where

$\|\cos(nx/l)\|=\left(\int_0^{l\pi}\cos^2(nx/l)\text{d}x\right)^{\frac{1}{2}}.$

For $\phi=(\phi^{^{(1)}},\phi^{^{(2)}})^{T}\in\mathcal{C}$, denote

$\phi_n=\langle \phi,\beta_n\rangle=\left(\langle \phi^{^{(1)}},b_n\rangle, \langle \phi^{^{(2)}},b_n\rangle\right)^{T}.$

Define $\mathcal{A}_{\epsilon, n}$ as

$\mathcal{A}_{\epsilon, n}(\phi_n(\theta)b_n)=\begin{cases} \dot{\phi}_n(\theta)b_n,& \theta\in[-1,0), \\ \int_{-1}^{0}\text{d}\eta_n(\epsilon,\theta)\phi_n(\theta)b_n , &\theta=0, \end{cases}$

(31)

and

$L_{\epsilon, n}(\phi_n)=(\tau^*+\epsilon)L_1\phi_n(0)+(\tau^*+\epsilon)L_2\phi_n(-1),$

$\int_{-1}^{0}\text{d}\eta_n(\epsilon,\theta)\phi_n(\theta)=-\cfrac{n^2}{l^2} \widetilde{D}\phi_n(0)+L_{\epsilon,n}(\phi_n),$

where

$\eta_n(\epsilon,\theta)=\begin{cases}\begin{array}{ll} -(\tau^*+\epsilon)L_2,&\theta=-1,\\ 0,&\theta\in(-1,0),\\ (\tau^*+\epsilon)L_1-\cfrac{n^2}{l^2}\widetilde{D},&\theta=0. \end{array}\end{cases}$

Denote $\mathcal{A}^*$ as the adjoint operator of $\mathcal{A}_0$ on $\mathcal{C}^*:=C([0,1],X)$.

$\mathcal{A}^*\psi(s)=\begin{cases}\begin{array}{ll} -\dot{\psi}(s),~& s\in(0,1],\\ \sum\limits_{n=0}^\infty\int_{-1}^0\text{d}\eta_n^T(0,\theta)\psi_n(-\theta)b_n,~&s=0. \end{array}\end{cases}$

Following [10], we introduce the bilinear formal $(\cdot,\cdot)$ on $\mathcal{C}^*\times\mathcal{C}$

$(\psi,\phi)=\sum\limits_{k,j=0}^\infty(\psi_k,\phi_j)_c\int_\Omega b_kb_j\text{d}x,$

where

$\psi=\sum\limits_{n=0}^\infty \psi_nb_n\in\mathcal{C}^*,~\phi=\sum\limits_{n=0}^\infty \phi_nb_n\in\mathcal{C},$

and

$\phi_n\in C:=C([-1,0],\mathbb{R}^2),~~\psi_n\in C^*:=C([0,1],\mathbb{R}^2).$

Notice that

$\int_\Omega b_kb_j\text{d}x=0~~\mbox{for}~~k\neq j,$

we have

$(\psi,\phi)=\sum\limits_{n=0}^\infty(\psi_n,\phi_n)_c|b_n|^2,$

where $(\cdot,\cdot)_c$ is the bilinear form defined on $C^*\times C$

$(\psi_n,\phi_n)_c=\overline{\psi}_n^T(0)\phi_n(0)-\int_{-1}^0\int_{\xi=0}^\theta\overline{\psi}_n^T(\xi-\theta) \text{d}\eta_n(0,\theta)\phi_n(\xi)\text{d}\xi.$

Let

$q(\theta)b_{n_0}=q(0)e^{i\omega_{n_0}\tau^*\theta}b_{n_0}, ~q^*(s)b_{n_0}=q^*(0)e^{i\omega_{n_0}\tau^* s}b_{n_0}$

be the eigenfunctions of $\mathcal{A}_0$ and $\mathcal{A}^*$ corresponding to the eigenvalues $i\omega_{n_0}\tau^*$ and $-i\omega_{n_0}\tau^*$, respectively. By direct calculations, we chose

$q(0)=(1, q_1)^{T},~q^*(0)=M(q_2, 1)^{T},$

so that $(q^*,q)_{c}=1$, where

$\begin{array}{l} q_1=-\cfrac{i\omega_{n_0}+d_1 n_0^2/l^2+\gamma u*}{m_1 u_*},~q_2=\cfrac{i\omega_{n_0}-d_2 n_0^2/l^2-\theta v_*}{m_1 u_*},\\ \overline{M}=\cfrac{(1+u_*)^2}{(q_1+\bar{q}_2)(1+u_*)^2+\tau^* m_2 v_*e^{-i\omega_{n_0}\tau^*}}. \end{array}$

Then we decompose the space $\mathcal{C}$ as follows

$\mathcal{C}=P\oplus Q,$

where

$P=\{zqb_{n_0}+\overline{z}\overline{q}b_{n_0}|z\in\mathbb{C}\},$

$Q=\{\phi\in\mathcal{C}|(q^*b_{n_0},\phi)=0~\text{and}~(\overline{q}^*b_{n_0},\phi)=0\}.$

That is $P$ is the 2-dimensional center subspace spanned by the basis vectors of the linear operator $\mathcal{A}_0$ associated with purely imaginary eigenvalues $\pm i\omega_{n_0}\tau_*$, and $Q$ is the complement space of $P$.

Thus, system (30) could be rewritten as

$U_t=z(t)q(\cdot)b_{n_0}+\bar{z}(t)\bar{q}(\cdot)b_{n_0}+W(t,\cdot),$

where

$z(t)=(q^*b_{n_0}, U_t),~~~W(t,\cdot)\in Q,$

(32)

and

$W(t,\theta)=U_t(\theta)-2\text{Re}\{z(t)q(\theta)b_{n_0}\}.$

(33)

Then we have

$\dot{z}(t)=i\omega_0z(t)+\bar{q}^{*T}(0)\langle F(0, U_t), \beta_{n_0}\rangle,$

(34)

where

$\langle F, \beta_{n} \rangle:=(\langle F_1, b_{n}\rangle,\langle F_2, b_{n} \rangle)^T.$

It follows from Appendix A of [13](also see [18]), there exists a center manifold $\mathscr{C}_0$ and we can write $W$ in the following form on $\mathscr{C}_0$ nearby $(0,0)$:

$W(t,\theta)=W(z(t),\bar{z}(t),\theta)=W_{20}(\theta)\frac{z^2}{2}+W_{11}(\theta)z\bar{z} +W_{02}(\theta)\frac{\bar{z}^2}{2}+\cdots,$

(35)

For solution $U_t\in\mathscr{C}_0$, we denote

$F(0, U_t)\mid _{\mathscr{C}_0}=\tilde{F}(0, z, \bar{z}),$

and

$\tilde{F}(0, z, \bar{z})=\tilde{F}_{20}\frac{z^2}{2}+\tilde{F}_{11}z\bar{z}+\tilde{F}_{02}\frac{\bar{z}^2}{2} +\tilde{F}_{21}\frac{z^2\bar{z}}{2}+\cdots.$

Therefore the system restricted to the center manifold is given by

$\dot{z}(t)=i\omega_0z(t)+g(z,\bar{z}),$

and denote

$g(z,\bar{z})=g_{20}\frac{z^2}{2}+g_{11}z\bar{z}+g_{02}\frac{\bar{z}^2}{2} +g_{21}\frac{z^2\bar{z}}{2}+\cdots.$

By direct calculation, we get

$\begin{align*} g_{20}=&\tau^*\bar{M}\int_0^{l\pi}b_{n_0}^3\text{d}x \Big[\bar{q}_2\left(-2\gamma-2m_1q_1\right)-2\theta q_1^2\\ &+\cfrac{2m_2q_1}{(1+u_*)^2}e^{-i\omega_{n_0}\tau^*}-\cfrac{2m_2 v_* }{(1+u_*)^3}e^{-i2\omega_{n_0}\tau^*}\Big], \\ g_{11}=&\tau^*\bar{M}\int_0^{l\pi}b_{n_0}^3\text{d}x \Big[\bar{q}_2\left(-2\gamma-m_1(q_1+\bar{q}_1)\right)-2\theta q_1\bar{q}_1\\ &+\cfrac{m_2}{(1+u_*)^2}(q_1e^{i\omega_{n_0}\tau^*}+\bar{q}_1e^{-i\omega_{n_0}\tau^*}+)-\cfrac{2m_2 v_*}{(1+u_*)^3}\Big], \end{align*}$

$\begin{split} g_{02}=&\tau^*\bar{M}\int_0^{l\pi}b_{n_0}^3\text{d}x \Big[\bar{q}_2\left(-2\gamma-2m_1\bar{q}_1\right)-2\theta\bar{q}_1^2\\ &+\cfrac{2m_2\bar{q}_1}{(1+u_*)^2}e^{i\omega_{n_0}\tau^*}-\cfrac{2m_2v_*}{(1+u_*)^3}e^{i2\omega_{n_0}\tau^*}\Big], \\ g_{21}=&\tau^*\bar{M} \left(Q_1\int_0^{l\pi}b_{n_0}^4\text{d}x+Q_2\int_0^{l\pi}b_{n_0}^2\text{d}x\right), \\ \end{split}$

where

$\begin{split} &Q_1=\cfrac{6m_2v_*}{(1+u_*)^4}e^{-i\omega_{n_0}\tau^*}-\cfrac{2m_2}{(1+u_*)^3}(2q_1+\bar{q}_1e^{-i2\omega_{n_0}\tau^*}), \\ &Q_2=\bar{q}_2\left\{-2\gamma\big[W_{20}^{(1)}(0)+2W_{11}^{(1)}(0)\big]-m_1\big[W_{20}^{(2)}(0)+2W_{11}^{(2)}(0) +\bar{q}_1W_{20}^{(1)}(0)\right.\\&\left.+2q_1W_{11}^{(1)}(0)\big] \right\} -2\theta\left[\bar{q}_1W_{20}^{(2)}(0)+2q_1W_{11}^{(2)}(0)\right] \\ &+\cfrac{m_2}{(1+u_*)^2}\left[\bar{q}_1W_{20}^{(1)}(-1)+W_{20}^{(2)}(0)e^{i\omega_{n_0}\tau^*} +2q_1W_{11}^{(1)}(-1)+2W_{11}^{(2)}(0)e^{-i\omega_{n_0}\tau^*}\right]\\ &-\cfrac{2m_2v_*}{(1+u_*)^3}\left[W_{20}^{(1)}(-1)e^{i\omega_{n_0}\tau^*}+2W_{11}^{(1)}(-1)e^{-i\omega_{n_0}\tau^*}\right]. \end{split}$

Since $g_{20}$, $g_{11}$, $g_{02}$ have no concern with $W(z(t),\bar{z}(t),\theta)$, then they can be calculated by Eq.(34). In order to get $g_{21}$, we need to compute $W_{20}$ and $W_{11}$. From (33), we have

$\begin{split} \dot{W}&=\dot{U}_t-\dot{z}qb_{n_0}-\dot{\bar{z}}\bar{q}b_{n_0} \\ &=\begin{cases} \mathcal{A}_0 W-2\text{Re}\{g(z,\bar{z})q(\theta)\}b_{n_0},& \theta\in[-r,0),\\ \mathcal{A}_0 W-2\text{Re}\{g(z,\bar{z})q(\theta)\}b_{n_0}+\tilde{F}, &\theta=0, \end{cases}\\ &\doteq \mathcal{A}_0 W + H(z,\bar{z},\theta), \end{split}$

(36)

where

$H(z,\bar{z},\theta)=H_{20}(\theta)\frac{z^2}{2}+H_{11}(\theta)z\bar{z}+H_{02}(\theta)\frac{\bar{z}^2}{2}+\cdots.$

Obviously,

$\begin{split} H_{20}(\theta)&=\begin{cases} -g_{20}q(\theta)b_{n_0}-\bar{g}_{02}\bar{q}(\theta)b_{n_0}, &\theta \in [-r,0),\\ -g_{20}q(0)b_{n_0}-\bar{g}_{02}\bar{q}(0)b_{n_0}+\tilde{F}_{20}, &\theta=0,\\ \end{cases}\\ H_{11}(\theta)&=\begin{cases} -g_{11}q(\theta)b_{n_0}-\bar{g}_{11}\bar{q}(\theta)b_{n_0}, &\theta \in [-r,0),\\ -g_{11}q(0)b_{n_0}-\bar{g}_{11}\bar{q}(0)b_{n_0}+\tilde{F}_{11}, &\theta=0,\\ \end{cases}\\ &\cdots. \end{split}$

Comparing the coefficients of (36) with the derived function of (35), we obtain

$(A_0 -2i\omega_0 I)W_{20}(\theta)=-H_{20}(\theta), A_0 W_{11}(\theta)=-H_{11}(\theta),~\cdots.$

(37)

From (29) and (37), for $\theta\in[-1,0)$, we have

$\begin{split} W_{20}(\theta)&=-\frac{g_{20}}{i\omega_{n_0}\tau^*}\begin{pmatrix} 1 \\ q_1 \end{pmatrix}e^{i\omega_{n_0}\tau^*\theta}b_{n_0}-\frac{\bar{g}_{02}}{3i\omega_{n_0}\tau^*}\begin{pmatrix} 1 \\ \bar{q}_1 \end{pmatrix}e^{-i\omega_{n_0}\tau^*\theta}b_{n_0}+E_1e^{2i\omega_{n_0}\tau^*\theta},\\ W_{11}(\theta)&=\frac{g_{11}}{i\omega_{n_0}\tau^*}\begin{pmatrix} 1 \\ q_1 \end{pmatrix}e^{i\omega_{n_0}\tau^*\theta}b_{n_0}-\frac{\bar{g}_{11}}{i\omega_{n_0}\tau^*}\begin{pmatrix} 1 \\ \bar{q}_1 \end{pmatrix}e^{-i\omega_{n_0}\tau^*\theta}b_{n_0}+E_2, \end{split}$

(38)

where $E_1$ and $E_2$ can be obtained by setting $\theta=0$ in $H$, that is

$(A_0 -2i\omega_{n_0}^+\tau^*I)E_1e^{2i\omega_{n_0}^+\tau^*\theta}\mid_{\theta=0}+\tilde{F}_{20}=0, A_0 E_2\mid_{\theta=0}+\tilde{F}_{11}=0.$

(39)

The terms $\tilde{F}_{20}$ and $\tilde{F}_{11}$ are elements in the space $\mathscr{C}$, and

$\tilde{F}_{20}=\sum\limits_{n=1}^{\infty}\langle \tilde{F}_{20}, \beta_n \rangle b_n, \tilde{F}_{11}=\sum\limits_{n=1}^{\infty}\langle \tilde{F}_{11}, \beta_n \rangle b_n.$

Denote

$E_1=\sum\limits_{n=0}^{\infty}E_1^n b_n,~~E_2=\sum\limits_{n=0}^{\infty}E_2^n b_n,$

then from (39) we have

$\begin{array}{ll} (A_0-2i\omega_{n_0}\tau^*I)E_1^n b_n e^{2i\omega_{n_0}\tau^*\theta}\mid_{\theta=0}=-\langle \tilde{F}_{20}, \beta_n \rangle b_n,\\ A_0 E_2^n b_n\mid_{\theta=0}=-\langle \tilde{F}_{11}, \beta_n \rangle b_n, \\ n=0,1,\cdots. \end{array}$

Thus, $E_1^n$ and $E_2^n$ could be calculated by

$\begin{array}{l} E_1^n=\left(2i\omega_{n_0}\tau^*I-\displaystyle{\int}_{-1}^0e^{2i\omega_{n_0}\tau^*\theta}\text{d}\eta_n(0,\theta)\right)^{-1}\langle \tilde{F}_{20}, \beta_n \rangle,\\ E_2^n=-\left(\displaystyle{\int}^0_{-1}\text{d}\eta_n(0,\theta)\right)^{-1}\langle \tilde{F}_{11}, \beta_n \rangle, \\ n=0,1,\cdots, \end{array}$

where

$\langle \tilde{F}_{20}, \beta_n \rangle=\begin{cases}\frac{1}{\sqrt{l\pi}}\hat{F}_{20}, &n_0\neq0,~n=0,\\ \frac{1}{\sqrt{2l\pi}}\hat{F}_{20}, &n_0\neq0,~n=2n_0,\\ \frac{1}{\sqrt{l\pi}}\hat{F}_{20}, &n_0=0,~n=0,\\ 0, &other,\end{cases}$

$\langle \tilde{F}_{11}, \beta_n \rangle=\begin{cases}\frac{1}{\sqrt{l\pi}}\hat{F}_{11}, &n_0\neq0,~n=0,\\ \frac{1}{\sqrt{2l\pi}}\hat{F}_{11}, &n_0\neq0,~n=2n_0,\\ \frac{1}{\sqrt{l\pi}}\hat{F}_{11}, &n_0=0,~n=0,\\ 0, &other,\end{cases}$

$\hat{F}_{20}=\left[\begin{array}{l} -2\gamma -2m_1q_1\\ -2\theta q_1^2+\cfrac{2m_2q_1}{(1+u_*)^2}e^{-i\omega_{n_0}\tau^*} -\cfrac{2m_2v_*}{(1+u_*)^3}e^{-i2\omega_{n_0}\tau^*}\end{array}\right],$

$\hat{F}_{11}=\left[\begin{array}{l} -2\gamma-m_1(q_1+\bar{q}_1)\\ -2\theta q_1\bar{q}_1+\cfrac{m_2}{(1+u_*)^2}(q_1e^{i\omega_{n_0}\tau^*}+\bar{q}_1e^{-i\omega_{n_0}\tau^*})-\cfrac{m_2v_*}{(1+u_*)^3} \end{array}\right].$

Hence, $g_{21}$ could be represented explicitly.

Denote

$\begin{split} &c_1(0)=\frac{i}{2\omega_{n_0}\tau^*}(g_{20}g_{11}-2|g_{11}|^2-\frac{1}{3}|g_{02}|^2)+\frac{1}{2}g_{21},\\ &\mu_2=-\frac{\text{Re}(c_1(0))}{\tau^*\text{Re}(\lambda'(\tau^*))},~~~ \beta_2=2\text{Re}(c_1(0)),\\ &T_2=-\frac{1}{\omega_{n_0}\tau^*}(\text{Im}(c_1(0))+\mu_2(\omega_{n_0}+\tau^*\text{Im}(\lambda'(\tau^*))). \end{split}$

(40)

Then by the general result of Hopf bifurcation theory (see [13]), we know that the parameters in (40) determine the properties of Hopf bifurcation which we can describe specifically: $\beta_2$ determines the stability of the bifurcating periodic solutions: the bifurcating periodic solutions are orbitally asymptotically stable(unstable) if $\beta_2<0(>0)$; $\mu_2$ determines the directions of the Hopf bifurcation: if $\mu_2>0(<0)$, then the direction of the Hopf bifurcation is forward (backward), that is the bifurcating periodic solutions exist when $\tau>\tau^*(<\tau^*)$; and $T_2$ determines the period of the bifurcating periodic solutions: when $T_2>0(<0)$, the period increases(decreases) as the $\tau$ varies away from $\tau^*$.

From 3.1 in Section 4, we know that $\text{Re}(\lambda'(\tau^*))>0$. Combining with above discuss, we obtain the following theorem

Theorem 4.1. If $\text{Re}(c_1(0))＜0(>0)$, then the bifurcating periodic solutions exists for $\tau>\tau^*(＜\tau^*)$ and are orbitally asymptotically stable(unstable).

---

5. Simulations

In this section, we make some simulations to support and extend our analytical results. Taking $l=2$, and choose

$\gamma=0.01 ,~~~\theta=0.05 ,~~~m_1=0.20 ,~~~m_2=0.30 ,~~~d_1=1 ,~~~d_2=0.50.$

Since $m_1=0.2＜1$, the positive equilibrium exists, through numerical calculation, we get $E_*(1.8663,4.9067)$. From a simple verification, we also obtain that $D_n-B_*＜0$ only for $n=0$. That is $\mathcal{S}=\{0\}$, and

$\omega\approx 0.2074,~~~~ \tau^*\approx 4.6242.$

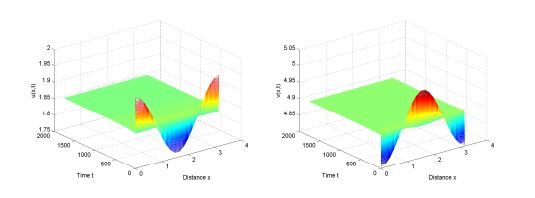
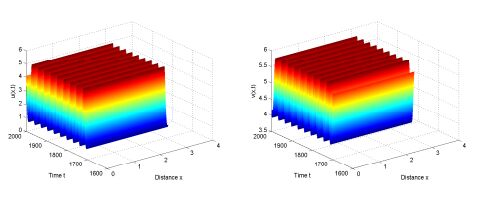
Furthermore, we have $c_1(0)\approx-0.08872+0.0200i$, that is $\beta＜0$. From Theorem 3.3 and 4.1, the positive equilibrium $E_*(1.8663,4.9067)$ is locally asymptotically stable when $\tau\in[0, \tau^*)$ (see Fig. 2), moreover, system (3) undergoes a Hopf bifurcation at $\tau=\tau^*$, the direction of the Hopf bifurcation is forward and bifurcating periodic solutions are orbitally asymptotically stable for $\tau>\tau^*$(see Fig. 3).

If we choose

$\gamma=0.01 ,~~~\theta=0.05 ,~~~m_1=2 ,~~~m_1=0.30 ,~~~d_1=1 ,~~~d_2=0.50, ~~~\tau=1.$

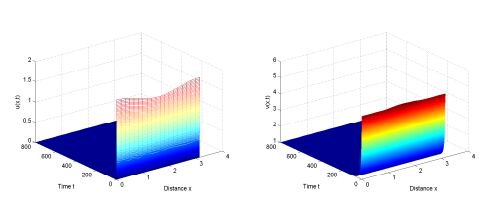
Here we chose $m_1=2>1$, then we know that the boundary equilibrium $E_1(0,1)$ is global asymptotically stable (see Fig. 4).

The initial conditions in all simulations are given by $u_0(x,t)=1.7+0.1\cos2x, ~v_0(x,t)=4.9-0.1\cos2x$, $(x,t)\in[0,2\pi]\times[-\tau,0]$.

Remark 3. Fig. 2 and Fig. 3 come into being on the precondition of $(H1)$, that is to say, when the delay $\tau$ is less than the critical value $\tau^*$, the population of predator and prey will tend to a relatively stable state (see Fig. 2); when the delay $\tau$ is a little larger than the critical value $\tau^*$, the polulation presents a periodic oscillation phenomenon near the equilibrium point(see Fig. 3). If the precondition of $(H1)$ is not satisfied, from Remark 1 and Remark 2, we know that the boundary equilibrium $E_1(0,1)$ is global asymptotically stable, the prey will go extinct at last, but the predator will increase and reach its carrying capacity(see Fig. 4).

---

Acknowledgments

The authors greatly appreciate the anonymous referees' careful reading and valuable comments. Their critical comments and helpful suggestions greatly improve the presentation of the manuscript.

---