1. Introduction

Psoriasis is a chronic, immune modulated autoimmune disease that affects the skin with localized inflammation reactions. It is one of the complicated and persistent skin disorders encountered till date. About $2-3\%$ individuals worldwide are suffering from this irritating skin disease. The common form of this disease is chronic plaque Psoriasis which occurs in nearly $90\%$ of cases [1,2]. Psoriasis is a special condition of the dermal layers where hyper-proliferation of Keratinocytes (skin cells) is chaotic due to interference's within immune cell signaling.

Basal Keratinocytes of dermis during cellular differentiation gradually migrates to the skin surface and forms the outermost layer. This process is highly synchronized by various co-stimulation factors within the immune cells. In the presence of Co-stimulation molecules cytokine secretion is more pronounced by T Cells [3,4]. Immune cell proliferation and polarization in organized pattern is controlled by the cytokine milieu. Cytokines are special messenger molecules secreted by immune cells and are associated with the cellular signal transduction, trafficking and its modulation to impose activation or suppression of immune system. Naive T Cells, after originated from bone marrow through thymus undergo a differentiation with interaction of DCs post-synapse to produce $\mbox{Th}_{1}$ and $\mbox{Th}_{2}$ subtypes [5,6] under selected cytokine milieu. It is interesting to know that the synaptic locks are short transient initially lasting from a few minutes to hours but in long run it can develop stable T-DC synapse to initiate a T Cell polarization [7]. Psoriatic hyper-proliferation of Keratinocytes is expressed by anomalous balance of immune cell activation and differentiation e.g., T Cells, Dendritic Cells, $\mbox{Th}_{1}$-Cells and $\mbox{Th}_{2}$-Cells [5,6] and its associated signal cascade elevating the Keratinocyte growth. The synaptic interactions may often produce asymmetric T Cell division and functional diversity of T Cell heterogeneity [10]. The enhancement of Keratinocytes population through different cytokine signaling by the immune cells is illustrated in Figure 1. Under $\mbox{IL}-{12}$ over crowded signaling molecules, T Cell differentiates into large amount of $\mbox{Th}_{1}$-Cells that secretes pro-inflammatory cytokines viz. $\mbox{IFN}-{\gamma}$, $\mbox{TGF}-\beta$ and $\mbox{TNF}-\alpha$ [11]. The role of $\mbox{TGF}-\beta$ differs with its target cell types. Keratinocytes has been shown to be a significant target tissue of $\mbox{TGF}-\beta$ and it differentiates by the influence of $\mbox{TGF}-\beta$ signaling [12]. Under $\mbox{IFN}-{\gamma}$ cytokine environment macrophages are activated and also stimulated to increase cellular activity [5]. Psoriasis is pronounced by $\mbox{Th}_{1}$-Cells disorder, characterized by the production of $\mbox{IFN}-{\gamma}$, $\mbox{TNF}-\alpha$ and $\mbox{TGF}-\beta$ under the effect of cytokine $\mbox{IL}-{12}$ [13]. $\mbox{TNF}-\alpha$ alone cannot elicit immunologic reaction although secreted from T Cell and APC but can raise a cytokine storm when combined with strong synergism with $\mbox{IL}-{17a}$ [14]. Recent studies suggest that if the periphery environment is $\mbox{IL}-{4}$ dominated at the time of naive T Cells activation, it results in enhancement of the density of $\mbox{Th}_{2}$-Cells. Cytokines expressed by each subset positively regulate itself and negatively regulate the other subset either in paracrine or autocrine signals [11,15]. $\mbox{IL}-{4}$ exerts pleiotropic effects on the immune system and may directly suppress $\mbox{Th}_{1}$-mediated inflammation by converting the T helper cell phenotype into $\mbox{Th}_{2}$-Cells [16,17,18]. It is reported that $\mbox{IL}-{10}$ cytokine promote the enlargement of an anti-inflammatory cytokines configuration by inhibiting the $\mbox{IFN}-{\gamma}$ production of T Cells and natural killer cells particularly via the conquest of $\mbox{IL}-{12}$ synthesis in adjunct cells [19]. Although anti-inflammatory cytokines secreted from $\mbox{Th}_{2}$-Cells negatively regulate the Keratinocytes population [20,21]. High level secretion of $\mbox{Th}_{1}$ mediated cytokines, generalized as pro-inflammatory cytokines are responsible for aggravating psoriatic lesion [6,21].

During the last few decades, widespread clinical and experimental investigations are being done for diagnosis of Psoriasis. Rapid cell cycle duration of psoriatic cell division elevates to $28$ fold ($35000$ cells/day in lieu of $1246$ cells/day) as estimated by Weinstein et al. following [22]. Baker et al. have already found that pro-inflammatory cytokine plays a significant role in this uncontrolled psoriatic cell division and also they shown that $\mbox{IFN}-{\gamma}$ is found at raised levels in psoriatic skin [23]. $\mbox{TNF}-\alpha$ has been secreted as a emergency or early psoriatic stages delivering inflammatory influence on the epidermal layers. Nockowski et al. observed that the concentrations of $\mbox{TGF}-\beta$ were significantly increased in level for patients with Psoriasis [24]. For psoriatic patients, Alefacept, Efalizumab, Etanercept, Infliximab and Adalimumab are most commonly used drugs and are active $\mbox{TNF}-\alpha$ blockers [25]. Recently, cytokine induced treatment for psoriatic patients is majorly suggested by many biological or clinical experimentalist proposing that the anti-inflammatory cytokine ($\mbox{IL}-{4}$ and $\mbox{IL}-{10}$) injecting may be a plausible treatment for Psoriasis [17,26]. $\mbox{IL}-{10}$ can be administered subcutaneously as described by Tzu et al. [27]. Clinical studies have demonstrated that $\mbox{IL}-{10}$ reduces $\mbox{Th}_{1}$-type cytokine levels and induced remission of Psoriasis [26]. Numerous studies have suggested the efficacy of recombinant human $\mbox{IL}-{10}$ ($\mbox{rhIL}-{10}$) in decreasing the Psoriasis activity and achieving long-term remissions [28,29,30,31,32]. Although a lot of experimental and clinical studies were performed yet a unified exploratory analysis to predict and intervene the Psoriasis in mathematical conjecture is highly needed.

In this direction Roy et al. have already instigated several mathematical models on Psoriasis regulation by formulating the individual cell population of T Cells, Dendritic Cells and Keratinocytes along with cytokine effect in a mechanistic approach described through a set of ordinary differential equations. They proposed the basic mathematical model on disease Psoriasis and extended the mathematical model introducing the half-saturation constant and negative feedback control approach in delay induced scheme [33]. Roy and Dutta already studied the effect of various Cytokines in the cell-biological network in this Psoriasis dynamics [34,35]. Recent theoretical works [36,37] have demonstrated how homoeostatic cell concentration, epidermal turnover time and the multilayered tissue structure are interlinked with disease pathogenesis has been observed and also a complete review using finite time stability properties of Psoriasis dynamics has been carried out. In the previous study of Psoriasis in mathematical perceptive, it was considered that only T Cells and Dendritic Cells play the crucial role. The interplay of cytokines associated with T Cells differentiation ($\mbox{Th}_{1}$ and $\mbox{Th}_{2}$) with pro-inflammatory and anti-inflammatory functionality is not mathematically well explored. In this research article, we are interested to observe the effect of $\mbox{Th}_{1}$ and $\mbox{Th}_{2}$ through their cytokines network mathematically on disease pathogenesis. Incorporating the therapeutic efficacy of the particular Biologic ($\mbox{IL}-{10}$) on $\mbox{Th}_{1}$-Cell and its anti-inflammatory impact on immunologic interactions, a mathematical model is demonstrated with the important biological connections for Psoriasis. We also study the effect of Biologic in continuous as well as impulsive mode and compared the results of the two strategies.

The article begins with a general introduction followed by our formulated mathematical model with assumptions and the basic property of the system is also discussed in Section 2. In Section 3, we have studied the model system analytically exploring the existence and stability criteria of endemic equilibria. In Section 4, we investigate the optimal control (drug) therapeutic approach and existence conditions integrating the dynamical nature of the system. Section 5, includes analysis of the explicit version of the system through impulsive therapy ($\mbox{IL}-{10}$) and the dynamical consequences with fixed impulse dosing. Section 6, represents the numerical simulation of system dynamics without and with therapy. Finally, we discuss about the results and concluding remarks which we have obtained in different sections in Section 7.

---

2. The model

---

2.1. Model formulation with suitable assumptions

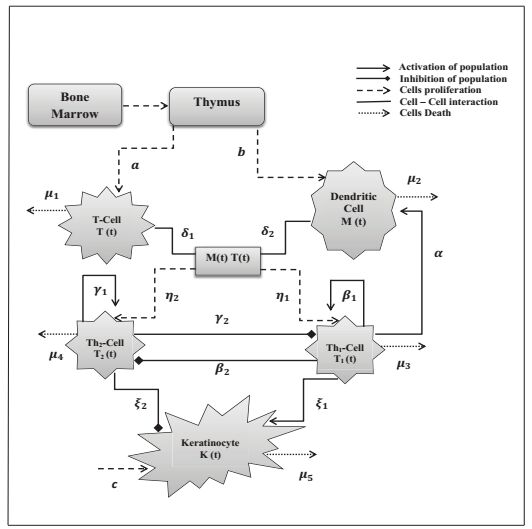
We develop a mathematical model of Psoriasis by introducing different cells to reflect the cell-biological relationships in expressing the disease. Here, $T(t)$, $M(t)$, $T_1(t)$, $T_2(t)$ and $K(t)$ represent the densities of naive T Cells, Dendritic Cells, $\mbox{Th}_{1}$-Cells, $\mbox{Th}_{2}$-Cells and epidermal Keratinocytes respectively at any time $t$. Naive T Cells and DCs strictly originated from bone marrow through thymus at a constant rate. The accumulation rate of naive T Cells and DCs in the area proximity at the suitable management are $a$ and $b$ respectively. T Cells and DCs are two different types of immune cells with dissimilar features in human immune system. Therefore, we have assumed different activation rates of T Cells and DCs for justification of our mathematical model. The rate at which T Cells trigger Dendritic Cells is denoted as $\delta_1$. On the other hand, $\delta_2$ is the rate of stimulation of Dendritic Cells with T Cells. In mathematical perceptive the interaction obey the Law of Mass Action. Under mixing homogeneity, the combined interaction of naive T Cells and DCs contributes the subtype of T Cells ($\mbox{Th}_{1}$ and $\mbox{Th}_{2}$) concentration. Rate of enhancement of the DC density is $\alpha$ due to effect of pro-inflammatory cytokines secreted by $\mbox{Th}_{1}$. The per capita removal rates of T Cells and DCs are assumed by $\mu_1$ and $\mu_2$ respectively throughout normal sequence. Based on the above considerations, growth rate of the T Cells and DCs can be demonstrated as follows :

$\begin{eqnarray} \nonumber\frac {dT}{dt}&=&a-\delta_1T M-\mu_1T,\\ \frac {dM}{dt}&=&b-\delta_2T M+\alpha T_1-\mu_2M. \end{eqnarray}$

(1)

Assumed that $\mbox{Th}_{1}$ ($T_1(t)$) and $\mbox{Th}_{2}$ ($T_2(t)$) cells are furnished due to cytokine conformational changes of naive T Cells after the interaction with Dendritic cells (DCs) at a rate $\eta_1$ and $\eta_2$ respectively. $\mbox{Th}_{1}$-Cells proliferation is motivated by itself through pro-inflammatory cytokine network a rate $\beta_1$ and also $\mbox{Th}_{1}$-Cells proliferation is inhibited by $\mbox{Th}_{2}$-Cells a rate $\beta_2$. We also consider that $\gamma_1$ is the rate of positive contribution of $\mbox{Th}_{2}$ on its own population and $\mbox{Th}_{1}$ gives negative effect on $\mbox{Th}_{2}$-Cell density at a rate $\gamma_2$. Apoptosis rate of $\mbox{Th}_{1}$ and $\mbox{Th}_{2}$ cells are noted by $\mu_3$ and $\mu_4$ respectively due to normal cell death. The equations for $\mbox{Th}_{1}$ and $\mbox{Th}_{2}$ cells :

$\begin{eqnarray} \nonumber\frac {dT_1}{dt}&=&\eta_1TM+\frac{\beta_1T_1}{1+\beta_2T_2}-\mu_3T_1,\\ \frac {dT_2}{dt}&= &\eta_2TM+\frac{\gamma_1T_2}{1+\gamma_2T_1}-\mu_4T_2. \end{eqnarray}$

(2)

Psoriasis is characterized by hyper-proliferation of Keratinocytes due to over expression of pro-inflammatory cytokines released by $\mbox{Th}_{1}$-Cells. Keratinocytes proliferation may reduced to a certain level by the effect of anti-inflammatory cytokines secreted by $\mbox{Th}_{2}$-Cells. $\xi_1$ and $\xi_2$ are denoted the cytokines effect on Keratinocytes by $\mbox{Th}_{1}$ and $\mbox{Th}_{2}$ cells respectively. Here we consider $c$ is the growth rate of Keratinocyte population due to cell migration from dermal layer to epidermal layer or protein and the removal rate of Keratinocytes is considered as $\mu_5$. The dynamics of Keratinocytes is furnished by the following equation

$\begin{eqnarray} \frac {dK}{dt}&= &c K+\frac{\xi_1T_1}{1+\xi_2T_2}-\mu_5K. \end{eqnarray}$

(3)

Assembling together the above three subsystems (1, 2, 3), we can rewrite the full mathematical model:

$\begin{eqnarray} \nonumber\frac{dT}{dt} &=&a-\delta_1T M-\mu_1T,\\ \nonumber\frac{dM}{dt} &=&b-\delta_2T M+\alpha T_1-\mu_2M,\\ \nonumber\frac{dT_1}{dt}& =&\eta_1TM+\frac{\beta_1T_1}{1+\beta_2T_2}-\mu_3T_1,\\ \nonumber\frac{dT_2}{dt}& =&\eta_2TM+\frac{\gamma_1T_2}{1+\gamma_2T_1}-\mu_4T_2,\\ \frac{dK}{dt} &=&cK+\frac{\xi_1T_1}{1+\xi_2T_2}-\mu_5K, \end{eqnarray}$

(4)

where $T(0)>0$, $M(0)>0$, $T_1(0)>0$, $T_2(0)>0$ and $K(0)>0$ are initial conditions.

---

2.2. Model properties

System (4) will be studied in a domain $\Omega \subset \mathbb{R}^5_+$, where all feasible solutions enter the region

$\Omega = \{ (T, M, T_1, T_2, K)\in \mathbb{R}^5_+: 0\leq T \leq a, 0\leq M\leq b, 0\leq T_1 \leq \frac{\eta_1ab}{\mu_3-\beta_1}, 0\leq T_2 \leq \frac{\eta_2ab}{\mu_4-\gamma_1}, 0\leq K \leq \frac{\xi_1\eta_1ab}{(\mu_3-\beta_1)(\mu_5-c)} \}.$

Considering the assumptions, we denote the accumulation of T Cells ($T(t)$) and DCs ($M(t)$) by $a$ and $b$ respectively. As the influx of T Cells and DCs are provided by blood circulation, so no residual cells exist in the concerned region and it constantly get replenished by new set of cells. Under this dynamical behaviour we assume that concentration level of two immune cells are assumed to be governed by, $T(t)\leq a$ and also $M(t)\leq b$ for any time $t$. Here, we take the one dimensional system and try to predict the maximum concentration of $\mbox{Th}_{1}$-Cells present in human body to exhibit Psoriasis,

$\begin{eqnarray} \frac{dT_1}{dt}&=&\eta_1 TM+\frac{\beta_1T_1}{1+\beta_2T_2}-\mu_3T_1. \end{eqnarray}$

(5)

The positive effect of $\mbox{Th}_{1}$-Cells on itself being very high in Psoriasis conferred by the imbalance in the $\mbox{Th}_{1}$ and $\mbox{Th}_{2}$. The suppression effect of $\mbox{Th}_{2}$-Cells is almost negligible to encounter the over population of $\mbox{Th}_{1}$-Cells. So we can infer that the effect of $\mbox{Th}_{2}$ on $\mbox{Th}_{1}$ is almost absent or masked to become exhibited. The term ($\beta_2 T_2$) is neglected from the above ODE for further calculation. Thus the system (5) is reduced to

$\frac{dT_1}{dt} = \eta_1TM+\beta_1T_1-\mu_3T_1.$

From this equation it follows that

$\begin{eqnarray} \frac{dT_1}{dt}&\leq&\eta_1ab-(\mu_3-\beta_1)T_1. \end{eqnarray}$

(6)

Solving the above inequality (6), we get

$\begin{eqnarray} T_1(t)&\leq&\frac{\eta_1ab}{\mu_3-\beta_1}+\Big(T_1(0)-\frac{\eta_1ab}{\mu_3-\beta_1}\Big)e^{-(\mu_3-\beta_1)t}.\nonumber \end{eqnarray}$

For the positive value of $(\mu_3 - \beta_1)$ and for long time, we get

$\begin{eqnarray} T_1(t)&\leq&\frac{\eta_1ab}{\mu_3-\beta_1}. \end{eqnarray}$

(7)

Similarly, we can consider the $\mbox{Th}_{2}$-Cell population from model system (4) to show that the cell concentration is also bounded. From the non-negative magnitude of $T_1(t)$ and the boundedness of the quantities $T(t)$ and $M(t)$ for the corresponding equation of the system (4), we obtain the inequality

$\begin{eqnarray} \frac {dT_2}{dt}&\leq&\eta_2ab-(\mu_4 - \gamma_1)T_2. \end{eqnarray}$

(8)

Solving the inequality (8) for the large value of $t$ we get

$\begin{eqnarray} T_2(t)&\leq&\frac{\eta_2ab}{\mu_4 - \gamma_1}. \end{eqnarray}$

(9)

We put the maximum value of $T_1(t)$ and neglecting the effect of $T_2(t)$ in the last equation of our considered model system (4) and try to predict the maximum level of Keratinocyte present in a psoriatic patient. Then, we have

$\begin{eqnarray} \frac {dK}{dt} &\leq&\frac{\xi_1\eta_1ab}{\mu_3-\beta_1}-(\mu_5-c)K. \end{eqnarray}$

(10)

After solving inequality (10) by considering large time duration and positive feature of $(\mu_5 - c)$, we get the maximum value of Keratinocytes

$\begin{eqnarray} K(t)&\leq&\frac{\xi_1\eta_1ab}{(\mu_3-\beta_1)(\mu_5-c)}. \end{eqnarray}$

(11)

From above discussion and using the inequations (7, 9, 11) we can conclude with the following theorem.

Theorem 2.1. The solutions of system (4) with initial conditions satisfy $T(t)>0, M(t)>0, T_1(t)>0, T_2(t)>0, K(t)>0$ for all $t>0$. The region $\Omega \subset \mathbb{R}^5_+$ is positively invariant and attracting with respect to system (4).

---

3. Equilibrium analysis

---

3.1. Existence condition

In this system, endemic equilibrium point $E$ is steady state solution where the excess production of Keratinocytes persist. For the existence of endemic equilibrium $E = (T^{*}, M^{*}, T_1^{*}, T_2^{*}, K^{*})$, its coordinates should satisfy the conditions; $E = (T^{*}, M^{*}, T_1^{*}, T_2^{*}, K^{*})\neq0$, where $T^{*}>0$; $M^{*}>0$; $T_1^{*}>0$; $T_2^{*}>0$; $K^{*}>0$. The endemic equilibrium point is obtained by setting equations of the system (4) to zero. Solving state variables in terms of $T^{*}$ we obtain the following

$\begin{eqnarray} M^{*}&=&\frac{p_1-p_2T^{*}}{T^{*}};\nonumber\\ T_1^{*}&=&\frac{q_1}{T^{*}}-q_2T^{*}-q_3;\nonumber\\ T_2^{*}&=&\frac{s_1T^{*}-s_2(T^{*})^2+s_3}{s_4(T^{*})^2-s_5T^{*}+s_6};\nonumber\\ K^{*}&=&\frac{(\xi_1q_1-\xi_1q_2(T^{*})^2-q_3T^{*})(s_4(T^{*})^2-T^{*}s_5+s_6)}{T^{*}(\mu_5-c)(m_1(T^{*})^2-T^{*}m_2+m_3)};\nonumber \end{eqnarray}$

where

$p_1=\frac{a}{\delta_1}$, $p_2=\frac{\mu_1}{\delta_1}$,

$q_1=\frac{\mu_2p_1}{\alpha}$, $q_2=\frac{\delta_2p_2}{\alpha}$, $q_3=\frac{b-\delta_2p_1+\mu_2p_2}{\alpha}$,

$s_1=\eta_1p_1+q_3\mu_3-\beta_1q_3$, $s_2=\beta_1q_2+\eta_1p_2-q_2\mu_3$, $s_3=\beta_1q_1-q_1\mu_3$,

$s_4=(\eta_1p_2-q_2\mu_3)\beta_2$, $s_5=(\eta_1p_1+q_3\mu_3)\beta_2$, $s_6=q_1\mu_3\beta_2$,

$m_1=s_4-\xi_2s_2$, $m_2=s_5-\xi_2s_1$, $m_3=s_6+\xi_2s_3$.

Now putting the value of $M^{*}$, $T_1^{*}$ and $T_2^{*}$ in $\eta_2T^{*}M^{*}+\frac{\gamma_1T_2^{*}}{1+\gamma_2T_1^{*}}-\mu_4T_2^{*} = 0$ we have an fifth degree polynomial of $T^{*}$ as

$f(T^{*})=(T^{*})^5+a_0(T^{*})^4+a_1(T^{*})^3+a_2(T^{*})^2+a_3T^{*}+a_4=0, \label{eq:12}$

(12)

where

$a_0=\frac{q_3d_5-d_6q_2-d_1}{q_2d_5}$, $a_1=\frac{d_2-q_1d_5+q_2d_7-q_3d_6}{q_2d_5}$, $a_2=\frac{q_3d_7-q_2d_8+q_1d_6-d_3}{q_2d_5}$,

$a_3=\frac{d_4-q_1d_7-q_3d_8}{q_2d_5}$, $a_4=\frac{q_1d_8}{q_2d_5}$

and $d_i$ ($i=1$ to $8$) are expressed as bellow,

$d_1=\eta_2p_2s_4$, $d_2=s_4\eta_2p_1+\eta_2p_2s_5-s_2\gamma_1+s_2\mu_4$,

$d_3=\eta_2p_2s_6-s_1\gamma_1+s_1\mu_4+s_5\eta_2p_1$, $d_4=\eta_2p_1s_6+s_3\gamma_1-s_3\mu_4$, $d_5=s_4\gamma_2\eta_2p_1$,

$d_6=s_5\gamma_2\eta_2p_1+s_4\gamma_2\eta_2p_1+\gamma_2\mu_4s_2$, $d_7=s_5\gamma_2\eta_2p_1+s_6\gamma_2\eta_2p_1+\gamma_2\mu_4s_1$,

$d_8=\gamma_2\eta_2p_1s_5-\gamma_2\mu_4s_3$.

Since $f(\infty)$ is always positive quantity for the polynomial $f(T^{*})$, so it has at least one root in $[0,\infty)$ if $f(0)<0$. The polynomial (12) has at least one positive root in $[0,\infty)$ if $a_4<0$. From this we can construct the following lemma.

Lemma 3.1. For the positive value of $T^{*}$, if $p_1 > p_2T^{*}$, $q_1 > q_2 (T^{*})^2+q_3 T^{*}$, $T_2^{*} > 0$ and $K^{*} > 0$ then the endemic equilibrium point exists.

---

3.2. Stability criteria

The Jacobian matrix for the endemic equilibrium of model system (4) is given by,

$J(T^{*}, M^{*}, T_1^{*}, T_2^{*}, K^{*})=\left[\begin{array}{ccccc} -\frac{a}{T^{*}}&-\delta_1T^{*}&0&0&0\\ -\delta_2M^{*}&-\frac{b+\alpha T_1^{*}}{M^{*}}&\alpha&0&0\\ \eta_1M^{*}&\eta_1T^{*}&-\frac{\eta_1T^{*}M^{*}}{T_1^{*}}&-\frac{\beta_1\beta_2T_1^{*}}{(1+\beta_2T_2^{*})^2}&0\\ \eta_2M^{*}&\eta_2T^{*}&-\frac{\gamma_1\gamma_2T_2^{*}}{(1+\gamma_2T_1^{*})^2}&-\frac{\eta_2T^{*}M^{*}}{T_2^{*}}&0\\ 0&0&\frac{\xi_1}{1+\xi_2T_2^{*}}&-\frac{\xi_1\xi_2T_1^{*}}{(1+\xi_2T_2^{*})^2}&c-\mu_5\\ \end{array}\right]$

After expanding with respect to the term $(c-\mu_5)$ we get the characteristic equation of the jacobian matrix in form,

$(\lambda+\mu_5-c)(\lambda^4+A_3\lambda^3+A_2\lambda^2+A_1\lambda+A_0)=0,\nonumber$

where

$A_0=s_{11}s_{22}s_{33}s_{44}+s_{12}s_{23}s_{31}s_{44}-s_{12}s_{23}s_{34}s_{41}+s_{21}s_{12}s_{43}s_{34}-s_{12}s_{21}s_{33}s_{44}-s_{11}s_{23}s_{32}s_{44}+s_{11}s_{23}s_{34}s_{42}-s_{11}s_{22}s_{34}s_{43}$,

$A_1=s_{11}s_{22}s_{33}+s_{44}s_{11}s_{22}+s_{11}s_{33}s_{44}+s_{22}s_{33}s_{44}+s_{23}s_{34}s_{42}+s_{12}s_{31}s_{23}-s_{12}s_{21}s_{44}-s_{21}s_{12}s_{33}-s_{23}s_{32}s_{44}-s_{22}s_{34}s_{43}-s_{11}s_{23}s_{32} -s_{11}s_{34}s_{43}$,

$A_2=s_{11}s_{22}+s_{11}s_{33}+s_{11}s_{44}+s_{22}s_{33}+s_{22}s_{44}+s_{33}s_{44}-s_{34}s_{43}-s_{23}s_{32}-s_{21}s_{12}$,

$A_3=s_{11}+s_{22}+s_{33}+s_{44}$,

and $s_{ij}$($i,j=1$ to $4$) are governed by the bellow expression,

$s_{11}=-\frac{a}{T^{*}}$, $s_{12}=-\delta_1T^{*}$, $s_{21}=-\delta_2M^{*}$, $s_{22}=-\frac{b+\alpha T_1^{*}}{M^{*}}$, $s_{23}=\alpha$,

$s_{31}=\eta_1M^{*}$, $s_{32}=\eta_1T^{*}$, $s_{33}=-\frac{\eta_1T^{*}M^{*}}{T_1^{*}}$, $s_{34}=-\frac{\beta_1\beta_2T_1^{*}}{(1+\beta_2T_2^{*})^2}$,

$s_{41}=\eta_2M^{*}$, $s_{42}=\eta_2T^{*}$, $s_{43}=-\frac{\gamma_1\gamma_2T_2^{*}}{(1+\gamma_2T_1^{*})^2}$, $s_{44}=-\frac{\eta_2T^{*}M^{*}}{T_2^{*}}$.

From the Routh-Hurwitz criteria(R-H criteria), if the three conditions viz. $A_n{>}0$ where $(n=0,1,2,3)$, $A_3A_2{>}A_1$ and $A_3A_2A_1{>}A_1^2+A_3^2A_0$ are satisfied then by the following two proposition we can describe the stability situation of our system [38,39,40]. Two proposition are established depending on $R_E$, where $R_E = \frac {c}{\mu_5}$.

Proposition 1. If $R_E < 1$ along with the R-H criteria the system will be stable at the endemic equilibrium point $E = (T^{*}, M^{*}, T_1^{*}, T_2^{*}, K^{*})$.

Proposition 2. If $R_E \geq 1$ and if R-H criteria is satisfied then $E$ is an unstable saddle point with four-dimensional stable manifold and one-dimensional unstable manifold.

---

4. Optimal control theoretic approach

Optimal control is suitable for monitoring a disease dynamics. By optimizing a particular performance, we usually solve these types of problems through finding the time dependent profiles of the control variable [41,42,43,44]. It is apparent from our preceding discussion that to control Psoriasis, it is obligatory to suppress the $\mbox{Th}_{1}$-Cells and Keratinocytes. This brings innovative results to treatment of Psoriasis and we are exploring approaches for such treatments by means of optimal control effort. We have taken our control set, defined on $[t_s,t_f]$ subject to the condition $0 \leq u(t) \leq u_{\max} < 1$, where $t_s$ and $t_f$ are starting and finishing time of treatment, respectively. Even though we do not study about the deviation or side effects of cytokine treatment i.e. $\mbox{IL}-{10}$ injecting, we can implement a state that arranges the complete effects of this period, which is programmed for any treatment [45]. We use the control effort to the $\mbox{Th}_{1}$-Cells regulation by various cytokines effect released by itself and also from $\mbox{Th}_{2}$-Cells. Hyper-proliferation of Keratinocytes due to pro-inflammatory cytokines which is totally uncontrolled by $\mbox{Th}_{2}$, is causal effect of Psoriasis. Treatment with $\mbox{IL}-{10}$ has also a significant effect on unbounded growth of Keratinocyte. Thus a same control profile is considered with the Keratinocyte proliferation term. We consider all possible Lebesgue measurable functions satisfying for almost all $t\in[t_{f},t_{s}]$ the following inequalities:

$0 \leq u(t) \leq u_{\max} < 1$

as controls that forming a control set $\mathcal{U}$, and then define on this set our objective functional for cost minimization fix it:

$\begin{eqnarray} J(u)&=&\int\limits^{t_f}_{t_s}\Bigl[K(t)+0.5B(u(t))^2\Bigr]dt, \end{eqnarray}$

(13)

The objective function (13) expresses our goal to minimize costs for $\mbox{IL}-{10}$ injecting, while minimize Keratinocytes. Where $u(t)$ is an admissible control representing the effect of $\mbox{IL}-{10}$ injecting. In the objective functional the weight constants of the Keratinocyte is considered as unity and $B \geq 0$ is weight constant for $\mbox{IL}-{10}$ injecting. The term $0.5 B(u(t))^2$ stands for the cost associated with $\mbox{IL}-{10}$ injecting in continuous way for psoriatic patient. We also assume that the cost is proportional to the square of the analogous control function [34,35,46]. Therefore, we seek an optimal control $u^{*}(t)$ such that

$\min\limits_{u(\cdot)\in\mathcal{U}}J(u) = J(u^*).$

(14)

If $u^*(t)$ is the optimal control, then the Pontryagin's Minimal Principal may functional to the reversed control approach [45,47]. One of our objectives is to simulate qualitatively the drug efficiency for $\mbox{Th}_{1}$-Cell and Keratinocyte. To represent the corresponding activity, we consider a control problem (14) together with the mathematical model described by system (4) such that:

$\begin{eqnarray} \nonumber\frac{dT}{dt} &=&a-\delta_1T M-\mu_1T,\\ \nonumber\frac{dM}{dt} &=&b-\delta_2T M+\alpha T_1-\mu_2M,\\ \nonumber\frac{dT_1}{dt}& =&\eta_1TM+(1-u)\frac{\beta_1T_1}{1+\beta_2T_2}-\mu_3T_1,\\ \nonumber\frac{dT_2}{dt}& =&\eta_2TM+\frac{\gamma_1T_2}{1+\gamma_2T_1}-\mu_4T_2,\\ \frac {dK}{dt}&=&cK+(1-u)\frac{\xi_1T_1}{1+\xi_2T_2}-\mu_5K, \end{eqnarray}$

(15)

with known initial values for $T$, $M$, $T_1$, $T_2$ and $K$ at $t_s$.

---

4.1. Existence of control problem:

In this section, to show the existence of the control problem, we study the system (15) with appropriate initial conditions. For any bounded Lebesgue measurable controls and non-negative initial conditions, it is obvious that non-negative bounded solutions to the state system exist [48]. Let us discuss about our constructed optimal control problem (15), (13). In order to obtain an optimal solution, first we discuss its existence by the following theorem.

Theorem 4.1. There exists an optimal control $u^*(\cdot) \in \mathcal{U}$ such that (14) subject to the control system (15) with the initial conditions at $t = t_s$.

Proof. Using the result demonstrated by Lukes et al., we wish to prove the existence of our optimal control [49]. The necessary condition in this minimizing problem, convexity of objective functional is satisfied. The set of the control variable $\mathcal{U}$ is also convex and closed by definition. The optimal system is bounded which governs the compactness required for the existence of the optimal control. Furthermore, the integrand in the functional $\left[K(t)+0.5{B(u(t))^2}\right]$ is convex on the control set $\mathcal{U}$. Note that the control parameter is nonnegative and the state variables are nonnegative and bounded.

$\begin{eqnarray} J(u)&\geq&0.5 B \lVert{u(\cdot)}\rVert^2_{L_2[0,T]}\nonumber \end{eqnarray}$

Where $\lVert{u(\cdot)}\rVert_{L_2[0,T]}$ is norm of function space $L_2[0,T]$, elements of which are admissible controls from the set $\mathcal{U}$. Which completes the existence of an optimal control [48,50].

---

4.2. Dynamics of the optimal system:

For optimal control system, we define the Hamiltonian,

$\begin{eqnarray} H &=& K+\frac{1}{2}{B(u)^2}+\vartheta_1[ a-\delta_1TM-\mu_1T ]+\vartheta_2[ b-\delta_2TM+\alpha T_1-\mu_2M ]\nonumber\\ &+& \vartheta_3[ \eta_1TM+(1-u)\frac{\beta_1T_1}{1+\beta_2T_2}-\mu_3T_1 ] + \vartheta_4[ \eta_2TM+\frac{\gamma_1T_2}{1+\gamma_2T_1}-\mu_4T_2 ]\nonumber\\ &+& \vartheta_5[ cK+(1-u)\frac{\xi_1T_1}{1+\xi_2T_2}-\mu_5K ]+v_1u+v_2(1-u),\nonumber \end{eqnarray}$

where $\vartheta_1$, $\vartheta_2$, $\vartheta_3$, $\vartheta_4$ and $\vartheta_5$ are adjoint variables and $v_1$, $v_2$ are penalty multipliers. Subject to the conditions, $u = 0$ when $v_1 \neq 0$ and $v_2 = 0$ and $u = u_{\max}$ when $v_1 = 0$ and $v_2 \neq 0$.

Given an optimal control and corresponding states, there exists adjoint variables $\vartheta_i~(i=1,2,...,5)$ satisfying the following equations:

$\begin{eqnarray} \frac{d\vartheta_1}{dt} &=& -\frac{\partial H}{\partial T} = \vartheta_1(\delta_1M+\mu_1)+\vartheta_2\delta_2M-\vartheta_3\eta_1M-\vartheta_4\eta_2M, \nonumber\\ \frac{d\vartheta_2}{dt} &=& -\frac{\partial H}{\partial M} = \vartheta_1\delta_1T+\vartheta_2(\delta_2T+\mu_2)-\vartheta_3\eta_1T-\vartheta_4\eta_2T, \nonumber\\ \frac{d\vartheta_3}{dt} &=& -\frac{\partial H}{\partial T_1} = -\vartheta_2\alpha+\vartheta_3\Big[ \mu_3-\frac{\beta_1(1-u)}{1+\beta_2T_2} \Big]+\vartheta_4 \frac{\gamma_1\gamma_2T_2}{(1+\gamma_2T_1)^2}-\vartheta_5\frac{\xi_1(1-u)}{1+\xi_2T_2},\nonumber\\ \frac{d\vartheta_4}{dt} &=& -\frac{\partial H}{\partial T_2} = \vartheta_3\frac{\beta_1\beta_2(1-u)T_1}{(1+\beta_2T_2)^2}+\vartheta_4\Big[ \mu_4- \frac{\gamma_1}{1+\gamma_2T_1} \Big]+\vartheta_5\frac{\xi_1\xi_2(1-u)T_1}{(1+\xi_2T_2)^2},\nonumber\\ \frac{d\vartheta_5}{dt} &=& -\frac{\partial H}{\partial K} = \vartheta_5[ \mu_5-c ]-1, \end{eqnarray}$

(16)

with transversality conditions (or boundary conditions) $\vartheta_i(t_f) = 0$, for $(i=1,...,5)$.

Again $H$ can be expressed as,

$\begin{eqnarray} H&=&\frac{1}{2}{B(u)^2}+ \vartheta_3\frac{\beta_1(1-u)T_1}{1+\beta_2T_2}+ \vartheta_5\frac{\xi_1(1-u)T_1}{1+\xi_2T_2}+v_1u+v_2(1-u)\nonumber\\ &&+\mbox{other terms without $u$}. \end{eqnarray}$

(17)

and differentiating the expression for $H$ with respect to $u$ give

$\begin{eqnarray} \frac{\partial H}{\partial u} &=& Bu-\vartheta_3\frac{\beta_1T_1}{1+\beta_2T_2}-\vartheta_5\frac{\xi_1T_1}{1+\xi_2T_2}+v_1-v_2. \end{eqnarray}$

(18)

The Hamiltonian (17) is minimized with respect to $u$ at the optimal value $u^*$, so the derivative of the $H$ with respect to $u$ furnished by the above equation (18) must be zero at $u^*$. Now, using the fact

$Bu^*-\vartheta_3\frac{\beta_1T_1}{1+\beta_2T_2}-\vartheta_5\frac{\xi_1T_1}{1+\xi_2T_2}+v_1-v_2 = 0. \label{eq:19}$

(19)

Solving the equation (19) for the optimal control, we have,

$\begin{eqnarray} u^* &=& \frac {\vartheta_3\frac{\beta_1T_1}{1+\beta_2T_2}+\vartheta_5\frac{\xi_1T_1}{1+\xi_2T_2}-v_1+v_2}{B}. \end{eqnarray}$

(20)

Now there are three cases to be observed.

Case 1. $0 < u^* < u_{\max}$, subject to the condition $v_1 = v_2 = 0$. Thus from equation (20)

$\begin{eqnarray} u^* &=& \frac {\vartheta_3\frac{\beta_1T_1}{1+\beta_2T_2}+\vartheta_5\frac{\xi_1T_1}{1+\xi_2T_2}}{B}. \end{eqnarray}$

(21)

Case 2. $u^* = 0$, subject to the condition $v_1 \neq 0$ and $v_2 = 0$. Hence from equation (20)

$\begin{eqnarray} v_1 &=& \vartheta_3\frac{\beta_1T_1}{1+\beta_2T_2}+\vartheta_5\frac{\xi_1T_1}{1+\xi_2T_2}. \end{eqnarray}$

(22)

Case 3. $u^* = u_{\max}$, subject to the condition $v_1 = 0$ and $v_2 \neq 0$. Therefore from equation (20)

$\begin{eqnarray} u_{\max} &=& \frac {\vartheta_3\frac{\beta_1T_1}{1+\beta_2T_2}-\vartheta_5\frac{\xi_1T_1}{1+\xi_2T_2}-v_2}{B}. \end{eqnarray}$

(23)

Consequently, we can conclude the optimal value of $u(t)$, i.e., $u^*(t)$ for the control $u$ from (21, 22, 23) that

$u^*= \left\{ \begin{array}{ll} 0, \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \mbox{if} \quad \frac {\vartheta_3\beta_1T_1(1+\xi_2T_2)+\vartheta_5\xi_1T_1(1+\beta_2T_2)}{B(1+\beta_2T_2)(1+\xi_2T_2)} \leq 0;&\hbox{}\\ \frac {\vartheta_3\beta_1T_1(1+\xi_2T_2)+\vartheta_5\xi_1T_1(1+\beta_2T_2)}{B(1+\beta_2T_2)(1+\xi_2T_2)}, \mbox{if} \quad 0<\frac {\vartheta_3\beta_1T_1(1+\xi_2T_2)+\vartheta_5\xi_1T_1(1+\beta_2T_2)}{B(1+\beta_2T_2)(1+\xi_2T_2)} < u_{\max};&\hbox{} \\ u_{\max}, \quad \quad \quad \quad \quad \quad \quad \quad \quad \mbox{if} \quad \frac {\vartheta_3\beta_1T_1(1+\xi_2T_2)+\vartheta_5\xi_1T_1(1+\beta_2T_2)}{B(1+\beta_2T_2)(1+\xi_2T_2)} \geq u_{\max}.&\hbox{} \end{array} \right.\nonumber$

Therefore, we have the following theorem.

Theorem 4.2. If the objective cost function $J(u)$ attains its minimum for the optimal control $u^*$, then there exist adjoint functions $\vartheta_1,\vartheta_2,\vartheta_3,\vartheta_4,\vartheta_5$ satisfying the equations (16) along with the transversality condition $\vartheta_i(t_f)=0, (i=1,...,5)$.

---

5. System with impulsive therapy

In this section, we analyse our drug induced system using modified impulsive method for better understanding of drug dynamics [51,52,53]. Here, we study the effect of impulse with fixed $\mbox{IL}-{10}$ injecting to control the Keratinocytes by reducing $\mbox{Th}_{1}$-Cells. During the period of Biologic ($\mbox{IL}-{10}$) taken through injection the cell density of $\mbox{Th}_{1}$ are made less by some proportion $r$. Here we assume that the injections are taken at different time interval and the direct effect of $\mbox{IL}-{10}$ on Keratinocytes and $\mbox{Th}_{2}$ is negligible. Now by taking the maximum concentration of $\mbox{Th}_{1}$ the one-dimensional impulsive differential equation takes the form:

$\begin{eqnarray} \frac {dT_1}{dt} &=& \eta_1ab-(\mu_3-\beta_1)T_1,~\mbox{for}~ t \neq t_k \nonumber\\ \Delta T_1 &=&-rT_1, ~\mbox{for}~ t=t_k ~\mbox{where}~k = 1, 2, 3,.....,n. \end{eqnarray}$

(24)

Here for single impulsive cycle $t_k \leq t \leq t_{k+1}$, the solution is

$\begin{eqnarray} T_1(t^-_{k+1}) &=& \frac{\eta_1ab}{\mu_3-\beta_1} \Big[1-e^{-(\mu_3-\beta_1)(t_{n+1}-t_n)}\Big]+T_1(t^+_n)e^{-(\mu_3-\beta_1)(t_{n+1}-t_n)}. \end{eqnarray}$

(25)

Where, $T_1(t^-_{k})$ is the value immediately before and $T_1(t^+_{k})$ is the value immediately after the impulse. For simplicity of notation we use $P$ instead of $\eta_1ab$ and $Q$ for ($\mu_3-\beta_1$). Now, for different successive time interval solutions become

$\begin{eqnarray} T_1(t^-_1)&=& \frac{P}{Q},\nonumber\\ T_1(t^+_1)&=&(1-r)\frac{P}{Q},\nonumber\\ T_1(t^-_2) &=& (1-r)\frac{P}{Q}e^{-Q(t_2-t_1)}+\frac{P}{Q} \Big[1-e^{-Q(t_2-t_1)}\Big],\nonumber\\ T_1(t^+_2) &=& (1-r)^2\frac{P}{Q}e^{-Q(t_2-t_1)}+(1-r)\frac{P}{Q}\Big[1-e^{-Q(t_2-t_1)}\Big],\nonumber\\ T_1(t^-_3) &=& \frac{P}{Q} \Big[(1-r)^2e^{-Q(t_3-t_1)}+(1-r)e^{-Q(t_3-t_2)}-(1-r)e^{-Q(t_3-t_1)}+ \nonumber\\ &&1-e^{-Q(t_3-t_2)}\Big],\nonumber\\ T_1(t^+_3) &=& \frac{P}{Q} \Big[(1-r)^3e^{-Q(t_3-t_1)}+(1-r)^2e^{-Q(t_3-t_2)}-(1-r)^2e^{-Q(t_3-t_1)}\nonumber\\ &&+ (1-r)-(1-r)e^{-Q(t_3-t_2)}\Big],\nonumber\\ T_1(t^-_4)&=& \frac{P}{Q} \Big[(1-r)^3e^{-Q(t_4-t_1)}+(1-r)^2e^{-Q(t_4-t_2)}+(1-r)e^{-Q(t_4-t_3)}+ \nonumber\\ &&1-(1-r)^2e^{-Q(t_4-t_1)}-(1-r)e^{-Q(t_4-t_2)}-e^{-Q(t_4-t_3)}\Big],\nonumber\\ T_1(t^+_4)&=& \frac{P}{Q} \Big[(1-r)^4e^{-Q(t_4-t_1)}+(1-r)^3e^{-Q(t_4-t_2)}+(1-r)^2e^{-Q(t_4-t_3)}+ \nonumber\\ &&(1-r)^3e^{-Q(t_4-t_1)}-(1-r)^2e^{-Q(t_4-t_2)}-(1-r)e^{-Q(t_4-t_3)}+(1-r)\Big].\nonumber\\ &&...................................................................................................\nonumber \end{eqnarray}$

The general solution becomes

$\begin{eqnarray} T_1(t^-_n) &=& \frac{P}{Q} \Big[(1-r)^{(n-1)}e^{-Q(t_n-t_1)}+(1-r)^{(n-2)}\nonumber\\ &&e^{-Q(t_n-t_2)}+{....}+(1-r)e^{-Q(t_n-t_{n-1})}+ 1-(1-r)^{(n-2)}e^{-Q(t_n-t_1)}\nonumber\\ &&-(1-r)^{(n-3)}e^{-Q(t_n-t_2)}-{....}-e^{-Q(t_n-t_{n-1})}\Big] \end{eqnarray}$

(26)

$\begin{eqnarray} T_1(t^+_n) &=& \frac{P}{Q} \Big[(1-r)^{n}e^{-Q(t_n-t_1)}+(1-r)^{(n-1)}\nonumber\\ &&e^{-Q(t_n-t_2)}+{....}+(1-r)^2e^{-Q(t_n-t_{n-1})}-(1-r)^{(n-1)}e^{-Q(t_n-t_1)}\nonumber\\ &&-(1-r)^{(n-2)}e^{-Q(t_n-t_2)}-{....}-(1-r)e^{-Q(t_n-t_{n-1})}+(1-r)\Big] \end{eqnarray}$

(27)

The above general solution (26, 27) helps to predict the maximal $\mbox{Th}_{1}$-Cells present in formation of Psoriasis just before injection process start. Note that solution does not depend on time between drug induced being fixed.

---

5.1. System under Fixed $\mbox{IL}-{10}$ injecting process

For fixed time period, i.e $\tau = t_{n+1}-t_n$ is constant, then we have

$\begin{eqnarray} T_1(t^-_n) &=& \frac{P}{Q} \Big[1+(1-r)e^{-Q\tau}+(1-r)^2e^{-2Q\tau}+{....}+(1-r)^{n-1}e^{-(n-1)Q\tau}\nonumber\\ &&-e^{-Q\tau}\Big(1+(1-r)e^{-Q\tau}+{....}+(1-r)^{n-2}e^{-(n-2)Q\tau}\Big)\Big]\nonumber\\ &=&\frac{P}{Q}\Big[\frac{1-(1-r)^ne^{-nQ\tau}}{1-(1-r)e^{-Q\tau}}-e^{-Q\tau}\frac{1-(1-r)^{n-1}e^{-(n-1)Q\tau}}{1-(1-r)e^{-Q\tau}}\Big]\nonumber\\ \lim\limits_{n\rightarrow\infty}T_1(t^-_n) &=& \frac{P}{Q}\Big[\frac{1}{1-(1-r)e^{-Q\tau}}-e^{-Q\tau}\frac{1}{1-(1-r)e^{-Q\tau}}\Big]\nonumber\\ &=&\frac{P}{Q}\Big[\frac{1-e^{-Q\tau}}{1-(1-r)e^{-Q\tau}}\Big].\nonumber \end{eqnarray}$

This is the long-term maximum value of $\mbox{Th}_{1}$-Cells. To keep this below a certain threshold $\tilde{T_1}$ of $T_1$, thus we have

$\begin{eqnarray} \tau&<&\frac{1}{Q} \ln\Big[\frac{P-(1-r)\tilde{T_1}Q}{P-\tilde{T_1}Q}\Big]\nonumber\\ \tau&< &\frac{1}{\mu_3-\beta_1} \ln\Big[\frac{\eta_1ab-(1-r)\tilde{T_1}(\mu_3-\beta_1)}{\eta_1ab-\tilde{T_1}(\mu_3-\beta_1)}\Big]\equiv{\tau}_{max}~(\mbox{say}). \end{eqnarray}$

(28)

The maximum period mentioned by the equation (28) between two consecutive $\mbox{IL}-{10}$ injection required to maintain the $\mbox{Th}_{1}$-Cell concentration below $\tilde{T_1}$. The threshold value $\tilde{T_1}$ must satisfy

$\begin{eqnarray} \tilde{T_1}&<&\frac{\eta_1ab}{\mu_3-\beta_1}. \end{eqnarray}$

(29)

It follows that, in the case of fixed $\mbox{IL}-{10}$ injecting process, we can derive a maximal gap of injection (28) which is fixed and that may keep concentration of $\mbox{Th}_{1}$ strictly below a threshold described by the equation (29). Pro-inflammatory cytokines released by $\mbox{Th}_{1}$, play a crucial role in Psoriasis pathogenesis so by controlling $\mbox{Th}_{1}$ using $\mbox{IL}-{10}$ as a therapeutic agent hyper-proliferation of Keratinocyte will be controlled.

---

6. Numerical simulations

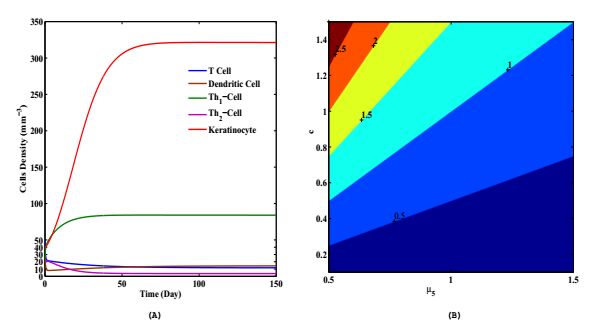
In the preceding section, we have used several analytic tools for a qualitative analysis of psoriatic case, both with and without drug induced system. In this section, we carry out the numerical simulation of our model system on the basis of analytical findings. Numerical values of the model parameters are collected from different journals represented in Table 1. To test the numerical experimentation we have used some initial values of model variables where it is obvious that the values must satisfy the initial condition of the analytical measures obtained from the study. So, applying the cardinal rule of scientific hypothesis we have chosen the initial values in a ratio dependent form as $T(0) = 50$, $M(0) = 40$, $T_1(0) = 20$, $T_2(0) = 20$, and $K(0) = 80$. Numerical simulations are done using Mathworks MATLAB (version 7.6.0). In this section, we have tried to focus dynamical cell interaction numerically towards the psoriatic expression that is considered in our model. Stability of the cells were enumerated and then further dynamical behavior of the cell components were numerically evaluated under control approach as well as impulse $\mbox{IL}-{10}$ therapy. Immune cells viz. T Cell, Dendritic Cell, $\mbox{Th}_{1}$-Cell, $\mbox{Th}_{2}$-Cell and Keratinocytes are plotted with respect to time to investigate the qualitative behavior of considered cells between $150$ days in Figure 2(A). From this figure it is evident that due to interaction between T Cell and Dendritic Cell both population will be decreased initially but due to the pro-inflammatory cytokines secreted from $\mbox{Th}_{1}$-Cells, DC population regains growth function. Both T-Cell and DC densities reached to a stable condition after $100$ days approximately. For cross and self-regulatory cytokine effect which have already discussed in introduction section, $\mbox{Th}_{1}$ is up-regulated and $\mbox{Th}_{2}$ is subjected to suppressed condition. After initial $50$ days both the population will be stable. For the cytokines viz. $\mbox{IFN}-{\gamma}$ and $\mbox{TGF}-\beta$ secreted by $\mbox{Th}_{1}$, Keratinocyte population is increased but the rate become slow due to cytokines ($\mbox{IL}-{10}$, $\mbox{IL}-{4}$ etc.) released from $\mbox{Th}_{2}$. Eventually, Keratinocyte population will be stable between $60-90$ days.

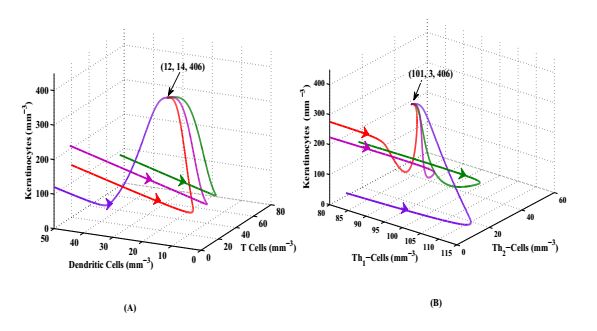
Figure 2(B) gives the graph of $R_E$ as a function of $c$ (growth of Keratinocyte due to cell migration and protein) and $\mu_5$ (death of Keratinocyte due to normal sequence). The figure illustrates that the change of the parameter $R_E$ as $c$ and $\mu_5$ vary. We observe that when the ratio of accumulation rate of Keratinocyte obtained from other growth factor (protein, cell migration etc.) and its natural death rate becomes less than unity, our system will be locally asymptotically stable indicated by dark blue region. It becomes unstable when the ratio will be greater than unity located in the figure in all parts other than the blue region. Analytically, we obtain the stability condition of all population i.e. $R_E < 1$, where $R_E = \frac {c}{\mu_5}$ and here we also emphasis the stability criteria through numerical studies. From this figure it is also clear that if the value of $c$ below a certain level (approximate $c \leq 0.75$) the system is always stable even if higher level of $\mu_5$. For other values of the parameters, however, $R_E$ is relatively stable with respect to variations.

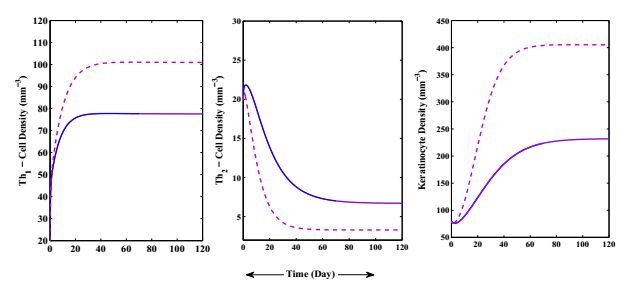
In Figures 3(A) and 3(B), we consider two different set of population to show our considered system ultimately reaches a stable state. Figures 3(A) indicates, for different initial values Keratinocyte, DC and T cell ultimately converge to the point ($12, 14,406$). Similarly, in 3(B) $\mbox{Th}_{1}$ and $\mbox{Th}_{2}$ cell also converges along with Keratinocyte at point ($101, 3,406$). As it is very stringent to evaluate the endemic equilibrium analytically, so Figures 3 enables us to deduce the unique endemic equilibrium numerically.

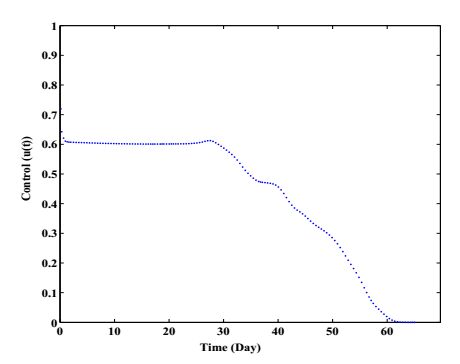
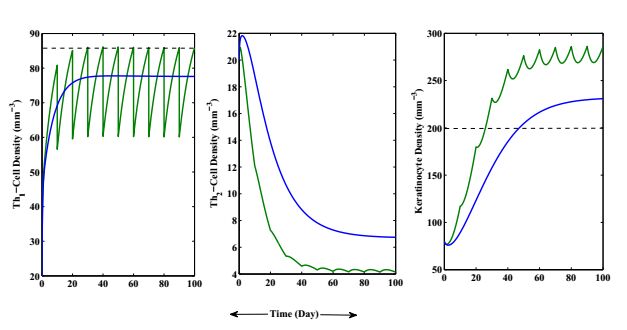
The variations of $\mbox{Th}_{1}$, $\mbox{Th}_{2}$ and Keratinocytes population with respect to time $t$ for without and with control approach are shown in Figure 4 where other parameters are fixed as in Table 1. The solid lines indicate the cells behavior when disease is under control with continuous dosing. Here, dotted line indicates the uncontrolled growth of cell density which is highly relevant with psoriatic plaque. After applying control input on $\mbox{Th}_{1}$ and Keratinocyte population we get a substantial impact on disease dynamics. $\mbox{Th}_{2}$ density will be increased to a noticeable state after applying control Biologic therapy which is also illustrated in Figure 4. It can be concluded from this figure that with proper inputs of control parameters $u(t)$, it yields more trustworthy results in decreasing the Keratinocyte and $\mbox{Th}_{1}$ population as well as increasing the $\mbox{Th}_{2}$ level. This reflects that people affected with Psoriasis need to take Biologic ($\mbox{IL}-{10}$) continuously through injecting process for $65-70$ days to control the disease.

In Figure 5, drug dose is described with respect to time. Very high drug dose is applied to control the high impact of pro-inflammatory cytokine effect at the initial stage of therapy. Subsequently, the dose is decreased in very low amount at the time interval $2-28$ days to maintain the $\mbox{Th}_{1}$ and $\mbox{Th}_{2}$ level. After $28$ days the dosing amount will be decreased and finally after $65-70$ days no drug will required. The change in slope of the curve indicate that the effect of $\mbox{IL}-{10}$ on disease dynamics is not always identical due to cross regulation between pro and anti-inflammatory cytokines.

Figure 6 depicts the comparative regulation of Keratinocyte and immune cells to achieve the termination of psoriatic lesions through continuous dosing (optimal drug dose) and impulsive dosing (drug efficacy $r = 0.3$, dosing interval $\tau = 10$ days)of biologic. From our analytical study we derived the upper threshold of $\mbox{Th}_{1}$ expressed by the equation (29), required to maintain normal Keratinocyte density as $84~\mbox{mm}^{-3}$. The natural growth of Keratinocyte is estimated $195 - 200~\mbox{mm}^{-3}$ compare with the ratio of the other cells taken in our model [22,61]. It is evident from this figure, for impulse dosing the $\mbox{Th}_{1}$ density is just below the threshold value and oscillating with fixed amplitude while in continuous mode the $\mbox{Th}_{1}$-Cells maintain a steady density much below the threshold boundary and maintaining a better regulation for longer periods. The impulse dosing has suppressed $\mbox{Th}_{1}$-Cell density to a magnitude of $84~\mbox{mm}^{-3}$ whereas the continuous dosing has suppressed the same cell to a density around $78~\mbox{mm}^{-3}$. We get a fruitful result for $\mbox{Th}_{2}$ density while applying the biologic in optimal dose. For continuous dosing the $\mbox{Th}_{2}$ cells reaches the cell density around $7~\mbox{mm}^{-3}$ and for impulsive dosing it is around $4~\mbox{mm}^{-3}$ keeping the other parameters constant. In the last panel, we observe that the Keratinocyte cells experience a reduction in density by the continuous and impulse therapy. It is to be noted that although the Keratinocyte population is more suppressed using $\mbox{IL}-{10}$ in continuous mode but it is still remains above the threshold for both the cases. Though Figure 6 illustrates that the optimal drug dose in continuous way is more effective compare with impulse therapy but there are some biological restrictions for such continued dosing as evident from clinical literatures [29,62]. in the case, we wise to improve the impulse dosing to achieve our goal.

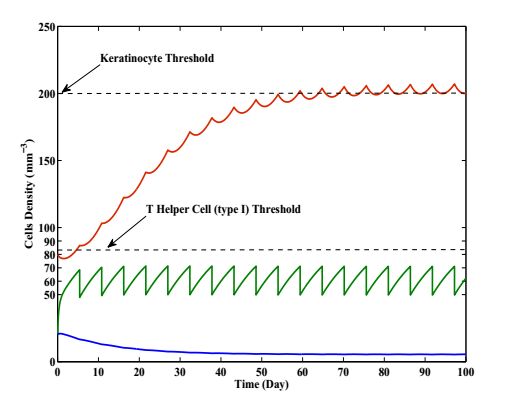
In order to find the safe and perfect dose of $\mbox{IL}-{10}$ injecting through impulse way we exhibit the Figures 7. The time gap between two consecutive $\mbox{IL}-{10}$ injecting will be $\tau$ which is less than or equal to $\tau_{max}$ i.e $\tau < \tau_{max}$. From the Table 1 putting values of parameter in the expression $\tau_{max}$ we get $\tau_{max}= 25~\mbox{days}~2~\mbox{hours}$, therefore $\tau < 25$ days $2$ hours. Here we consider the drug efficacy $r = 0.3$ depending upon our assumption the decay rate of $\mbox{Th}_{1}$-Cells due to $\mbox{IL}-{10}$ injecting process is fixed and dosing interval $5.4$ days. It is noticeable from this figure the $\mbox{Th}_{1}$ density oscillates with fixed amplitude between $70 - 50 \mbox{mm}^{-3}$ which is lower than its threshold and the $\mbox{Th}_{2}$ density increased to around $6~\mbox{mm}^{-3}$. In this figure we get a sufficient change in behavior of Keratinocyte population which is suppressed to its normal density ($195 - 200~\mbox{mm}^{-3}$) and also oscillates. The magnitude of oscillation of Keratinocyte become fixed after $55~\mbox{days}$. From this figure we can conclude that the impulse dose of Biologic (drug efficacy $r = 0.3$, dosing interval $5.4$ days) is more appreciable for psoriatic patients.

---

7. Discussion and conclusion

In this paper, we have studied the role of pro-inflammatory and anti-inflammatory cytokines for psoriatic patient by considering a mathematical model. In our analytical study, we have verified the existence condition and also we established the stability criterion of endemic equilibrium depending on Routh-Hurwitz criteria and the condition $R_E$ is greater or less than unity. Restriction on $R_E$ suggests, Keratinocyte will prevail with restrained growth function only when the growth rate of the Keratinocyte originating from dermal cell migration and protein is below the natural mortality rate of the Keratinocytes. It is found that after $70$ days of continuous therapeutic intervention, the disease reaches normal state as observed through numerical analysis. We have analytically determined the threshold for $\mbox{Th}_{1}$-Cell and we also get the theoretical value of normal Keratinocyte proliferation rate from various clinical studies. We have compared the balance of the cell population through numerical experimentations and observed that on accounting the value of $\tau = 10$ and $\tau = 5.4$ days respectively the $\mbox{Th}_{1}$-Cell populations assumes normalcy with the drug efficacy parameter (r) being fixed at $0.3$. We conclude that, when Biologic ($\mbox{IL}-{10}$) is applied in an impulsive fashion, we obtained $\tau = 5.4$ days the exact dose interval which is less than to $\tau_{max} = 25$ days $2$ hours. Our numerical outcomes associated with analytical results which allow more precise prediction of model system connecting to impulsive dose and optimal control to avoid the psoriatic lesion. Our study reveals that control of $\mbox{Th}_{1}$-Cells through an impulse based optimization reduces the hyper-proliferation of Keratinocytes induced by Biologic ($\mbox{IL}-{10}$) application is much safer and better treatment than continuous treatment with Biologic.

---