Persistence and stability in an SVIR epidemic model with relapse on timescales

1.   Introduction

In many mathematical models, it is required to finding the solutions of a stationary problem, which can be formulated as an equation

where $F$ is a nonlinear smooth mapping defined on $(\lambda, u)\in \mathbb{R}\times X$ and mapped to $Y$, $\lambda$ is a parameter, and $X, Y$ are Banach spaces. Often the system Eq (1.1) has a trivial state $u = u_0$ for all parameter values $\lambda$, and it may have other nontrivial solutions near $(\lambda_0, u_0)$ for some $\lambda_0$. Such $\lambda_0$ is called a bifurcation point for Eq (1.1), and the bifurcating nontrivial solutions near a bifurcation point are often with significance for the models as they represent states breaking from the symmetric or uniform ones.

If the Fréchet derivative $F_u(\lambda_0, u_0)$ of $F$ at $(\lambda_0, u_0)$ is invertible, then $(\lambda_0, u_0)$ is not a bifurcation point from the Implicit Function Theorem ^[1,2,3]. Hence a necessary condition for the bifurcation to occur is that $F_u(\lambda_0, u_0)$ is not invertible. The most useful bifurcation occurs when that $0$ is a simple eigenvalue of the linearized operator $F_u(\lambda_0, u_0)$, that is

${\bf(F1)}$ $\dim N(F_u(\lambda_0, u_0)) = {\rm{codim}} R(F_u(\lambda_0, u_0)) = 1$, and $N(F_u(\lambda_0, u_0)) = {\rm{span}}\{w_0\}$,

where $N(F_u)$ and $R(F_u)$ are the null space and the range of linear operator $F_u$. Crandall and Rabinowitz ^[2] prove the following celebrated "bifurcation from a simple eigenvalue" theorem (see [2,Theorem 1.7]). Here is an expanded version of the theorem for our purpose:

Theorem 1.1. Let $U$ be a neighborhood of $(\lambda_0, u_0)$ in $\mathbb{R} \times X$, and let $F:U\to Y$ be a twice continuously differentiable mapping. Assume that $F(\lambda, u_0) = 0$ for $(\lambda, u_0) \in U$. At $(\lambda_0, u_0)$, $F$ satisfies (F1) and ${\bf (F3)}$ $F_{ \lambda u}(\lambda_0, u_0)[w_0] \not\in R(F_u(\lambda_0, u_0)).$

Let $Z$ be any complement of ${\rm{span}}\{w_0\}$ in $X$. Thenthe solution set of (1.1) near $(\lambda_0, u_0)$ consistsprecisely of the curves $\Gamma_0 = \{(\lambda, u_0)\}$ and $\Gamma_1 = \{(\lambda(s), u(s)):s \in|s| < \delta \}$, where $\lambda: I \to \mathbb{R}$, $z: I\to Z$are $C^1$ functionssuch that $u(s) = u_0+sw_0+sz(s)$, $\lambda(0) = \lambda_0$, $z(0) = 0$, and

where $l\in Y^*$satisfying $N(l) = R(F_{u}(\lambda_0, u_0))$. If $F$ also satisfies

${\bf (F4)}$ $F_{uu}(\lambda_0, u_0)[w_0]^2\not\in R(F_u(\lambda_0, u_0))$,

then we have $\lambda'(0)\not = 0$, and it is called a transcritical bifurcation; If $F$ satisfies

${\bf (F4 ^\prime)}$ $F_{uu}(\lambda_0, u_0)[w_0]^2\in R(F_u(\lambda_0, u_0))$,

and in addition $F\in C^3$, then $\lambda'(0) = 0$ and

where $\theta_1$ satisfies

If $\lambda'(0) = 0$ and $\lambda''(0)\ne 0$, then it is called a pitchfork bifurcation.

Note that the classification of transcritical and pitchfork bifurcations using (F4) and (F4$^\prime$) was first used in reference ^[4], although this has been widely used in finite dimensional dynamical systems ^[5].

The transversality condition (F3) holds in most practical situations, but there are also important exceptional cases for which (F3) fail. In reference ^[6], we considered a degenerate bifurcation scenario in which (F3) is not satisfied. In this case, we prove that, under some higher order transversality conditions on $F$, the local solution set of Eq (1.1) near the bifurcation point $(\lambda_0, u_0)$ consists of the line of trivial solutions, and two other solution curves. First we recall a degenerate version of Theorem 1.1, which can be used to obtain more than two intersecting solution curves near the bifurcation point.

Theorem 1.2. ([6,Theorem 2.3]) Let $U$ be a neighborhood of $(\lambda_0, u_0)$ in $\mathbb{R} \times X$, and let $F\in C^3(U, Y)$.Assume that $F(\lambda, u_0) = 0$ for $(\lambda, u_0) \in U$ and at$(\lambda_0, u_0)$, $F$ satisfies (F1), (F4$^\prime$), and

${\bf (F3')}$ $F_{ \lambda u}(\lambda_0, u_0)[w_0] \in R(F_u(\lambda_0, u_0))$.

Let $X = N(F_u(\lambda_0, u_0))\oplus Z$ be a fixed splitting of $X$, and let $l\in Y^*$ such that $R(F_u(\lambda_0, u_0)) = \{v\in Y: \langle l, v\rangle = 0\}$.Denote by $\theta_2\in Z$ the unique solution of

and recall $\theta_1$ to be the unique solution of Eq (1.4). We assume that the matrix (all derivatives areevaluated at $(\lambda_0, u_0)$)

is non-degenerate, i.e., $\det(H)\ne 0$, where $H_{ij}$ is given by

1) If $H$ is definite, i.e., $\det(H) > 0$, then the solution set of Eq (1.1) near $(\lambda, u) = (\lambda_0, u_0)$ is the line $\Gamma_0 = \{(\lambda, u_0)\}$.

2) If $H$ is indefinite, i.e., $\det(H) < 0$, then the solution set of Eq (1.1) near $(\lambda, u) = (\lambda_0, u_0)$ is the union of $C^1$curves intersecting at $(\lambda_0, u_0)$, including the line of trivial solutions $\Gamma_0 = \{(\lambda, u_0)\}$and two other curves $\Gamma_i = \{(\lambda_i(s), u_i(s)):|s| < \delta\}$ ($i = 1, 2$) for some$\delta > 0$, with

where $(\mu_1, \eta_1)$ and $(\mu_2, \eta_2)$ are non-zerolinear independent solutions of the equation

$\alpha_i(0) = \alpha_i'(0) = 0$, $\beta_i(s)\in Z$, and$\beta_i(0) = \beta_i'(0) = 0$, $i = 1, 2$.

In this paper, we prove another bifurcation result when the transversality condition (F3) fails. In this case, under the complement (F3$^\prime$) of (F3), and as well as (F4), we show that the solution set of Eq (1.1) near the bifurcation point $(\lambda_0, u_0)$ consists of the line of trivial solution, and another curve of nontrivial solutions which is tangent to the line of trivial ones.

Theorem 1.3. Let $U$ be a neighborhood of $(\lambda_0, u_0)$ in $\mathbb{R} \times X$, and let $F\in C^2(U, Y)$. Assume that $F(\lambda, u_0) = 0$ for any $\lambda \in \mathbb{R}$. At$(\lambda_0, u_0)$, $F$ satisfies (F1), (F3$^\prime$) and (F4).Then the solution set of Eq (1.1) near $(\lambda, u) = (\lambda_0, u_0)$ is the union of two $C^2$ curves which are tangent to each other at $(\lambda_0, u_0)$, including the line of trivial solutions $\Gamma_0 = \{(\lambda, u_0)\}$ and $\Gamma_1 = \{(\lambda, u(\lambda)): \lambda\in I\}$ for some $\delta > 0$, where $I = (\lambda_0-\delta, \lambda_0+\delta)$, $u(\lambda) = u_0+t(\lambda)w_0+g(\lambda, t(\lambda))$, $t:I\to V$ and $g: I\times V\to Z$ are continuously differentiable functions, $t(\lambda_0) = t'(\lambda_0) = 0$, and $g(\lambda, 0) = g_{ \lambda}(\lambda_0, 0) = g_{t}(\lambda_0, 0) = 0$, where $V\subset \mathbb{R}$ is a neighborhood of $t = 0$. Moreover if $F\in C^4(U, Y)$, then $t(\lambda)$ is $C^3$ and

where $\theta_2$ is defined by Eq (1.5).

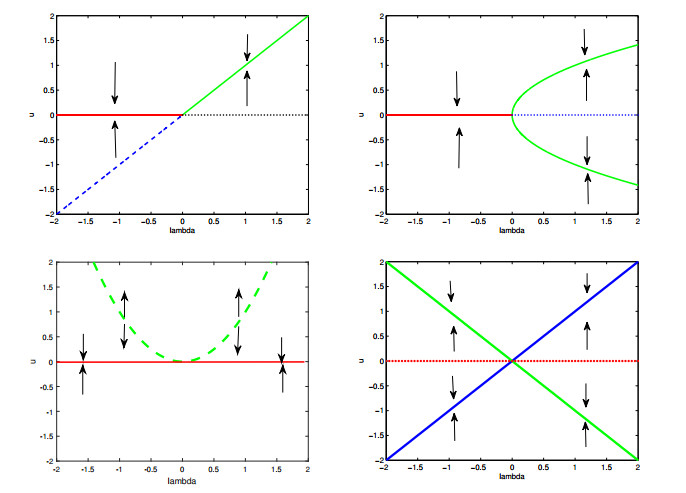
If $F$ satisfies $F_{ \lambda \lambda u}(\lambda_0, u_0)[w_0]+3F_{ \lambda u}(\lambda_0, u_0)[\theta_2]\not\in R(F_u(\lambda_0, u_0)$, then the solution set of Eq (1.1) near $(\lambda_0, u_0)$ in Theorem 1.3 is the union of a line and a parabola-like curve which is tangent to the line. The simplest example for Theorem 1.3 is the function $f: \mathbb{R}^2\to \mathbb{R}$ defined by $f(\lambda, u) = u(u- \lambda^2)$, and its solution set of $f(\lambda, u) = 0$ near $(\lambda, u) = (0, 0)$ is the union of the line $u = 0$ and the curve of nontrivial solutions $u = \lambda^2$ which are tangent to each other at $(0, 0)$ (see the lower left panel of Figure 1).

Theorem 1.1, Theorem 1.2 and Theorem 1.3 together provide a complete classification of bifurcation scenarios for Eq (1.1) under the conditions (F3) or (F3$^\prime$), and (F4) or (F4$^\prime$), while $F(\lambda, u_0)\equiv 0$ and (F1) are assumed:

$(a)$ Transcritical: (F3) and (F4), a crossing curve of nontrivial solutions (Theorem 1.1);

$(b)$ Pitchfork: (F3) and (F4$^\prime$), a crossing curve of nontrivial solutions bending leftward or rightward (Theorem 1.1);

$(c)$ Tangential: (F3$^\prime$) and (F4), a tangential curve of nontrivial solutions bending upward or downward (Theorem 1.3); and

$(d)$ Double transcritical: (F3$^\prime$) and (F4$^\prime$), two crossing curves of nontrivial solutions (Theorem 1.2).

Because of the condition (F3$^\prime$), the tangential and the double transcritical bifurcations are called degenerate ones. Figure 1 shows examples of each types of bifurcations using simple mappings $F_i: \mathbb{R}\times \mathbb{R}\to \mathbb{R}$, and these mappings can be regarded as normal forms of these bifurcations.

Another bifurcation result with solution set being two tangential curves was proved in reference ^[7] but it is under the assumption that the kernel $N(F_u(\lambda_0, u_0))$ is of two-dimensional and it is of saddle-node bifurcation type. It is applied to a nonlinear Schrödinger system with quadratic nonlinearity ^[8], where one of the two tangential curves is indeed vertical in a form $\{(\lambda_0, k\varphi_1): k\in \mathbb{R}\}$. Here one of the two tangential curves is horizontal in a form $\{(\lambda, u_0): \lambda\in \mathbb{R}\}$.

We also remark that transversality conditions like (F3) or (F4) are not needed for global bifurcation theorems concerning the topological structure of the solution continuum. Indeed in the celebrated Rabinowitz global bifurcation theorem ^[9] (see also extensions in ^[10,11]), only the odd algebraic multiplicity was assumed, thus all four scenarios shown in Figure 1 can occur as local pictures for the global bifurcation diagrams in reference ^[9,10,11].

We prove Theorem 1.3 in Section 2, and we consider the stability of the bifurcating solutions obtained in Theorem 1.3 in Section 3. Finally in Section 4 we show some examples to apply Theorem 1.3. Throughout the paper, we use the same labeling of conditions such as (F1) and ${\bf (F2)}$ on $F$ as in our previous work ^[4,6,12], and we use the convention that (Fi$^{\prime}$) stands for the negation of (Fi) for i$\in \mathbb{N}$. We use $||\cdot||$ as the norm of Banach space $X$, $\langle \cdot, \cdot\rangle$ as the duality pair of a Banach space $X$ and its dual space $X^*$. For a linear operator $L$, we use $N(L)$ as the null space of $L$ and $R(L)$ as the range space of $L$, and we use $L[w]$ to denote the image of $w$ under the linear mapping $L$. For a multilinear operator $L$, we use $L[w_1, w_2, \cdots, w_k]$ to denote the image of $(w_1, w_2, \cdots, w_k)$ under $L$, and when $w_1 = w_2 = \cdots = w_k$, we use $L[w_1]^k$ instead of $L[w_1, w_1, \cdots, w_1]$. For a nonlinear operator $F$, we use $F_u$ as the partial derivative of $F$ with respect to argument $u$.

2.   Proof of Theorem 1.3

First we recall an important lemma from our previous work ^[12]. First is the well-known Lyapunov-Schmidt reduction under the condition (F1) which is standard from many textbooks in nonlinear analysis (see for example ^[1,3,13]).

Lemma 2.1. Supposethat $F:\mathbb{R} \times X\to Y$ is a $C^p$ ($p\ge 1$) mapping such that $F(\lambda_0, u_0) = 0$, and $F$ satisfies (F1) at $(\lambda_0, u_0)$. Thenthe equation $F(\lambda, u) = 0$ for $(\lambda, u)$ near $(\lambda_0, u_0)$ can be reduced to

where $t\in (-\delta, \delta)$, $\lambda\in (\lambda_0-\delta, \lambda_0+\delta)$ where $\delta$ is a small constant, $l\in Y^*$ such that $\langle l, v\rangle = 0$ if and only if $v\in R(F_u(\lambda_0, u_0))$, and $g$ is a $C^p$ function into $Z$ such that $g(\lambda_0, 0) = 0$ and $Z$ is acomplement of $N(F_u(\lambda_0, u_0))$ in $X$.

Proof of Theorem 1.3. We denote the projection from $Y$ into $R(F_u(\lambda_0, u_0))$ by $Q$. Applying Lemma 2.1 to $F$ in Theorem 1.3 at $(\lambda_0, u_0)$, we have that the function $g(\lambda, t)$ in Lemma 2.1 is obtained from (see ^[12]),

Since $u_0$ is a trivial solution for all $\lambda$ near $\lambda_0$, that is, $F(\lambda, u_0)\equiv 0$, then by Lemma 2.1 we have $g(\lambda, 0)\equiv 0$, hence $g_{ \lambda}(\lambda_0, 0) = g_{ \lambda \lambda}(\lambda_0, 0) = 0$. Differentiating $f_1$ and evaluating at $(\lambda, t) = (\lambda_0, 0)$, we obtain

Since $F_u [w_0] = 0$ and $g_t\in Z$, and $F_u(\lambda_0, c_0u_*)|_Z$ is an isomorphism, then $g_t(\lambda_0, 0) = 0$.

Next we calculate the second derivatives of $f_1$:

thus $g_{ \lambda t}(\lambda_0, 0) = \theta_2$ from (F3'), where $\theta_2$ is defined as in Eq (1.5). We define the bifurcation function

From the assumptions, $f$ is $C^2$ in $U$ and $f(\lambda, 0) = 0$. Next we apply the Implicit Function Theorem to the equation $h(\lambda, t) = 0$ where the function $h(\lambda, t)$ is defined by

Then $h(\lambda, 0) = 0$ from the assumption that $F(\lambda, u_0) = 0$, and from (F4), we have

By the Implicit Function Theorem, there exists a unique continuously differentiable function $t = t(\lambda)\in \mathbb{R}$ satisfying $h(\lambda, t(\lambda)) = 0$ and $t(\lambda_0) = 0$, and

Now we assume that $F\in C^4(U, Y)$. Let $u(\lambda) = u_0+t(\lambda)w_0+g(\lambda, t(\lambda))$. Then we have

Differentiating Eq (2.6) with respect to $\lambda$ twice and evaluating at $\lambda = \lambda_0$, we obtain that

Here all partial derivatives are evaluated as $\lambda = \lambda_0$. By applying $l\in Y^*$ to Eq (2.7), we have $t'(\lambda_0) = 0$ from (F3$^\prime$) and (F4), and we also have $u_{ \lambda} = 0$ and $u_{ \lambda \lambda} = t''(\lambda_0)w_0$. Differentiating Eq (2.6) with respect to $\lambda$ three times and evaluating at $\lambda = \lambda_0$, we obtain that

which implies that $u_{ \lambda \lambda \lambda} = 3t''(\lambda_0)\theta_2$. Finally differentiating Eq (2.6) with respect to $\lambda$ four times and evaluating at $\lambda = \lambda_0$, we obtain that

By applying $l\in Y^*$ to Eq (2.9), we can obtain Eq (1.11).

3.   Stability

In this section, we consider the stability of the bifurcating solutions obtained in Theorem 1.3. First similar to [14,Corollary 1.13], we have the

Proposition 3.1. Let $X$, $Y$, $U$, $F$, $Z$, $\lambda_0$, $w_0$, $\theta_2$ be the same as in Theorem 1.3, and let all assumptions in Theorem 1.3 on $F$ be satisfied.In addition we assume that $X\subset Y$, and the inclusion mapping $i:X\to Y$ is continuous. Let $\Gamma_1 = \{(\lambda, u(\lambda)):| \lambda- \lambda_0| < \delta\}$ be the solution curve in Theorem 1.3.Then there exist $\varepsilon > 0$, $C^2$ functions $\gamma: (\lambda_0- \varepsilon, \lambda_0+ \varepsilon)\to \mathbb{R}$, $\mu:(\lambda_0- \varepsilon, \lambda_0+ \varepsilon)\to \mathbb{R}$, $v:(\lambda_0- \varepsilon, \lambda_0+ \varepsilon)\to X$ and $\omega:(\lambda_0- \varepsilon, \lambda_0+ \varepsilon)\to X$ such that

where $\gamma(\lambda_0) = \mu(\lambda_0) = 0$, $v(\lambda_0) = \omega(\lambda_0) = w_0$, $v(\lambda)-w_0\in Z$ and $\omega(\lambda)-w_0\in Z$.

We have the following result on the stabilities of the bifurcating solution $(\lambda, u(\lambda))$ obtained in Theorem 1.3.

Proposition 3.2. Let the assumptions of Proposition 3.1 hold, and let $\gamma(\lambda)$ and $\mu(\lambda)$ be the functions defined in Proposition 3.1.In addition, we assume that

Then$\gamma'(\lambda_0) = \mu'(\lambda_0) = 0$ and

Proof. We differentiate Eq (3.1) to obtain

Setting $\lambda = \lambda_0$ and applying $l$ to the equation, we get $\gamma'(\lambda_0) = 0$ and $v'(\lambda_0) = \theta_2$ by (F3$^\prime$). Differentiating Eq (3.6) again, we have

Setting $\lambda = \lambda_0$, we get

Thus by applying $l$ to Eq (3.8), we obtain Eq (3.4).

On the other hand, we differentiate Eq (3.2) to obtain

Setting $\lambda = \lambda_0$, we have

we get $\mu'(\lambda_0) = 0$ and $\omega'(\lambda_0) = \theta_2$. We differentiate Eq (3.9) again and set $\lambda = \lambda_0$, and we have

by $u'(\lambda_0) = 0$ and $u''(\lambda_0) = t''(\lambda_0)w_0$. Thus by applying $l$ to Eq (3.11) and using Eq (1.11), we obtain Eq (3.5).

Proposition 3.2 implies that the trivial solution $u = u_0$ on $\Gamma_0$ and the non-trivial solution $u(\lambda)$ on $\Gamma_1$ in Theorem 1.3 both have the same stability before and after the bifurcation point. Thus there is no exchange of stability occurring in the tangential bifurcation described in Theorem 1.3. Furthermore, the stability of the trivial solution $u_0$ on $\Gamma_0$ and the one of the non-trivial solution $u(\lambda)$ on $\Gamma_1$ in Theorem 1.3 are always opposite: while one is stable, the other is unstable, or vice versa, if $\gamma(\lambda_0) = \mu(\lambda_0) = 0$ is the principal eigenvalue of $F_u(\lambda_0, u_0)$.

4.   Examples

We show that the tangential bifurcations described in Theorem 1.3 occurs for the following semilinear elliptic equations.

Example 4.1.

where $\lambda$ is a positive parameter, $\Omega$ is a bounded region with smooth boundary in $\mathbb{R}^n$ for $n\ge 1$.

It is easy to see $(\lambda, 0)$ is a trivial solution of Eq (4.1). Define a nonlinear mapping $F:\mathbb{R}\times X\to Y$ by

where $X = \left\{u\in W^{2, p}(\Omega)\; : \dfrac{\partial u}{\partial n} = 0 \right\}$ and $Y = L^p(\Omega)$. It is easy to verify that $F_u(0, 0)[\phi] = \Delta\phi$, we have $N(F_u(0, 0)) = {\rm{span}}\{1\}$, $R(F_u(0, 0)) = \{y\in Y: \int_ \Omega ydx = 0\}$. And $F_{ \lambda u}(0, 0)[1] = 0$, $\theta_2 = 0$, $F_{uu}(0, 0)[1]^2 = 2$, $F_{ \lambda \lambda u}(0, 0)[1] = -2$, so (F1), (F3$^\prime$), (F4) are satisfied. We can apply Theorem 1.3 to $F$. Then the solution set of Eq (4.1) near $(\lambda, u) = (0, 0)$ is the union of two $C^1$ curves which are tangent to each other at $(0, 0)$, including the line of trivial solutions $\Gamma_0 = \{(\lambda, 0)\}$ and $\Gamma_1 = \{(\lambda, u(\lambda)):| \lambda| < \delta\}$ for some $\delta > 0$, where $u(\lambda)$ is a continuously differentiable function, $u(\lambda) = t(\lambda)+g(\lambda, t(\lambda))$, $t(0) = t'(0) = 0$ and $t''(0) = 2$. Furthermore from Proposition 3.2, we have $\gamma''(0) = -\mu''(0) = -2$. It implies the trivial solution $(\lambda, 0)$ is stable and the nontrivial solution $(\lambda, u(\lambda))$ is unstable. Note that this example is rather trivial as $u(\lambda) = \lambda^2$ is a constant solution of Eq (4.1).

Example 4.2.

where $\lambda$ is a positive parameter, $\Omega$ is a bounded region with smooth boundary in $\mathbb{R}^n$ for $n\ge 1$, and $\mu_1$ is the principal eigenvalue of $-\Delta$ on $H^1_0(\Omega)$.

For any $\lambda > 0$, $u = 0$ is a trivial solution of (4.3). Define a nonlinear mapping $F:\mathbb{R}\times X\to Y$ by

where $X = W^{2, p}(\Omega)\cap W^{1, p}_0(\Omega)$ and $Y = L^p(\Omega)$. We show that $\lambda = \sqrt{\mu_1}$ is a bifurcation point for the trivial solution $u = 0$. We can verify that $F_u(\sqrt{\mu_1}, 0)[\phi] = \Delta \phi+\mu_1\phi$, we have $N(F_u(\sqrt{\mu_1}, 0)) = {\rm{span}}\{\varphi_1\}$, $R(F_u(\sqrt{\mu_1}, 0)) = \{y\in Y: \int_ \Omega y \varphi_1 dx = 0\}$, where $\varphi_1 > 0$ is the principal eigenfunction of $-\Delta$ on $H^1_0(\Omega)$ corresponding to $\mu_1$. Moreover we can verify that $F_{ \lambda u}(\sqrt{\mu_1}, 0)[\varphi_1] = 0$, $\theta_2 = 0$, $F_{uu}(\sqrt{\mu_1}, 0)[\varphi_1]^2 = 2\varphi_1^2$, $F_{ \lambda \lambda u}(\sqrt{\mu_1}, 0)[\varphi_1] = -2\varphi_1$. so the conditions (F1), (F3$^\prime$), (F4) are satisfied. We can apply Theorem 1.3 to $F$ at $\lambda = \sqrt{\mu_1}$. The solution set of Eq (4.3) near $(\lambda, u) = (\sqrt{\mu_1}, 0)$ is the union of two $C^1$ curves which are tangent to each other at $(\sqrt{\mu_1}, 0)$, including the line of trivial solutions $\Gamma_0 = \{(\lambda, 0): \lambda > 0\}$ and $\Gamma_1 = \{(\lambda, u(\lambda)):| \lambda-\sqrt{\mu_1}| < \delta\}$ for some $\delta > 0$, where $u(\lambda) = t(\lambda)\varphi_1+g(\lambda, t(\lambda))$ is smooth, $t(\sqrt{\mu_1}) = t'(\sqrt{\mu_1}) = 0$, $t''(\sqrt{\mu_1}) = 2A > 0$ where $A = \int_{\Omega}\varphi_1^2/\int_{\Omega}\varphi_1^3 > 0$, and $g(\lambda, 0) = g_{ \lambda}(\sqrt{\mu_1}, 0) = g_{t}(\sqrt{\mu_1}, 0) = 0$. Thus Eq (4.3) has a positive solution $u(\lambda)\approx A(\lambda-\sqrt{\mu_1})^2\varphi_1$ for any $0 < | \lambda-\sqrt{\mu_1}| < \delta$. Furthermore from Proposition 3.2, we have $\gamma''(0) = -\mu''(0) = -2$. It implies the trivial solution $(\lambda, 0)$ is stable and the nontrivial solution $(\lambda, u(\lambda))$ is unstable when $\lambda\ne \sqrt{\mu_1}$.

Acknowledgments

P. Liu is partially supported by NSFC grant 11571086, and J. Shi is partially supported by NSF grant DMS-1853598.

Conflict of interest

The authors declare there is no conflicts of interest.