Efficient solutions for time fractional Sawada-Kotera, Ito, and Kaup-Kupershmidt equations using an analytical technique

Humaira Yasmin; Aljawhara H. Almuqrin; Humaira Yasmin; Aljawhara H. Almuqrin

doi:10.3934/math.2024994

AIMS Mathematics

2024, Volume 9, Issue 8: 20441-20466. doi: 10.3934/math.2024994

Previous Article Next Article

Research article Special Issues

Efficient solutions for time fractional Sawada-Kotera, Ito, and Kaup-Kupershmidt equations using an analytical technique

Humaira Yasmin ^{1,2
,
,},
Aljawhara H. Almuqrin ³

1.
Department of Basic Sciences, General Administration of Preparatory Year, King Faisal University, P.O. Box 400, Al Ahsa 31982, Saudi Arabia
2.
Department of Mathematics and Statistics, College of Science, King Faisal University, P.O. Box 400, Al Ahsa 31982, Saudi Arabia
3.
Department of Physics, College of Science, Princess Nourah bint Abdulrahman University, P.O. Box 84428, Riyadh 11671, Saudi Arabia

Received: 24 March 2024 Revised: 27 May 2024 Accepted: 12 June 2024 Published: 24 June 2024
MSC : 34G20, 35A20, 35A22, 35R11

We focused on the analytical solution of strong nonlinearity and complicated time-fractional evolution equations, including the Sawada-Kotera equation, Ito equation, and Kaup-Kupershmidt equation, using an effective and accurate method known as the Aboodh residual power series method (ARPSM) in the framework of the Caputo operator. Therefore, the Caputo operator and the ARPSM are practical for figuring out a linear or nonlinear system with a fractional derivative. This technique was effectively proposed to obtain a set of analytical solutions for various types of fractional differential equations. The derived solutions enabled us to understand the mechanisms behind the propagation and generation of numerous nonlinear phenomena observed in diverse scientific domains, including plasma physics, fluid physics, and optical fibers. The fractional property also revealed some ambiguity that may be observed in many natural phenomena, and this is one of the most important distinguishing factors between fractional differential equations and non-fractional ones. We also helped clarify fractional calculus in nonlinear dynamics, motivating researchers to work in mathematical physics.
- fractional PDE,
- fractional Sawada-Kotera equation,
- fractional Ito equation,
- fractional Kaup-Kupershmidt equation,
- Aboodh residual power series method,
- Caputo operator,
- solitary waves
Citation: Humaira Yasmin, Aljawhara H. Almuqrin. Efficient solutions for time fractional Sawada-Kotera, Ito, and Kaup-Kupershmidt equations using an analytical technique[J]. AIMS Mathematics, 2024, 9(8): 20441-20466. doi: 10.3934/math.2024994

Related Papers:

Abstract

We focused on the analytical solution of strong nonlinearity and complicated time-fractional evolution equations, including the Sawada-Kotera equation, Ito equation, and Kaup-Kupershmidt equation, using an effective and accurate method known as the Aboodh residual power series method (ARPSM) in the framework of the Caputo operator. Therefore, the Caputo operator and the ARPSM are practical for figuring out a linear or nonlinear system with a fractional derivative. This technique was effectively proposed to obtain a set of analytical solutions for various types of fractional differential equations. The derived solutions enabled us to understand the mechanisms behind the propagation and generation of numerous nonlinear phenomena observed in diverse scientific domains, including plasma physics, fluid physics, and optical fibers. The fractional property also revealed some ambiguity that may be observed in many natural phenomena, and this is one of the most important distinguishing factors between fractional differential equations and non-fractional ones. We also helped clarify fractional calculus in nonlinear dynamics, motivating researchers to work in mathematical physics.

References

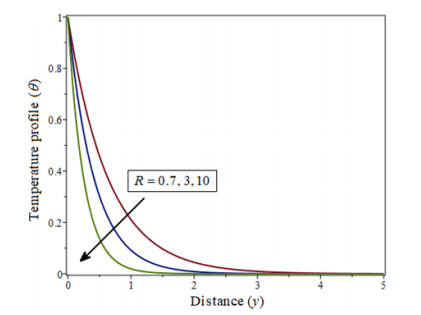
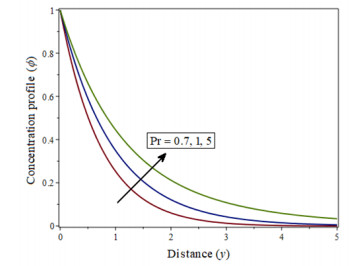
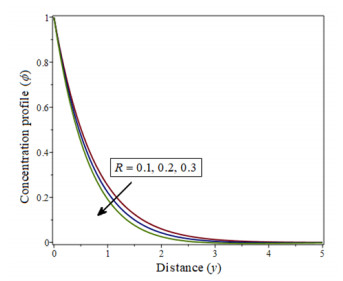
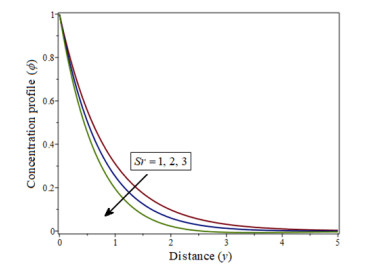
[1]	R. Khalil, M. Al Horani, A. Yousef, M. Sababheh, A new definition of fractional derivative, J. Comput. Appl. Math., 264 (2014), 65–70. http://dx.doi.org/10.1016/j.cam.2014.01.002 doi: 10.1016/j.cam.2014.01.002
[2]	R. Mabel Lizzy, K. Balachandran, J. Trujillo, Controllability of nonlinear stochastic fractional neutral systems with multiple time varying delays in control, Chaos Soliton. Fract., 102 (2017), 162–167. http://dx.doi.org/10.1016/j.chaos.2017.04.024 doi: 10.1016/j.chaos.2017.04.024
[3]	K. Diethelm, The analysis of fractional differential equations, Berlin: Springer, 2010. http://dx.doi.org/10.1007/978-3-642-14574-2
[4]	H. Yasmin A. Alderremy, R. Shah, A. Hamid Ganie, S. Aly, Iterative solution of the fractional Wu-Zhang equation under Caputo derivative operator, Front. Phys., 12 (2024), 1333990. http://dx.doi.org/10.3389/fphy.2024.1333990 doi: 10.3389/fphy.2024.1333990
[5]	M. Kbiri Alaoui, K. Nonlaopon, A. Zidan, A. Khan, R. Shah, Analytical investigation of fractional-order Cahn-Hilliard and gardner equations using two novel techniques, Mathematics, 10 (2022), 1643. http://dx.doi.org/10.3390/math10101643 doi: 10.3390/math10101643
[6]	T. Botmart, R. Agarwal, M. Naeem, A. Khan, R. Shah, On the solution of fractional modified Boussinesq and approximate long wave equations with non-singular kernel operators, AIMS Mathematics, 7 (2022), 12483–12513. http://dx.doi.org/10.3934/math.2022693 doi: 10.3934/math.2022693
[7]	H. Yasmin, N. Aljahdaly, A. Saeed, R. Shah, Probing families of optical soliton solutions in fractional perturbed radhakrishnan-kundu-akshmanan model with improved versions of extended direct algebraic method, Fractal Fract., 7 (2023), 512. http://dx.doi.org/10.3390/fractalfract7070512 doi: 10.3390/fractalfract7070512
[8]	H. Yasmin, N. Aljahdaly, A. Saeed, R. Shah, Investigating families of soliton solutions for the complex structured coupled fractional biswas-arshed model in birefringent fibers using a novel analytical technique, Fractal Fract., 7 (2023), 491. http://dx.doi.org/10.3390/fractalfract7070491 doi: 10.3390/fractalfract7070491
[9]	L. Barros, M. Lopes, F. Pedro, E. Esmi, J. Santos, D. Sanchez, The memory effect on fractional calculus: an application in the spread of COVID-19, Comp. Appl. Math., 40 (2021), 72. http://dx.doi.org/10.1007/s40314-021-01456-z doi: 10.1007/s40314-021-01456-z
[10]	R. Pakhira, U. Ghosh, S. Sarkar, Study of memory effects in an inventory model using fractional calculus, Applied Mathematical Sciences, 12 (2018), 797–824. http://dx.doi.org/10.12988/ams.2018.8578 doi: 10.12988/ams.2018.8578
[11]	S. Alkhateeb, S. Hussain, W. Albalawi, S. El-Tantawy, E. El-Awady, Dissipative Kawahara ion-acoustic solitary and cnoidal waves in a degenerate magnetorotating plasma, J. Taibah Univ. Sci., 17 (2023), 2187606. http://dx.doi.org/10.1080/16583655.2023.2187606 doi: 10.1080/16583655.2023.2187606
[12]	R. Alharbey, W. Alrefae, H. Malaikah, E. Tag-Eldin, S. El-Tantawy, Novel approximate analytical solutions to the nonplanar modified Kawahara equation and modeling nonlinear structures in electronegative plasmas, Symmetry, 15 (2023), 97. http://dx.doi.org/10.3390/sym15010097 doi: 10.3390/sym15010097
[13]	S. El-Tantawy, A. Salas, H. Alyouse, M. Alharthi, Novel exact and approximate solutions to the family of the forced damped Kawahara equation and modeling strong nonlinear waves in a plasma, Chinese J. Phys., 77 (2022), 2454–2471. http://dx.doi.org/10.1016/j.cjph.2022.04.009 doi: 10.1016/j.cjph.2022.04.009
[14]	H. Alyousef, A. Salas, M. Alharthi, S. El-tantawy, New periodic and localized traveling wave solutions to a Kawahara-type equation: applications to plasma physics, Complexity, 2022 (2022), 9942267. http://dx.doi.org/10.1155/2022/9942267 doi: 10.1155/2022/9942267
[15]	M. Alharthi, R. Alharbey, S. El-Tantawy, Novel analytical approximations to the nonplanar Kawahara equation and its plasma applications, Eur. Phys. J. Plus, 137 (2022), 1172. http://dx.doi.org/10.1140/epjp/s13360-022-03355-6 doi: 10.1140/epjp/s13360-022-03355-6
[16]	S. El-Tantawy, L. El-Sherif, A. Bakry, W. Alhejaili, A. Wazwaz, On the analytical approximations to the nonplanar damped Kawahara equation: cnoidal and solitary waves and their energy, Phys. Fluids, 34 (2022), 113103. http://dx.doi.org/10.1063/5.0119630 doi: 10.1063/5.0119630
[17]	R. Shah, H. Khan, P. Kumam, M. Arif, An analytical technique to solve the system of nonlinear fractional partial differential equations, Mathematics, 7 (2019), 505. http://dx.doi.org/10.3390/math7060505 doi: 10.3390/math7060505
[18]	H. Khan, R. Shah, D. Baleanu, P. Kumam, M. Arif, Analytical solution of fractional-order hyperbolic telegraph equation, using natural transform decomposition method, Electronics, 8 (2019), 1015. http://dx.doi.org/10.3390/electronics8091015 doi: 10.3390/electronics8091015
[19]	X. Li, Y. Sun, Application of RBF neural network optimal segmentation algorithm in credit rating, Neural Comput. Appl., 33 (2021), 8227–8235. http://dx.doi.org/10.1007/s00521-020-04958-9 doi: 10.1007/s00521-020-04958-9
[20]	T. Ali, Z. Xiao, H. Jiang, B. Li, A class of digital integrators based on trigonometric quadrature rules, IEEE T. Ind. Electron., 71 (2024), 6128–6138. http://dx.doi.org/10.1109/TIE.2023.3290247 doi: 10.1109/TIE.2023.3290247
[21]	B. Chen, J. Hu, B. Ghoso, Finite-time observer based tracking control of heterogeneous multi-AUV systems with partial measurements and intermittent communication, Sci. China Inform. Sci., 67 (2024), 152202. http://dx.doi.org/10.1007/s11432-023-3903-6 doi: 10.1007/s11432-023-3903-6
[22]	B. Chen, J. Hu, Y. Zhao, B. Ghosh, Finite-time observer based tracking control of uncertain heterogeneous underwater vehicles using adaptive sliding mode approach, Neurocomputing, 481 (2022), 322–332. http://dx.doi.org/10.1016/j.neucom.2022.01.038 doi: 10.1016/j.neucom.2022.01.038
[23]	C. Guo, J. Hu, Time base generator based practical predefined-time stabilization of high-order systems with unknown disturbance, IEEE T. Circuits-II, 70 (2023), 2670–2674. http://dx.doi.org/10.1109/TCSII.2023.3242856 doi: 10.1109/TCSII.2023.3242856
[24]	S. Lin, J. Zhang, C. Qiu, Asymptotic analysis for one-stage stochastic linear complementarity problems and applications, Mathematics, 11 (2023), 482. http://dx.doi.org/10.3390/math11020482 doi: 10.3390/math11020482
[25]	L. Liu, S. Zhang, L. Zhang, G. Pan, J. Yu, Multi-UUV maneuvering counter-game for dynamic target scenario based on fractional-order recurrent neural network, IEEE T. Cybernetics, 53 (2023), 4015–4028. http://dx.doi.org/10.1109/TCYB.2022.3225106 doi: 10.1109/TCYB.2022.3225106
[26]	Y. Kai, S. Chen, K. Zhang, Z. Yin, Exact solutions and dynamic properties of a nonlinear fourth-order time-fractional partial differential equation, Wave. Random Complex, in press. http://dx.doi.org/10.1080/17455030.2022.2044541
[27]	D. Kaup, On the inverse scattering problem for cubic eigenvalue problems of the class $\psi_{xxx}+ 6Q \psi_{x}+ 6R_{\psi} = \lambda \psi $, Stud. Appl. Math., 62 (1980), 189–216. http://dx.doi.org/10.1002/sapm1980623189 doi: 10.1002/sapm1980623189
[28]	B. Kupershmidt, A super Korteweg-de Vries equation: an integrable system, Phys. Lett. A, 102 (1984), 213–215. http://dx.doi.org/10.1016/0375-9601(84)90693-5 doi: 10.1016/0375-9601(84)90693-5
[29]	O. Abdulaziz, I. Hashim, M. Chowdhury, A. Zulkifle, Assessment of decomposition method for linear and nonlinear fractional differential equations, Far East Journal of Applied Mathematics, 28 (2007), 95–112.
[30]	J. He, X. Wu, Construction of solitary solution and compacton-like solution by variational iteration method, Chaos Soliton. Fract., 29 (2006), 108–113. http://dx.doi.org/10.1016/j.chaos.2005.10.100 doi: 10.1016/j.chaos.2005.10.100
[31]	Z. Odibat, S. Momani, Application of variational iteration method to nonlinear differential equations of fractional order, Int. J. Nonlin. Sci. Num., 7 (2006), 27–34. http://dx.doi.org/10.1515/IJNSNS.2006.7.1.27 doi: 10.1515/IJNSNS.2006.7.1.27
[32]	J. He, Application of homotopy perturbation method to nonlinear wave equations, Chaos Soliton. Fract., 26 (2005), 695–700. http://dx.doi.org/10.1016/j.chaos.2005.03.006 doi: 10.1016/j.chaos.2005.03.006
[33]	Z. Odibat, Exact solitary solutions for variants of the KdV equations with fractional time derivatives, Chaos Soliton. Fract., 40 (2009), 1264–1270. http://dx.doi.org/10.1016/j.chaos.2007.08.080 doi: 10.1016/j.chaos.2007.08.080
[34]	Q. Wang, Homotopy perturbation method for fractional KdV-Burgers equation, Chaos Soliton. Fract., 35 (2008), 843–850. http://dx.doi.org/10.1016/j.chaos.2006.05.074 doi: 10.1016/j.chaos.2006.05.074
[35]	S. Liao, An approximate solution technique not depending on small parameters: a special example, Int. J. NonLin. Mech., 30 (1995), 371–380. http://dx.doi.org/10.1016/0020-7462(94)00054-E doi: 10.1016/0020-7462(94)00054-E
[36]	M. El-Tawil, S. Huseen, The q-homotopy analysis method (q-HAM), Int. J. Appl. Math. Mech., 8 (2012), 51–75.
[37]	J. Biazar, K. Hosseini, P. Gholamin, Homotopy perturbation method for solving KdV and Sawada-Kotera equations, Journal of Operational Research in its Applications, 6 (2009), 11–16.
[38]	S. Dinarvand, S. Khosravi, A. Doosthoseini, M. Rashidi, The homotopy analysis method for solving the Sawada-Kotera and Lax's fifth-order KdV equations, Adv. Theor. Appl. Mech., 1 (2008), 327–335.
[39]	O. Abu Arqub, Series solution of fuzzy differential equations under strongly generalized differentiability, J. Adv. Res. Appl. Math., 5 (2013), 31–52. http://dx.doi.org/10.5373/jaram.1447.051912 doi: 10.5373/jaram.1447.051912
[40]	O. Abu Arqub, Z. Abo-Hammour, R. Al-Badarneh, S. Momani, A reliable analytical method for solving higher-order initial value problems, Discrete Dyn. Nat. Soc., 2013 (2013), 673829. http://dx.doi.org/10.1155/2013/673829 doi: 10.1155/2013/673829
[41]	O. Abu Arqub, A. El-Ajou, Z. Zhour, S. Momani, Multiple solutions of nonlinear boundary value problems of fractional order: a new analytic iterative technique, Entropy, 16 (2014), 471–493. http://dx.doi.org/10.3390/e16010471 doi: 10.3390/e16010471
[42]	A. El-Ajou, O. Abu Arqub, S. Momani, Approximate analytical solution of the nonlinear fractional KdV-Burgers equation: a new iterative algorithm, J. Comput. Phys., 293 (2015), 81–95. http://dx.doi.org/10.1016/j.jcp.2014.08.004 doi: 10.1016/j.jcp.2014.08.004
[43]	F. Xu, Y. Gao, X. Yang, H. Zhang, Construction of fractional power series solutions to fractional Boussinesq equations using residual power series method, Math. Probl. Eng., 2016 (2016), 5492535. http://dx.doi.org/10.1155/2016/5492535 doi: 10.1155/2016/5492535
[44]	J. Zhang, Z. Wei, L. Li, C. Zhou, Least-squares residual power series method for the time-fractional differential equations, Complexity, 2019 (2019), 6159024. http://dx.doi.org/10.1155/2019/6159024 doi: 10.1155/2019/6159024
[45]	I. Jaradat, M. Alquran, R. Abdel-Muhsen, An analytical framework of 2D diffusion, wave-like, telegraph, and Burgers' models with twofold Caputo derivatives ordering, Nonlinear Dyn., 93 (2018), 1911–1922. http://dx.doi.org/10.1007/s11071-018-4297-8 doi: 10.1007/s11071-018-4297-8
[46]	I. Jaradat, M. Alquran, K. Al-Khaled, An analytical study of physical models with inherited temporal and spatial memory, Eur. Phys. J. Plus, 133 (2018), 162. http://dx.doi.org/10.1140/epjp/i2018-12007-1 doi: 10.1140/epjp/i2018-12007-1
[47]	M. Alquran, K. Al-Khaled, S. Sivasundaram, H. Jaradat, Mathematical and numerical study of existence of bifurcations of the generalized fractional Burgers-Huxley equation, Nonlinear Stud., 24 (2017), 235–244.
[48]	M. Alquran, M. Alsukhour, M. Ali, I. Jaradat, Combination of Laplace transform and residual power series techniques to solve autonomous n-dimensional fractional nonlinear systems, Nonlinear Engineering, 10 (2021), 282–292. http://dx.doi.org/10.1515/nleng-2021-0022 doi: 10.1515/nleng-2021-0022
[49]	A. Khan, M. Junaid, I. Khan, F. Ali, K. Shah, D. Khan, Application of homotopy analysis natural transform method to the solution of nonlinear partial differential equations, Sci. Int. (Lahore), 29 (2017), 297–303.
[50]	M. Zhang, Y. Liu, X. Zhou, Efficient homotopy perturbation method for fractional non-linear equations using Sumudu transform, Therm. Sci., 19 (2015), 1167–1171.
[51]	R. Al-Deiakeh, M. Ali, M. Alquran, T. Sulaiman, S. Momani, M. Al-Smadi, On finding closed-form solutions to some nonlinear fractional systems via the combination of multi-Laplace transform and the Adomian decomposition method, Rom. Rep. Phys., 74 (2022), 111.
[52]	H. Eltayeb, A. Kilicman, A note on double Laplace transform and telegraphic equations, Abstr. Appl. Anal., 2013 (2013), 932578. http://dx.doi.org/10.1155/2013/932578 doi: 10.1155/2013/932578
[53]	M. Alquran, K. Al-Khaled, M. Ali, A. Ta'any, The combined Laplace transform-differential transform method for solving linear non-homogeneous PDEs, J. Math. Comput. Sci., 2 (2012), 690–701.
[54]	K. Aboodh, The new integral transform "Aboodh transform'', Global Journal of Pure and Applied Mathematics, 9 (2013), 35–43.
[55]	S. Aggarwal, R. Chauhan, A comparative study of Mohand and Aboodh transforms, International Journal of Research in Advent Technology, 7 (2019), 520–529.
[56]	M. Benattia, K. Belghaba, Application of the Aboodh transform for solving fractional delay differential equations, Universal Journal of Mathematics and Applications, 3 (2020), 93–101. http://dx.doi.org/10.32323/ujma.702033 doi: 10.32323/ujma.702033
[57]	B. Delgado, J. Macias-Diaz, On the general solutions of some non-homogeneous Div-curl systems with Riemann-Liouville and Caputo fractional derivatives, Fractal Fract., 5 (2021), 117. http://dx.doi.org/10.3390/fractalfract5030117 doi: 10.3390/fractalfract5030117
[58]	S. Alshammari, M. Al-Smadi, I. Hashim, M. Alias, Residual power series technique for simulating fractional Bagley-Torvik problems emerging in applied physics, Appl. Sci., 9 (2019), 5029. http://dx.doi.org/10.3390/app9235029 doi: 10.3390/app9235029
[59]	S. Almutlak, S. Parveen, S. Mahmood, A. Qamar, B. Alotaibi, S. El-Tantawy, On the propagation of cnoidal wave and overtaking collision of slow shear Alfvén solitons in low $\beta-$magnetized plasmas, Phys. Fluids, 35 (2023), 075130. http://dx.doi.org/10.1063/5.0158292 doi: 10.1063/5.0158292
[60]	W. Albalawi, S. El-Tantawy, A. Salas, On the rogue wave solution in the framework of a Korteweg-de Vries equation, Results Phys., 30 (2021), 104847. http://dx.doi.org/10.1016/j.rinp.2021.104847 doi: 10.1016/j.rinp.2021.104847
[61]	T. Hashmi, R. Jahangir, W. Masood, B. Alotaibi, S. Ismaeel, S. El-Tantawy, Head-on collision of ion-acoustic (modified) Korteweg-de Vries solitons in Saturn's magnetosphere plasmas with two temperature superthermal electrons, Phys. Fluids, 35 (2023), 103104. http://dx.doi.org/10.1063/5.0171220 doi: 10.1063/5.0171220
[62]	A. Wazwaz, W. Alhejaili, S. El-Tantawy, Physical multiple shock solutions to the integrability of linear structures of Burgers hierarchy, Phys. Fluids, 35 (2023), 123101. http://dx.doi.org/10.1063/5.0177366 doi: 10.1063/5.0177366
[63]	S. El-Tantawy, R. Matoog, R. Shah, A. Alrowaily, S. Ismaeel, On the shock wave approximation to fractional generalized Burger-Fisher equations using the residual power series transform method, Phys. Fluids, 36 (2024), 023105. http://dx.doi.org/10.1063/5.0187127 doi: 10.1063/5.0187127
[64]	S. El-Tantawy, A. Salas, H. Alyousef, M. Alharthi, Novel approximations to a nonplanar nonlinear Schrodinger equation and modeling nonplanar rogue waves/breathers in a complex plasma, Chaos Soliton. Fract., 163 (2022), 112612. http://dx.doi.org/10.1016/j.chaos.2022.112612 doi: 10.1016/j.chaos.2022.112612
[65]	S. El-Tantawy, A. Wazwaz, R. Schlickeiser, Solitons collision and freak waves in a plasma with Cairns-Tsallis particle distributions, Plasma Phys. Control. Fusion, 57 (2015), 125012. http://dx.doi.org/10.1088/0741-3335/57/12/125012 doi: 10.1088/0741-3335/57/12/125012

Reader Comments

Your name:*

Email:*
© 2024 the Author(s), licensee AIMS Press. This is an open access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0)