Quasi-autocorrelation coefficient change test of heavy-tailed sequences based on M-estimation

1.   Introduction

Detecting a change-point in a time series has received considerable attention for a long time, originating from in quality control [1]. It remains a popular field of research today due to the occurrence of sudden changes in various areas, such as financial data, signal processing, genetic engineering, and machine learning. There is an important issue in detecting structural breaks in time series data, which involves identifying changes in a sequence of parameters, numerical characteristics, or distributions that alter the model, such as a shift in mean [2], a change in variance [3], a change in tail index [4], or a change in persistence [5,6], etc.

However, Mandelbrot [7] has pointed out that many financial asset return distributions exhibit characteristics, such as peakedness and heavy tails, that cannot be adequately described by traditional normal distributions. Heavy-tailed series are better suited for capturing the distributional features of peaks and heavy tails in financial data due to their additivity and consistency with market observations. The distributions of commodity and stock returns often exhibit heavy tails with a possible infinite variance, as subsequently pointed out by Fama [8] and Mandelbrot [9]. They have initiated an investigation into time series models in which the marginal distributions exhibit regularly varying tails. Recently, there has been increasing interest in modeling change-point phenomena using heavy-tailed noise variables.

Developing estimation procedures for statistical models has received a great deal of interest, which are designed to represent data with infinite variance. Under the assumption of heavy-tailed time series with infinite variance, Paulauskas and Paulauskas [10] developed the asymptotic theory for econometric co-integration processes. Knight [11] investigated the limiting distribution of M-estimation for autoregressive parameters in the context of an integral linear process with infinite variance data. These findings demonstrate that, in terms of a heavier sequence, M-estimation is asymptotically more robust than least squares estimation (LS-estimation). M-estimation is a widely used and important method, which was first introduced by Huber [12] in 1964 for the location parameter model. Since then, many statisticians have shown interest in studying M-estimation, and this led to the establishment of a series of useful results. Hušková [13] proposed and investigated a method based on the moving sum of M-residuals to detect parameter changes and estimate the change position. Davis [14] studied the M-estimation of general autoregressive moving average (ARMA) processes with infinite variance, where the innovation follows a non-Gaussian stability law in its domain of attraction, and they derived a functional limit theorem for stochastic processes and established asymptotic properties of M-estimation. The asymptotic distribution of the M-estimation for parameters in an unstable AR($p$) process was presented in Sohrabi [15], who suggested that the M-estimation exhibits a higher asymptotic convergence rate compared to LS-estimation due to the fact that the LS-estimation of the mean is expressed as $\hat{\mu}-\mu = O_p(T^{1/\kappa-1})$, whose consistency is destroyed if $\kappa\in(0, 1)$. Knight [16] investigated the asymptotic behavior of LS- and M-estimation for autoregressive parameters in the context of a data generation process with an infinite variance random walk. The study demonstrated that certain M-estimation converges more rapidly than LS-estimation, especially in heavy-tailed distributions. Therefore, this paper employs M-estimation to estimate the parameters.

In time series analysis, covariance, the correlation coefficient, and their sample form are fundamental tools for studying parameter estimation, goodness of fit, change-point detection, and other related researches. For instance, classic monographs [17,18] have extensively discussed these topics, and introduced numerous practical applications. Furthermore, Wang et al. [19] proposed two semiparametric additive mean models for clustered panel count data and derived estimation equations to estimate the regression parameters of interest for the proposed models. Xu et al. [20] provided a bivariate Wiener model to capture the degradation patterns of two key performance characteristics of permanent magnet brakes, and considered an objective Bayesian method to analyze degradation data with small sample sizes. Additionally, in Yaghi's [21] doctoral dissertation, he proposed a novel method to detect change in the covariance of time series by converting the change in auto-covariance into a change in slope. Jarušková [22] investigated the equivalence of two covariance operators, and utilized the functional principal component analysis method, which can verify the equality of the largest eigenvalues and their corresponding eigenfunctions. Furthermore, Wied [23] proposed a test statistic

to study the change in the correlation coefficient between two time series over an unknown time period, where $\hat{\rho}$ is the estimated autocorrelation coefficient, and $\hat{D}$ is the regulatory parameter associated with the long-run variance. Na [24] applied the monitoring procedure

to identify changes in the autocorrelation function, parameter instability, and distribution shifts within the GARCH model, where $\hat{\gamma}$ is the autocorrelation coefficient, $\hat{\Sigma}$ is the long-run variance, and $b\left (\cdot \right)$ is a given boundary function. Dette [25] proposed to use

to detect relevant changes in time series models, where $\hat{e}_i$ denotes the nonparametric residuals, and $\hat{\sigma}$ is the variance function estimation.

This paper extends previous research to heavy-tailed innovation processes and utilizes the moving window method to convert the problem of detecting change in QAC into a change in mean. The methods for testing mean change-points primarily include the maximum likelihood method, least squares method, cumulative sum method (also known as CUSUM), Bayesian method, empirical quantile method, wavelet method, and others. Among these methods, the most commonly used test statistics for change-point problems is cumulative sum statistics. Yddter [26] and Hawkins [27] utilized the maximum likelihood approach to investigate the mean change-point of a normal sequence, while Kim [28] employed Incán's [29] cumulative sum of squares (SCUSUM) method to examine parameter changes in the generalized autoregressive conditional heteroskedasticity (GARCH). Lee [30] utilized the residual cumulative sum method (RCUSUM) to enhance the detection of parameter changes in GARCH (1, 1). Han [31] investigated the change-point estimation of the mean for heavy-tailed dependent sequences, and provided the consistency of the CUSUM statistics. However, due to the non-monotonic empirical powers issue with CUSUM statistics, ratio-typed statistics were subsequently proposed as a suitable alternative to CUSUM, particularly in cases of infinite variance since they do not require any variance estimation for normalization. As a result, Horváth [32] proposed a robust ratio test statistic to test the mean change-point of weakly dependent stable distribution sequences. Jin et al. [33] applied this ratio test statistic to investigate the mean change in their research.

The remainder of this paper is organized as follows. In Section 2, we introduce our ratio-typed test and derive its asyptotic properties under both the null hypothesis and the alternative, and the asymptotic behavior of the parameter estimation and ratio-typed test is studied. Section 3 presents the Monte Carlo simulation results. Section 4 offers an empirical application example and Section 5 concludes the paper.

2.   Materials and methods

2.1.   Model and hypothesis

The above-mentioned methods require estimation of the long-run variance to execute the test for the change in the autocorrelation coefficient. However, since the heavy-tailed sequence has an infinite variance, the results of these tests are not applicable. We use Yaghi [21]'s moving window method to combine the QAC of each window into a new series and utilize ratio test statistics to test mean change, which avoids the need for estimating long-run variance. In this paper, the primitive time series $\left\{y_{t}, 1\le t\le T \right\}$ would satisfy the following conditions,

where $\mu$ and $\beta$ are the intercept and the time trend, and $T$ is the sample size. $\xi_{t}$ refers to a $p$-order autoregressive process. We assume throughout this paper that the error term $\eta_{t}$ belongs to the domain of attraction of a stable law. For any $x > 0$, then

where $a_{T} = \inf\{x:P(|\eta_t| > x)\leq T^{-1}\}$, and

The tail thickness of the observed data is determined by tail index $\kappa$, which is unknown. Well-known special cases of $\eta_t$ are the Gaussian $(\kappa = 2)$ and Cauchy $(\kappa = 1)$ distributions. When $\kappa\in (0, 2)$, the distribution has the moment behavior: $E|\eta_t|^\nu = \infty$ once $\nu\geq\kappa$, and thus $\eta_t$ has infinite variance, it is heavy-tailed.

The variance of the heavy-tailed sequence $y_{t}$ is infinite, but the variance of $T^{\frac{\kappa}{2}-1}y_{t}$ is finite.

Proof. Multiply both sides of the model (1.1) by a control velocity $T^{\frac{\kappa}{2}-1}$,

where $\kappa\in \left (0, 2 \right)$, and $T$ represents the sample size. We then prove the existence of the first and second moments of $T^{(\frac{\kappa}{2}-1)}\xi_{t}$. According to the definition of the stable distribution, we obtain

where $C\left (\sigma, \beta, \mu \right)$ is bounded. This means that there is at least one sufficiently large $M$, that when $T > M$, there is $P\left (X > T \right) = O\left (T^{-\kappa } \right)$.

Note that

Since as $T\rightarrow \infty$, then $T^{\frac{\kappa}{2}-1}\to 0$, and ${\int}_{-M}^{M} \xi dF\left (\xi \right)\le M{\int}_{-\infty}^{+\infty} 1\mathrm{d}F\left (\xi \right) = M$. Here, the second term tends to zero. Next, we only prove the third term, and the proof for the first term is similar.

Let $P\left (X > T \right) = \overline{F}(T) = 1-F(T)$, then $\overline{F}(\infty) = 0$, and we get

Because $T^{\frac{\kappa }{2} -1}M\overline{F}(M) = T^{\frac{\kappa }{2} -1}M^{1-\kappa } M^{\kappa } \overline{F}(M){\rightarrow } 0$, then $T^{\frac{\kappa }{2} -1} \xi \overline{F}(\xi){\rightarrow } 0$, as $\xi \rightarrow \infty$. On the other hand, due to $\overline{F}(\infty) = 0$, it leads to $T^{\frac{\kappa }{2} -1}\int_{M}^{+\infty }\overline{F} (\xi)\mathrm{d} \xi \rightarrow0$, and $E(T^{(\frac{\kappa}{2}-1)} \xi _{t}) = 0$.

Similarly, the existence of $E(T^{\kappa-1} \xi^2 _{t})$ can be dealt with the same way. We complete the proof of the variance of $T^{\frac{\kappa}{2}-1}\xi_{t}$.

In this study, our primary objective is to attain a more significant leap in amplitude. Consequently, we concentrate on the first-order autocorrelation coefficient, whereas the second-order and higher-order autocorrelation coefficients tend to diminish or fluctuate within the interval of $\left (-1, 1 \right)$. We define the first-order QAC of the heavy-tailed sequences as follows, $t = 1, \cdots, T$,

Thus, the corresponding sample correlation coefficient is defined as

where $\bar{y} = \frac{1}{T}\sum^T_{i = 1}y_i$.

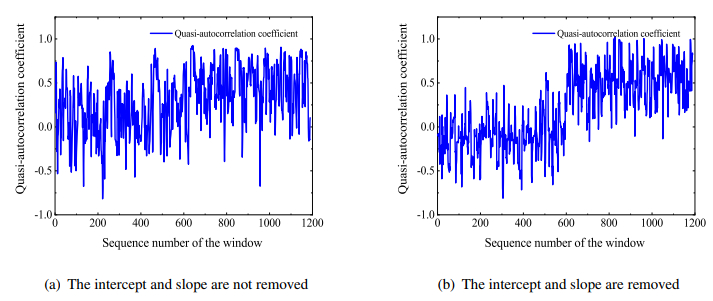
Through simulation experiments, it was found that the presence of intercept and slope parameters had a significant impact on the changes in the QAC. Therefore, it is crucial to detrend the intercept and slope parameters in the model because noticeable variations occur in the QAC when the regression coefficient of the AR$(p)$ series alters. Now, we use a simple example to employ a moving window method to simulate this phenomenon. Suppose the sequence follows an AR(1) model with a change in autoregressive parameter,

Now, we conside a window width $m = 10$, lag number $d = 1$, sample size $T = 1200$, change position $\tau^* = 0.5$, and tail index $\kappa = 1.2$. Since each window has a width of $m$ and a lag of $d$, it results in the number of windows $n = floor((T-m)/d)+1$ and obtains $n = T-m+1$ sets of the sub-sample, namely, $\{y_t, t = 1, \cdots, m\}$, $\{y_t, t = 2, \cdots, m+1\}$, $\cdots, \{y_t, t = T-m+1, \cdots, T\}$.

Figure 1(a) indicates that the change in $\hat{\alpha}_j(1)$ based on the sub-sample $\{y_j, \cdots, y_{j+m-1}\}$, $j = 1, \cdots, n$, is not obvious, where

and $\bar{y}_{j} = \frac{1}{m}\sum^{j+m-1}_{t = j}y_j$. Under some regular conditions, it has beem proven that $\alpha_{j}(1)$ can converge to $\alpha(1)$ in probability. On the other hand, if there are consistent estimates of parameters $\mu$ and $\beta$, we can have the residuals $\{\hat{\xi}_j, \cdots, \hat{\xi}_{j+m-1}\}$, $j = 1, \cdots, n$, where $\hat{\xi}_t = y_t-\hat{\mu}-\hat{\beta}t$. This means that the intercept and slope have detrended. Thus, Figure 1(b) shows that $\hat{\alpha}_j(1)$ based on the sub-sample $\{\hat{\xi}_j, \cdots, \hat{\xi}_{j+m-1}\}$, $j = 1, \cdots, n$, have more pronounced fluctuation, where

and $\bar{\hat{\xi}}_{j} = \frac{1}{m}\sum^{j+m-1}_{t = j}\hat{\xi}_j$.

Moreover, it is worth noting that

Because $\hat{\alpha}_{j}(1)$ can converge to $\alpha(1)$ in probability, we focus on an autocorrelation coefficient consisting of $\hat{\xi}_t$, not $y_t$. As shown in Figure 1, if a change in mean is observed in the new series $\hat{\alpha}_1(1), \cdots, \hat{\alpha}_n(1)$, it can be explained that the QAC of the primitive sequence $y_t$ has changed. The problem of testing the null hypothesis of no QAC change can be illustrated as

against the alternative hypothesis

Therefore, we would convert the QAC change to the mean change.

2.2.   Asymptotic properties of M-estimation

Prior to deriving the asymptotic properties of the following ratio-typed test, it is necessary to establish a lemma that proves the consistency of M-estimations for both intercept and slope parameters under the null hypothesis for all $\kappa\in(0, 2]$. To estimate the parameters $\mu$ and $\beta$ by M-estimation, $\hat{\mu}$ and $\hat{\beta}$ are defined as solutions of the minimization problem

where $\rho$ is a convex loss function. The estimations in equation (2.5) are sometimes also defined as the solution to the following equation,

Throughout this paper, we will make the following assumptions about the loss function $\rho$ and the distribution of random variables $\xi_1, \cdots, \xi_T$.

Assumption 1. The distribution $F_\xi$ of random error term $\xi_t$ is in the domain of attraction of a stable law with index $\kappa\in(0, 2)$, and $\eta_t$ is an independent identically distributed sequence $(i.i.d)$.

(1) If $\kappa > 1$, then $E(\xi_t) = 0$;

(2) while if $\kappa < 1$, $\xi_t$ has a symmetric distribution.

Assumption 2. Let $\rho$ be a convex and twice differentiable function, and take $\rho' = \phi$, where $\phi$ is Lipschitz continuous, then there is a real number $K\ge 0$ made for all $x$ and $y$ thus that $\left | \phi '(x)-\phi '(y) \right | \le K\left | x-y \right |$.

Assumption 3. Finally, we will make the following assumptions about the random variable $\phi(\xi_t)$:

(1) $E(\phi(\xi_t)) = 0$;

(2) $0 < \sigma^2_{\xi}(\phi) = E\phi^2(\xi_t)+2\sum_{i = 0}^\infty{E\phi(\xi_t)\phi(\xi_{t+i})} < \infty$.

Assumptions 1, 2, and 3 are standard conditions for deriving the asymptotic properties based on M-estimation, although extra moment conditions are imposed on $\phi$ and $\phi'$. Note that $\rho$ is an almost everywhere differentiable convex function that ensures the uniqueness solution. Although $\rho'$ may not exist in this case, M-estimation can still be counted under certain additional conditions for the asymptotic theory. This paper only considers situations where $\rho'$ exists. We mainly consider two types of estimation methods, $\phi(x) = x$ (LS-estimation) and $\phi(x) = xI\{{\vert x\vert\leq K}\}+Ksgn(x)I\{{\vert x\vert > K}\}$ (M-estimation).

In the view of the moving window method for fixed $d$, we can rewrite formula (2.3) and obtain the following first-order QAC $\hat{\alpha}_{j}(1), j = 1, \cdots, n,$

where $\bar{\hat{\xi } } _{j} = \frac{1}{m} \sum_{i = d(j-1)+1}^{d(j-1)+m} \hat{\xi } _{i}$ and $\hat{\xi}_{t} = y_{t} -\hat{\mu } -\hat{\beta } t$. The QAC of all windows based on the residuals $\hat{\xi}_{k}$ constitute a new sequence of $\{\hat{\alpha}_{j}(1), j = 1, 2, \dots, n\}$. Recall that $n = floor((T-m)d)+1$ represents the sequence number of windows. Here, $\overset{d}{\rightarrow }$ and $\overset{p}{\rightarrow }$ denote convergence in distribution and convergence in probability, respectively.

Lemma 2.1. If Assumptions 1–3 hold, $\hat{\mu}$ and $\hat{\beta}$ minimize formula (2.5), and under the null hypothesis, then

where $W(\cdot)$ is a Wiener process.

Proof. The proof is essentially the same as that in Knight [16]. Define the process

with $(u, v) = (T^{3/2}(\hat{\beta} -\beta), T^{1/2}(\hat{\mu}-\mu))$ minimizing $Z(u, v)$. By a Taylor series expansion of each summand of $Z$ around $u = 0, v = 0$, then

where $\xi_{t}^{*} \in\left(\xi_{t} \pm\left|T^{-3 / 2} u t+T^{-1 / 2} v\right|\right)$. Using the Lipschitz continuity of $\phi'$, then

with bounded $C$, and we get

Thus, $\phi'(\xi_{t}^{*})$ can be approximately replaced by $\phi'(\xi_{t})$.

Under Assumptions 1–3, since $\phi\left(\xi_{t}\right)$ satisfies the central limit theorem, it yields

where $\sigma^2(\phi) = E\phi^2(\xi_t)+2\sum_{i = 0}^\infty{E\phi(\xi_t)\phi(\xi_{t+i})}$. By some algebraic derivation, we have

and

By the theorem of large numbers, we get

This shows that $\phi'(\xi_{t})$ can be asympotically replaced by $E\phi'(\xi_{t})$, resulting in

and

Together with (3)–(7), we can rewrite (1) as

and take the partial derivative on it with respect to $u$ and $v$

The solution is

This, in turn, implies that

Therefore, the proof is complete.

Lemma 2.1 shows the convergence rate for $\hat{\mu}$ and $\hat{\beta}$ based on M-estimation are $T^{-1/2}$ and $T^{-3/2}$ under the heavy-tail environment, which are the same as those in the case of a Gaussian process. Furthermore, the simulation study has revealed that the parameter estimations based on M-estimation are consistent and more robust than those based on the LS-method. The QAC plays a crucial role in time series analysis by measuring the degree to which successive observations are correlated with each other over time. The consistency of these estimations ensures that our comprehension of such correlations remains robust and trustworthy. Consequently, we can present the ratio-typed test to detect a change in mean and discuss its asymptotic properties.

2.3.   Ratio-typed test

For the sake of convenience, we define $\omega_j = \hat{\alpha}_{j}(1)$. Without loss of generality, we suppose $\omega_j$ follows an AR$(p)$ process with a drift, that is, $\omega _{t} = \gamma +\gamma _{1} \omega _{t-1}+\cdots + \gamma _{p} \omega _{t-p}+\varepsilon _{t}$. By using a $t$-test to fit the QAC sequence, it is found that when $p = 1$, the P-value is $0.0086$, which is greater than $0.001$; whereas when $p = 0$, the P-value is $6\times 10^{-213}$, which is much smaller than $0.001$. The smaller the P-value is, the better the goodness-of-fit is. This means that, under the null hypethesis of no change, the QAC series can be fitted by the mean model

where $\varepsilon_{t}$ is assumed to meet Assumption 1. However, under the alternative hypothesis, the QAC series would follow the mean model with a change,

where $\gamma^*_1\neq \gamma^*_2$ and $\tau$ is an unknown change-point.

Hence, for testing a change in the QAC under original sequence $\{y_t, t = 1, \cdots, T\}$, it can be converted into mean change detection with sequence $\{\omega _{1}, \omega _{2}, \cdots, \omega _{n}\}$. The mean change test has been extensively studied and is relatively mature. Because these innovations $\{\varepsilon_{t}, t = 1, \cdots, n\}$ in sequence $\{\omega _{1}, \omega _{2}, \cdots, \omega _{n}\}$ maybe follow a heavy-tailed distribution, this paper extensively studies test procedures that utilize the ratio-typed test based on M-residuals to detect changes in mean.

Our inspiration is derived from Horváth's description (2008) [32] of ratio-typed tests and their robustness performance, and by the framework of test statistics, which is on the basis of Peštová and Pešta (2018) [34]. The ratio-typed test based on M-residuals is expressed as

The score function $\phi$ is chosen in two forms. The problem of testing the null hypothesis of no QAC change can be illustrated as: $\phi(x) = x, x\in R$, and these procedures could be reduced to classic LS procedures (Csörgo and Horváth (1997) [35]). In a similar vein, these procedures are simplified to the Huber function truncation process if $\phi(x) = xI\{{\vert x\vert\leq K}\}+Ksgn(x)I\{{\vert x\vert > K}\}$. $\hat{\gamma }({\phi })$ is the M-estimation of parameter $\gamma$ generated by a score function $\rho$ with sequence $\{\omega _{1}, \omega _{2}, \cdots, \omega _{n}\}$, i.e., it is defined as a solution of the minimization problem

where $\rho$ is a convex loss function. Sometimes, the estimation in (2.9) is also defined as a solution of the following equation:

where $\rho$ and $\phi$ satisfy Assumption 2.

Analogous to $\hat{\gamma }({\phi })$, the M-estimates $\hat{\gamma }_1({\phi })$ and $\hat{\gamma }_2({\phi })$ are computed, respectively, from sequences $\omega_1, \cdots, \omega_{[ns]}$ and $\omega_{[ns]+1}, \cdots, \omega_n$. They are solutions to these equations:

and

Prior to deriving asymptotic properties of the proposed ratio-typed test, we assume that $\phi(\varepsilon_{t})$ follows Assumption 3 and give the lemma that, under the null hypothesis, the M-estimation should be consistent for all $\kappa \in \left (0, 2 \right ]$.

Lemma 2.2. If Assumptions 4–6 hold, under the null hypothesis, we have

Similarly

where $\sigma^2_\varepsilon(\phi) = E\phi^2(\varepsilon_t)+2\sum_{i = 0}^\infty{E\phi(\varepsilon_t)\phi(\varepsilon_{t+i})}$ and $W(\cdot)$ is a Wiener process.

Proof. Define the process

with $u = n^{1/2}(\gamma-\hat{\gamma}(\phi))$. By a Taylor series expansion of each summand of $Z$ around $u = 0$, then

where $\varepsilon_t^*\in(\varepsilon_t, \varepsilon_t\pm|un^{-1/2}|)$. Using the Lipschitz continuity of $\phi'$, then $|\phi'(\varepsilon_t)-\phi'(\varepsilon_t^*)|\leq C|un^{-1/2}|$ with bounded $C$, and we get

uniformly over $u$ in compact sets. By the theorem of large numbers, then

Combining $n^{-1/2}\sum\limits_{t = 1}^{[ns]}\phi(\varepsilon_t)\xrightarrow{d}\sigma_\varepsilon(\phi)W(s)$ with (9) and (10), it yields

Find the minimum value in (11), and we have

so it turns out

Similarly, the asymptotic distributions of $n^{1/2}(\hat{\gamma}_1(\phi)-\gamma)$ and $n^{1/2}(\hat{\gamma}_2(\phi)-\gamma)$ can be obtained in the same way. Therefore, the proof is complete.

Subsequently, we examine the performance of the ratio-typed test in the presence of a mean change. The ensuing lemma serves as a crucial tool for achieving the desired outcomes under the alternative hypothesis.

Lemma 2.3. If Assumptions 4–6 hold, and under the alternative hypothesis, we have:

(i) for $i = 1, 2$, both $\hat{\gamma}(\phi)-\gamma^*_i = O_p(1)$ hold,

(ii) let a constant $\theta\neq0$, then

if $s\in(0, \tau-\theta]$, we have $\hat{\gamma}_1(\phi)-\gamma^*_1 = O_p(n^{-1/2})$, and $\hat{\gamma}_2(\phi)-\gamma^*_2 = O_p(1)$,

if $s\in[\tau+\theta, 1)$, we have $\hat{\gamma}_1(\phi)-\gamma^*_1 = O_p(1)$, and $\hat{\gamma}_2(\phi)-\gamma^*_2 = O_p(n^{-1/2})$,

(iii) if $s = \tau$, $n^{1/2}(\hat{\gamma}_1(\phi)-\gamma^*_1)$ and $n^{1/2}(\hat{\gamma}_2(\phi)-\gamma^*_2)$ have the same asymptotic distributions as those in Lemma 2.2.

Proof.(ⅰ) To confirm $\hat{\gamma}(\phi)-\gamma_1 = O_p(1)$, it is sufficient to prove that $\hat{\gamma}(\phi)-\gamma_1$ does converge to nonzero in probability. Without loss of generality, we assume $n^{1/2}(\hat{\gamma}(\phi)-\gamma_1) = O_p(1)$. Under the alternative hypothesis, define the process

where $u = n^{1/2}(\gamma_1-\hat{\gamma}(\phi))$.

By a Taylor series expansion of each summand of $Q_{n, 1}(u)$, it yields

where $\tilde{\varepsilon}_t\in(\varepsilon_t, \varepsilon_t\pm n^{-1/2}|u|)$. Similarly, we can get a Taylor series expansion of each summand $Q_{n2}(u)$ as follows

where $\tilde{\tilde{\varepsilon}}_t\in(\varepsilon_t, \varepsilon_t\pm|n^{-1/2}u+(\gamma_2-\gamma_1)|)$.

In view of (13) and (14), to find ind the minimum value in (11), it turns out that

Using the Lipschitz continuity of $\phi'$, we have

However, because of $\gamma_2\neq\gamma_1$, then

Thus, because of the fact that

we rewrite (15) as follows

To find the solution to the equation $Q_{n}'(u) = 0$, we have

which holds due to $E(\tilde{\tilde{\varepsilon}}) = O_p(1)$. Recall that $u = n^{1/2}(\gamma_1-\hat{\gamma}(\phi))$, and it shows that $\hat{\gamma}(\phi)-\gamma_1$ should converge to nonzero, which contradicts the artificial assumption. Hence, we prove that $\hat{\gamma}(\phi)-\gamma_1 = O_p(1)$, and can deal with $\hat{\gamma}(\phi)-\gamma_2 = O_p(1)$ in the same way.

(ⅱ) Since the estimator $\hat{\gamma}(\phi)$ is constructed on the basic of data $\omega_1, \cdots, \omega_n$, which involve the structural change in location, it turns out that $\hat{\gamma}_1(\phi)-\gamma_i = O_p(1)$, $i = 1, 2$. For the same reason, we still suppose that $u = n^{1/2}(\gamma_1-\hat{\gamma}(\phi))$ is bounded. If $s\in(\tau+\theta, 1)$, because the estimator $\hat{\gamma}_1(\phi)$ consists of data $\omega_1, \cdots, \omega_{[ns]}$, we rewrite (12) in the form

Using the same proof process as discussed above, we obtain

Note that $\theta = s-\tau\neq0$, and it again leads to $u = O_p(n^{1/2})$, which is inconsistent with $u$ being bounded. Hence, it turns out that $\hat{\gamma}_1(\phi)-\gamma_1 = O_p(1)$. While the estimator $\hat{\gamma}_2(\phi)$ consists of data $\omega_{[ns]+1}, \cdots, \omega_{n}$ which are not contaminated, it implies that the asymptotic distribution of $n^{1/2}(\hat{\gamma}_2(\phi)-\gamma_2)$ is asymptotically equivalent to that shown in Lemma 2.2. Similarly, if $s\in(0, \tau-\theta)$, the assertions of $\hat{\gamma}_1(\phi)-\gamma_1 = O_p(n^{-1/2})$ and $\hat{\gamma}_2(\phi)-\gamma_2 = O_p(1)$ do hold.

(ⅲ) When $s = \tau$, the two sets of data $\omega_1, \cdots, \omega_{[ns]}$ and $\omega_{[ns]+1}, \cdots, \omega_{n}$ do not become contaminated even if under the alternative hypothesis. Thus, the convergence of $\hat{\gamma}_1(\phi)$ and $\hat{\gamma}_2(\phi)$ still exists, and the proof of their asympotic distribution is similar to that in Theorem 2.1 Thus, the proof is complete.

As stated in Lemma 2.3, if any of the estimation equations (2.10)–(2.13) involve observations with a change in mean, the corresponding M-estimation will be biased. If $s = \tau$, the asymptotic results for $\hat{\gamma}_1(\phi)$ and $\hat{\gamma}_2(\phi)$ are consistent with Lemma 2.2.

Theorem 2.1. $(Under\; null)$ Suppose sequences $\{\omega_1, \cdots, \omega_n\}$ follow model (2.8) under the null hypothesis, as $n\rightarrow \infty$, and we have,

Proof. The proof is analogous in several steps with the proof of Theorem 1.1 in Horváth [32]. By the mean value theorem, it leads to

where $\varepsilon_t^{**}$ satisfies $|\phi'(\varepsilon_t)-\phi'(\varepsilon_t^{**})|\leq C|\gamma-\hat{\gamma}(\phi)|$.

Combining Lemma 2.2 with (9) and (10), we have

which holds due to $n^{-1/2}(\gamma-\hat{\gamma}(\phi))\max\limits_{0\leq s\leq1}\sum_{t = 1}^{[ns]}\left|\phi'(\varepsilon_t)-\phi'(\varepsilon_t^{**})\right|\leq C|n^{-1/2}n^{-1}(\gamma-\hat{\gamma}(\phi))^2|\xrightarrow{d}0.$

Actually, the proof of the first and second terms of the denominators is roughly analogous, so we just handle the second one.

where $\varepsilon_t^{***}\in(\varepsilon_t, \varepsilon_t\pm n^{1/2}|\gamma-\hat{\gamma}_2(\phi)|)$. Similarly, we can obtain

Therefore, together with (17), (18), and (19), it yields

Therefore, the proof is complete.

Theorem 2.1 demonstrates that, under the null hypothesis, the proposed test $V_n$ converges to a function of the Wiener process. In comparison with existing results, the asymptotic distribution remains robust against variations in tail index and therefore yields a unique critical value for any given significance level. Thus, the ratio-typed test is robust to heavy-tailed series with infinite variance, which has the advantage of avoiding tail index estimation for real data and greatly improves operational efficiency.

Next, we study the behavior of the ratio-typed test if there is a mean change. The following theorem is crucial for obtaining the desired results under the alternative hypothesis.

Theorem 2.2. $(Under\; alternative)$ Suppose sequences $\{\omega_1, \cdots, \omega_n\}$ follow model $(2.9)$ under the alternative hypothesis, as $n\rightarrow \infty$, and we have

Proof. When $s \in(\tau+\theta, 1)$, according to the proofs of Lemma 2.3 and Theorem 2.1, we have $\hat{\gamma}_1(\phi)-\gamma_1 = O_p(1)$, $\hat{\gamma}_2(\phi)-\gamma_2 = O_p(1)$, and $\hat{\gamma}_2(\phi)-\gamma_2 = O_p(n^{-1/2})$ under the alternative hypothesis. For the numerator of $V_n$, by the mean value theorem, it yields

where $\hat{\varepsilon}_t\in{(\varepsilon_t, \varepsilon_t+|\gamma_1-\hat{\gamma}(\phi)|)}$, and $\hat{\hat{\varepsilon}}_t\in{(\varepsilon_t, \varepsilon_t+|\gamma_2-\hat{\gamma}(\phi)|)}$. Since the second and third terms play a major role in the convergent rate $O_p(n)$, it follow that

Now, we deal with the first term of the denominator.

(ⅰ) If $1\leq [nv]\leq [n\tau]$, we have

where $\tilde{\varepsilon}_i^*\in(\varepsilon_i, \varepsilon_i\pm|(\gamma_1-\hat{\gamma}_1(\phi))|)$.

(ⅱ) If $[n\tau]+1\leq [nv]\leq [ns]$,

where $\hat{\varepsilon}_i^*\in(\varepsilon_i, \varepsilon_i\pm|(\gamma_1-\hat{\gamma}_1(\phi))|), \hat{\varepsilon}_i^{**}\in(\varepsilon_i, \varepsilon_i\pm|(\gamma_2-\hat{\gamma}_2(\phi))|)$. Hence, we obtain

For the second term of the denominator, its asymptotic disbribution is the same as the null hypothesis, because data $\omega_{[ns]+1}, \cdots, \omega_n$ are free of the influnence caused by the change-point. Thus, we have

Combining (20)–(22), we end up with $\max\limits_{0\leq s \leq 1}V_n = O_p(1)$. When $s\in(0, \tau-\theta)$, we can similarly prove that $\max\limits_{0\leq s \leq 1}V_n = O_p(1)$. Finally, when $s\in(\tau-\theta, \tau+\theta)$, we just consider the special case of $s = \tau$. Since both ot the two sets $\omega_1, \cdots, \omega_{[ns]}$ and $\omega_{[ns]+1}, \cdots, \omega_{n}$ are not affected by the mean change, the asymptotic distribution of the denominator is the same as in Theorem 2.1. However, the numerator always diverges. Consequently, we get

Therefore, the proof is complete.

According to Theorem 2.2, the ratio-typed test is consistent under the alternative hypothesis. However, unlike the result provided in Theorem 2.1, a closed-form asymptotic distribution cannot be obtained due to the unknown explicit expression of the objective function for M-estimation. The simulation study has revealed an intriguing finding that the divergence appears to be independent of the tail index in theory, yet it significantly affects the validity in practice.

3.   Simulation results

In this section, we present simulation results to investigate the performance of the ratio-typed test $V$ on empirical sizes and empirical powers using LS-estimation and M-estimation, i.e., $\phi_{LS}(x) = x$ and $\phi_{M}(x) = xI\{{\vert x\vert\leq K}\}+K sgn(x)I\{{\vert x\vert > K}\}$. The validity of the theory will be verified by the portfolio of the change position, magnitude of the change-point, tail index, window width, lag number and so on. Empirical sizes refer to the rejection rates at a significance level of 0.05 under the null hypothesis, while empirical powers denote rejection rates in the presence of a change-point. All results are based on 2000 replications.

We adopt the following DGP (data generating process):

where $\eta_t$ is a heavy-tailed sequence. The remaining parameters are set as follows: threshold value $K = 1.345$; autoregressive coefficient $c_1 = -0.3, 0, 0.3$; sample size $T = 300,600, 1200$; tailed index $\kappa = 0.4, 0.8, 1.2, 1.6, 2.0$; intercept and slope $\mu = 5$, $\beta = 0.2$; change position $\tau = 0, 0.3, 0.5, 0.7$; magnitude of change $\delta = 0.3, 0.6$; window width $m = 10, 20, 30$; and lag number $d = 1, 2, 3, 10, 15, 25$.

3.1.   Asymptotic critical values

In this subsection, our objective is to discuss the critical values of the ratio-typed test. Critical values of M-estimation and LS-estimation corresponding to changes in the tail index under different coefficients $c_{1}$ are obtained and presented in Table 1.

For the sake of simplicity, $V_{M}$ is defined as a ratio-typed test based on M-estimation with Huber function, and the definition of $V_{LS}$ relies on LS-estimation. It is not surprising that the simulated critical values of $V_{LS}$ are functional to tail index $\kappa$, whereas this phenomenon does not occur in $V_{M}$. That is consistent with the conclusion of Jin et al. [36,37]. It is noteworthy that critical values of two test statistics are not sensitive to the variations in $c_1$. Thus, for the $V_{LS}$ test, prior estimation of the tail index is necessary to conduct change-point tests with corresponding critical values. However, accurately estimating the unknown and elusive tail index in practical applications remains challenging. On the other hand, the simulated critical value of $V_{M}$ shows minimal fluctuations, which greatly facilitates its practical application.

3.2.   Empirical sizes and empirical powers

In this subsection, we aim to investigate empirical sizes and empirical powers of ratio-typed tests under various profiles of sample size, score function, change position, window width, and lag number. Figure 2 illustrates the curve of empirical sizes for $V_{M}$ and $V_{LS}$ under the null hypothesis, where the $x$-axis represents the tail index and the $y$-axis represents empirical sizes.

The empirical sizes of $V_{M}$, as shown in Figure 2, have greater stability compared to that of $V_{LS}$, because they nearly fluctuate around the 0.05 confidence level. It is notable that, the rejection rate of $V_{M}$ performs well regardless of the window width, but for $V_{LS}$, the empirical sizes are sensitive to the window width. When $m = 10$, there is a slight distortion, but the distortion becomes more pronounced as the window width expands to 20 and 30, which indicates that the rejection rate is unstable with larger window widths, in particular $T = 300$. It means that when sample size is small, the increase in window width may result in a slight growth of distortion. The reason for this is that a larger amount of data within each window is more prone to outliers, which in turn triggers an over-rejection. However, as the sample size increases, empirical sizes approach satisfactory and fluctuate around the significance level. There is no significant difference in empirical sizes when various lag numbers are considered. In short, the rejection rate of $V_{LS}$ is higher for a smaller sample size with a larger tail index, while the phenomenon does not occur for $V_{M}$. These results indicate that the convergence rate estimated by M-estimation is independent of tail thickness, as confirmed by Lemmas 2.1 and 2.2.

Figures 3–5 show the sensitivity analysis of the ratio-typed test under the alternative hypothesis, in terms of sample size, tail index, window width, lag number, change location, and magnitude of change. With an increase in the tail index, there is a decrease in the empirical powers of $V_{M}$, while there is an increase in those of $V_{LS}$. The ratio-typed test based on M-estimation appears to have a higher level of empirical powers if $\kappa\leq1.4$, while the test based on LS-estimation exhibits larger empirical powers if $\kappa > 1.4$. The Huber function truncates outliers to normality, by which the M-estimation enables more accurate estimation in heavy-tailed sequences while it involves more bias in light-tailed observations. This indicates that M-estimation is better suited for heavy-tail sequences. As expected, both tests have excellent performance on empirical powers with sample size growth, for example, when $\tau = 0.5$ and $\kappa = 1.6$ for $m = 20$ and $d = 1$, the rejection rates of $V_{M}$ are 80.7$\%$, 93.2$\%$, and 99.35$\%$, respectively, for $T = 300,600, 1200$.

It is interesting that, compared to that of $\tau = 0.3$ and $\tau = 0.7$, the empirical powers exhibit superior performance when $\tau = 0.5$ for both $V_{M}$ and $V_{LS}$. Furthermore, it is found that a wider window width leads to larger empirical powers when the lag number is fixed. For example, when $d = 1$, $\tau = 0.5$, and $T = 600$, if the window width $m$ is 10, the empirical powers obtained from M-estimation are 99.95$\%$, 99.2$\%$, 93.3$\%$, 83.55$\%$, and 72.85$\%$ under various tail indices, while the empirical powers are 100$\%$, 99.35$\%$, 97.8$\%$, 93.2$\%$, and 87.8$\%$ when $m = 20$. The empirical powers still remain insensitive to the lag number when the window width is fixed. When $m = 30$, $\tau = 0.7$, $T = 300$, and $d = 1$, the empirical powers based on M-estimation are 98.2$\%$, 93$\%$, 85.4$\%$, 76.8$\%$, and 69.1$\%$; but for $d = 2$, the empirical powers are 96.35$\%$, 92.25$\%$, 85$\%$, 75.15$\%$, and 67.75$\%$. This highlights the criticality of selecting an appropriate window width.

The relationship between empirical powers and lag numbers $d = 1, 2, 3$ is present in Figures 3–5. The line charts reveal an intuitive result that there is a slight difference in the empirical powers when the lag number is small. Therefore, to account for the impact of lag numbers on empirical powers, we consider three distinct lag numbers with $d = 10, 15, 25$. As depicted in Figure 6, the empirical powers decrease as the lag number increases. For example, when $\kappa = 0.8$, $\tau = 0.3$, $T = 1200$, and $m = 20$, empirical powers of $V_{M}$ are 80.52$\%$, 76.12$\%$, and 57.38$\%$ for $d = 10, 15, 25$. This phenomenon is attributed to the sample size of the mean change-point test reduction caused by a larger lag number and a smaller window width.

Recall that empirical powers decrease with an increase in lag numbers; therefore, we choose a relatively optimal lag number of $d = 3$ and explore window widths of $m = 10, 20, 30$ to analyze calculation efficiency. Actually, when the sample size is large, $d = 3$ can be selected due to computation cost reduction. However, when the sample size is small, we choose $d = 1$ as the optimal lag number to ensure no loss of samples and maximize the change-point test efficiency. Figures 2–7 indicate that when $m = 30$, both $V_{M}$ and $V_{LS}$ obtain outstanding empirical power. Consequently, we adopt $m = 30$ as the optimal window width in the practical example. In other words, the empirical powers of the ratio-typed test based on M-estimation are higher than those of the ratio-typed test based on LS-estimation, especially in the case of heavy-tailed sequences.

Figures 3–6 report the simulated results of $\delta = 0.3$, and we also are interested in the case of $\delta = 0.6$. As shown in Figure 7, it is not surprising that empirical powers enhance with the growth in $\delta$. Additionally, when $\delta = 0.3$, empirical powers tend to decrease as $\tau$ is far away from the middle of the sample. But for $\delta = 0.6$, the difference in empirical powers is very small no matter whether $\tau = 0.3$, $\tau = 0.5$, or $\tau = 0.7$. In other words, when $\delta$ is large, the influence of the change position on the empirical power is negligible.

4.   Empirical applications

In this section, the ratio-typed test based on M-estimation is used to test the QAC change in USD/CNY exchange rate data, by which the validity of the aforementioned method is confirmed. Figure 8(a) shows a total of 581 daily data points of the USD/CNY exchange rate from May 12, 2009 to August 31, 2011, which were drawn from https://www.economagic.com. Through the use of software [38] to find the rough estimate of the tail index, we have $\hat{\kappa} = 1.0515$. Thus, we suppose that this set of exchange rate data is $y_{t} = \mu+\beta t+\xi_{t}, t = 1, 2, \dots 581$, where innovation $\xi_t$ is heavy-tailed. In view of this, the test statistics in [23,24,25] for the change in correlation coefficients detection are invalidated, because this method requires long-run variance estimation, which is difficult and redundant for heavy-tailed sequences.

Note that the method proposed in this paper not only avoids long-term variance estimation, but also expands the application range and greatly improves practicability and convenience by converting the change in the autocorrelation coefficient into the change in mean. For a mean change problem, we provide the ratio-typed test based on M-estimation to execute for the heavy-tailed series. The exchange rate sequence $y_{t}$ is detrended in advance. The intercept and the slope are estimated through M-estimation, resulting in $\hat{\xi}_{t}$ = $y_{t}-\hat{\mu}$$-\hat{\beta} t$, $t = 1, 2, \dots, 581$, where $\hat{\mu} = 6.9401$ and $\hat{\beta} = -0.00078$. The residuals $\hat{\xi}_{t}$ are depicted in Figure 8(b). Thus, we set $d = 1$ and $m = 30$, and get a new sequence $\omega_{t}$ composed of 550 QAC structure, as shown in Figure 9.

By BIC or AIC criteria, the QAC data $\omega_{t}$ is fitted by the the mean model, namely, $\omega_{t} = \gamma+\varepsilon_{t}, t = 1, 2, \dots, 550$. We substitute the $\omega_{t}$ sequence into the ratio-typed test based on M-estimation, and find $V_{M} = 3.6375 > 1.4133$ at $s^{*} = 348$. That is, $\omega_{t}$ occured a change in mean at $s^{*} = 348$ (the red dashed line in Figure 9), and is divided into two segments. The first part is $\gamma_{1}, \gamma_{2}, \dots, \gamma_{348}$ with a sample mean of $\gamma_{1}^{\ast } = 0.9155$, and the second one involves $\gamma_{349}, \gamma_{350}, \dots, \gamma_{580}$ with a sample mean of $\gamma_{2}^{\ast } = 0.6373$. The standard error of the mean estimate based on M-estimation is 0.0075, which indicates that our proposed method is highly reliable. By this, we verify that the daily data of the USD/CNY exchange rate $y_{t}$ from May 12, 2009 to August 31, 2011 has a change in the autocorrelation coefficient.

5.   Conclusions

In this paper, we primarily studied the change-point test of the QAC for heavy-tailed sequences. In order to improve the efficiency, the moving window method was used to convert the QAC change to the mean change, and the ratio-typed test based on M-estimation was proposed to test the mean change. The methods not only eliminated the influence of outliers, but also extended the theory on QAC change detection of Gaussian sequences to heavy-tail process with tail index $\kappa \in (0, 2)$. Under some regular conditions, the asymptotic distribution under the null hypothesis was a functional of a Wiener process, which was independent of the tail index, and the consistency was also obtained under the alternative hypothesis. The simulation results revealed that these procedures have good performance even if the sequence was heavy-tailed. In summary, we can combine the moving window method with a ratio-typed test based on M-estimation to test the change in the QAC with a heavy-tailed series.

Author contributions

Xiaofeng Zhang: Writing-original draft, Software; Hao Jin: Methodology, Writing-review & editing; Yunfeng Yang: Validation. All authors have read and agreed to the published version of the manuscript.

Use of AI tools declaration

All authors declare that they have not used Artificial Intelligence tools in the creation of this article.

Acknowledgments

The authors would like to thank Prof. John Nolan who provided the software for generating stable innovations and fitting the tail index. The authors are also thankful for the financial support from NNSF (Nos.71473194) and SNSF (Nos.2020JM-513).

Conflict of interest

All authors disclose no conflicts of interest.