Fractional generalized cumulative residual entropy: properties, testing uniformity, and applications to Euro Area daily smoker data

1.   Introduction

Rao et al. ^[17] presented the concept of cumulative residual entropy (CRE) for a random variable (RV) X, which plays a significant role across various scientific disciplines for quantifying the uncertainty measure in the RV X. In this paper, X represents a non-negative RV characterized by the continuous cumulative distribution function (CDF) $F$ along with its associated probability density function (PDF) $f$. The CRE is expressed as

where $\Theta(x) = \log(\overline{F}(x)),$ $x > 0$. Numerous extensions of the CRE have been proposed, incorporating additional parameters to enhance their adaptability to a wide range of probability distribution shapes. Di Crescenzo and Longobardi ^[6], as well as Navarro et al. ^[13], introduced and examined a similar model known as cumulative entropy. This model is described concerning the CDF $F$ as follows:

where $X$ is supported by $(0, d)$. Xiong et al. ^[22] presented the fractional cumulative residual entropy in the following manner:

Adding a further term can result in a better relationship with other valuable measures. In particular, Di Crescenzo et al. ^[5] considered fractional generalized cumulative residual entropy (FGCRE) for any non-negative RV X. FGCRE is expressed as

where $G(\gamma) = \frac{1}{\Gamma(\gamma+1)}$, $\gamma\geq0$. Moreover, if $\gamma = n\in \mathbb{N}$, thus $G(n) = \frac{1}{n!}$ which is the case studied by Psarrakos and Navarro ^[15] as the generalized cumulative residual entropy. It is evident that $FGCRn_{\gamma}(X)$ is regarded as a dispersion measure. Additionally, the measure relates to a nonhomogeneous Poisson process's inter-epoch intervals and relevance transformation, as shown in Toomaj and Di Crescenzo ^[19]. Moreover, Alomani and Kayid ^[3] discussed further properties of the FGCRE.

A helpful manual for goodness-of-fit testing with statistics derived from the empirical CDF was given by Stephens ^[18]. Moreover, ^[18] carried out power comparisons of several uniformity tests. Dudewicz and Van der Meulen ^[8] examined the power analysis of the uncertainty when employed for the uniformity test. Additionally, by contrasting it with other uniformity tests, they demonstrated that the entropy-based test has strong power attributes for diverse alternatives. Noughabi ^[14] examined some of the aspects of the CRE and created a uniformity test based on it. He also contrasted the power and percentage points of seven different distributions. To test for consistency, Mohamed et al. ^[11,12] employed fractional CRE and cumulative residual Tsallis entropy measurements, respectively.

In this consideration, the FGCRE is employed to conduct a uniformity test. It is found in the study that the test conducted under FGCRE is being compared with other tests in terms of power. The succeeding contents of this article are arranged in the subsequent order: In Section 2, we reintroduce and modify some properties of the FGCRE. Section 3 introduces the FGCRE test statistic for assessing uniformity and examines specific characteristics, such as stability. In Section 4, we suggest techniques for determining the percentile values of FGCRE. Moreover, we compute the percentile values of FGCRE. Section 5 employs a Monte Carlo method to compare the power of various tests for uniformity against alternative distributions. Besides, we use the real data of the daily smokers in the countries of the Euro Area to get the test power estimations. At the end of the article, we apply the empirical form of the FGCRE to the exponential distribution.

2.   Some features of the fractional generalized cumulative residual entropy

This section will discuss some further aspects of the FGCRE. Alomani and Kayid presented the following theorem ^[3], and we will represent its proof with more details and modifications.

Theorem 2.1. Provided that the random vector (RVT) $X = \{X_{j}\}_{j = 1}^{n}$ in $\mathbb{R}^{n}$. Therefore, from (1.4), we have:

(1) For some $m > \frac{1}{\gamma}$, $X_{j}\in \mathbb{L}^{m}$, $E[|X_{j}|^{m}] < \infty$, $1\leq j\leq n$. Thus, for all $0 < \gamma < 1$, $FGCRn_{\gamma}(X) < \infty$.

(2) For some $m > \gamma$, $X_{j}\in \mathbb{L}^{m}$, $E[|X_{j}|^{m}] < \infty$, $1\leq j\leq n$. Thus, for all $\gamma\geq1$, $FGCRn_{\gamma}(X) < \infty$.

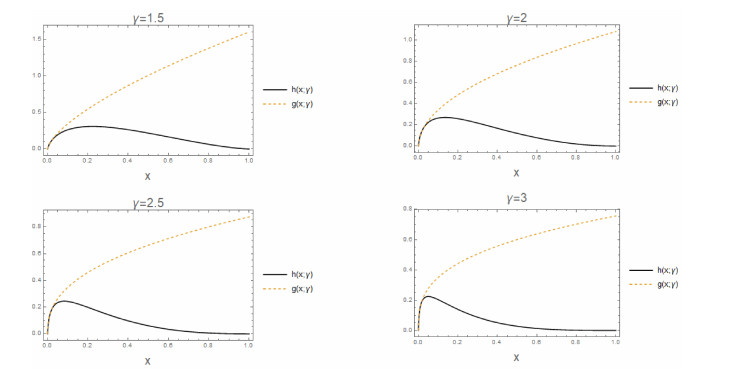
Proof. We can readily verify that the function defined by $h(x; \gamma) = G(\gamma)x[-\Theta(x)]^{\gamma}$ reaches its maximum value $\frac{G(\gamma)\gamma^{\gamma}}{ e^{\gamma}},$ at $x_0 = e^{-\gamma}$, for all $0\leq x\leq 1$ and $\gamma\geq0$. In addition, we have

In the sequel, it is important to prove the following inequality:

where $w(x; \gamma) = \frac{x^{\lambda}}{(1-\lambda)^{\gamma}}$, $\lambda = \gamma$ when $0\leq\gamma\leq1$, $\lambda = \frac{1}{\gamma}$ when $\gamma\geq1$, and in both cases we have $0\leq\lambda\leq1$. The inequality (2.2) has two cases: first, if $w(x; \gamma)\geq1$ it holds, Second, if $w(x; \gamma) < 1$, we get $x < (1-\lambda)^{\frac{\gamma}{\lambda}}$. Therefore, the ratio

where the last line is obtained from (2.1) (i.e. $G(\gamma)(1-\lambda)^{\frac{\gamma}{\lambda}}\left(-\log \left[(1-\lambda)^{\frac{\gamma}{\lambda}}\right]\right)^{\gamma} \leq \frac{G(\gamma)\gamma^{\gamma}}{ e^{\gamma}}$, $0\leq\lambda\leq1$). Figure 1 shows the behavior of functions.

Next, for each $\gamma\geq0$, from the inequality (2.2), we have

By integrating both sides of (2.3) across $\mathbb{R}^{n}_{+} = \{x_j\in\mathbb{R}^{n}; x_j\geq0\}$ and employing the Markov inequality, the result obtained is:

if $\frac{m\lambda}{n} > 1$, then it is finite. Therefore, for any $m > n$, we can select $\lambda < 1$ (close to one sufficiently) such that $\frac{m\lambda}{n} > 1$, and consequently, the outcome holds. □

Theorem 2.2. Suppose that the $N$-dimensional RVTs $X_{n}$ is converge in distribution to a RVT $X$ (i.e., $X_{n}$ ${ \begin{array}{c} \stackrel{dis}{\longrightarrow}\\ {n}\end{array}} X$). Moreover, let $m > N$, $X_n\in L^{m}$, for all $n$. Then,

[Weak convergence]

Proof. Since $X_{n}$ ${ \begin{array}{c} \stackrel{dis}{\longrightarrow}\\ {n}\end{array}} X,$ we have

On the other hand, from (2.3), we have

The $j$th component of the RVT $X_n$ is denoted by $X_{n_{j}}$, and $I_\mathbb{A}(x)$ represents the indicator function, defined as $I_\mathbb{A}(x) = 1$ if $x\in \mathbb{A}$, and $I_\mathbb{A}(x) = 0$ if $x\notin \mathbb{A}$. Hence, when $\frac{m \lambda}{N} > 1$, the expression $\overline{F}_{|X{n}|}(x)(-\log \overline{F}_{|X{n}|}(x))^{\gamma}$ is constrained by a function that is integrable. Additionally, for any $m > N$, it is possible to select $\lambda < 1$ close enough to one such that $\frac{m\lambda}{N} > 1$. The proof is concluded by applying the dominated convergence theorem. □

Alomani and Kayid presented the following theorem ^[3], and we will represent its proof with modifications and more details. Below, we demonstrate that the measure $FGCRn_{\gamma}(X)$ prevails over the classical Shannon entropy, a condition that can occur when $X$ possesses a density.

Theorem 2.3. Provided that the non-negative RV $X$ follows CDF $F_X(x)$, thus, we have

where $T(\gamma) = e^{\int_{0}^{1}\log\left(G(\gamma)x(-\log x)^{\gamma}\right)dx} < \infty$ and $SHn(X) = -\int_{0}^{\infty}f(x)\log f(x) dx$ is the classical Shannon entropy.

Proof. Since, the log-sum inequality indicates for the following expression that

Moreover, the expression on the left-hand side in Eq (2.4) is obtained as

Therefore,

After exponentiating both sides of (2.5) and employing (2.1), the outcome emerges, wherein $T(\gamma) = e^{\int_{0}^{1}\ln\left(G(\gamma)x(-\log x)^{\gamma}\right)dx}\leq \frac{G(\gamma)\gamma^{\gamma}}{ e^{\gamma}}\leq1$ remains finite. This concludes the proof. □

3.   Additional theoretical elements and a statistic for testing uniformity

Suppose we have $X_{1}, X_{2}, ..., X_{n}$ as a random sample following a continuous CDF $F$ supported in the interval $[0, 1]$. Additionally, the corresponding order statistics are denoted by $X_{(1)}\leq X_{(2)}\leq...\leq X_{(n)}$. For $FGCRn_{\gamma}(F)$, we can propose its estimator as $FGCRn_{\gamma}(F_{n}) = \int_{0}^{\infty} g({\bar F}{n}(x); \gamma) dx, \; \gamma > 0,$ where $\bar{F}{n}(x) = 1-F_{n}(x)$ and $F_{n}(x)$ represents the empirical CDF, which is expressed as

Furthermore, for the purpose of obtaining a consistent test of the uniformity hypothesis, we think of employing a consistent statistical test as follows:

where ${\cal M}_{j} = G(\gamma)\left(1-\frac{j}{n}\right)\left[-\log\left(1-\frac{j}{n}\right)\right]^{\gamma},$ $\gamma > 0,$ and $\Omega_j = (X_{(j+1)}-X_{(j)}),$ $j = 1, 2, ..., n-1.$

Theorem 3.1. The test relying on the sample estimate ${\cal T}_{n}(\gamma)$ maintains its consistency.

Proof. Based on the Glivenko-Cantelli theorem, as discussed in Howard ^[9], it can be inferred that $\sup_{y} |F_{n}(y)-F(y) | { \begin{array}{c} \stackrel{a.s.}{\longrightarrow}\\ {n}\end{array}}0$ (i.e., almost surely as $n$ tends to $\infty$). Furthermore, it can be readily claimed that $FGCRn_{\gamma}(F_{n}) { \begin{array}{c} \stackrel{a.s.}{\longrightarrow}\\ {n}\end{array}}FGCRn_{\gamma}(F)$, and the proof holds. □

In order to set up the uniformity test based on the null hypothesis $H_{0}$, the following theorem is required.

Theorem 3.2. If the non-negative RV $X$ adheres to a CDF $F$ with support on $[0, 1]$, then $0 \leq FGCRn_{\gamma}(F) \leq \frac{G(\gamma)\gamma^{\gamma}}{ e^{\gamma}}$ holds. Additionally, the value $\frac{1}{2^{\gamma+1}}$ is exclusively achieved by the standard uniform distribution (i.e., $U(0, 1)$) for all $\gamma > 0$.

Proof. We can see that the inequality $0\leq FGCRn_{\gamma}(F)\leq \frac{G(\gamma)\gamma^{\gamma}}{ e^{\gamma}}$ can be readily derived from (2.1). Simultaneously, leveraging the strict concavity of $h(x; \gamma) = G(\gamma)x(-\log x)^{\gamma}$, we establish that $FGCRn_{\gamma}(F)$ returns a distributions of concave function supporting with $[0, 1]$. Consequently, $FGCRn_{\gamma}(F) = \frac{1}{2^{\gamma+1}}$ is exclusively attained by the $U(0, 1)$ distribution. This validates the proof. □

Remark 3.1. Due to the convergence in probability as $n$ approaches to $\infty$, we have $FGCRn_{\gamma}(F_{n}){ \begin{array}{c} \stackrel{p}{\longrightarrow}\\ {n}\end{array}}FGCRn_{\gamma}(F)$, therefore we observe ${\cal T}_{n}(\gamma) { \begin{array}{c} \stackrel{p}{\longrightarrow}\\ {n}\end{array}} \frac{1}{2^{\gamma+1}}$ under the null hypothesis $H_{0}$. Conversely, under the hypothesis of alternative (that $F$ represents any CDF supported with the interval $[0, 1],$ except for the $U(0, 1)$ distribution), ${\cal T}_{n}(\gamma) { \begin{array}{c} \stackrel{p}{\longrightarrow}\\ {n}\end{array}}\delta$, where $\delta$ could be either smaller or larger than $\frac{1}{2^{\gamma+1}}$.

Theorem 3.3. If $X_{1}, X_{2}, ..., X_{n}$ are defined as a random sample taken from an unspecified continuous CDF $F$ on the interval $[0, 1]$, then ${\cal T}{n}(\gamma)$ satisfies the inequality $0\leq {\cal T}{n}(\gamma)\leq \frac{G(\gamma)\gamma^{\gamma}}{ e^{\gamma}}$, where $\gamma > 0$.

Proof. Considering Eq (2.1), we find that

This concludes the result. □

Theorem 3.4. Under the null hypothesis $H_{0}$, the mean and variance of the statistic ${\cal T}_{n}(\gamma)$ are provided, respectively, by

Proof. It is evident that for every $j = 1, 2, ..., n-1,$ the RV ${\Omega}_j,$ which follows a $U(0, 1)$ distribution, possesses a beta distribution based on the $(1, n)$ parameter-vector, denoted as $\Omega_j\sim Beta(1, n)$ (cf. ^[4]). This concludes the proof. □

Remark 3.2. Under $H_{0},$ we obtain $\lim_{n\rightarrow \infty}\mbox{E}({\cal T}_{n}(\gamma)) = \frac{1}{2^{\gamma+1}}$ and $\lim_{n\rightarrow \infty}\mbox{Var}({\cal T}_{n}(\gamma)) = 0.$

The interval $[lower, upper]: = [FGCRn^{o}_{\gamma, \frac{\alpha}{2}}, FGCRn^{o}_{\gamma, 1-\frac{\alpha}{2}}]$ delineates the region crucial for defining the uniformity test, where $\alpha$ denotes the specified level of significance, and $FGCRn^{o}_{\gamma, \alpha}$ represents the $\alpha-$quantile function of the approximate or asymptotic CDF $FGCRn_{\gamma}(F_{n})$ test statistic under the null hypothesis $H_{0}$.

The stability of information measures has been explored in various literature sources, as noted in references ^[1,2,22]. Similarly, we introduce the concept of stability for the $FGCRn_{\gamma}$ in the subsequent definition.

Definition 3.1. If $X_{1}, X_{2}, ..., X_{n}$ constitute a random sample following a continuous CDF $F$, and $\chi_{1}, \chi_{2}, ..., \chi_{n}$ represent any minor alterations from this random sample. The empirical $FGCRn_{\gamma}$ remains stable provided that for every $\tau > 0$, $\exists$ $\theta > 0$, the condition $\sum_{k = 1}^{n}|X_{k}- \chi{k}| < \theta$ implies $|FGCRn{\gamma}(\bar{F}{n}(X))-FGCRn{\gamma}(\bar{F}_{n}(\chi))| < \tau$, where $n \in \mathbb{Z}^{+}$.

The following theorem provides a condition sufficient for determining the stability of the empirical $FGCRn_{\gamma}$.

Theorem 3.5. Provided any continuous RV $X,$ the empirical $FGCRn_{\gamma}$ is stable if $X$ is distributed on finite, closed, or open intervals.

Proof. Assuming that the RV $X$ is confined within the finite interval $[\alpha, \beta]$, where $\alpha\geq0$ and $\beta < \infty$. For the brevity sake, denote $W_k = g\left({\bar F}_{n}(X_{(k)}); \gamma\right)$, $W_k' = g\left({\bar F}_{n}(\chi_{(k)}); \gamma\right)$, and $\Omega_k' = \chi_{(k+1)}-\chi_{(k)}$, then, the empirical $FGCRn_{\gamma}$ can be obtained based on (3.2) as $FGCRn_{\gamma}(\bar{F}_{n}(X)) = G(\gamma)\sum_{k = 1}^{n-1}W_k\; \Omega_k$, $\gamma\geq0$. Thus, when $\sum_{k = 1}^{n}|X_{k}- \chi_{k}| < \theta,$ we get

The validity of the second part in the second inequality line is justified concerning (2.1). Conversely, the justification for the first part of that inequality stems from the reality that, for any $t'$, $t''$, and arbitrarily small $\theta^\star > 0$, there exists $\tau^\star > 0$ where $|{\bar F}n(x')-{\bar F}n(x'')| < \tau^\star$ whenever $|t'-t''| < \theta^\star$ (cf. ^[22]), which implies $\left|W_k-W_k'\right|\leq \frac{\tau}{2 (\beta-\alpha)}$ whenever $\sum{k = 1}^{n}|X{k}- \chi_{k}| < \theta$. Now, selecting $\theta = \frac{\tau}{4}$ yields $G(\gamma)\frac{\tau}{2 (b-a)}(X_{(n)}-X_{(1)})+2\theta\leq \tau$. This concludes the proof. □

4.   Percentage points of the empirical $FGCRn_{\gamma}$ test statistic

In this part, we figure out the asymptotic distribution of ${\cal T}_{n}(\gamma)$, assuming the null hypothesis, by using three different methods. From (3.2), recall the test statistic ${\cal T}_{n}(\gamma) = \sum_{j = 1}^{n-1}{\cal R}_{j} = \sum_{j = 1}^{n-1}{\cal M}_{j}\Omega_j$, then we have

where the RV ${\cal R}_{j}$ has the PDF

the RV $Z$ represents the standard normal distribution (i.e., $N(0, 1)$), and $\Omega_j\sim \; Beta(1, n)$. Therefore, the mean and variance of ${\cal R}_{j}$ are $\mu_{j} = E({\cal R}_{j}) = {\cal M}_{j}\mbox{E}(\Omega_j) = \frac{{\cal M}_{j}}{n+1}$ and $\sigma^{2}_{j} = \mbox{Var}(R_{i}) = {\cal M}^{2}_{i}\mbox{Var}(\Omega_j) = \frac{n {\cal M}^2_{i}}{(n+1)^{2}(n+2)}$. Therefore, the first procedure to obtain the percentage point $FGCRn^{o}_{\gamma, \alpha}$ by using the normal asymptotic of ${\cal T}_{n}(\gamma)$ (normal approximation percentage points) is given by

Johannesson and Giri ^[10] illustrated an approximation method for the CDF of a linear combination of a limited number of RVs following the beta distribution. Noughabi ^[14] employed this finding to approximate and estimate the percentage points of the $FGCRn_{\gamma}$ for finite values of $n$. By employing a comparable approach, an approximation method for ${\cal T}_{n}(\gamma)$ for limited values of $n$ can be derived from the following expression (beta approximation percentage points):

such that $Beta^{-1}(\nu_{1}, \nu_{2})$ is the function of quantile of $Beta(\nu_{1}, \nu_{2})$ distribution, with

Moreover, in this second procedure, we have

We produce $50,000$ with $n = 10, 20, 30, 40, 50, 70,100$, samples of sizes from $U(0, 1)$. Employing (3.2), the test statistic ${\cal M}_{n}(\gamma)$ is assessed through the empirical FGCRE for each sample. Additionally, $FGCRn_{1.5}(U) = 0.1767$, $FGCRn_{2}(U) = 0.125$, $FGCRn_{2.5}(U) = 0.0883$, $FGCRn_{3}(U) = 0.0625$, $FGCRn_{3.5}(U) = 0.04419$, and $FGCRn_{4}(U) = 0.03125$, where $FGCRn_{\gamma}(U)$ represents the FGCRE of the CDF $U(0, 1)$. Consequently, for ${\cal M}_{n}(\gamma)$, the percentage points of the Monte Carlo procedure, asymptotic normality, and beta approximation are presented. Table 1 indicates that:

(1) Under fixed $n$ and increasing $\gamma$, the discrepancy between percentage points diminishes.

(2) Under fixed $\gamma$ and increasing $n$, the discrepancy between percentage points diminishes.

Moreover, it transpires that the difference among the three methods is not significant for ${\cal M}_{n}(\gamma)$. Figure 2 illustrates the empirical PDFs of the test statistics via Monte Carlo simulation samples with $n = 10, 20, 30, 50,100.$ It is observed that the test statistics converge closer to the exact values as $n$ increases, implying a reduction in bias and variance with increasing $n$.

5.   Uniformity test via power analysis

In this section, we investigate the power analysis of the Monte Carlo simulation procedure across different distributions. The value of the power of ${\cal T}_{n}(\gamma)$ is gauged by the ratio of generated samples falling within the critical region. Across the distributions of seven alternatives, the power analysis of ${\cal T}_{n}(\gamma)$ is evaluated using the Monte Carlo procedure with 50,000 generated samples for each sample size of $n = 10, 20, 30$. The alternative distributions, as outlined by Stephens ^[18] in the investigation of uniformity tests, are utilized for this analysis by

According to Stephens' report ^[18], family $U1_p$ yields points closer to zero than expected under the assumption of uniformity, understood as a shift in the mean. Alternative $U2_p$ produces points near 0.5, indicating a trend towards reduced variance, while family $U3_p$ exhibits two clusters near 0 and 1, suggesting an increase in variance. Consequently, Stephens proposed that alternatives $U1$ and $U2$ yield points near 0 and 1, respectively, while alternative $U3$ produces points near 0 and 1. Our test's performance is compared to several omnibus tests, including Kolmogorov-Smirnov (Ko-S), Kuiper (Ku), Cramer-von Mises (C-v-M), Watson (Wn), and Anderson-Darling (An-D). These tests enjoy widespread popularity among practitioners in various fields. Based on the information presented in Table 2, the following conclusions can be drawn:

$(1)$ Under fixed $n$ and increasing $\gamma$, the power of the $FGCRn_{\gamma}$ test increases for alternative $U1$ and decreases for alternatives $U2$ and $U3$.

$(2)$ The power of the $FGCRn_{\gamma}$ test increases by increasing $n$ as $\gamma$ is fixed.

In this section, we will study the uniformity of the FGCRE among the daily smokers of the countries in the Euro Area, see ^[7]. Figure 3 shows the data analysis, where the daily smokers are individuals aged 15 and above who report smoking daily. The goodness-of-fit test problem is for the $U(\alpha, \beta)$ distribution. The PDF of the $U(\alpha, \beta)$ distribution is expressed as $f(r) = \frac{1}{\beta-\alpha}$; where $\alpha < r < \beta$. If $(\alpha, \beta)$ are provided, then the transformation $Z = \frac{U-\alpha}{\beta-\alpha}$ provides a random sample from the $U(0, 1)$ distribution. Thus, tests can be readily applied by converting them into standard uniform samples. The power analysis of these tests remains unaffected for assessing the $U(\alpha, \beta)$ distribution when $(\alpha, \beta)$ are given. In cases where the parameters are unknown, they can be estimated from the data using maximum likelihood estimators. Let $U_{1}, U_{2}, ..., U_{n}$ be an $n$ size random sample that follows the $U(\alpha, \beta)$ distribution. The maximum likelihood estimators for $\alpha$ and $\beta$ are the first and $nth$ order statistics $U_{(1)}$ and $U_{(n)}$, respectively. Next, by the transformation $Z_{i} = \frac{U(i+1)-U(1)}{U(n)-U(1)}$, $i = 1, 2, ..., n-2$, a random sample of size $n-2$ from the $U(0, 1)$ distribution is obtained. Consequently, this conversion changes the testing of $U(\alpha, \beta)$ from a sample size of $n$ to testing $U(0, 1)$ from a sample size of $n-2$. Therefore, we apply the chi-squared test for the given data, which returns p-value = 0.7788. Furthermore, to transform the data to fit $U(0, 1)$ using the quantile function, we apply a one-sample Kolmogorov-Smirnov test, which returns p-value = 0.8743, see Figure 4. Figure 5 shows the empirical and theoretical values of the $FGCRn_{\gamma}$ of the data set's uniform and standard uniform distribution. We can see that it decreases as $\gamma$ increases.

To study the test of uniformity for the real set of data we performed 50000 bootstrap samples each of sizes $n = 8, 12, 15$. We have illustrated the method by the algorithm as shown in Figure 6.

Similarly, the steps for the rest of the alternatives. Table 3 shows the test power estimations at a significance level of $\alpha = 0.05$ of the daily smokers of the countries in the Euro Area data. Therefore, we can see that by increasing the sample size, the power increases.

6.   Features on fractional cumulative residual entropy via exponential distribution

This part discusses some features of the FGCRE and uses non-parametric estimation techniques under the exponential distribution.

Example 6.1. If the RV X follows an exponential distribution having parameter $\theta$ (i.e. $exp(\theta)$) follows CDF $F(x) = 1-e^{-\theta x}$. Then, from (1.4), we have $FGCRn_{\gamma}(X) = \frac{1}{\theta}$.

In the following example, we discuss the first-order statistic of FGCRE under the exponential distribution.

Example 6.2. Based on the order statistics $X_{(1)}\leq X_{(2)}\leq...\leq X_{(n)}$, and the first order statistic $X_{(1)}$ follows a CDF $F(X_{(1)}) = 1-(1-F(x))^{n}$. Then, we can see that the FGCRE, under the exponential distribution, is given by $FGCRn_{\gamma}(X_{(1)}) = \frac{1}{n \; \theta}$.

The primary benefit of the new FGCRE measure is its applicability to heavy-tailed distributions where the mean $E(X) < \infty$ but $E(X^2)$ is infinite. At the same time, the standard deviation does not exist. Yang ^[23] discusses the cumulative residual entropy as an alternative risk measure. Moreover, Ramsay ^[16] illustrated that the standard deviation is not an appropriate measure for large insurance risks with long-tailed skewed distributions. The next example discusses this issue.

Example 6.3.3 Let the standard deviation $\sqrt{Var(X)}$ of a risk $X$ be a common risk measure in insurance. Moreover, Wang ^[20] presents the right-tail deviation risk measure as

Therefore, under the exponential distribution, we see that

which is independent of $\gamma$. Then, we can see no difference among the three measures.

Remark 6.1. In the exponential distribution, where the $FGCRn_{\gamma}$ measure equals $\frac{1}{\theta}$. Then, it usually refers to the distribution's average or expected value, which offers crucial details regarding the RV's central tendency.

We can illustrate the uses of Remark (6.1) by studying the increasing failure rate average (IFRA) and decreasing failure rate average (DFRA) of the FGCRE. Let $X$ be the lifetime of a component or a system with an absolutely continuous CDF $F$. We say that F is IFRA (DFRA) if $\frac{[-\Theta(x)]}{x}$ is an increasing (decreasing) function in $x > 0$.

Proposition 6.1. If X is IFRA (DFRA), then, from (1.4), we have

and for the exponential distribution, the equality holds.

Proof. Suppose that X is IFRA (DFRA), then

then, from (1.4) with $\gamma\geq1$, we get

According to Remark (6.1), equality is held for the exponential distribution. □

In the next step, we can use the empirical measure of the FGCRE introduced in (3.2), which depends on the empirical CDF given in (3.1) as ${\cal T}_{n}(\gamma) = \sum_{j = 1}^{n-1}{\cal M}_{j}\Omega_j$.

Proposition 6.2. Provided that the random sample $X_{1}, X_{2}, ..., X_{n}$ follows $exp(\theta)$. From (3.2), due to the independence of sample spacings, $\Omega_{p}$ adheres to the exponential distribution with parameter $\theta(n - p)$, $p = 1, 2, ..., n-1$. Therefore, we obtain

(1) The expectation and variance of $FGCRn_{\gamma}(F_{n})$ are

(2) For any $\gamma > 0$, we have

Proof. Part (ⅰ) follows directly. In part (ⅱ), we observe that $FGCRn_{\gamma}(F_{n})$ may be represented as the accumulation of independent exponential RVs $\Omega_p$ having an expected value of $\frac{{\cal M}_{p}}{\theta(n-p)}$. The remainder of the proof proceeds with analogous reasoning from ^[12]. Therefore, it is excluded. □

Figure 7 shows the empirical and theoretical $FGCRn_{\gamma}$ of $exp(\theta)$ under different values of $\theta$ and a sample size of $n = 5000$. We can see that the empirical $FGCRn_{\gamma}$ is far from the theoretical by increasing $\theta$.

Table 4 shows the expected value and variance of the empirical $FGCRn_{\gamma}$ under different values of $\theta$ and $n = 5000$. Therefore, we can see that

$(1)$ For fixed $\gamma$, the variance decreases as $\theta$ increases.

$(2)$ For fixed $\theta$, the variance increases as $\gamma$ increases.

7.   Conclusions

By the end of this paper, we have represented and modified some features of FGCRE and illustrated its weak convergence. Based on the empirical version of our model, we study the stability, and using three approximation methods, we obtain the percentage points whose accuracy depends on the increasing and decreasing of $n$ and $\gamma$. Moreover, we perform the uniformity test with the power estimates of our test statistic and other tests. We conclude that our test statistic accuracy depends on the value of $\gamma$ to achieve its priority. Under the real data of the daily smokers of the countries in the Euro Area, we have fitted it to uniform distribution and given the algorithm to show how to make the test of uniformity with the power analysis. Finally, we apply the empirical version of our form to the exponential distribution and figure out that the variance depends on the values of $\gamma$ and $\theta$. In forthcoming research, certain studies related to entropy, such as quantum X-entropy in generalized quantum evidence theory (Xiao ^[21]), will be explored.

Author contributions

All authors have equally contributed to this work, and all authors have read and approved the final version of the manuscript for publication.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This study is supported via funding from Prince sattam bin Abdulaziz University project number (PSAU/2024/R/1445).

The authors extend their appreciation to the Deanship of Scientific Research at Northern Border University, Arar, KSA for funding this research work through the project number "NBU-FFR-2024-2727-04".

Conflict of interest

The authors confirm no conflict of interest.