Stochastic inequalities involving past extropy of order statistics and past extropy of record values

1.   Introduction

Information theory plays a crucial role in the quantification of the uncertainty present in probability distributions. One of the fundamental measures in information theory is entropy, which was introduced by Shannon ^[33]. Entropy is a quantity with many applications in various fields, namely information science, statistical mechanics, probability and statistical analysis, communication and also economics. Let us consider a random variable (rv) $X$, which represents the length of life of a life unit. Let us assume that $X$ has a probability density function (pdf) $f(x)$. Then the Shannon differential entropy, denoted as $H(X)$, is defined as the negative expected value of the logarithm of $f(X)$, provided that the expected value is meaningful. Recently Lad et al. ^[19] introduced a new measure of uncertainty called "differential extropy". To simplify the terminology, we will refer to "differential extropy" simply as "extropy" hereafter. This quantity acts as the dual complement of entropy. For a non-negative rv $X$ with pdf $f(x)$ and survival function (sf) $S(x)$, the extropy of $X$, denoted by $J(X)$, is obtained as follows:

where $\mathbb{E}(\cdot)$ represents the expectation operator, $U$ is a random number from $[0, 1]$ and $F^{-1}(u)$ stands for the right-hand inverse function of $F$. This measure has proven to be a powerful tool for quantifying uncertainty, and it is widely used in various fields of research. Qiu and Jia ^[26] considered an estimator of extropy to create a goodness-of-fit test for the uniform distribution. Qiu et al. ^[28] applied extropy to analyze the lifetime of mixed-reliability systems. Balakrishnan et al. ^[4] provided an application of Tsallis extropy in pattern recognition.

It is often necessary to consider the current age of the system in order to estimate the uncertainty regarding the remaining lifetime of the system. For example, operators want to estimate the uncertainty regarding the remaining lifetime of the system if they have information about the operation of the system at a certain time $t$. This remaining lifetime, denoted as $X^t = [X-t \mid X > t]$, corresponds to the time remaining for the system if it has already been operated for a duration of $t$. In this situation, the extropy measure $J(X)$ may not be appropriate. Qiu and Jia ^[26] a novel method, which is described as follows:

for all $t > 0,$ where ${f(x+t)}/{S(t)}$ denotes the pdf of $X^t.$

In the realm of real systems, uncertainty is a pervasive feature that affects future events and past events. This realization has motivated the development of a complementary concept of extropy that specifically captures uncertainty related to past events and differs from the traditional notion of extropy for the remaining lifetime, which is used to evaluate uncertainty related to future events. Imagine an rv $X$ that represents the lifetime of a system. Note that the pdf of $X_t = [X \mid X < t]$ is captured as $f_t(x) = \frac{f(x)}{F(t)}$ such that $x\in (0, t)$. In view of this, the past extropy (PEX) at time $t$ for rv $X$ is defined as follows (see ^[17,36])

for all $t > 0.$ Note that $\bar{J}(X; t)$ has a wide range of possible values, from negative infinity to positive infinity. In the context of analyzing system failures, $\bar{J}(X; t)$ serves as a valuable metric to quantify the uncertainty caused by the past lifetime or inactivity time of a system, especially in scenarios in which the system is inactive at time $t$. This metric proves particularly useful when comparing random lifetimes, as it allows the identification of subtle variations in the underlying distributions of past lifetimes.

Order statistics play an essential role in the construction of a model for the lifetime of systems. This study is concerned by exploring the PEX for typical ordered rvs derived from a continuous distribution. Order statistics have proven useful in structural reliability engineering (see Bulleit and Liu ^[7], Rosowsky and Bulleit ^[29], van de Lindt and Goh ^[37], Diamoutene et al. ^[10], and Yamakawa and Ohsaki ^[42]). Record values and extreme value theory have also proven useful in construction (see e.g., Dymiotis et al. ^[11], Saini and Ray-Chaudhuri ^[30], and Ozer and Feng ^[22]). In reliability theory, order statistics are crucial, especially when analyzing the lifetime characteristics of coherent systems and when performing lifetime tests with censored data. For a comprehensive understanding of this topic, the work of David and Nagaraja ^[9] is recommended, which provides a comprehensive overview.

In addition, the lower record statistic of a sequence of identical and independently distributed (i.i.d.) rvs $\{X_i; i = 1, 2, \ldots\}$ is examined. The analogous analysis is also applied to the order statistics. A lower data set exists if an observation $X_j$ has a value that is smaller than all previous observations, i.e. $X_i > X_j$ applies to every $i$ for which $i < j$. Records are important in numerous real-world scenarios and statistical applications. They are often of interest when it comes to observing new records, such as Olympic records, and they prove useful in areas such as reliability theory. Consider, for example, the scenario in which wooden beams are tested for their breaking strength, as Glick ^[13] has explained. Further insights into records and their many applications can be found in the work by Arnold et al. ^[2] a comprehensive resource. Jose and Sathar ^[16] focused on studying the residual extropy of k-data sets derived from various continuous probability distributions. They investigated the properties and characteristics of extropy with respect to these data sets. In another study, Xiong et al. ^[41] presented a new test for evaluating the symmetry of continuous distributions. This test was based on the symmetric nature of the extropy of data set values and included specific characterizations of exponential distributions (EDs).

The study of information properties in the context of organized data has received considerable attention from various researchers. Notable contributions in this area include the work of Wong and Chen ^[39], Park ^[23], Ebrahimi et al. ^[12], Zarezadeh and Asadi ^[43], and Baratpour et al. ^[6]. These researchers have made considerable efforts to investigate the information properties that are inherent in ordered data and to shed light on the underlying characteristics and structures. In recent years, extropy has emerged as a measure of information that is attracting considerable attention. Notable studies in this area include the work of Lad et al. ^[19], Qiu ^[25], and Qiu and Jia ^[26], among others. Qiu ^[25] presented insightful comparative results on extropy and investigated the conditions for the uniqueness of extropy in terms of the order statistics and record values. They also investigated the monotonic properties and lower bounds of extropy for the order statistics and record values, as further discussed by Qiu and Jia ^[26]. In a recent study by Shrahili and Kayid ^[34], they developed the concept of residual extropy for the i-th order statistic. In particular, they focused on establishing the link between the residual extropy of the $i$-th order statistic and the residual extropy of the $i$-th order statistic derived from a random sample generated from a uniform distribution; they then obtained several useful results.

The aforementioned works have examined the extropy of the order statistics and the record values for the remaining terms. Building on these foundations, here we investigate the extropy of the order statistics and lower record values for past lifetimes, an area that has received little attention. The main focus of this study is to fill the existing gap in the literature regarding the study of the extropy properties of order statistics and record values in the past. In particular, the use of extropy in this study provides computational simplicity compared to other information measures discussed by Zarezadeh and Asadi ^[43]. Consequently, it is possible to calculate the PEX of order statistics and capture values for different distribution functions. This computational simplicity increases the practicality and applicability of the proposed approach and enables efficient analysis in different scenarios.

Moreover, the proposed method proves its effectiveness in the evaluation of distribution functions, which is confirmed by previous research. The applicability of the method also extends to the area of reliability systems, where the interpretation of order statistics as lifetimes of $i$-out-of-$n$ systems becomes relevant. This demonstrates the extensive versatility and broad applicability of the proposed method in the comprehensive analysis of reliability and distribution tests. By using this method, researchers and practitioners can gain valuable insights into the performance and behavior of systems, which can improve their understanding and enable informed decisions in various fields. In addition, the results of this study have the potential to be used to predict the remaining useful life of lithium-ion batteries by using extropy feature extraction and support vector regression techniques. An important reference related to this context is the work of Jia et al. ^[15], which investigates the use of similar approaches.

Here one will find some background information on this application. Since lithium batteries are used in many different types of electronic devices, it is possible to avoid unexpected device failures by accurately predicting their remaining useful life. In a recent study by Weddington et al. ^[38]; they focused on improving the reliability of remaining useful life predictions by integrating prediction results obtained by using different techniques. The aim was to reduce the uncertainty associated with these predictions. Specifically, models based on the extended Kalman filter and the particle filter were developed by using feature data. A fusion approach using the Dempster-Shafer theory was then applied to combine the results obtained with the Kalman filter and the particle filter. Chen et al. ^[8] presented a new method for online prediction of the remaining useful life of lithium-ion batteries based on permutation entropy. Qu et al. ^[24] proposed an adaptive noise suppression method to predict the remaining useful life of lithium-ion batteries.

The concepts and methods discussed can be applied in these areas and benefit from related research, such as that contributed by Al-Qazzaz et al. ^[1], Wu et al. ^[40], and Liu et al. ^[20]. By utilizing the insights and techniques explored in these publications, researchers and practitioners in the field of machine learning and deep learning can further improve their models and algorithms.

The contents of the paper are organized as follows. In Section 2, we present a representation of the PEX of the ordered rv $X_{i:n}$, the $i$-th smallest value among $X_1, \ldots, X_n$ as an i.i.d sample, which is taken from the cumulative distribution function (cdf) $F$. A lower boundary condition is derived for the PEX of the order statistics, since closed-form expressions for the PEX of the order statistics are often not available in many statistical models. In order to provide practical insights, several illustrative examples are presented that show the application of these bounds. It is shown that the PEX of the minimum and maximum values in a random sample exhibits monotonic behavior with respect to the number of observations under mild conditions. Section 3 considers the properties of the PEX of lower record values. Constraints are placed on the PEX of lower record statistics and it is confirmed that the PEX of records under appropriate conditions grows monotonically with the number of records in the underlying sequence of rvs. By studying the relationships, deriving bounds, and investigating the monotonic behavior, this paper contributes to a comprehensive understanding of the PEX of ordered rvs. Section 4 presents some computational results that validate some of the conclusions drawn from this study. Estimators for calculating the PEX of the ED are offered. For this reason, the maximum likelihood estimator (MLE) is derived. Section 5 concludes the study conducted in this paper.

In the remaining part of the paper, the notations "$\le_{st}$", "$\le_{hr}$", "$\le_{lr}$" and "$\le_{d}$" are used to signify the usual stochastic order, the hazard rate order, the likelihood ratio order and the dispersion order. Further properties and a more detailed discussion of these stochastic orders can be found in ^[31].

2.   Derivation of PEX for order statistics

We attempt here to find an expression that relates the PEX of order statistics obtained from a randomly distributed population to the PEX of order statistics obtained from a uniformly distributed population. To facilitate the analysis, the terms $f_{X_{i:n}}(x)$ and $F_{X_{i:n}}(x)$ are used to represent the pdf and cdf of the $i$-th order statistic $X_{i:n}$, respectively, where $i$ ranges from 1 to $n$. The density of $X_{i:n}$ is therefore

Further, the cdf of $X_{i:n}$ is:

where

in which $\bar{x} = 1-x$ and $a, b \in (0, +\infty).$ The function $I(\cdot, \cdot)$ is known in the literature as a complete beta function (see ^[9]). Another useful representation of the cdf $F_{X_{i:n}}$ is based on the imperfect beta function, which is obtained as

where

In this section, the notation $Y\sim B_t(a, b)$ indicates that the rv $Y$ satisfies the condition of the next density:

Our focus is on the study of the PEX associated with the order statistic $X_{i:n}$. The PEX of $X_{i:n}$ provides information about the extent and magnitude of uncertainty regarding the results of the conditional rv $[t-X_{i:n}| X_{i:n}\leq t]$. In this context, let us consider a system consisting of $n$ units, where the system operates as long as at least $(n-i+1)$ of the $n$ units are in operation. The lifetime of the system is represented by $X_{i:n}$, so $i$ denotes the situation of the underlying ordered rv. In the case of $i = 1$, the system operates as a system with a serial structure, while for $i = n$ it operates as a system with a parallel structure. In order to facilitate the computation of the PEX, a lemma is presented that establishes a connection between the PEX of the underlying ordered rv in the unitary case and the imperfect beta function. The next lemma plays a crucial role in the subsequent analysis and simplifies the computation of the PEX. The proof of this lemma is not included here as it is simple and follows directly from the definition of the PEX.

Lemma 2.1. Let $U_{i:n}$ stand as the $i$-th order statistic of a set of $n$ random numbers generated from $(0, 1)$ with equal chances. Then,

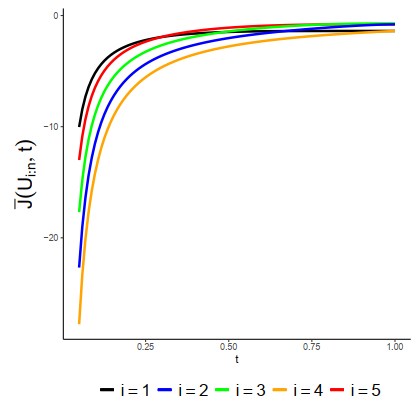
With the imperfect beta function and a uniform distribution, this lemma simplifies the calculation of the PEX of the order statistic. This makes it easier to apply the PEX in many contexts. The values of $\bar{J}(U_{i:n}; t)$ are shown in Figure 1 for certain cases when $i = 1, 2, \cdots, 5$ and $n = 5$. From the diagram shown, it can be seen that $\bar{J}(U_{i:n}; t)$ decreases with respect to $t.$

The following theorem establishes a connection between the PEX of order statistics from a uniform population and the PEX of $X_{i:n}$.

Theorem 2.1. If $X_{i:n}$ stands as the $i$-th order statistic of a set of $n$ random values adopted from cdf $F,$ then the PEX of $X_{i:n}$ is derived as follows:

where $Y_i\sim I_{F(t)}(i-\bar{i}, 2n-(i-\bar{i}))$ with $\bar{i} = 1-i.$

Proof. Making use of the change of variable $u = F(x)$, one extracts the following expressions by utilizing Eqs (1.2), (2.1) and (2.3):

The final equality is derived by applying Lemma 2.1. This step concludes the proof. □

For $t = +\infty$, the particular case of this result is provided by

such that $Y_i\sim I(i-\bar{i}, 2n-(i-\bar{i})),$ where $\bar{i} = 1-i.$ In the following result, a basic result is established regarding the monotonicity of the PEX of $X_{i:n}$ by assuming a descending reversed hazard rate of the component lifetimes $X$. Specifically, this means that the rv $X$ is a a distribution with the descending reverse hazard rate (DRHR) property if the reverse hazard rate (rhr) function of $X$, i.e., the function $\tau$ given by $\tau(x) = f(x)/F(x)$, decreases in $x$ for $x\in (0, +\infty)$.

Theorem 2.2. If $X$ has a distribution with the DRHR property, then $\bar{J}(X_{i:n}; t)$ increases in $t.$

Proof. The DRHR property of the distribution of $X$ allows $X_{i:n}$ to have a distribution with the DRHR property. Therefore, the proof follows directly from Theorem 1 of ^[18]. □

Remark 2.1. If $X$ is an absolutely continuous nonnegative rv with the support $(0, \infty),$ cdf $F$ and pdf $f,$ then $X$ is said to have the decreasing likelihood ratio (DLR) property if $f(x)$ is log-convex or, equivalently, if the function $f'(x)/f(x)$ is increasing in $x > 0.$ Since the DLR property implies the DRHR propery, if $X$ is DLR, then $\bar{J}(X_{i:n}; t)$ increases in $t.$

Using the upcoming example, the application of Theorems 2.1 and 2.2 is illustrated.

Example 2.1. Let us contemplate an rv $X$ with the cdf given by:

It is found that $f(F^{-1}(u)) = ku(-\ln u)^{\frac{k+1}{k}}$ for $0 < u < 1$ upon using the method of inverse transformation. After performing some manipulations, the following expression is obtained:

Numerical methods have been employed to investigate the relationship between the extropy of $\bar{J}(X_{i:n}; t)$ and the time $t$, as it is difficult to derive an explicit formula. The PEX trends with respect to $t$ for various choices of $k$, specifically $k = 0.5$, $k = 1$, and $k = 2$, are illustrated in Figure 2. It is plainly shown that $X$ possesses the DRHR property. Consequently, in line with Theorem 2.2 it is seen that as $t$ increases, so does the extropy of $\bar{J}(X_{i:n}; t)$.

Since the PEX of the underlying ordered rv has no explicit solution for many distributions, it is necessary to explore alternative approaches to characterize the PEX of order statistics. Given this restriction, one could explore the use of bounds to express the PEX of $X_{i:n}$. To this end, the next result is presented, which establishes a lower constraint for the PEX of order statistics and sheds light on their behavior in practical scenarios.

Theorem 2.3. For a nonnegative continuous rv $X$ with density $f$ and distribution function $F,$ let $\mathfrak{M} = f(m)$ be finite with $m: = \sup\{x:f(x)\in [0, \mathfrak{M}]\}$ as the mode of $F$. One has the following:

Proof. Because $f(F^{-1}(u))\leq \mathfrak{M}, \ \; \text{for every} \; u \in (0, 1),$ one thus gets

The proof is now complete, and the result may be obtained with ease from Eq (2.5). □

A lower constraint on the PEX of $X_{i:n}$ is provided by the following theorem. This lower limit is dependent on the mode of the base distribution, $m$, and the PEX of the underlying ordered rv in the uniform case. This solution provides a quantifiable lower bound for the PEX based on the mode of the distribution, and it provides relevant information about $X_{i:n}$. For a few common distributions, Theorem 3.3 is used to determine the PEX limits of the order statistics. A table showing the results is Table 1.

The next finding provides an upper bound on the parallel system's PEX in terms of the parent distribution's rhr function.

Theorem 2.4. Let $X$ denote a nonnegative continuous rv with the DRHR property. Then,

where $\tau(t)$ is the rhr of $X$.

Proof. If $X$ has the DRHR property, then Theorem 2.2 implies that $\bar{J}(X_{n:n}; t)$ increases in $t$. Therefore, based on Theorem 2.1 of ^[17] one has:

Since $\tau_{n:n}(t) = n\tau(t) \geq \tau(t)$, the last inequality is easily obtained which completes the proof. □

The monotonicity of the PEX of extreme order statistics with uniformly distributed components' lifetimes is explored in the ensuing lemma.

Lemma 2.2. The PTE of the system lifetime drops with an increasing number of components in a parallel (serial) structure with $n$ components whose lifetimes are evenly distributed over the unit interval.

Proof. The presumption is that the system operates in parallel. Analogous reasoning can be applied to a series system. Let us contemplate the rvs $Z_1$ and $Z_2$ with pdfs $f_{1, t}(z)$ and $f_{2, t}(z)$, respectively, given by:

It is then deduced that

By assuming that $\Theta(n)$ is a differentiable function of $n$, one can obtain

where

It is observed plainly that

where

It can be observed that $Z_{2}$ is greater than $Z_1$ in the usual stochastic order. Consequently, as $\ln(z)$ increases in $z$, by applying Theorem 1.A.3. of ^[31] one thus obtains that $\mathbb{E}[\ln(Z_2)]\geq(\leq)\mathbb{E}[\ln(Z_1)]$. This suggests that $\Theta(n)$ is a descending function of $n$ since (2.9) is positive (negative). That is, as the number of components increases, the PTE of the parallel system decreases. □

Theorem 2.5. Think of a parallel system made up of $n$ units with i.i.d. component lifetimes $X_1, \ldots, X_n$. Let us assume that $X_1$ has a growing pdf $f$. The system lifetime's PTE then has descending characteristics as $n$ increases.

Proof. Assuming that $Y_n\sim B_{F(t)}(2n-1, 1),$ $f_{Y_n}(y)$ indicates the pdf of $Y_n.$ Evidently,

increases in $y.$ It is deduced that $Y_n$ is less than $Y_{n+1}$ in likelihood ratio order and, therefore, $Y_n$ is also less than $Y_{n+1}$ in the usual stochastic order. In addition, $f(F^{-1}(x))$ increases with respect to $x.$ Therefore

From Theorem 2.1, one obtains

The first inequality is obtained by noting that $\bar{J}(U_{n:n}; F(t))$ is non-positive. The last inequality is obtained from Lemma 2.2. Thus, it can be inferred that $\bar{J}(X_{n:n}; t)\geq \bar{J}(X_{n+1:n+1};t)$ for every nonnegative $t.$ □

Certain distributions, like the power distribution, possess pdfs that exhibit increasing behavior. It is remarked that the result obtained from Theorem 2.5 does not hold universally for all systems with an $(n-i+1)$-out-of-$n$ structure. To illustrate this point, an example is given that demonstrates the deviation from the general validity of the theorem.

Example 2.2. Assume that for the system to function, at least $(n-1)$ of its $n$ components must function. Then, $X_{2:n}$, i.e., the second-smallest component lifetime, is the lifespan of the system. On $(0, 1)$, the components' lifetimes are uniformly distributed. The effect of $n$ on the PEX of $X_{2:n}$ at $t = 0.2$ is seen in Figure 3. The graph makes it abundantly evident that the system's PEX does not change monotonically as $n$ increases.

3.   Past extropy of lower record values

Let $\{X_i, i = 1, 2, \ldots\}$ be a sequence of i.i.d. rvs with the cdf $F(x)$ and pdf $f(x).$ Let us assume that $X_{i:n}$ is the $i$-th order statistic arising from $X_1\ldots, X_n.$ The $n$-th lower record time $L(n), n = 1, 2, \ldots$ with $L(1) = 1$ is stated as

and the $n$-th lower record is enumerated as $Z_n = X_{1:L(n)}, n = 1, 2, \ldots.$ The pdf of $Z_n$ can be acquired as follows:

Moreover, $Z_n$ has the following cdf:

where

stands as the imperfect gamma function (see e.g., ^[3]). Let us write $V\sim \Gamma_t(a, b)$ to specify that the rv $V$ follows a truncated gamma distribution with the following density

where $a, b \in (0, +\infty).$ Hereafter, the PEX of the rv $Z_n$ is concentrated, and it yields the degree of uncertainty present in the density of $[t-Z_n | Z_n\leq t]$. The predictability of the system's inactivity time is assessed in this way. To facilitate the efficiency of computations, a lemma is introduced that proves a formula that connects the PEX of order statistics in the uniform case with the imperfect beta function. Practically speaking, this connection is essential as it makes calculating the PEX easier. This lemma's demonstration, which comes immediately from the PEX's definition, is left out because it only requires a few simple computations.

Lemma 3.1. Let $\{U_i, i = 1, 2, \ldots\}$ be a sequence of i.i.d. rvs adopted for a uniformly distributed population. In addition, let $Z^\star_n$ denote the $n$-th lower records of $\{U_i, i = 1, 2, \ldots\}$. Then

Researchers and practitioners can easily use the well-known imperfect gamma function to determine the PEX of record values from a uniform distribution by utilizing this lemma. The PEX is more useful and applicable in a variety of situations as a result of this computational reduction. The PEX of record values $Z_n$ and the PEX of record values from a uniform distribution are related, as will be shown in the following theorem.

Theorem 3.1. Let $\{X_i, i = 1, 2, \ldots \}$ be a sequence of i.i.d. rvs with the cdf $F$ and pdf $f.$ Let $Z_n$ denote the $n$-th lower record value of the sequence $\{X_i\}.$ Then, the PEX of $Z_n,$ is obtained as follows:

such that $V_n\sim \Gamma_{-\ln F(t)}(2n-1, 1).$

Proof. By appealing to the change in variable of $u = F(x),$ and in the spirit of Eqs (1.3), (3.1) and (3.2) one gets

The proof is finished when Lemma 3.1 yields the final equality. □

In the next theorem, a clear breakup of the historical extropy of lower record statistics is found. In particular, it is shown that this extropy metric can be written as the product of two essential elements: the expectation of a truncated gamma rv and the historical extropy of the lower records from the uniform distribution.

Theorem 3.2. If $X$ has a distribution which processes the DRHR property, then $\bar{J}(Z_n; t)$ increases in $t.$

Proof. It is well known that if $X$ has the DRHR property, then $Z_n$ also has the DRHR property. Therefore, the proof follows directly by using Theorem 1 of ^[18].

□ Using the example given below, the application of Theorems 3.1 and 3.2 is illustrated.

Example 3.1. Let us contemplate a sequence of i.i.d. rvs $\{X_i, i = 1, 2, \ldots\}$ following power law distribution. The associated pdf is

The right-continuous inverse cdf of $X$ is $f(F^{-1}(u)) = \beta u^{\frac{\beta-1}{\beta}}, \ u\in (0, 1).$ Then, one can calculate

It can also be obtained that

Therefore, using Eq (3.5), one gets

A theoretical result is now developed that states that the PEX of lower records from any continuous distribution has a lower bound. Two important aspects affect the lower bound for the PEX of lower records: the original distribution's mode and the PEX of lower records from the uniform distribution on the interval $(0, 1)$.

Theorem 3.3. Under the circumstances mentioned in Theorem 3.1, let us assume that $\mathfrak{M} = f(m) < +\infty$, where $m$ denotes the mode of the underlying distribution with density $f$. Based on this assumption, one can arrive at the following result:

Proof. Since

one can write

The proof is now complete, and the result may be obtained with ease from Eq (3.5). □

Consequently, a result was proved that provides a lower bound for $\bar{J}(Z_n; t)$, the PEX of $Z_n$. This lower bound depends on the mode of the pdf, $\mathfrak{M}$, the original distribution and the PEX of the record values from the uniform case. This solution provides a measurable lower bound for the PEX with respect to the mode of the underlying distribution and sheds light on several intriguing informational properties of $Z_n$.

The monotonic behavior of the PEX of $n$-th lower records with respect to $n$ is proved in the next theorem. First, the lemma that follows is required.

Lemma 3.2. Let $\{X_i, i = 1, 2, \ldots\}$ be a sequence of i.i.d. rvs with the cdf $F$ and pdf $f.$ Further, assume that $Z^\star_n$ signifies the $n$-th lower record in the uniform case. Then $\bar{J}(Z^\star_{n}; F(t))\geq \bar{J}(Z^\star_{n+1};F(t))$ for all $t\in (0, +\infty).$

Proof. Let us set two rvs $Z_1$ and $Z_2$ having densities $f_{1, t}(z)$ and $f_{2, t}(z)$ which are respectively derived as follows:

Moreover, one has

One can get

where

Easily, one can write the following:

so that

One can observe that $Z_{1}\geq_{lr}Z_2$ and hence $Z_{1}\geq_{st}Z_2.$ As a result, as $\ln(-\ln(z))$ decreases in $z$, one can deduce upon using Theorem 1.A.3. of ^[31] that $\mathbb{E}[\ln(-\ln(Z_2))]\geq\mathbb{E}[\ln(-\ln(Z_1))]$. Now, it follows that Eq (2.9) is positive; thus, $\Theta(n)$ decreases as $n$ grows. □

Theorem 3.4. Let $\{X_i, i = 1, 2, \ldots\}$ represent a sequence of i.i.d. rvs with the cdf $F$ and associated pdf $f.$ Let $Z_n,$ signify the $n$-th lower record of the sequence $\{X_i, i = 1, 2, \ldots\}.$ If $f(F^{-1}(x))$ increases with respect to $x,$ then $\bar{J}(Z_n; t)$ decreases in $n$ as $n$ grows.

Proof. Let us suppose that $V_n\sim \Gamma_{-\ln F(t)}(2n-1, 1).$ Then, one can demonstrate that $V_n$ is less than $V_{n+1}$ in likelihood ratio order and, as a result, $V_n$ is also less than $V_{n+1}$ in the usual stochastic order. Since $f(F^{-1}(x))$ increases with respect to $x,$ it follows that

So using Eq (3.5), one gets

The inequality given firstly follows because $\bar{J}(U_{n:n}; F(t))$ is non-positive. The inequality given lastly is due to Lemma 3.2. Consequently, it is proved that $\bar{J}(Z_n; t)\geq \bar{J}(Z_{n+1};t)$ for every $t\in (0, +\infty).$ □

Using the example given below, the application of Theorem 3.4 is illustrated.

Example 3.2. Assume a sequence of i.i.d. rvs $\{X_i, i = 1, 2, \ldots\}$ following uniform distribution on $[0, 1].$ It is evident that $f(F^{-1}(e^{-u})) = 1, \ u\in (0, 1).$ Then, one can calculate the following:

and hence we have

The effect of $n$ on the PEX of $Z_{n}$ at $t = 0.2$ is seen in Figure 4. It is evident that the PEX of $Z_n$ decreases with the increase of $n.$

4.   Computational results

Hereafter, the value of $\bar{J}(X_{i:n}; t), \ i = 1, 2, \cdots, n,$ is estimated for an ED with mean $1/\lambda.$ Equation (2.5) will be used to obtain the PEX of order statistics based on an ED with mean $1/\lambda$ as follows:

Toward this aim, the MLE of $\lambda$ is employed to estimate the value of $\bar{J}(X_{i:n}; t)$ for simulated exponential data. Let us consider a random sample $X_1, X_2, \cdots, X_m$ adopted from an ED with a mean of $1/\lambda.$ The MLE of $\lambda$ is calculated as $\widehat{\lambda} = m/\sum_{i = 1}^{m}X_i = 1/\overline{X}.$ It is significant to remember that the Monte Carlo simulation is used to generate the statistical data. The parameters are estimated based on $5000$ samples with various sizes of the sample, such as $m = n = 5, 10, 20, 25, 30$ and different parameter values of $\lambda = 0.5, 1, 2,$ and values of $t = 0.5, 1, 1.5, 2.$ Since the MLE is an invariant estimator, one can estimate $\bar{J}(X_{i:n}; t)$ for an ED by using the MLE as follows:

for $i = 1, 2, \cdots, n.$ To maintain simplicity, we focus on presenting the results specifically for series and parallel systems. Nevertheless, it is worth noting that similar trends have been observed across different parameter values and sample sizes.

To assess the performance of the proposed estimator, we computed the bias and mean squared error (MSE) of MLEs for different values of $n$. We used 5000 simulated samples and various values of the parameter $\lambda$. The results can be found in Tables 2–4. Based on the obtained results, it can be inferred that there is a clear relationship between the sample size $n$, parameter $\lambda$, bias and MSE. Based on the results, it is evident that the extropy estimator of the parallel system outperforms the extropy estimator of the series system. This can be observed by comparing the MSE and bias of the MLE for the extropy of both systems. The MLE of the parallel system exhibits a smaller MSE and bias, indicating better performance than the series system.

Let us present an investigation with real data to evaluate the performance of the proposed estimators.

Example 4.1. The strength of 1.5 cm glass fibers recorded at the National Physical Laboratory in England by using a dataset from Smith and Naylor ^[35] has been analyzed.

Data Set: 0.55, 0.93, 1.25, 1.36, 1.49, 1.52, 1.58, 1.61, 1.64, 1.68, 1.73, 1.81, 2.00, 0.74, 1.04, 1.27, 1.39, 1.49, 1.53, 1.59, 1.61, 1.66, 1.68, 1.76, 1.82, 2.01, 0.77, 1.11, 1.28, 1.42, 1.50, 1.54, 1.60, 1.62, 1.66, 1.69, 1.76, 1.84, 2.24, 0.81, 1.13, 1.29, 1.48, 1.50, 1.55, 1.61, 1.62, 1.66, 1.70, 1.77, 1.84, 0.84, 1.24, 1.30, 1.48, 1.51, 1.55, 1.61, 1.63, 1.67, 1.70, 1.78, 1.89

Shanker et al. ^[32] established that the ED provides a good fit for the dataset given in ^[35]. Using this dataset, the MLE of the parameter $\lambda$ is computed as $\widehat{\lambda} = 0.663647.$

In Table 5, the computed values of $\widehat{\bar{J}}(X_{1:n}; t)$ for the provided data are presented, considering various values of $t = 0.5, 1, 1.5, 2$ and different sample sizes $n = 10, 15, 20, 25, 30.$ The results demonstrate a notable trend: as the sample size $n$ increases, the uncertainty decreases significantly in terms of the extropy measure.

5.   Conclusions

The aim of this study was to investigate the idea of the PEX in relation to order statistics and record values. It was found that the PEX of order statistics (or record values) derived from a uniform distribution and the PEX of order statistics (or record values) derived from a continuous distribution are significantly related. Since it is difficult to obtain closed formulas for the PEX, a number of constraints were presented that provide useful methods for estimating the PEX of dataset values and, furthermore, the PEX of order statistics. A comprehensive study was conducted on the monotonic trend of data set values with respect to the set of observations. This study sheds important light on the patterns and behavior of data set values as sample size increases. Numerous illustrated situations have been included to demonstrate the practical implications and implementations of the given findings to enhance understanding and provide tangible examples. In addition, the method can be effectively used to test distribution functions presented in the existing literature. Furthermore, it is relevant in the area of reliability systems, where order statistics can be interpreted as the lifetimes of $i$-out-of-$n$ systems. This underlines the versatility and wide range of applications of the proposed method as a tool to analyze the reliability and distribution tests. In summary, this research has significantly expanded the knowledge of the PEX of order statistics and record values. By defining correlations, examining thresholds, and looking at monotonic behavior, insight was gained into the properties and estimation of the PEX under different circumstances. The knowledge gained from this study will help researchers and practitioners to make defensible decisions and draw insightful conclusions in a number of areas in which the analysis of order statistics and record values is important.

In addition to the results presented in this paper, there is the possibility of generalizing the results of this paper to other measures of information proposed in the literature, such as cumulative past entropy and generalized cumulative past entropy. Moreover, an interesting direction for future research is to study the PEX of order statistics in the presence of dependent lifetimes by implementing the results from ^[5,14,21] and the references therein. Exploring the behavior and properties of extropy when the lifetimes of individuals or events are not independent opens up exciting opportunities to gain new insights. This type of investigation promises to uncover the intricate relationship between order statistics and dependent lifetime distributions.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

The authors are thankful to the three anonymous reviewers for their constructive comments and suggestions.

The authors acknowledge financial support from the Researchers Supporting Project number (RSP2024R464), King Saud University, Riyadh, Saudi Arabia.

Conflict of interest

There is no conflict of interest declared by the authors.