Continuous Tsallis and Renyi extropy with pharmaceutical market application

1.   Introduction

Supported by R, the continuous Shannon entropy (Shannon ^[14]) of the random variable (RV) X is given by

where $\mathfrak{h}(.)$ is the probability density function (pdf). Lad et al. ^[5] produced the extropy as a dual Shannon entropy measure. The extropy of the discrete RV X supported on $Q = \{x_{1}, ..., x_{N}\}$ and with corresponding probability vector $p = (p_{1}, ..., p_{N})$, is

Moreover, the view of the extropy of the continuous RV X supported on R has been introduced in many pieces of literature, see for example Raqab and Qiu ^[11] and Qiu ^[9], can be shown as follows:

The literature has offered several entropy measures and their generalizations. Through the various uncertainty generalizations, Tsallis ^[15] presented the Tsallis entropy. The continuous Tsallis (C-Ts) entropy of the continuous RV X supported on R, $1\neq\eta > 0$, is defined as follows:

when $\eta$ is 1, then $\lim_{\eta\rightarrow 1}TEn_{\eta }(X) = SH(X)$.

Renyi ^[12] suggested a model referred to as continuous Renyi (C-Re) entropy of order $\eta$ of the continuous RV $X$ with pdf $\mathfrak{h}(x)$ as

where $1\neq\eta > 0$. It's simple to see that, when $\eta \rightarrow 1$, $REn_{\eta }(X)$ tends to $SH(X)$.

The Tsallis and Renyi extropy under the discrete distribution have been presented in the literature. Xue and Deng ^[19] suggested the model Tsallis of extropy, the dual of Tsallis entropy function, and examined its maximum value. Besides, Balakrishnan et al. ^[2] study the Tsallis of extropy and apply it to pattern recognition. Liu and Xiao ^[6] introduced Renyi extropy and looked at the maximum value of it. Jawa et al. ^[4] discuss the past and residual of Tsallis and Renyi extropy via the softmax function.

This paper introduces the C-Ts and C-Re extropy under the continuous distribution lifetime. Moreover, presenting the maximum of both models. The remainder of this article is as follows: Section 2 discusses the C-Ts extropy model with its properties and their connection to other measures. Furthermore, examples of the models for different distributions are introduced. Section 3 gives the maximum C-Ts extropy and some properties depending on it. Section 4 provides the maximum CRe extropy. Finally, Section 5 ends the article with some non-parametric estimations of C-Ts extropy applied to simulated and real data and discusses the estimation for the forecasting time series of OECD pharmaceutical market data.

2.   Continuous Tsallis extropy

In this section, we introduce the rendition of the C-Ts extropy based on the continuous distribution lifetime.

In the same manner, introduced in Lad et al. ^[5], we can present the extropy of the continuous RV X supported on R as follows:

In our work, we will deal with both Eqs (1.3) and (2.1) as a representative form of extropy.

Inspired by the idea of discrete Tsallis of extropy, and the continuous distribution lifetime, we present the C-Ts extropy by the following definition.

Definition 2.1. Let X be a continuous RV supported in $[a, b]$, $-\infty < a < b < \infty$, having a pdf $\mathfrak{h}(.)$. Before we introduce the concept of C-Ts extropy, we must mention that the value of the expression $(1-\mathfrak{h}(x))^{\eta}$ can be negative or non-negative according to the value of the pdf $\mathfrak{h}(x) > 1$ or $\mathfrak{h}(x)\leq1$, respectively. If $\mathfrak{h}(x)\leq1$, then $(1-\mathfrak{h}(x))^{\eta}$ gives real value for all $1\neq \eta > 0$. If $\mathfrak{h}(x) > 1$, then $(1-\mathfrak{h}(x))^{\eta}$ gives real value when $\eta\in \mathbb{Z}^{+}\backslash \{1\}$. Otherwise, it gives a complex result when $\eta$ is a non-positive integer. Then, the C-Ts extropy can be given as

where the conditions on $\eta$ can be given in two cases:

(1) $1\neq\eta > 0$ if $\mathfrak{h}(x) \leq 1$.

(2) $\eta\in \mathbb{Z}^{+}\backslash \{1\}$ if $\mathfrak{h}(x) > 1$.

Proposition 2.1. Assume that X is a continuous RV supported in $[a, b]$, $-\infty < a < b < \infty$. From (2.2), where $1\neq \eta > 0$, if $\mathfrak{h}(x)\leq1$ then the C-Ts extropy is non-negative.

Proof. From (2.2), the C-Ts extropy can be rewritten as

Provided that $\mathfrak{h}(x)\leq1$, when $\eta > 1$, the function $z(y) = y^{\eta -1}$ is increasing, $y > 0$, therefore $1-(1-\mathfrak{h}(x))^{\eta -1}$$\geq0$. While, when $0 < \eta < 1$, the function $z(y) = y^{\eta -1}$ is decreasing, $y > 0$, therefore $1-(1-\mathfrak{h}(x))^{\eta -1}$$\leq0$. Then, the C-Ts extropy is non-negative. □

Example 2.1. Assume that the continuous RV X has a continuous uniform distribution over $[a, b]$, $-\infty < a < b < \infty$ symbolize by $U(a, b)$ with pdf $\mathfrak{h}(x) = \frac{1}{b-a}$. Then, from (2.2), the C-Ts extropy is given by

where $1\neq\eta > 0$ if $\mathfrak{h}(x) \leq 1$ and $\eta\in \mathbb{Z}^{+}\backslash \{1\}$ if $\mathfrak{h}(x) > 1$. In particular, the C-Ts extropy equals zero if $b - a = 1$.

Example 2.2. Consider that the continuous RV X has power function distribution with pdf given by

Then, from (2.2), the C-Ts extropy is given by

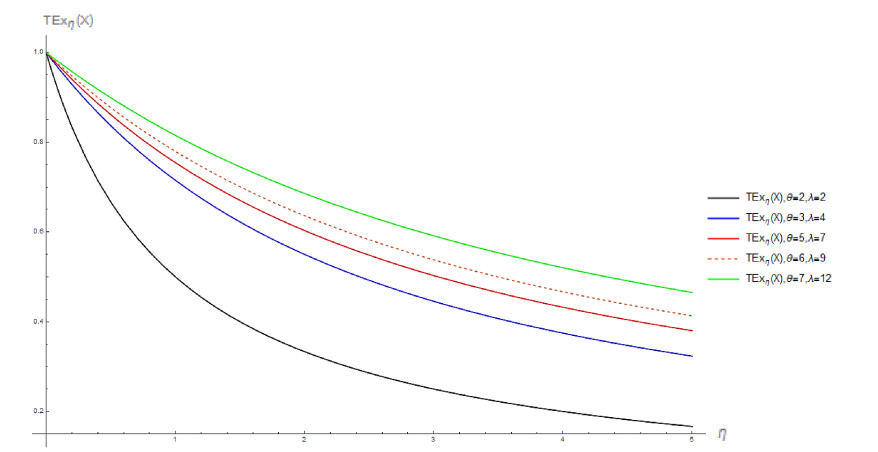
where $1\neq\eta > 0$ if $\mathfrak{h}(x) \leq 1$ and $\eta\in \mathbb{Z}^{+}\backslash \{1\}$ if $\mathfrak{h}(x) > 1$. Figure 1 shows the C-Ts extropy of power function distribution with different values of $\theta$ and $\lambda$. Furthermore, we can see that when the difference between $\theta$ and $\lambda$ increases, the C-Ts extropy increases.

In view of Figure 1, we can see that all the given values of $\theta$ and $\lambda$ of the power function distribution satisfy the condition $\mathfrak{h}(x) \leq 1$ in Eq (2.2) and C-Ts extropy exist where $1\neq\eta > 0$. For example, Figure 2 shows the plot of $\mathfrak{h}(x)\leq 1$ when $\theta = 5$ and $0 < \lambda\leq7$. In contrast, Figure 2 shows that $\mathfrak{h}(x)$ has the values $\mathfrak{h}(x) \leq 1$ and $\mathfrak{h}(x) > 1$, for values like $\theta = 6$ and $0 < \lambda \leq4$. As a result, the value of C-Ts extropy will only exist under the conditions described in Definition 2.1.

The next proposition discuss the C-Ts extropy when $\eta$ tends to 1.

Proposition 2.2. Providing that X is a continuous RV supported in $[a, b]$, $-\infty < a < b < \infty$. Then, from (2.1) and (2.2), we have

which is valid only for $1\neq\eta > 0$ and $\mathfrak{h}(x) \leq 1$.

Proof. From (2.2), with applying $L'H\hat{o}pital's$ rule, we get

If $\mathfrak{h}(x) \geq 1$, then $\eta\in \mathbb{Z}^{+}\backslash \{1\} = \{2, 3, ...\}$, which can't be tends to 1. Thus, $\lim_{\eta \rightarrow1} TEx_{\eta }(X) = Ex(X)$ only when $1\neq\eta > 0$ and $\mathfrak{h}(x) \leq 1$ □

In the next, we will obtain some significant results of C-Ts extropy when the parameter $\eta = 2$ is selected.

Remark 2.1. From Definition 2.1, when the parameter $\eta = 2$ is selected, then the C-Ts extropy is valid for $\mathfrak{h}(x) \leq 1$ or $\mathfrak{h}(x) > 1$.

Proposition 2.3. Assume that X is a continuous RV supported in $[a, b]$, $-\infty < a < b < \infty$. Then, from (1.3), (1.4), Definition 2.1 and Remark 2.1, we have

Proof. From (2.2), at $\eta = 2$, we have

□

Definition 2.2. (Shaked and Shanthikumar ^[13]) Provided that X and Y be RV's with pdf's $\mathfrak{h}$ and $\mathfrak{g}$, cdf's $\mathfrak{H}$ and $\mathfrak{G}$, respectively. In the dispersive order, it is said that X is smaller than Y, symbolized by $X \leq_{DIS} Y$, if $\mathfrak{G}^{-1}(\mathfrak{H}(x)) - x$ is increasing in $x \geq 0$.

Lemma 2.1. If $X \leq_{DIS} Y$, then $TEx_{2}(X)\leq TEx_{2}(Y)$.

Proof. From Definition 2.1 and Remark 2.1, at $\eta = 2$, we have

If $X \leq_{DIS} Y$, thus, by (2.2), we have $\mathfrak{h}(\mathfrak{H}^{-1}(u))\geq \mathfrak{g}(\mathfrak{G}^{-1}(u))$, $\forall u\in (0, 1)$. Therefore,

□

Based on the independent and identically distributed observations (iid) $X_{1}, X_{2}, ..., X_{n}$ and $Y_{1}, Y_{2}, ..., Y_{n}$. If $X \leq_{DIS} Y$, then we have

$(1)$ $X_{i:n} \leq_{DIS} Y_{i:n}$ (see Theorem 3.B.26 in Shaked and Shanthikumar ^[13]), $i = 1, 2, ..., n$.

$(2)$ $P_{n}^{X} \leq_{DIS} P_{n}^{Y}$ (see Belzunce et al. ^[3]).

Where $X_{i:n}$ and $Y_{i:n}$, $i = 1, 2, ..., n$, are the ith order statistics of $X_{1}, X_{2}, ..., X_{n}$ and $Y_{1}, Y_{2}, ..., Y_{n}$, respectively, and $P_{n}^{X}$ and $P_{n}^{Y}$ are the nth upper records of X and Y, respectively. Thus, we can conclude with the following results.

Proposition 2.4. If $X \leq_{DIS} Y$, thus

(1) $TEx_{2}(X_{i:n})\leq TEx_{2}(Y_{i:n})$, $i = 1, 2, ..., n$.

(2) $TEx_{2}(P_{n}^{X})\leq TEx_{2}(P_{n}^{Y})$.

The pdf of the jth order statistics $X_{j:n}$ in a sample of size n is

where $\textbf{B}(j, n-j+1)$ is the beta function, $\overline{\mathfrak{H}}(.) = 1-\mathfrak{H}(.)$ and $\mathfrak{H}(.)$ is the cumulative distribution function (cdf). In the following example, based on $U(a, b)$ distribution, we will obtain the C-Ts extropy of the jth order statistics $X_{j:n}$ as follows.

Example 2.3. Provided that X is a continuous RV supported in $[a, b]$, $-\infty < a < b < \infty$. Thus, from (2.6), Definition 2.1 and Remark 2.1, the C-Ts extropy of the jth order statistics $X_{j:n}$ of the $U(a, b)$ distribution is given by

Based on the jth order statistics $X_{j:n}$, we will obtain some significant results of C-Ts extropy when the choice of $\eta = 2$.

Proposition 2.5. Provided that X is a continuous RV supported in $[a, b]$, $-\infty < a < b < \infty$. Then, from (1.3), (1.4), (2.6), Definition 2.1 and Remark 2.1, we have

Proposition 2.6. Let X and Y be two continuous RV's with cdf's $\mathfrak{H}$ and $\mathfrak{G}$, respectively. Moreover, X and Y supports in $[a, b_{1}]$ and $[a, b_{2}]$, respectively, where $-\infty < a < b_{1} < \infty$ and $-\infty < a < b_{2} < \infty$. Provided that $\int_{a}^{b_{1}} dx$ and $\int_{a}^{b_{2}} dy$ exists, then, for a fixed j $(1 \leq j \leq n)$, X and Y have a common distribution iff $TEx_{2}(X_{j:n}) = TEx_{2}(Y_{j:n})$.

Proof. Proof of sufficiency is sufficient. Suppose that $TEx_{2}(X_{j:n}) = TEx_{2}(Y_{j:n})$, then, from (2.6), we have

after simplification, we get

which is equivalent to

where $\tau_{X}(x) = \frac{\mathfrak{h}(x)}{\overline{\mathfrak{H}}(x)}$ and $\tau_{Y}(x) = \frac{\mathfrak{g}(x)}{\overline{\mathfrak{G}}(x)}$. Setting $w = \overline{\mathfrak{H}}^{2}(x)$ or $w = \overline{\mathfrak{G}}^{2}(x)$, thus, we have

Equivalently

From Stone-Weierstrass Theorem and its corollary (Aliprantis and Burkinshaw ^[1]): If $\chi$ is a continuous function on (0, 1) such that $\int_{0}^{1} x^{n} \chi(x) dx = 0$ $\forall n \geq 0$, then $\chi(x) = 0$, $x \in (0, 1)$. Thus, from (1.5), we have $\tau_{X}(\mathfrak{H}^{-1}(1-\sqrt{w})) = \tau_{Y}(\mathfrak{G}^{-1}(1-\sqrt{w}))$, $w\in [0, 1]$. Put $1-\sqrt{w} = u$, then we have $\mathfrak{H}^{-1}(u) = \mathfrak{G}^{-1}(u)$, $u \in (0, 1)$, and the result follows. □

3.   The maximum C-Ts extropy

In this section, we will present the maximum C-Ts extropy by the following theorem.

Theorem 3.1. Provided that X is a continuous RV supported in $[a, b]$, $-\infty < a < b < \infty$. Thus, from (2.2), X has the maximum C-Ts extropy iff it follows the continuous uniform distribution, where $1\neq\eta > 0$ if $\mathfrak{h}(x) \leq 1$ and $\eta\in \mathbb{Z}^{+}\backslash \{1\}$ if $\mathfrak{h}(x) > 1$.

Proof. From Definition 2.1, we have

subject to

We can obtain the maximization of $TEx_{\eta }(X)$, using Lagrange multipliers method as follows:

Differentiating $L(X)$ with respect to $\mathfrak{h}(x)$ then equating to zero, we obtain

therefore, we get

To find the value of $\mu$, we substitute (3.2) in the constrain (3.1), thus

Substituting (3.3) in (3.2), it holds $\mathfrak{h}(x) = \frac{1}{b-a}$ is the pdf of the continuous $U(a, b)$ distribution. □

Proposition 3.1. Provided that X is a continuous RV supported in $[a, b]$, $-\infty < a < b < \infty$, provided that $b-a\geq 2$. Then, from (1.4) and Definition 2.1, we have

(1) $TEx_{\eta }(X)\leq TEn_{\eta }(X)$, if $0 < \eta < 2$.

(2) $TEx_{\eta }(X)\geq TEn_{\eta }(X)$, if $\eta > 2$.

Proof. From (1.4) and Definition 2.1, we have

Therefore, the Lagrange function $(L(X))$ is given by

Then, the derivative with respect to $\mathfrak{h}(x)$ is

thus, we can note the vanishing equation

and the rest of the proof will be in the same manner given in Balakrishnan et al. ^[2]. □

Figure 3 shows the comparison between $TEx_{\eta }(X)$ and $TEn_{\eta }(X)$ according to Proposition 3.1 of uniform and power function distributions.

Theorem 3.2. Provided that X is a continuous RV supported in $[a, b]$, $-\infty < a < b < \infty$. Then, from Definition 2.1, The C-Ts extropy is less than or equal to 1.

Proof. We can see that the C-Ts extropy of the continuous uniform distribution increases to 1 as $(b-a)$ increases. From (2.4), assume the function

then, its derivative is given by

its sign, by mean value theorem, is given by $\eta(Z-1+\varepsilon)^{\eta-1}-\eta(Z-1)^{\eta-1}$, for some $\varepsilon \in (0, 1)$. Therefore, we can see that $T(Z)$ increases for $\eta > 1$ and decreases for $0 < \eta < 1$. Moreover, as Z tends to $\infty$, we have the limit of uniform C-Ts extropy as follows:

From the maximum C-Ts extropy given in Theorem 3.1, C-Ts extropy is less than or equal to 1. Or, we can implement the proof simply by using Bernoulli's inequality, as follows:

□

4.   Continuous Renyi extropy

Inspired by the idea of the discrete Renyi extropy introduced by Liu and Xiao ^[6], we presented the C-Re extropy in this section. Let X be a continuous RV supported in $[a, b]$, $-\infty < a < b < \infty$, having a pdf $\mathfrak{h}(.)$. It is obvious from the logarithmic function that its domain is $(o, \infty)$. Therefore, the C-Re extropy exists only when $h(x)\leq 1$ and $b-a > 1$. Otherwise, it will return to a complex result or vanish. Then, the C-Re extropy, $1\neq \eta > 0$, is given by

where $h(x)\leq 1$ and $b-a > 1$.

Proposition 4.1. Provided that X is a continuous RV supported in $[a, b]$, $-\infty < a < b < \infty$. Then, from (2.1) and (4.1), we have

Proof. From (4.1), with applying $L'H\hat{o}pital's$ rule, we get

□

Example 4.1. Suppose that the continuous RV X has $U(a, b)$ distribution, provided that $b-a\neq1$. Then, the C-Re extropy is given by

where $b-a\neq1$.

4.1.   The maximum C-Re extropy

In this subsection, we will present the maximum C-Re extropy by the following theorem.

Theorem 4.1. Provided that X is a continuous RV supported in $[a, b]$, $-\infty < a < b < \infty$. Thus, from (4.1), X has the maximum C-Re extropy iff it follows the continuous uniform distribution.

Proof. From (4.1), we have

subject to

We can obtain the maximization of $REx_{\eta }(X)$, using Lagrange multipliers method as follows:

Differentiating $L(X)$ with respect to $\mathfrak{h}(x)$ then equating to zero, we obtain

therefore, we get

To find the value of $\mu$, we substitute (4.5) in the constrain (4.4), thus

Substituting (4.6) in (4.5), it holds $\mathfrak{h}(x) = \frac{1}{b-a}$ is the pdf of the continuous $U(a, b)$ distribution. □

5.   Non-parametric estimation

The non-parametric estimation is used in many works to estimate the extropy and its related measures. The non-parametric kernel density estimation is a common procedure used in many works of literature as a smoothed estimator, see, for example, Qiu and Jia ^[5], Noughabi and Jarrahiferiz ^[10] and Jahanshahi et al. ^[12]. In this section, we present the empirical estimator of the pdf to estimate the C-Ts extropy using the kernel non-parametric estimator. Let the sequence $\{X_{j}, 1\leq j\leq n\}$ be a random sample drawn from a population with pdf $\mathfrak{h}(.)$. From Definition 2.1, the empirical Tsallis extropy is defined as

where $X_{1:n}\leq X_{2:n}\leq... \leq X_{n:n}$ is the order statistic of the random sample. Furthermore, $\mathfrak{h}_{n}(.)$ is the density kernel estimator of $\mathfrak{h}(.)$ defined by (see, Parzen ^[8])

where $kr(x)$ is the kernel function (we use the Gaussian kernel) and $B$ is the bandwidths. To choose the bandwidths, we use different methods like plug-in selectors (includes rule-of-thumb $B_{RT}$ and direct plug-in $B_{DPI}$) and cross-validation selectors (includes unbiased cross-validation $B_{UCV}$ and biased cross-validation $B_{BCV}$). Figure 4 shows the Gaussian kernel density estimator rule-of-thumb bandwidth $(B_{RT-Gaussian})$ compared with different bandwidths selection. Tables 1 and 2 show the Tsallis extropy estimator with different values of $\eta$ and sample size $n = 10, 20, 30, 70, 90, 100, 150, 200$, and we can conclude the following:

$(1)$ For fixed $\eta$ and $n$ increases, Tsallis extropy decreases.

$(2)$ For fixed $n$ and $\eta$ increases, Tsallis extropy decreases.

$(3)$ The Tsallis extropy under the bandwidths $B_{RT}$ gives a large value than the other bandwidths selections.

5.1.   Pharmaceutical market dataset

In this subsection, we illustrate a dataset that compares sales and consumption across several countries in the pharmaceutical business. From Figures 5 and 6, this study focuses on the OECD countries which contain 8 countries in the pharmaceutical market variables (Antidepressants; Anxiolytics; Drugs used in diabetes; Respiratory system) from 2010 to 2021 (Defined daily dosage per 1000 inhabitants per day), see ^[7]. Table 3 shows the Tsallis extropy estimator with different values of $\eta$ and we can conclude the following:

$(1)$ When $\eta$ increases, Tsallis extropy decreases.

$(2)$ The Tsallis extropy under the bandwidths $B_{DPI}$ gives a large value than the other bandwidths selections.

5.1.1.   Forecasting time series

In this part, we study the forecasting time series of Austria pharmaceutical market from 2021 to 2030 for the two variables, anxiolytics and drugs used in diabetes. Then, we obtain the Tsallis extropy estimator of the obtained results. Figures 7 and 8 show the fitted model to the anxiolytics and drugs used in diabetes variables which both fitted to $ARIMA(0, 1, 0)$ with (AIC = 54.09, BIC = 54.39 and p-value 0.74) and (AIC = 14.13, BIC = 14.44 and p-value 0.505), respectively.

Figure 9 shows the time series and its forecasting of Austria pharmaceutical market from 2021 to 2030 for the two variables Anxiolytics and Drugs used in diabetes. Tables 4 and 5 show the Tsallis extropy estimator of $80%$ and $95%$ forecasting interval of anxiolytics and drugs used in diabetes of Austria pharmaceutical market, respectively, and we can conclude the following:

$(1)$ When $\eta$ increases, Tsallis extropy decreases.

$(2)$ The Tsallis extropy under the bandwidths $B_{RT}$ gives a large value than the other bandwidths selections.

6.   Conclusions

In this consideration, we have discussed the C-Ts and C-Re extropy under the continuous case, and discuss the conditions when the continuous distributions can be valid to apply in C-Ts and C-Re extropy. We have illustrated some properties of the presented models with examples of some distributions like uniform and power function distributions. Besides, our models with the other uncertainty measures and order statistics are compared. Moreover, we have discussed the condition of the maximum C-Ts and C-Re extropy, which both returned to the uniform distribution. A non-parametric estimation has been introduced of the Tsallis extropy and we see that its increases depend on the values of $n$, $\eta$ and the selection of the bandwidth. In comparing C-Ts and C-Re extropy with the original version of entropy, we can see that no constraints are held on the pdf of the entropy measures. Moreover, we must have some restrictions on the pdf in C-Ts and C-Re extropy. Furthermore, when the Tsallis entropy parameter $\eta$ approaches 1, it converges to the classical Shannon entropy. In contrast, the C-Ts extropy converges to the extropy measure when $\eta$ tends to 1, only at $\mathfrak{h}(x)\leq1$. The choice of the non-extensive parameter $\eta$ can significantly impact the behavior and interpretation of the entropy measure; therefore, when $\eta = 2,$ the C-Ts extropy and entropy coincide, which means that the two models have the same performance in evaluating uncertain information. In future work, some relative works of entropy, e.g., Quantum X-entropy in generalized quantum evidence theory (Xiao ^[16]); On the maximum entropy negation of a complex-valued distribution (Xiao ^[17]); Evidential fuzzy multicriteria decision making based on belief entropy (Xiao ^[18]) can be implemented in extropy and its related measures.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This research is supported by researchers supporting project number (RSPD2023R548), King Saud University, Riyadh, Saudi Arabia.

Conflict of interest

The authors declare no conflict of interest.