Coupled systems of nonlinear sequential proportional Hilfer-type fractional differential equations with multi-point boundary conditions

Ayub Samadi; Sotiris K. Ntouyas; Jessada Tariboon; Ayub Samadi; Sotiris K. Ntouyas; Jessada Tariboon

doi:10.3934/math.2024633

AIMS Mathematics

2024, Volume 9, Issue 5: 12982-13005. doi: 10.3934/math.2024633

Previous Article Next Article

Research article Special Issues

Coupled systems of nonlinear sequential proportional Hilfer-type fractional differential equations with multi-point boundary conditions

1.
Department of Mathematics, Miyaneh Branch, Islamic Azad University, Miyaneh 5315836511, Iran
2.
Department of Mathematics, University of Ioannina, Ioannina 45110, Greece
3.
Intelligent and Nonlinear Dynamic Innovations Research Center, Department of Mathematics, Faculty of Applied Science, King Mongkut's University of Technology North Bangkok, Bangkok 10800, Thailand

Received: 27 February 2024 Revised: 27 March 2024 Accepted: 29 March 2024 Published: 07 April 2024
MSC : 26A33, 34A08, 34B15

In this paper, we studied the existence of solutions for a coupled system of nonlinear sequential proportional $\psi$ -Hilfer fractional differential equations with multi-point boundary conditions. By using a Burton's version of the Krasnosel'ski $\breve{{\rm{i}}}$ 's fixed-point theorem we established sufficient conditions for the existence result. An example illustrating our main result was also provided.

Keywords:

coupled system,
Hilfer fractional proportional derivative,
multi-point boundary conditions,
fixed-point theorem

Citation: Ayub Samadi, Sotiris K. Ntouyas, Jessada Tariboon. Coupled systems of nonlinear sequential proportional Hilfer-type fractional differential equations with multi-point boundary conditions[J]. AIMS Mathematics, 2024, 9(5): 12982-13005. doi: 10.3934/math.2024633

Related Papers:

[1]	Rashad M. EL-Sagheer, Mohamed S. Eliwa, Khaled M. Alqahtani, Mahmoud El-Morshedy . Bayesian and non-Bayesian inferential approaches under lower-recorded data with application to model COVID-19 data. AIMS Mathematics, 2022, 7(9): 15965-15981. doi: 10.3934/math.2022873
[2]	I. H. K. Premarathna, H. M. Srivastava, Z. A. M. S. Juman, Ali AlArjani, Md Sharif Uddin, Shib Sankar Sana . Mathematical modeling approach to predict COVID-19 infected people in Sri Lanka. AIMS Mathematics, 2022, 7(3): 4672-4699. doi: 10.3934/math.2022260
[3]	Peter Joseph Witbooi, Sibaliwe Maku Vyambwera, Mozart Umba Nsuami . Control and elimination in an SEIR model for the disease dynamics of COVID-19 with vaccination. AIMS Mathematics, 2023, 8(4): 8144-8161. doi: 10.3934/math.2023411
[4]	Sofia Tedim, Vera Afreixo, Miguel Felgueiras, Rui Pedro Leitão, Sofia J. Pinheiro, Cristiana J. Silva . Evaluating COVID-19 in Portugal: Bootstrap confidence interval. AIMS Mathematics, 2024, 9(2): 2756-2765. doi: 10.3934/math.2024136
[5]	Oluwaseun F. Egbelowo, Justin B. Munyakazi, Manh Tuan Hoang . Mathematical study of transmission dynamics of SARS-CoV-2 with waning immunity. AIMS Mathematics, 2022, 7(9): 15917-15938. doi: 10.3934/math.2022871
[6]	Said Gounane, Jamal Bakkas, Mohamed Hanine, Gyu Sang Choi, Imran Ashraf . Generalized logistic model with time-varying parameters to analyze COVID-19 outbreak data. AIMS Mathematics, 2024, 9(7): 18589-18607. doi: 10.3934/math.2024905
[7]	Yahia Abdel-Aty, Mohamed Kayid, Ghadah Alomani . Generalized Bayesian inference study based on type-Ⅱ censored data from the class of exponential models. AIMS Mathematics, 2024, 9(11): 31868-31881. doi: 10.3934/math.20241531
[8]	Rahat Zarin, Amir Khan, Aurangzeb, Ali Akgül, Esra Karatas Akgül, Usa Wannasingha Humphries . Fractional modeling of COVID-19 pandemic model with real data from Pakistan under the ABC operator. AIMS Mathematics, 2022, 7(9): 15939-15964. doi: 10.3934/math.2022872
[9]	Xiaoying Pan, Longkun Tang . A new model for COVID-19 in the post-pandemic era. AIMS Mathematics, 2024, 9(8): 21255-21272. doi: 10.3934/math.20241032
[10]	Mohamed A. H. Sabry, Ehab M. Almetwally, Osama Abdulaziz Alamri, M. Yusuf, Hisham M. Almongy, Ahmed Sedky Eldeeb . Inference of fuzzy reliability model for inverse Rayleigh distribution. AIMS Mathematics, 2021, 6(9): 9770-9785. doi: 10.3934/math.2021568

Abstract

1. Introduction

In the present context, quantum technology enhances a wide range of application areas, such as 5G wireless connections, the IoT, wearable technology, and artificial intelligence (AI). Quantum computing is a highly centralized computing infrastructure that processes and caches data from both the site of generation and cloud. Quantum computing extends cloud computing and complements the concept of agile devices that can operate at the network's fringes ^[1]. Quantum computing delivers various services while handling diverse sensors, processes, users, actuators, and connectivity by bringing processing capability closer to the users. Quantum setups are proficient at processing diverse volumes of data locally, operating under the assumption that they are fully compact and can be integrated into integrated hardware ^[2]. Quantum computing could help with IoT applications and address the limitations of the cloud when it comes to handling time-sensitive apps ^[3].

However, quantum computing, characterized as an augmentation of cloud computing, exhibits unique attributes in wireless connectivity, regional subtlety, and geographical responsiveness, which give rise to new concerns about security and forensics ^[1]. Many threats in the context of cloud security and forensics remain inadequately addressed. Quantum operations are primarily driven by service and user requirements, often leading to the neglect of security considerations or treating them as an afterthought. The privacy and security threats and assets related to quantum computing have not been systematically analyzed. The exploration of privacy and security threats in quantum computing for the IoT is in its infancy. The security threats to quantum computing provoke a fascinating debate within academia ^[2]. Since quantum computing is assumed to be a significant expansion of the cloud, it is expected that many privacy and security threats from the cloud computing environment will inevitably impact quantum computing. Quantum computing faces new privacy and security threats in addition to those rooted in cloud computing. While some security threats can be mitigated through appropriate mechanisms, the distinctive features of quantum computing introduce significant challenges and threats ^[3].

In this study, we aimed to investigate more feasible and practical solutions for security concerns in quantum computing. To achieve this, we extensively covered various security aspects of quantum computing, including their sub-components, to facilitate the systematic management of quantum layer security. Furthermore, we developed a ranking system to prioritize and manage these security aspects. The resulting ranking will assist both academics and industry experts in dealing with security issues in quantum computing systematically.

In addition to the above, the rest of this research work is organized as follows: Section 2 discusses recent work in this domain, followed by an exploration of the recognized quantum-level security attributes and their sub-attributes. Subsequently, Section 3 outlines the materials and methods used to evaluate the impact of the key security attributes selected by the researchers in constructing their hierarchical model. Section 4 presents a comparison of the results obtained through this method with those obtained using the classical AHP-TOPSIS method. Section 5 delves into the discussion of the research findings. The conclusion and future guidelines are presented in Section 6.

2. Literature review

To explore the scope of studies cited by various researchers and practitioners, we identified commonly used substitutes and synonyms for words to conduct a comprehensive literature review for this research study. A thorough analysis of previous research literature available in this context reveals that the current security threats and challenges can be classified as follows: Privacy, trust, authentication, threats and attacks, security audits, and access control. This section also examines and highlights security threats and explanations of auxiliary areas, including edge computing and cloud computing, which encompass the quantum computing landscape. To ensure a comprehensive survey and analysis for our study, we conducted manual searches using different search engines in the areas of quantum and cloud security to meet the section's needs.

As the users' primary concern is the privacy of their data ^[4], privacy preservation has become a crucial issue in quantum computing ^[3]. The information used in quantum computing originates from various sources, including wireless networks, IoT devices, and cloud networks. Consequently, safeguarding privacy is a significant security threat in the quantum environment ^[2]. In 2020, L. Zhao introduced a new distributed algorithm for data analytics on quantum-enabled IoT devices ^[5]. By integrating this algorithm with homomorphic encryption, the author devised a method to protect the privacy of edge devices. Vehicular cloud computing has emerged as one of the most significant threats to this technology.

Xue et al. ^[5] also presented a study in the same context. They securely outsourced a sophisticated computation burden to cloud and quantum servers, emphasizing privacy preservation and confidentiality. Wang et al. ^[6] discussed data privacy and confidentiality in 2018, focusing on quantum oriented public cloud computing and pioneering the concepts of anonymity and secure accumulation. Pseudonyms and combinatorial cryptographic techniques were among their contributions. In 2017, Lu et al. ^[7] investigated device and data privacy using lightweight privacy-preserving data accumulation techniques for quantum and IoT processes ^[8,9]. They employed homomorphic cryptography, the Chinese Remainder Theorem, and a hash chain method.

In 2018, Rauf et al. ^[8] proposed a risk-oriented trust prototype method for the IoT setting, introducing a dynamic domain-adaptive security solution. They used criteria based on response time, availability, and reliability, incorporating both direct and indirect perception for reliance estimation ^[9]. J. Zhao et al. worked on securing trust formation among vehicles ^[10]. The authors proposed a fuzzy trust structure based on validity and understanding and conducted a series of security investigations. In 2017, Dang et al. ^[10] pro-posed a dynamic data prevention scheme for quantum computing in mobility management services, addressing privacy-aware, role-centric access control techniques and introducing quantum-based region verification.

In 2019, Wazid et al. ^[11] established that the security of quantum devices can be ensured with the help of key management and authentication schemes. The authors performed adequate and lightweight exercises. Dsouza et al. ^[12] introduced policy-oriented resource management in the quantum network in 2014, supporting interoperability and secure association among various resources in the quantum system. In 2018, Zhang et al. ^[13] proposed an encouraging CP-ABE-centric access controller for a quantum computing environment where encryption and decryption are outsourced. In 2018, Vohra et al. ^[14] also presented a quantum-based distributed multi-authority credit-based data access protocol. In 2017, Xiao et al. ^[15] proposed a comprehensive solution for fine-grained owner-enforced exploration and access control, addressing user-quantum-cloud interaction and the limitations of end procedures.

Stojmenovic et al. ^[16], in 2016, proposed an authentication scheme to mitigate MITM attacks. The authors concluded that encryption and decryption methods are not always well-suited due to the system's constraints. Homayoun et al. ^[17], employed entirely automated and quantum node ransomware detection methods for the quantum layer. They also demonstrated that deep learning methods can be used for this purpose.

Undoubtedly, quantum computing is considered more secure than cloud computing. The collected data in quantum computing is cultivated and evaluated on local quantum nodes near data sources ^[19], reducing dependence on network connections. Additionally, local data storage, transactions, and analysis make it more challenging for intruders to gain access to users' information. However, there are security risks associated with data transactions between the user's device and the quantum computing node or among different quantum nodes ^[20]. Therefore, multiple threats exist in the process, and safeguarding privacy and security in quantum computing is not straightforward. Security issues can arise in various areas of quantum computing, with critical areas including networks, service infrastructure, virtualization, and users' devices.

Aggregating all quantum security-related concerns exhibits inconsistency, and there are limited solutions available to detect and prevent malicious attacks on the quantum platform. Optimal security is essential to ensure the effectiveness of quantum computing systems, making it a crucial research question ^[21]. None of the scholarly works we referenced provided a comprehensive assessment of all aspects of quantum security. Quantum computing is vulnerable to significant threats due to its unique features ^[3]. In the quantum computing environment, devices are primarily managed by different users, and the resources utilized by these devices are not typically examined by regulatory bodies, amplifying security threats in the quantum environment.

3. Quantum security issues and alternatives

3.1. Hierarchical structure for evaluation

As a centralized resource, the cloud presents a significant opportunity to breach privacy. Current cloud-based security services continue to focus on perimeter-based safety ^{[18,19,20,21,22]}. However, these services may impose extreme delays on numerous applications and systems that require impractically long-term communication bandwidth. If a threat manages to breach these barriers, a system with security measures in place will typically have limited and outdated capabilities to counter the compromises. Consequently, the current security model is insufficient for protecting a wide variety of IoT systems, devices, and applications. Therefore, the unique IoT security challenges outlined below need to be addressed: (1) Ensuring secure operation for a diverse array of devices. (2) Securing a wide range of resource-constrained devices. (3) Dynamically responding to security breaches based on system requirements and breach risk levels.

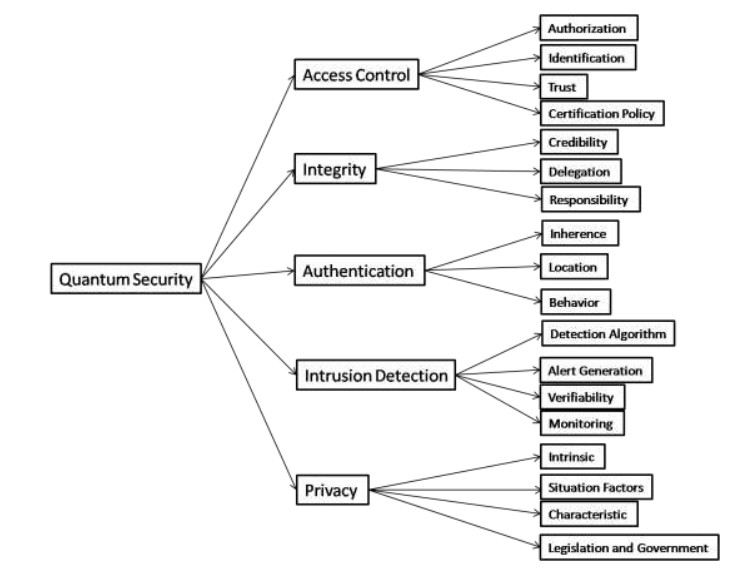
Quantum computing plays a pivotal role in this new security paradigm, offering a solution to enhance end-user privacy demands. Quantum systems are well-suited to provide security services across a diverse spectrum of IoT devices ^[23]. They are physically and logically close to the endpoints, allowing for comprehensive and authentic oversight of various devices and the execution of time-sensitive and re-source-intensive security tasks on behalf of the endpoints ^[24]. Consequently, it is essential to thoroughly examine the security fundamentals and requirements of any platform or system from the ground up. The interaction between quantum computing and heterogeneous smart devices introduces significant complexities to security management in the quantum paradigm. Consequently, a comprehensive analysis of all security elements is imperative. The structured hierarchy of various security concerns related to quantum computing, based on research findings and discussions with experts in the field. Quantum computers are capable of cracking encryption systems ^[3], as shown in Figure 1. According to experts, quantum computers will eventually be able to break all current cryptographic coding schemes, including RSA, Diffie-Hellman, and elliptic curve approaches ^[2]. Quantum-safe algorithms are currently under development. When quantum computers render today's encryption technologies obsolete, these quantum safe approaches will become essential for government and commercial enterprises. This event has been coined as "Q-Day" ^[25].

Figure 1. Tree structure of quantum security issues.

DownLoad: Full-Size Img PowerPoint

3.1.1. Access control [F1]

Access management is a security strategy in a virtualized environment that governs who or what can gain access to or use resources. It is a fundamental security notion that mitigates the threat to an organization ^[28]. There are two kinds of access control systems: physical and logical. Physical access controls the access to academic institutions, buildings, and spaces, as well as tangible IT resources. Logical access controls the restriction of access to computer network systems, system files, and data ^[26]. Workforce access to confined business locations as well as proprietary territories, like data centers, is monitored through security access control models that depend on login details, access card users, auditing, and reports. A few of these systems have access control panels that restrict who can gain entry to rooms and housing developments. They also have alarms and lockdown mechanisms to keep individuals at bay and prevent them from entering or doing things they shouldn't ^[29].

Authorization [F11]: The process of permitting someone the right to use a resource is known as authorization ^[27]. Obviously, this explanation may appear ambiguous, but many real-life circumstances can exemplify what authorization implies and how to apply those notions to computer systems. The household's ownership is a perfect example. The landlord has complete control over the assets (resources), and he or she can command the right of entry.

Identification [F12]: Identification is a subject's claim to its own identity ^[28]. Authentication is the process of proving one's identity by supplying credentials to an access control system. The technique that determines the subject's access level(s) to the objects are called authorization.

Trust [F13]: The belief in a machine's or sensor's ability to act consistently and securely, as well as consistently within a given environment is known as trust ^[30]. Cryptography, digital signatures, and electronic certificates are often used in M2M networks to establish trust. This method develops and assesses a trust chain among devices; however, it does not provide sufficient information about the feature of data transmission between machines. Information security is only one aspect of trust; it also comprises subjective criteria and experience.

Certification Policy [F14]: Policy for users is a process in which you validate that someone who is at-tempting to access services and applications is indeed the one who he or she claims to be ^[30]. This can be accomplished through a variety of certification methods.

3.1.2. Integrity [F2]

The ability to ensure that a framework and its data have not even been tampered with is referred to as integrity. Not only is data protected by integrity preservation, but even operating systems, applications, and hardware are protected from unauthorized access ^[31].

Credibility [F21]: A key concern is the increased onus on the companies to reduce vulnerability in their systems due to the threat of legal action when something goes wrong ^[32]. If data and security aren't managed carefully, this is a real risk. An example we've considered is that of an autonomous car. With no one in the driver's seat, human error is eliminated, leaving only the systems to blame when something goes wrong.

Delegation [F22]: Delegation is the procedure of a computer consumer handing over its authentication credentials to another user ^[31]. In role-based access control models, delegation of authority involves dele-gating the roles that a user can assume or the set of permissions that the user can acquire to other users.

Responsibility [F23]: This implies using the advanced software security techniques in accordance with the technical reference architecture, implementing, testing, and running those ^[33]. To increase software security, undertake ongoing security testing and code review. Issues that develop are troubleshot and debugged.

3.1.3. Authentication [F3]

Authentication is the procedure of validating the identity of the user or information ^[31]. User authentication is the process of verifying the user's identity at the time of login. Single-Factor Authentication (SFA): This was the first security solution devised.

Inherence [F31]: The inherent risk is a vulnerability that exists within an organization prior to the implementation of security measures ^[33]. On the other side, residual risk is evaluated after all of these inherent hazards have been mitigated by cybersecurity measures. It considers every possible attack vector that could compromise a system or its data.

Location [F32]: A secure location is an area in a defined site where entry is regulated by lock and key, backed up by an adequate security system, and only the authorized company employees have access to that ^[34].

Behavior [F33]: Behavior-based access control is a proactive strategy of protection in which all applicable actions are supervised to identify and address variances from regular patterns of behavior as soon as they occur ^[35].

3.1.4. Intrusion detection [F4]

An intrusion detection system, or IDS for short, keeps an eye on network and system traffic for any unusual activities ^[36]. Intrusion detection software will provide you with a notice after possible threats have been identified.

Detection Algorithm [F41]: An intrusion detection system (IDS) is a network traffic analysis system that identifies strange activities and notifies the users when they are discovered ^[6,7,8]. It is software that scans a computer system or network for malicious activity. Any malicious activity or policy violations are notified to an operations manager or central monitoring unit using a SIEM scheme. A SIEM scheme can collect data from various sources and use alarm scanning methods to differentiate between harmful and false alarms.

Alert Generation [F42]: IT alerting software sends out notifications when a computer system fails ^[9,10,11,12]. These tools will keep an eye on systems for issues including slow performance, infrastructure problems, and other IT management difficulties. Email, SMS, or other forms of communication may be used to provide these notifications. These tools are used by businesses to identify problems with their networks, IT infrastructure, and other IT systems in order to save time and prevent irreversible damage. By capturing incidents, collecting historical records, and analyzing them, some tools can help speed up the resolution and recovery procedures.

Verifiability [F43]: Software verification pledges that "you built it right" as well as that the artifact, when carried, meets the developers' expectations ^[13]. Software authentication guarantees that "you produced the proper thing" as well as that the invention, as delivered, meets the stakeholders' intended use and goals.

Monitoring [F44]: Security monitoring is the automated process of acquiring and analyzing signals of potential security threats, prioritizing them, and taking appropriate action to address them ^[14].

3.1.5. Privacy [F5]

The term "privacy software" refers to applications that are designed to keep their users' confidential ^[15]. The program is generally used in combination with Internet usage to handle or restrict the amount of data made publicly available to third-party companies. The application is capable of a wide range of encryption and filtration.

Intrinsic [F51]: The intrinsic security model replaces the reactive model with a framework that enables the company to be proactive ^[16]. Security is built into all of your environment's critical control points, including the network, the cloud, endpoints, workloads, and identity management.

Situation Factors [F52]: Human variables are psychological, physiological, and environmental characteristics that are both inherent in humans and influence how they interact with the rest of the world ^[17,18]. Human variables such as fatigue, time of day, diversions, and the way information is displayed on a screen are used to demonstrate the impact on how successfully individuals perform their tasks and how secure they are in industries such as aviation, trucking, healthcare, manufacturing, and nuclear power.

Legislation and Government [F53]: Security legislation refers to all the laws that govern security protocols from time to time, along with the Aviation and Maritime Security Act of 1990, the International Code for the Security of Ships, as well as Port Facilities, and any manually configuring or substituting security legislative action ^[36].

4. Materials and methods

The Managing security in software is the task of design management ^{[28,29,30,31]}. To make an effective and secure software design, it is always significant to work on the tactics of the design management ^[32]. Hence, prioritizing this approach, we consulted several industry experts and researchers working in this area. After collating the recommendations given by these experts, we classified the various tactics and their sub-tactics. Thereafter, the next step was to design the computational model. For this, we adopted the most significant MCDM approach in the current era, i.e., fuzzy AHP-TOPSIS ^{[36,37,38,39]}. This approach provides an efficient and effective outcome in a situation where the user has more than one option to choose from. A descriptive discussion of the methodology is enunciated below.

Its fundamental precept is to find the highest-quality viable replacement among a set of alternative strategies and then rank all of them on the basis of their evaluation metrics. Fuzzy-based AHP is used throughout for the research to demonstrate the weights of the criterion (characteristics), as well as fuzzy-based TOPSIS, which is used to prioritize the alternatives ^[40]. To figure out how to calculate the results for this method, we did the following:

Step 1: Triangular Fuzzy Number (TFN) is architecturally a triplet (f1, f2, f3) wherein f1 < f2 < f3 and f1 represent minor importance, f2 middle one and < f3 signifies upper importance. The membership function of the fuzzy number ~T is confirmed with the assistance of Eqs (1) and (2) as well as the quantity is documented as TFN. Figure 2 demonstrates the structure of a TFN.

${\mathrm{\mu }}_{\mathrm{a}}\left(\mathrm{x}\right) = \mathrm{F}\to \left[\mathrm{0, 1}\right]$

(1)

${\mathrm{\mu }}_{\mathrm{a}}\left(\mathrm{x}\right) = \left\{\begin{array}{c}\frac{\mathrm{x}}{\mathrm{m}\mathrm{i}-\mathrm{l}\mathrm{o}}-\frac{\mathrm{b}}{\mathrm{m}\mathrm{i}-\mathrm{l}\mathrm{o}}x\in \left[\mathrm{l}\mathrm{o}, \mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{m}\mathrm{i}\right]\\ \frac{\mathrm{x}}{\mathrm{m}\mathrm{i}-\mathrm{u}\mathrm{p}}-\frac{\mathrm{u}}{\mathrm{m}\mathrm{i}-\mathrm{u}\mathrm{p}}x\in \left[\mathrm{m}\mathrm{i}, \mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{u}\mathrm{p}\right]\\ 0 \;\;\;\;\;\; \mathrm{Otherwise}\end{array}\right.$

(2)

As per the triangular membership function, Eq (l), mi and u represent the lower, middle, and upper limit for triangular membership numbers.

Figure 2. Triangular Fuzzy Number.

DownLoad: Full-Size Img PowerPoint

After that, a fuzzy transformation is completed on these numeric statistics. To transform the numeric data into TFNs, Eqs (3)–(6) are employed as well as represented as (f1ij, f2ij, f3ij), where f1ij grants low importance, f2ij grants middle importance, and f3ij grants upper importance (Table 1). Additional TFN [ij] is distinct, such as:

${\mathrm{n}}_{\mathrm{i}\mathrm{j}} = ({\mathrm{l}}_{\mathrm{i}\mathrm{j}}, {\mathrm{m}}_{\mathrm{i}\mathrm{j}, }{\mathrm{u}}_{\mathrm{i}\mathrm{j}})$

(3)

Where, ${\mathrm{l}}_{\mathrm{i}\mathrm{j}}\le {\mathrm{m}}_{\mathrm{i}\mathrm{j}}\le {\mathrm{u}}_{\mathrm{i}\mathrm{j}}$

${\mathrm{l}}_{\mathrm{i}\mathrm{j}} = \left({\mathrm{J}}_{\mathrm{i}\mathrm{j}\mathrm{d}}\right)$

(4)

${\mathrm{m}}_{\mathrm{i}\mathrm{i}\mathrm{j}} = {({\mathrm{J}}_{\mathrm{i}\mathrm{j}1}, {\mathrm{J}}_{\mathrm{i}\mathrm{j}2}, {\mathrm{J}}_{\mathrm{i}\mathrm{j}3})}^{\frac{1}{\mathrm{x}}}$

(5)

${\mathrm{a}\mathrm{n}\mathrm{d}\;\;\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{u}}_{\mathrm{i}\mathrm{j}} = \left({\mathrm{J}}_{\mathrm{i}\mathrm{j}\mathrm{d}}\right)$

(6)

Table 1. TFN scale.

Saaty Scale Definition	Scale
Equally significant	(1, 1, 1)
Inadequately significant	(2, 3, 4)
Equitably significant	(4, 5, 6)
Sturdily significant	(6, 7, 8)
Categorically significant	(9, 9, 9)

| Show Table

DownLoad: CSV

The Table 1, mention the literature value of the initial data. The 'Jijk' denotes the degree of importance of attributes among some of the two factors using professional opinion as well as the expressions presented above. I and j are the element pairs that are evaluated and symbolized. Furthermore, the processes on the two TFNs are carried out with the assistance of Eqs (7)–(9). Supposing T1 and T2 are two TFNs, T1 = (f11, f21, f31) and T2 = (f12, f22, f32). At that moment, the functioning rules for them would be:

$\left({\mathrm{l}}_{1}, {\mathrm{m}}_{\mathrm{i}1, }{\mathrm{u}}_{1}\right)+\left({\mathrm{l}}_{2}, {\mathrm{m}}_{\mathrm{i}2, }{\mathrm{u}}_{2}\right) = \left({\mathrm{l}}_{1}+{\mathrm{l}}_{2}, {{\mathrm{m}}_{\mathrm{i}1}+{\mathrm{m}}_{\mathrm{i}2}}_{, }{\mathrm{u}}_{1}+{\mathrm{u}}_{2}\right)$

(7)

$\left({\mathrm{l}}_{1}, {\mathrm{m}}_{\mathrm{i}1, }{\mathrm{u}}_{1}\right)\times \left({\mathrm{l}}_{2}, {\mathrm{m}}_{\mathrm{i}2, }{\mathrm{u}}_{2}\right) = \left({\mathrm{l}}_{1}\times {\mathrm{l}}_{2}, {{\mathrm{m}}_{\mathrm{i}1}\times {\mathrm{m}}_{\mathrm{i}2}}_{, }{\mathrm{u}}_{1}\times {\mathrm{u}}_{2}\right)$

(8)

$\left({\mathrm{l}}_{1}, {\mathrm{m}}_{\mathrm{i}1, }{\mathrm{u}}_{1}\right)-1 = (\frac{1}{{\mathrm{u}}_{1}}, \frac{1}{{\mathrm{m}}_{\mathrm{i}1}}, \frac{1}{{\mathrm{l}}_{1}})$

(9)

$\widetilde {{\mathrm{A}}^{\mathrm{d}}} = \left[\begin{array}{ccc}\widetilde {\rm{k}}_{11}^{\mathrm{d}}& \widetilde {\rm{k}}_{12}^{\mathrm{d}}& \widetilde {\rm{k}}_{1\mathrm{n}}^{\mathrm{d}}\\ \dots \dots & \dots \dots & \dots \dots \\ \widetilde {\rm{k}}_{\mathrm{n}1}^{\mathrm{d}}& \widetilde {\rm{k}}_{\mathrm{n}2}^{\mathrm{d}}& \widetilde {\rm{k}}_{\mathrm{n}\mathrm{n}}^{\mathrm{d}}\end{array}\right]$

(10)

$\widetilde {\rm{k}}_{\mathrm{i}\mathrm{j}} = {\sum }_{\mathrm{d} = 1}^{\mathrm{d}}\widetilde {\rm{k}}_{\mathrm{i}\mathrm{j}}^{\mathrm{d}}$

(11)

Using Eq (12), we integrate the experts' opinions into the mathematical function and try to elaborate on them in it.

$\widetilde{\mathrm{A}}=\left[\begin{array}{ccc} \widetilde{\mathrm{k}_{11}} & \cdots & \widetilde{\mathrm{k}_{1 \mathrm{n}}} \\ \cdots & \ddots & \cdots \\ \widetilde{\mathrm{k}_{\mathrm{n} 1}} & \cdots & \tilde{\mathrm{k}}_{\mathrm{nn}} \end{array}\right]$

(12)

We use the following Eqs (13)–(16) to normalize the value and find the geometric mean of functions.

${\widetilde {\rm{P}}_{\rm{i}}} = {\left( {\prod_{{\rm{j}} = 1}^{\rm{n}} {{{{\rm{\tilde k}}}_{{\rm{ij}}}}} } \right)^{1/{\rm{n}}}},{\rm{i}} = 1,2,3,4, \ldots ..{\rm{n}}$

(13)

$\widetilde{\mathrm{w}_1}=\widetilde{\mathrm{p}_1} \otimes\left(\widetilde{\mathrm{p}_1} \oplus \widetilde{\mathrm{p}_2} \oplus \widetilde{\mathrm{p}_3} \ldots \ldots \oplus \widetilde{\mathrm{p}_{\mathrm{n}}}\right)^{-1}$

(14)

${\mathrm{M}}_{\mathrm{i}} = \frac{ \widetilde {\rm{w}}_{1} \oplus \widetilde {\rm{w}}_{2}\dots .. \oplus \widetilde {\rm{w}}_{\mathrm{n}}}{\mathrm{n}}$

(15)

${\mathrm{N}\mathrm{r}}_{\mathrm{i}} = \frac{{\mathrm{M}}_{\mathrm{i}}}{{\mathrm{M}}_{1} \oplus {\mathrm{M}}_{2} \oplus \dots \dots \oplus {\mathrm{M}}_{\mathrm{n}}}$

(16)

Now, after conducting all these steps and solving the equations, the BNP value is determined using Eq (17).

$\mathrm{B}\mathrm{N}\mathrm{P}\mathrm{w}\mathrm{D}1 = \frac{\left[\left(\mathrm{u}\mathrm{w}1-\mathrm{l}\mathrm{w}1\right)+\left(\mathrm{m}\mathrm{i}\mathrm{w}1-\mathrm{l}\mathrm{w}1\right)\right]}{3}+\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{l}\mathrm{w}1$

(17)

This completes the process for the fuzzy-AHP methodology. After this, the TOPSIS part begins. We adopt the TOPSIS methodology to test the ranking and effectiveness of the evaluated outcomes in a simulation scenario to validate the outcomes. The descriptive steps that were followed during this methodology are discussed below:

Using Table 2 and Eq (18), we prepared the correlation between the previously evaluated data and the tested alternatives.

$\begin{array}{ccc}{\mathrm{C}\mathrm{r}}_{1}& \dots .& {\mathrm{C}\mathrm{r}}_{\mathrm{n}}\end{array}$

$\widetilde {\rm{K}} = \begin{array}{c}{\mathrm{A}}_{1}\\ \dots \\ {\mathrm{A}}_{\mathrm{m}}\end{array}\left[\begin{array}{ccc}{ \widetilde {\mathrm{\alpha }}}_{11}& \cdots & { \widetilde {\mathrm{\alpha }}}_{1\mathrm{n}}\\ \cdots & \ddots & \cdots \\ { \widetilde {\mathrm{\alpha }}}_{\mathrm{m}1}& \cdots & { \widetilde {\mathrm{\alpha }}}_{\mathrm{m}\mathrm{n}}\end{array}\right]$

(18)

Table 2. Ranking scale.

Linguistic Variable	Corresponding TFN
Exact Pitiable (EP)	(0, 1, 3)
Pitiable (P)	(1, 3, 5)
Rational (R)	(3, 5, 7)
Worthy (W)	(5, 7, 9)
Exact Worthy (EW)	(7, 9, 10)

| Show Table

DownLoad: CSV

To make the standard of the function, Eq (19) is used, and after that, to create the grid, Eq (20) is utilized.

$\widetilde {\mathrm{P}} = {\left[ \widetilde {\rm{P}}_{\mathrm{i}\mathrm{j}}\right]}_{\mathrm{m}\times \mathrm{n}}$

(19)

$\widetilde {\mathrm{Q}} = {\left[{ \widetilde {\mathrm{q}}}_{\mathrm{i}\mathrm{j}}\right]}_{\mathrm{m}\times \mathrm{n}}\mathrm{i} = \mathrm{1, 2}, 3, \mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\dots \dots .\mathrm{m};\mathrm{j} = \mathrm{1, 2}, \mathrm{3, 4}, \mathrm{ }\dots \dots \mathrm{n}$

(20)

After identifying all these attributes and equations, the next step is to evaluate the gap degree by the following Eq (21).

$\mathrm{C} \widetilde {\rm{C}} = \frac{\widetilde {\rm{k}}_{\mathrm{i}}^{-}}{\widetilde {\rm{k}}_{\mathrm{i}}^{+}+\widetilde {\rm{k}}_{\mathrm{i}}^{-}} = 1-\frac{\widetilde {\rm{k}}_{\mathrm{i}}^{+}}{\widetilde {\rm{k}}_{\mathrm{i}}^{+}{+ \widetilde {\rm{k}}}_{\mathrm{i}}^{-}}, \mathrm{ }\mathrm{i} = \mathrm{1, 2}, \mathrm{ }\dots \dots ., \mathrm{ }\mathrm{m}$

(21)

After evaluating all these equations and formulae, we found the whole simulated scenario of security tactics. This computational methodology is most effective in the current situation of its real-world application capability. We attempted a simulator approach to test the efficacy of the above technique.

5. Data analysis and results

5.1. Statistical findings

To apply the above-discussed technique in a real-world scenario, we prepared a security tactic based on the tree structure that has already been discussed in Figure 1. We applied the adopted approach of fuzzy-AHP-TOPSIS to the stated readings in Figure 1 and evaluated the results in a computational manner that would facilitate the industry's development. Moreover, the hierarchical structure has different security issues and tactics that will enhance the development of software. Using the method described in the previous section, we performed the computational analysis to come up with Table 1 and Eqs (1) to (17). Further, from Table 3 to Table 8, we are showing the integrated fuzzy-based comparison matrices as per Figure 1. In addition, Table 9 to Table 14 shows the defuzzified values for various groups, and Table 15 represents the final weights of the attributes.

Table 3. Integrated fuzzy based comparison matrix at level 1.

	F1	F2	F3	F4	F5
F1	1.000000, 1.000000, 1.000000	1.872022, 2.527010, 3.203105	1.461400, 1.681042, 1.974301	1.441601, 2.431805, 3.386105	0.461707, 0.572104, 0.784501
F2	-	1.000000, 1.000000, 1.000000	0.601083, 0.771504, 1.021065	0.771008, 0.950400, 1.213601	0.161300, 0.195013, 0.249017
F3	-	-	1.000000, 1.000000, 1.000000	0.716904, 1.015002, 1.351503	0.201806, 0.241602, 0.311107
F4	-	-	-	1.000000, 1.000000, 1.000000	0.195106, 0.228103, 0.219003
F5	-	-	-	-	1.000000, 1.000000, 1.000000

| Show Table

DownLoad: CSV

Table 4. Integrated fuzzy based comparison matrix for F1 at level 2.

	F11	F12	F13	F14
F11	1.00000, 1.00000, 1.00000	1.75540, 2.34580, 3.03630	1.48540, 1.95750, 2.52630	1.12980, 1.55510, 1.98950
F12	-	1.00000, 1.00000, 1.00000	0.57000, 0.78600, 1.16000	0.56000, 0.72000, 0.96990
F13	-	-	1.00000, 1.00000, 1.00000	0.62860, 0.81750, 1.07560
F14	-	-	-	1.00000, 1.00000, 1.00000

| Show Table

DownLoad: CSV

Table 5. Integrated fuzzy based comparison matrix for F2 at level 2.

	F21	F22	F23
F21	1.00000, 1.00000, 1.00000	0.23750, 0.28790, 0.36750	0.3421, 0.4477, 0.8247
F22	-	1.00000, 1.00000, 1.00000	0.66140, 1.17250, 1.69360
F23	-	-	1.00000, 1.00000, 1.00000

| Show Table

DownLoad: CSV

Table 6. Integrated fuzzy based comparison matrix for F3 at level 2.

	F31	F32	F33
F31	1.00000, 1.00000, 1.00000	0.66503, 1.17230, 1.69740	1.15760, 1.44720, 1.70430
F32	-	1.00000, 1.00000, 1.00000	1.00770, 1.52470, 1.93430
F33	-	-	1.00000, 1.00000, 1.00000

| Show Table

DownLoad: CSV

Table 7. Integrated fuzzy based comparison matrix for F4 at level 2.

	F41	F42	F43	F44
F41	1.00000, 1.00000, 1.00000	0.69410, 0.89530, 1.11240	0.23450, 0.28780, 0.36410	0.71120, 0.95410, 1.35120
F42	-	1.00000, 1.00000, 1.00000	0.49310, 0.64230, 1.24140	0.27130, 0.35150, 0.52160
F43	-	-	1.00000, 1.00000, 1.00000	1.08540, 1.32970, 1.55820
F44	-	-	-	1.00000, 1.00000, 1.00000

| Show Table

DownLoad: CSV

Table 8. Integrated fuzzy based comparison matrix for F5 at level 2.

	F51	F52	F53
F51	1.00000, 1.00000, 1.00000	1.19780, 1.58803, 2.15640	0.49110, 0.64202, 1.00990
F52	-	1.00000, 1.00000, 1.00000	0.22410, 0.29560, 0.42790
F53	-	-	1.00000, 1.00000, 1.00000

| Show Table

DownLoad: CSV

Table 9. Integrated comparison matrix and local weights at level 1.

	F1	F2	F3	F4	F5	Weights
F1	1.000000	2.551440	1.710170	2.421740	0.591930	0.2400000
F2	0.391150	1.000000	0.791640	0.971690	0.201730	0.0952000
F3	0.581760	1.255160	1.000000	1.051630	0.251320	0.1200000
F4	0.411200	1.021360	0.941670	1.000000	0.231570	0.1032000
F5	1.661860	4.821390	3.941950	4.214270	1.000000	0.4416000
CR= 0.0025025

| Show Table

DownLoad: CSV

Table 10. Integrated comparison matrix and local weights for F1 at level 2.

	F11	F12	F13	F14	Weights
F11	1.000000	2.372300	1.981900	1.556400	0.3900000
F12	0.421500	1.000000	0.824300	0.744700	0.1700000
F13	0.504600	1.213200	1.000000	0.830900	0.2000000
F14	0.642500	1.342800	1.203500	1.000000	0.2400000
CR=0.0015400

| Show Table

DownLoad: CSV

Table 11. Integrated comparison matrix and local weights for F2 at level 2.

	F21	F22	F23	Weights
F21	1.000000	1.173000	0.494000	0.2749000
F22	0.852500	1.000000	1.172000	0.3296000
F23	2.024300	0.853200	1.000000	0.3955000
CR=0.0024500

| Show Table

DownLoad: CSV

Table 12. Integrated comparison matrix and local weights for F3 at level 2.

	F31	F32	F33	Weights
F31	1.000000	1.172000	1.363000	0.3843000
F32	0.853300	1.000000	1.491000	0.3562000
F33	0.733700	0.670700	1.000000	0.2595000
CR= 0.0025000

| Show Table

DownLoad: CSV

Table 13. Integrated comparison matrix and local weights for F4 at level 2.

	F41	F42	F43	F44	Weights
F41	1.000000	0.892000	1.173000	0.994000	0.2463000
F42	1.121100	1.000000	0.691000	0.372000	0.1820000
F43	0.852500	1.447200	1.000000	1.298000	0.2724000
F44	1.006100	2.688200	0.770400	1.000000	0.2993000
CR=0.0025400

| Show Table

DownLoad: CSV

Table 14. Integrated comparison matrix and local weights for F5 at level 2.

	F51	F52	F53	Weights
F51	1.000000	1.633000	0.691000	0.3159000
F52	0.612400	1.000000	0.303000	0.1731000
F53	1.447200	3.300300	1.000000	0.5110000
CR= 0.005200

| Show Table

DownLoad: CSV

Table 15. Final weights.

Attributes of Level 1	Independent Weights	Attributes of Level 2	Independent Weights	Dependent Weights
F1	0.2400000	F11	0.3900000	0.0093600
		F12	0.1700000	0.0040800
		F13	0.2000000	0.0048000
		F14	0.2400000	0.0057600
F2	0.0952000	F21	0.2749000	0.0261705
		F22	0.3296000	0.0313779
		F23	0.3955000	0.0376516
F3	0.1200000	F31	0.3843000	0.0461160
		F32	0.3562000	0.0427440
		F33	0.2595000	0.0311400
F4	0.1032000	F41	0.2463000	0.0254182
		F42	0.1820000	0.0187824
		F43	0.2724000	0.0281117
		F44	0.2993000	0.0308878
F5	0.4416000	F51	0.3159000	0.1395014
		F52	0.1731000	0.0764410
		F53	0.5110000	0.2269824

| Show Table

DownLoad: CSV

Tables 3–8 are showing the initial value of the pairwise comparison matrix. The values are further evaluated by the Eqs 1 to 10.

The Tables 9 to 14 are evaluating the weight of the factors related to the quantum security.

After analyzing the fuzzy AHP technique and its priority list, we evaluated the overall impact by adopting the TOPSIS approach. To perform this approach, we took fifteen real-time projects from Babasaheb Bhimrao Ambedkar University, Lucknow, Uttar Pradesh, India. These projects' data comprised a repository of the results of quiz competitions and entrance tests held at the university over a two- to five-year period. The selected projects were taken as the alternatives in this study. The sensitivity of these selected alternatives was very high. Table 16 and Table 17 demonstrate the use of the fuzzy TOPSIS method (Table 2 and Eqs (18)–(21)) to evaluate the results.

Table 16. Subjective cognition results.

Alternatives/ Attributes	A1	A2	A3	A4	A5	A6	A7
F11	6.3800, 8.3800, 9.6900	4.3800, 6.3800, 8.3800	7.0000, 9.0000, 10.0000	6.3800, 8.3800, 9.6900	4.3800, 6.3800, 8.3800	7.0000, 9.0000, 10.0000	3.0000, 5.0000, 7.0000
F12	7.0000, 9.0000, 10.000	6.3800, 8.3800, 9.6900	4.3800, 6.3800, 8.3800	7.0000, 9.0000, 10.000	7.0000, 9.0000, 10.000	6.2400, 8.2400, 9.6200	5.0000, 7.0000, 9.0000
F13	3.0000, 5.0000, 7.0000	7.0000, 9.0000, 10.000	7.0000, 9.0000, 10.000	3.0000, 5.0000, 7.0000	7.0000, 9.0000, 10.000	5.6200, 7.6200, 9.3100	7.0000, 9.0000, 10.000
F14	7.0000, 9.0000, 10.000	3.0000, 5.0000, 7.0000	7.0000, 9.0000, 10.000	7.0000, 9.0000, 10.000	7.0000, 9.0000, 10.000	5.7600, 7.7600, 9.3800	3.0000, 5.0000, 7.0000
F21	6.3800, 8.3800, 9.6900	4.3800, 6.3800, 8.3800	6.3800, 8.3800, 9.6900	4.3800, 6.3800, 8.3800	7.0000, 9.0000, 10.0000	3.0000, 5.0000, 7.0000	3.0000, 5.0000, 7.0000
F22	7.0000, 9.0000, 10.000	7.0000, 9.0000, 10.000	6.3800, 8.3800, 9.6900	4.3800, 6.3800, 8.3800	7.0000, 9.0000, 10.0000	3.0000, 5.0000, 7.0000	3.0000, 5.0000, 7.0000
F23	3.0000, 5.0000, 7.0000	7.0000, 9.0000, 10.000	7.0000, 9.0000, 10.000	6.3800, 8.3800, 9.6900	4.3800, 6.3800, 8.3800	7.0000, 9.0000, 10.0000	3.0000, 5.0000, 7.0000
F31	7.0000, 9.0000, 10.000	7.0000, 9.0000, 10.000	3.0000, 5.0000, 7.0000	7.0000, 9.0000, 10.000	7.0000, 9.0000, 10.000	6.2400, 8.2400, 9.6200	5.0000, 7.0000, 9.0000
F32	5.6200, 7.6200, 9.3100	3.7600, 5.7600, 7.7600	7.0000, 9.0000, 10.000	3.0000, 5.0000, 7.0000	7.0000, 9.0000, 10.000	5.6200, 7.6200, 9.3100	7.0000, 9.0000, 10.000
F33	5.6200, 7.6200, 9.3100	8.3800, 9.6900, 10.0000	5.6200, 7.6200, 9.3100	7.0000, 9.0000, 10.000	7.0000, 9.0000, 10.000	5.7600, 7.7600, 9.3800	3.0000, 5.0000, 7.0000
F41	6.3800, 8.3800, 9.6900	4.3800, 6.3800, 8.3800	7.0000, 9.0000, 10.0000	3.0000, 5.0000, 7.0000	3.0000, 5.0000, 7.0000	4.3800, 6.3800, 8.3800	3.0000, 5.0000, 7.0000
F42	7.0000, 9.0000, 10.000	7.0000, 9.0000, 10.000	6.3800, 8.3800, 9.6900	4.3800, 6.3800, 8.3800	7.0000, 9.0000, 10.0000	3.0000, 5.0000, 7.0000	3.0000, 5.0000, 7.0000
F43	3.0000, 5.0000, 7.0000	7.0000, 9.0000, 10.000	7.0000, 9.0000, 10.000	7.0000, 9.0000, 10.000	6.2400, 8.2400, 9.6200	5.0000, 7.0000, 9.0000	3.7600, 5.7600, 7.7600
F44	7.0000, 9.0000, 10.000	7.0000, 9.0000, 10.000	3.0000, 5.0000, 7.0000	6.3800, 8.3800, 9.6900	4.3800, 6.3800, 8.3800	7.0000, 9.0000, 10.0000	3.0000, 5.0000, 7.0000
F51	5.6200, 7.6200, 9.3100	3.7600, 5.7600, 7.7600	7.0000, 9.0000, 10.000	7.0000, 9.0000, 10.000	7.0000, 9.0000, 10.000	6.2400, 8.2400, 9.6200	5.0000, 7.0000, 9.0000
F52	5.6200, 7.6200, 9.3100	8.3800, 9.6900, 10.0000	5.6200, 7.6200, 9.3100	3.0000, 5.0000, 7.0000	7.0000, 9.0000, 10.000	5.6200, 7.6200, 9.3100	7.0000, 9.0000, 10.000
F53	5.6200, 7.6200, 9.3100	9.0000, 10.0000, 10.000	5.6200, 7.6200, 9.3100	7.0000, 9.0000, 10.000	7.0000, 9.0000, 10.000	5.7600, 7.7600, 9.3800	3.0000, 5.0000, 7.0000

| Show Table

DownLoad: CSV

Table 17. Weighted normalized fuzzy-decision matrix.

Alternative/ Attributes	A1	A2	A3	A4	A5	A6	A7
F11	0.00400, 0.00600, 0.00800	0.00300, 0.00400, 0.00600	0.00900, 0.01400, 0.02000	0.02500, 0.03400, 0.04100	0.02800, 0.04100, 0.05400	0.02000, 0.03300, 0.04600	0.00900, 0.01400, 0.02000
F12	0.00000, 0.00100, 0.00300	0.00000, 0.00200, 0.00300	0.00400, 0.00600, 0.00800	0.00300, 0.00400, 0.00600	0.00900, 0.01400, 0.02000	0.02500, 0.03400, 0.04100	0.02800, 0.04100, 0.05400
F13	0.00100, 0.00300, 0.00500	0.00000, 0.00000, 0.00100	0.00000, 0.00100, 0.00300	0.00000, 0.00200, 0.00300	0.00900, 0.01400, 0.02000	0.00300, 0.01000, 0.01900	0.00400, 0.01500, 0.02800
F14	0.00400, 0.00600, 0.00800	0.00300, 0.00400, 0.00600	0.00900, 0.01400, 0.02000	0.02500, 0.03400, 0.04100	0.02800, 0.04100, 0.05400	0.03100, 0.04000, 0.04400	0.05900, 0.06600, 0.06600
F21	0.00000, 0.00100, 0.00300	0.00000, 0.00200, 0.00300	0.00900, 0.01400, 0.02000	0.00300, 0.01000, 0.01900	0.00400, 0.01500, 0.02800	0.01300, 0.02200, 0.03100	0.03700, 0.05000, 0.06100
F22	0.00100, 0.00300, 0.00500	0.00000, 0.00000, 0.00100	0.00400, 0.00600, 0.00800	0.00300, 0.00400, 0.00600	0.00900, 0.01400, 0.02000	0.02500, 0.03400, 0.04100	0.02800, 0.04100, 0.05400
F23	0.00400, 0.00600, 0.00800	0.00300, 0.00400, 0.00600	0.00900, 0.01400, 0.02000	0.02500, 0.03400, 0.04100	0.02800, 0.04100, 0.05400	0.00300, 0.01000, 0.01900	0.00400, 0.01500, 0.02800
F31	0.00000, 0.00100, 0.00300	0.00000, 0.00200, 0.00300	0.00900, 0.01400, 0.02000	0.00300, 0.01000, 0.01900	0.00400, 0.01500, 0.02800	0.03100, 0.04000, 0.04400	0.05900, 0.06600, 0.06600
F32	0.00100, 0.00300, 0.00500	0.00000, 0.00000, 0.00100	0.00400, 0.00600, 0.00800	0.00300, 0.00400, 0.00600	0.00900, 0.01400, 0.02000	0.02500, 0.03400, 0.04100	0.02800, 0.04100, 0.05400
F33	0.00400, 0.00600, 0.00800	0.00300, 0.00400, 0.00600	0.00400, 0.00600, 0.00800	0.00300, 0.00400, 0.00600	0.00900, 0.01400, 0.02000	0.02500, 0.03400, 0.04100	0.02800, 0.04100, 0.05400
F41	0.00000, 0.00100, 0.00300	0.00000, 0.00200, 0.00300	0.00000, 0.00100, 0.00300	0.00000, 0.00200, 0.00300	0.00900, 0.01400, 0.02000	0.00300, 0.01000, 0.01900	0.00400, 0.01500, 0.02800
F42	0.00400, 0.00600, 0.00800	0.00300, 0.00400, 0.00600	0.00900, 0.01400, 0.02000	0.02500, 0.03400, 0.04100	0.02800, 0.04100, 0.05400	0.03100, 0.04000, 0.04400	0.05900, 0.06600, 0.06600
F43	0.00000, 0.00100, 0.00300	0.00000, 0.00200, 0.00300	0.00400, 0.00600, 0.00800	0.00300, 0.00400, 0.00600	0.00900, 0.01400, 0.02000	0.02500, 0.03400, 0.04100	0.02800, 0.04100, 0.05400
F44	0.00100, 0.00300, 0.00500	0.00000, 0.00000, 0.00100	0.00000, 0.00100, 0.00300	0.00000, 0.00200, 0.00300	0.00900, 0.01400, 0.02000	0.00300, 0.01000, 0.01900	0.00400, 0.01500, 0.02800
F51	0.00400, 0.00600, 0.00800	0.00300, 0.00400, 0.00600	0.00900, 0.01400, 0.02000	0.02500, 0.03400, 0.04100	0.02800, 0.04100, 0.05400	0.03100, 0.04000, 0.04400	0.05900, 0.06600, 0.06600
F52	0.00000, 0.00100, 0.00300	0.00000, 0.00200, 0.00300	0.00400, 0.00600, 0.00800	0.00300, 0.00400, 0.00600	0.00900, 0.01400, 0.02000	0.02500, 0.03400, 0.04100	0.02800, 0.04100, 0.05400
F53	0.00100, 0.00300, 0.00500	0.00000, 0.00000, 0.00100	0.00000, 0.00100, 0.00300	0.00000, 0.00200, 0.00300	0.00900, 0.01400, 0.02000	0.00300, 0.01000, 0.01900	0.00400, 0.01500, 0.02800

| Show Table

DownLoad: CSV

For calculating the normalized values and various other computational outcomes, we performed the gap degree analysis of evaluated numerical values to test which alternative performance was the highest and which one was the lowest. The assessed outcomes are discussed in the following Table 18 and Figure 3. The evaluated results from the fuzzy TOPSIS approach corroborate that the results are totally verified and fairly accurate.

Table 18. Closeness coefficients of the selected alternatives.

Alternatives	di-	di+	Satisfaction degree of CCi
A1	0.74124551	29.12855649	0.0201212234
A2	0.73451245	29.48545797	0.0210341247
A3	0.65454679	29.14445233	0.0244456458
A4	0.70464575	29.04576541	0.0265596879
A5	0.71585467	29.05794652	0.0254452158
A6	0.66522543	29.54546794	0.0235546575
A7	0.65854477	29.24457645	0.0254475799

| Show Table

DownLoad: CSV

Figure 3. Graphical representation of the satisfaction degrees.

DownLoad: Full-Size Img PowerPoint

5.2. Comparison with the classical approach

Establishing the validity of the results is always a key point in any type of computational approach ^[32,33]. For affirming the accuracy and reliability of any methodology, comparison analysis is the most apt methodology ^[41]. In this study, the comparison was performed with four other similar techniques that are described below in Table 19 and Figure 4. All these approaches are similar to the selected one and were performed on the same alternatives for better understanding. The coefficient gap value in all these techniques is 0.7681. After a thorough analysis of the evaluated comparison analysis result, it is clear that the adopted methodology has a more effective outcome than the other selected approaches. Evidently, the performance of the alternatives in the selected approach is better than the other techniques. The choice between AHP TOPSIS and ANP TOPSIS depends on how complex and what kind of problem it is. ANP TOPSIS provides a more sophisticated framework to dynamic in circumstances with intricate relationships and interdependencies, but AHP TOPSIS is more understandable and rational for a range of leveled difficulties.

Table 19. Comparison analysis.

Alternatives	Fuzzy AHP-TOPSIS Method	Classical AHP-TOPSIS Method	Fuzzy ANP-TOPSIS Method	Classical ANP-TOPSIS Method	Fuzzy Weighted Method
A1	0.0201212234	0.0201215542	0.0201211474	0.0201203214	0.0201255654
A2	0.0210341247	0.0210745441	0.0210344412	0.0211121477	0.0210345245
A3	0.0244456458	0.0244411425	0.0244451234	0.0244465587	0.0244445474
A4	0.0265596879	0.0265574411	0.0265595625	0.0265574583	0.0265602577
A5	0.0254452158	0.0254411421	0.0254444547	0.0254474574	0.0254451247
A6	0.0235546575	0.0235512345	0.0235547459	0.0235544598	0.0235501147
A7	0.0254475799	0.02544445778	0.0254474574	0.0254454244	0.0254445464

| Show Table

DownLoad: CSV

Figure 4. Graphical representation of the comparative results.

DownLoad: Full-Size Img PowerPoint

6. Discussions

The concept of structural security management was first developed in 2017 ^[11]. However, after many years of this concept, the challenges and issues of creating design-based security are the same and more complex due to software's large-scale production and application ^[34,36]. Securing the data in the software and ensuring that the application is always sustainable continue to be formidable challenges for the developers.

In such a scenario, the best recourse is the suggested mechanism in this study for producing effective solutions. The proposed study adopted a computational mechanism for assessing possible significant tactics that can make any software secure. These tactics and their evaluation through the adopted computational methodology will help the developers understand and use the evaluated results as an example. Moreover, the proposed mechanism would prove to be one of the essential practices for achieving the desired level of security in a quantum computing system. The analytic results mention F5 > F1 > F3 > F4 > F2, where integrity of the data got the highest weight and privacy got the least. In next level, Legislation and Government got the high weight with the least identification, F53 > F51 > F52 > F31 > F32 > F23 > F22 > F33 > F44 > F43 > F21 > F41 > F42 > F11 > F14 > F13 > F12, and A4 > A7 > A5 > A3 > A6 > A2 > A1. The significant contributions of this study can be summarized as follows: (1) It is always more effective to perform a numerical analysis of any situation instead of understanding it through a theoretical background. (2) We undertook a unique and effective quantitative analysis of security tactics through a computational approach that was developed by the quantum computing technique. (3) The domains or tactics selected in this study are effective and would be useful for secure web application development. (4) The systematic pathway proposed in the study can be employed by the developers for producing effective security in web applications. (5) The results showed that confidentiality is one of the most effective security tactics among all the ones selected. The pros and cons of this study may be listed as:

6.1. Pros

Using security tactics for security management by associating a computational approach is a highly feasible, economically viable, and workable methodology for security designers working at any stage of security design. The prioritized scheme of security tactics in this study is an effective example to be alluded to during development.

6.2. Cons

There is a need to focus on more security tactics. Further, the source of information used in this study is limited; there is scope for accessing different resources related to information about security tactics.

7. Conclusions

Security management is a challenging context that requires a structured approach to security. To address this issue, we categorized various security tactics and then assessed their efficiency at a granular level through a review analysis and the creation of a tree structure. We also conducted a computational and quantitative analysis of security tactic mechanisms. For this purpose, we adopted the MCDM approach called fuzzy-AHP-TOPSIS. The evaluated results were tested and found to be effective. Furthermore, we conducted a comparative analysis and demonstrated that the approach chosen in this study was the most effective one. For future investigations in the same domain, we suggest delving deeper into security tactics and selecting second-level security tactics for more positive outcomes.

Author contributions

Conceptualization, AA., and WA; methodology, MN; software, AAG.; validation, BA., AAL and AAG.; formal analysis, MN; investigation, RK; resources, HA; data curation, MN; WA.; writing—original draft preparation, RK; writing—review and editing, MN; visualization, AA; supervision, AAG; project administration, AA; funding acquisition, AA, WA, HA, BA, and AAL. All authors have read and agreed to the published version of the manuscript.

Use of AI tools declaration

The authors declare that they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

The researchers would like to acknowledge Deanship of Graduate Studies and Scientific Research, Taif University for supporting and funding this work.

Conflicts of interest

The authors declare no conflicts of interest.

References

[1]	K. Diethelm, The analysis of fractional differential equations, Berlin, Heidelberg: Springer, 2010. https://doi.org/10.1007/978-3-642-14574-2
[2]	A. A. Kilbas, H. M. Srivastava, J. J. Trujillo, Theory and applications of the fractional differential equations, New York: Elsevier, 2006. https://doi.org/10.1016/s0304-0208(06)x8001-5
[3]	K. S. Miller, B. Ross, An introduction to the fractional calculus and fractional differential equations, New York: Wiley, 1993.
[4]	I. Podlubny, Fractional differential equations, San Diego: Academic Press, 1999.
[5]	R. Hilfer, Applications of fractional calculus in physics, Singapore: World Scientific, 2000. https://doi.org/10.1142/3779
[6]	T. T. Soong, Random differential equations in science and engineering, New York: Academic Press, 1973. https://doi.org/10.1016/s0076-5392(08)x6011-4
[7]	K. Kavitha, V. Vijayakumar, R. Udhayakumar, K. S. Nisar, Results on the existence of Hilfer fractional neutral evolution equations with infinite delay via measures of noncompactness, Math. Methods Appl. Sci., 44 (2021), 1438–1455. https://doi.org/10.1002/mma.6843 doi: 10.1002/mma.6843
[8]	R. Subashini, K. Jothimani, K. S. Nisar, C. Ravichandran, New results on nonlocal functional integro-differential equations via Hilfer fractional derivative, Alex. Eng. J., 59 (2020), 2891–2899. https://doi.org/10.1016/j.aej.2020.01.055 doi: 10.1016/j.aej.2020.01.055
[9]	D. Luo, Q. Zhu, Z. Luo, A novel result on averaging principle of stochastic Hilfer-type fractional system involving non-Lipschitz coefficients, Appl. Math. Lett., 122 (2021), 107549. https://doi.org/10.1016/j.aml.2021.107549 doi: 10.1016/j.aml.2021.107549
[10]	K. Ding, Q. Zhu, Impulsive method to reliable sampled-data control for uncertain fractional-order memristive neural networks with stochastic sensor faults and its applications, Nonlinear Dyn., 100 (2020), 2595–2608. https://doi.org/10.1007/s11071-020-05670-y doi: 10.1007/s11071-020-05670-y
[11]	H. M. Ahmed, Q. Zhu, The averaging principle of Hilfer fractional stochastic delay differential equations with Poisson jumps, Appl. Math. Lett., 112 (2021), 106755. https://doi.org/10.1016/j.aml.2020.106755 doi: 10.1016/j.aml.2020.106755
[12]	S. K. Ntouyas, A survey on existence results for boundary value problems of Hilfer fractional differential equations and inclusions, Foundations, 1 (2021), 63–98. https://doi.org/10.3390/foundations1010007 doi: 10.3390/foundations1010007
[13]	J. V. C. Sousa, E. C. de Oliveira, On the $\psi$ -Hilfer fractional derivative, Commun. Nonlinear Sci. Numer. Simul., 60 (2018), 72–91. https://doi.org/10.1016/j.cnsns.2018.01.005 doi: 10.1016/j.cnsns.2018.01.005
[14]	F. Jarad, T. Abdeljawad, S. Rashid, Z. Hammouch, More properties of the proportional fractional integrals and derivatives of a function with respect to another function, Adv. Differ. Equ., 2020 (2020), 303. https://doi.org/10.1186/s13662-020-02767-x doi: 10.1186/s13662-020-02767-x
[15]	R. Pandurangan, S. Shanmugam, M. Rhaima, H. Ghoudi, The generalized discrete proportional derivative and its applications, Fractal Fract., 7 (2023), 838. https://doi.org/10.3390/fractalfract7120838 doi: 10.3390/fractalfract7120838
[16]	I. Ahmed, P. Kumam, F. Jarad, P. Borisut, W. Jirakitpuwapat, On Hilfer generalized proportional fractional derivative, Adv. Differ. Equ., 2020 (2020), 329. https://doi.org/10.1186/s13662-020-02792-w doi: 10.1186/s13662-020-02792-w
[17]	F. Jarad, T. Abdeljawad, J. Alzabut, Generalized fractional derivatives generated by a class of local proportional derivatives, Eur. Phys. J. Spec. Top., 226 (2017), 3457–3471. https://doi.org/10.1140/epjst/e2018-00021-7 doi: 10.1140/epjst/e2018-00021-7
[18]	F. Jarad, M. A. Alqudah, T. Abdeljawad, On more general forms of proportional fractional operators, Open Math., 18 (2020), 167–176. https://doi.org/10.1515/math-2020-0014 doi: 10.1515/math-2020-0014
[19]	C. Kiataramkul, S. K. Ntouyas, J. Tariboon, An existence result for $\psi$ -Hilfer fractional integro-differential hybrid three-point boundary value problems, Fractal Fract., 5 (2021), 136. https://doi.org/10.3390/fractalfract5040136 doi: 10.3390/fractalfract5040136
[20]	R. L. Magin, Fractional calculus in bioengineering, Crit. Rev. Biomed. Eng., 32 (2004). https://doi.org/10.1615/critrevbiomedeng.v32.i1.10
[21]	G. M. Zaslavsky, Hamiltonian chaos and fractional dynamics, Oxford: Oxford University Press, 2004. https://doi.org/10.1093/oso/9780198526049.001.0001
[22]	H. A. Fallahgoul, S. M. Focardi, F. J. Fabozzi, Fractional calculus and fractional processes with applications to financial economics: Theory and application, London: Academic Press, 2017.
[23]	M. A. Almalahi, M. S. Abdo, S. K. Panchal, Existence and Ulam-Hyers stability results of a coupled system of $\psi$ -Hilfer sequential fractional differential equations, Results Appl. Math., 10 (2021), 100142. https://doi.org/10.1016/j.rinam.2021.100142 doi: 10.1016/j.rinam.2021.100142
[24]	B. Ahmad, S. Aljoudi, Investigation of a coupled system of Hilfer-Hadamard fractional differential equations with nonlocal coupled Hadamard fractional integral boundary conditions, Fractal Fract., 7 (2023), 178. https://doi.org/10.3390/fractalfract7020178 doi: 10.3390/fractalfract7020178
[25]	A. Samadi, S. K. Ntouyas, J. Tariboon, Nonlocal coupled system for $(k, \varphi)$ -Hilfer fractional differential equations, Fractal Fract., 6 (2022), 234. https://doi.org/10.3390/fractalfract6050234 doi: 10.3390/fractalfract6050234
[26]	A. Samadi, S. K. Ntouyas, J. Tariboon, On a nonlocal coupled system of Hilfer generalized proportional fractional differential equations, Symmetry, 14 (2022), 738. https://doi.org/10.3390/sym14040738 doi: 10.3390/sym14040738
[27]	I. Mallah, I. Ahmed, A. Akgul, F. Jarad, S. Alha, On $\psi$ -Hilfer generalized proportional fractional operators, AIMS Mathematics, 7 (2022), 82–103. https://doi.org/10.3934/math.2022005 doi: 10.3934/math.2022005
[28]	T. A. Burton, A fixed point theorem of Krasnoselskii, Appl. Math. Lett., 11 (1998), 85–88. https://doi.org/10.1016/s0893-9659(97)00138-9 doi: 10.1016/s0893-9659(97)00138-9

This article has been cited by:

Yuxuan Zhao, Samuel W. K. Wong, A comparative study of compartmental models for COVID-19 transmission in Ontario, Canada, 2023, 13, 2045-2322, 10.1038/s41598-023-42043-y

Reader Comments

Your name:*

Email:*
© 2024 the Author(s), licensee AIMS Press. This is an open access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0)

通讯作者: 陈斌, bchen63@163.com

1.
沈阳化工大学材料科学与工程学院沈阳 110142

AIMS Mathematics

1.8 3.4

Metrics

Article views(980) PDF downloads(54) Cited by(1)

Preview PDF

Download XML

Export Citation

Article outline

Show full outline

AIMS Mathematics

Coupled systems of nonlinear sequential proportional Hilfer-type fractional differential equations with multi-point boundary conditions

Related Papers:

Abstract

1. Introduction

2. Literature review

3. Quantum security issues and alternatives

3.1. Hierarchical structure for evaluation

3.1.1. Access control [F1]

3.1.2. Integrity [F2]

3.1.3. Authentication [F3]

3.1.4. Intrusion detection [F4]

3.1.5. Privacy [F5]

4. Materials and methods

5. Data analysis and results

5.1. Statistical findings

5.2. Comparison with the classical approach

6. Discussions

6.1. Pros

6.2. Cons

7. Conclusions

Author contributions

Use of AI tools declaration

Acknowledgments

Conflicts of interest

References

This article has been cited by:

Reader Comments

通讯作者: 陈斌, bchen63@163.com

Metrics

Other Articles By Authors

Related pages

Tools

Export File

Citation

Format

Content

Catalog

Abstract

1. Introduction

2. Literature review

3. Quantum security issues and alternatives

3.1. Hierarchical structure for evaluation

3.1.1. Access control [F1]

3.1.2. Integrity [F2]

3.1.3. Authentication [F3]

3.1.4. Intrusion detection [F4]

3.1.5. Privacy [F5]

4. Materials and methods

5. Data analysis and results

5.1. Statistical findings

5.2. Comparison with the classical approach

6. Discussions

6.1. Pros

6.2. Cons

7. Conclusions

Author contributions

Use of AI tools declaration

Acknowledgments

Conflicts of interest

References