Exponential stability of stochastic complex networks with multi-weights driven by second-order process based on graph theory

1.   Introduction

During the past decades, complex networks have attracted widespread attention of many mathematicians, physicists, and other scientists because of their extensive applications in many fields, such as transportation networks ^[1], social networks ^[2], and neural networks ^[3]. There are many studies examining unweighted complex networks or complex networks with single weights ^{[4,5,6,7,8,9,10]}. However, there are many complex networks with multi-weights in real life, especially in transportation networks. If a place is regarded as the vertex, people can take various kinds of public transportation from place A to place B, such as bus, subway, taxi, and so on. Meanwhile, in a social network, in which a person could be regarded as a vertex, they can communicate with each other in different ways such as WeChat, Facebook, Instagram, and so on. Therefore, complex networks with multi-weights have a wider range of applications than the single ones. An et al.^[1] analyzed synchronization of complex networks with multi-weights and applied it to traffic networks. Qin et al.^[11] investigated the synchronization and $\mathcal{H}_\infty$ synchronization of multi-weighted complex dynamical networks with fixed and switching topologies. Feng et al.^[12] analyzed traffic flow patterns through complex networks with multi-weights based on trip data and an operation timetable obtained from the Beijing Subway System.

However, these systems are always impacted by uncertain external noise including white noise and colored noise ^[13,14]. To describe these systems more precisely, many researchers introduce Brownian motion to simulate white noise on the basis of complex networks with multi-weights. Zhang et al.^[15] proposed several sufficient conditions to ascertain the moment exponential stability and almost surely exponential stability of stochastic complex networks with multi-weights(SCNMW) driven by second-order process. Zhou et al.^[16] studied synchronization of stochastic Lévy noise systems on a multi-weight network and applied it to Chua's circuits. Li et al.^[17] investigated the exponential stability of SCNMW with time-varying delay driven by G-Brownian motion via aperiodically intermittent adaptive control.

However, white noise has certain limitations. Its bandwidth is infinite ^[18], and it is not differentiable almost everywhere ^[19]. Especially in the modeling of engineering issues the variance of Brownian motion is infinite at any time, which means that the power of the signal is unbounded. Besides, for some intelligent control systems based on neural networks, as the spectral power distribution of the noise may be unevenly distributed in the whole frequency domain, most of the noises under the specific environment are not white noises ^[20]. So, it is reasonable to describe the acceleration of random oscillation by a second-order process. A new model of SCNMW driven by a second-order process is proposed in this paper. For more details about the second-order process, please see ^[21,22,23].

To disclose how the uncertain external noise affect the dynamical properties of SCNMW driven by second-order process, stability is a crucial topic that needs to be considered ^[19]. Exponential stability is one of the best stabilities: The convergence to the equilibrium position is swift, and the rapidity of convergence is referred to as the quality index of the transition process in control theory ^[24]. Especially in traffic networks, studying the exponential stability of the uncongested equilibrium point can aid in devising more efficient public transportation routes ^[25]. In addition, the majority of existing studies analyzing the stability of systems driven by the second-order process focus on the noise-to-state stability ^[18,19,26], while few consider exponential stability. Therefore, this paper aims to study the exponential stability of SCNMW driven by second-order process.

It is common knowledge that the Lyapunov method is a potent tool to analyze the stability issues of systems. Unfortunately, in the model of SCNMW driven by second-order process, there are a great number of vertices. So, it is challenging to construct the global Lyapunov function of the system. All along, many scholars have long been devoted to researching how to construct Lyapunov functions for arbitrary systems. Fortunately, complex networks with multi-weights can be split into multiple different complex networks with single weights according to the method of network split mentioned in ^[27,28]. Then, motivated by Li ^[29] and Zhang ^[15], combined with Lyapunov method and Kirchhoff's matrix-tree theorem, the global Lyapunov function can be simply established by the Lyapunov function of every subsystem. Furthermore, the outstanding work of Wu ^[21] has provided a framework for analyzing the stability of random nonlinear systems driven by second-order process, which has also facilitated our work significantly.

Our contributions in this paper are as follows:

1) A new model of stochastic complex networks with multi-weights driven by second-order process is proposed in this paper. Since the second-order process is a stationary process, the new model is more suitable for the engineering task than the model which is driven by Brownian motion. So, our research can broaden the application scope of SCNMW.

2) Since SCNMW driven by second-order process cannot be described by Itô integral equation, it precludes us from analyzing its dynamical properties using traditional means. According to the properties of second-order process, we can take the derivative for the equation. Then, with the help of the Bellman-Gronwall inequality and some relaxed assumptions, we can deal with the term of the second-order process by a certain function. This enables us to obtain the sufficient criterion for exponential stability more easily.

3) Our results can also lay the foundation for studies of some other problems for SCNMW driven by second-order process, such as noise-to-state stability, input-to-state stability, synchronization, and so on.

The rest of this paper is organized as follows. In Section 2, we provide a detailed introduction to the relevant knowledge of graph theory and present the corresponding lemmas. Also, we present a model of the multi-weighted complex network driven by second-order process. Then, we provide some lemmas and definitions related to the model. Our main conclusions will be presented in Section 3, where we firstly provide the Lyapunov-type sufficiency criterion, followed by the corresponding coefficient-type sufficiency criterion. In order to verify the correctness of the theorems, we present the corresponding numerical examples in Section 4. Finally, the conclusion is provided in Section 5.

2.   Preliminary and model description

In this section, we introduce some important notations, and lemmas which are used throughout this paper in Section 2.1. Then, the details of SCNMW driven by second-order process are described in Section 2.2.

2.1.   Preliminary

$(\Omega, \mathcal{F}, \mathbb{F}, \mathbb{P})$ is a complete probability space with a filtration $\mathbb{F} = \{\mathcal{F}_t\}_{t\ge 0}$ satisfying the usual conditions(i.e., the filtration is right continuous, and $\mathcal{F}_0$ contains all $\mathbb{P}$-null sets). $\mathbb{P}$ is a probability measure, and $\mathbb{E}(\cdot)$ is the mathematical expectation. Let $\xi(t)\in\mathbb{R}^n$ be a stochastic process vector defined on the complete probability space which satisfies $\sup_{t_0\le s\le t}\mathbb{E}|\xi(s)|^2 < K$ in which $K$ is a constant. $|\cdot|$ is the Euclidean norm for vectors or the trace norm for matrices. Denote by $||A||$ the 2-norm of a matrix $A$. Denote by $A^T$ the transpose of a matrix $A$. The family of all non-negative functions $V(x, t)\in C^{2, 1}(\mathbb{R}^n\times\mathbb{R}^+; \mathbb{R}^+)$ has functions that are twice continuous differentiable in $x$ and once in $t$.

Meanwhile some fundamental principles in graph theory are introduced from ^[30,31]. A diagraph $\mathcal{G} = (V, E)$ contains a set $V = \{1, 2, \cdots, l\}$ of vertices and a set $E$ of edges $(k, h)$ leading from initial vertex $k$ to terminal vertex $h$. The digraph $\mathcal{G}$ is regarded as a weighted digraph if each edge $(h, k)$ is assigned a positive weight $a_{kh}$. $a_{kh} = 0$ if there are no edges from vertex $h$ to vertex $k$ in $\mathcal{G}$. $A = (a_{kh})_{l\times l}$ is the weight matrix of $\mathcal{G}$. $\omega(\mathcal{G})$ is the product of the weights of all its edges. A subgraph $\mathcal{H}$ of $\mathcal{G}$ is regarded to be spanning if $\mathcal{H}$ and $\mathcal{G}$ have the same vertex set. A directed path $\mathcal{P}$ in $\mathcal{G}$ is a subgraph with distinct vertices $\{k_1, k_2, \cdots, k_s\}$ such that its set of edges is $\{(k_i, k_{i+1}):i = 1, 2, \cdots, s-1\}$. If $k_s = k_1$, we name $\mathcal{P}$ as a directed cycle. A tree $\mathcal{T}$ is rooted at vertex $k$, called the root, if $k$ is not a terminal vertex of any edges, and each of the remaining vertices is a terminal vertex of exactly one edge. A connected subgraph $\mathcal{T}$ is a tree if it contains no cycles. A subgraph $\mathcal{Q}$ is unicyclic if it is a disjoint union of rooted trees whose roots form a directed cycle. A digraph $\mathcal{G}$ is strongly connected if there exists a directed path from any vertex to another. If $\omega(\mathcal{C}) = \omega(-\mathcal{C})$ for all directed cycles $\mathcal{C}$, the weighted digraph $(\mathcal{G}, A)$ is said to be balanced, where $-\mathcal{C}$ denotes the reverse of $\mathcal{C}$ and is constructed by reversing the directions of all edges in $\mathcal{C}$. For a unicyclic graph $\mathcal{Q}$ with cycle $\mathcal{C}_{\mathcal{Q}}$, let $\tilde{\mathcal{Q}}$ be the unicyclic graph obtained by replacing $\mathcal{C}_{\mathcal{Q}}$ with $-\mathcal{C}_{\mathcal{Q}}$.

Then, we state some significant lemmas about the graph theory.

Lemma 1. (Kirchhoff's Matrix-Tree Theorem)^[29]. Let $l \geq 2$ and $(\mathcal{G}, A)$, $A = \left(a_{kh}\right)_{l \times l}$ be a weighted digraph. Define $L = (p_{kh})_{l\times l}$ as the Laplacian matrix of $(\mathcal{G}, A)$, where $p_{kh} = -a_{kh}$ for $h\neq k$ and $p_{kh} = \sum_{j\neq k}a_{kj}$ for $h = k$, and let $c_k$ be the cofactor of the $k$th diagonal element of $L$. Then, it holds that

where $\mathbb{T}_{k}$ is the set of all spanning trees $\mathcal{T}$ of $(\mathcal{G}, A)$ that are rooted at vertex $k$, and $w(\mathcal{T})$ is the weight of $\mathcal{T}$. Additionally, if $(\mathcal{G}, A)$ is strongly connected, then $c_{k} > 0$ for $k = 1, 2, \ldots, l$.

Lemma 2. ^[15]. Assume $(\mathcal{G}, A), A = \left(a_{i j}\right)_{l \times l}$ is a weighted digraph in which $l \geq 2$. Define $\mathbb{Q}$ as the set of all spanning unicyclic graphs $\mathcal{Q}$ of $(\mathcal{G}, A)$, $C_{\mathcal{Q}}$ as the cycle of $\mathcal{Q}$, and $W(\mathcal{Q})$ as the weight of $\mathcal{Q}$. $c_{k}$ is defined as in Lemma 1. Then, for arbitrary functions $Q_{k h}\left(x_{k}, x_{h}\right), k, h = 1, 2, \ldots, l$, it holds that

Next, we introduce some important lemmas that we will use in the proofs.

Lemma 3. ^[32]. $\forall p > 0, x\in\mathbb{R}^n_+$, it holds that

Lemma 4. (Bellman-Gronwall inequality)^[33]. Let the function $y(t)$ be absolutely continuous for $t\ge t_0$ and let its derivative satisfy the inequality

Then, for almost all $t\ge t_0$, where $k(t)$ and $h(t)$ are almost everywhere continuous functions integrable over every finite interval. Then, for $t\ge t_0$, it holds that

2.2.   Model description

In this paper we consider a network $\mathcal{G}$ with $N$ vertices and $l$ different kinds of weights $(b_{ij}^1, b_{ij}^2, \cdots, b_{ij}^l)$. The network can be split into multiple subnetworks in many ways. According to the network split method, the principle is to split based on the different properties of the edges. So, SCNMW driven by second-order process can be described as

in which $x_i\in \mathbb{R}^n$ is the state vector of vertex $i$, and $\xi_i(t)\in\mathbb{R}^n$ is a second-order moment stochastic process which is $\mathcal{F}_t$-adapted. Vector function $f_i, g_i:\mathbb{R}^n\times\mathbb{R}_+^1\rightarrow \mathbb{R}^n$ is continuously differentiable for $i = 1, 2, \cdots, N$, where $f_i$ is the drift coefficient and $g_i$ is the diffusion coefficient. Assume that $f_i(0, t) = g_i(0, t) = 0, \forall t\in [t_0, \infty)$, which means that $x(t) = (x_1^T, x_2^T, \cdots, x_N^T)^T = (0, 0, \cdots, 0)^T_{1\times nN}$ is a trivial solution of the system, and they all satisfy the usually local Lipschitz condition and linear growth condition. Moreover $\delta_m(m = 1, 2, \cdots, l)$ is the coupling strength of the $m$th sub-network, and $b_{ij}^m$ is the $m$th weight from $j$th vertex to $i$th vertex. $H_m = diag(h_{11}^m, h_{22}^m, \cdots, h_{nn}^m)(m = 1, 2, \cdots, l)$ is a positive diagonal $n\times n$ matrix standing for the $k$th sub-network inner coupling.

Furthermore, in brief, we have some definitions as follow:

Then, we give a lemma and definition from ^[21].

Lemma 5. (Existence and uniqueness of solutions)^[21]. For system (2.1) there exists a unique solution $x_i(t)$ on $[t_0, \infty)$ for any given initial value $x(t_0) = x_0$ if the following assumptions hold.

A1. For $i = 1, 2, \cdots, N$, process $\xi_i(t)$ is $\mathcal{F}_t$-adapted and piecewise continuous, and satisfies

A2. For any $M > 0$ and $i = 1, 2, \cdots, N$, there exits a constant $L_M$ possibly depending on $M$ such that $\forall x_1, x_2\in U_M$, $x_1\neq x_2$

A3. There exists a constant $d_o\ge 0$ such that

A4. There exit a positive function $V(x(t), t)\in C^{2, 1}(\mathbb{R}^n\times\mathbb{R}^+; \mathbb{R}^+)$ and constants $c, d > 0$ such that for all $t\ge t_0$

and let $\sigma_k = \inf\{t\ge t_0:|x(t)|\ge k\}$, $\sigma_{\infty} = \lim\limits_{k\to\infty}\sigma_k$. Then it holds that

Definition 1. (ES-p-M)^[21]. For system (2.1) the equilibrium $x(t)\equiv 0$ is said to be exponentially stable in $p$th($p > 0$) moment if there exist constants $k_1, k_2$ such that $\forall t\ge t_0, x_0\in \mathbb{R}^n\setminus\{0\}$

As $p = 2$, it is said to be exponentially stable in mean square.

3.   Exponential stability analysis for SCNMW driven by second-order process

In the section, we will present Lyapunov-type sufficient criterion for SCNMW driven by second-order process to satisfy ES-p-M in Section 3.1, and give coefficients-type sufficient criterion in Section 3.2.

3.1.   Lyapunov-type sufficient criterion

First of all, we state some assumptions.

B1. For any $i, j\in\{1, 2, \cdots, N\}$ and $p\ge2$, there exist positive constants $\alpha_i, \beta_i, \lambda_i, \gamma_i$, $A = (a_{ij})_{N\times N}, a_{ij}\ge0$ and functions $V_i(x_i, t), Q_{ij}(x_i, x_j, t)$ such that

where $\frac{\partial V_i(x_i, t)}{\partial x_i} = \bigg(\frac{\partial V_i(x_i, t)}{\partial x_i^{(1)}}, \cdots, \frac{\partial V_i(x_i, t)}{\partial x_i^{(n)}}\bigg)$.

B2. For $\forall x_i, x_j\in\mathbb{R}^n$ along each directed cycle $\mathcal{C}$ of the weighted digraph $(\mathcal{G}, A)$, it follows that

B3. For any $\varepsilon > 0, t_1\ge t_0$, there exists a function $\varphi(\cdot)$ such that

where the function $\varphi(\cdot)$ satisfies $\varphi(\max\limits_{1\le i\le l}\gamma_i) < \min\limits_{1\le i\le l}\lambda_i$ for any $i\in \{1, 2, \cdots, N\}$.

Theorem 1. Let $(\mathcal{G}, A)$ be strongly connected. If Assumptions B1–B3 hold, then for system (2.1) the equilibrium $|x(t)|\equiv 0$ is $p$th moment exponentially stable.

Proof. Fix any $x_0\in\mathbb{R}^n$ and write $x(t; t_0, x_0)$ as $x(t)$ for short. Let $V(x, t) = \sum_{i = 1}^{N}c_iV_i(x_i, t)$, where $c_i$ is defined as Lemma 1. Then, we can derive from (3.1) that

Then, according to Lemma 3, we can easily derive that

Combining with inequalities (3.6) and (3.7), we can obtain that

Then, taking (3.2)–(3.4) together with Lemmas 1 and 2 and taking the derivative for $V(x, t)$ along the trajectory of system (2.1), in terms of $W(\mathcal{Q}) > 0$, we have

where $\hat{\lambda} = \min\limits_{1\le k\le l}{\lambda_k}, \check{\gamma} = \max\limits_{1\le k\le l}\gamma_k$. According to Lemma 4, it can easily be deduced that

Then, we define a stopping time sequence $\{\eta_k\}_{k = 1}^\infty$ in which $\eta_k = \inf\{t\ge t_0:|x(t)| > k\}(k = 1, 2, \cdots)$. Obviously, $\eta_k \rightarrow \infty$ almost surely as $k\rightarrow \infty$. Moreover, take the expectation on both sides of inequality (3.10), and we can obtain that

Because $f_i, g_i$ satisfy the usually local Lipschitz condition and linear growth condition, and $\sup_{t_0\le s\le t}\mathbb{E}|\xi(s)|^2 < K$ in which $K$ is a constant, we can easily verify that the above conditions in Lemma 5 are satisfied. Therefore, there exists a unique solution to system (2.1).

Then, let $k\rightarrow \infty$ in accordance with (3.8), and we can get that

In terms of Assumption B3, it yields that

Therefore, by Definition 1, for system (2.1) the equilibrium $|x(t)|\equiv 0$ is $p$th moment exponentially stable, which means the proof is complete. □

Remark 1. The requirements in Assumption B3 are feasible in practical applications. According to (1.7.15) in ^[34], if $\xi(t)\in\mathbb{R}^n$ is a Gaussian process, for all $t\ge t_0$ there exist $c_1, c_2 > 0$ such that

Then, for all $t_1 > t_0$ it holds that

So that the Assumption B3 is rational.

Remark 2. The large number of directed cycles possessed by a complex network as well as the uncertainty in $x_i$ and $x_j$ have made it difficult to verify the validity of Assumption B2. Therefore, we need to find a more convenient method. Fortunately, we can find some suitable functions $Q_{i j}, i, j = 1, ... N$, so that for $\forall i, j\in\{1, 2, \cdots, N\}$, there exists a function $L_i$ such that the following equation holds:

Naturally, we have

This approach makes it easier to test out Assumption B2.

Remark 3. If $(\mathcal{G}, A)$ is balanced, then the following equation holds:

Thus, Assumption B2 can be replaced by

Remark 4. Compared with our research on stochastic complex networks with multi-weights in Zhang et al. ^[15], the oscillation of surroundings in this paper is described by a second-order process rather than Brownian motion. Since SCNMW driven by second-order process cannot be described by Itô integral equation, it precludes us from analyzing its dynamical properties using traditional means. According to the properties of the second-order process, we can take the derivative for the equation. Then, with the help of Bellman-Gronwall inequality and some relaxed assumptions, we can deal with the term of second-order process by a certain function. This enables us to obtain the sufficient criterion for exponential stability more easily.

On the basis of Kirchhoff's matrix-tree theorem, the global Lyapunov function can be simply established by the Lyapunov function of every subsystem and the properties of the network. This solves the challenge of constructing a global Lyapunov function due to the number of vertices.

3.2.   Coefficients-type sufficient criterion

In Theorem 1, exponential stability sufficient criterion is given in the Lyapunov-type. Therefore, Theorem 1 is not applicable to the practical system (2.1). Subsequently, we will establish coefficients-type Theorem 2 based on Theorem 1.

First, we give some assumptions on the coefficients of system (2.1). For simplify, we define as follows

C1. For any $i\in\{1, 2, \cdots, N\}$, there exist positive constants $\alpha_i$, $\gamma_i$ such that

C2. For $p\ge 2$, it follows that

C3. For any $\varepsilon > 0, t_1\ge t_0, p\ge 2$, there exists a function $\varphi(\cdot)$ such that

where the function $\varphi(\cdot)$ satisfies for any $\varphi(\max\limits_{1\le i\le N}\gamma_i) < \min\limits_{1\le i\le N}\{p\alpha_i-lp\sum_{j = 1}^NB_{ij}\}$.

Theorem 2. If Assumptions C1–C3 hold, then for system (2.1), the equilibrium $|x(t)|\equiv 0$ is $p$th moment exponentially stable.

Proof. Define functions $V_i:\mathbb{R}^n\rightarrow \mathbb{R}^1_+, V_i(x_i) = |x_i|^p$ for the $i$th subsystem. We can derive that

where $a_{ij} = lB_{ij} > 0, Q_{ij}(x_i, x_j, t) = x_j^2-x_i^2$. Therefore, along each directed cycle $\mathcal{C}$ of weighted digraph $(\mathcal{G}, A)(A = (a_{ij})_{N\times N})$, it holds that

Furthermore, according to Assumption C2, we can know that $\lambda_i = p\alpha_i-lp\sum_{j = 1}^NB_{ij} > 0$. Finally by using Assumptions C1 and C3, all the assumptions in Theorem 1 have been verified successfully, which means for system (2.1) the equilibrium $|x(t)|\equiv 0$ is $p$th moment exponentially stable. The proof is completed. □

Remark 5. Theorem 2 states that the system (2.1) is $p$th moment exponentially stable if the multiple weights, coupling strengths, and second-order process satisfy Assumption C2. When $B_{i j} > 0$, for any $i, j = 1, 2, \ldots, N$, $(G, (B_{i j})_{N \times N})$ is strongly connected. Nevertheless, we have $B_{i j} = \max _{1 \leq k \leq l}\{b_{i j}^k \delta_k \breve{h}^k\}, \delta_k > 0, \breve{h}^k > 0$ for $k = 1, 2, \ldots, l$. Thus, whenever there exists a $k$ such that $b_{i j}^k > 0$ holds, there will be $B_{i j} > 0$. This shows that for any $k$, $b_{i j}^k > 0$ is not needed. That is, not all subnetworks must satisfy strong connectivity. Theorem 1 and Theorem 2 utilize the weighted sum of the vertex Lyapunov functions to derive the Lyapunov function of a multi-weighted complex network system, whose relationship can be represented by $\sum_{i = 1}^N c_i V_i$, where $c_i$ is the cofactor of the $i$th diagonal element of the Laplace matrix for $(G, (lB_{i j})_{N \times N})$.

Remark 6. A sufficient criterion for exponential stability is provided in Theorem 2. By observing the three Assumptions, we can find that multi-weights and the second-order process all affect the exponential stability of the system. According to Assumption C2, we can observe that $\sum_{j = 1}^NB_{ij}$ needs to be within a certain range. $B_{ij} = \max _{1 \leq k \leq l}\{b_{i j}^k \delta_k \breve{h}^k\}$ is closely related with the weights and coupling strength. So, the value of weights and $\delta_k$ should not be excessively large. Further, second-order process can also affect $\varphi(\cdot)$ which is a positive-definite function. And $g_i$ that is the diffusion coefficient determines the value of $\gamma_i$ to affect the exponential stability of the system. We will discuss more details in the Numerical example section.

Remark 7. When $0 < p < 2$, according to Jensen's inequality, the following equation holds

So if the trivial solution of system (2.1) is exponentially stable in mean square, system (2.1) is also $p$th exponentially stable when $0 < p < 2$.

Remark 8. Most of the literature studies the stability of complex networks with single weight ^[29,35,36]. However, in real life, there are many networks with more than one kind of weight, such as traffic networks, social networks, and epidemiological networks. Due to the diversity of weights, complex networks with multi-weights will exhibit more intricate dynamical properties than the single ones. Therefore, studying the stability of SCNMW is essential. Besides, SCNMW can also address the situation with single weight by adjusting certain parameters.

4.   Numerical example

To demonstrate the validity of the theorem, some numerical tests are provided in this section. For better fitting reality, refer to ^[1,27]. We consider a traffic network fulfilling the Lorenz chaotic system which has three bus lines. In order to satisfy the assumptions in Theorem 2, we adjust some parameters and choose the wide stationary process as the influence of the second-order process in the dynamical equations of nodes. The revised type can be described as follows:

When $i = 1$,

When $i = 2$,

When $i = 3$,

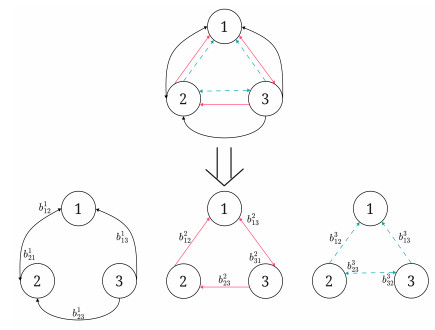
where $\delta_1 = 0.2, \delta_2 = 0.3, \delta_3 = 0.3$, and $\xi_i(t) = (2cos(it+\phi), 2cos(2it+\phi), 2cos(3it+\phi))^T$ where the random variable $\phi$ is uniformly distributed in $(0, 2\pi)$. The first kind of weights are $b_{12}^1 = 0.3, b_{13}^1 = 0.15, b_{23}^1 = 0.3, b_{21}^1 = 0.2$. The second kind of weights are $b_{12}^2 = 0.1, b_{13}^2 = 0.1, b_{23}^2 = 0.2, b_{31}^2 = 0.2$. The third kind of weights are $b_{12}^3 = 0.15, b_{13}^3 = 0.1, b_{23}^3 = 0.2, b_{32}^3 = 0.1$. Thus, in accordance with the network split method, this network with three-weights can be shown as Figure 1.

Subsequently, we shall proceed to verify the assumptions in Theorem 2 to ascertain their validity. By routine calculation we can get $B_{11} = B_{22} = B_{33} = 0,$ $B_{12} = 0.06, B_{13} = 0.03,$ $B_{21} = 0.04,$ $B_{23} = 0.06, B_{31} = 0.06, B_{32} = 0.03,$ and we can unequivocally ascertain that $(\mathcal{G}, (B_{ij})_{3\times 3})$ is strongly connected.

Then, in terms of $f_i(x_i, t) = (10(x_{i2}-x_{i1}), 2x_{i1}-10x_{i2}-x_{i1}x_{i3}, x_{i1}x_{i2}-8/3x_{i3})^T$, we can derive that

This means that $\alpha_i\le\frac{8}{3}$. We consider the exponential stability for $p = 2$. We choose $\alpha_i = 2.6$ so that

Moreover due to $g_i(x, t) = (0.375x_{i1}, 0.35x_{i2}, 0.36x_{i3})^T$, we can obtain that

which means that $\gamma_i\ge 0.75$. According to $\xi_i(t) = (2cos(it+\phi), 2cos(2it+\phi), 2cos(3it+\phi))^T$, it holds that $|\xi(t)|\le 6$. We choose the proper function $\varphi(\varepsilon) = 6\varepsilon$ and constant $\gamma_i = 0.75$ to satisfy that $\varphi(\max_{1\le i\le 3}\gamma_i) = 4.5 < \min_{1\le i\le l}\lambda_i = 4.6$.

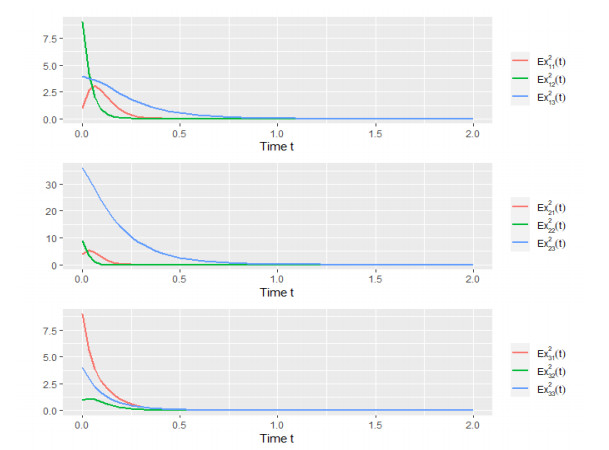
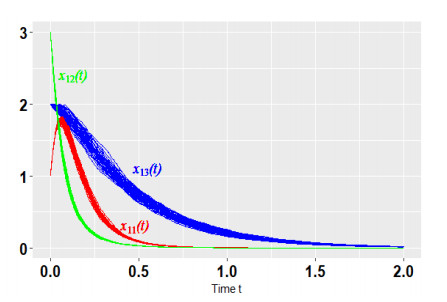
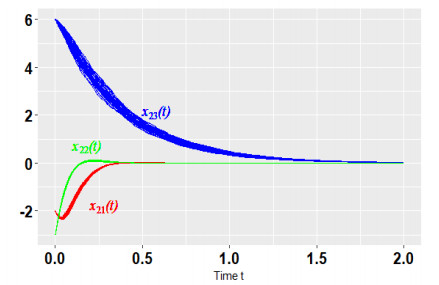
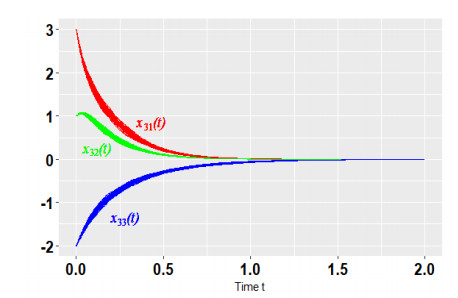
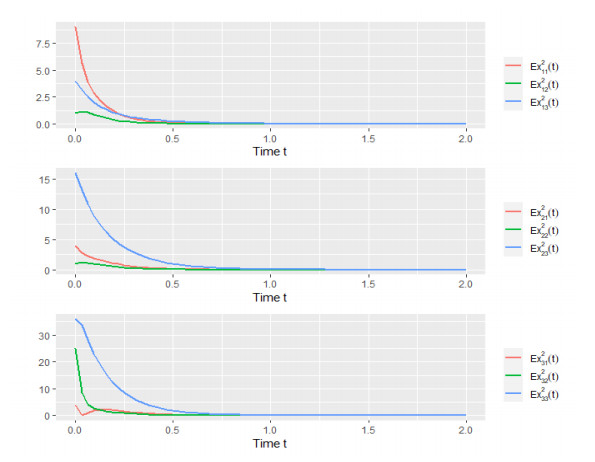
All the aforementioned assumptions hold true. Therefore, the equilibrium $|x(t)|\equiv 0$ is exponentially stable in mean square. Choose the initial value as $(1, 3, 2, -2, -3, 6, 3, 1, -2)^T$, and from Figures 2–5, we can observe that the numerical tests correspond to the expectation of Theorem 2.

Next, we will adjust the initial value and the parameters of multi-weights, coupling strength, and second-order process to make comparisons.

Example 1. The modified parameters are as follows:

$\delta_1 = 0.1, \delta_2 = 0.2, \delta_3 = 0.2$, $\xi_i(t) = (2.04cos(it+\phi), 2.04cos(2it+\phi), 2.04cos(3it+\phi))^T$ where the random variable $\phi$ is uniformly distributed in $(0, 2\pi)$. The first kind of weights are $b_{12}^1 = 0.4, b_{13}^1 = 0.3, b_{23}^1 = 0.4, b_{21}^1 = 0.3$. The second kind of weights are $b_{12}^2 = 0.2, b_{13}^2 = 0.2, b_{23}^2 = 0.3, b_{31}^2 = 0.3$. The third kind of weights are $b_{12}^3 = 0.2, b_{13}^3 = 0.2, b_{23}^3 = 0.3, b_{32}^3 = 0.2$.

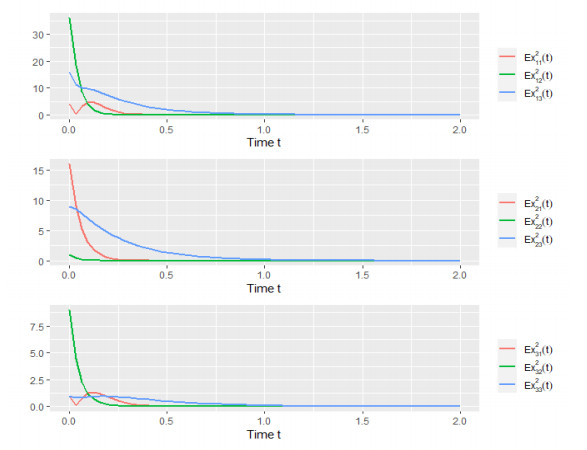
After calculation we can obtain that $\lambda_1 = 4.72 > 0, \lambda_2 = 4.66 > 0, \lambda_3 = 4.6 > 0$. We choose the proper function $\varphi(\varepsilon) = 6.12\varepsilon$ and constant $\gamma_i = 0.75$ to satisfy that $\varphi(\max_{1\le i\le 3}\gamma_i) = 4.59 < \min_{1\le i\le l}\lambda_i = 4.6$. Thus, according to Theorem 2, the equilibrium is exponentially stable in mean square. We choose the initial value as $(3, 1, -2, 2, 1, -4, -2, 5, -6)^T$, and the numerical simulation is shown in Figure 6.

Example 2. The modified parameters are as follows:

$\delta_1 = 0.4, \delta_2 = 0.6, \delta_3 = 0.5$, $\xi_i(t) = (1.5cos(it+\phi), 1.5cos(2it+\phi), 1.5cos(3it+\phi))^T$ where the random variable $\phi$ is uniformly distributed in $(0, 2\pi)$. The first kind of weights are $b_{12}^1 = 0.4, b_{13}^1 = 0.3, b_{23}^1 = 0.4, b_{21}^1 = 0.3, b_{31}^1 = 0.2, b_{32}^1 = 0.3$. The second kind of weights are $b_{12}^2 = 0.2, b_{13}^2 = 0.2, b_{23}^2 = 0.3, b_{21}^2 = 0.2, b_{31}^2 = 0.3, b_{32}^2 = 0.2$. The third kind of weights are $b_{12}^3 = 0.2, b_{13}^3 = 0.2, b_{23}^3 = 0.3, b_{21}^3 = 0.2, b_{31}^3 = 0.2, b_{32}^3 = 0.2$.

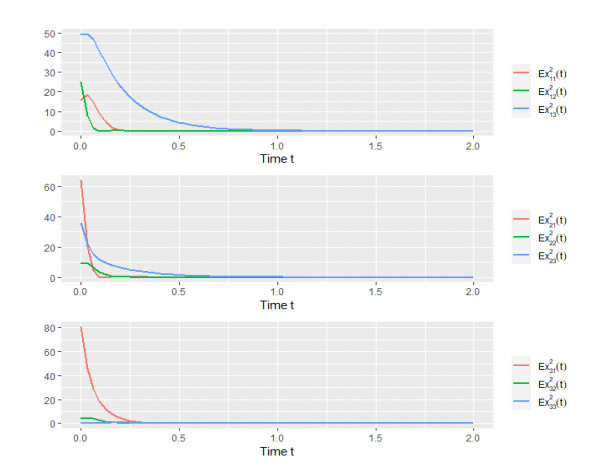
After calculation we can obtain that $\lambda_1 = 3.52 > 0, \lambda_2 = 3.4 > 0, \lambda_3 = 3.4 > 0$. We choose the proper function $\varphi(\varepsilon) = 4.5\varepsilon$ and constant $\gamma_i = 0.75$ to satisfy that $\varphi(\max_{1\le i\le 3}\gamma_i) = 3.375 < \min_{1\le i\le l}\lambda_i = 3.4$. Thus, according to Theorem 2, the equilibrium is exponentially stable in mean square. We choose the initial value as $(-2, 6, 4, 4, 1, 3, -1, 3, 1)^T$, and the numerical simulation is shown in Figure 7.

Example 3. The modified parameters are as follows:

$\delta_1 = 0.1, \delta_2 = 0.1, \delta_3 = 0.1$, $\xi_i(t) = (2.2cos(it+\phi), 2.2cos(2it+\phi), 2.2cos(3it+\phi))^T$ where the random variable $\phi$ is uniformly distributed in $(0, 2\pi)$. The first kind of weights are $b_{12}^1 = 0.1, b_{13}^1 = 0.05, b_{23}^1 = 0.1, b_{21}^1 = 0.2, b_{31}^1 = 0.1$. The second kind of weights are $b_{12}^2 = 0.1, b_{13}^2 = 0.1, b_{23}^2 = 0.2, b_{31}^2 = 0.1, b_{32}^2 = 0.05$. The third kind of weights are $b_{12}^3 = 0.05, b_{13}^3 = 0.1, b_{23}^3 = 0.15, b_{21}^3 = 0.15, b_{31}^3 = 0.05, b_{32}^3 = 0.1$.

After calculation we can obtain that $\lambda_1 = 5.08 > 0, \lambda_2 = 4.96 > 0, \lambda_3 = 5.08 > 0$. We choose the proper function $\varphi(\varepsilon) = 6.6\varepsilon$ and constant $\gamma_i = 0.75$ to satisfy that $\varphi(\max_{1\le i\le 3}\gamma_i) = 4.95 < \min_{1\le i\le l}\lambda_i = 4.96$. Thus, according to Theorem 2, the equilibrium is exponentially stable in mean square. We choose the initial value as $(4, 5, 7, -8, 3, -6, 9, 2, -1)^T$, and the numerical simulation is shown in Figure 8.

From Figures 6–8, we can find that the initial value which is not 0 does not affect the stability of the system. Comparing Example 1 with Example 2, we can get the conclusion of Remark 5.

Remark 9. From Figures 3–5, we can find that the moments of approaching zero are different. We need to point out that in the coupling terms, $x_{11}(t)$ is only related to both $x_{21}(t)$ and $x_{31}(t)$, and not to $x_{12}(t)$ or $x_{13}(t)$. So, when $x_{12}(t)$ and $x_{13}(t)$ approach zero over time, $x_{11}(t)$ does not necessarily approach zero. Apart from the coupling term, $x_{11}(t)$ is also related to $x_{12}(t)$. So, we can derive that $x_{11}(t)$ approaches zero when $x_{21}(t)$, $x_{31}(t)$ and $x_{12}(t)$ all approach zero.

5.   Conclusions and discussion

In this paper, we have analyzed the exponential stability of SCNMW driven by second-order process. A Lyapunov-type sufficient criterion is provided in Theorem 1. Building upon Theorem 1, a coefficient-type sufficient criterion is established in Theorem 2. Through the assumptions in Theorem 2, we find that this sufficient criterion is influenced by coupling strength, weights, and second-order process. Finally, an example of a complex network with multi-weights in traffic is provided by adjusting its parameters to satisfy the corresponding assumptions of Theorem 2. Subsequently, we have verified the effectiveness of the theorems through numerical simulations. Then, in order to illustrate how weights and second-order process affect the stability of the system, we adjust the parameters of second-order process and weights to verify the conclusion.

Compared with our research on SCNMW in Zhang et al. ^[15], the oscillation of surroundings in this paper is described by a second-order process rather than Brownian motion. Brownian motion is not well-suited for modeling in many engineering applications. Thus, this new model driven by second-order process can be applied in more fields. For example, our results can be applied for the derivation of sufficient conditions of exponential stability of the uncongested equilibrium point in traffic networks to devise more efficient public transportation routes. Our work can also lay the foundation for the research of some other problems for SCNMW driven by second-order processes such as noise-to-state stability, input-to-state stability, synchronization, and so on. Furthermore, in practical life, many complex networks are also subject to disturbances such as time delays or pulse noise ^[37,38,39], which are worth studying.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgement

This study was supported by the National Natural Science Foundation of China (11401085), Hei-longjiang Province Postdoctoral Funding Program (LBH-Q21059), Fundamental Research Projects of Chinese Central Universities (2572021DJ04).

Conflict of interest

The authors declare no conflicts of interest.