This work utilizes generalized order statistics (GOSs) to study the q-Weibull distribution from several statistical perspectives. First, we explain how to obtain the maximum likelihood estimates (MLEs) and utilize Bayesian techniques to estimate the parameters of the model. The Fisher information matrix (FIM) required for asymptotic confidence intervals (CIs) is generated by obtaining explicit expressions. A Monte Carlo simulation study is conducted to compare the performances of these estimates based on type Ⅱ censored samples. Two well-established measures of information are presented, namely extropy and weighted extropy. In this context, the order statistics (OSs) and sequential OSs (SOSs) for these two measures are studied based on this distribution. A bivariate q-Weibull distribution based on the Farlie-Gumbel-Morgenstern (FGM) family and its relevant concomitants are studied. Finally, two concrete instances of medical real data are ultimately provided.
Citation: M. Nagy, H. M. Barakat, M. A. Alawady, I. A. Husseiny, A. F. Alrasheedi, T. S. Taher, A. H. Mansi, M. O. Mohamed. Inference and other aspects for q−Weibull distribution via generalized order statistics with applications to medical datasets[J]. AIMS Mathematics, 2024, 9(4): 8311-8338. doi: 10.3934/math.2024404
| [1] | H. M. Barakat, M. A. Alawady, I. A. Husseiny, M. Nagy, A. H. Mansi, M. O. Mohamed . Bivariate Epanechnikov-exponential distribution: statistical properties, reliability measures, and applications to computer science data. AIMS Mathematics, 2024, 9(11): 32299-32327. doi: 10.3934/math.20241550 |
| [2] | Areej M. AL-Zaydi . On concomitants of generalized order statistics arising from bivariate generalized Weibull distribution and its application in estimation. AIMS Mathematics, 2024, 9(8): 22002-22021. doi: 10.3934/math.20241069 |
| [3] | Jumanah Ahmed Darwish, Saman Hanif Shahbaz, Lutfiah Ismail Al-Turk, Muhammad Qaiser Shahbaz . Some bivariate and multivariate families of distributions: Theory, inference and application. AIMS Mathematics, 2022, 7(8): 15584-15611. doi: 10.3934/math.2022854 |
| [4] | Mansour Shrahili, Mohamed Kayid, Mhamed Mesfioui . Stochastic inequalities involving past extropy of order statistics and past extropy of record values. AIMS Mathematics, 2024, 9(3): 5827-5849. doi: 10.3934/math.2024283 |
| [5] | Ramy Abdelhamid Aldallal, Haroon M. Barakat, Mohamed Said Mohamed . Exploring weighted Tsallis extropy: Insights and applications to human health. AIMS Mathematics, 2025, 10(2): 2191-2222. doi: 10.3934/math.2025102 |
| [6] | Nora Nader, Dina A. Ramadan, Hanan Haj Ahmad, M. A. El-Damcese, B. S. El-Desouky . Optimizing analgesic pain relief time analysis through Bayesian and non-Bayesian approaches to new right truncated Fréchet-inverted Weibull distribution. AIMS Mathematics, 2023, 8(12): 31217-31245. doi: 10.3934/math.20231598 |
| [7] | Haiping Ren, Xue Hu . Estimation for inverse Weibull distribution under progressive type-Ⅱ censoring scheme. AIMS Mathematics, 2023, 8(10): 22808-22829. doi: 10.3934/math.20231162 |
| [8] | A. M. Abd El-Raheem, Ehab M. Almetwally, M. S. Mohamed, E. H. Hafez . Accelerated life tests for modified Kies exponential lifetime distribution: binomial removal, transformers turn insulation application and numerical results. AIMS Mathematics, 2021, 6(5): 5222-5255. doi: 10.3934/math.2021310 |
| [9] | Mohamed Said Mohamed, Najwan Alsadat, Oluwafemi Samson Balogun . Continuous Tsallis and Renyi extropy with pharmaceutical market application. AIMS Mathematics, 2023, 8(10): 24176-24195. doi: 10.3934/math.20231233 |
| [10] | Qasim Ramzan, Muhammad Amin, Ahmed Elhassanein, Muhammad Ikram . The extended generalized inverted Kumaraswamy Weibull distribution: Properties and applications. AIMS Mathematics, 2021, 6(9): 9955-9980. doi: 10.3934/math.2021579 |
This work utilizes generalized order statistics (GOSs) to study the q-Weibull distribution from several statistical perspectives. First, we explain how to obtain the maximum likelihood estimates (MLEs) and utilize Bayesian techniques to estimate the parameters of the model. The Fisher information matrix (FIM) required for asymptotic confidence intervals (CIs) is generated by obtaining explicit expressions. A Monte Carlo simulation study is conducted to compare the performances of these estimates based on type Ⅱ censored samples. Two well-established measures of information are presented, namely extropy and weighted extropy. In this context, the order statistics (OSs) and sequential OSs (SOSs) for these two measures are studied based on this distribution. A bivariate q-Weibull distribution based on the Farlie-Gumbel-Morgenstern (FGM) family and its relevant concomitants are studied. Finally, two concrete instances of medical real data are ultimately provided.
Ordered random variables (RVs) can be found in various practical contexts. For example, we might want to determine the price trends of commodities by arranging them in ascending (or descending) order, or we might want to examine the lifetime of a specific type of product by subjecting some product items to a life test so that you get automatically arranged data. As a result of arranging data in ascending or descending order, OSs are generated, which can be used to understand data features such as maximum, minimum, range, etc. In any life test, if the failure of any component possibly influences the other components, we get what are called SOSs. Other models of ordered RVs such as record values and Pfeifer's record values are frequently used in the literature. Kamps [1] created the idea of GOSs, a unification of many ordered RV models, based on his observations of multiple ordered RV models. Additionally, Kamps [1] defined a crucial submodel of GOSs known as m−GOSs, which characterizes the aforesaid ordered RV models. The following is a description of the mathematical expression for GOSs: Consider a sequence of independent and identically distributed RVs Z1,Z2,…,Zn with a common cumulative distribution function (CDF), FZ(z), and a matching probability density function (PDF), fZ(z). Further, let n be a natural number more than or equal to 2, and let k be a positive integer. Define γr=k+(n−r)(m+1),r∈{1,2,…,n−1}. Then, the marginal PDF of the rth m−GOS, Z(r,n,m,k), is given by
| fZ(r,n,m,k)(z)=Cr−1(r−1)![ˉFZ(z)]γr−1gr−1m(FZ(z))fZ(z), | (1.1) |
where ˉFZ(z)=1−FZ(z), Cr−1=∏ri=1γi,r=1,2,...,n,
| hm(z)={−1m+1(1−z)m+1,m≠−1,−ln(1−z),m=−1, |
and gm(z)=hm(z)−hm(0),z∈[0,1). Given (1.1), the model can be readily simplified to OSs for m=0,k=1. When the value of m is equal to −1, it is possible to simplify it as the k-th upper record values, while for m=k=1, we get a model of SOSs.
q-type distributions are a class of probability distributions that have been proposed to characterize intricate systems. They have been extensively utilized across various disciplines, including physics, biology, mathematics, geography, economics, medicine, and informatics. The notion of q-distributions was first presented by Charalambides [2] in the discrete case, and the continuous case by Diaz, Parguan [3] and Diaz et al. [4]. One of the most popular q-type distributions is the q-Weibull distribution. It is a generalization of the Weibull distribution, which is a commonly used distribution to describe lifetime data. The q-Weibull distribution can exhibit a wider range of shapes for its hazard rate function than the Weibull distribution, making it a more versatile tool for modeling complex systems. Jia et al. [5] provided a detailed description of the q-Weibull distribution and its parameter estimation. Singh et al. [6] conducted a study to examine several defining outcomes of the q-Weibull distribution. The outcomes encompass many statistical measures, such as conditional expectation, recurrence relations for both individual and combined moments, and truncated moment calculations using GOSs. In the study conducted by Jia [7], the focus was on investigating the dependability of the q-Weibull distribution using multiple Type-Ⅰ censored data. This type of data represents the general form of Type-Ⅰ censored data. The PDF for the q-Weibull distribution can be expressed as follows:
| fZ(z;q,δ,η)=(2−q)δη(zη)δ−1expq[−(zη)δ], | (1.2) |
where
| expq(t)={[1+(1−q)t]11−q,1+(1−q)t>0,0,otherwise, |
δ>0 and q<2 are shape parameters, and η>0 is a scale parameter. By incorporating the variable θ=η−δ and utilizing the function expq(t) in Eq (1.2), it is possible to rephrase the PDF of the q-Weibull distribution as
| fZ(z;q,δ,θ)=(2−q)θδzδ−1[1−(1−q)θzδ]11−q,z∈{[0,+∞),1<q<2,[0,[θ(1−q)]−1δ],q<1. | (1.3) |
For q=1, the limiting PDF is
| limq→1fZ(z;q,δ,θ)=θδzδ−1limq→1{[1−(1−q)θzδ]−1(1−q)θzδ}−θzδ=θδzδ−1e(−θzδ)=fZ(z;δ,θ), | (1.4) |
the PDF of Weibull distribution.
The CDF and reliability function of the q-Weibull distribution are, respectively,
| FZ(z;q,δ,θ)=1−[1−(1−q)θzδ]2−q1−q | (1.5) |
and
| Rq(z)=[1−(1−q)θzδ]2−q1−q. |
The mean and variance of the q-Weibull RV are
| E(Z)={2−q(q−1)1+1δθ1δB(1δ+1,1q−1−1δ−1),1<q<2,2−q(1−q)1+1δθ1δB(1δ+1,2−q1−q),q<1,Var(Z)={2−q(q−1)1+2δθ2δ[B(2δ+1,1q−1−2δ−1)−2−qq−1B2(1δ+1,1q−1−1δ−1)],1<q<2,2−q(1−q)1+2δθ2δ[B(2δ+1,2−q1−q)−2−q1−qB2(1δ+1,2−q1−q)],q<1, |
where
| B(u,v)=∫10tu−1(1−t)v−1dt=∫+∞0tu−1(1+t)u+vdt |
denotes the beta function.
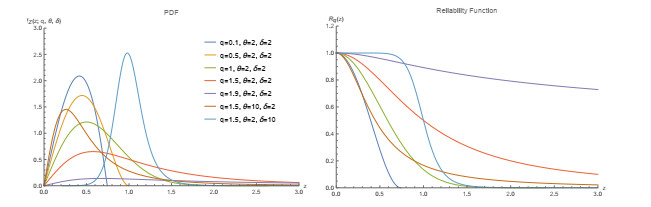
Figure 1 shows the PDF and reliability function for the q-Weibull distribution for a few specific parameter selections.
Singh et al. [6] primarily conducted a study that centered on the characterization of the q-Weibull distribution based on moments of GOSs and truncated moments. The jth moment, E[Zj(r,n,m,k)],m≠−1, based on the q-Weibull distribution can clearly be computed via the moment generating function
| M(r,n,m,k)(t)=Cr−1(r−1)!(m+1)r−1∫∞0etz[ˉFZ(z)]γr−1[1−ˉFZ(z)m+1]r−1fZ(z)dz. |
Using the binomial expansion for [1−(ˉFZ(z))m+1]r−1, we get
| M_{(r, n, m, k)}(t) = \frac{C_{r-1}}{(r-1) !(m+1)^{r-1}} \sum\limits_{u = 0}^{r-1}(-1)^u\binom{r-1}{u} \int_0^{\infty} e^{t z}[\bar{F}_Z(z)]^{\gamma_{r-u}-1} f_Z(z) d z, |
and, by (1.3) and (1.5), we get
| M_{(r, n, m, k)}(t) = \frac{C_{r\!-\!1}}{(r\!-\!1) !(m\!+\!1)^{r\!-\!1}} \sum\limits_{u = 0}^{r\!-\!1}(\!-\!1)^u\binom{r\!-\!1}{u} \mathbb{E}\left(e^{t Z}\left[1\!-\!(1\!-\!q) \theta Z^{\delta}\right]^{\frac{(2\!-\!q)(\gamma_{r\!-\!u}\!-\!1)}{1\!-\!q}}\right), |
where
| \begin{equation*} \mathbb{E}\left(e^{t Z}\left[1\!-\!(1\!-\!q) \theta Z^{\delta}\right]^{\frac{(2\!-\!q)(\gamma_{r\!-\!u}\!-\!1)}{1\!-\!q}}\right) = \left\{\begin{array}{lc} {(2\!-\!q) \theta \delta \int_0^{\infty} e^{t z}\left[1\!-\!(1\!-\!q) \theta z^{\delta}\right]^{\frac{(2\!-\!q)(\gamma_{r\!-\!u}\!-\!1)\!+\!1}{1\!-\!q}} z^{\delta\!-\!1} d z, }\!\!\!\! &\!\!\!\! \!\!\!\!\!\!1 < q < 2, \\ {(2\!-\!q) \theta \delta\int_0^{[\theta(1\!-\!q)]^{\!-\!\frac{1}{\delta}}} e^{t z}\left[1\!-\!(1\!-\!q) \theta z^{\delta}\right]^{\frac{(2\!-\!q)(\gamma_{r\!-\!u}\!-\!1)\!+\!1}{1\!-\!q}} z^{\delta\!-\!1} d z, } & q < 1. \end{array} \right. \end{equation*} |
The integrations in \mathbb{E}\left(e^{t Z}\left[1\!-\!(1\!-\!q) \theta Z^{\delta}\right]^{\frac{(2\!-\!q)(\gamma_{r\!-\!u}\!-\!1)}{1\!-\!q}}\right) can be evaluated using the Mathematica 12 software.
Extropy is a measure of uncertainty that functions as a dual of the entropy measure and works in conjunction with the measures that are currently in place. It was first described by Lad et al. [8] in the context of information measures. Both measures of uncertainty exhibit invariance under permutations of their mass functions, and the maximal extropy distribution is equivalent to the uniform distribution, similar to the case of entropy, the maximal extropy distribution is equal to the uniform distribution, and both measures of uncertainty show invariance under permutations of their mass functions. They do, however, differ noticeably in how sophisticated they judge a distribution to be. The dualism displayed by the subjects in the study by Lad et al. [8] was accepted as legitimate, according to their findings. The following is the formal definition of the extropy of a nonnegative RV Z (cf. Husseiny and Syam, [9]) with a continuous PDF f_Z and CDF F_Z :
| \begin{equation*} J(Z) = -\frac{1}{2} \int_{0}^{+\infty}[f_Z(z)]^{2} \mathrm{\; d} z = -\frac{1}{2} \int_{0}^{1} f_Z\left(Q_Z(u)\right) d u, \end{equation*} |
where Q_Z(.) = F_Z^{-1}(.) is the quantile function of F_Z(.).
Bansal and Gupta [10] have provided a definition for the weighted extropy of a non-negative absolutely continuous RV Z as
| \begin{equation*} \mathcal{J^{ \text w}}(Z) = -\frac{1}{2} \int_{0}^{+\infty}z[f_Z(z)]^{2} dz. \end{equation*} |
We can identify two distinct distributions with the same extropy, yet each of the two distributions has a different weighted extropy (eg., J(Z) = J(Y) = - 2/3, while \mathcal{J^{ \text w}}(Z) = -1/2 and \mathcal{J^{ \text w}}(Y) = -1/6 for the two RVs Z and Y, which have the PDFs f_Z(z) = 2z, \; 0 \leq z \leq 1, and f_Y(y) = 2(1-y), \; 0 \leq y \leq 1, respectively). This may represent an advantage of the weighted extropy for use instead of the extropy in some cases.
The main purpose of this article is to study the q-Weibull distribution from various statistical angles. The Weibull distribution, which is frequently used in reliability engineering, has been generalized to a q-Weibull distribution by Picoli et al. [11]. Unlike the Weibull distribution, which can only explain monotonic hazard rate functions, this distribution can describe several behaviors of the hazard rate function, including the unimodal, bathtub-shaped, monotonic (monotonically increasing and decreasing), and constant. As a result, the q-Weibull distribution, which is adaptable for fitting failure data, unifies monotonic and non-monotonic hazard rate functions using a single set of parameters. This work compares the performance of Bayesian and non-Bayesian (MLEs) inferences regarding the q-Weibull distribution's parameters using a simulation study based on the GOSs model. We present two recent and widely used information measures: extropy and weighted extropy. This context looks at the OSs and SOSs for these two measures based on this distribution. A bivariate q-Weibull distribution obtained from the FGM family and its associated concomitants are examined in this work. Lastly, two specific examples of actual medical data are offered.
The ensuing sections of the paper are structured in the following manner: In Section 2, we introduce the MLEs and Bayesian methods for estimating the q -Weibull parameters based on GOSs. Furthermore, we construct asymptotic CIs. In Section 3, we study the extropy and weighted extropy for the q -Weibull distribution. Section 4 delves into the examination of a bivariate q -Weibull distribution and its associated concomitant. Section 5 encompasses reviews of two real-world data sets. In conclusion, the paper is finalized in Section 6.
In this section, we present the methods for acquiring the MLEs and Bayesian estimates of the q -Weibull parameters via m- GOSs. The FIM necessary for the calculation of asymptotic CIs is derived by obtaining explicit expressions. We ignore the case q = 1 throughout this section based on the fact given in (1.4). This is because other authors, including Aboeleneen [12] and Jafari and Zakerzadeh [13], have studied Bayesian and non-Bayesian estimations for the Weibull distribution under GOSs.
Consider a GOS sample \underline Z = (Z(1, n, m, k), Z(2, n, m, k), ..., Z(n, n, m, k)) of size n chosen from the q -Weibull distribution. The PDF and CDF of this distribution are given by (1.3) and (1.5), respectively. The following expression can be used to formulate the likelihood function.
| \begin{eqnarray} L \left(\underline z|\Theta\right)& = & k\left(\prod\limits_{j = 1}^{n-1} \gamma_{j}\right)\left(\prod\limits_{i = 1}^{n-1}\left[1-(1-q) \theta z_i^{\delta}\right]^{\frac{{m}(2-q)}{1-q}} (2-q) \theta \delta z_i^{\delta-1}\left[1-(1-q) \theta z_i^{\delta}\right]^{\frac{1}{1-q}}\right)\\\!& \times&\! \left[1-(1-q) \theta z_n^{\delta}\right]^{\frac{({k-1})(2-q)}{1-q}} (2-q) \theta \delta z_n^{\delta-1}\left[1-(1-q) \theta z_n^{\delta}\right]^{\frac{1}{1-q}}, \end{eqnarray} | (2.1) |
where \Theta = (q, \delta, \theta). After simplifying and applying the logarithm function to both sides of the equation, we obtain
| \begin{eqnarray*} \ln L\left(\underline z|\Theta\right)& = & \ln k \!+\!\sum\limits_{j = 1}^{n-1}\ln \gamma_{j}\!+\! n[ \ln (2-q)+ \ln \delta+ \ln \theta] +\frac{(k-1)(2-q)+1}{1-q} \ln \left[1-(1-q) \theta z_{n}^{\delta}\right]\nonumber\\ &+&{\frac{{m}(2-q)+1}{1-q}}\sum\limits_{i = 1}^{n-1} \ln \left[1-(1-q) \theta z_i^{\delta}\right]+({\delta-1}) \sum\limits_{i = 1}^{n} \ln z_i. \end{eqnarray*} |
The partial derivatives of the log-likelihood function with respect to q, \delta, and \theta are
| \begin{eqnarray} \frac{\partial \ln L\left(\underline z|\Theta\right)}{\partial q}& = &\frac{n}{q-2}+ \frac{(k(2-q)+q-1)\theta z_{n}^{\delta}}{(1-q)(1-(1-q) \theta z_{n}^{\delta})}+\frac{k}{(1-q)^{2}} \ln \left[1-(1-q) \theta z_{n}^{\delta}\right]\\ &+\!&\!{\frac{m+1}{(1-q)^2}}\sum\limits_{i = 1}^{n-1} \ln \left[1-(1-q) \theta z_i^{\delta}\right]+{\frac{{m}(2-q)+1}{1-q}}\sum\limits_{i = 1}^{n-1} \frac{ \theta z_i^{\delta}}{ \left[1-(1-q) \theta z_i^{\delta}\right]}, \end{eqnarray} | (2.2) |
| \begin{eqnarray} \frac{\partial \ln L\left(\underline z|\Theta\right)}{\partial \delta} = \frac{n}{\delta}-\frac{(k(2-q)+q-1)\theta z_{n}^{\delta} \ln z_{n}}{1-(1-q) \theta z_{n}^{\delta}}-({m}(2-q)+1)\sum\limits_{i = 1}^{n-1} \frac{\theta z_{i}^{\delta} \ln z_{i}}{1-(1-q)\theta z_{i}^{\delta}}+\sum\limits_{i = 1}^{n} \ln z_{i}, \end{eqnarray} | (2.3) |
and
| \begin{eqnarray} \frac{\partial \ln L\left(\underline z|\Theta\right)}{\partial \theta} = \frac{n}{\theta}-\frac{(k(2-q)+q-1)z_{n}^{\delta}}{1-(1-q) \theta z_{n}^{\delta}}-({m}(2-q)+1)\sum\limits_{i = 1}^{n} \frac{z_{i}^{\delta}}{1-(1-q) \theta z_{i}^{\delta}}. \end{eqnarray} | (2.4) |
The equations given by (2.2)–(2.4) (the resultant zero-equations) may be solved to obtain the MLEs for the parameters ({q}, {\theta}, {\delta}) , denoted as (\hat{q}, \hat{\theta}, \hat{\delta}) . However, the derivatives exhibit nonlinearity. Therefore, obtaining closed-form solutions for the MLEs poses a challenging task. Thus, for the computation of numerical solutions we use Mathematica Ver. 12 software, see Table 1.
| \delta =1.5, q=1.3, \theta =0.354 | \delta =3, q=0.9, \theta =0.579 | |||||||||
| MLE | Bayes | MLE | Bayes | |||||||
| n | r | Bias | MSE | Bias | MSE | Bias | MSE | Bias | MSE | |
| 20 | 1 | \delta | 0.924 | 0.812 | 0.911 | 0.798 | 0.345 | 0.278 | 0.333 | 0.268 |
| q | 0.301 | 0.187 | 0.298 | 0.178 | 0.475 | 0.296 | 0.465 | 0.289 | ||
| \theta | 0.115 | 0.128 | 0.109 | 0.113 | 0.125 | 0.189 | 0.121 | 0.178 | ||
| 3 | \delta | 0.916 | 0.796 | 0.901 | 0.789 | 0.328 | 0.263 | 0.314 | 0.254 | |
| q | 0.299 | 0.178 | 0.287 | 0.169 | 0.463 | 0.276 | 0.456 | 0.269 | ||
| \theta | 0.107 | 0.119 | 0.098 | 0.105 | 0.112 | 0.168 | 0.102 | 0.156 | ||
| 10 | \delta | 0.898 | 0.782 | 0.879 | 0.779 | 0.309 | 0.211 | 0.298 | 0.201 | |
| q | 0.287 | 0.169 | 0.275 | 0.157 | 0.419 | 0.251 | 0.405 | 0.243 | ||
| \theta | 0.095 | 0.102 | 0.089 | 0.096 | 0.106 | 0.146 | 0.097 | 0.138 | ||
| 12 | \delta | 0.859 | 0.767 | 0.843 | 0.759 | 0.268 | 0.198 | 0.234 | 0.168 | |
| q | 0.281 | 0.165 | 0.275 | 0.152 | 0.389 | 0.228 | 0.356 | 0.213 | ||
| \theta | 0.074 | 0.099 | 0.054 | 0.091 | 0.078 | 0.123 | 0.056 | 0.114 | ||
| 17 | \delta | 0.811 | 0.759 | 0.745 | 0.682 | 0.225 | 0.153 | 0.205 | 0.132 | |
| q | 0.279 | 0.164 | 0.198 | 0.155 | 0.335 | 0.214 | 0.312 | 0.298 | ||
| \theta | 0.058 | 0.091 | 0.035 | 0.084 | 0.031 | 0.103 | 0.012 | 0.009 | ||
| 19 | \delta | 0.753 | 0.669 | 0.658 | 0.569 | 0.211 | 0.146 | 0.198 | 0.134 | |
| q | 0.208 | 0.052 | 0.189 | 0.045 | 0.289 | 0.195 | 0.231 | 0.178 | ||
| \theta | 0.038 | 0.076 | 0.024 | 0.062 | 0.029 | 0.098 | 0.012 | 0.078 | ||
| 50 | 1 | \delta | 0.954 | 0.857 | 0.935 | 0.847 | 0.215 | 0.195 | 0.204 | 0.193 |
| q | 0.214 | 0.178 | 0.203 | 0.165 | 0.211 | 0.187 | 0.200 | 0.182 | ||
| \theta | 0.116 | 0.125 | 0.103 | 0.118 | 0.117 | 0.124 | 0.112 | 0.121 | ||
| 3 | \delta | 0.932 | 0.842 | 0.924 | 0.832 | 0.201 | 0.187 | 0.196 | 0.181 | |
| q | 0.201 | 0.165 | 0.189 | 0.146 | 0.203 | 0.176 | 0.195 | 0.169 | ||
| \theta | 0.111 | 0.121 | 0.098 | 0.104 | 0.103 | 0.115 | 0.097 | 0.111 | ||
| 25 | \delta | 0.898 | 0.821 | 0.872 | 0.802 | 0.195 | 0.175 | 0.191 | 0.163 | |
| q | 0.197 | 0.152 | 0.185 | 0.146 | 0.196 | 0.164 | 0.185 | 0.156 | ||
| \theta | 0.101 | 0.105 | 0.092 | 0.101 | 0.089 | 0.099 | 0.085 | 0.092 | ||
| 27 | \delta | 0.852 | 0.785 | 0.824 | 0.752 | 0.191 | 0.152 | 0.184 | 0.143 | |
| q | 0.178 | 0.135 | 0.169 | 0.126 | 0.192 | 0.142 | 0.187 | 0.141 | ||
| \theta | 0.089 | 0.098 | 0.068 | 0.076 | 0.054 | 0.095 | 0.046 | 0.085 | ||
| 45 | \delta | 0.746 | 0.658 | 0.647 | 0.587 | 0.189 | 0.138 | 0.154 | 0.121 | |
| q | 0.159 | 0.107 | 0.142 | 0.095 | 0.182 | 0.135 | 0.163 | 0.128 | ||
| \theta | 0.034 | 0.071 | 0.022 | 0.059 | 0.022 | 0.094 | 0.009 | 0.079 | ||
| 47 | \delta | 0.732 | 0.637 | 0.632 | 0.523 | 0.154 | 0.125 | 0.132 | 0.116 | |
| q | 0.179 | 0.118 | 0.132 | 0.106 | 0.165 | 0.115 | 0.156 | 0.105 | ||
| \theta | 0.023 | 0.063 | 0.019 | 0.045 | 0.013 | 0.086 | 0.008 | 0.048 | ||
| 100 | 1 | \delta | 0.528 | 0.425 | 0.495 | 0.405 | 0.115 | 0.135 | 0.105 | 0.126 |
| q | 0.136 | 0.125 | 0.128 | 0.112 | 0.245 | 0.175 | 0.235 | 0.169 | ||
| \theta | 0.102 | 0.119 | 0.099 | 0.100 | 0.109 | 0.114 | 0.099 | 0.111 | ||
| 3 | \delta | 0.504 | 0.398 | 0.487 | 0.365 | 0.112 | 0.131 | 0.108 | 0.128 | |
| q | 0.131 | 0.111 | 0.121 | 0.101 | 0.236 | 0.162 | 0.228 | 0.152 | ||
| \theta | 0.099 | 0.102 | 0.086 | 0.098 | 0.095 | 0.102 | 0.083 | 0.099 | ||
| 50 | \delta | 0.478 | 0.315 | 0.466 | 0.302 | 0.096 | 0.125 | 0.084 | 0.112 | |
| q | 0.127 | 0.105 | 0.112 | 0.091 | 0.224 | 0.154 | 0.215 | 0.143 | ||
| \theta | 0.078 | 0.095 | 0.069 | 0.091 | 0.074 | 0.094 | 0.052 | 0.088 | ||
| 52 | \delta | 0.411 | 0.297 | 0.398 | 0285 | 0.087 | 0.121 | 0.078 | 0.118 | |
| q | 0.113 | 0.098 | 0.089 | 0.072 | 0.212 | 0.151 | 0.200 | 0.136 | ||
| \theta | 0.056 | 0.084 | 0.035 | 0.067 | 0.032 | 0.072 | 0.027 | 0.058 | ||
| 96 | \delta | 0.346 | 0.222 | 0.245 | 0.186 | 0.079 | 0.119 | 0.063 | 0.109 | |
| q | 0.099 | 0.076 | 0.078 | 0.065 | 0.198 | 0.141 | 0.165 | 0.126 | ||
| \theta | 0.021 | 0.061 | 0.013 | 0.059 | 0.007 | 0.054 | 0.001 | 0.034 | ||
| 98 | \delta | 0.309 | 0.197 | 0.298 | 0.185 | 0.035 | 0.103 | 0.012 | 0.095 | |
| q | 0.076 | 0.069 | 0.054 | 0.052 | 0.075 | 0.107 | 0.062 | 0.084 | ||
| \theta | 0.015 | 0.052 | 0.009 | 0.036 | 0.002 | 0.023 | 0.0009 | 0.008 | ||
When m = 0, k = 1, and \gamma_r = n-r+1, we get the model of OSs. Therefore, (2.2)–(2.4) can be utilized to compute the MLEs of the parameters inside the OSs framework. Moreover, when m = k = 1, and \gamma_i = 2(n-i)+1 (cf. Kamps, [1]), we get the model of SOSs. Thus, (2.2)–(2.4) can be utilized to compute the MLEs of the parameters inside the SOSs framework.
A commonly used and suitable choice for the prior distributions of \theta, \; \delta , and q would be to assume that the three quantities (as RVs) are independent and that \theta \sim G(a_1, b_1) and \delta \sim G(a_2, b_2), where G(a, b) denotes the gamma distribution with mean \frac{a}{b} and variance \frac{a}{b^2}. Moreover, q has a truncated positive exponential distribution with parameter \xi > 0, i.e.,
| \pi(q) = \frac{\xi e^{-\xi q}}{1-e^{-2 \xi }}, \; 0 < q < 2. |
The hyperparameters a_1, b_1, a_2, b_2, \; \text{ and}\; \xi are chosen to reflect prior knowledge about \theta, \; \delta, and q. For example, a_1, b_1, a_2, \; \text{and}\; b_2 can be assessed to match the experimenter's notion of the average and precision of their prior for \theta and \delta, while \xi could be obtained by using the experimenters prior median for q. Nonetheless, Garthwaite et al. [14] provided a thorough analysis of the elicitation of hyperparameters. Nevertheless, we shall move forward by carefully selecting the hyperparameter values that will be applied to the Bayesian analysis.
The prior joint density of \theta, \; \delta, and q can be written as
| \begin{equation} \pi(\Theta)\propto \frac{\xi \theta^{a_1-1}\delta^{a_2-1}e^{-\xi q-\theta b_1-\delta b_2}}{1-e^{-2 \xi }}. \end{equation} | (2.5) |
The posterior likelihood, \pi^*(\Theta|\underline Z = \underline z): = \pi^*(\Theta|\underline z), can be represented as proportional to the product of the likelihood given in (2.1) and the joint prior densities given by (2.5). That can be rewritten as
| \begin{eqnarray*} \pi^*(\Theta|\underline z)&\propto& k(2-q) \theta \delta\left(\prod\limits_{j = 1}^{n-1} \gamma_{j}\right)\left(\prod\limits_{i = 1}^{n-1}\left[1-(1-q) \theta z_i^{\delta}\right]^{\frac{{m}(2-q)}{1-q}} (2-q) \theta \delta z_i^{\delta-1}\left[1-(1-q) \theta z_i^{\delta}\right]^{\frac{1}{1-q}}\right)\nonumber\\\!& \times&\! \left[1-(1-q) \theta z_n^{\delta}\right]^{\frac{({k-1})(2-q)}{1-q}} z_n^{\delta-1}\left[1-(1-q) \theta z_n^{\delta}\right]^{\frac{1}{1-q}} \frac{\xi \theta^{a_1-1}\delta^{a_2-1}e^{-\xi q-\theta b_1-\delta b_2}}{1-e^{-2 \xi }}. \end{eqnarray*} |
The marginal posterior distributions \pi^*(\theta|\underline z), \pi^*(\delta|\underline z), and \pi^*(q|\underline z) of the parameters \theta, \; \delta, and q may be found by integrating out the nuisance parameters from the posterior distribution \pi^*(\Theta|\underline z) as follows:
| \begin{eqnarray*} \pi^*(\theta|\underline z) = \int_{\delta = 0}^\infty \int_{q = 0}^2 \pi^*(\Theta|\underline z)dq d\delta, \end{eqnarray*} |
| \begin{eqnarray*} \pi^*(\delta|\underline z) = \int_{\theta = 0}^\infty \int_{q = 0}^2 \pi^*(\Theta| \underline z)dq d\theta, \end{eqnarray*} |
and
| \begin{eqnarray*} \pi^*(q|\underline z) = \int_{\theta = 0}^\infty \int_{\delta = 0}^\infty \pi^*(\Theta|\underline z)d\delta d\theta. \end{eqnarray*} |
We use the well-known squared error loss function that yields the posterior means as the Bayes estimates of \Theta, say (\hat{\theta}_B, \hat{\delta}_B, \hat{q}_B), which are given by
| \begin{eqnarray} \hat{\theta}_B = \int_0^\infty \theta\pi^*(\theta|\underline z) d\theta, \end{eqnarray} | (2.6) |
| \begin{eqnarray} \hat{\delta}_B = \int_0^\infty \delta \pi^*(\delta|\underline z) d\delta, \end{eqnarray} | (2.7) |
and
| \begin{eqnarray} \hat{q}_B = \int_0^2 q \pi^*(q|\underline z)d q. \end{eqnarray} | (2.8) |
It is noticed that the integrals given by (2.6)–(2.8) cannot be obtained explicitly. Because of that, we use the Monte Carlo method to find an approximate value of the integrals in (2.6)–(2.8). We refer the interested reader to Hamdia et al. [15] for a comparable use of data fitting and Bayesian updating.
Based on the asymptotic normality of the MLEs, the FIM is frequently used to create CIs for parameters. Let us consider the parameter \Theta as the focal point of our investigation. Under specific assumptions of regularity, the MLEs denoted as \widehat{\Theta} are distributed according to the normal distribution. As the sample size n tends to infinity, the distribution of the estimator \widehat\Theta approaches a normal distribution with mean \Theta and covariance matrix equal to the inverse of the FIM, denoted by I^{-1}(\Theta). The FIM consists of the negative expected values of the second order derivatives of \ln L, as
| \begin{equation} I(\Theta) = -\mathbb{E}\left[\begin{array}{lll} \frac{\partial^{2} \ln L}{\partial q^{2}} & \frac{\partial^{2} \ln L}{\partial q \partial \delta} & \frac{\partial^{2} \ln L}{\partial q \partial \theta} \\ \frac{\partial^{2} \ln L}{\partial \delta \partial q} & \frac{\partial^{2} \ln L}{\partial \delta^{2}} & \frac{\partial^{2} \ln L}{\partial \delta \partial \theta} \\ \frac{\partial^{2} \ln L}{\partial \theta \partial q} & \frac{\partial^{2} \ln L}{\partial \theta \partial \delta} & \frac{\partial^{2} \ln L}{\partial \theta^{2}} \end{array}\right] . \end{equation} | (2.9) |
According to Jia et al. [16], in cases where it is challenging to obtain the anticipated values directly, an alternative approach is to estimate them by calculating the negative second-order derivatives of the natural logarithm of the likelihood function, evaluated at the MLEs. The CIs for the q -Weibull parameters were derived by Xu et al. [17] using the approximation method. In this analysis, we calculate the anticipated values for the q -Weibull distribution using the GOS setup. The second-order derivatives of \ln L are given by
| \begin{eqnarray*} \frac{\partial^{2} \ln L}{\partial q^{2}}\!\!\!& = &\!\!\!-\frac{n}{(q-2)^{2}}+\frac{\theta {z_n}^{\delta } \left(2 k-\theta (q-1) (k (q-4)-q+1) {z_n}^{\delta }\right)}{(q-1)^2\left(1-\theta (1-q) {z_n}^{\delta }\right)^2}-\frac{2 k \ln \left(1-(1-q) \theta z_n^{\delta}\right)}{(q-1)^3}\nonumber\\\!\!\!&+&\!\!\!\frac{2 (m+1) }{(1-q)^3}\sum\limits_{i = 1}^{n-1}\ln \left(1\!-\!(1\!-\!q) \theta z_i^{\delta}\right)\!+\!\frac{ \theta}{(q-1)^2 }\sum\limits_{i = 1}^{n-1}\frac{ z_i^{\delta } \left(2 (m+1)\!-\theta (q-1) (m (q\!-\!4)\!-\!3) z_i^{\delta }\right)}{ \left(1-(1-q) \theta z_i^{\delta}\right)^2}, \nonumber\\ \frac{\partial^{2} \ln L}{\partial q \partial \delta}& = &\frac{\theta z_n^{\delta } \ln (z_n) \left(k \theta z_n^{\delta }+k-1\right)}{\left(1-(1-q) \theta z_n^{\delta}\right)^2} +\sum\limits_{i = 1}^{n-1}\frac{\theta z_i^{\delta } \ln (z_i) \left(\theta (m+1) z_i^{\delta }+m\right)}{\left(1-(1-q) \theta z_i^{\delta}\right)^2} , \nonumber\\ \frac{\partial^{2} \ln L}{\partial q \partial \theta}& = & \frac{z_n^{\delta } \left(k \theta z_n^{\delta }+k-1\right)}{\left(1-(1-q) \theta z_n^{\delta}\right)^2} +\sum\limits_{i = 1}^{n-1} \frac{z_i^{\delta } \left(\theta (m+1) z_i^{\delta }+m\right)}{\left(1-(1-q) \theta z_i^{\delta}\right)^2}, \nonumber\\ \frac{\partial^{2} \ln L}{\partial \delta^{2}}& = &-\frac{n}{\delta^{2}}+\frac{\theta (k (q-2)-q+1) z_n^{\delta } \ln ^2(z_n)}{\left(1-(1-q) \theta z_n^{\delta}\right)^2}+\sum\limits_{i = 1}^{n-1} \frac{\theta (m (q-2)-1) z_i^{\delta } \ln ^2(z_i)}{\left(1-(1-q) \theta z_i^{\delta}\right)^2}, \\ \frac{\partial^{2} \ln L}{\partial \delta \partial \theta}& = &\frac{(k (q-2)-q+1) z_n^{\delta } \ln (z_n)}{\left(1-(1-q) \theta z_n^{\delta}\right)^2} +\sum\limits_{i = 1}^{n-1}\frac{(m (q-2)-1) z_i^{\delta } \ln (z_i)}{\left(1-(1-q) \theta z_i^{\delta}\right)^2}, \nonumber\\ \frac{\partial^{2} \ln L}{\partial \theta^{2}}& = &-\frac{n}{\theta ^2}+\frac{(1-q) (k (q-2)-q+1) z_n^{2 \delta }}{\left(1-(1-q) \theta z_n^{\delta}\right)^2}+\sum\limits_{i = 1}^{n-1} \frac{(1-q) (m (q-2)-1) z_i^{2 \delta }}{\left(1-(1-q) \theta z_i^{\delta}\right)^2} . \end{eqnarray*} |
The following moments are required to calculate the elements in the matrix given in (2.9), according to the aforementioned second-order derivatives. If 0 < q < 1, we have
| \begin{eqnarray*} \mathbb{E}\left(\frac{Z^{ \delta}}{\left[1-(1-q) \theta Z^{\delta}\right]^{2}}\right)& = &\frac{2-q}{(1-q)^{2} \theta} B\left(2, \frac{q}{1-q}\right), \nonumber\\ \mathbb{E}\left(\frac{Z^{2 \delta}}{\left[1-(1-q) \theta Z^{\delta}\right]^{2}}\right)& = &\frac{2-q}{(1-q)^{3} \theta^{2}} B\left(3, \frac{q}{1-q}\right), \nonumber\\ \mathbb{E}\left(\frac{Z^{\delta}}{1-(1-q) \theta Z^{\delta}}\right)& = &\frac{2-q}{(1-q)^{2} \theta} B\left(2, \frac{1}{1-q}\right), \nonumber\\ \mathbb{E}\left(\frac{Z^{\delta} \ln Z}{\left[1-(1-q) \theta Z^{\delta}\right]^{2}}\right)& = &\frac{2-q}{(1-q)^{2} \theta \delta} B\left(2, \frac{q}{1-q}\right)(J_1-J_2), \nonumber\\\mathbb{E}\left(\frac{Z^{2 \delta} \ln Z}{\left[1-(1-q) \theta Z^{\delta}\right]^{2}}\right)& = &\frac{2-q}{(1-q)^{3} \theta^{2} \delta} B\left(3, \frac{q}{1-q}\right)(J_3-J_2), \\ \mathbb{E}\left(\frac{Z^{\delta} \ln ^{2} Z}{\left[1-(1-q) \theta Z^{\delta}\right]^{2}}\right)& = &\frac{2-q}{(1-q)^{2} \theta \delta^{2}} B\left(2, \frac{q}{1-q}\right)\left[(J_1-J_2)^{2}+J_4\right], \nonumber\\ \mathbb{E}\left(\ln \left[1-(1-q) \theta Z^{\delta}\right]\right)& = &\frac{q-1}{2-q}, \end{eqnarray*} |
where J_1 = \psi^{(1)}(2)-\psi^{(1)}\left(2+\frac{q}{1-q}\right), \; J_2 = \ln \theta+\ln (1-q), \; \; J_3 = \psi^{(1)}(3)-\psi^{(1)}\left(3+\frac{q}{1-q}\right), \; \; J_4 = \psi^{(2)}(2)-\psi^{(2)}\left(2+\frac{q}{1-q}\right), \; and \; \psi^{(k)}(x) = \frac{d^{k} \ln \Gamma(x)}{d z^{k}}. Therefore, the FIM, when 0 < q < 1, is
| I(q, \delta, \theta) = n\left[\begin{array}{lll} {\mathbf E}_{11} & {\mathbf E}_{12} & {\mathbf E}_{13} \\ {\mathbf E}_{21} & {\mathbf E}_{22} & {\mathbf E}_{23} \\ {\mathbf E}_{31} & {\mathbf E}_{32} & {\mathbf E}_{33} \end{array}\right], |
where
| \begin{eqnarray*} {\mathbf E}_{11}\!\!\!\!& = &\!\!\!\!\frac{2\!-\!q }{(q\!-\!1)^4}\left[2 \left( k\!+\!(n\!-\!1)(m\!+\!1)\right) B\left(2, \frac{q}{1\!-\!q}\right)\!+\! \left( (k (q\!-\!4)\!-\!q\!+\!1)\!+\!(n\!-\!1)(m (q\!-\!4)\!-\!3) \right) \right. \nonumber\\\!\!\!\!&\times&\!\!\!\! \left.B\left(3, \frac{q}{1\!-\!q}\right)-\frac{n}{(q-2)^{2}}-\frac{2(k+ (m+1)(n-1)) }{(1-q)^2(2-q)}\right], \nonumber\\ {\mathbf E}_{12}\!\!\!\!& = &\!\!\!\!{\mathbf E}_{21} = \frac{(2\!-\!q)}{\delta} \left( \frac{(k\!+\!(n\!-\!1) (m\!+\!1))(J_3\!-\!J_2) }{(1\!-\!q)^{3} } B\!\!\left(\!3, \frac{q}{1\!-\!q}\right)\!+\!\frac{(k\!-\!1\!+\!m (n\!-\!1))(J_1\!-\!J_2)}{(1\!-\!q)^{2} } B\!\!\left(\!2, \frac{q}{1\!-\!q}\right)\right) , \nonumber\\ {\mathbf E}_{13}\!\!\!\!& = &\!\!\!\!{\mathbf E}_{31} = \frac{(k-1+m(n-1))(2-q)}{(1-q)^{2} \theta} B\left(2, \frac{q}{1-q}\right)+\frac{(k+(m+1)(n-1)) (2-q)}{(1-q)^{3} \theta} B\left(3, \frac{q}{1-q}\right), \\ {\mathbf E}_{22}\!\!\!\!& = &\!\!\!\!-\frac{n}{\delta^{2}}+\left[(k (q-2)-q+1)+(n-1)(m (q-2)-1)\right]\frac{ (2-q)}{(1-q)^{2} \delta^{2}} B\left(2, \frac{q}{1-q}\right)\left[(J_1-J_2)^{2}+J_4\right], \nonumber\\ {\mathbf E}_{23}\!\!\!\!& = &\!\!\!\!{\mathbf E}_{32} = \left((k (q-2)-q+1) +(n-1)(m (q-2)-1) \right) \frac{2-q}{(1-q)^{2} \theta \delta} B\left(2, \frac{q}{1-q}\right)(J_1-J_2), \nonumber\\ {\mathbf E}_{33}\!\!\!\!& = &\!\!\!\!-\frac{n}{\theta ^2}+\frac{(2-q)}{(1-q)^2 \theta ^2}( (k(q-2)-q+1)+(n-1) (m(q-2)-1)) B\left(3, \frac{q}{1-q}\right). \end{eqnarray*} |
Moreover, the following moments are required to calculate the elements in the matrix given in (2.9), according to the second-order derivatives, if 1 < q < 2
| \begin{eqnarray*} \mathbb{E}\left(\frac{Z^{2 \delta}}{\left[1-(1-q) \theta Z^{\delta}\right]^{2}}\right)& = &\frac{2-q}{(q-1)^{3} \theta^{2}} B\left(3, \frac{2-q}{q-1}\right), \\ \mathbb{E}\left(\frac{Z^{\delta}}{\left[1-(1-q) \theta Z^{\delta}\right]^{2}}\right)& = &\frac{2-q}{(q-1)^{2} \theta} B\left(2, \frac{2-q}{q-1}\right), \\ \mathbb{E}\left(\frac{Z^{\delta} \ln Z}{\left[1-(1-q) \theta Z^{\delta}\right]^{2}}\right)& = &\frac{2-q}{(q-1)^{2} \theta \delta} B\left(2, \frac{1}{q-1}\right)(J_5-J_6), \\\mathbb{E}\left(\frac{Z^{2 \delta} \ln Z}{\left[1-(1-q) \theta Z^{\delta}\right]^{2}}\right)& = &\frac{2-q}{(q-1)^{3} \theta^{2} \delta} B\left(3, \frac{2-q}{q-1}\right)(J_7-J_6), \\ \mathbb{E}\left(\frac{Z^{\delta} \ln ^{2} Z}{\left[1-(1-q) \theta Z^{\delta}\right]^{2}}\right)& = &\frac{2-q}{(q-1)^{2} \theta \delta^{2}} B\left(2, \frac{1}{q-1}\right)\left[(J_5-J_6)^{2}+J_8\right], \\ \mathbb{E}\left(\ln \left[1-(1-q) \theta Z^{\delta}\right]\right)& = &\frac{2-q}{q-1}, \end{eqnarray*} |
where J_5 = \psi^{(1)}(2)-\psi^{(1)}\left(\frac{1}{q-1}\right), \; J_6 = \ln \theta+\ln (q-1), \; J_7 = \psi^{(1)}(3)-\psi^{(1)}\left(\frac{2-q}{q-1}\right), \; and J_8 = \psi^{(2)}(2)+\psi^{(2)}\left(\frac{1}{q-1}\right). Thus, if 1 < q < 2, the FIM is
| I(q, \delta, \theta) = n\left[\begin{array}{lll} {\mathbf E}_{11} & {\mathbf E}_{12} & {\mathbf E}_{13} \\ {\mathbf E}_{21} & {\mathbf E}_{22} & {\mathbf E}_{23} \\ {\mathbf E}_{31} & {\mathbf E}_{32} & {\mathbf E}_{33} \end{array}\right], |
where
| \begin{eqnarray*} {\mathbf E}_{11}\!\!\!\!& = &\!\!\!\!\frac{2\!-\!q }{(q\!-\!1)^4}\left[2 \left( k\!+\!(n\!-\!1)(m\!+\!1)\right) B\left(2, \frac{2\!-\!q}{q\!-\!1}\right)\!-\! \left( (k (q\!-\!4)\!-\!q\!+\!1)\!+\!(n\!-\!1)(m (q\!-\!4)\!-\!3) \right) \right.\nonumber\\\!\!\!\!&\times&\!\!\!\!\left.B\left(3, \frac{2\!-\!q}{q\!-\!1}\right)\right] -\frac{n}{(q-2)^{2}}+\frac{2(2-q)(k+ (m+1)(n-1)) }{(1-q)^4}, \nonumber\\ {\mathbf E}_{12}\!\!\!\!& = &\!\!\!\!{\mathbf E}_{21}\! = \!\frac{(2\!-\!q)}{\delta} \left( \frac{(k\!+\!(n\!-\!1) (m\!+\!1))(J_7\!\!-\!\!J_6) }{(q\!-\!1)^{3} } B\!\!\left(\!3, \frac{2\!-\!q}{q\!-\!1}\right)\!+\!\frac{(k\!-\!1\!+\!m (n\!-\!1))(J_5\!\!-\!\!J_6)}{(1\!-\!q)^{2} } B\!\!\left(\!2, \frac{1}{1\!-\!q}\right)\right) , \nonumber\\ {\mathbf E}_{13}\!\!\!\!& = &\!\!\!\!{\mathbf E}_{31} = \frac{(k-1+m(n-1))(2-q)}{(1-q)^{2} \theta} B\left(2, \frac{2\!-\!q}{q\!-\!1}\right)+\frac{(k+(m+1)(n-1)) (2-q)}{(q-1)^{3} \theta} B\left(3, \frac{2\!-\!q}{q\!-\!1}\right), \nonumber\\ {\mathbf E}_{22}\!\!\!\!& = &\!\!\!\!-\frac{n}{\delta^{2}}\!+\!\left[(k (q-2)-q+1)+(n-1)(m (q-2)\!-\!1)\right]\frac{2\!-\!q}{(q-1)^{2} \delta^{2}} B\!\left(2, \frac{1}{q-1}\right)\left[(J_5\!-\!J_6)^{2}\!+\!J_8\right], \end{eqnarray*} |
| \begin{eqnarray*} {\mathbf E}_{23}\!\!\!\!& = &\!\!\!\!{\mathbf E}_{32} = \left((k (q-2)-q+1) +(n-1)(m (q-2)-1) \right) \frac{2-q}{(q-1)^{2} \theta \delta} B\left(2, \frac{1}{q-1}\right)(J_5-J_6), \nonumber\\ {\mathbf E}_{33}\!\!\!\!& = &\!\!\!\!-\frac{n}{\theta ^2}-\frac{(2-q)}{(q-1)^2 \theta ^2}( (k(q-2)-q+1)+(n-1) (m(q-2)-1)) B\left(3, \frac{2-q}{q-1}\right). \end{eqnarray*} |
The remaining scenario to consider is q \leq 0. The arguments of the beta function B(x, y) must satisfy x > 0 and y > 0 . So, in this case, the beta function is no longer applicable and the expectations are intractable. Hence, we approximate the expected values by the negatives of the second-order derivatives evaluated at the MLEs \widehat{q_{m}}, \widehat{\delta_{m}}, and \widehat{\theta_{m}}, that is
| d_{a p p}(\widehat{q}, \widehat{\delta}, \widehat{\theta}) = -\left[\begin{array}{c} \frac{\partial^{2} \ln L}{\partial q^{2}} \frac{\partial^{2} \ln L}{\partial q \partial \delta} \frac{\partial^{2} \ln L}{\partial q \partial \theta} \\ \frac{\partial^{2} \ln L}{\partial \delta \partial q} \frac{\partial^{2} \ln L}{\partial \delta^{2}} \frac{\partial^{2} \ln L}{\partial \delta \partial \theta} \\ \frac{\partial^{2} \ln L}{\partial \theta \partial q} \frac{\partial^{2} \ln L}{\partial \theta \partial \delta} \frac{\partial^{2} \ln L}{\partial \theta^{2}} \end{array}\right] |
evaluated at q = \widehat{q_{m}}, \delta = \widehat{\delta_{m}}, and \theta = \widehat{\theta_{m}} . The covariance matrix of the MLEs is the inverse matrix of the FIM, that is
| C = I^{-1}(q, \delta, \theta) = \left[\begin{array}{lll} c_{11} & c_{12} & c_{13} \\ c_{21} & c_{22} & c_{23} \\ c_{31} & c_{32} & c_{33} \end{array}\right]. |
Hence, the 100(1-\alpha) percent asymptotic CIs for q, \delta, and \theta are {\left[\widehat{q}_{m}+U_{\frac{\alpha}{2}} \sqrt{c_{11}}, \min \left(2, \widehat{q}_{m}-U_{\frac{\alpha}{2}} \sqrt{c_{11}}\right)\right]}, \; {\left[\max \left(0, \widehat{\delta}_{m}+U_{\frac{\alpha}{2}} \sqrt{c_{22}}\right), \; \widehat{\delta}_{m}-U_{\frac{\alpha}{2}} \sqrt{c_{22}}\right]}, \; and {\left[\max \left(0, \widehat{\theta}_{m}+U_{\frac{\alpha}{2}} \sqrt{c_{33}}\right), \; \widehat{\theta}_{m}-U_{\frac{\alpha}{2}} \sqrt{c_{33}}\right]}, respectively, where \widehat{q}_{m}, \widehat{\delta}_{m}, and \widehat{\theta}_{m} are the MLEs and U_{\alpha} is the \alpha -quantile of the standard normal distribution. Here, the max and min operations are used to ensure that \delta > 0, \theta > 0, and q < 2.
In this subsection, the numerical performances of MLE and Bayesian estimates are assessed and compared based on Type Ⅱ censored samples from the q- Weibull distribution. After 10,000 samples of size n from the q- Weibull distribution were collected, the Mathcad 2001 package was utilized. The parameters' values can be described as \delta = 1.5, q = 1.3, \theta = 0.354, and \delta = 3, q = 0.9, \theta = 0.579. The following Type Ⅱ censored samples are used in this study: \underline Z = (Z(1, n, 0, 1), Z(2, n, 0, 1), ..., Z(r, n, 0, 1)), where n = 20, \; r = 1, 3, 10, 12, 17, 19; \; n = 50, \; r = 1, 3, 25, 27, 45, 47; \; n = 100, \; r = 1, 3, 50, 52, 96, 98. Table 1 displays the mean average of bias and mean squared error (MSE) simulation results for over 10,000 Monte Carlo simulation cycles. Table 1 allows for the following conclusions to be made:
(1) It is clear that MLE and Bayesian estimates of unknown parameters are fairly good in terms of the bias and MSE.
(2) For all unknown parameters, the Bayesian estimates outperform the MLE estimates based on the bias and MSE.
(3) With an increase in sample size, it is shown that MSEs, as well as biases, decrease.
(4) In most cases, with increasing r the performance of the estimators becomes better, i.e., the biases and MSEs diminish.
The extropy for the q -Weibull distribution with the PDF given in (1.3) is given by
| \begin{eqnarray*} J(Z)& = &-\frac{1}{2}\int_{0}^{\infty}f_{Z}^2(z;q, \delta, \theta)dz. \end{eqnarray*} |
If q < 1, we have
| \begin{eqnarray*} J(Z)& = &-\frac{1}{2} \int_0^{[\theta(1-q)]^{-\frac{1}{\delta}} } \left(\delta \theta (2-q) z^{\delta -1} \left(1- (1-q)\theta z^{\delta }\right)^{\frac{1}{1-q}}\right)^2 \, dz \nonumber\\& = &\frac{-\delta (q-2)^2 (\theta)^{\frac{1}{\delta}} }{2 (1-q )^{2-\frac{1}{\delta}} } B\left(2-\frac{1}{\delta }, \frac{2}{1-q}+1\right). \end{eqnarray*} |
On the other hand, if 1 < q < 2, we have
| \begin{eqnarray*} J(Z)& = &-\frac{1}{2} \int_0^{\infty} \left(\delta \theta (2-q) z^{\delta -1} \left(1- (1-q)\theta z^{\delta }\right)^{\frac{1}{1-q}}\right)^2 \, dz \nonumber\\& = &\frac{-\delta (q-2)^2 (\theta)^{\frac{1}{\delta} } }{2 (q-1)^{2-\frac{1}{\delta}} } B\left(2-\frac{1}{\delta }, \frac{2}{q-1}-2+\frac{1}{\delta }\right). \end{eqnarray*} |
Figure 2 consists of the following three parts:
({\rm{a}}) when \theta = 2 , \delta = 2, and various values of q,
({\rm{b}}) when q = 1.5, \delta = 2, and various values of \theta,
({\rm{c}}) when q = 1.5, \theta = 1, and various values of \delta.
It is easy to see from the parts of Figure 2 that the value of extropy increases with an increase in q, while it decreases with an increase in \theta. It can also be seen that it decreases in most cases with an increase in \delta, except in a very short interval where it has an increase.
If Z(r, n, m, k) is the r th GOS based on (1.1) and (1.3), then the extropy measure is provided by
| \begin{eqnarray} J\left(Z{(r, n, m, k)}\right)& = &-\frac{1}{2} \int_{0}^{\infty} f_{Z(r, n, m, k)}^{2}(z;q, \delta, \theta) d z\\ & = &-\frac{1}{2} \int_0^{\infty} \left(\frac{C_{r-1}}{(r-1) !}[\bar{F}_Z(z)]^{\gamma_{r}-1} g_{m}^{r-1}(F_Z(z)) f_Z(z)\right)^2dz. \end{eqnarray} | (3.1) |
On expanding g_m^{2(r-1)}(F(x)) = \left(\frac{1}{m+1}\left\{1-\bar{F}(x)^{m+1}\right\}\right)^{2(r-1)} binomially in (3.1), we get
| \begin{equation*} J\left(Z{(r, n, m, k)}\right) = - \frac{C_{r-1}^2}{2((r-1) !(m+1)^{r-1})^2} \sum\limits_{i = 0}^{2(r-1)}(-1)^i\binom{2(r-1)}{i} \int_0^{\infty}[\bar{F}_Z(z)]^{2\gamma_{r-\frac{1}{2}i}-2} f_Z^2(z) d z. \end{equation*} |
Thus, if q < 1, we get
| \begin{eqnarray} J\left(Z{(r, n, m, k)}\right)& = &- \frac{(\delta \theta (2-q)C_{r-1})^2}{2((r-1) !(m+1)^{r-1})^2} \sum\limits_{i = 0}^{2(r-1)}(-1)^i\binom{2(r-1)}{i} \int_0^{[\theta(1-q)]^{-\frac{1}{\delta}} } \\&\times&\left[1-(1-q) \theta z^{\delta}\right]^{\frac{(2-q)({2\gamma_{r-\frac{1}{2}i}-2})}{1-q}} \left( z^{\delta -1} \left(1- (1-q)\theta z^{\delta }\right)^{\frac{1}{1-q}}\right)^2 d z\\& = &- \frac{\delta \theta^{\frac{1}{\delta}} ((2-q)C_{r-1})^2}{2(1-q)^{2-\frac{1}{\delta}} ((r-1) !(m+1)^{r-1})^2} \sum\limits_{i = 0}^{2(r-1)}(-1)^i\binom{2(r-1)}{i} \\&\times&B\left(2-\frac{1}{\delta}, \frac{(2-q)({2\gamma_{r-\frac{1}{2}i}})}{1-q}-1\right). \end{eqnarray} | (3.2) |
Moreover, if 1 < q < 2, we get
| \begin{eqnarray} J\left(Z{(r, n, m, k)}\right)& = &- \frac{(\delta \theta (2-q)C_{r-1})^2}{2((r-1) !(m+1)^{r-1})^2} \sum\limits_{i = 0}^{2(r-1)}(-1)^i\binom{2(r-1)}{i} \int_0^{\infty} \\&\times&\left[1-(1-q) \theta z^{\delta}\right]^{\frac{(2-q)({2\gamma_{r-\frac{1}{2}i}-2})}{1-q}} \left( z^{\delta -1} \left(1- (1-q)\theta z^{\delta }\right)^{\frac{1}{1-q}}\right)^2 d z\\& = &- \frac{\delta \theta^{\frac{1}{\delta}} ((2-q)C_{r-1})^2}{2(q-1)^{2-\frac{1}{\delta}} ((r-1) !(m+1)^{r-1})^2} \sum\limits_{i = 0}^{2(r-1)}(-1)^i\binom{2(r-1)}{i} \\&\times&B\left(2-\frac{1}{\delta}, \frac{(2-q)({2\gamma_{r-\frac{1}{2}i}})}{q-1}+\frac{1}{\delta}\right). \end{eqnarray} | (3.3) |
When m = 0, k = 1, C_{r:n} = \frac{n!}{(r-1)!(n-r)!}, and \gamma_{r-\frac{1}{2}i} = n-r+\frac{1}{2}i+1, Eqs (3.2) and (3.3) are simplified to the case of OSs. Therefore,
| \begin{equation*} \label{eq 3.7} J\left(Z{(r, n, 0, 1)}\right) = \left\{\begin{array}{ll} {- \frac{\delta \theta^{\frac{1}{\delta}} ((2-q)C_{r:n})^2}{2(q-1)^{2-\frac{1}{\delta}} } \sum\limits_{i = 0}^{2(r-1)}(-1)^i\binom{2(r-1)}{i} B\left(2-\frac{1}{\delta}, \frac{2(2-q)({n-r+\frac{1}{2}i+1})}{q-1}+\frac{1}{\delta}\right), } & 1 < q < 2, \\ {- \frac{\delta \theta^{\frac{1}{\delta}} ((2-q)C_{r:n})^2}{2(1-q)^{2-\frac{1}{\delta}} } \sum\limits_{i = 0}^{2(r-1)}(-1)^i\binom{2(r-1)}{i}B\left(2-\frac{1}{\delta}, \frac{2(2-q)({n-r+\frac{1}{2}i+1})}{1-q}-1\right), } & q < 1. \end{array} \right. \end{equation*} |
When m = k = 1 and \gamma_i = 2(n-i)+1, Eqs (3.2) and (3.3) are simplified to the case of SOSs. Therefore,
| \begin{equation*} J\left(Z{(r, n, 1, 1)}\right)\!\! = \!\!\left\{\begin{array}{ll} {- \frac{\delta \theta^{\frac{1}{\delta}} ((2-q)C_{r-1})^2}{8(q-1)^{2-\frac{1}{\delta}} ((r-1)!^2)}\sum\limits_{i = 0}^{2(r-1)}(-1)^i\binom{2(r-1)}{i} B\!\!\left(\!2-\frac{1}{\delta}, \frac{2(2-q)({2(n-r+\frac{1}{2}i)+1})}{q-1}+\frac{1}{\delta}\right), } &\!\! 1\! < \!q\! < \!2, \\ {- \frac{\delta \theta^{\frac{1}{\delta}} ((2-q)C_{r-1})^2}{8(1-q)^{2-\frac{1}{\delta}} ((r-1)!^2)} \sum\limits_{i = 0}^{2(r-1)}(-1)^i\binom{2(r-1)}{i}B\!\!\left(2-\frac{1}{\delta}, \frac{2(2-q)({2(n-r+\frac{1}{2}i)+1})}{1-q}-1\right), } &\!\! q\! < \!1. \end{array}\right. \end{equation*} |
Table 2 displays the values of J\left(Z{(r, n, 0, 1)}\right) for the q -Weibull distribution based on OSs for n = 1, ..., 5, \; r = 1, ..., n. We can extract the following properties. In most cases, the extropy J\left(Z{(r, n, 0, 1)}\right) decreases as r increases, except for some of our values approaching the maximum and increasing again when 1 < q < 2. In general, the extropy J\left(Z{(r, n, 0, 1)}\right) decreases as \delta increases. Moreover, J\left(Z{(r, n, 0, 1)}\right) increases as q increases and the extropy J\left(Z{(r, n, 0, 1)}\right) decreases as \theta increases.
| n | r | \theta=0.25 | \theta= 0.5 | \theta=1 | \theta= 1.5 | \theta= 2 | \theta= 3 | \theta=0.25 | \theta= 0.5 | \theta=1 | \theta= 1.5 | \theta= 2 | \theta= 3 |
| \delta=20, q=0.2 | \delta=20, q=0.6 | ||||||||||||
| 1 | 1 | -3.1491 | -3.2601 | -3.3751 | -3.4442 | -3.4941 | -3.5657 | -2.8168 | -2.9161 | -3.0190 | -3.0808 | -3.1254 | -3.1894 |
| 2 | 1 | -2.8455 | -2.9458 | -3.0497 | -3.1122 | -3.1573 | -3.2219 | -2.6874 | -2.7822 | -2.8803 | -2.9393 | -2.9819 | -3.0429 |
| 2 | 2 | -5.0267 | -5.2039 | -5.3874 | -5.4978 | -5.5774 | -5.6916 | -4.2827 | -4.4337 | -4.5901 | -4.6841 | -4.7519 | -4.8492 |
| 3 | 1 | -2.7852 | -2.8834 | -2.9851 | -3.0463 | -3.0904 | -3.1537 | -2.6724 | -2.7666 | -2.8642 | -2.9229 | -2.9652 | -3.0259 |
| 3 | 2 | -4.4275 | -4.5837 | -4.7453 | -4.8425 | -4.9127 | -5.0133 | -4.0546 | -4.1976 | -4.3456 | -4.4346 | -4.4988 | -4.5910 |
| 3 | 3 | -6.5114 | -6.741 | -6.9787 | -7.1216 | -7.2248 | -7.3728 | -5.369 | -5.5583 | -5.7543 | -5.8722 | -5.9573 | -6.07930 |
| 4 | 1 | -2.769 | -2.8666 | -2.9677 | -3.0285 | -3.0724 | -3.1353 | -2.6769 | -2.7713 | -2.8690 | -2.9278 | -2.9702 | -3.0310 |
| 4 | 2 | -4.2582 | -4.4084 | -4.5639 | -4.6573 | -4.7248 | -4.8216 | -3.9948 | -4.1356 | -4.2815 | -4.3692 | -4.4325 | -4.5232 |
| 4 | 3 | -5.7058 | -5.9070 | -6.1153 | -6.2406 | -6.3310 | -6.4606 | -5.1042 | -5.2842 | -5.4706 | -5.5826 | -5.6635 | -5.7795 |
| 4 | 4 | -7.7753 | -8.0495 | -8.3333 | -8.5040 | -8.6272 | -8.8039 | -6.2535 | -6.4741 | -6.7024 | -6.8397 | -6.9387 | -7.0809 |
| 5 | 1 | -2.7668 | -2.8643 | -2.9654 | -3.0261 | -3.0699 | -3.1328 | -2.6866 | -2.7813 | -2.8794 | -2.9384 | -2.9809 | -3.0420 |
| 5 | 2 | -4.1852 | -4.3328 | -4.4856 | -4.5774 | -4.6438 | -4.7389 | -3.9749 | -4.1151 | -4.2602 | -4.3474 | -4.4104 | -4.5008 |
| 5 | 3 | -5.4454 | -5.6374 | -5.8362 | -5.9557 | -6.0420 | -6.1658 | -5.0160 | -5.1929 | -5.3761 | -5.4862 | -5.5657 | -5.6796 |
| 5 | 4 | -6.8161 | -7.0565 | -7.3053 | -7.4549 | -7.5629 | -7.7178 | -5.9828 | -6.1938 | -6.4122 | -6.5435 | -6.6383 | -6.7743 |
| 5 | 5 | -8.8926 | -9.2062 | -9.5308 | -9.726 | -9.8669 | -10.0690 | -7.0093 | -7.2565 | -7.5124 | -7.6662 | -7.7773 | -7.9366 |
| \delta=20, q=1.3 | \delta=20, q=1.6 | ||||||||||||
| 1 | 1 | -1.9042 | -1.9714 | -2.0409 | -2.0827 | -2.1129 | -2.1561 | -1.2665 | -1.3111 | -1.3574 | -1.3852 | -1.4052 | -1.4340 |
| 2 | 1 | -2.1679 | -2.2444 | -2.3235 | -2.3711 | -2.4054 | -2.4547 | -1.6859 | -1.7454 | -1.8069 | -1.8439 | -1.8706 | -1.9089 |
| 2 | 2 | -2.4306 | -2.5163 | -2.6051 | -2.6584 | -2.6969 | -2.7522 | -1.3535 | -1.4012 | -1.4506 | -1.4803 | -1.5018 | -1.5325 |
| 3 | 1 | -2.2880 | -2.3687 | -2.4523 | -2.5025 | -2.5387 | -2.5907 | -1.8986 | -1.9656 | -2.0349 | -2.0766 | -2.1066 | -2.1498 |
| 3 | 2 | -2.8969 | -2.9991 | -3.1048 | -3.1684 | -3.2143 | -3.2802 | -1.9544 | -2.0233 | -2.0947 | -2.1376 | -2.1685 | -2.2130 |
| 3 | 3 | -2.7159 | -2.8117 | -2.9108 | -2.9705 | -3.0135 | -3.0752 | -1.3575 | -1.4054 | -1.455 | -1.4848 | -1.5063 | -1.5371 |
| 4 | 1 | -2.3616 | -2.4448 | -2.5311 | -2.5829 | -2.6203 | -2.6740 | -2.0307 | -2.1023 | -2.1765 | -2.221 | -2.2532 | -2.2994 |
| 4 | 2 | -3.1194 | -3.2294 | -3.3432 | -3.4117 | -3.4611 | -3.5320 | -2.307 | -2.3884 | -2.4726 | -2.5232 | -2.5598 | -2.6122 |
| 4 | 3 | -3.3326 | -3.4502 | -3.5718 | -3.6450 | -3.6978 | -3.7735 | -2.0357 | -2.1075 | -2.1819 | -2.2265 | -2.2588 | -2.3051 |
| 4 | 4 | -2.9031 | -3.0055 | -3.1114 | -3.1752 | -3.2212 | -3.2871 | -1.3462 | -1.3937 | -1.4428 | -1.4724 | -1.4937 | -1.5243 |
| 5 | 1 | -2.4132 | -2.4983 | -2.5864 | -2.6394 | -2.6776 | -2.7325 | -2.1224 | -2.1973 | -2.2748 | -2.3214 | -2.3550 | -2.4032 |
| 5 | 2 | -3.2564 | -3.3712 | -3.4901 | -3.5616 | -3.6132 | -3.6872 | -2.5435 | -2.6332 | -2.7261 | -2.7819 | -2.8222 | -2.8800 |
| 5 | 3 | -3.6407 | -3.7691 | -3.9020 | -3.9819 | -4.0396 | -4.1223 | -2.4682 | -2.5552 | -2.6453 | -2.6995 | -2.7386 | -2.7947 |
| 5 | 4 | -3.6363 | -3.7645 | -3.8973 | -3.9771 | -4.0347 | -4.1173 | -2.0612 | -2.1339 | -2.2091 | -2.2543 | -2.2870 | -2.3338 |
| 5 | 5 | -3.0385 | -3.1457 | -3.2566 | -3.3233 | -3.3714 | -3.4405 | -1.3318 | -1.3788 | -1.4274 | -1.4567 | -1.4778 | -1.508 |
| \delta=40, q=0.2 | \delta=40, q=1.6 | ||||||||||||
| 1 | 1 | -6.3621 | -6.4733 | -6.5865 | -6.6536 | -6.7016 | -6.7699 | -2.6887 | -2.7357 | -2.7835 | -2.8119 | -2.8322 | -2.8610 |
| 2 | 1 | -5.6569 | -5.7558 | -5.8564 | -5.9161 | -5.9588 | -6.0195 | -3.5004 | -3.5616 | -3.6238 | -3.6608 | -3.6872 | -3.7247 |
| 2 | 2 | -10.2589 | -10.4382 | -10.6206 | -10.7289 | -10.8063 | -10.9164 | -2.9479 | -2.9994 | -3.0518 | -3.0829 | -3.1052 | -3.1368 |
| 3 | 1 | -5.4836 | -5.5794 | -5.6769 | -5.7348 | -5.7762 | -5.8350 | -3.8962 | -3.9643 | -4.0336 | -4.0746 | -4.1041 | -4.1459 |
| 3 | 2 | -8.9294 | -9.0855 | -9.2443 | -9.3385 | -9.4059 | -9.5017 | -4.1554 | -4.2280 | -4.3019 | -4.3457 | -4.3771 | -4.4217 |
| 3 | 3 | -13.3429 | -13.5762 | -13.8135 | -13.9542 | -14.0549 | -14.1981 | -3.0001 | -3.0526 | -3.1059 | -3.1376 | -3.1602 | -3.1924 |
| 4 | 1 | -5.4137 | -5.5083 | -5.6046 | -5.6617 | -5.7025 | -5.7606 | -4.1342 | -4.2064 | -4.28 | -4.3236 | -4.3548 | -4.3992 |
| 4 | 2 | -8.5209 | -8.6698 | -8.8214 | -8.9112 | -8.9756 | -9.0670 | -4.8443 | -4.9290 | -5.0152 | -5.0663 | -5.1028 | -5.1548 |
| 4 | 3 | -11.5790 | -11.7814 | -11.9874 | -12.1095 | -12.1969 | -12.3212 | -4.3869 | -4.4636 | -4.5416 | -4.5879 | -4.6210 | -4.6681 |
| 4 | 4 | -15.9696 | -16.2488 | -16.5328 | -16.7012 | -16.8218 | -16.9932 | -3.0060 | -3.0586 | -3.1120 | -3.1437 | -3.1664 | -3.1987 |
| 5 | 1 | -5.3799 | -5.4740 | -5.5696 | -5.6264 | -5.667 | -5.7247 | -4.2949 | -4.3700 | -4.4464 | -4.4917 | -4.5241 | -4.5702 |
| 5 | 2 | -8.3253 | -8.4708 | -8.6189 | -8.7067 | -8.7695 | -8.8589 | -5.2964 | -5.3890 | -5.4832 | -5.5391 | -5.5791 | -5.6359 |
| 5 | 3 | -10.9769 | -11.1687 | -11.364 | -11.4797 | -11.5626 | -11.6804 | -5.2501 | -5.3419 | -5.4353 | -5.4906 | -5.5303 | -5.5866 |
| 5 | 4 | -13.8827 | -14.1254 | -14.3723 | -14.5187 | -14.6235 | -14.7725 | -4.4845 | -4.5629 | -4.6426 | -4.6899 | -4.7238 | -4.7719 |
| 5 | 5 | -18.2923 | -18.6121 | -18.9374 | -19.1303 | -19.2684 | -19.4647 | -2.9981 | -3.0505 | -3.1038 | -3.1354 | -3.1581 | -3.1902 |
The weighted extropy for the q -Weibull distribution with PDF given in (1.3) is given by
| \begin{eqnarray*} \mathcal{J^{ \text w}}(Z)& = &\frac{-1}{2} \int_{0}^{\infty} z f_{Z}^2(z) dz. \end{eqnarray*} |
Thus, if q < 1, we have
| \begin{eqnarray*} \mathcal{J^{ \text w}}(Z)& = &-\frac{1}{2} \int_0^{[\theta(1-q)]^{-\frac{1}{\delta}} }z \left(\delta \theta (2-q) z^{\delta -1} \left(1- (1-q)\theta z^{\delta }\right)^{\frac{1}{1-q}}\right)^2 dz. \nonumber\\& = &\frac{-\delta (q-2)^2 }{2 (1-q )^{2} } B\left(2, \frac{2}{1-q}+1\right). \end{eqnarray*} |
Moreover, if 1 < q < 2, we get
| \begin{eqnarray*} \mathcal{J^{ \text w}}(Z)& = &-\frac{1}{2} \int_0^{\infty} z\left(\delta \theta (2-q) z^{\delta -1} \left(1- (1-q)\theta z^{\delta }\right)^{\frac{1}{1-q}}\right)^2 \, dz \nonumber\\& = &\frac{-\delta (q-2)^2 }{2 (q-1)^{2} } B\left(2, \frac{2}{q-1}-2\right). \end{eqnarray*} |
It is easy to notice that the value of the weighted extropy does not depend on \theta. Consequently, Figure 3 consists of the following parts:
({\rm{a}}) when \delta = 2 and various values of q,
({\rm{b}}) when q = 1.5 and various values of \delta.
It is easy to see from the parts of Figure 3 that the value of the weighted extropy increases with an increase in q, while it decreases with an increase in \delta.
If Z(r, n, m, k) is the r th GOS based on (1.1) and (1.3), where q < 1, then the weighted extropy measure is provided by
| \begin{eqnarray} \mathcal{J^{ \text w}}\left(Z{(r, n, m, k)}\right)& = &- \frac{(\delta \theta (2-q)C_{r-1})^2}{2((r-1) !(m+1)^{r-1})^2} \sum\limits_{i = 0}^{2(r-1)}(-1)^i\binom{2(r-1)}{i} \int_0^{[\theta(1-q)]^{-\frac{1}{\delta}} } \\&\times&z\left[1-(1-q) \theta z^{\delta}\right]^{\frac{(2-q)({2\gamma_{r-\frac{1}{2}i}-2})}{1-q}} \left( z^{\delta -1} \left(1- (1-q)\theta z^{\delta }\right)^{\frac{1}{1-q}}\right)^2 d z\\& = &- \frac{\delta ((2-q)C_{r-1})^2}{2(1-q)^{2} ((r-1) !(m+1)^{r-1})^2} \sum\limits_{i = 0}^{2(r-1)}(-1)^i\binom{2(r-1)}{i} \\&\times&B\left(2, \frac{(2-q)({2\gamma_{r-\frac{1}{2}i}})}{1-q}-1\right). \end{eqnarray} | (3.4) |
Moreover, if \; 1 < q < 2, we get
| \begin{eqnarray} \label{eq 3.11} \mathcal{J^{ \text w}}\left(Z{(r, n, m, k)}\right)& = &- \frac{(\delta \theta (2-q)C_{r-1})^2}{2((r-1) !(m+1)^{r-1})^2} \sum\limits_{i = 0}^{2(r-1)}(-1)^i\binom{2(r-1)}{i} \int_0^{\infty} \\&\times&z\left[1-(1-q) \theta z^{\delta}\right]^{\frac{(2-q)({2\gamma_{r-\frac{1}{2}i}-2})}{1-q}} \left( z^{\delta -1} \left(1- (1-q)\theta z^{\delta } \right)^{\frac{1}{1-q}}\right)^2 d z\\ & = &- \frac{\delta ((2-q)C_{r-1})^2}{2(q-1)^{2} ((r-1) !(m+1)^{r-1})^2} \sum\limits_{i = 0}^{2(r-1)}(-1)^i\binom{2(r-1)}{i} \\ &\times&B\left(2, \frac{(2-q)({2\gamma_{r-\frac{1}{2}i}})}{q-1}\right). \end{eqnarray} |
When m = 0, k = 1, C_{r:n} = \frac{n!}{(r-1)!(n-r)!}, and \gamma_{r-\frac{1}{2}i} = n-r+\frac{1}{2}i+1, we get the OSs. Therefore, Eqs (3.4) and (3.5) can be utilized to compute the weighted extropy based on OSs.
| \begin{equation} \mathcal{J^{ \text w}}\left(Z{(r, n, 0, 1)}\right) = \left\{\begin{array}{ll} {- \frac{\delta ((2-q)C_{r:n})^2}{2(q-1)^{2} } \sum\limits_{i = 0}^{2(r-1)}(-1)^i\binom{2(r-1)}{i} B\left(2, \frac{2(2-q)({n-r+\frac{1}{2}i+1})}{q-1}\right), } & 1 < q < 2, \\ {- \frac{\delta ((2-q)C_{r:n})^2}{2(1-q)^{2 }} \sum\limits_{i = 0}^{2(r-1)}(-1)^i\binom{2(r-1)}{i}B\left(2, \frac{2(2-q)({n-r+\frac{1}{2}i+1})}{1-q}-1\right), } & q < 1. \end{array}\right. \end{equation} | (3.5) |
When m = k = 1 and \gamma_i = 2(n-i)+1, we get the SOSs. Therefore, Eqs (3.4) and (3.5) yield the weighted extropy based on SOSs.
| \begin{equation*} \mathcal{J^{ \text w}}\left(Z{(r, n, 1, 1)}\right) = \left\{\begin{array}{ll} {- \frac{\delta ((2-q)C_{r-1})^2}{8(q-1)^{2} ((r-1)!^2)} \sum\limits_{i = 0}^{2(r-1)}(-1)^i\binom{2(r-1)}{i} B\left(2, \frac{2(2-q)({2(n-r+\frac{1}{2}i)+1})}{q-1}\right), } & 1 < q < 2, \\ {- \frac{\delta ((2-q)C_{r-1})^2}{8(1-q)^{2 }((r-1)!^2)} \sum\limits_{i = 0}^{2(r-1)}(-1)^i\binom{2(r-1)}{i}B\left(2, \frac{2(2-q)({2(n-r+\frac{1}{2}i)+1})}{1-q}-1\right), } & q < 1. \end{array} \right. \end{equation*} |
Table 3 displays the values of \mathcal{J^{ \text w}}\left(Z{(r, n, 0, 1)}\right) for the q -Weibull distribution based on OSs for n = 1, ..., 5, r = 1, ..., n. We can extract the following properties. In most cases, \mathcal{J^{ \text w}}\left(Z{(r, n, 0, 1)}\right) decreases as r increases, except for certain values that approach the maximum and then increase again when 1 < q < 2. In general, \mathcal{J^{ \text w}}\left(Z{(r, n, 0, 1)}\right) decreases as \delta increases. In general, \mathcal{J^{ \text w}}\left(Z{(r, n, 0, 1)}\right) increases as q increases. Moreover, \mathcal{J^{ \text w}}\left(Z{(r, n, 0, 1)}\right) from (3.4)–(3.5) does not depend on \theta.
| n | r | \delta=1 | \delta=3 | \delta=5 | \delta= 10 | \delta= 20 | \delta= 40 | \delta=1 | \delta=3 | \delta=5 | \delta= 10 | \delta= 20 | \delta= 40 |
| q=0.2 | q=0.6 | ||||||||||||
| 1 | 1 | -0.1607 | -0.4821 | -0.8036 | -1.6071 | -3.2143 | -6.4286 | -0.1458 | -0.4375 | -0.7292 | -1.4583 | -2.9167 | -5.8333 |
| 2 | 1 | -0.1406 | -0.4219 | -0.7031 | -1.4062 | -2.8125 | -5.6250 | -0.1346 | -0.4038 | -0.6731 | -1.3462 | -2.6923 | -5.3846 |
| 2 | 2 | -0.2617 | -0.7852 | -1.3087 | -2.6174 | -5.2349 | -10.4697 | -0.2267 | -0.6802 | -1.1336 | -2.2672 | -4.5344 | -9.0688 |
| 3 | 1 | -0.1350 | -0.4050 | -0.6750 | -1.3500 | -2.7000 | -5.4000 | -0.1312 | -0.3937 | -0.6562 | -1.3125 | -2.6250 | -5.2500 |
| 3 | 2 | -0.2251 | -0.6754 | -1.1257 | -2.2514 | -4.5027 | -9.0055 | -0.2093 | -0.6278 | -1.0463 | -2.0927 | -4.1853 | -8.3706 |
| 3 | 3 | -0.3418 | -1.0254 | -1.7090 | -3.4180 | -6.8359 | -13.6718 | -0.2869 | -0.8607 | -1.4345 | -2.8690 | -5.7379 | -11.4758 |
| 4 | 1 | -0.1324 | -0.3971 | -0.6618 | -1.3235 | -2.6471 | -5.2941 | -0.1296 | -0.3889 | -0.6481 | -1.2963 | -2.5926 | -5.1852 |
| 4 | 2 | -0.2132 | -0.6395 | -1.0658 | -2.1316 | -4.2632 | -8.5265 | -0.2028 | -0.6085 | -1.0142 | -2.0284 | -4.0567 | -8.1135 |
| 4 | 3 | -0.2937 | -0.8812 | -1.4687 | -2.9374 | -5.8749 | -11.7498 | -0.2670 | -0.8009 | -1.3349 | -2.6698 | -5.3396 | -10.6792 |
| 4 | 4 | -0.4100 | -1.2301 | -2.0501 | -4.1002 | -8.2003 | -16.4007 | -0.3360 | -1.0080 | -1.6800 | -3.3599 | -6.7199 | -13.4398 |
| 5 | 1 | -0.1308 | -0.3924 | -0.6541 | -1.3081 | -2.6163 | -5.2326 | -0.1287 | -0.3860 | -0.6434 | -1.2868 | -2.5735 | -5.1471 |
| 5 | 2 | -0.2070 | -0.6211 | -1.0352 | -2.0704 | -4.1408 | -8.2817 | -0.1994 | -0.5981 | -0.9969 | -1.9938 | -3.9876 | -7.9753 |
| 5 | 3 | -0.2766 | -0.8298 | -1.3831 | -2.7661 | -5.5323 | -11.0646 | -0.2587 | -0.7760 | -1.2933 | -2.5866 | -5.1732 | -10.3464 |
| 5 | 4 | -0.3535 | -1.0604 | -1.7673 | -3.5346 | -7.0693 | -14.1385 | -0.3155 | -0.9464 | -1.5773 | -3.1545 | -6.3091 | -12.6181 |
| 5 | 5 | -0.4704 | -1.4111 | -2.3518 | -4.7036 | -9.4073 | -18.8145 | -0.3780 | -1.1340 | -1.8900 | -3.7800 | -7.5600 | -15.1199 |
| q=1.3 | q=1.6 | ||||||||||||
| 1 | 1 | -0.1029 | -0.3088 | -0.5147 | -1.0294 | -2.0588 | -4.1176 | -0.0714 | -0.2143 | -0.3571 | -0.7143 | -1.4286 | -2.8571 |
| 2 | 1 | -0.1129 | -0.3387 | -0.5645 | -1.1290 | -2.2581 | -4.5161 | -0.0909 | -0.2727 | -0.4545 | -0.9091 | -1.8182 | -3.6364 |
| 2 | 2 | -0.1358 | -0.4073 | -0.6789 | -1.3578 | -2.7156 | -5.4312 | -0.0803 | -0.2410 | -0.4016 | -0.8033 | -1.6065 | -3.2131 |
| 3 | 1 | -0.1167 | -0.3500 | -0.5833 | -1.1667 | -2.3333 | -4.6667 | -0.1000 | -0.3000 | -0.5000 | -1.0000 | -2.0000 | -4.0000 |
| 3 | 2 | -0.1565 | -0.4694 | -0.7824 | -1.5648 | -3.1296 | -6.2592 | -0.1105 | -0.3315 | -0.5524 | -1.1049 | -2.2098 | -4.4196 |
| 3 | 3 | -0.1542 | -0.4625 | -0.7709 | -1.5417 | -3.0835 | -6.1669 | -0.0830 | -0.2489 | -0.4148 | -0.8295 | -1.6590 | -3.3180 |
| 4 | 1 | -0.1186 | -0.3559 | -0.5932 | -1.1864 | -2.3729 | -4.7458 | -0.1053 | -0.3158 | -0.5263 | -1.0526 | -2.1053 | -4.2105 |
| 4 | 2 | -0.1652 | -0.4957 | -0.8262 | -1.6523 | -3.3047 | -6.6093 | -0.1272 | -0.3816 | -0.6360 | -1.2720 | -2.5440 | -5.0880 |
| 4 | 3 | -0.1833 | -0.5500 | -0.9166 | -1.8332 | -3.6665 | -7.3330 | -0.1182 | -0.3547 | -0.5911 | -1.1822 | -2.3644 | -4.7288 |
| 4 | 4 | -0.1665 | -0.4996 | -0.8326 | -1.6653 | -3.3305 | -6.6611 | -0.0840 | -0.2519 | -0.4199 | -0.8398 | -1.6795 | -3.3591 |
| 5 | 1 | -0.1199 | -0.3596 | -0.5993 | -1.1986 | -2.3973 | -4.7945 | -0.1087 | -0.3261 | -0.5435 | -1.0870 | -2.1739 | -4.3478 |
| 5 | 2 | -0.1701 | -0.5103 | -0.8505 | -1.7011 | -3.4021 | -6.8042 | -0.1379 | -0.4137 | -0.6895 | -1.3791 | -2.7581 | -5.5162 |
| 5 | 3 | -0.1966 | -0.5898 | -0.9830 | -1.9660 | -3.9320 | -7.8641 | -0.1396 | -0.4189 | -0.6982 | -1.3964 | -2.7928 | -5.5856 |
| 5 | 4 | -0.2024 | -0.6072 | -1.0121 | -2.0242 | -4.0483 | -8.0967 | -0.1220 | -0.3660 | -0.6101 | -1.2201 | -2.4402 | -4.8804 |
| 5 | 5 | -0.1756 | -0.5269 | -0.8782 | -1.7563 | -3.5127 | -7.0254 | -0.0844 | -0.2533 | -0.4222 | -0.8443 | -1.6887 | -3.3773 |
A method commonly employed in statistical literature for producing bivariate distributions involves the utilization of a copula, as described by Nelsen [18]. The utilization of copulas can be advantageous in the characterization of bivariate distributions that possess a well-defined dependency structure. This function facilitates the merging of bivariate data frames with uniform margins ranging from 0 to 1. The selection of the copula function is contingent upon the type of dependence structure exhibited by the two RVs. Copulas are widely employed in high-dimensional statistical applications due to their ability to facilitate the modeling and estimation of the distribution of random vectors. This is achieved by separately estimating the marginals and copula, hence simplifying the overall process. Given two marginal univariate distributions, denoted as F_Z(z) = P(Z \leq z) and F_Y(y) = P(Y \leq y), as well as a copula C(u, v) and its PDF denoted as c(u, v) = \frac{\partial^2C(u, v)}{\partial u \partial v}, Sklar [19] introduced the joint CDF and joint PDF (JPDF) in the following manner:
| F_{Z, Y}(z, y) = C(F_Z(z), F_Y(y)) |
and
| f_{Z, Y}(z, y) = f_Z(z) f_Y(y) c(F_Z(z), F_Y(y)). |
The FGM copula is widely acknowledged as a prevalent parametric copula family that is frequently employed in many applications. The family in question has been examined by Gumbel [20] in his scholarly research. The CDF and PDF for the FGM copula are
| C(u, v) = u v[1+\rho(1- u)(1-v)], \; -1\leq\rho\leq1, |
and
| c(u, v) = [1+\rho(1- 2u)(1-2v)], |
respectively. For more details about this family and its generalizations, see [21,22,23,24,25,26,27,28,29,30].
The JPDF of an FGM bivariate q -Weibull distribution (denoted by FGMBq-W) can be expressed as follows:
| \begin{eqnarray*} f_{Z, Y}(z, y)& = & (2-q_1) \theta_1 \delta_ z^{\delta_1-1}\left[1-(1-q_1) \theta_1 z^{\delta_1}\right]^{\frac{1}{1-q_1}}(2-q_2) \theta_2 \delta_2 y^{\delta_2-2}\left[1-(1-q_2) \theta_2 y^{\delta_2}\right]^{\frac{1}{1-q_2}}\\&\times&\left[1+\rho(1-2\left[1-(1-q_1) \theta_1 z^{\delta_1}\right]^{\frac{2-q_1}{1-q_1}})(1-2\left[1-(1-q_2) \theta_2 y^{\delta_2}\right]^{\frac{2-q_2}{1-q_2}})\right]. \end{eqnarray*} |
The JPDF of the FGMBq-W is plotted in Figure 4. The figure presents subfigures featuring distinct parameter values. The parameter values in the vector form (\theta _1, \delta _1, q_1, \theta _2, \delta _2, q_2, \rho) were placed under each subfigure from (a) to (i).
Remark 4.1. Since the correlation between the marginals whatever they may be in the FGM family does not exceed 0.33 (cf., Schucany et al., [31]), the FGMBq-W is used for describing bivariate data that have a weak correlation between variables in lifetime data. Attwa et al. [32] studied the FGMBq-W in a more general framework. They considered the bivariate extension distribution, q-EWF, and the FGM copula (denoted by FGMq-EWF), where EWF is the extended Weibull family of distributions that was suggested by Gurvich et al. [33]. The family FGMq-EWF contains many submodels, among them FGMBq-W. However, the study of Attwa et al. [32] focused only on the correlation coefficient. It is worth mentioning that some of the correlation values given for the considered submodels in this paper are greater than 0.33 and this result, unfortunately, interferes with the result of Schucany et al. [31]. Moreover, many values of the correlation in Attwa et al. [32] are zero, although the marginal variances are finite and the value of the shape parameter in the FGM is positive. The reason for these illogical results is often that the admissible range of the parameter vector in FGMq-EWF was incorrect and required radical adjustment.
The concomitants are a vital tool when selection and prediction problems are involved. The idea of concomitants of OSs was first proposed by David [34]. Later, many studies have been published on the concomitants of the m- GOSs model. Researchers, such as [35,36,37,38,39,40], have studied this issue.
Let (Z_i, Y_i), i = 1, 2, ..., n, be a random sample from the FGMBq-W F_{Z, Y}(z, y). If Z(r, n, m, k) is the r th GOS of the Z sample values, then the Y values associated with Z(r, n, m, k) is called the concomitant of the r th GOS and is denoted by Y[r, n, m, k], \; r = 1, 2, ..., n. The PDF of the concomitant of the r th GOS is given by
| \begin{eqnarray*} g_{[r, n, m, k]}(y) = \int_{0}^{\infty}f_{Y|Z}(y|z)f_{Z(r, n, m, k)}(z)dz, \end{eqnarray*} |
where f_{Y|Z}(y|z) is the conditional PDF of Y given Z. Therefore, after simple algebra, the PDF and CDF of the concomitant, Y[r, n, m, k], of the r th GOS Z(r, n, m, k), 1 \leq r \leq n, are respectively given by
| \begin{eqnarray*} g_{[r, n, m, k]}(y) & = &f_Y(y)+\rho\left(2 F_Y(y)-1\right) f_Y(y) C^*(r, n, m, k), \end{eqnarray*} |
and
| \begin{eqnarray} G_{[r, n, m, k]}(y) & = &F_Y(y)+\rho\left( F_Y(y)-1\right) F_Y(y) C^*(r, n, m, k), \end{eqnarray} | (4.1) |
where C^*(r, n, m, k) = 1-2\left(\frac{\gamma_1 \gamma_2 \cdots \gamma_r}{\left(\gamma_1+1\right)\left(\gamma_2+1\right) \cdots\left(\gamma_r+1\right)}\right). Note that
| C^*(r, n, 0, 1) = -\left(\frac{n-2 r+1}{n+1}\right). |
By using (1.3), (1.5), and (4.1), after simple algebra, we get
| \begin{equation} g_{[r, n, m, k]}\!(\!y\!)\! = \!(\!2\!-\!q_2\!) \theta_2 \delta_2 y^{\delta_2\!-\!1}\left[\!1\!-\!\!(\!1\!-\!q_2\!) \theta_2 y^{\delta_2}\!\right]^{\frac{1}{1\!-\!q_2}}\left(\!1\!+\!\rho\left(\! 2\left(\!\!\!1\!-\!\left[1\!-\!\!(\!1\!-\!q_2\!) \theta_2 y^{\delta_2}\right]^{\frac{2\!-\!q_2}{1\!-\!q_2}}\right)\! \!-\!1\right)\! C^*\!(\!r\!, n\!, m\!, k\!)\!\right), \end{equation} | (4.2) |
and
| \begin{equation*} G_{[r\!, n\!, m\!, k]}(y) = \left(\!1\!-\!\left[\!1\!-\!\!(\!1\!-\!q_2) \theta_2 y^{\delta_2}\!\right]^{\frac{2\!-\!q_2}{1\!-\!q_2}} \right)\!\left(\!1\!+\!\rho\left(\! \left(\!1\!-\!\left[1\!-\!\!(\!1\!-\!q_2) \theta_2 y^{\delta_2}\right]^{\frac{2\!-\!q_2}{1\!-\!q_2}} \right)\! \!-\!1\right) C^*\!(\!r\!, n\!, m\!, k\!)\right). \end{equation*} |
From (4.2), the l th moment of Y[r, n, m, k] is
| \begin{eqnarray*} \mu_{[r, n, m, k]}^{(l)} & = &\mathbb{E}\left(Y^l[r, n, m, k]\right) = \int_{0}^{\infty} y^l g_{[r, n, m, k]}(y) \mathrm{d} y \nonumber\\ & = &\left(1-\rho C^*(r, n, m, k)\right) \mu_Y^{(l)}+2\rho C^*(r, n, m, k) (\mu_Y^{(l)}-I^{*}), \end{eqnarray*} |
where
| \mu_{Y}^{(l)} = \mathbb{E}\left(Y^l\right) = \left\{\begin{array}{ll} {\frac{2-q_2}{(q_2-1)^{1+\frac{l}{\delta_2}} \theta_2^{\frac{l}{\delta_2}}} B\left(\frac{l}{\delta_2}+1, \frac{2-q_2}{q_2-1}-\frac{l}{\delta_2}\right) , } & 1 < q_2 < 2, \\ {\frac{2-q_2}{(1-q_2)^{1+\frac{l}{\delta_2} }\theta_2^{\frac{l}{\delta_2}} }B\left(\frac{l}{\delta_2}+1, \frac{2-q_2}{1-q_2}\right), } & q_2 < 1, \end{array} \right. |
and
| I^{*} = \mathbb{E}\left(Y^l\left[1\!-\!(\!1\!-\!q_2\!) \theta_2 Y^{\delta_2}\right]^{\frac{2\!-\!q_2}{1\!-\!q_2}}\right) = \left\{\begin{array}{ll} {\frac{2-q_2}{(q_2-1)^{1+\frac{l}{\delta_2}} \theta_2^{\frac{l}{\delta_2}}} B\left(\frac{l}{\delta_2}+1, \frac{2(2-q_2)}{q_2-1}-\frac{l}{\delta_2}\right), } & 1 < q_2 < 2, \\ {\frac{2-q_2}{(1-q_2)^{1+\frac{l}{\delta_2}}\theta_2^{\frac{l}{\delta_2}} }B\left(\frac{l}{\delta_2}+1, \frac{2(2-q_2)}{1-q_2}\right), } & q_2 < 1. \end{array} \right. |
In this section, we demonstrate the applicability of the q -Weibull distribution. For the sake of comparison, we consider the generalized exponential distribution (GE), F_Z(z) = (1-e^{-\theta z})^{\lambda}, z; \lambda, \theta > 0, and its special case the exponential distribution "E" at \lambda = 1. Finally, we consider the Weibull distribution "W" and the q -Weibull distribution q -W (\theta, \delta, q), which is defined by (1.3).
Example 5.1 (COVID-19 data). The q -Weibull distribution is applied to a data set concerned with the COVID-19 data set. The data represents COVID-19 pandemic data from Canada for 36 days, from 10 April to 15 May 2020, from Klakattawi et al. [41]. The considered data set has 36 observations and is given in Table 4. Furthermore, some summary plots of the data set are presented in Figure 5.
| 3.1091 | 3.3825 | 3.1444 | 3.2135 | 2.4946 | 3.5146 | 4.9274 | 3.3769 | 6.8686 | 3.0914 | 4.9378 | 3.1091 | 3.2823 | 3.8594 |
| 4.0480 | 4.1685 | 3.6426 | 3.2110 | 2.8636 | 3.2218 | 2.9078 | 3.6346 | 2.7957 | 4.2781 | 4.2202 | 1.5157 | 2.6029 | 3.3592 |
| 2.8349 | 3.1348 | 2.5261 | 1.5806 | 2.7704 | 2.1901 | 2.4141 | 1.9048 |
Table 5 discusses the MLE with standard error (SE), -\ln L, and different measures, namely the Akaike information criterion (AIC), corrected AIC (AICc), Bayesian information criterion (BIC), Hannan-Quinn information criterion (HQIC), and consistent AIC (CAIC). The Kolmogorov -Smirnov goodness of fit (K-S) test is employed for real data where we obtained the Kolmogorov- Smirnov distance, KSSTAT (the maximum difference between the data and fitting curve), and its p-value for the W, GE, q -W, and E distributions fit for COVID-19 data. Table 5 shows that the q -W fits the data better than W, GE, and E distributions based on different measures and the K-S test. Figure 6 shows the fit of the empirical CDF, histogram, and the fitted PDF. Figure 7 examines the extropy for the model q -W (6.15825, 0.00148, 1.47004) for the OSs Z_{r:36}, \; r = 1, ..., 36. This Figure shows that the extropy has fairly large values at the minimum. In addition, when r increases, the value of the extropy gradually decreases until it reaches close to the median, at which point it increases until it finally becomes as large as possible at the maximum in such a way that the information contained in the minimum is twice that of the maximum.
| Estimates | SE | -\ln L | AIC | AICc | BIC | HQIC | CAIC | KSSTAT | p-value | |
| W | 3.3136 | 0.38184 | 51.4743 | 106.949 | 107.312 | 110.116 | 108.054 | 107.312 | 0.14997 | 0.39295 |
| 0.01386 | 0.00810 | |||||||||
| GE | 29.0724 | 12.5274 | 48.5134 | 101.027 | 101.39 | 104.194 | 102.132 | 101.39 | 0.12359 | 0.64141 |
| 1.19845 | 0.15728 | |||||||||
| q-W | 6.15825 | 0.00633 | 47.0659 | 100.132 | 100.882 | 104.882 | 101.79 | 100.882 | 0.09918 | 0.87071 |
| 0.00148 | 0.00068 | |||||||||
| 1.47004 | 0.08778 | |||||||||
| E | 0.30473 | 0.05079 | 78.7798 | 159.56 | 159.677 | 161.143 | 160.112 | 159.677 | 0.4097 | 0.00001 |
Example 5.2 (Bladder cancer patients data). This data set represents the remission times (in months) of a random sample of 128 bladder cancer patients, as reported by Lee and Wang [42]. This data is given in Table 6. Furthermore, some summary plots of the data set are presented in Figure 8. We compare the fits of the q -W distribution with the W, GE, and E distributions.
| 0.08 | 2.09 | 3.48 | 4.87 | 6.94 | 8.66 | 13.11 | 23.63 | 0.20 | 2.23 | 3.52 | 4.98 | 6.97 | 8.65 |
| 9.02 | 13.29 | 0.40 | 2.26 | 3.57 | 5.06 | 7.09 | 9.22 | 13.80 | 25.74 | 0.50 | 2.46 | 3.64 | 5.09 |
| 7.26 | 9.47 | 14.24 | 25.82 | 0.51 | 2.54 | 3.70 | 5.17 | 7.28 | 9.74 | 14.76 | 26.31 | 0.81 | 2.62 |
| 3.82 | 5.32 | 7.32 | 10.06 | 14.77 | 32.15 | 2.64 | 3.88 | 5.32 | 7.39 | 10.34 | 14.83 | 34.26 | 0.90 |
| 2.69 | 4.18 | 5.34 | 7.59 | 10.66 | 15.96 | 36.66 | 1.05 | 2.69 | 4.23 | 5.41 | 7.62 | 10.75 | 16.62 |
| 43.01 | 1.19 | 2.75 | 4.26 | 5.41 | 7.63 | 17.12 | 46.12 | 1.26 | 2.83 | 4.33 | 5.49 | 7.66 | 11.25 |
| 17.14 | 79.05 | 1.35 | 2.87 | 5.62 | 7.87 | 11.64 | 17.36 | 1.40 | 3.02 | 4.34 | 5.71 | 7.93 | 11.79 |
| 18.10 | 1.46 | 4.40 | 5.85 | 8.26 | 11.98 | 19.13 | 1.76 | 3.25 | 4.50 | 6.25 | 8.37 | 12.02 | 2.02 |
| 3.31 | 4.51 | 6.54 | 8.53 | 12.03 | 20.28 | 2.02 | 3.36 | 6.76 | 12.07 | 21.73 | 2.07 | 3.36 | 6.93 |
| 12.63 | 22.69 | ||||||||||||
Table 7 discusses the MLE with the standard error (SE), -\ln L, and the different measures: AIC, AICc, BIC, HQIC, and CAIC. The K-S test is employed for real data where we obtained the KSSTAT and its p-value for the W, GE, q -W, and E distributions. Table 7 shows that the q -W fits the data better than W, GE, and E distributions based on different measures and the K-S test. Figure 9 shows the CDF curve, empirical CDF, histogram, and the fitted PDF. Figure 10 examines the extropy for the model q -W (1.4276, 0.08806, 1.32572) for the OSs Z_{r:128}, \; r = 1, ..., 128. This figure shows that the extropy has its lowest values at the minimum. In addition, when r increases, the value of the extropy gradually increases, until it finally becomes as large as possible at the maximum.
| estimates | SE | -\ln L | AIC | AICc | BIC | HQIC | CAIC | KSSTAT | p-value | |
| W | 1.04783 | 0.06758 | 414.087 | 832.174 | 832.27 | 837.878 | 834.491 | 832.27 | 0.07002 | 0.55697 |
| 0.09389 | 0.01908 | |||||||||
| GE | 1.21795 | 0.01357 | 413.078 | 830.155 | 830.251 | 835.859 | 832.473 | 830.251 | 0.07251 | 0.51132 |
| 0.12117 | 0.14884 | |||||||||
| q-W | 1.4276 | 0.17789 | 409.74 | 825.48 | 825.673 | 834.036 | 828.956 | 825.673 | 0.03506 | 0.99752 |
| 0.08806 | 0.02193 | |||||||||
| 1.32572 | 0.10271 | |||||||||
| E | 0.10677 | 0.00944 | 414.342 | 830.684 | 830.716 | 833.536 | 831.843 | 830.716 | 0.08463 | 0.31833 |
Based on the GOS model, this paper proposes Bayesian and non-Bayesian approaches to estimate the three unknown parameters for the q -Weibull distribution. We have compared the performances of the different estimates based on Type Ⅱ censored samples from the q -Weibull distribution. It was revealed that for all unknown parameters the Bayesian estimates outperform the MLEs based on the bias and MSE. For interval estimation, we have proposed the asymptotic CIs based on the MLEs. For the asymptotic CIs, explicit expressions have been derived for the FIM. There were two well-known information measures given: extropy and weighted extropy. The q -Weibull distribution was used to study the OSs and SOSs for these two measures in this context. A bivariate q -Weibull distribution and its relevant concomitants based on the FGM family were studied. Some recently published erroneous results were pointed out, see Remark 4.1. These results concern the bivariate q -extended Weibull Morgenstern family. Finally, we demonstrated the applicability of the q -Weibull distribution compared to other known distributions via two real medical data sets.
The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.
The authors are grateful to the editor and anonymous referees for their insightful comments and suggestions, which helped to improve the paper's presentation. The authors extend their appreciation to King Saud University for funding this work through Researchers Supporting Project number (RSP2024R323), King Saud University, Riyadh, Saudi Arabia.
The authors declare no conflicts of interest.
| [1] |
U. Kamps, A concept of generalized order statistics, J. Statist. Plan. Inf., 48 (1995), 1–23. https://doi.org/10.1016/0378-3758(94)00147-N doi: 10.1016/0378-3758(94)00147-N

|
| [2] |
C. A. Charalambides, Discrete q-distributions on Bernoulli trials with a geometrically varying success probability, J. Statist. Plann. Inf., 140 (2010), 2355–2383. https://doi.org/10.1016/j.jspi.2010.03.024 doi: 10.1016/j.jspi.2010.03.024

|
| [3] |
R. Diaz, E. Pariguan, On the Gaussian q-distribution, J. Math. Anal. Appl., 358 (2009), 1–9. https://doi.org/10.1016/j.jmaa.2009.04.046 doi: 10.1016/j.jmaa.2009.04.046

|
| [4] |
R. Diaz, C. Ortiz, E. Pariguan, On the k-gamma q-distribution, Cent. Eur. J. Math., 8 (2010), 448–458. https://doi.org/10.2478/s11533-010-0029-0 doi: 10.2478/s11533-010-0029-0

|
| [5] |
X. Jia, S. Nadarajah, B. Guo, Inference on q-Weibull parameters, Statist. Papers, 61 (2020), 575–593. http://doi.org/10.1007/s00362-017-0951-3 doi: 10.1007/s00362-017-0951-3

|
| [6] |
B. Singh, R. U. Khan, M. A. Khan, Characterizations of q-Weibull distribution based on generalized order statistics, J. Statist. Manag. Sys., 22 (2019), 1573–1595. http://doi.org/10.1080/09720510.2019.1643554 doi: 10.1080/09720510.2019.1643554

|
| [7] |
X. Jia, Reliability analysis for q-Weibull distribution with multiply type-Ⅰ censored data, Qual. Reliab. Eng. Int., 37 (2021), 2790–2817. http://doi.org/10.1002/qre.2890 doi: 10.1002/qre.2890

|
| [8] |
F. Lad, G. Sanflippo, G. Agro, Extropy: complementary dual of entropy, Statist. Sci., 30 (2015), 40–58. http://doi.org/10.1214/14-sts430 doi: 10.1214/14-sts430

|
| [9] |
I. A. Husseiny, A. H. Syam, The extropy of concomitants of generalized order statistics from Huang-Kotz-Morgenstern bivariate distribution, J. Math., 2022 (2022), 6385998. http://dx.doi.org/10.1155/2022/6385998 doi: 10.1155/2022/6385998

|
| [10] |
S. Bansal, N. Gupta, Weighted extropies and past extropy of order statistics and k-record values, Commun. Statist. Theory Meth., 51 (2022), 6091–6108. http://dx.doi.org/10.1080/03610926.2020.1853773 doi: 10.1080/03610926.2020.1853773

|
| [11] |
S. Picoli, R. S. Mendes, L. C. Malacarne, q-exponential, Weibull, and q-Weibull distributions: an empirical analysis, Phys. A, 324 (2003), 678–688. http://doi.org/10.1016/s0378-4371(03)00071-2 doi: 10.1016/s0378-4371(03)00071-2

|
| [12] |
Z. A. Aboeleneen, Inference for Weibull distribution under generalized order statistics, Math. Comput. Sim., 81 (2010), 26–36. http://dx.doi.org/10.1016/j.matcom.2010.06.013 doi: 10.1016/j.matcom.2010.06.013

|
| [13] | A. A. Jafari, H. Zakerzadeh, Inference on the parameters of the Weibull distribution using records, SORT, 39 (2015), 3–18. |
| [14] |
P. H. Garthwaite, J. B. Kadane, A. OHagan, Statistical methods for eliciting probability distributions, J. Am. Stat. Assoc., 100 (2005), 680–701. http://dx.doi.org/10.1198/016214505000000105 doi: 10.1198/016214505000000105

|
| [15] |
K. M. Hamdia, X. Zhuang, P. He, T. Rabczuk, Fracture toughness of polymeric particle nanocomposites: Evaluation of models performance using Bayesian method, Composites Sci. Tech., 126 (2016), 122–129. http://dx.doi.org/10.1016/j.compscitech.2016.02.012 doi: 10.1016/j.compscitech.2016.02.012

|
| [16] |
X. Jia, D. Wang, P. Jiang, B. Guo, Inference on the reliability of Weibull distribution with multiply type-Ⅰ censored data, Reliab. Eng. Syst. Saf., 150 (2016), 171–181. http://doi.org/10.1016/j.ress.2016.01.025 doi: 10.1016/j.ress.2016.01.025

|
| [17] |
M. Xu, E. L. Droguett, I. D. Lins, M. das Chagas Moura, On the q-Weibull distribution for reliability applications: An adaptive hybrid artificial bee colony algorithm for parameter estimation, Reliab. Eng. Syst. Saf., 158 (2017), 93–105. http://doi.org/10.1016/j.ress.2016.10.012 doi: 10.1016/j.ress.2016.10.012

|
| [18] | R. B. Nelsen, An Introduction to Copulas, New York: Springer-Verlag, 2006. |
| [19] | A. Sklar, Random variables, joint distribution functions, and copulas, Kybernetika, 9 (1973), 449–460. |
| [20] | E. J. Gumbel, Bivariate exponential distributions, J. Am. Stat. Assoc., 55 (1960), 698–707. |
| [21] |
M. A. Alawady, H. M. Barakat, M. A. Abd Elgawad, Concomitants of generalized order statistics from bivariate Cambanis family of distributions under a general setting, Bull. Malays. Math. Sci. Soc., 44 (2021), 3129–3159. http://dx.doi.org/10.1007/s40840-021-01102-1 doi: 10.1007/s40840-021-01102-1

|
| [22] |
M. A. Alawady, H. M. Barakat, S. Xiong, M. A. Abd Elgawad, Concomitants of generalized order statistics from iterated Farlie-Gumbel-Morgenstern type bivariate distribution, Commun. Statist. Theory Meth., 51 (2022), 5488–5504. http://dx.doi.org/10.1080/03610926.2020.1842452 doi: 10.1080/03610926.2020.1842452

|
| [23] |
S. P. Arun, C. Chesneau, R. Maya, M. R. Irshad, Farlie-Gumbel-Morgenstern bivariate moment exponential distribution and its inferences based on concomitants of order statistics, Stats, 6 (2023), 253–267. http://dx.doi.org/10.3390/stats6010015 doi: 10.3390/stats6010015

|
| [24] |
H. M. Barakat, M. A. Alawady, I. A. Husseiny, G. M. Mansour, Sarmanov family of bivariate distributions: statistical properties, concomitants of order statistics, and information measures, Bull. Malays. Math. Sci. Soc., 45 (2022), 49–83. http://dx.doi.org/10.1007/s40840-022-01241-z doi: 10.1007/s40840-022-01241-z

|
| [25] |
H. M. Barakat, E. M. Nigm, M. A. Alawady, I. A. Husseiny, Concomitants of order statistics and record values from the generalization of FGM bivariate-generalized exponential distribution, J. Statist. Theory Appl., 18 (2019), 309–322. http://dx.doi.org/10.2991/jsta.d.190822.001 doi: 10.2991/jsta.d.190822.001

|
| [26] |
H. M. Barakat, E. M. Nigm, M. A. Alawady, I. A. Husseiny, Concomitants of order statistics and record values from the iterated FGM type bivariate-generalized exponential distribution, REVSTAT Statist. J., 19 (2021), 291–307. http://dx.doi.org/10.2298/fil1809313b doi: 10.2298/fil1809313b

|
| [27] |
S. Cambanis, Some properties and generalizations of multivariate Eyraud-Gumbel-Morgenstern distributions, J. Mul. Anal., 7 (1977), 551–559. http://dx.doi.org/10.1016/0047-259x(77)90066-5 doi: 10.1016/0047-259x(77)90066-5

|
| [28] |
I. A. Husseiny, H. M. Barakat, G. M. Mansour, M. A. Alawady, Information measures in record and their concomitants arising from Sarmanov family of bivariate distributions, J. Comput. Appl. Math., 408 (2022), 114120. http://doi.org/10.1016/j.cam.2022.114120 doi: 10.1016/j.cam.2022.114120

|
| [29] |
I. A. Husseiny, M. A. Alawady, H. M. Barakat, M. A. Abd Elgawad, Information measures for order statistics and their concomitants from Cambanis bivariate family, Commun. Statist. Theory Meth., 53 (2024), 865–881. http://doi.org/10.1080/03610926.2022.2093909 doi: 10.1080/03610926.2022.2093909

|
| [30] | J. Scaria, B. Thomas, Second order concomitants from the Morgenstern family of distributions, J. Appl. Statist. Sci., 21 (2014), 63–76. |
| [31] |
W. Schucany, W. C. Parr, J. E. Boyer, Correlation structure in Farlie-Gumbel-Morgenstern distributions, Biometrika, 65 (1978), 650–653. http://doi.org/10.1093/biomet/65.3.650 doi: 10.1093/biomet/65.3.650

|
| [32] |
R. A. Attwa, T. Radwan, E. O. Abo Zaid, Bivariate q-extended Weibull Morgenstern family and correlation coefficient formulas for some of its sub-models, AIMS Math., 8 (2023), 25325–25342. http://dx.doi.org/10.3934/math.20231292 doi: 10.3934/math.20231292

|
| [33] | M. Gurvich, A. Dibenedetto, S. Ranade, A new statistical distribution for characterizing the random strength of brittle materials, J. Mater. Sci., 32 (1997), 2559–2564. |
| [34] | H. A. David, Concomitants of order statistics, Bull. Int. Statist. Inst., 45 (1973), 295–300. |
| [35] |
I. Bairamov, S. Kotz, M. Becki, New generalized Farlie-Gumbel-Morgenstern distributions and concomitants of order statistics, J. Appl. Statist., 28 (2001), 521–536. http://dx.doi.org/10.1080/02664760120047861 doi: 10.1080/02664760120047861

|
| [36] |
M. I. Beg, M. Ahsanullah, Concomitants of generalized order statistics from Farlie-Gumbel-Morgenstern distributions, Statist. Methodol., 5 (2008), 1–20. http://dx.doi.org/10.1016/j.stamet.2007.04.001 doi: 10.1016/j.stamet.2007.04.001

|
| [37] |
F. Domma, S. Giordano, Concomitants of m-generalized order statistics from generalized Farlie-Gumbel-Morgenstern distribution family, J. Comput. Appl. Math., 294 (2016), 413–435. http://dx.doi.org/10.1016/j.cam.2015.08.022 doi: 10.1016/j.cam.2015.08.022

|
| [38] |
S. Eryilmaz, On an application of concomitants of order statistics, Commun. Statist. Theory Meth., 45 (2016), 5628–5636. http://dx.doi.org/10.1080/03610926.2014.948201 doi: 10.1080/03610926.2014.948201

|
| [39] |
J. Scaria, N. U. Nair, Distribution of extremes of rth concomitant from the Morgenstern family, Statist. Papers, 49 (2008), 109–119. http://doi.org/10.1007/s00362-006-0365-0 doi: 10.1007/s00362-006-0365-0

|
| [40] |
S. Tahmasebi, A. A. Jafari, Concomitants of order statistics and record values from Morgenstern type bivariate-generalized exponential distribution, Bull. Malays. Math. Sci. Soc., 38 (2015), 1411–1423. http://doi.org/10.1007/s40840-014-0087-8 doi: 10.1007/s40840-014-0087-8

|
| [41] |
H. S. Klakattawi, W. H. Aljuhani, L. A. Baharith, Alpha power exponentiated new Weibull-Pareto distribution: Its properties and applications, Pakistan J. Statist. Oper. Res., 18 (2022), 703–720. http://doi.org/10.18187/pjsor.v18i3.3937 doi: 10.18187/pjsor.v18i3.3937

|
| [42] | E. T. Lee, J. Wang, Statistical Methods for Survival Data Analysis, New york: John Wiley & Sons, 2003. |
| 1. | I. A. Husseiny, M. Nagy, A. H. Mansi, M. A. Alawady, Some Tsallis entropy measures in concomitants of generalized order statistics under iterated FGM bivariate distribution, 2024, 9, 2473-6988, 23268, 10.3934/math.20241131 | |
| 2. | H. M. Barakat, M. A. Alawady, I. A. Husseiny, M. Nagy, A. H. Mansi, M. O. Mohamed, Bivariate Epanechnikov-exponential distribution: statistical properties, reliability measures, and applications to computer science data, 2024, 9, 2473-6988, 32299, 10.3934/math.20241550 | |
| 3. | M. A. Alawady, H. M. Barakat, T. S. Taher, I. A. Husseiny, Measures of Extropy for $$k-$$Record Values and Their Concomitants Based on Cambanis Family, 2025, 19, 1559-8608, 10.1007/s42519-024-00423-1 |
| \delta =1.5, q=1.3, \theta =0.354 | \delta =3, q=0.9, \theta =0.579 | |||||||||
| MLE | Bayes | MLE | Bayes | |||||||
| n | r | Bias | MSE | Bias | MSE | Bias | MSE | Bias | MSE | |
| 20 | 1 | \delta | 0.924 | 0.812 | 0.911 | 0.798 | 0.345 | 0.278 | 0.333 | 0.268 |
| q | 0.301 | 0.187 | 0.298 | 0.178 | 0.475 | 0.296 | 0.465 | 0.289 | ||
| \theta | 0.115 | 0.128 | 0.109 | 0.113 | 0.125 | 0.189 | 0.121 | 0.178 | ||
| 3 | \delta | 0.916 | 0.796 | 0.901 | 0.789 | 0.328 | 0.263 | 0.314 | 0.254 | |
| q | 0.299 | 0.178 | 0.287 | 0.169 | 0.463 | 0.276 | 0.456 | 0.269 | ||
| \theta | 0.107 | 0.119 | 0.098 | 0.105 | 0.112 | 0.168 | 0.102 | 0.156 | ||
| 10 | \delta | 0.898 | 0.782 | 0.879 | 0.779 | 0.309 | 0.211 | 0.298 | 0.201 | |
| q | 0.287 | 0.169 | 0.275 | 0.157 | 0.419 | 0.251 | 0.405 | 0.243 | ||
| \theta | 0.095 | 0.102 | 0.089 | 0.096 | 0.106 | 0.146 | 0.097 | 0.138 | ||
| 12 | \delta | 0.859 | 0.767 | 0.843 | 0.759 | 0.268 | 0.198 | 0.234 | 0.168 | |
| q | 0.281 | 0.165 | 0.275 | 0.152 | 0.389 | 0.228 | 0.356 | 0.213 | ||
| \theta | 0.074 | 0.099 | 0.054 | 0.091 | 0.078 | 0.123 | 0.056 | 0.114 | ||
| 17 | \delta | 0.811 | 0.759 | 0.745 | 0.682 | 0.225 | 0.153 | 0.205 | 0.132 | |
| q | 0.279 | 0.164 | 0.198 | 0.155 | 0.335 | 0.214 | 0.312 | 0.298 | ||
| \theta | 0.058 | 0.091 | 0.035 | 0.084 | 0.031 | 0.103 | 0.012 | 0.009 | ||
| 19 | \delta | 0.753 | 0.669 | 0.658 | 0.569 | 0.211 | 0.146 | 0.198 | 0.134 | |
| q | 0.208 | 0.052 | 0.189 | 0.045 | 0.289 | 0.195 | 0.231 | 0.178 | ||
| \theta | 0.038 | 0.076 | 0.024 | 0.062 | 0.029 | 0.098 | 0.012 | 0.078 | ||
| 50 | 1 | \delta | 0.954 | 0.857 | 0.935 | 0.847 | 0.215 | 0.195 | 0.204 | 0.193 |
| q | 0.214 | 0.178 | 0.203 | 0.165 | 0.211 | 0.187 | 0.200 | 0.182 | ||
| \theta | 0.116 | 0.125 | 0.103 | 0.118 | 0.117 | 0.124 | 0.112 | 0.121 | ||
| 3 | \delta | 0.932 | 0.842 | 0.924 | 0.832 | 0.201 | 0.187 | 0.196 | 0.181 | |
| q | 0.201 | 0.165 | 0.189 | 0.146 | 0.203 | 0.176 | 0.195 | 0.169 | ||
| \theta | 0.111 | 0.121 | 0.098 | 0.104 | 0.103 | 0.115 | 0.097 | 0.111 | ||
| 25 | \delta | 0.898 | 0.821 | 0.872 | 0.802 | 0.195 | 0.175 | 0.191 | 0.163 | |
| q | 0.197 | 0.152 | 0.185 | 0.146 | 0.196 | 0.164 | 0.185 | 0.156 | ||
| \theta | 0.101 | 0.105 | 0.092 | 0.101 | 0.089 | 0.099 | 0.085 | 0.092 | ||
| 27 | \delta | 0.852 | 0.785 | 0.824 | 0.752 | 0.191 | 0.152 | 0.184 | 0.143 | |
| q | 0.178 | 0.135 | 0.169 | 0.126 | 0.192 | 0.142 | 0.187 | 0.141 | ||
| \theta | 0.089 | 0.098 | 0.068 | 0.076 | 0.054 | 0.095 | 0.046 | 0.085 | ||
| 45 | \delta | 0.746 | 0.658 | 0.647 | 0.587 | 0.189 | 0.138 | 0.154 | 0.121 | |
| q | 0.159 | 0.107 | 0.142 | 0.095 | 0.182 | 0.135 | 0.163 | 0.128 | ||
| \theta | 0.034 | 0.071 | 0.022 | 0.059 | 0.022 | 0.094 | 0.009 | 0.079 | ||
| 47 | \delta | 0.732 | 0.637 | 0.632 | 0.523 | 0.154 | 0.125 | 0.132 | 0.116 | |
| q | 0.179 | 0.118 | 0.132 | 0.106 | 0.165 | 0.115 | 0.156 | 0.105 | ||
| \theta | 0.023 | 0.063 | 0.019 | 0.045 | 0.013 | 0.086 | 0.008 | 0.048 | ||
| 100 | 1 | \delta | 0.528 | 0.425 | 0.495 | 0.405 | 0.115 | 0.135 | 0.105 | 0.126 |
| q | 0.136 | 0.125 | 0.128 | 0.112 | 0.245 | 0.175 | 0.235 | 0.169 | ||
| \theta | 0.102 | 0.119 | 0.099 | 0.100 | 0.109 | 0.114 | 0.099 | 0.111 | ||
| 3 | \delta | 0.504 | 0.398 | 0.487 | 0.365 | 0.112 | 0.131 | 0.108 | 0.128 | |
| q | 0.131 | 0.111 | 0.121 | 0.101 | 0.236 | 0.162 | 0.228 | 0.152 | ||
| \theta | 0.099 | 0.102 | 0.086 | 0.098 | 0.095 | 0.102 | 0.083 | 0.099 | ||
| 50 | \delta | 0.478 | 0.315 | 0.466 | 0.302 | 0.096 | 0.125 | 0.084 | 0.112 | |
| q | 0.127 | 0.105 | 0.112 | 0.091 | 0.224 | 0.154 | 0.215 | 0.143 | ||
| \theta | 0.078 | 0.095 | 0.069 | 0.091 | 0.074 | 0.094 | 0.052 | 0.088 | ||
| 52 | \delta | 0.411 | 0.297 | 0.398 | 0285 | 0.087 | 0.121 | 0.078 | 0.118 | |
| q | 0.113 | 0.098 | 0.089 | 0.072 | 0.212 | 0.151 | 0.200 | 0.136 | ||
| \theta | 0.056 | 0.084 | 0.035 | 0.067 | 0.032 | 0.072 | 0.027 | 0.058 | ||
| 96 | \delta | 0.346 | 0.222 | 0.245 | 0.186 | 0.079 | 0.119 | 0.063 | 0.109 | |
| q | 0.099 | 0.076 | 0.078 | 0.065 | 0.198 | 0.141 | 0.165 | 0.126 | ||
| \theta | 0.021 | 0.061 | 0.013 | 0.059 | 0.007 | 0.054 | 0.001 | 0.034 | ||
| 98 | \delta | 0.309 | 0.197 | 0.298 | 0.185 | 0.035 | 0.103 | 0.012 | 0.095 | |
| q | 0.076 | 0.069 | 0.054 | 0.052 | 0.075 | 0.107 | 0.062 | 0.084 | ||
| \theta | 0.015 | 0.052 | 0.009 | 0.036 | 0.002 | 0.023 | 0.0009 | 0.008 | ||
| n | r | \theta=0.25 | \theta= 0.5 | \theta=1 | \theta= 1.5 | \theta= 2 | \theta= 3 | \theta=0.25 | \theta= 0.5 | \theta=1 | \theta= 1.5 | \theta= 2 | \theta= 3 |
| \delta=20, q=0.2 | \delta=20, q=0.6 | ||||||||||||
| 1 | 1 | -3.1491 | -3.2601 | -3.3751 | -3.4442 | -3.4941 | -3.5657 | -2.8168 | -2.9161 | -3.0190 | -3.0808 | -3.1254 | -3.1894 |
| 2 | 1 | -2.8455 | -2.9458 | -3.0497 | -3.1122 | -3.1573 | -3.2219 | -2.6874 | -2.7822 | -2.8803 | -2.9393 | -2.9819 | -3.0429 |
| 2 | 2 | -5.0267 | -5.2039 | -5.3874 | -5.4978 | -5.5774 | -5.6916 | -4.2827 | -4.4337 | -4.5901 | -4.6841 | -4.7519 | -4.8492 |
| 3 | 1 | -2.7852 | -2.8834 | -2.9851 | -3.0463 | -3.0904 | -3.1537 | -2.6724 | -2.7666 | -2.8642 | -2.9229 | -2.9652 | -3.0259 |
| 3 | 2 | -4.4275 | -4.5837 | -4.7453 | -4.8425 | -4.9127 | -5.0133 | -4.0546 | -4.1976 | -4.3456 | -4.4346 | -4.4988 | -4.5910 |
| 3 | 3 | -6.5114 | -6.741 | -6.9787 | -7.1216 | -7.2248 | -7.3728 | -5.369 | -5.5583 | -5.7543 | -5.8722 | -5.9573 | -6.07930 |
| 4 | 1 | -2.769 | -2.8666 | -2.9677 | -3.0285 | -3.0724 | -3.1353 | -2.6769 | -2.7713 | -2.8690 | -2.9278 | -2.9702 | -3.0310 |
| 4 | 2 | -4.2582 | -4.4084 | -4.5639 | -4.6573 | -4.7248 | -4.8216 | -3.9948 | -4.1356 | -4.2815 | -4.3692 | -4.4325 | -4.5232 |
| 4 | 3 | -5.7058 | -5.9070 | -6.1153 | -6.2406 | -6.3310 | -6.4606 | -5.1042 | -5.2842 | -5.4706 | -5.5826 | -5.6635 | -5.7795 |
| 4 | 4 | -7.7753 | -8.0495 | -8.3333 | -8.5040 | -8.6272 | -8.8039 | -6.2535 | -6.4741 | -6.7024 | -6.8397 | -6.9387 | -7.0809 |
| 5 | 1 | -2.7668 | -2.8643 | -2.9654 | -3.0261 | -3.0699 | -3.1328 | -2.6866 | -2.7813 | -2.8794 | -2.9384 | -2.9809 | -3.0420 |
| 5 | 2 | -4.1852 | -4.3328 | -4.4856 | -4.5774 | -4.6438 | -4.7389 | -3.9749 | -4.1151 | -4.2602 | -4.3474 | -4.4104 | -4.5008 |
| 5 | 3 | -5.4454 | -5.6374 | -5.8362 | -5.9557 | -6.0420 | -6.1658 | -5.0160 | -5.1929 | -5.3761 | -5.4862 | -5.5657 | -5.6796 |
| 5 | 4 | -6.8161 | -7.0565 | -7.3053 | -7.4549 | -7.5629 | -7.7178 | -5.9828 | -6.1938 | -6.4122 | -6.5435 | -6.6383 | -6.7743 |
| 5 | 5 | -8.8926 | -9.2062 | -9.5308 | -9.726 | -9.8669 | -10.0690 | -7.0093 | -7.2565 | -7.5124 | -7.6662 | -7.7773 | -7.9366 |
| \delta=20, q=1.3 | \delta=20, q=1.6 | ||||||||||||
| 1 | 1 | -1.9042 | -1.9714 | -2.0409 | -2.0827 | -2.1129 | -2.1561 | -1.2665 | -1.3111 | -1.3574 | -1.3852 | -1.4052 | -1.4340 |
| 2 | 1 | -2.1679 | -2.2444 | -2.3235 | -2.3711 | -2.4054 | -2.4547 | -1.6859 | -1.7454 | -1.8069 | -1.8439 | -1.8706 | -1.9089 |
| 2 | 2 | -2.4306 | -2.5163 | -2.6051 | -2.6584 | -2.6969 | -2.7522 | -1.3535 | -1.4012 | -1.4506 | -1.4803 | -1.5018 | -1.5325 |
| 3 | 1 | -2.2880 | -2.3687 | -2.4523 | -2.5025 | -2.5387 | -2.5907 | -1.8986 | -1.9656 | -2.0349 | -2.0766 | -2.1066 | -2.1498 |
| 3 | 2 | -2.8969 | -2.9991 | -3.1048 | -3.1684 | -3.2143 | -3.2802 | -1.9544 | -2.0233 | -2.0947 | -2.1376 | -2.1685 | -2.2130 |
| 3 | 3 | -2.7159 | -2.8117 | -2.9108 | -2.9705 | -3.0135 | -3.0752 | -1.3575 | -1.4054 | -1.455 | -1.4848 | -1.5063 | -1.5371 |
| 4 | 1 | -2.3616 | -2.4448 | -2.5311 | -2.5829 | -2.6203 | -2.6740 | -2.0307 | -2.1023 | -2.1765 | -2.221 | -2.2532 | -2.2994 |
| 4 | 2 | -3.1194 | -3.2294 | -3.3432 | -3.4117 | -3.4611 | -3.5320 | -2.307 | -2.3884 | -2.4726 | -2.5232 | -2.5598 | -2.6122 |
| 4 | 3 | -3.3326 | -3.4502 | -3.5718 | -3.6450 | -3.6978 | -3.7735 | -2.0357 | -2.1075 | -2.1819 | -2.2265 | -2.2588 | -2.3051 |
| 4 | 4 | -2.9031 | -3.0055 | -3.1114 | -3.1752 | -3.2212 | -3.2871 | -1.3462 | -1.3937 | -1.4428 | -1.4724 | -1.4937 | -1.5243 |
| 5 | 1 | -2.4132 | -2.4983 | -2.5864 | -2.6394 | -2.6776 | -2.7325 | -2.1224 | -2.1973 | -2.2748 | -2.3214 | -2.3550 | -2.4032 |
| 5 | 2 | -3.2564 | -3.3712 | -3.4901 | -3.5616 | -3.6132 | -3.6872 | -2.5435 | -2.6332 | -2.7261 | -2.7819 | -2.8222 | -2.8800 |
| 5 | 3 | -3.6407 | -3.7691 | -3.9020 | -3.9819 | -4.0396 | -4.1223 | -2.4682 | -2.5552 | -2.6453 | -2.6995 | -2.7386 | -2.7947 |
| 5 | 4 | -3.6363 | -3.7645 | -3.8973 | -3.9771 | -4.0347 | -4.1173 | -2.0612 | -2.1339 | -2.2091 | -2.2543 | -2.2870 | -2.3338 |
| 5 | 5 | -3.0385 | -3.1457 | -3.2566 | -3.3233 | -3.3714 | -3.4405 | -1.3318 | -1.3788 | -1.4274 | -1.4567 | -1.4778 | -1.508 |
| \delta=40, q=0.2 | \delta=40, q=1.6 | ||||||||||||
| 1 | 1 | -6.3621 | -6.4733 | -6.5865 | -6.6536 | -6.7016 | -6.7699 | -2.6887 | -2.7357 | -2.7835 | -2.8119 | -2.8322 | -2.8610 |
| 2 | 1 | -5.6569 | -5.7558 | -5.8564 | -5.9161 | -5.9588 | -6.0195 | -3.5004 | -3.5616 | -3.6238 | -3.6608 | -3.6872 | -3.7247 |
| 2 | 2 | -10.2589 | -10.4382 | -10.6206 | -10.7289 | -10.8063 | -10.9164 | -2.9479 | -2.9994 | -3.0518 | -3.0829 | -3.1052 | -3.1368 |
| 3 | 1 | -5.4836 | -5.5794 | -5.6769 | -5.7348 | -5.7762 | -5.8350 | -3.8962 | -3.9643 | -4.0336 | -4.0746 | -4.1041 | -4.1459 |
| 3 | 2 | -8.9294 | -9.0855 | -9.2443 | -9.3385 | -9.4059 | -9.5017 | -4.1554 | -4.2280 | -4.3019 | -4.3457 | -4.3771 | -4.4217 |
| 3 | 3 | -13.3429 | -13.5762 | -13.8135 | -13.9542 | -14.0549 | -14.1981 | -3.0001 | -3.0526 | -3.1059 | -3.1376 | -3.1602 | -3.1924 |
| 4 | 1 | -5.4137 | -5.5083 | -5.6046 | -5.6617 | -5.7025 | -5.7606 | -4.1342 | -4.2064 | -4.28 | -4.3236 | -4.3548 | -4.3992 |
| 4 | 2 | -8.5209 | -8.6698 | -8.8214 | -8.9112 | -8.9756 | -9.0670 | -4.8443 | -4.9290 | -5.0152 | -5.0663 | -5.1028 | -5.1548 |
| 4 | 3 | -11.5790 | -11.7814 | -11.9874 | -12.1095 | -12.1969 | -12.3212 | -4.3869 | -4.4636 | -4.5416 | -4.5879 | -4.6210 | -4.6681 |
| 4 | 4 | -15.9696 | -16.2488 | -16.5328 | -16.7012 | -16.8218 | -16.9932 | -3.0060 | -3.0586 | -3.1120 | -3.1437 | -3.1664 | -3.1987 |
| 5 | 1 | -5.3799 | -5.4740 | -5.5696 | -5.6264 | -5.667 | -5.7247 | -4.2949 | -4.3700 | -4.4464 | -4.4917 | -4.5241 | -4.5702 |
| 5 | 2 | -8.3253 | -8.4708 | -8.6189 | -8.7067 | -8.7695 | -8.8589 | -5.2964 | -5.3890 | -5.4832 | -5.5391 | -5.5791 | -5.6359 |
| 5 | 3 | -10.9769 | -11.1687 | -11.364 | -11.4797 | -11.5626 | -11.6804 | -5.2501 | -5.3419 | -5.4353 | -5.4906 | -5.5303 | -5.5866 |
| 5 | 4 | -13.8827 | -14.1254 | -14.3723 | -14.5187 | -14.6235 | -14.7725 | -4.4845 | -4.5629 | -4.6426 | -4.6899 | -4.7238 | -4.7719 |
| 5 | 5 | -18.2923 | -18.6121 | -18.9374 | -19.1303 | -19.2684 | -19.4647 | -2.9981 | -3.0505 | -3.1038 | -3.1354 | -3.1581 | -3.1902 |
| n | r | \delta=1 | \delta=3 | \delta=5 | \delta= 10 | \delta= 20 | \delta= 40 | \delta=1 | \delta=3 | \delta=5 | \delta= 10 | \delta= 20 | \delta= 40 |
| q=0.2 | q=0.6 | ||||||||||||
| 1 | 1 | -0.1607 | -0.4821 | -0.8036 | -1.6071 | -3.2143 | -6.4286 | -0.1458 | -0.4375 | -0.7292 | -1.4583 | -2.9167 | -5.8333 |
| 2 | 1 | -0.1406 | -0.4219 | -0.7031 | -1.4062 | -2.8125 | -5.6250 | -0.1346 | -0.4038 | -0.6731 | -1.3462 | -2.6923 | -5.3846 |
| 2 | 2 | -0.2617 | -0.7852 | -1.3087 | -2.6174 | -5.2349 | -10.4697 | -0.2267 | -0.6802 | -1.1336 | -2.2672 | -4.5344 | -9.0688 |
| 3 | 1 | -0.1350 | -0.4050 | -0.6750 | -1.3500 | -2.7000 | -5.4000 | -0.1312 | -0.3937 | -0.6562 | -1.3125 | -2.6250 | -5.2500 |
| 3 | 2 | -0.2251 | -0.6754 | -1.1257 | -2.2514 | -4.5027 | -9.0055 | -0.2093 | -0.6278 | -1.0463 | -2.0927 | -4.1853 | -8.3706 |
| 3 | 3 | -0.3418 | -1.0254 | -1.7090 | -3.4180 | -6.8359 | -13.6718 | -0.2869 | -0.8607 | -1.4345 | -2.8690 | -5.7379 | -11.4758 |
| 4 | 1 | -0.1324 | -0.3971 | -0.6618 | -1.3235 | -2.6471 | -5.2941 | -0.1296 | -0.3889 | -0.6481 | -1.2963 | -2.5926 | -5.1852 |
| 4 | 2 | -0.2132 | -0.6395 | -1.0658 | -2.1316 | -4.2632 | -8.5265 | -0.2028 | -0.6085 | -1.0142 | -2.0284 | -4.0567 | -8.1135 |
| 4 | 3 | -0.2937 | -0.8812 | -1.4687 | -2.9374 | -5.8749 | -11.7498 | -0.2670 | -0.8009 | -1.3349 | -2.6698 | -5.3396 | -10.6792 |
| 4 | 4 | -0.4100 | -1.2301 | -2.0501 | -4.1002 | -8.2003 | -16.4007 | -0.3360 | -1.0080 | -1.6800 | -3.3599 | -6.7199 | -13.4398 |
| 5 | 1 | -0.1308 | -0.3924 | -0.6541 | -1.3081 | -2.6163 | -5.2326 | -0.1287 | -0.3860 | -0.6434 | -1.2868 | -2.5735 | -5.1471 |
| 5 | 2 | -0.2070 | -0.6211 | -1.0352 | -2.0704 | -4.1408 | -8.2817 | -0.1994 | -0.5981 | -0.9969 | -1.9938 | -3.9876 | -7.9753 |
| 5 | 3 | -0.2766 | -0.8298 | -1.3831 | -2.7661 | -5.5323 | -11.0646 | -0.2587 | -0.7760 | -1.2933 | -2.5866 | -5.1732 | -10.3464 |
| 5 | 4 | -0.3535 | -1.0604 | -1.7673 | -3.5346 | -7.0693 | -14.1385 | -0.3155 | -0.9464 | -1.5773 | -3.1545 | -6.3091 | -12.6181 |
| 5 | 5 | -0.4704 | -1.4111 | -2.3518 | -4.7036 | -9.4073 | -18.8145 | -0.3780 | -1.1340 | -1.8900 | -3.7800 | -7.5600 | -15.1199 |
| q=1.3 | q=1.6 | ||||||||||||
| 1 | 1 | -0.1029 | -0.3088 | -0.5147 | -1.0294 | -2.0588 | -4.1176 | -0.0714 | -0.2143 | -0.3571 | -0.7143 | -1.4286 | -2.8571 |
| 2 | 1 | -0.1129 | -0.3387 | -0.5645 | -1.1290 | -2.2581 | -4.5161 | -0.0909 | -0.2727 | -0.4545 | -0.9091 | -1.8182 | -3.6364 |
| 2 | 2 | -0.1358 | -0.4073 | -0.6789 | -1.3578 | -2.7156 | -5.4312 | -0.0803 | -0.2410 | -0.4016 | -0.8033 | -1.6065 | -3.2131 |
| 3 | 1 | -0.1167 | -0.3500 | -0.5833 | -1.1667 | -2.3333 | -4.6667 | -0.1000 | -0.3000 | -0.5000 | -1.0000 | -2.0000 | -4.0000 |
| 3 | 2 | -0.1565 | -0.4694 | -0.7824 | -1.5648 | -3.1296 | -6.2592 | -0.1105 | -0.3315 | -0.5524 | -1.1049 | -2.2098 | -4.4196 |
| 3 | 3 | -0.1542 | -0.4625 | -0.7709 | -1.5417 | -3.0835 | -6.1669 | -0.0830 | -0.2489 | -0.4148 | -0.8295 | -1.6590 | -3.3180 |
| 4 | 1 | -0.1186 | -0.3559 | -0.5932 | -1.1864 | -2.3729 | -4.7458 | -0.1053 | -0.3158 | -0.5263 | -1.0526 | -2.1053 | -4.2105 |
| 4 | 2 | -0.1652 | -0.4957 | -0.8262 | -1.6523 | -3.3047 | -6.6093 | -0.1272 | -0.3816 | -0.6360 | -1.2720 | -2.5440 | -5.0880 |
| 4 | 3 | -0.1833 | -0.5500 | -0.9166 | -1.8332 | -3.6665 | -7.3330 | -0.1182 | -0.3547 | -0.5911 | -1.1822 | -2.3644 | -4.7288 |
| 4 | 4 | -0.1665 | -0.4996 | -0.8326 | -1.6653 | -3.3305 | -6.6611 | -0.0840 | -0.2519 | -0.4199 | -0.8398 | -1.6795 | -3.3591 |
| 5 | 1 | -0.1199 | -0.3596 | -0.5993 | -1.1986 | -2.3973 | -4.7945 | -0.1087 | -0.3261 | -0.5435 | -1.0870 | -2.1739 | -4.3478 |
| 5 | 2 | -0.1701 | -0.5103 | -0.8505 | -1.7011 | -3.4021 | -6.8042 | -0.1379 | -0.4137 | -0.6895 | -1.3791 | -2.7581 | -5.5162 |
| 5 | 3 | -0.1966 | -0.5898 | -0.9830 | -1.9660 | -3.9320 | -7.8641 | -0.1396 | -0.4189 | -0.6982 | -1.3964 | -2.7928 | -5.5856 |
| 5 | 4 | -0.2024 | -0.6072 | -1.0121 | -2.0242 | -4.0483 | -8.0967 | -0.1220 | -0.3660 | -0.6101 | -1.2201 | -2.4402 | -4.8804 |
| 5 | 5 | -0.1756 | -0.5269 | -0.8782 | -1.7563 | -3.5127 | -7.0254 | -0.0844 | -0.2533 | -0.4222 | -0.8443 | -1.6887 | -3.3773 |
| 3.1091 | 3.3825 | 3.1444 | 3.2135 | 2.4946 | 3.5146 | 4.9274 | 3.3769 | 6.8686 | 3.0914 | 4.9378 | 3.1091 | 3.2823 | 3.8594 |
| 4.0480 | 4.1685 | 3.6426 | 3.2110 | 2.8636 | 3.2218 | 2.9078 | 3.6346 | 2.7957 | 4.2781 | 4.2202 | 1.5157 | 2.6029 | 3.3592 |
| 2.8349 | 3.1348 | 2.5261 | 1.5806 | 2.7704 | 2.1901 | 2.4141 | 1.9048 |
| Estimates | SE | -\ln L | AIC | AICc | BIC | HQIC | CAIC | KSSTAT | p-value | |
| W | 3.3136 | 0.38184 | 51.4743 | 106.949 | 107.312 | 110.116 | 108.054 | 107.312 | 0.14997 | 0.39295 |
| 0.01386 | 0.00810 | |||||||||
| GE | 29.0724 | 12.5274 | 48.5134 | 101.027 | 101.39 | 104.194 | 102.132 | 101.39 | 0.12359 | 0.64141 |
| 1.19845 | 0.15728 | |||||||||
| q-W | 6.15825 | 0.00633 | 47.0659 | 100.132 | 100.882 | 104.882 | 101.79 | 100.882 | 0.09918 | 0.87071 |
| 0.00148 | 0.00068 | |||||||||
| 1.47004 | 0.08778 | |||||||||
| E | 0.30473 | 0.05079 | 78.7798 | 159.56 | 159.677 | 161.143 | 160.112 | 159.677 | 0.4097 | 0.00001 |
| 0.08 | 2.09 | 3.48 | 4.87 | 6.94 | 8.66 | 13.11 | 23.63 | 0.20 | 2.23 | 3.52 | 4.98 | 6.97 | 8.65 |
| 9.02 | 13.29 | 0.40 | 2.26 | 3.57 | 5.06 | 7.09 | 9.22 | 13.80 | 25.74 | 0.50 | 2.46 | 3.64 | 5.09 |
| 7.26 | 9.47 | 14.24 | 25.82 | 0.51 | 2.54 | 3.70 | 5.17 | 7.28 | 9.74 | 14.76 | 26.31 | 0.81 | 2.62 |
| 3.82 | 5.32 | 7.32 | 10.06 | 14.77 | 32.15 | 2.64 | 3.88 | 5.32 | 7.39 | 10.34 | 14.83 | 34.26 | 0.90 |
| 2.69 | 4.18 | 5.34 | 7.59 | 10.66 | 15.96 | 36.66 | 1.05 | 2.69 | 4.23 | 5.41 | 7.62 | 10.75 | 16.62 |
| 43.01 | 1.19 | 2.75 | 4.26 | 5.41 | 7.63 | 17.12 | 46.12 | 1.26 | 2.83 | 4.33 | 5.49 | 7.66 | 11.25 |
| 17.14 | 79.05 | 1.35 | 2.87 | 5.62 | 7.87 | 11.64 | 17.36 | 1.40 | 3.02 | 4.34 | 5.71 | 7.93 | 11.79 |
| 18.10 | 1.46 | 4.40 | 5.85 | 8.26 | 11.98 | 19.13 | 1.76 | 3.25 | 4.50 | 6.25 | 8.37 | 12.02 | 2.02 |
| 3.31 | 4.51 | 6.54 | 8.53 | 12.03 | 20.28 | 2.02 | 3.36 | 6.76 | 12.07 | 21.73 | 2.07 | 3.36 | 6.93 |
| 12.63 | 22.69 | ||||||||||||
| estimates | SE | -\ln L | AIC | AICc | BIC | HQIC | CAIC | KSSTAT | p-value | |
| W | 1.04783 | 0.06758 | 414.087 | 832.174 | 832.27 | 837.878 | 834.491 | 832.27 | 0.07002 | 0.55697 |
| 0.09389 | 0.01908 | |||||||||
| GE | 1.21795 | 0.01357 | 413.078 | 830.155 | 830.251 | 835.859 | 832.473 | 830.251 | 0.07251 | 0.51132 |
| 0.12117 | 0.14884 | |||||||||
| q-W | 1.4276 | 0.17789 | 409.74 | 825.48 | 825.673 | 834.036 | 828.956 | 825.673 | 0.03506 | 0.99752 |
| 0.08806 | 0.02193 | |||||||||
| 1.32572 | 0.10271 | |||||||||
| E | 0.10677 | 0.00944 | 414.342 | 830.684 | 830.716 | 833.536 | 831.843 | 830.716 | 0.08463 | 0.31833 |
| \delta =1.5, q=1.3, \theta =0.354 | \delta =3, q=0.9, \theta =0.579 | |||||||||
| MLE | Bayes | MLE | Bayes | |||||||
| n | r | Bias | MSE | Bias | MSE | Bias | MSE | Bias | MSE | |
| 20 | 1 | \delta | 0.924 | 0.812 | 0.911 | 0.798 | 0.345 | 0.278 | 0.333 | 0.268 |
| q | 0.301 | 0.187 | 0.298 | 0.178 | 0.475 | 0.296 | 0.465 | 0.289 | ||
| \theta | 0.115 | 0.128 | 0.109 | 0.113 | 0.125 | 0.189 | 0.121 | 0.178 | ||
| 3 | \delta | 0.916 | 0.796 | 0.901 | 0.789 | 0.328 | 0.263 | 0.314 | 0.254 | |
| q | 0.299 | 0.178 | 0.287 | 0.169 | 0.463 | 0.276 | 0.456 | 0.269 | ||
| \theta | 0.107 | 0.119 | 0.098 | 0.105 | 0.112 | 0.168 | 0.102 | 0.156 | ||
| 10 | \delta | 0.898 | 0.782 | 0.879 | 0.779 | 0.309 | 0.211 | 0.298 | 0.201 | |
| q | 0.287 | 0.169 | 0.275 | 0.157 | 0.419 | 0.251 | 0.405 | 0.243 | ||
| \theta | 0.095 | 0.102 | 0.089 | 0.096 | 0.106 | 0.146 | 0.097 | 0.138 | ||
| 12 | \delta | 0.859 | 0.767 | 0.843 | 0.759 | 0.268 | 0.198 | 0.234 | 0.168 | |
| q | 0.281 | 0.165 | 0.275 | 0.152 | 0.389 | 0.228 | 0.356 | 0.213 | ||
| \theta | 0.074 | 0.099 | 0.054 | 0.091 | 0.078 | 0.123 | 0.056 | 0.114 | ||
| 17 | \delta | 0.811 | 0.759 | 0.745 | 0.682 | 0.225 | 0.153 | 0.205 | 0.132 | |
| q | 0.279 | 0.164 | 0.198 | 0.155 | 0.335 | 0.214 | 0.312 | 0.298 | ||
| \theta | 0.058 | 0.091 | 0.035 | 0.084 | 0.031 | 0.103 | 0.012 | 0.009 | ||
| 19 | \delta | 0.753 | 0.669 | 0.658 | 0.569 | 0.211 | 0.146 | 0.198 | 0.134 | |
| q | 0.208 | 0.052 | 0.189 | 0.045 | 0.289 | 0.195 | 0.231 | 0.178 | ||
| \theta | 0.038 | 0.076 | 0.024 | 0.062 | 0.029 | 0.098 | 0.012 | 0.078 | ||
| 50 | 1 | \delta | 0.954 | 0.857 | 0.935 | 0.847 | 0.215 | 0.195 | 0.204 | 0.193 |
| q | 0.214 | 0.178 | 0.203 | 0.165 | 0.211 | 0.187 | 0.200 | 0.182 | ||
| \theta | 0.116 | 0.125 | 0.103 | 0.118 | 0.117 | 0.124 | 0.112 | 0.121 | ||
| 3 | \delta | 0.932 | 0.842 | 0.924 | 0.832 | 0.201 | 0.187 | 0.196 | 0.181 | |
| q | 0.201 | 0.165 | 0.189 | 0.146 | 0.203 | 0.176 | 0.195 | 0.169 | ||
| \theta | 0.111 | 0.121 | 0.098 | 0.104 | 0.103 | 0.115 | 0.097 | 0.111 | ||
| 25 | \delta | 0.898 | 0.821 | 0.872 | 0.802 | 0.195 | 0.175 | 0.191 | 0.163 | |
| q | 0.197 | 0.152 | 0.185 | 0.146 | 0.196 | 0.164 | 0.185 | 0.156 | ||
| \theta | 0.101 | 0.105 | 0.092 | 0.101 | 0.089 | 0.099 | 0.085 | 0.092 | ||
| 27 | \delta | 0.852 | 0.785 | 0.824 | 0.752 | 0.191 | 0.152 | 0.184 | 0.143 | |
| q | 0.178 | 0.135 | 0.169 | 0.126 | 0.192 | 0.142 | 0.187 | 0.141 | ||
| \theta | 0.089 | 0.098 | 0.068 | 0.076 | 0.054 | 0.095 | 0.046 | 0.085 | ||
| 45 | \delta | 0.746 | 0.658 | 0.647 | 0.587 | 0.189 | 0.138 | 0.154 | 0.121 | |
| q | 0.159 | 0.107 | 0.142 | 0.095 | 0.182 | 0.135 | 0.163 | 0.128 | ||
| \theta | 0.034 | 0.071 | 0.022 | 0.059 | 0.022 | 0.094 | 0.009 | 0.079 | ||
| 47 | \delta | 0.732 | 0.637 | 0.632 | 0.523 | 0.154 | 0.125 | 0.132 | 0.116 | |
| q | 0.179 | 0.118 | 0.132 | 0.106 | 0.165 | 0.115 | 0.156 | 0.105 | ||
| \theta | 0.023 | 0.063 | 0.019 | 0.045 | 0.013 | 0.086 | 0.008 | 0.048 | ||
| 100 | 1 | \delta | 0.528 | 0.425 | 0.495 | 0.405 | 0.115 | 0.135 | 0.105 | 0.126 |
| q | 0.136 | 0.125 | 0.128 | 0.112 | 0.245 | 0.175 | 0.235 | 0.169 | ||
| \theta | 0.102 | 0.119 | 0.099 | 0.100 | 0.109 | 0.114 | 0.099 | 0.111 | ||
| 3 | \delta | 0.504 | 0.398 | 0.487 | 0.365 | 0.112 | 0.131 | 0.108 | 0.128 | |
| q | 0.131 | 0.111 | 0.121 | 0.101 | 0.236 | 0.162 | 0.228 | 0.152 | ||
| \theta | 0.099 | 0.102 | 0.086 | 0.098 | 0.095 | 0.102 | 0.083 | 0.099 | ||
| 50 | \delta | 0.478 | 0.315 | 0.466 | 0.302 | 0.096 | 0.125 | 0.084 | 0.112 | |
| q | 0.127 | 0.105 | 0.112 | 0.091 | 0.224 | 0.154 | 0.215 | 0.143 | ||
| \theta | 0.078 | 0.095 | 0.069 | 0.091 | 0.074 | 0.094 | 0.052 | 0.088 | ||
| 52 | \delta | 0.411 | 0.297 | 0.398 | 0285 | 0.087 | 0.121 | 0.078 | 0.118 | |
| q | 0.113 | 0.098 | 0.089 | 0.072 | 0.212 | 0.151 | 0.200 | 0.136 | ||
| \theta | 0.056 | 0.084 | 0.035 | 0.067 | 0.032 | 0.072 | 0.027 | 0.058 | ||
| 96 | \delta | 0.346 | 0.222 | 0.245 | 0.186 | 0.079 | 0.119 | 0.063 | 0.109 | |
| q | 0.099 | 0.076 | 0.078 | 0.065 | 0.198 | 0.141 | 0.165 | 0.126 | ||
| \theta | 0.021 | 0.061 | 0.013 | 0.059 | 0.007 | 0.054 | 0.001 | 0.034 | ||
| 98 | \delta | 0.309 | 0.197 | 0.298 | 0.185 | 0.035 | 0.103 | 0.012 | 0.095 | |
| q | 0.076 | 0.069 | 0.054 | 0.052 | 0.075 | 0.107 | 0.062 | 0.084 | ||
| \theta | 0.015 | 0.052 | 0.009 | 0.036 | 0.002 | 0.023 | 0.0009 | 0.008 | ||
| n | r | \theta=0.25 | \theta= 0.5 | \theta=1 | \theta= 1.5 | \theta= 2 | \theta= 3 | \theta=0.25 | \theta= 0.5 | \theta=1 | \theta= 1.5 | \theta= 2 | \theta= 3 |
| \delta=20, q=0.2 | \delta=20, q=0.6 | ||||||||||||
| 1 | 1 | -3.1491 | -3.2601 | -3.3751 | -3.4442 | -3.4941 | -3.5657 | -2.8168 | -2.9161 | -3.0190 | -3.0808 | -3.1254 | -3.1894 |
| 2 | 1 | -2.8455 | -2.9458 | -3.0497 | -3.1122 | -3.1573 | -3.2219 | -2.6874 | -2.7822 | -2.8803 | -2.9393 | -2.9819 | -3.0429 |
| 2 | 2 | -5.0267 | -5.2039 | -5.3874 | -5.4978 | -5.5774 | -5.6916 | -4.2827 | -4.4337 | -4.5901 | -4.6841 | -4.7519 | -4.8492 |
| 3 | 1 | -2.7852 | -2.8834 | -2.9851 | -3.0463 | -3.0904 | -3.1537 | -2.6724 | -2.7666 | -2.8642 | -2.9229 | -2.9652 | -3.0259 |
| 3 | 2 | -4.4275 | -4.5837 | -4.7453 | -4.8425 | -4.9127 | -5.0133 | -4.0546 | -4.1976 | -4.3456 | -4.4346 | -4.4988 | -4.5910 |
| 3 | 3 | -6.5114 | -6.741 | -6.9787 | -7.1216 | -7.2248 | -7.3728 | -5.369 | -5.5583 | -5.7543 | -5.8722 | -5.9573 | -6.07930 |
| 4 | 1 | -2.769 | -2.8666 | -2.9677 | -3.0285 | -3.0724 | -3.1353 | -2.6769 | -2.7713 | -2.8690 | -2.9278 | -2.9702 | -3.0310 |
| 4 | 2 | -4.2582 | -4.4084 | -4.5639 | -4.6573 | -4.7248 | -4.8216 | -3.9948 | -4.1356 | -4.2815 | -4.3692 | -4.4325 | -4.5232 |
| 4 | 3 | -5.7058 | -5.9070 | -6.1153 | -6.2406 | -6.3310 | -6.4606 | -5.1042 | -5.2842 | -5.4706 | -5.5826 | -5.6635 | -5.7795 |
| 4 | 4 | -7.7753 | -8.0495 | -8.3333 | -8.5040 | -8.6272 | -8.8039 | -6.2535 | -6.4741 | -6.7024 | -6.8397 | -6.9387 | -7.0809 |
| 5 | 1 | -2.7668 | -2.8643 | -2.9654 | -3.0261 | -3.0699 | -3.1328 | -2.6866 | -2.7813 | -2.8794 | -2.9384 | -2.9809 | -3.0420 |
| 5 | 2 | -4.1852 | -4.3328 | -4.4856 | -4.5774 | -4.6438 | -4.7389 | -3.9749 | -4.1151 | -4.2602 | -4.3474 | -4.4104 | -4.5008 |
| 5 | 3 | -5.4454 | -5.6374 | -5.8362 | -5.9557 | -6.0420 | -6.1658 | -5.0160 | -5.1929 | -5.3761 | -5.4862 | -5.5657 | -5.6796 |
| 5 | 4 | -6.8161 | -7.0565 | -7.3053 | -7.4549 | -7.5629 | -7.7178 | -5.9828 | -6.1938 | -6.4122 | -6.5435 | -6.6383 | -6.7743 |
| 5 | 5 | -8.8926 | -9.2062 | -9.5308 | -9.726 | -9.8669 | -10.0690 | -7.0093 | -7.2565 | -7.5124 | -7.6662 | -7.7773 | -7.9366 |
| \delta=20, q=1.3 | \delta=20, q=1.6 | ||||||||||||
| 1 | 1 | -1.9042 | -1.9714 | -2.0409 | -2.0827 | -2.1129 | -2.1561 | -1.2665 | -1.3111 | -1.3574 | -1.3852 | -1.4052 | -1.4340 |
| 2 | 1 | -2.1679 | -2.2444 | -2.3235 | -2.3711 | -2.4054 | -2.4547 | -1.6859 | -1.7454 | -1.8069 | -1.8439 | -1.8706 | -1.9089 |
| 2 | 2 | -2.4306 | -2.5163 | -2.6051 | -2.6584 | -2.6969 | -2.7522 | -1.3535 | -1.4012 | -1.4506 | -1.4803 | -1.5018 | -1.5325 |
| 3 | 1 | -2.2880 | -2.3687 | -2.4523 | -2.5025 | -2.5387 | -2.5907 | -1.8986 | -1.9656 | -2.0349 | -2.0766 | -2.1066 | -2.1498 |
| 3 | 2 | -2.8969 | -2.9991 | -3.1048 | -3.1684 | -3.2143 | -3.2802 | -1.9544 | -2.0233 | -2.0947 | -2.1376 | -2.1685 | -2.2130 |
| 3 | 3 | -2.7159 | -2.8117 | -2.9108 | -2.9705 | -3.0135 | -3.0752 | -1.3575 | -1.4054 | -1.455 | -1.4848 | -1.5063 | -1.5371 |
| 4 | 1 | -2.3616 | -2.4448 | -2.5311 | -2.5829 | -2.6203 | -2.6740 | -2.0307 | -2.1023 | -2.1765 | -2.221 | -2.2532 | -2.2994 |
| 4 | 2 | -3.1194 | -3.2294 | -3.3432 | -3.4117 | -3.4611 | -3.5320 | -2.307 | -2.3884 | -2.4726 | -2.5232 | -2.5598 | -2.6122 |
| 4 | 3 | -3.3326 | -3.4502 | -3.5718 | -3.6450 | -3.6978 | -3.7735 | -2.0357 | -2.1075 | -2.1819 | -2.2265 | -2.2588 | -2.3051 |
| 4 | 4 | -2.9031 | -3.0055 | -3.1114 | -3.1752 | -3.2212 | -3.2871 | -1.3462 | -1.3937 | -1.4428 | -1.4724 | -1.4937 | -1.5243 |
| 5 | 1 | -2.4132 | -2.4983 | -2.5864 | -2.6394 | -2.6776 | -2.7325 | -2.1224 | -2.1973 | -2.2748 | -2.3214 | -2.3550 | -2.4032 |
| 5 | 2 | -3.2564 | -3.3712 | -3.4901 | -3.5616 | -3.6132 | -3.6872 | -2.5435 | -2.6332 | -2.7261 | -2.7819 | -2.8222 | -2.8800 |
| 5 | 3 | -3.6407 | -3.7691 | -3.9020 | -3.9819 | -4.0396 | -4.1223 | -2.4682 | -2.5552 | -2.6453 | -2.6995 | -2.7386 | -2.7947 |
| 5 | 4 | -3.6363 | -3.7645 | -3.8973 | -3.9771 | -4.0347 | -4.1173 | -2.0612 | -2.1339 | -2.2091 | -2.2543 | -2.2870 | -2.3338 |
| 5 | 5 | -3.0385 | -3.1457 | -3.2566 | -3.3233 | -3.3714 | -3.4405 | -1.3318 | -1.3788 | -1.4274 | -1.4567 | -1.4778 | -1.508 |
| \delta=40, q=0.2 | \delta=40, q=1.6 | ||||||||||||
| 1 | 1 | -6.3621 | -6.4733 | -6.5865 | -6.6536 | -6.7016 | -6.7699 | -2.6887 | -2.7357 | -2.7835 | -2.8119 | -2.8322 | -2.8610 |
| 2 | 1 | -5.6569 | -5.7558 | -5.8564 | -5.9161 | -5.9588 | -6.0195 | -3.5004 | -3.5616 | -3.6238 | -3.6608 | -3.6872 | -3.7247 |
| 2 | 2 | -10.2589 | -10.4382 | -10.6206 | -10.7289 | -10.8063 | -10.9164 | -2.9479 | -2.9994 | -3.0518 | -3.0829 | -3.1052 | -3.1368 |
| 3 | 1 | -5.4836 | -5.5794 | -5.6769 | -5.7348 | -5.7762 | -5.8350 | -3.8962 | -3.9643 | -4.0336 | -4.0746 | -4.1041 | -4.1459 |
| 3 | 2 | -8.9294 | -9.0855 | -9.2443 | -9.3385 | -9.4059 | -9.5017 | -4.1554 | -4.2280 | -4.3019 | -4.3457 | -4.3771 | -4.4217 |
| 3 | 3 | -13.3429 | -13.5762 | -13.8135 | -13.9542 | -14.0549 | -14.1981 | -3.0001 | -3.0526 | -3.1059 | -3.1376 | -3.1602 | -3.1924 |
| 4 | 1 | -5.4137 | -5.5083 | -5.6046 | -5.6617 | -5.7025 | -5.7606 | -4.1342 | -4.2064 | -4.28 | -4.3236 | -4.3548 | -4.3992 |
| 4 | 2 | -8.5209 | -8.6698 | -8.8214 | -8.9112 | -8.9756 | -9.0670 | -4.8443 | -4.9290 | -5.0152 | -5.0663 | -5.1028 | -5.1548 |
| 4 | 3 | -11.5790 | -11.7814 | -11.9874 | -12.1095 | -12.1969 | -12.3212 | -4.3869 | -4.4636 | -4.5416 | -4.5879 | -4.6210 | -4.6681 |
| 4 | 4 | -15.9696 | -16.2488 | -16.5328 | -16.7012 | -16.8218 | -16.9932 | -3.0060 | -3.0586 | -3.1120 | -3.1437 | -3.1664 | -3.1987 |
| 5 | 1 | -5.3799 | -5.4740 | -5.5696 | -5.6264 | -5.667 | -5.7247 | -4.2949 | -4.3700 | -4.4464 | -4.4917 | -4.5241 | -4.5702 |
| 5 | 2 | -8.3253 | -8.4708 | -8.6189 | -8.7067 | -8.7695 | -8.8589 | -5.2964 | -5.3890 | -5.4832 | -5.5391 | -5.5791 | -5.6359 |
| 5 | 3 | -10.9769 | -11.1687 | -11.364 | -11.4797 | -11.5626 | -11.6804 | -5.2501 | -5.3419 | -5.4353 | -5.4906 | -5.5303 | -5.5866 |
| 5 | 4 | -13.8827 | -14.1254 | -14.3723 | -14.5187 | -14.6235 | -14.7725 | -4.4845 | -4.5629 | -4.6426 | -4.6899 | -4.7238 | -4.7719 |
| 5 | 5 | -18.2923 | -18.6121 | -18.9374 | -19.1303 | -19.2684 | -19.4647 | -2.9981 | -3.0505 | -3.1038 | -3.1354 | -3.1581 | -3.1902 |
| n | r | \delta=1 | \delta=3 | \delta=5 | \delta= 10 | \delta= 20 | \delta= 40 | \delta=1 | \delta=3 | \delta=5 | \delta= 10 | \delta= 20 | \delta= 40 |
| q=0.2 | q=0.6 | ||||||||||||
| 1 | 1 | -0.1607 | -0.4821 | -0.8036 | -1.6071 | -3.2143 | -6.4286 | -0.1458 | -0.4375 | -0.7292 | -1.4583 | -2.9167 | -5.8333 |
| 2 | 1 | -0.1406 | -0.4219 | -0.7031 | -1.4062 | -2.8125 | -5.6250 | -0.1346 | -0.4038 | -0.6731 | -1.3462 | -2.6923 | -5.3846 |
| 2 | 2 | -0.2617 | -0.7852 | -1.3087 | -2.6174 | -5.2349 | -10.4697 | -0.2267 | -0.6802 | -1.1336 | -2.2672 | -4.5344 | -9.0688 |
| 3 | 1 | -0.1350 | -0.4050 | -0.6750 | -1.3500 | -2.7000 | -5.4000 | -0.1312 | -0.3937 | -0.6562 | -1.3125 | -2.6250 | -5.2500 |
| 3 | 2 | -0.2251 | -0.6754 | -1.1257 | -2.2514 | -4.5027 | -9.0055 | -0.2093 | -0.6278 | -1.0463 | -2.0927 | -4.1853 | -8.3706 |
| 3 | 3 | -0.3418 | -1.0254 | -1.7090 | -3.4180 | -6.8359 | -13.6718 | -0.2869 | -0.8607 | -1.4345 | -2.8690 | -5.7379 | -11.4758 |
| 4 | 1 | -0.1324 | -0.3971 | -0.6618 | -1.3235 | -2.6471 | -5.2941 | -0.1296 | -0.3889 | -0.6481 | -1.2963 | -2.5926 | -5.1852 |
| 4 | 2 | -0.2132 | -0.6395 | -1.0658 | -2.1316 | -4.2632 | -8.5265 | -0.2028 | -0.6085 | -1.0142 | -2.0284 | -4.0567 | -8.1135 |
| 4 | 3 | -0.2937 | -0.8812 | -1.4687 | -2.9374 | -5.8749 | -11.7498 | -0.2670 | -0.8009 | -1.3349 | -2.6698 | -5.3396 | -10.6792 |
| 4 | 4 | -0.4100 | -1.2301 | -2.0501 | -4.1002 | -8.2003 | -16.4007 | -0.3360 | -1.0080 | -1.6800 | -3.3599 | -6.7199 | -13.4398 |
| 5 | 1 | -0.1308 | -0.3924 | -0.6541 | -1.3081 | -2.6163 | -5.2326 | -0.1287 | -0.3860 | -0.6434 | -1.2868 | -2.5735 | -5.1471 |
| 5 | 2 | -0.2070 | -0.6211 | -1.0352 | -2.0704 | -4.1408 | -8.2817 | -0.1994 | -0.5981 | -0.9969 | -1.9938 | -3.9876 | -7.9753 |
| 5 | 3 | -0.2766 | -0.8298 | -1.3831 | -2.7661 | -5.5323 | -11.0646 | -0.2587 | -0.7760 | -1.2933 | -2.5866 | -5.1732 | -10.3464 |
| 5 | 4 | -0.3535 | -1.0604 | -1.7673 | -3.5346 | -7.0693 | -14.1385 | -0.3155 | -0.9464 | -1.5773 | -3.1545 | -6.3091 | -12.6181 |
| 5 | 5 | -0.4704 | -1.4111 | -2.3518 | -4.7036 | -9.4073 | -18.8145 | -0.3780 | -1.1340 | -1.8900 | -3.7800 | -7.5600 | -15.1199 |
| q=1.3 | q=1.6 | ||||||||||||
| 1 | 1 | -0.1029 | -0.3088 | -0.5147 | -1.0294 | -2.0588 | -4.1176 | -0.0714 | -0.2143 | -0.3571 | -0.7143 | -1.4286 | -2.8571 |
| 2 | 1 | -0.1129 | -0.3387 | -0.5645 | -1.1290 | -2.2581 | -4.5161 | -0.0909 | -0.2727 | -0.4545 | -0.9091 | -1.8182 | -3.6364 |
| 2 | 2 | -0.1358 | -0.4073 | -0.6789 | -1.3578 | -2.7156 | -5.4312 | -0.0803 | -0.2410 | -0.4016 | -0.8033 | -1.6065 | -3.2131 |
| 3 | 1 | -0.1167 | -0.3500 | -0.5833 | -1.1667 | -2.3333 | -4.6667 | -0.1000 | -0.3000 | -0.5000 | -1.0000 | -2.0000 | -4.0000 |
| 3 | 2 | -0.1565 | -0.4694 | -0.7824 | -1.5648 | -3.1296 | -6.2592 | -0.1105 | -0.3315 | -0.5524 | -1.1049 | -2.2098 | -4.4196 |
| 3 | 3 | -0.1542 | -0.4625 | -0.7709 | -1.5417 | -3.0835 | -6.1669 | -0.0830 | -0.2489 | -0.4148 | -0.8295 | -1.6590 | -3.3180 |
| 4 | 1 | -0.1186 | -0.3559 | -0.5932 | -1.1864 | -2.3729 | -4.7458 | -0.1053 | -0.3158 | -0.5263 | -1.0526 | -2.1053 | -4.2105 |
| 4 | 2 | -0.1652 | -0.4957 | -0.8262 | -1.6523 | -3.3047 | -6.6093 | -0.1272 | -0.3816 | -0.6360 | -1.2720 | -2.5440 | -5.0880 |
| 4 | 3 | -0.1833 | -0.5500 | -0.9166 | -1.8332 | -3.6665 | -7.3330 | -0.1182 | -0.3547 | -0.5911 | -1.1822 | -2.3644 | -4.7288 |
| 4 | 4 | -0.1665 | -0.4996 | -0.8326 | -1.6653 | -3.3305 | -6.6611 | -0.0840 | -0.2519 | -0.4199 | -0.8398 | -1.6795 | -3.3591 |
| 5 | 1 | -0.1199 | -0.3596 | -0.5993 | -1.1986 | -2.3973 | -4.7945 | -0.1087 | -0.3261 | -0.5435 | -1.0870 | -2.1739 | -4.3478 |
| 5 | 2 | -0.1701 | -0.5103 | -0.8505 | -1.7011 | -3.4021 | -6.8042 | -0.1379 | -0.4137 | -0.6895 | -1.3791 | -2.7581 | -5.5162 |
| 5 | 3 | -0.1966 | -0.5898 | -0.9830 | -1.9660 | -3.9320 | -7.8641 | -0.1396 | -0.4189 | -0.6982 | -1.3964 | -2.7928 | -5.5856 |
| 5 | 4 | -0.2024 | -0.6072 | -1.0121 | -2.0242 | -4.0483 | -8.0967 | -0.1220 | -0.3660 | -0.6101 | -1.2201 | -2.4402 | -4.8804 |
| 5 | 5 | -0.1756 | -0.5269 | -0.8782 | -1.7563 | -3.5127 | -7.0254 | -0.0844 | -0.2533 | -0.4222 | -0.8443 | -1.6887 | -3.3773 |
| 3.1091 | 3.3825 | 3.1444 | 3.2135 | 2.4946 | 3.5146 | 4.9274 | 3.3769 | 6.8686 | 3.0914 | 4.9378 | 3.1091 | 3.2823 | 3.8594 |
| 4.0480 | 4.1685 | 3.6426 | 3.2110 | 2.8636 | 3.2218 | 2.9078 | 3.6346 | 2.7957 | 4.2781 | 4.2202 | 1.5157 | 2.6029 | 3.3592 |
| 2.8349 | 3.1348 | 2.5261 | 1.5806 | 2.7704 | 2.1901 | 2.4141 | 1.9048 |
| Estimates | SE | -\ln L | AIC | AICc | BIC | HQIC | CAIC | KSSTAT | p-value | |
| W | 3.3136 | 0.38184 | 51.4743 | 106.949 | 107.312 | 110.116 | 108.054 | 107.312 | 0.14997 | 0.39295 |
| 0.01386 | 0.00810 | |||||||||
| GE | 29.0724 | 12.5274 | 48.5134 | 101.027 | 101.39 | 104.194 | 102.132 | 101.39 | 0.12359 | 0.64141 |
| 1.19845 | 0.15728 | |||||||||
| q-W | 6.15825 | 0.00633 | 47.0659 | 100.132 | 100.882 | 104.882 | 101.79 | 100.882 | 0.09918 | 0.87071 |
| 0.00148 | 0.00068 | |||||||||
| 1.47004 | 0.08778 | |||||||||
| E | 0.30473 | 0.05079 | 78.7798 | 159.56 | 159.677 | 161.143 | 160.112 | 159.677 | 0.4097 | 0.00001 |
| 0.08 | 2.09 | 3.48 | 4.87 | 6.94 | 8.66 | 13.11 | 23.63 | 0.20 | 2.23 | 3.52 | 4.98 | 6.97 | 8.65 |
| 9.02 | 13.29 | 0.40 | 2.26 | 3.57 | 5.06 | 7.09 | 9.22 | 13.80 | 25.74 | 0.50 | 2.46 | 3.64 | 5.09 |
| 7.26 | 9.47 | 14.24 | 25.82 | 0.51 | 2.54 | 3.70 | 5.17 | 7.28 | 9.74 | 14.76 | 26.31 | 0.81 | 2.62 |
| 3.82 | 5.32 | 7.32 | 10.06 | 14.77 | 32.15 | 2.64 | 3.88 | 5.32 | 7.39 | 10.34 | 14.83 | 34.26 | 0.90 |
| 2.69 | 4.18 | 5.34 | 7.59 | 10.66 | 15.96 | 36.66 | 1.05 | 2.69 | 4.23 | 5.41 | 7.62 | 10.75 | 16.62 |
| 43.01 | 1.19 | 2.75 | 4.26 | 5.41 | 7.63 | 17.12 | 46.12 | 1.26 | 2.83 | 4.33 | 5.49 | 7.66 | 11.25 |
| 17.14 | 79.05 | 1.35 | 2.87 | 5.62 | 7.87 | 11.64 | 17.36 | 1.40 | 3.02 | 4.34 | 5.71 | 7.93 | 11.79 |
| 18.10 | 1.46 | 4.40 | 5.85 | 8.26 | 11.98 | 19.13 | 1.76 | 3.25 | 4.50 | 6.25 | 8.37 | 12.02 | 2.02 |
| 3.31 | 4.51 | 6.54 | 8.53 | 12.03 | 20.28 | 2.02 | 3.36 | 6.76 | 12.07 | 21.73 | 2.07 | 3.36 | 6.93 |
| 12.63 | 22.69 | ||||||||||||
| estimates | SE | -\ln L | AIC | AICc | BIC | HQIC | CAIC | KSSTAT | p-value | |
| W | 1.04783 | 0.06758 | 414.087 | 832.174 | 832.27 | 837.878 | 834.491 | 832.27 | 0.07002 | 0.55697 |
| 0.09389 | 0.01908 | |||||||||
| GE | 1.21795 | 0.01357 | 413.078 | 830.155 | 830.251 | 835.859 | 832.473 | 830.251 | 0.07251 | 0.51132 |
| 0.12117 | 0.14884 | |||||||||
| q-W | 1.4276 | 0.17789 | 409.74 | 825.48 | 825.673 | 834.036 | 828.956 | 825.673 | 0.03506 | 0.99752 |
| 0.08806 | 0.02193 | |||||||||
| 1.32572 | 0.10271 | |||||||||
| E | 0.10677 | 0.00944 | 414.342 | 830.684 | 830.716 | 833.536 | 831.843 | 830.716 | 0.08463 | 0.31833 |