Efficient numerical method for multi-term time-fractional diffusion equations with Caputo-Fabrizio derivatives

1.   Introduction

Fractional differential equations have developed rapidly due to their applications, see^{[1,2,3,4,5,6,7]}. Compared to classical integer-order equations, fractional differential equations offer a more accurate representation of memory effects in diverse materials and processes. Many scholars have devoted their efforts to exploring this topic and have achieved significant advancements. By using semigroup theory, the noncompact measures conditions, the references ^[8] studied local and global existence and uniqueness of mild solutions for fractional impulisive evolution differential equations of order $0 < \alpha \leq 1$. By using semigroup theory, the properties of noncompact measures, the references ^[10,11,12] studied local and global existence of solutions for a class of fractional evolution equations of order $0 < \alpha \leq 1.$ By the generalized Darbo fixed point theorem and Schauder fixed point theorem, the reference ^[14] investigated the existence and uniqueness of mild solutions for fractional impulsive integro-differential evolution equations of order $1 < \beta\leq2$ with nonlocal conditions. By using the cosine family theory, the Mönch fixed point theorem, the reference ^[15] studied the existence of mild solutions for fractional impulsive integro-differential evolution equations of order $1 < \beta\leq2$ with nonlocal conditions. By using the two-step Adomian decomposition method, the reference ^[16,17] found an analytical solution of for fractional order integro-differential equation, meanwhile, established results for the existence and uniqueness of a solution with the help of some fixed point theorems and the Banach contraction principle. Many evolution processes are characterized by abrupt state changes, which can be effectively modeled using impulsive differential equations. There are two types of impulses: instantaneous impulses and non-instantaneous impulses. The theory of instantaneous impulses often describes some processes which have a sudden change in their states at certain times, particularly in the fields of biology, dynamics, physics, and engineering. However, in the management and optimal control of life phenomena, there exist numerous non-instantaneous impulsive phenomena. The classical instantaneous impulsive differential system is not suitable to describe such phenomena, whereas differential equations with the non-instantaneous impulse offer a more suitable framework. Differential equations with non-instantaneous impulses have found extensive applications in areas such as pesticide dynamics, pest control, integrated environmental management, and fishery resources. Therefore, it is worthwhile to explore the non-instantaneous impulsive differential system. Many scholars have dedicated their efforts to investigating this subject and have achieved notable advancements. For further details, please refer to^{[18,19,20,21,22,23]}. In comparison to the results of differential equations with instantaneous impulses, there are fewer results available for differential equations with non-instantaneous impulses.

The non-instantaneous impulses were first proposed by Hernandez and Regan^[18]. In ^[18], the authors studied the following integer order equations:

where $A:D(A)\subset X \rightarrow X$ is the generator of a $C_{0}$-semigroup of bounded linear operators $(T(t)), {t\geq 0}$ is defined on a Banach space $X$, and the impulses start abruptly at the points $t_{i}$ and their action continues on the interval $[t_{i}, s_{i}]$. Utilizing the semigroup theory and fixed point theory, they established the existence of mild solutions.

Pierri et al.^[20] studied the following differential equation:

where they gave the existence of mild solutions on $[0, +\propto)$.

The literature^[21] considered the following fractional nonautonomous evolution equations with delay:

where ${A(t)}_{t\in J}$ is a family of closed and linear operators defined on a dense domain $D(A)$ in Banach space $E$ into $E$ and the operator $A(t)$ depends on $t$.

In ^[18,20], the authors studied the integer order equation with non-instantaneous impulse, where the operator $A$ did not depend on $t.$ In the process of proving the theorem, the nonlinear function $f$ required the Lipschitz condition; meanwhile, the compression coefficient was less than 1. In ^[21], the authors derived mild solutions using the Banach contraction mapping principle without employing the contraction coefficient $0 < k < 1$.

Inspired by the literature mentioned earlier, we explore the following nonlinear fractional integro-differential equations with nonlocal conditions and non-instantaneous impulses:

where $^{C}_{0}D^{\beta}_{t}$ represents the Caputo fractional derivatives of order $\beta\in(0, 1]$, $u(\cdot)\in X$, $A(t)\subset X$ is a closed linear operator, and $A(t)$ depends on $t$. $J = [0, T], \; 0 = s_{0} < t_{1}\leq s_{1} < t_{2}\leq... < t_{n}\leq s_{n} < t_{n+1} = T < +\infty$. $f\in C [J\times X^{3}, X], \; l_{i}:J\times X\rightarrow X,$ and $g_{1}: X\rightarrow X$ are also continuous. $H_{1}$ and $H_{2}$ are defined by

In this paper, we utilize the Mönch fixed point theorem, the non-compact measure, and the method of stepwise estimation to eliminate the Lipschitz condition for the nonlinear function $f$. Additionally, we do not require the compressibility coefficient to be less than 1. The key findings in this study enhance and extend some previous results.

2.   Preliminaries

We suppose that $(X, \parallel \cdot\parallel)$ is a Banach space, $J = [0, T]$, $J_{0} = [0, t_{1}], J_{i} = (t_{i}, t_{i+1}], i = 1, 2, ...n-1, J_{n} = (t_{n}, T],$ and

and there exist

Obviously, $PC[J, X]$ is a Banach space endowed with $PC$-norm $\|u\|_{pc} = \sup_{t\in J}u(t).$

Definition 2.1. ^[2] The Caputo fractional derivative of order $\beta \in (0, 1]$ for a function $u(t)$ is given by

where $p = [\beta]+1$.

Definition 2.2. ^[24] We assume that $A(t):D(A)\subset E\rightarrow E$ is a closed linear operator. We define the resolvent set of $A(t)$ by $\rho[A(t)]$. If there exist a nonnegative constant $\omega\geq 0$ and a strongly continuous function $U_{\beta}:R_{+}^{2}\rightarrow B(E)$ satisfying

then we call $A(t)$ the generator of a $\beta$-resolvent family. $U_{\beta}(t, s)$ is called the $\beta$-resolvent family generated by $A(t)$.

Property 2.1. ^[24] $U_{\beta}(x, y)$ has the following properties:

(1) $U_{\beta}(x, x) = I, U_{\beta}(x, y) = U_{\beta}(x, r)U_{\beta}(r, y)$ for $0\leq x\leq r\leq y\leq T$;

(2) For $0\leq x\leq y\leq T, \; (x, y)\rightarrow U_{\beta}(x, y)$ is strongly continuous.

Definition 2.3. ^[25] We suppose that $D$ is a space and mapping $T:D\rightarrow D$. If there exists $x_{0}\in D$ such that $Tx_{0} = x_{0},$ then $x_{0}\in D$ is called the fixed point of operator $T.$

Lemma 2.1. ^[14] Suppose $B \subset PC[J, X]$ is equi-continuous and bounded, then for $t\in J_{i}$, $\alpha(\{u(t)|u\in B\})$ is continuous and

Lemma 2.2. ^[26] Suppose $B\subset PC[J, X]$ is equi-continuous and bounded, then $\overline{Co}B\subset PC[J, X]$ is equi-continuous and bounded.

Lemma 2.3. ^[27] For any $R > 0$, the function $f$ is uniformly continuous and bounded on $J\times B_{R}^{4}$ where $B_{R} = \{u\in X : \| u\| \leq R\}$, if $B\subset PC[J, X]$ is equi-continuous and bounded, then $\{f(t, u(t), u(\tau(t)), (H_{1}u)(t), (H_{2}u)(t): u\in B\}\subset PC[J, X]$ is also equi-continuous and bounded.

Lemma 2.4. ^[27] Suppose $B\subset PC[J, X]$ is bounded and equi-continuous, then

Lemma 2.5. ^[6] Suppose $B\subset PC[J, X]$ is a bounded set, then

Lemma 2.6. ^[27] Suppose that $r\in C[J, R^{+}]$ meets

where $N_{1} > 0, N_{2}\geq 0, N_{3}\geq 0$ are constants. If one of the following conditions holds

(i) $TN_{3}(e^{T(N_{1}+TN_{2})}-1) < N_{1}+TN_{2},$

(ii) $T(2N_{1}+TN_{2}+TN_{3}) < 2,$

then $r(t)\equiv 0$, $t\in J.$

Lemma 2.7. (Mönch fixed point theorem) ^[7] We assume that $X$ is a Banach space, $\Omega \subset X$ is open and bounded, $\theta\in\Omega,$ and $Q:\overline{\Omega} \rightarrow \overline{\Omega}$ is a continuous operator and meets the following condition:

(i) $u\neq\lambda Qu, 0\leq\lambda \leq 1, u\in\partial\Omega;$

(ii) If $W\subset \overline{\Omega}$ is countable and $W\subset\overline{co}(\{\theta\}\cup Q(W))$, then $W$ is relatively compact.

Thus, $Q$ exists at least a fixed point on $\Omega.$

Definition 2.4. $u\in PC[J, X]$ is called a mild solution of $(1.1)$ if $u(t)$ satisfies equations:

3.   Main results

We first give the following hypotheses.

(H$_{1}$) $f:J\times T_{R}^{3}\rightarrow X$ is uniformly continuous and bounded, where $T_{R} = \{u\in PC[J, X] : \| u\|_{PC} \leq R\}$.

(H$_{2}$) There exist $p(t, \cdot), q(t, \cdot)\in L[J, R^{+}],$ such that

(H$_{3}$) There exist $b_{1}\in L[J, R^{+}], b_{2}, b_{3}\in L^{2}[J, R^{+}]$ satisfying

(H$_{4}$) Suppose $l_{i}\in C[J\times X, X], g_{1}\in C[PC[J, X], X].$ For $u\in PC[J, X],$ there are nonnegative constants $d\geq 0, e\geq 0$ such that

(H$_{5}$) There exist nonnegative constants $L_{h}, L_{g}, L_{l_{i}}(i = 1, 2, ..., n)$ such that for any bounded subset $B\subset X,$ we have

(H$_{6}$) There exist constants $L_{k}\geq 0(k = 1, 2, 3)$ satisfying one of the following conditions:

$(i)$$TM^{*}(2(L_{1}+L_{l_{i}})+TL_{h}L_{2}+TL_{g}L_{3}) < 2,$

$(ii)$$TL_{g}L_{3}(e^{TM^{*}(L_{1}+L_{l_{i}}+TL_{2}L_h)}-1) < (L_{1}+L_{l_{i}})+TL_{2}L_h,$

and for any bounded subset $S_{k}\subset X(k = 1, 2, 3)$, we have

(H$_{7}$) There exists a constant $L_{g_{1}} > 0$ such that for any bounded subset $B\subset PC[J, X],$ we obtain

(H$_{8}$) There exist constants $Y_{k}\geq 0(k = 1, 2, 3)$ meeting conditions $(i)$ or $(ii)$:

(i) $TL_{g}Y_{3}(e^{TM^{*}(Y_{1}+L_{l_{i}}+L_{g_{1}}+TY_{2}L_h)}-1) < (Y_{1}+L_{l_{i}}+L_{g_{1}})+TY_{2}L_h,$

(ii) $TM^{*}(2(Y_{1}+L_{l_{i}}+L_{g_{1}})+TL_{h}Y_{2}+TL_{g}Y_{3}) < 2,$

and for any bounded subset $S_{k}\subset X(k = 1, 2, 3)$,

Theorem 3.1. We assume that conditions $(H_{1})-(H_{6})$ are fulfilled, and $g_{1}$ is compact, then the problem $(1.1)$ exists at least one mild solution.

Proof. We initially define the operator $Q:PC[J, X]\rightarrow PC[J, X]$ by

The fixed point of operator $Q$ in $PC[J, X]$ is a solution of problem $(1.1)$. Next, we will prove that operator $Q$ has a fixed point in $PC[J, X]$.

As $f$ is uniformly continuous, $g_{1}, l_{i}$ are continuous, and $U_{\beta}(t, s)$ is strongly continuous, we can get that $Q$ is continuous.

Next, we prove that $\Omega_{0} = \{u\in PC[J, X]|u = \lambda Qu, \lambda\in[0, 1]\}$ is bounded. In fact, if $y_{0}\in \Omega_{0},$ then there exists $0\leq\lambda_{0}\leq 1$ satisfying $y_{0}(t) = \lambda_{0}(Qy_{0})(t), t\in J.$

When $t\in [0, t_{1}],$ we have

Let $y(t) = \parallel y_{0}(t) \parallel.$ By $(H_{2})-(H_{4})$ and (3.2), we get

where $M^{*} = \max_{0\leq s\leq t\leq a}\parallel U_{\beta}(t, s)\parallel.$

Since

similarly, we can get $\parallel H_{2}y_{0}(t)\parallel \leq t_{1}g_{0}y(s)+t_{1}e_{g},$ then

where

Therefore $F: C[J_{0}, R^{+}]\rightarrow C[J_{0}, R^{+}]$ is completely continuous.

As $b_{2}, b_{3}, b_{4}\in L^{2}[J, R^{+}],$ then

Next, we will demonstrate $r_{\sigma}(F) = 0.$ Because

for any $n\in N,$ by mathematical induction, we can obtain

then

There is a nonnegative constant $C_{1}\geq 0$ independent of function $u$ satisfying

Since $l_{1}$ is continuous, there is a nonnegative constant $\beta_{1}\geq 0$ satisfying

Let

then $z_{0}\in C[[t_{1}, t_{2}], X]$ and

Similar to the method from the previous step, we get that there exists $C_{2} \geq 0$ satisfying

therefore,

Likewise, we obtain that there exist $C_{n+1} \geq 0$ satisfying

Let

then

Hence

so $\Omega_{0}$ is bounded.

We take a constant $R$ satisfying $R > C$ and $\Omega = \{u\in PC[J, X]| \|u\|_{PC}\leq R \},$ then $\Omega$ is bounded and open. When $u\in \partial\Omega, 0\leq \lambda \leq 1,$ we obtain

We suppose that $W\subset \overline{\Omega}$ is a countable set and $W\subset\overline{co}(\{\theta\}\cup Q(W)), \; \theta \in \Omega,$ then $W$ is relatively compact.

In fact, as $U_{\beta}(t, s)$ is strong continuity, by the assumption $(H_{1})$, we obtain that $Q(W)$ is equi-continuous on $J_{i}(i = 0, 1, ...n)$, then $W$ is equi-continuous on $J_{i}. \; \forall u\in T_{R}, u_{1}, u_{2}\in[0, t_{1}].$

Case 1: $\forall t\in J_{0} = [0, t_{1}].$ Since $g_{1}$ is compact, by the assumption $(H_{6})$ and Lemma 2.1, we obtain

because

then

Similarly, we can obtain

hence

By assumption $(H_{6})$ and Lemma 2.6, we get $\alpha(W(t)) = 0, t\in J_{0} = [0, t_{1}],$ and especially $\alpha(W(t_{1})) = 0,$ then $W$ is relatively compact on $C[J_{0}, X]$.

Case 2: $\forall t\in (t_{1}, s_{1}].$ We obtain

By the assumption $(H_{6})$ and Lemma 2.6, we have $\alpha(W(t)) = 0, t\in (t_{1}, s_{1}].$

Case 3: $\forall t\in (s_{1}, t_{2}].$ We obtain

since

Thus

By $(H_{6})$ and Lemma 2.6, we get $\alpha(W(t)) = 0, t\in (s_{1}, t_{2}],$ then $\alpha(W(t)) = 0, t\in J_{1} = (t_{1}, t_{2}],$ especially $\alpha(W(t_{2})) = 0;$ then $W$ is relatively compact on $C[J_{1}, X]$.

Similarly, we can prove that $W$ is relatively compact on $C[J_{i}, X](i = 2, 3, ..., n)$, so $W$ is relatively compact on $C[J, X].$

By Lemma 2.7, $Q$ exists a fixed point, thus problem (1.1) exists a solution $u^{*} \in PC[J, X].$

Theorem 3.2. We suppose that $(H_{1}-H_{5}), (H_{7}), (H_{8})$ are fulfilled, then problem $(1.1)$ exists at least a mild solution.

Proof. By Theorem 3.1, we obtain that $\Omega_{0} = \{u\in PC[J, X]|u = \lambda Qu, \lambda\in[0, 1] \}$ is bounded. $\forall t\in J_{0},$ by $(H_{8}).$ We obtain

since

then

By assumption $(H_{8})$ and Lemma 2.6, we get $\alpha(W(t)) = 0, t\in J_{0} = [0, t_{1}],$ especially $\alpha(W(t_{1})) = 0,$ then $W$ is relatively compact on $C[J_{0}, X]$. $\forall t\in J_{1} = (t_{1}, s_{1}],$

by assumption $(H_{8})$ and Lemma 2.6, we get $\alpha(W(t)) = 0, t\in (t_{1}, s_{1}].$

$\forall t\in (s_{1}, t_{2}],$ resembling Theorem 3.1. We obtain

By $(H_{8})$ and Lemma 2.6, we get $\alpha(W(t)) = 0, t\in (s_{1}, t_{2}];$ hence, $\alpha(W(t)) = 0, t\in J_{1} = (t_{1}, t_{2}],$ especially $\alpha(W(t_{2})) = 0,$ then $W$ is relatively compact on $C[J_{1}, X]$.

Similarly, we obtain that $W$ is relatively compact on $C[J_{i}, X], (i = 2, 3, ..., n)$, then $W$ is relatively compact on $C[J, X].$ By Lemma 2.7, $Q$ exists a fixed point; therefore, problem (1.1) exists a solution.

Remark 3.1. When $L_{4} = 0,$ the condition (ii) in assumption $(H_{6})$ is clearly valid. In this situation, the assumption $(H_{6})$ can be removed.

4.   Example

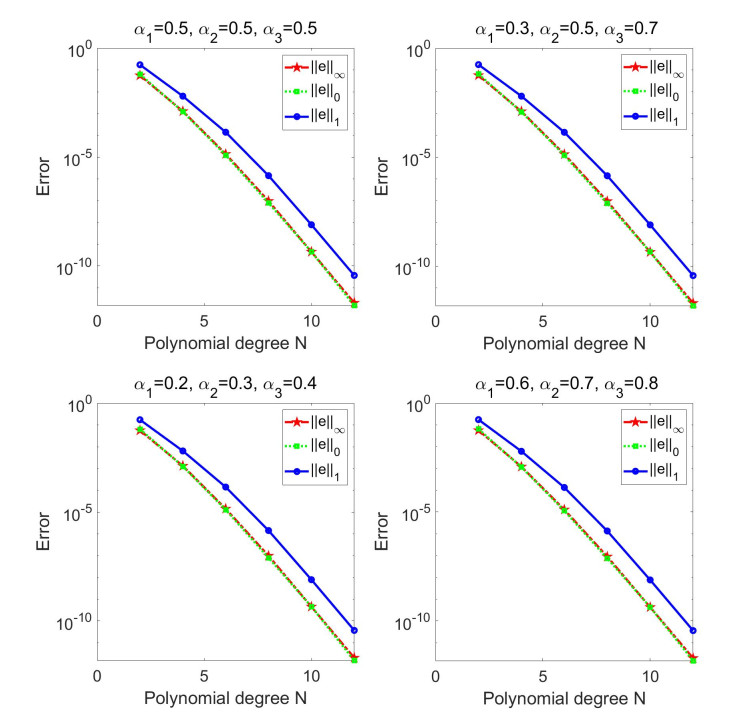
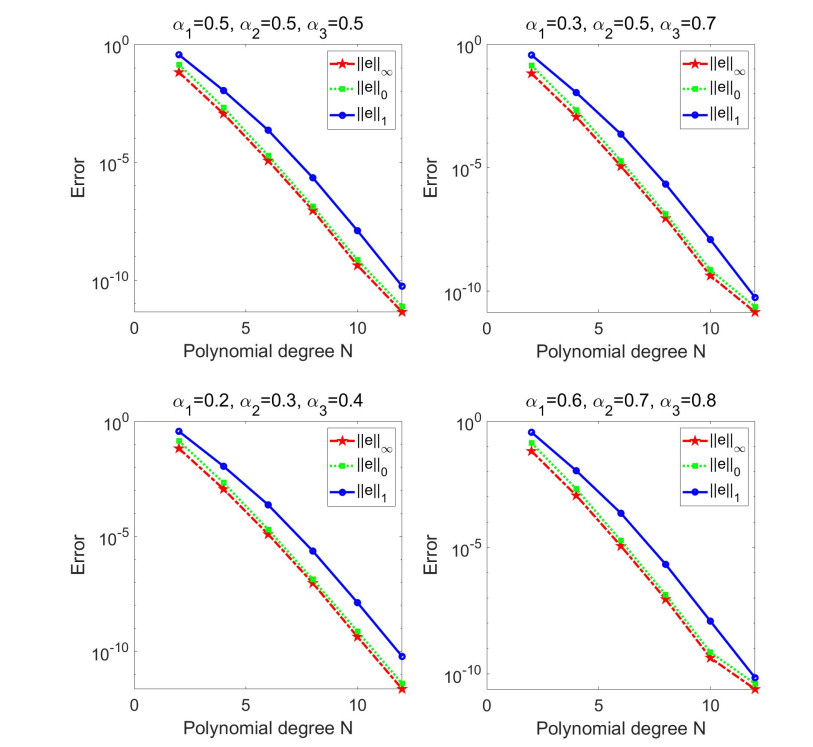
We study the following problem:

Define

then Eq (4.1) can be transformed into the following form:

For any $x_{k}, y_{k}\in X(k = 1, 2, 3, 4), t\in[0, 1]$, we obtain

If other assumptions of Theorem 3.1 are fulfilled, then system (4.1) exists a mild solution.

5.   Conclusions

The literatures ^[15,17] studied the problem of non-instantaneous impulses of integer order. In process of proving the theorem, the author used the Lipschitz condition and required the compression coefficient to be less than 1. By employing the non-compact measure, the method of stepwise estimation, and the Mönch fixed point theorem, we eliminated the need for the Lipschitz condition and the requirement of a compressibility coefficient less than 1. The literature ^[18] studied the problem of non-instantaneous impulses of fractional order. They gave the mild solutions via the Banach contraction mapping principle without the condition of compressibility coefficient less than 1, but did not consider the impulses and nonlocal conditions. Through the use of the $\beta$-order solution operator, the Mönch fixed point theorem, and the method of stepwise estimation, we eliminated the Lipschitz condition and the requirement of the compressibility coefficient less than 1. This work discusses the existence of mild solutions, with our future focus directed toward investigating the stability outcomes of fractional non-instantaneous impulse integro-differential equations.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This research was funded by the Project of Shandong Province Teaching Reform(M2021049).

Conflict of interest

The authors declare there is no conflicts of interest.