Mathematical analysis and numerical simulations of the piecewise dynamics model of Malaria transmission: A case study in Yemen

1.   Introduction

Malaria, caused by the Plasmodium parasite and transmitted through infected mosquitoes, is a significant global health concern ^[1]. The parasite enters the bloodstream, multiplying and infecting red blood cells, resulting in symptoms like high fever, chills, and fatigue. Severe cases can lead to organ failure and even death, particularly in vulnerable populations. Certain groups, such as those with HIV/AIDS, young children, and pregnant women, are more susceptible ^[2,3]. While Malaria predominantly affects rural areas, urban residents benefit from improved housing and healthcare services ^[4,5]. Prevention and control strategies include raising awareness about the disease and promoting preventive measures like bed nets and insecticides ^[6]. Public health campaigns play a crucial role in educating communities and encouraging proactive measures. Eliminating mosquito breeding sites and promoting environmental control further reduce transmission. Addressing misconceptions and promoting behavior change are essential aspects of effective awareness campaigns. By empowering individuals with knowledge, these efforts contribute to reducing the disease burden, improving health outcomes, and saving lives ^[7,8].

Fractional calculus, a branch of mathematics ^[9,10], focuses on derivatives and integrals of non-integer orders. This mathematical framework has gained considerable interest among researchers due to its ability to model real-world phenomena that integer-order calculus cannot accurately describe. Through the exploration of various fractional derivatives and integral operators, researchers aim to enhance their understanding of complex systems and phenomena in real-world scenarios. This approach enables more comprehensive and accurate mathematical modeling techniques.

Recent studies in fractional calculus have made significant contributions to the field. Caputo and Fabrizio introduced a new fractional derivative with an exponential kernel, expanding the possibilities for modeling phenomena with specific characteristics ^[11]. Atangana and Baleanu extended fractional derivatives by considering Mittag-Leffler kernels and higher orders, broadening the understanding of fractional calculus ^[12]. Adel et al. studied the Caputo-Fabrizio fractional COVID-19 model, providing valuable insights into the virus's multidimensional nature ^[13]. El-Mesady et al. ^[14] investigated monkeypox spread using a Caputo fractional order epidemic model, considering population interaction and control signals. Elsonbaty et al. ^[15] analyzed lumpy skin disease dynamics using a discrete fractional model, discussing equilibrium points and stability. Wenjie Li et al. ^[16] examined avian influenza transmission dynamics using a degenerate diffusion system, establishing the global stability of the disease-free equilibrium. Furthermore, the dynamics of malicious signal transmission in wireless sensor networks were studied, analyzing local stability and optimal control ^[17].

A novel technique involving piecewise differential and integral operators has been developed by Atangana-Seda for the Caputo-Fabrizio fractional derivative ^[18]. This technique offers a fresh approach to modeling some real-world problems and provides additional tools for researchers to analyze and solve complex problems ^{[19,20,21,22,23,24,25]}.

In the last few years, some researchers studied the behavior and properties of the mathematical models of Malaria and provided important which offer more nuanced and comprehensive insights into the multidimensional nature of the virus's behavior. For example, Sinan et al. ^[26] studied theoretical properties such as existence, uniqueness, and Ulam-Hyers stability for the Malaria model with the Atangana-Baleanu fractional derivative. Rezapour et al. ^[27] employed a mathematical framework to examine the impact of control factors on the fractal-fractional hybrid Mittag-Leffler model of Malaria. Abioye et al. ^[28] studied the important properties of a new mathematical model for Malaria and COVID-19 co-infection dynamics. In ^[29] the authors proposed a mathematical model to reduce Malaria by dividing the infected population into two sub-populations: unaware and aware individuals. They assumed that awareness program growth is proportional to the number of unaware individuals and that aware individuals avoid mosquito contact. Olaniyi et al. ^[30] studied a social hierarchy-structured model to understand the dynamics of Malaria transmission, and they focused on utilizing mathematical techniques to investigate the intricate relationships between social hierarchy and the spread of Malaria. Basir and Abraha ^[31] studied the behavior and some properties of the mathematical model and optimal control of Malaria using Awareness-Based interventions. Muhammad et al. ^[32] studied the existence, uniqueness, and numerical algorithm of the Malaria transmission model under piecewise derivatives with both kernels. They discuss the stability result for the proposed model using Ulam-Hyers stability. The models mentioned above have successfully investigated the qualitative aspects of Malaria, but the issue of crossover behaviors associated with the disease remains unexplored by researchers thus far.

In this work, we investigate the dynamics of Malaria transmission within a social hierarchy structure, conduct a comprehensive theoretical analysis, and explore the crossover effect within the Malaria model by dividing the study interval into two subintervals. In the first subinterval, we employ classical derivatives to examine the qualitative properties of the Malaria model, while in the second subinterval, we utilize the Caputo-Fabrizio fractional differential operator to gain insights into the interaction and influence of different scales on the overall behavior of the Malaria model.

The advantages of using piecewise Caputo-Fabrizio derivatives in mathematical models are their ability to analyze systems with multi-scale dynamics and capture different temporal scales within a single model. This enables a comprehensive understanding of system behavior across various time domains. Incorporating these derivatives provides enhanced capabilities for analyzing and predicting system behavior, leading to improved decision-making, optimization, and control in real-world applications.

The novelty and contributions of this study include:

● Integration of piecewise derivatives: The study employs piecewise derivatives in the mathematical model of Malaria, allowing for the analysis of multi-scale dynamics and the exploration of the interaction and influence of different scales on the overall behavior of the model.

● Investigation of crossover effects: The study explores the crossover effects within the Malaria model, shedding light on critical transitions and providing insights into the complex nature of the disease. This expands knowledge and understanding of Malaria dynamics.

● Empirical analysis of real-world data: The study incorporates an analysis of statistical data on Malaria cases diagnosed and confirmed by a laboratory in Yemen, providing valuable insights into the practical implications of the model in a real-world context.

● Comprehensive theoretical analysis: The study conducts a thorough theoretical analysis of the model, including identifying an invariant region, studying solution positivity, equilibrium points, and the basic reproduction number. This contributes to a deeper understanding of the behavior and properties of the Malaria model within a social hierarchy structure.

● Fractional-order system analysis: The study extends the analysis to fractional calculus, examining the fractional-order system. This demonstrates the existence, uniqueness, and stability of solutions, providing insights into the system dynamics at finer temporal scales.

● Numerical solutions and graphical representations: The study presents numerical solutions and graphical representations of the piecewise fractional-order model, enhancing the understanding of the model's behavior and facilitating result interpretation.

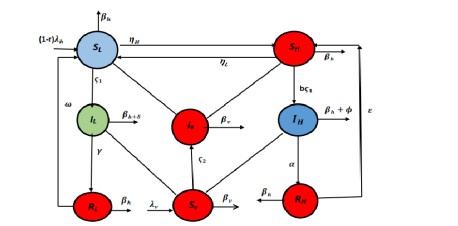
Our paper is structured as follows: In Section 2, we describe the mathematical model of Malaria within the framework of piecewise derivatives. In section 3, we analyze the collected statistical data on total cases of Malaria that were diagnosed and confirmed by the laboratory in Yemen. In section 4, we present the behavior and properties of the model such as the identification of an invariant region and the positivity of solutions as well as equilibrium point and basic reproduction number. The basic definitions and results that will be necessary for later discussions are present in section 5. Moving on to Section 6, we analyze the fractional-order system, demonstrating the existence and uniqueness of the solution as well as stability analysis. Section 7 presents the numerical solutions of the piecewise fractional-order model. Section 8 focuses on providing graphical representations of the Malaria model. Finally, we conclude the paper with some concluding remarks. Here, we aim to generalize the Malaria model studied by ^[30] within the framework of piecewise derivatives. By incorporating evolutionary dynamics and examining the various dynamics between humans and mosquito populations within each social class, our study will provide a comprehensive understanding of Malaria transmission dynamics. This knowledge will inform the development of effective interventions and policies to control and mitigate the impact of Malaria, ultimately aiming to reduce the disease burden and improve public health outcomes. Our model can be expressed as follows:

with the initial conditions $\mathcal{S}_{L}(0), \mathcal{S}_{H}(0), \mathcal{I }_{L}(0), \mathcal{I}_{H}(0)\mathcal{R}_{L}(0), \mathcal{R}_{H}(0), \mathcal{S} _{v}(0), \mathcal{I}_{v}(0) > 0.$ The schematic diagram of our proposed model is given in Figure 1.

To investigate the crossover effect within the Malaria model, we divide the interval of study $\left[0, T\right]$ into two subintervals $\left[0, \tau _{1}\right]$ and $\left[\tau _{1}, T\right]$ and consider that $_{0}^{PCF} \mathbf{D}_{\tau }^{\varrho }$ represents the classical derivative on $\tau \in \left[0, \tau _{1}\right]$ and Caputo–Fabrizio fractional derivative on $\tau \in \left[\tau _{1}, T\right]$. Thus, the restructuring of the model (1.1) as the following:

where

and

The model (1.1) includes a unique feature and distinguishing factors when compared to existing models discussed in the current literature. The model (1.1) is a social hierarchy-structured system that aims to examine the influence of social hierarchy on the dynamics of Malaria disease within populations of humans and mosquitoes. The total human population in the model (1.1) is stratified into two main social classes: low and high. This stratification reflects the division of individuals based on their socioeconomic status, with the low social class representing individuals with lower socioeconomic backgrounds and high social class representing those with higher socioeconomic backgrounds. Due to differences in social and economic factors between social classes (Low and High), such as access to health care, housing conditions, and preventive measures that may affect the extent of susceptibility to Malaria infection, we divided the study population $\mathcal{P}(\tau)$ in the model (1.1) at time $\tau$ into two classes as follows:

● Total human population $\mathcal{P}_{h}(\tau)\ $which divided into three classes as follows

- susceptible humans which are divided into two classes as follows

* Low social-class $\mathcal{S}_{L}(\tau).$

* High social-class $\mathcal{S}_{H}(\tau).$

- infectious humans which are divided into two classes as follows

* Low social-class $\mathcal{I}_{L}(\tau).$

* High social-class $\mathcal{I}_{H}(\tau)$

- recovered humans which are divided into two classes as follows

* Low social-class $\mathcal{R}_{L}(\tau).$

* High social-class $\mathcal{R}_{H}(\tau).$

● Total mosquito population $\mathcal{P}_{v}(\tau)\ $which divided into two classes as follows

- Susceptible mosquitoes $\mathcal{S}_{v}(\tau).$

- Infectious mosquitoes $\mathcal{I}_{v}(\tau).$

Hence, $\mathcal{P}_{h}(\tau) = \mathcal{S}_{L}(\tau)+\mathcal{I}_{L}(\tau)+ \mathcal{R}_{L}(\tau)+\mathcal{S}_{H}(\tau)+\mathcal{I}_{H}(\tau)+ \mathcal{R}_{H}(\tau)$ and $\mathcal{P}_{v}(\tau) = \mathcal{S}_{v}(\tau)+ \mathcal{I}_{v}(\tau).$ The model assumes that a portion $r$ of the recruitment rate $\lambda _{h}$ corresponds to the susceptible individuals from the higher social class. These individuals have unrestricted access to medical resources but are still susceptible to infection. On the other hand, the remaining fraction, $1-r$, represents susceptible individuals from the lower social class who face limited or no access to resources, making them highly vulnerable to Malaria disease. When these susceptible lower social class individuals come into contact with infectious mosquitoes, they transition to the infectious state with a transmission probability $\varsigma _{1}$. Lower-class individuals who become infected transition to the infectious state and subsequently recover at a rate $\gamma$. Once they have recovered, these lower-class individuals can become susceptible again due to temporary immunity acquired, which occurs at a rate $\omega$. Additionally, the Malaria-induced death rate for the lower social class population is denoted by $\delta$.

On the contrary, susceptible individuals from the higher social class become infectious after effective contact occurs at a rate $b\varsigma _{1}$. Here, the modification parameter $b$ represents a reduction in the transmission of infection within the higher social class population, with $0 < b < 1$. Infectious individuals transition to the recovered state at a rate $\alpha$, and the acquired immunity gradually diminishes at a rate $\varepsilon$. For the higher social class population, the disease-induced mortality rate is denoted by $\phi$, where $\delta > \phi$. Additionally, the natural mortality rate for the human population as a whole is represented by $\beta _{h}$. Regarding the lower social class, susceptible individuals improve their status at a rate $\eta _{L}$, indicating a potential upward movement within the social hierarchy. On the other hand, susceptible individuals from the higher social class experience a decline in their social status at a rate $\eta _{H}$. Both lower and higher social class individuals in the infectious state can transmit the infection to susceptible mosquitoes with a transmission probability $\varsigma _{2}$. However, the transmission from the higher social class is subject to a reduction determined by the modification parameter $\theta$.

The model (1.1) allows for the examination of various dynamics between the human and mosquito populations within each social class. It can capture interactions such as mosquito feeding preferences, human mobility patterns, and the effectiveness of control measures in different social classes. By analyzing the impact of social hierarchy on Malaria dynamics, we can gain insight into the complex relationship between socioeconomic factors and disease transmission. This knowledge can inform the development of targeted interventions and policies to reduce Malaria burden, particularly among vulnerable populations.

2.   Statistical analysis

This section is devoted to analyzing the collected statistical data on total cases of Malaria that were diagnosed and confirmed by the laboratory in Yemen ^[33]. Also, to predict the future instances of the spread of Malaria to draw decision-makers and specialists' attention to work on monitoring and combating it. A brief discussion of the significant results obtained was presented. Now, we will introduce definitions of the statistical methods used:

ARIMA model: ARIMA stands for autoregressive integrated moving average. It is a popular and widely used time series forecasting model that incorporates autoregressive (AR), differencing (I), and moving average (MA) components. The ARIMA model is designed to capture and forecast the patterns and trends observed in time series data. The three components of the ARIMA model are the following:

$(1)$ Autoregressive (AR): This component considers the relationship between the current observation and a specified number of lagged observations (i.e., previous values in the series). It assumes that the current value of the series can be predicted based on its past values.

$(2)$ Integrated (I): This component involves differencing the series to make it stationary. Differencing is the process of computing the differences between consecutive observations in the time series. It helps remove trends and seasonality from the data, making it suitable for modeling with AR and MA components.

$(3)$ Moving Average (MA): This component considers the dependency between the current observation and a residual error term based on a moving average of the lagged forecast errors. It helps capture the short-term fluctuations and noise in the data.

The ARIMA model is typically denoted as ARIMA ($p, d, q$), where $p$ represents the order of the autoregressive component, $d$ represents the order of differencing required to make the series stationary, and $q$ represents the order of the moving average component.

In the context of time series analysis, estimating coefficients refers to the process of determining the values of the parameters in a given model. Two commonly used techniques for estimating coefficients are:

Autocorrelation Function (ACF): The ACF is a statistical tool used to assess the correlation between a time series and its lagged values. It measures the linear relationship between a time series observation and its past observations at different lags. By examining the ACF plot, one can identify the significant lags and infer the appropriate order of the autoregressive or moving average components in a model.

Partial Autocorrelation Function (PACF): The PACF measures the correlation between an observation and its lagged values while controlling for the influence of intermediate lags. It helps identify the direct relationship between an observation and its specific lagged values, excluding the influence of other lags. The PACF plot displays the partial correlation coefficients at different lags.

Estimating coefficients, whether through ACF or PACF involves finding the parameter values that best fit the observed data. This estimation process is crucial for accurately modeling and forecasting time series data and is typically performed using statistical techniques such as maximum likelihood estimation (MLE) or least squares estimation (LSE).

2.1.   Significance of the statistical methods used

The usefulness of the methods used to predict the behavior of cases for different phenomena over time to develop a system capable of predicting cases that will occur in the future. The models used in predicting the future must be understandable and straightforward to be implemented by decision-makers efficiently ^[34,35]. By fitting an ARIMA model to historical time series data, one can estimate the model parameters and use the model to make future predictions or forecast future values of the series. The ARIMA model is widely used in various fields, including finance, economics, and climate science, for analyzing and predicting time series data. Statistical modelling plays a crucial role in the field of epidemiology, serving as a potent tool for examining the dynamics of Malaria disease and forecasting potential future trends. The utilization of the ARIMA model is particularly significant in predicting the occurrence of Malaria, as it leverages historical data to generate forecast future patterns ^[36]. This predictive capability holds immense importance in public health planning, enabling authorities to anticipate the likely occurrence of new cases. Consequently, it facilitates timely interventions and the provision of healthcare services.

2.2.   Descriptive data

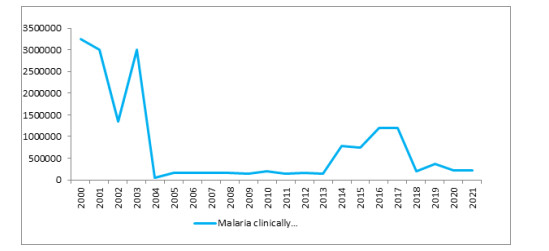
Table 1 displays the total diagnosed and laboratory-confirmed Malaria cases, which were collected from epidemiological surveillance data issued by the Central Bureau of Statistics. It is noted that the fluctuation in the total cases examined by the laboratory increased and decreased. We find a decrease in the total cases from 3246504 cases in 2000 to 51992 cases in 2004, with a relative decline (98.4%). After that, the number of Malaria cases increased during the period (2005–2010), reaching 1988963 cases in 2010, then decreased cases during the period (2011–2015), and then rose again for the two years (2016 and 2017). After that, it decreased continuously during the period (2018–2021), as the year 2021 reached 212132 cases. We find that the total number of people infected with Malaria decreased from 3246504 in 2000 to 212132 cases in 2021, with 93% during the entire period (2000–2021). The graphical representation of this trend can be observed in Figure 2.

2.3.   Forecasts and data analysis

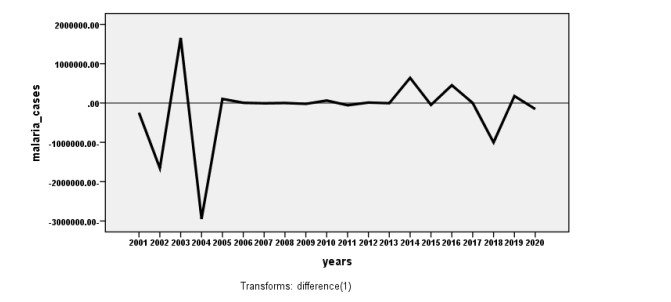
The main purpose and benefit of time series models are to use them in the estimation process of the variables' behavior and various phenomena and their future trends in epidemiology, diseases, economics, management, climate sciences, and other sciences. Recently, mathematical and statistical modeling has been used to predict the behavior and trends of some diseases and epidemics ^[37]. These models include four basic procedures for the prediction process: determining the model, followed by estimation of unknown parameters, then the diagnostic process and the last stage is the prediction process ^[38]. The models (MA, AR, ARMA, ARIMA) are within the time series models most used for forecasting ^[39]. The data collected about the total Malaria cases from 2000 to 2020 were investigated. The assumptions and tests for the stability of these data were examined to be used in the prediction process. Estimating coefficients (APCF & ACF) and unit root testing Augmented, Dickey-Fuller & Phillips-Perron showed that the time series is unstable, which means that the general trend exists, as shown in Figure 2. After taking the first differences shown in Figure 3, as for the unit root test, the calculated values are more significant than the critical values for all confidence levels shown in Table 2.

The probabilistic values (Prob. = 0.0000) are less than 5%. Therefore, the null hypothesis can be rejected, which states that the time series has a unit root; the alternative hypothesis was accepted that the time series does not have a unit root. Therefore the time series of Malaria cases is stable after taking the first differences. Furthermore, we examined the autocorrelation and partial autocorrelation functions, and the following models can be proposed for prediction: ARIMA(1, 1, 1), ARIMA(1, 1, 0), ARIMA(0, 1, 1), and ARIMA(4, 1, 1). All coefficients of the proposed models have been estimated using the method of ordinary least squares (OLS). The ARIMA (1, 1, 0) model which is considered the best was selected according to specific criteria, including that the model's coefficients are statistically significant, and the coefficient of determination is greater than the rest of the models. It achieves the slightest variance, less volatility, and the lowest value of the indicator AIC, as shown in Table 3.

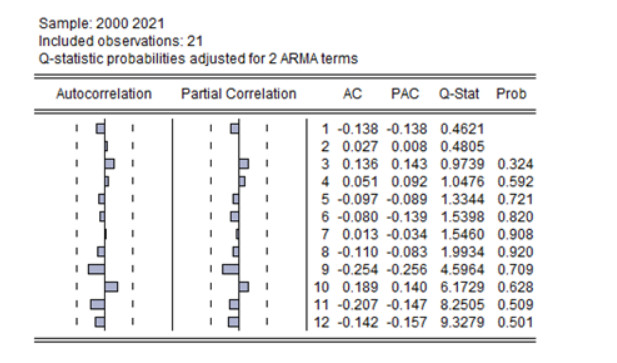
In addition, we examined the best model through the residual test to determine the extent to which the original observations match the estimated values from the candidate model and the validity of the model's hypotheses. The strength of the appropriateness of the selected statistical model was also verified through residual randomness, the shape of the autocorrelation, and partial autocorrelation functions. Figure 4 shows no autocorrelation between errors. That is, autocorrelation and partial autocorrelation are within confidence limits, and it can be said that the residuals are white noise.

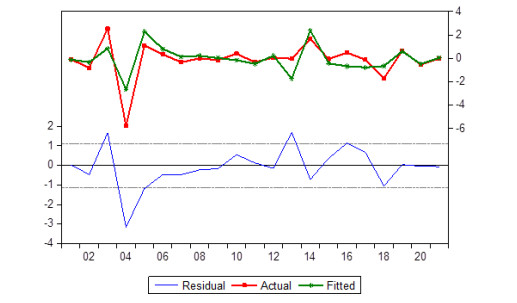
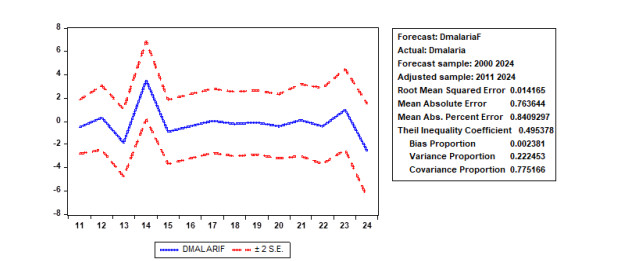
The estimated and the actual values were verified by drawing them together as shown in Figure 5, which shows the closeness of the estimated values to the actual values as well as to the quality of the model. The selected and problem-free ARIMA (1, 1, 0) model was applied to predict the behavior and future trends of the total Malaria cases of infected persons. A decrease in Malaria cases in Yemen was observed in the future, as shown in Figure 6.

3.   Fundamental characteristics of the model (1.1)

The fundamental characteristics of the Malaria model (1.1), which incorporates social hierarchy and tracks the interactions between humans and mosquito populations are established based on the following outcomes: the identification of an invariant region and the positivity of solutions. These results provide essential insights into the behavior and properties of the model.

3.1.   Non-negativity and boundedness of the solutions

In this section, we discuss the effects of awareness on the transmission dynamics of Malaria, represented by $\mathcal{S}_{L}, \mathcal{I}_{L}, \mathcal{R}_{L}, \mathcal{S}_{H}, \mathcal{I}_{H}, \mathcal{R}_{H}$, $\mathcal{S} _{v}, \mathcal{I}_{v}$ that will be analyzed within a biologically and mathematically feasible region such that this region should be suitable for the habitation of both human and mosquito populations. In the following theorems, we demonstrate the boundedness and positivity of solutions for the piecewise fractional model (1.1) within a viable region $\Omega = \Omega _{h}\times \Omega _{V}\subset \mathbb{R} _{+}^{6}\times \mathbb{R} _{+}^{2},$ where

and

Theorem 3.1. The region $\Omega$ is positively invariant with respect to the piecewise fractional model (1.1)$.$

Proof. First, at the time $\tau,$ the piecewise derivative of the total human population is

where

Clearly,

From (3.1), we have

By definition 4.1, the inequality (3.2), can be rewritten in two cases as follows:

Case (1): For $\tau \in \left[0, \tau _{1}\right]$, we have

Thus,

Consequently, $\mathcal{P}_{h}(\tau)$ is bounded by $\frac{\lambda _{h}}{ \beta _{h}}.$

Case (2): For $\tau \in \left[\tau _{1}, T\right]$, we have

Apply the Laplace transform on both sides of (3.3), we obtain

Further simplification yields

where $\mathcal{P}_{h}(s) = \mathcal{L}\left[\mathcal{P}_{h}(\tau)\right] \left(s\right)$ and $\mathcal{P}_{h}(0)$ is $\mathcal{P}_{h}$ at $\tau = 0.$ Thus,

Applying the inverse Laplace transformation yields

where $\mathcal{M = -}\frac{\beta _{h}\varrho }{\left(1+\beta _{h}-\beta _{h}\varrho \right) }$ and $\mathbb{E}_{\alpha, \varsigma }$ is the Mittag-Leffler function with two parameters $\alpha, \varsigma > 0.$ We utilize the asymptotic behavior of the Mittag-Leffler function in the inequality(3.4). As $\tau \rightarrow \infty,$ we conclude that $\mathcal{P}_{h}(\tau)\leq \frac{\lambda _{h}}{\beta _{h}}.$ Consequently, $\mathcal{P}_{h}(\tau)$ is bounded by $\frac{\lambda _{h}}{\beta _{h}}.$

From the above cases, we conclude that $\mathcal{P}_{h}(\tau)$ is bounded by $\frac{\lambda _{h}}{\beta _{h}}$ within the region $\Omega _{h}$. In the same manner, we can prove that the $\mathcal{P}_{v}(\tau)$ is bounded within the region $\Omega _{V}.$ As a result, the solution trajectory of the model (1.1) is bounded within region $\Omega$, demonstrating the positive invariance of the region $\Omega$. □

Theorem 3.2. Under the assumption of the specified set of non-negative initial conditions, the solutions of the model (1.1) are positive.

Proof. Let us examine the first equation of model (1.1), which can be expressed as follows

Then, we have

By definition 4.1, the inequality (3.5), can be rewritten in two cases as follows

Case (1): For $\tau \in \left[0, \tau _{1}\right]$, we have

which on integration gives

This proves the positivity of solution $\mathcal{S}_{L}(\tau)$ in case $\tau \in \left[0, \tau _{1}\right].$

Case (2): For $\tau \in \left[\tau _{1}, T\right]$, we have

Since all solutions are bounded. Let the solution $\mathcal{I}_{v}$ is bounded by $\wp.$ Then, we get

where $\ell = \sup \left\{ \varsigma _{1}\wp +\beta _{h}+\eta _{L}\right\}.$ By applying the Laplace transform to both sides of equation (3.6), we obtain

Thus, we get

Applying the inverse Laplace transformation, we have

Since $\mathcal{S}_{L}(0) > 0$ and $0\leq \mathbb{E}_{1, 1}\leq 1,$ we conclude that $\mathcal{S}_{L}(\tau)$ is positive solution in case $\tau \in \left[ \tau _{1}, T\right].$ Thus, by above cases we conclude that $\mathcal{S} _{L}(\tau)$ is positive solution for $\tau \in \left[0, T\right].$ By same techniques, we can prove that solutions of the model (1.1) are positive. □

3.2.   Equilibrium point and basic reproduction number

The equilibrium points help characterize the stable states of disease dynamics, while the basic reproduction number provides a measure of the disease's transmission potential. Both concepts are essential for understanding and managing infectious diseases, enabling informed decision-making in public health interventions and control strategies ^[40]. The disease-free equilibrium point of model (1.1) obtained by putting

In view of the above equations, the disease-free equilibrium point of model (1.1) is given as

To compute the value of $R_{0}$ using the next-generation matrix method, let $\mathbb{Y} = \left(\mathcal{I}_{L}, \mathcal{I}_{H}, \mathcal{I}_{v}\right) ^{T}$ be the infected compartments

Then, the above model can be written as $_{0}^{PCF}\mathbf{D}_{\tau }^{\varrho }\mathbb{Y\left(\tau \right) = }\mathcal{F}\left(\tau \right) - \mathcal{V}\left(\tau \right),$ where

The expressions $\mathcal{F}\left(x\right)$ and $\mathcal{V}\left(x\right)$ represents the rate of new infection appearance in the population and the rate of individuals' transfer within the infectious classes, respectively. The Jacobian matrices $F$ and $V$, corresponding to $\mathcal{F }\left(x\right)$ and $\mathcal{V}\left(x\right)$ respectively, can be expressed as follows

Therefore, using the fact that $R_{0} = \rho \left(FV^{-1}\right)$, we obtain the basic reproduction number $R_{0}$ for the model (1.1)

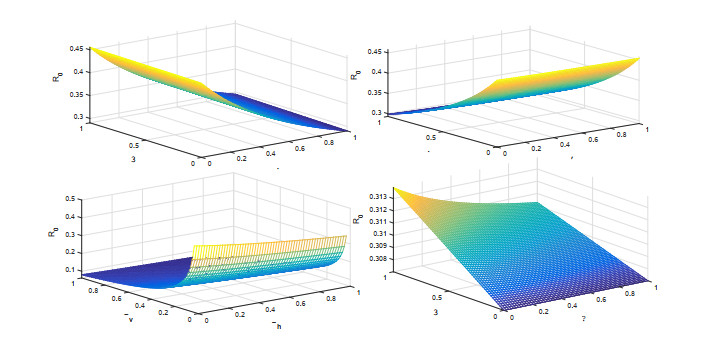
The Eq (3.7) defines the basic reproduction number $R_{0}$, which quantifies the number of secondary Malaria cases generated by a single infectious individual, regardless of their social class or mosquito category, within populations where all individuals are susceptible to the disease. By examining the parameters associated with $R_{0}$, as defined in Eq (3.7), we can analyze their impacts and gain insights into intervention strategies needed to control and prevent Malaria transmission within a population structured by social hierarchy. Here in Figure 7, we describe 3D profile against various parameters of the basic reproductive number computed in (3.7).

3.3.   Stability analysis

Stability analysis in the Ulam sense plays a vital role in understanding and managing dengue transmission. It facilitates epidemic control, prediction of outbreaks, development of optimal control strategies, robustness assessment, and model validation. By studying the stability properties of the dengue model, we gain valuable insights into the behavior of the disease and can make informed decisions to prevent and control its spread. Before giving the fundamental theorem of stability, we restructure the model (1.1) as a compact initial value problem as follows:

where $\mathbb{Y}(\tau), \mathbb{Y}(0)$ and $\mathbb{F}\left(\tau, \mathbb{Y }(\tau)\right)$ are defined in (1.3) and (1.4). The system (3.8) can be converted into the following fractional form (see ^[18])

Definition 3.3. The piecewise fractional model (1.1) of Malaria is Ulam-Hyers stable if there is a constant number $\mathfrak{M} > 0$ such that, for each $\varepsilon = \max \left(\varepsilon _{1}, \varepsilon _{2}, \varepsilon _{3}, \varepsilon _{4}, \varepsilon _{5}, \varepsilon _{6}, \varepsilon _{7}, \varepsilon _{8}\right) > 0$ and for each $\widetilde{ \mathbb{Y}}\in \mathcal{E}$ of the inequality

there is $\mathbb{Y}\in \mathcal{E}$ satisfying piecewise CF-fractional-order model (1.1) of Malaria with

Remark 3.4. $\widetilde{\mathbb{Y}}\in \mathcal{E}$ is a solution of the inequality

if and only if there exists a small perturbation $Z\in \mathcal{E}$ such that for each $\tau \in \mathcal{J},$ $\left\vert Z(\tau)\right\vert \leq \varepsilon,$ we have

where

Lemma 3.5. Let $\varrho > 0.$ For every $\varepsilon > 0$. Suppose that $\widetilde{\mathbb{Y}}\in \mathcal{E}$ satisfies (3.9). Then, $\widetilde{\mathbb{Y}}$ satisfies the following integral inequalities

and

Proof. Since $\widetilde{\mathbb{Y}}$ satisfies (3.9), then by Remark 3.4, we have

It follows that

Then, we estimate

and

Thus

and

□

Theorem 3.6. Assume that for any $\mathbb{Y}_{1}, \mathbb{Y}_{2}\in \mathcal{E}$ and $\tau \in \mathcal{J},$ there exists constant number $\psi > 0$ such that

If

then the piecewise fractional model (1.1) of Malaria will be UH stable.

Proof. Let $\varepsilon > 0\ $ and $\widetilde{\mathbb{Y}}\in \mathcal{E}$ be satisfying (3.9) and let $\mathbb{Y}\in \mathcal{E}$ be the unique solution of piecewise fractional model (1.1) of Malaria. It implies that

Thus

and

Hence, from (3.10) and Lemma 3.5, we have two cases as follows:

Case (1): $\tau \in \left[0, \tau _{1}\right].$ The equation (3.11) becomes

which implies

Case (2): $\tau \in \left[\tau _{1}, T\right].$ The equation (3.12) becomes

which implies

From (3.13) and (3.14), we get

where

Hence, the piecewise fractional model (1.1) of Malaria is UH stable. □

4.   Existence and uniqueness of model (1.1)

In this part, we address the existence and uniqueness of the solution for piecewise fractional model (1.1) of Malaria by utilizing the fixed point technique. We present some definitions and basic auxiliary results of piecewise derivative and integral with classical and Caputo-Fabrizio that are required throughout our paper. Let $\mathcal{J = }\left[0, \tau \right] \subset \mathbb{R} ^{+},$ we define the Banach space $\mathcal{E} = C\left(\mathcal{J}, \mathbb{R} ^{+}\right) \times C\left(\mathcal{J}, \mathbb{R} ^{+}\right) \times C\left(\mathcal{J}, \mathbb{R} ^{+}\right) \times C\left(\mathcal{J}, \mathbb{R} ^{+}\right) \times C\left(\mathcal{J}, \mathbb{R} ^{+}\right) \times C\left(\mathcal{J}, \mathbb{R} ^{+}\right) \times C\left(\mathcal{J}, \mathbb{R} ^{+}\right) \times C\left(\mathcal{J}, \mathbb{R} ^{+}\right)$ under the norm

where $\mathcal{S}_{L}, \mathcal{S}_{H}, \mathcal{I}_{L}, \mathcal{I}_{H}, \mathcal{R}_{L}, \mathcal{R}_{H}, \mathcal{S}_{v}, \mathcal{I}_{v}\in C\left(\mathcal{J}, \mathbb{R} ^{+}\right).$

Definition 4.1 ^[18] The piecewise derivative, incorporating both classical and Caputo-Fabrizio can be defined as follows:

where

i) $_{0}^{PCF}\mathbf{D}_{\tau }^{\varrho }\mathbb{Y}(\tau)$ represents the classical derivative on $\tau \in \left[0, \tau _{1}\right]$ and Caputo–Fabrizio fractional derivative on $\tau \in \left[\tau _{1}, T\right]$.

ii) $\frac{d}{d\tau }\mathbb{Y}(\tau)$ is the classical derivative on $\tau \in \left[0, \tau _{1}\right]$.

iii) $^{CF}\mathbf{D}_{0}^{\varrho }\mathbb{Y}(\tau)$ is the Caputo–Fabrizio fractional derivative on $\tau \in \left[\tau _{1}, T\right].$

Definition 4.2. [^[18] Definition 8] Let $f$ be continuous. A piecewise integral of $f$ with respect to $\mathbb{Y}$ is given as

where

i) $_{0}^{PCF}\mathbf{I}_{\tau }^{\varrho }$ represents classical integral on $\tau \in \left[0, \tau _{1}\right]$ and Caputo–Fabrizio fractional integral on $\tau \in \left[\tau _{1}, T\right]$.

ii) $\int_{0}^{\tau }\mathbb{Y}(s)ds$ is the classical integral on $\tau \in \left[0, \tau _{1}\right]$.

iii) $^{CF}\mathbf{I}^{\varrho }\mathbb{Y}(\tau) = \frac{1-\varrho }{\Upsilon \mathcal{(}\varrho \mathcal{)}}\mathbb{Y}(\tau)+\frac{\varrho }{\Upsilon \mathcal{(}\varrho \mathcal{)}}\int_{\tau _{1}}^{\tau }\mathbb{Y}(s)ds$ is the Caputo–Fabrizio integral on $\tau \in \left[\tau _{1}, T\right]$.

Clearly, the model (1.2) can be converted into the following fractional form (see ^[18]):

To transform the model (1.2) into the fixed point problem, we define the operator $\mathcal{Q}:\mathcal{E}\rightarrow \mathcal{E}$ by

In the following theorem, we shall apply the Schauder fixed-point theorem to prove the existence result.

Theorem 4.3. Assume that the function $\mathbb{F}:\mathcal{J}\times \mathcal{E}\rightarrow \mathbb{R}$ is continuous and there exist two constants $\mu, \hslash > 0$ such that

Then, the piecewise fractional model (1.1) of Malaria has a solution, provided that

Proof. First, we will prove that $\mathcal{Q}:\mathcal{E}\rightarrow \mathcal{E}$ defined by (4.2) is a completely continuous operator. By considering the definition of the operator $\mathcal{Q}$ and the continuity of the functions $\mathbb{F}$, we can conclude that $\mathcal{Q}$ is continuous. Let $\mathbb{Q}\subset \mathcal{E}$ be a bounded set. Then, for all $\mathbb{Y }\in \mathbb{Q}$, there exists $\Delta > 0$, such that $\left\vert \mathbb{F} \left(\tau, \mathbb{Y}(\tau)\right) \right\vert \leq \Delta, \tau \in \left[0, T\right].$Thus, for any $\mathbb{Y}\in Q,$ we have two cases as follows:

Case (1): For $\tau \in \left[0, \tau _{1}\right]$ and $\mathbb{Y}\in \mathbb{Q},$ we have

Hence, the operator $\mathcal{Q}$ is uniformly bounded for any $\tau \in \left[0, \tau _{1}\right].$

Case (2): For $\tau \in \left[\tau _{1}, T\right]$ and $\mathbb{Y}\in \mathbb{Q},$ we have

Hence, the operator $\mathcal{Q}$ is uniformly bounded for any $\tau \in \left[\varrho _{1}, T\right].$

By (4.3) and (4.4), we conclude that the operator $\mathcal{Q}$ is uniformly bounded in the interval $\left[0, T\right].$ Now, we show that $\mathcal{Q}$ is equicontinuous. We have two cases as follows:

Case (1): For $\tau \in \left[0, \tau _{1}\right], 0\leq \tau _{a} < \tau _{b}\leq \tau _{1}$ and $\mathbb{Y}\in \mathbb{Q},$ we have

It is clear that, when $\tau _{b}-\tau _{a}\rightarrow 0$, the right-hand sides of Eq (4.5) tend to zero.

Case (2): For $\tau \in \left[\tau _{1}, T\right], \tau _{1}\leq \tau _{a} < \tau _{b}\leq T$ and $\mathbb{Y}\in \mathbb{Q},$ we have

It is clear that, when $\tau _{b}-\tau _{a}\rightarrow 0$, the right-hand sides of Eq. (4.6) tend to zero. Thus, from Eqs (4.5) and (4.6), we conclude that the operator $\mathcal{Q}$ is equicontinuous and therefore it is completely continuous. Finally, we show, the following set $\mathbb{Z}$ is bounded

Case (1): For $\tau \in \left[0, \tau _{1}\right]$ and $\mathbb{Y}\in \mathbb{Z},$ we have

Consequently, for all $\tau \in \left[\tau _{1}, T\right]$, we have

Thus, the set $\mathbb{Z}$ is bounded in case $\tau \in \left[0, \tau _{1} \right].$

Case (2): For $\tau \in \left[\tau _{1}, T\right]$ and $\mathbb{Y}\in \mathbb{Z},$ we have

Consequently, for all $\tau \in \left[\tau _{1}, T\right]$, we have

Hence, from (4.8) and (4.10), we conclude that the set $\mathbb{Z}$ is bounded in the interval $\left[0, T\right].$ in view of Schauder fixed point theorem, the operator $\mathcal{Q}$ has at least one fixed point. Therefore, the piecewise fractional model (1.1) of Malaria has at least one solution. □

Theorem 4.4. Assume that the function $\mathbb{F}:\mathcal{J}\times \mathcal{E }\rightarrow \mathbb{R}$ is continuous and there exist constant $\psi > 0$ such that

If

then, the piecewise fractional model (1.1) of Malaria has unique solution.

Proof. Take the operator $\mathcal{Q}:\mathcal{E}\rightarrow \mathcal{E}$ defined by (4.2).

Case (1): For $\tau \in \left[0, \tau _{1}\right],$ $\mathbb{Y}_{1}, \mathbb{ Y}_{2}\in \Psi _{\zeta }$, we have

Thus

Case (2): For $\tau \in \left[\tau _{1}, T\right],$ $\mathbb{Y}_{1}, \mathbb{ Y}_{2}\in \Psi _{\zeta }$ with (H$_{2}$), we have

Hence

From the above cases, we get

Thus, $\mathcal{Q}$ is contraction due to (4.11). Consequently, the piecewise fractional model (1.1) of Malaria has a unique solution. □

5.   Numerical scheme with piecewise derivative

The use of numerical schemes with piecewise derivatives is important due to their ability to accurately simulate complex phenomena, improve accuracy and efficiency, offer flexibility and facilitate the development of new models and algorithms. These schemes play a crucial role in advancing scientific research, engineering design, and decision-making processes across various disciplines. This section presents the numerical resolution of the adopted fractional order model (1.1). By applying the piecewise integral, we have

and

At $\tau = \tau _{n+1}$, we write

and

By applying Newton Polynomial interpolation scheme we have

and

6.   Numerical Simulations and Discussion

We consider the initial data as

In addition, we consider the following numerical values for the parameters involved in our proposed model as described in Table 4.

● We find that the total number of people infected with Malaria decreased from 3246504 in 2000 to 212132 cases in 2021, with 93% during the entire period (2000–2021). The graphical representation of this trend can be observed in Figure 2.

● The assumptions and tests for the stability of these data were examined to be used in the prediction process. Estimating coefficients (APCF & ACF) and unit root testing Augmented, Dickey-Fuller & Phillips-Perron showed that the time series is unstable, which means that the general trend exists, as shown in Figure 2. After taking the first differences shown in Figure 3, as for the unit root test, the calculated values are more significant than the critical values for all confidence levels shown in Table 2.

● Figure 4 shows no autocorrelation between errors. That is, autocorrelation and partial autocorrelation are within confidence limits, and it can be said that the residuals are white noise.

● The selected and problem-free ARIMA (1, 1, 0) model was applied to predict the behavior and future trends of the total Malaria cases of infected persons. A decrease in Malaria cases in Yemen was observed in the future, as shown in Figure 6.

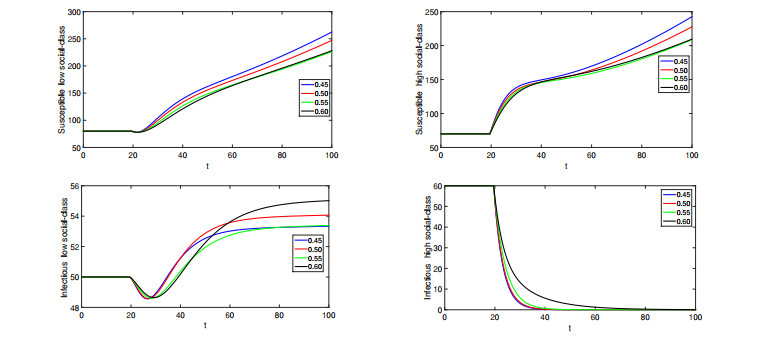
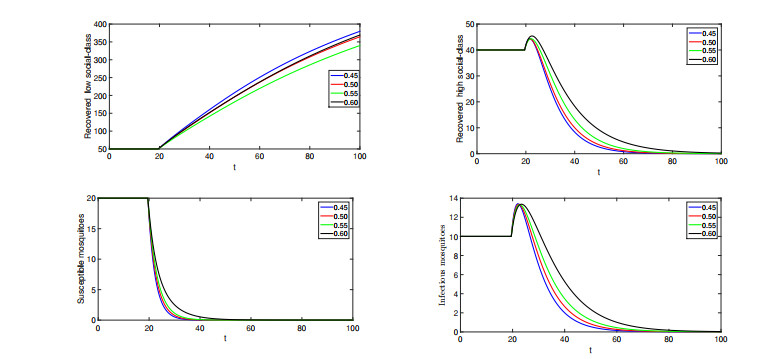
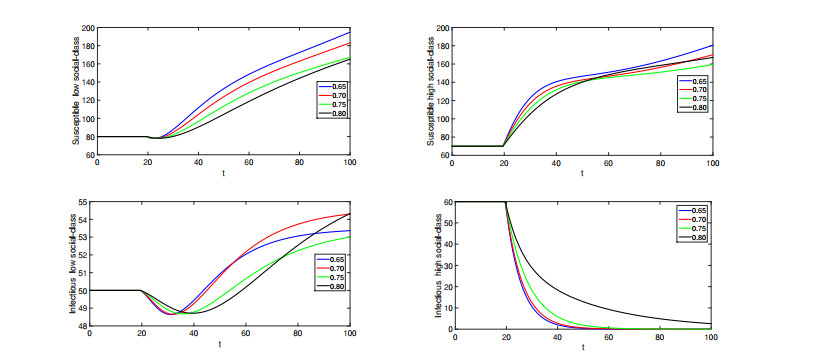
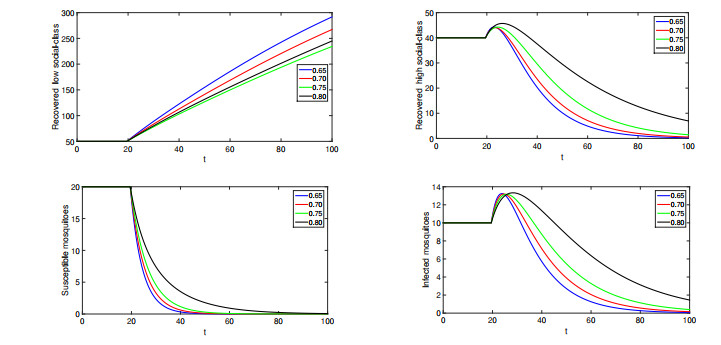
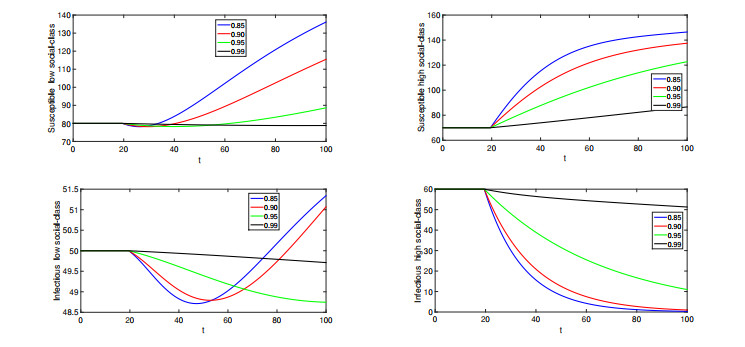
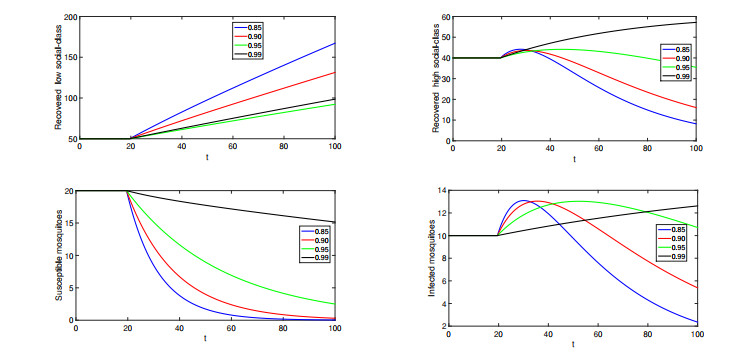
● When $\varrho \in (0, 0.60]$. We simulate the numerical solutions for different compartments using various values of fractional orders lies in $(0, 0.60]$. Here, we see that solutions show crossover behaviors.

● When $\varrho \in (0.60, 0.80]$. We have presented the approximate solutions for various values of fractional orders in $(0.60, 0.80]$.

● When $\varrho \in (0.80, 1.0]$. Again, we simulate the numerical interpretations for various compartments of the proposed model, we choose fractional orders values from $(0.80, 1.0]$. In Figures 8–13, we have presented the graphical presentation for various compartments using different fractional orders values. We have taken the domain as $[0, 40]$, and $(40, 120]$. Three sets of fractional orders have been used. The crossover dynamics in each compartment can be clearly observed.

7.   Conclusions

The piecewise derivatives with classical and Caputo-Fabrizio is a powerful tool for capturing the intricacies of functions and systems that exhibit diverse behaviors across different regions. Its inherent flexibility and versatility make it an indispensable asset in mathematical analysis and modeling, facilitating a deeper understanding of real-world phenomena.

In this study, we have investigated the dynamics of Malaria transmission within a social hierarchy structure, employing piecewise Caputo-Fabrizio derivatives of fractional orders with both non-local and singular kernels. On the other hand, we collected and analyzed statistical data on Malaria prevalence in Yemen from 2000 to 2021. By utilizing the statistical analysis program Eviews and employing ARIMA models, we present predictions for the approximate number of Malaria cases in Yemen from 2022 to 2024.

Additionally, we examined the crossover effect within the Malaria model by dividing the study interval into two subintervals. We established the existence and uniqueness of solutions for the model in both intervals by employing fixed-point techniques and functional analysis. The positivity and boundedness of the solutions are demonstrated using the fractional-order properties of the Laplace transformation.

Furthermore, we computed the basic reproduction number for the model using a next-generation technique, enabling us to handle the future dynamics of the pandemic effectively. To obtain numerical solutions for the fractional model, we employed a computationally efficient Adams-Bashforth method. These numerical results are thoroughly discussed and visually presented through graphs, providing valuable insights into the dynamic behavior of the model. The model numerical demonstrated the crossover effect in the dynamics using the time domain for transmission $[0, 200]$ near the point where $t_{1} < 100$.

The patients who have HIV/AIDS, children under five years of age, infants, and pregnant women are more susceptible to Malaria than others. Malaria affects the poor in rural areas more than urban residents due to the health services provided for urban residents. We concluded that decreasing the mobility rate among individuals from high social-class populations and increasing mobility within low social-class populations can potentially contribute to a decrease in the basic reproduction number (R0) of malaria. By reducing R0, the burden of malaria transmission within the community can be effectively reduced.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgements

This work was supported by the Deanship of Scientific Research, Vice Presidency for Graduate Studies and Scientific Research, King Faisal University, Saudi Arabia (grant no. 5423). This study is supported via funding from Prince Sattam bin Abdulaziz University, project number (PSAU/2024/R/1445). The researchers wish to extend their sincere gratitude to the Deanship of Scientific Research at the Islamic University of Madinah for the support provided to the Post-Publishing Program.

Conflict of interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.