A novel analytical treatment for the Ambartsumian delay differential equation with a variable coefficient

1.   Introduction

Malaria is a lethal infectious disease caused by Plasmodium parasites, which infects humans through the bite of infected female geneus Anopheles mosquitoes. It is endemic in about 100 countries and an estimated 3.3 billion people are at risk of being infected in the word ^[1]. Therefore, it is necessary to study the spread of malaria in the population. The pioneering work was given by Ross ^[2] which showed that malaria is transmitted by mosquitoes and proposed the first mathematical model of this disease. Subsequently, Macdonald promoted this ^[3], which plays a particularly important role in understanding the disease. However, the Ross-Macdonald model is extremely simplified, ignoring many critical factors of real-world ecology and epidemiology ^[4]. One omission is spatial heterogeneity, for example, the distribution of urban and rural areas and the spatial movement of mosquitoes and people, which increases the spatial transmission of malaria. Hence, in the malaria epidemiological model, spatial heterogeneity must be considered ^[5,6,7]. In 1951, Skellam specially examined the reaction-diffusion model of species population density in a bounded habitat ^[8]. One advantage of reaction-diffusion models is that they can easily incorporate simple rules about edge effects. Use these features of reaction-diffusion model to study how environmental heterogeneity affects malaria ^[9,10,11]. However, in these studies, it seems that the following important biological aspects are rarely paid, simultaneously.

First, "vector-bias" is a typical feature of malaria transmission, which describes the different probabilities of a mosquito bitting humans. Lacroix et al. ^[12] proved that mosquitoes are generally more inclined to bite infected individuals. To describe this preference, Chamchod and Britton incorporated the vector-bias effect into malaria model ^[13]. Subsequently, a wealth of papers take into account the effect of vector-bias when studying malaria transmission ^[14,15,16]. Due to the different densities of mosquitoes in various regions, the infectivity of malaria is also different. The analysis of vector-bias effects is of great significance for understanding the dynamics of malaria transmission.

Secondly, in recent years, climate has become more fluctuating ^[17], and the rise in temperature is related to global warming. Climate warming is directly connected with the number of Anopheles, the main vector of malaria. Because temperature affects the immature development rate, immature stage survival rate, adult size, adult lifespan, blood feeding, and reproduction ability of mosquitoes ^[18]. It is widely accepted that both the life cycle of mosquitoes and the development of parasites are extremely sensitive to temperature. Empirical evidence indicates that the life cycle of mosquitoes experiences four different stages: eggs, larvae, pupae and adults. The first three stages are also called aquatic or immature stages ^[19]. In addition, a very important process in the development of parasites is the extrinsic incubation period (EIP), i.e., mosquitoes may not be able to transmit the disease to humans for a period of time after taking infected blood meal. The lifespan of female adult mosquitoes is generally 3 to 100 days, and EIP can reach 30 days ^[20]. These infected mosquitoes that live pass EIP will keep infectious until they die. There is considerable evidence that temperature rise will shorten the length of each immature stage ^[21] and EIP is extremely sensitive to seasonal changes in temperature ^[22,23]. In view of climate change, exploring the effect of temperature in the spread of malaria is particularly essential. Therefore, these seasonal forced EIP and mosquito life cycles need to be considered in the malaria model.

Note that mathematical models of malaria transmission rarely consider key features such as vector-bias, climate/seasonality, temperature-dependent mosquito life cycle and EIP in a spatially heterogeneous environment, simultaneously. A reaction-diffusion model with periodic delays is proposed to study the influence of the above factors on the transmission of malaria. This work is inspired by the following biological questions: (I) What is the impact of vector-bias on malaria transmission? (II) What effect does the maturity and incubation period of seasonal temperature changes have on the spread of malaria? (III) Does the movement of mosquitoes and humans have different effects for the transmission of malaria in different areas? These issues that are closely related to the spread and control of malaria need to be explored in more depth. How to add the temperature-dependent maturity period to the model is the first issue we consider, and the detailed model derivation is also the difficulty of this paper. The existence of temperature-dependent periodic delays makes it difficult to understand the asymptotic behavior of the model. We consider the stage structure, because the mosquitoes in the aquatic stage cannot fly, which makes it impossible for us to directly use the theoretical results in references ^[22,24]. Our theoretical results indicate the model has a threshold parameter, the basic reproduction number $R_{0}$, which determines wether the malaria can persist or become extinct in susceptible populations.

The structure of the rest of this paper is shown below. Section 2 establishes human and mosquito populations models and malaria transmission model. This section also gives the biological significance of these parameters in models. Section 3 is devoted to well-posedness and some properties of the model. In Section 4, we first define the basic reproduction number $R_{0}$, and then analyze the threshold dynamics of models in terms of $R_{0}$. Section 5 gives the basic framework of the system threshold dynamics through numerical simulation, and discusses the influence of parameters on basic reproduction number, mosquitoes and humans in the process of malaria transmission. A brief discussion section concludes the paper.

2.   The models

2.1.   Mosquito stage structure model with seasonal effect

Motivated by models in references ^[19,25,26], we introduce a seasonal stage-structured model of malaria to explain the cross-infection between mosquitoes and individuals. In this subsection, we first consider the mosquito population. According to the biological cycle, mosquitoes can go through several stages and have different habits at various stages. We divide them into immature aquatic stage $M(t, x)$ and mature stage $V(t, x)$ at time $t\geq0$ and location $x$ in a spatial bounded domain $\Omega\in \mathbb{R}^{n}$ with smooth boundary $\partial\Omega$. Let $\eta(t, a, x)$ denote the density of the mosquito population at time $t$, chronological age $a\geq0$, and location $x$. Metz and Diekmann ^[27] gave

through the standard argument for structured populations and spatial diffusion. Here, $\Delta$ denotes the usual Laplacian operator. $\hat{\phi}(\cdot, x)$ represents the non-negative initial age and location distribution of mosquitoes, the term $\Lambda_{v}(t, x)$ is the recruitment rate of the immature stage, which is Hölder continuous and nonnegative function on $\mathbb{R}\times \bar{\Omega}$, $D(a)$ is the age-related diffusion coefficient, and $d(t, a, x)$ indicates the death rate of mosquitoes with time $t$, age $a$ and location $x$, which is Hölder continuous and positive on $\mathbb{R}\times \bar{\Omega}$. $\Lambda_{v}(t, \cdot)$ and $d(t, \cdot, \cdot)$ are periodic in $t$ and have the same period $\omega$.

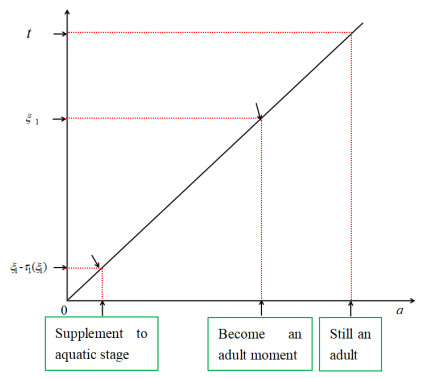
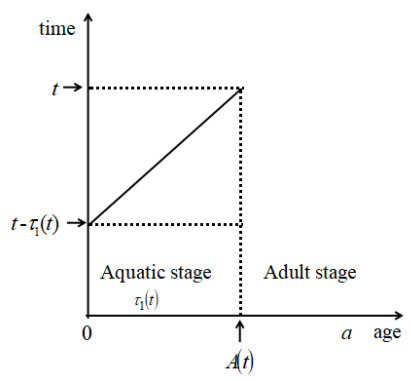
Let us first assume some age thresholds so that the growth of mosquitoes can be divided into discrete age stages. When modeling species dynamics with a stage structure, we divide mosquitoes into immature stage (also known as aquatic stage) and mature stage, the time delay is the mature period. The temperature $T(t)$ is an $\omega$-periodic function of time $t$. Generally speaking, the maturity age is determined by seasonal changes in temperature. We will use a time-dependent positive function $\tau_{1}(t)$ to describe the duration from newborn to adult. That is, an individual at time $t$ becomes mature only if its age exceeds $\tau_{1}(t)$, in other words, the adult mosquitoes that develop at time $t$ enter the aquatic stage at $t-\tau_{1}(t)$. We assume that the maximum chronological age of aquatic mosquitoes at time $t$ is $A(t)$. Here and in the following, $\tau_{1}(t)$ and $A(t)$ are $C^{1}$ (a section of continuous differentiable functions) periodic functions of time $t$ with the same periodic $\omega$. The relationship between time-dependent threshold age and time-dependent delay can be indicated as follows:

Here we introduce another quantity $f$ to describe the maturity level of mosquitoes. Let $f = f_{M} = 0$, that is, the maturity level of mosquitoes that have just entered the aquatic stage is $0$. At time $t$, the mosquitoes reach the maximum chronological age $A(t)$ of the aquatic stage. At this time, the maturity level is also the maximum, $f_{V}$. Then one has

where $\hat{\rho}(r_{1})$ is the proportion of maturity at time $r_{1}$. Taking the derivative of the above formula with respect to $t$, we can get

and hence $1-\tau^{\prime}_{1}(t) > 0$. Recall that $\tau_{1}(t)$ represents the time it takes for a mosquito to go from the aquatic stage to the adult stage at time $t$. For the case where $\delta > 0$ is small enough, if the mosquito is an adult mosquito at time $t$, then it is still an adult mosquito at time $t+\delta$. Thus $\tau_{1}(t+\delta) < \tau_{1}(t)+\delta$, and hence, $\tau^{\prime}_{1}(t) = \lim\limits_{\delta\rightarrow 0}\frac{\tau_{1}(t+\delta)-\tau_{1}(t)}{\delta} \leq 1$. This condition also makes sense biologically. $1-\tau^{\prime}_{1}(t) > 0$, is called maturation rate ^[26], which excludes the possibility of mosquitoes returning from the mature stage to the immature stage unless they are born. Mathematically speaking, $t-\tau_{1}(t)$ is strictly increased with respect to $t$, that is, since the developmental rate depends only on time, it is impossible for juveniles to reach maturity before they are born.

$M(t, x)$ and $V(t, x)$ denote the density of mosquitoes in the aquatic and mature stages at time $t$ and location $x$, respectively. The accumulative density between the two age thresholds can be recorded as the population size at each stage. In particular, for the aquatic stage $M$ and the mature stage $V$ (for the sake of simplicity, we use $M$ and $V$ instead of $M(t, x)$ and $V(t, x)$, respectively), we have the following mathematical expressions:

Next, we put forward natural biological assumptions about birth rate, death rate and diffusion coefficient in Eq (2.1). Since immature mosquitoes cannot fly, we assume that the diffusion coefficient satisfies

At each age stage, all mosquitoes undergo the same birth rate and death rate which are age-independent, then the natural death rates in the aquatic and mature stages are $\mu_{m}(t, x)$ and $\mu_{v}(t, x)$, respectively, i.e.,

where $\mu_{m}(t, x)$ and $\mu_{v}(t, x)$ are non-negative non-trivial and Hölder continuous on $\mathbb{R}\times \bar{\Omega}$ and $\omega$-periodic in $t$. Differentiating the equations in system (2.2) with respect to time $t$ on both sides yields

and

In a biological sense, because no mosquito can live forever, $\eta(t, \infty, x) = 0$. $\eta(t, 0, x)$ represents the inflow rate of mosquitoes in the aquatic stage at time $t$, then $\eta(t, 0, x) = \Lambda_{v}(t, x)$ is a function of $t$.

Mathematically, assume that the delay $\tau_{1}(t)$ is continuously differentiable in $[0, \infty)$, bounded and far away from zero and infinity. The expression of $\eta(t, A(t), x)$ in the above system will be obtained by integrating along characteristics. For $t\geq A(t)$ and $t < A(t)$, $\eta(t, A(t), x)$ has different expressions. Without loss of generality, we study $t \geq A(t)$ (see, ^[28]), which is practicable due to the boundedness of $A(t)$, because we are concerned with long-term behavior of population dynamics. Here, $\eta(t-\tau_{1}(t), 0, \cdot) = \Lambda_{v}(t-\tau_{1}(t), \cdot)$. Let $t = t_{0}+h$, $a = a_{0}+h$, $P(h, x) = \eta(t_{0}+h, a_{0}+h, x)$ and $\hat{d}(h, x) = d(t_{0}+h, a_{0}+h, x)$, then

Integrating Eq (2.3) from $h_{1}$ to $h_{2}$ yields

For $t\geq A(t)$, setting $t_{0} = t-A(t)$, $h = A(t)$ and $a_{0} = 0$, we have

Since we are concerned about the long-term behavior of population dynamics, the model for $t\geq A(t)$ is as follows

where $\nu$ is the outward unit normal vector on $\partial\Omega$ and $\frac{\partial}{\partial \nu}$ indicates the normal derivative along $\nu$ on $\partial\Omega$, $e^{-\int_{t-\tau_{1}(t)}^{t}\mu_{m}(r_{2}, x) {\rm{d}}r_{2}}$ represents probability surviving through natural death during aquatic stage. It is easy to see that the equation $V(t, x)$ is decoupled, so we can get the following system

for any $t\geq A(t)$. Alternatively, according to biological significance, $M$ and $V$ can be written as integral form. Note that $\tau_{1}(t)$ is the maturation time of aquatic mosquitoes at time $t$. Thence, aquatic mosquitoes at time $t$ contain all newly born mosquitoes at a previous time $\xi_{1}$ with $\xi_{1}\in(t-\tau_{1}(t), t)$ and survive to time $t$. Hence, one has

Similarly, for any $x\in \bar{\Omega}$,

where $V(0, \cdot)$ is the initial data of $V(t, \cdot)$.

The first term in Eq (2.7) represents those mosquitoes that were adults at time $0$ at position $y$ and are still in $V$ class at time $t$ at position $x$ by diffusion. The second term in Eq (2.7) denotes the total density of mosquitoes at time $t$. These mosquitoes were newly developed adults at time $\xi_{1}$ and survived until time $t$. These new adults developed from the aquatic stage at previous time $\xi_{1}-\tau_{1}(\xi_{1})$, which grown through $\tau_{1}(\xi_{1})$ periodic of time and developed into adult stage at time $\xi_{1}$ with "maturation rate" $1-\tau^{\prime}_{1}(\xi_{1})$. $\Gamma (t, t_{0}, x, y)$ with $t\geq t_{0}\geq 0$ is the Green function related to $\frac{\partial V}{\partial t} = D_{v}\Delta V-\mu_{v}(t, x)V$ that meets the Neumann boundary condition.

2.2.   The human population dynamics model

Since the incubation period of the pathogen in the human is 1–12 days, which is short compared with the human life span, we do not consider the incubation period of the pathogen in the human body. In this subsection, inspired by ^{[13,19,20,24,29]}, we give a model of malaria transmission, including the mobility of mosquitoes and individuals, vector-bias, temperature-dependent maturation delay and EIP. Because mosquitoes are the vectors of malaria transmission from person to person, the modeling takes into account the dynamics of human and mosquito populations. One supposes that individuals will become susceptible again after recovery. Thus, humans include two epidemiological types: susceptible $(S_{h})$ and infected $(I_{h})$ compartments. Assume that all populations walk unbiased and random. Since climate change has almost no impact on human birth and death, according to ^[29], the following reaction-diffusion equation is suitable:

$D_{h} > 0$ is the human diffusion coefficient. Suppose the dispersal pattern is random diffusion, that is, individual walkers use a fixed step to walk randomly on the solid line ^[30,31]. $\Lambda_{h}(x)$ and $\mu_{h}(x)$ are the recruitment rate and natural death rate of human at location $x$, respectively. In particular, we should note that the disease dose not have a significant impact on the mobility of individuals and mosquitoes. It is mathematically assumed that the diffusion coefficient $D_{h} > 0$ of all individuals is the same, and the diffusion coefficient $D_{v} > 0$ of all mosquitoes is recognized as the same. Assuming that no population flow crosses the boundary $\partial\Omega$, therefore, the Neumann boundary condition is imposed:

here, the definition of $\nu$ is same as Section 2.1. Following Theorems 3.1.5 and 3.1.6 in reference ^[32] and Section 2 in reference ^[29], we realize that the positive steady state $N(x)\in C\left(\bar{\Omega}, \mathbb{R}_{+}\right)\backslash \{0\}$ of systems (2.8) and (2.9) is globally attractive, where $C\left(\bar{\Omega}, \mathbb{R}_{+}\right)$ is Banach space of continuous functions from $\bar{\Omega}$ to $\mathbb{R}_{+}$. According to Appendix 8.1 in reference ^[33], it is assumed that the total human density of at time $t$ and location $x$ is stable at $N(x)$, i.e., $N_{h}(t, x)\equiv N(x)$, for $\forall t\geq 0$ and $x\in \Omega$. Then we know that $S_{h} = N(x)-I_{h}$. Here and later, for the sake of simplicity, we use $S_{h}$ and $I_{h}$ instead of $S_{h}(t, x)$ and $I_{h}(t, x)$, respectively.

From a biological and epidemiological point of view, immature mosquitoes do not take part in infection, and are primarily in a waiting period, because they cannot fly and bite humans. Since adult male mosquitoes do not eat blood meal, they cannot transmit and acquire the virus, so only adult female mosquitoes are modeled. Mature female mosquitoes are divided into susceptible ($S_{v}(t, x)$), exposed ($E_{v}(t, x)$) and infectious ($E_{v}(t, x)$), $t$ is time and $x$ denotes location. The exposed mosquitoes are already infected, but not infectious. From Section 2.1, we know that $V = S_{v}+E_{v}+I_{v}$ is the total density of female adult mosquitoes and satisfies reaction-diffusion system (2.5). Here and later, for the sake of simplicity, we use $V$, $S_{v}$, $E_{v}$ and $I_{v}$ instead of $V(t, x)$, $S_{v}(t, x)$, $E_{v}(t, x)$ and $I_{v}(t, x)$, respectively.

Vector-bias effect is a situation in which mosquitoes display the weight of preference when choosing a host. In order to add a vector-bias term to the model, parameters $p$ and $l$ are introduced, which are the probability of mosquitoes arriving at humans randomly, and select infectious and susceptible humans, respectively ^[13]. Since mosquitoes are more attracted to infected humans, we assume that the vector-bias parameter $\chi = \frac{p}{l}\geq 1$. To comprehend the influences of spatial structure and climate change, we allow a space-dependent bite rate $\beta(t, x)$ of female mosquitoes to be Hölder continuous non-negative non-trivial on $\mathbb{R}\times \bar{\Omega}$ with $\beta(t, x)\not\equiv 0$, representing the number of mosquitoes biting per unit time at location $x$, and $\beta(t, \cdot)$ is a $\omega$-period function of time $t$. Let $B$ represent the mosquitoes bite incident, and $A$ be the event of mosquitoes reaching humans infected with malaria. Then $P(A) = \frac{I_{h}}{N(x)}$, $P(A^{c}) = 1-\frac{I_{h}}{N(x)}$, $P(B|A) = p$ and $P(B|A^{c}) = l$. So the probability that an infectious human is chosen as $P(A|B)$,

then one has

which are the probability of infected individuals and susceptible individuals are bitten. Then at time $t$ and location $x$, the numbers of newly infected individuals and mosquitoes per unit time are

respectively, where $c$ is the probability that an infected mosquito will spread to susceptible individuals per bite, and $\alpha$ is probability that an infected individual will transmission to susceptible mosquitoes per bite.

During the malaria transmission cycle, the EIP of parasite in mosquitoes is one of the most pivotal parameters. Mosquitoes can fly around during EIP. The malaria parasites undergo different growth stages before migrating to the salivary glands where can spread to humans. The degree of this development is related to environmental factors, such as temperature. EIP is exceedingly sensitive to temperature. Therefore, it is necessary to incorporate this seasonal forced incubation period when describing malaria transmission. We will use a time-dependent positive function $\tau_{2}(t)$ to describe the duration from new infection to infectiousness. That is, a mosquito is infectious at time $t$ only if its age of infection exceeds $\tau_{2}(t)$, where $\tau_{2}(t)$ is a $C^{1}$ periodic function in $[0, \infty)$ with the periodic $\omega$, and $t-\tau_{2}(t)$ is strictly increasing in $t$.

Based on the above discussions, we will pay attention to the dynamics of the following malaria transmission reaction-diffusion model

for $t > 0$. Similar to the derivation in Section 2.1, we get

Substituting $E_{m}(t, x)$ into system (2.10), one has

for $t > 0,$ where $\alpha$, $p$, $l$ and $c$ are positive constants, and $\varrho(x)$ denotes the recovery rate of humans in position $x$, which is Hölder continuous and positive on $\Omega$. Neumann boundary condition indicates that all individuals and mosquitoes still remain in this domain $\Omega$.

Since $M(t, x)$ and $E_{v}(t, x)$ of the system (2.11) are decoupled from the other equations, it is sufficient to explore the system

for $t > 0$, where $(u_{1}, u_{2}, u_{3}) = (S_{v}, I_{v}, I_{h})$.

3.   Well-posedness

In this section, the well-posedness of the model is proved. Let $\mathbb{X}_{1}: = C\left(\bar{\Omega}, \mathbb{R}^{3}\right)$ be the Banach space of continuous functions from $\bar{\Omega}$ to $\mathbb{R}^{3}$ the supremum norm be $\|\cdot\|_{\mathbb{X}}$, and $\mathbb{X}_{1}^{+}: = C\left(\bar{\Omega}, \mathbb{R}_{+}^{3}\right)$. Let $\hat{\tau}_{1}: = \max\limits _{t \in[0, \omega]}\tau_{1}(t)$, $\hat{\tau}_{2}: = \max\limits _{t \in[0, \omega]}\tau_{2}(t)$, and $\hat{\tau}: = \max\left\{\hat{\tau}_{1}, \hat{\tau}_{2}\right\}$. Define $\mathcal{X}_{1}: = C([-\hat{\tau}, 0], \mathbb{X}_{1})$ to be a Banach space, with the norm $\|\phi\| = \max\limits_{\theta\in[-\hat{\tau}, 0]}\|\phi(\theta)\|_{\mathbb{X}_{1}}$, $\forall \phi\in \mathcal{X}_{1}$, and $\mathcal{X}_{1}^{+}: = C([-\hat{\tau}, 0], \mathbb{X}_{1}^{+})$. Then $(\mathbb{X}_{1}, \mathbb{X}_{1}^{+})$ and $(\mathcal{X}_{1}, \mathcal{X}_{1}^{+})$ are order Banach spaces. A function $z:[-\hat{\tau}, \sigma)\rightarrow \mathbb{X}_{1}$ for $\sigma > 0$ is given and $z_{t}\in \mathcal{X}_{1}$ is defined by

for any $t\in[0, \sigma)$.

Denote $\mathbb{Y}: = C\left(\bar{\Omega}, \mathbb{R}\right)$, $\mathbb{Y}^{+}: = C\left(\bar{\Omega}, \mathbb{R}_{+}\right)$, $\mathbb{Y}_{h}: = \{\varphi \in \mathbb{Y}^{+}:0\leq \varphi(x)\leq N(x), \forall x\in \bar{\Omega}\}$. Suppose that $T_{1}(t, s), T_{2}(t, s): \mathbb{Y}\rightarrow \mathbb{Y}$, are the evolution operators associated

and

obey the Neumann boundary condition, respectively. Since $T_{i}(t, s) = T_{i}(t-s)$ $(i = 1, 2)$ and $\mu_{v}(t, \cdot)$ is $\omega$-periodic in $t$, = [34,Lemma 6.1] indicates that $T_{i}(t+\omega, s+\omega) = T_{i}(t, s)$ for $(t, s)\in \mathbb{R}^{2}$ with $t\geq s$. Furthermore, $T_{i}(t, s)$ is compact and strongly positive [35,Section 7.1 and Corollary 7.2.3] for $(t, s)\in \mathbb{R}^{2}$ with $t > s$ $(i = 1, 2)$. Let $T(t, s) = {\rm{diag}}\{T_{1}(t, s), T_{1}(t, s), T_{2}(t, s)\}: \mathbb{X}_{1}\rightarrow \mathbb{X}_{1}$, $t\geq s$, is a strongly continuous semigroup and $A(t) = {\rm{diag}}\{A_{1}(t), A_{1}(t), A_{2}\}$, defined on $D(A(t)) = D(A_{1}(t))\times D(A_{1}(t))\times D(A_{2})$. $A_{1}(t)$ is defined by

and $A_{2}$ is defined by

Set

Write $F = (F_{1}, F_{2}, F_{3}):[0, \infty)\times W_{h}\rightarrow \mathbb{X}_{1}$ as

for $t\geq 0$, $x\in\bar{\Omega}$ and $\phi = (\phi_{1}, \phi_{2}, \phi_{3})\in W_{h}$. Rewrite system (2.12) as

it then follows from references [36,Corollary 4 and Theorem 1] and [37,Corollary 8.1.3] that for any $\phi \in W_{h}$, a mild solution can be get as a continuous solution of the integral equation:

Lemma 3.1. For any $\phi\in W_{h}$, system (2.12) has the unique solution, denoted by $z(t, \cdot, \phi)$ on its maximal existence interval $[0, t_{\phi})$ with $z_{0} = \phi$, where $t_{\phi}\leq \infty$.Moreover, $z(t, \cdot, \phi)\in \mathbb{Y}^{+}\times\mathbb{Y}^{+}\times\mathbb{Y}_{h}$ for any $t\in [0, t_{\phi})$, andthis solution is a classical solution of system (2.12) for all $t > \hat{\tau}$.

Before studying the global existence, go back to system (2.11) to make more information. We impose the compatibility conditions based on the biological meaning of $\tau_{1}(t)$ and $\tau_{2}(t)$:

and

Now we define

Next, for any $\psi\in \mathcal{D}$, system (2.11) has the unique solution $U(t, \cdot) = (M(t, \cdot), S_{v}(t, \cdot), E_{v}(t, \cdot), I_{v}(t, \cdot), I_{h}(t, \cdot))$ satisfying $U_{0} = \psi$. Corollary 4 in reference ^[36] implies that $S_{v}(t, x)\geq 0$, $I_{v}(t, x)\geq 0$ and $I_{h}(t, x)\geq 0$ on maximal existence interval. According to the uniqueness of the solutions and the compatibility conditions (3.4) and (3.5), one has $M(t, \cdot)$ (see(2.6)) and

Hence, $M(t, x)\geq 0$ and $E_{v}(t, x)\geq 0$ on the maximal interval of existence.

Lemma 3.2. For any $\phi\in W_{h}$, system (2.12)has a unique solution $u(t, \cdot, \phi)$ on $[0, \infty)$ with $u_{0} = \phi$.Moreover, system (2.12) generates an $\omega$-periodic semiflow$Q_{t}:W_{h}\rightarrow W_{h}$, defined by $Q_{t}: = u_{t}(\cdot)$, $\forall t\geq 0$, i.e., $Q_{t}(\phi)(s, x) = u(t+s, x, \phi)$, $\forall\phi\in W_{h}$, $t\geq 0$, $s\in [-\hat{\tau}, 0]$, $x\in \Omega$, and $Q: = Q_{\omega}$ has a strong global attractor in $W_{h}$.

The proof of Lemma 3.2 is given in Appendix A.

4.   Threshold dynamics

Here, the basic reproduction number are introduced by the theory in reference ^[41], and then investigate the dynamics of system (2.12).

4.1.   Threshold dynamics

The current main work is to explore the extinction and persistence of malaria in a spatially heterogeneous environment. The basic reproduction number $R_{0}$ is one of the most necessary concepts in epidemiology. It is usually defined as the mean number of secondary infections during the entire period when a typical infected person is introduced into a completely susceptible population. From a biological point of view, the basic reproduction number is a characteristic of the risk of infection. More meaningfully, it describes the threshold behavior of many infectious disease models.

Let $u_{2} = u_{3} = 0$, we have the equation of mosquitoes compartment

obeys the Neumann boundary condition. Based on reference [38,Lemma 2.1], it is easy to know that system (4.1) has a unique globally attractive positive $\omega$-periodic solution $u_{1}^{*}(t, \cdot)$ in $\mathbb{Y}^{+}\backslash \{0\}$. Linearize system (2.12) at $(u_{1}^{*}(t, \cdot), 0, 0)$ and consider the equations of infectious compartments,

for $t > 0$. Denote $w: = (w_{1}, w_{2}) = (u_{2}, u_{3})$.

Set $\mathbb{X}_{2}: = C\left(\bar{\Omega}, \mathbb{R}^{2}\right)$, $\mathbb{X}_{2}^{+}: = C\left(\bar{\Omega}, \mathbb{R}_{+}^{2}\right)$, and $C_{\omega}(\mathbb{R}, \mathbb{X}_{2})$ to be the Banach space consisting of all $\omega$-periodic and continuous functions from $\mathbb{R}$ to $\mathbb{X}_{2}$, where $\|\psi\|_{C_{\omega}(\mathbb{R}, \mathbb{X}_{2})}: = \max\limits_{\theta\in[0, \omega]}\|\psi(\theta)\|_{\mathbb{X}_{2}}$ for any $\psi\in C_{\omega}(\mathbb{R}, \mathbb{X}_{2})$. Let $\mathcal{X}_{2}: = C([-\hat{\tau}_{2}, 0], \mathbb{X}_{2})$ and $\mathcal{X}_{2}^{+}: = C([-\hat{\tau}_{2}, 0], \mathbb{X}_{2}^{+})$. Write $\mathcal{F}(t):\mathcal{X}_{2} \rightarrow \mathbb{X}_{2}$ as

for any $t\in \mathbb{R}$, $\tilde{\psi} = \left(\tilde{\psi}_{1}, \tilde{\psi}_{2}\right)\in \mathcal{X}_{2}$ and $-V_{1}(t)w = \bar{D}\Delta w-W(t)w$, where $\bar{D} = {\rm{diag}}(D_{v}, D_{h})$ and

Denote that $\Phi(t, s) = {\rm{diag}}(T_{1}(t, s), T_{2}(t, s))$ is an evolution operator related to the following system

$t\geq s$, with the Neumann boundary condition. Obviously, $\Phi(t, s)$ is a positive operator, that is, $\Phi(t, s)\mathbb{X}_{2}^{+}\subseteq \mathbb{X}_{2}^{+}$ for all $t\geq s$. Then $-V_{1}(t)$ is resolvent positive, based on reference [39,Theorem 3.12].

The exponential growth bound of $\Phi(t, s)$ can be written as

By [39,Proposition A.2], one has

According to Krein-Rutman theorem and [40,Lemma 14.2], one has

here, $r(\Phi(\omega, 0))$ denotes the spectral radius of $\Phi(\omega, 0)$. By [39,Proposition 5.6] with $s = 0$, we obtain $\bar{\omega}(\Phi) < 0$. Obviously, $\mathcal{F}(t)$ and $W(t)$ meet the assumptions: (1) $\mathcal{F}(t): \mathcal{X}_{2} \rightarrow \mathbb{X}_{2}$ is positive, i.e., $\mathcal{F}(t)\mathcal{X}_{2}^{+}\subseteq\mathbb{X}_{2}^{+}$, for any $t\geq 0$. (2) $-W(t)$ is cooperative, and $\bar{\omega}(\Phi) < 0$.

To introduce $R_{0}$ of system (2.12) based on references ^[41] and ^[42], it is assumed that both human and mosquito populations are close to $(u_{1}^{*}(t, \cdot), 0, 0)$. Suppose $w\in C_{\omega}(\mathbb{R}, \mathbb{X}_{2})$, and $w(t) = w(t)$ is the initial distribution of infected mosquitoes and humans at $t\in\mathbb{R}$. For any fixed $s\geq 0$, the distribution of newly infected mosquitoes and individuals at time $t-s$ $(t\geq s)$ is $\mathcal{F}(t-s)w_{t-s}$, which is engendered by the infectious mosquitoes and humans introduced in $[t-s-\hat{\tau}_{2}, t-s]$. Thus, the distribution of infectious who were newly infected at time $t-s$ and keep survive at time $t$, is $\Phi(t, t-s)\mathcal{F}(t-s)w_{t-s}$, $t\geq s$. Then, at time $t$, the distribution of the accumulative infectious humans and mosquitoes produced by all people introduced to $t$ at all previous times is

Define the next generation operator $L$ associated with system (2.12) as

Inspired by the definition of next generation operators in references ^[39,42], the basic reproduction number of system (2.12) is defined by the spectral radius $L$, i.e.,

For any $\tilde{\psi} \in \mathcal{X}_{2}$, set $\bar{Q}_{t}$ to be solution map of system (4.2) on $\mathcal{X}_{2}$, i.e., $\bar{Q}_{t}(\tilde{\psi}) = w_{t}(\tilde{\psi})$, $t\geq 0$, where $w_{t}(\tilde{\psi})(\theta)(x) = w(t+\theta, x, \tilde{\psi}) = (w_{1}(t+\theta, x, \tilde{\psi}), w_{2}(t+\theta, x, \tilde{\psi}))$, and $w(t, x, \tilde{\psi})$ is the unique solution of system (4.2) with $w(\theta, x) = \tilde{\psi}(\theta, x)$ for all $\theta\in[-\hat{\tau}_{2}, 0]$, $x\in \bar{\Omega}$. Thus $\bar{Q}: = \bar{Q}_{\omega}$ is the Poincaré map related to system (4.2). $r(\bar{Q})$ represents the spectral radius of $\bar{Q}$. Based on reference [41,Theorem 3.7], the following result can be obtained.

Lemma 4.1. $R_{0}-1$ has the same sign as $r(\bar{Q})-1$.

To explore the global dynamic behaviors of system (2.12) according to $R_{0}$, we demonstrate that system (4.2) engenders an eventually strong monotone periodic semiflow on the phase space:

Thus $(\mathcal{E}_{1}, \mathcal{E}_{1}^{+})$ is an ordered Banach space. For every $\hat{\psi}\in \mathcal{E}_{1}^{+}$, $\tilde{w}(t, x, \hat{\psi}) = (\tilde{w}_{1}(t, x, \hat{\psi}), \tilde{w}_{2}(t, x, \hat{\psi}))$ denotes the unique solution of (4.2) with $\tilde{w}_{0}(\hat{\psi})(\theta, x)$ for $x\in \bar{\Omega}$, $\theta\in [-\tau_{2}(0), 0]$, where

Lemma 4.2. For any $\hat{\psi}\in \mathcal{E}_{1}^{+}$, system (4.2)has a unique nonnegative solution $\tilde{w}(t, \cdot, \hat{\psi})$ on $[0, \infty)$with $\tilde{w}_{0} = \hat{\psi}$.

The proof of Lemma 4.2 is given in Appendix B.

Remark 1. Through the uniqueness of solutions in Lemmas 3.2 and 4.2, then for any $\tilde{\psi}\in \mathcal{X}_{2}^{+}$ and $\hat{\psi} \in \mathcal{E}_{1}^{+}$ with $\tilde{\psi}_{1}(\cdot) = \hat{\psi}_{1}(\cdot)$ and $\tilde{\psi}_{2}(\theta, \cdot) = \hat{\psi}_{2}(\theta, \cdot)$, $\forall \theta\in[-\tau_{2}(0), 0]$, one has $w(t, \cdot, \tilde{\psi}) = \tilde{w}(t, \cdot, \hat{\psi})$, $t\geq 0$, where $w(t, \cdot, \tilde{\psi})$ and $\tilde{w}(t, \cdot, \hat{\psi})$ are solutions of system (4.2) meeting $w_{0} = \tilde{\psi}$ and $\tilde{w}_{0} = \hat{\psi}$, respectively.

For every fixed $t\geq 0$, let $\tilde{Q}_{t}$ be the solution map of system (4.2) on the space $\mathcal{E}_{1}$, i.e., $\tilde{Q}_{t}(\hat{\psi}) = \tilde{w}_{t}(\hat{\psi})$, for $t\geq 0$ and $\forall \hat{\psi}\in\mathcal{E}_{1}$. Thus, $\tilde{Q}: = \tilde{Q}_{\omega}$ is the Poincaré map related to system (4.2) and $r(\tilde{Q})$ is the spectral radius of $\tilde{Q}$. The next lemma indicates that the periodic semiflow $\tilde{Q}_{t}$ is eventually strongly positive.

Lemma 4.3. For each $\xi$ in $\mathcal{E}_{1}^{+}$, with $\xi\not\equiv 0$, the solution $\tilde{w}(t, \cdot, \xi)$ of (4.2) with $\tilde{w}_{0} = \xi$, meets $\tilde{w}_{i}(t, \cdot) > 0$ $(i = 1, 2)$ for all $t > 2\hat{\tau}$, therefore, $\tilde{Q}_{t}\xi \gg 0$ for every $t > 3\hat{\tau}$.

The proof of Lemma 4.3 is given in Appendix C.

Fix an integer $n_{0}$ satisfying $n_{0}\omega > 3\hat{\tau}$. Obviously, $\tilde{Q}^{n_{0}} = \tilde{Q}_{n_{0}\omega}$ is strongly monotone, according to proof of Lemma 4.3. In addition, through similar arguments in reference [43,Lemma 2.6], one can get that $\tilde{Q}^{n_{0}}$ is compact. Apply the Krein-Rutman theorem to the linear operator $\tilde{Q}^{n_{0}}$, and because $r(\tilde{Q}^{n_{0}}) = (r(\tilde{Q}))^{n_{0}}$, one has $\bar{\lambda} = r(\tilde{Q}) > 0$, among them $\bar{\lambda}$ is the simple eigenvalue of $\tilde{Q}$ and there is a eigenvector $\vartheta\in Int(\mathcal{E}_{1}^{+})$ that is strongly positive. Based on reference [22,Lemma 3.8], one has the following lemma.

Lemma 4.4. The spectral radii of the two Poincaré maps $\bar{Q}:\mathcal{X}_{2}\rightarrow \mathcal{X}_{2}$and $\tilde{Q}:\mathcal{E}_{1}\rightarrow \mathcal{E}_{1}$ are the samei.e., $r(\bar{Q}) = r(\tilde{Q})$.Furthermore, $R_{0}-1$ has the same sign as $r(\tilde{Q})-1$.

The fact that system has a special solution is given by the following lemma, which can be used to study long-term dynamics. The following argument is inspired by references [29,Lemma 5] and [44,Proposition 1.1].

Lemma 4.5. There is a positive $\omega$-periodic function $w^{*}(t, x)$, such that $e^{\tilde{\mu}t}w^{*}(t, x)$ is a solution of (4.2), where $\tilde{\mu} = \frac{\ln r(\tilde{Q})}{\omega}$.

The proof of Lemma 4.5 is given in Appendix D.

Next, we use $R_{0}$ to give the threshold results of the global dynamics of system (2.12).

Denote

Through similar arguments in Lemma 4.2, it can be concluded that for any $\phi\in W_{h}$ and $\bar{\varphi}\in \mathcal{E}_{2}$ with $\phi_{1}(\theta, \cdot) = \bar{\varphi}_{1}(\theta, \cdot)$, $\phi_{2}(0, \cdot) = \bar{\varphi}_{2}(\cdot)$, and $\phi_{3}(\theta, \cdot) = \bar{\varphi}_{3}(\theta, \cdot)$, $\forall\theta\in [-\tau_{2}(0), 0]$, $z(t, \cdot, \phi) = \bar{z}(t, \cdot, \bar{\varphi})$ is established, $t\geq 0$, where $z(t, \cdot, \phi)$ and $\bar{z}(t, \cdot, \bar{\varphi})$ are solutions of system (2.12) meeting $z_{0} = \phi$ and $\bar{z}_{0} = \bar{\varphi}$, respectively. Then we get that solutions of system (2.12) on $\mathcal{E}_{2}$ exist globally on $[0, +\infty)$ and ultimately bounded. In addition, it is easy to get the next result based on the discussion on references [22,Lemma 3.5], ^[43] and [45,Theorem 2.9].

Lemma 4.6. Set $\hat{Q}_{t}$ to be the solution map of system (2.12) on the space$\mathcal{E}_{2}$, i.e., $\hat{Q}_{t}(\bar{\varphi}) = u_{t}(\bar{\varphi})$, for $t\geq 0$ and $\forall \bar{\varphi}\in\mathcal{E}_{2}$. Thus, $\hat{Q}_{t}$ is an $\omega$-periodic semiflow on $\mathcal{E}_{2}$, in this sense, one has

(i) $\hat{Q}_{0} = I$;

(ii) $\hat{Q}_{t+\omega} = \hat{Q}_{t}\circ\hat{Q}_{\omega}$, $\forall t\geq 0$;

(iii) $\hat{Q}_{t}(\bar{\varphi})$ is continuous in $(t, \bar{\varphi})\in[0, \infty)\times \mathcal{E}_{2}$.

Furthermore, $\hat{Q}: = \hat{Q}_{\omega}$ admits a strong global attractor in $\mathcal{E}_{2}$.

Next, we prove that the solution of system (2.12) is strictly positive.

Lemma 4.7. Use $u(t, \cdot, \bar{\varphi}) = (u_{1}(t, \cdot, \bar{\varphi}), u_{2}(t, \cdot, \bar{\varphi}), u_{3}(t, \cdot, \bar{\varphi}))$ to be the solution of (2.12) with the initial data $u_{0} = \bar{\varphi}\in \mathcal{E}_{2}$, if there is $t_{1}\geq 0$ such that $u_{2}(t_{1}, \cdot, \bar{\varphi})\not\equiv 0$, and$u_{3}(t_{1}, \cdot, \bar{\varphi})\not\equiv 0$, in that way, the solution of system (2.12) meets

Besides, for $\forall t > 0$, $x\in \bar{\Omega}$ and any initial data $\bar{\varphi}\in \mathcal{E}_{2}$, one has $u_{1}(t, x, \bar{\varphi}) > 0$, and

where $\varepsilon > 0$ is a $\bar{\varphi}$-independent positive constant.

Proof. According to the comparison principle for cooperative systems, we have $u_{2}(t, x)\geq 0$ and $u_{3}(t, x)\geq 0$ for $t > 0$ and $x\in \bar{\Omega}$. Moreover, for a fixed $\bar{\varphi}\in \mathcal{E}_{2}$, it is easy to know that $u_{2}(t, x, \bar{\varphi})$ and $u_{3}(t, x, \bar{\varphi})$ satisfy

where $\hat{\mu}_{v} = \max\limits_{t\in[0, \omega], x\in\bar{\Omega}}\mu(t, x)$, $\hat{\mu}_{h} = \max\limits_{x\in\bar{\Omega}}\mu_{h}(x)$ and $\hat{\varrho} = \max\limits_{x\in\bar{\Omega}}\varrho(x)$. If there exists $t_{1}\geq 0$, such that $u_{2}(t_{1}, \cdot, \bar{\varphi})\neq 0$ and $u_{3}(t_{1}, \cdot, \bar{\varphi})\neq 0$, one has $u_{2}(t, \cdot, \bar{\varphi}) > 0$ and $u_{3}(t, \cdot, \bar{\varphi}) > 0$, $\forall t > t_{1}$ based on the strong maximum principle [40,Proposition 13.1]. For $t > 0$, let $\bar{n}(t, x, \bar{\varphi}_{2})$ be the solution of

Clearly, $\Lambda_{v}(t, x)\not \equiv 0$ is non-negative non-trivial and Hölder continuous on $\mathbb{R}\times \bar{\Omega}$. Using the comparison principle, one has

In addition, from reference [38,Lemma 2.1], system (4.8) allows a unique globally attractive periodic solution $\bar{n}^{*}(t, \cdot)$. Then

This proof is complete.

For every fixed $\bar{\varphi}\in \mathcal{E}_{2}$, $u(t, x, \bar{\varphi})$ is the unique solution of system (2.12) with $u_{0} = \bar{\varphi}$. The following conclusion indicates that $R_{0}$ is a threshold for the transmission of disease.

Theorem 4.8. Let $R_{0}$ be defined in (4.4).We have the following statements:

(i) When $R_{0} < 1$, the disease-free $\omega$-periodic solution $(u_{1}^{*}(t, x), 0, 0)$ of system (2.12) is globally attractive.

(ii) When $R_{0} > 1$, system (2.12) has at least one positive $\omega$-periodic solution $(\bar{z}_{1}^{*}(t, x), \bar{z}_{2}^{*}(t, x), \bar{z}_{3}^{*}(t, x))$, and there exists a constant $\bar{\sigma} > 0$such that for every $\bar{\varphi}\in \mathcal{E}_{2}$ with$\bar{\varphi}_{2}(\cdot)\not\equiv 0$, $\bar{\varphi}_{3}(0, \cdot)\not\equiv 0$, on has

Proof. Since $\hat{Q}_{t}$ is the solution map of system (2.12) on $\mathcal{E}_{2}$, based on reference [22,Lemma 3.5], $\hat{Q}_{t}$ is an $\omega$-periodic semiflow of system (2.12). Thence, $\hat{Q}: = \hat{Q}_{\omega}$ is the Poincaré map, and $\{\hat{Q}^{n}\}_{n\geq 0}$ is a discrete-time system on $\mathcal{E}_{2}$. For every fixed $\bar{\varphi} \in \mathcal{E}_{2}$, the omega limit set of the orbit $\{\hat{Q}^{n}(\bar{\varphi})\}_{n\geq 0}$ is $\omega(\bar{\varphi})$. Then $\omega(\bar{\varphi})$ is an internally chain transitive set for $\{\hat{Q}^{n}\}$ on $\mathcal{E}_{2}$.

(i) As $R_{0} < 1$, according to Lemma 4.4, one has $r(\tilde{Q}) < 1$, and therefore $\tilde{\mu} = \frac{\ln r(\tilde{Q})}{\omega} < 0$. For $t > 0$, discuss the following system with parameter $\epsilon > 0$,

Denote $w^{\epsilon}(t, x, \hat{\varphi}) = (w^{\epsilon}_{1}(t, x, \hat{\varphi}), w^{\epsilon}_{2}(t, x, \hat{\varphi}))$ to be the unique solution of system (4.10) for any $\hat{\varphi}\in \mathcal{E}_{1}$, with $w^{\epsilon}_{0}(\hat{\varphi})(\theta, x) = (\hat{\varphi}(0, x), \hat{\varphi}(\theta, x))$ for all $\theta\in [-\tau_{2}(0), 0]$, $x\in \bar{\Omega}$, where

Let $\tilde{Q}_{t}^{\epsilon}: = \mathcal{E}_{1}\rightarrow \mathcal{E}_{1}$ be the solution map of system (4.10) and $\tilde{Q}^{\epsilon}: = \tilde{Q}_{\omega}^{\epsilon}$ be the corresponding Poincaré map, i.e., $\tilde{Q}^{\epsilon}(\hat{\varphi}) = w^{\epsilon}_{\omega}(\hat{\varphi})$, for $\forall \hat{\varphi}\in \mathcal{E}_{1}$, and make $r(\tilde{Q}^{\epsilon})$ be the spectral radius of $\tilde{Q}^{\epsilon}$. Then the eventual strong monotonicity and compactness of $\tilde{Q}^{\epsilon}$ on $\mathcal{E}_{1}$ are easy to prove, for $t\geq 3\hat{\tau}_{2}$. From the continuity of the principle eigenvalue to parameters, one has $\lim\limits_{\epsilon\rightarrow 0}r(\tilde{Q}^{\epsilon}) = r(\tilde{Q})$. Allow $\epsilon > 0$ to be small enough, one has $r(\tilde{Q}^{\epsilon}) < 1$. From Lemma 4.5, a positive $\omega$-periodic function $w^{*}_{\epsilon}(t, x)$ exists such that $w^{\epsilon}(t, x) = e^{\tilde{\mu}_{\epsilon } t}w^{*}_{\epsilon}(t, x)$ is a solution of system (4.10), where $\tilde{\mu}_{\epsilon} = \frac{\ln r(\tilde{Q}^{\epsilon})}{\omega} < 0$. By system (4.1), $u_{1}^{*}(t, \cdot)$ is globally attractive and the comparison principle, there must be a large enough integer $n_{1} > 0$ such that $n_{1}\omega > \hat{\tau}_{2}$ and

Thus, as $t\geq n_{1}\omega$, one has

there exists some $C_{1} > 0$, for any given $\bar{\varphi}\in \mathcal{E}_{2}$, such that

Using systems (4.10) and (4.11), and the comparison theorem [36,Proposition 1], we have

Accordingly, $\lim\limits_{t\rightarrow \infty}\left(u_{2}(t, x, \bar{\varphi}), u_{3}(t, x, \bar{\varphi})\right) = (0, 0)$ uniformly for $x\in \bar{\Omega}$. Using the theory of internally chain transitive sets [32,Section 1.2], we can prove that $\lim\limits_{t\rightarrow \infty}(u_{1}(t, x, \bar{\varphi})-u_{1}^{*}(t, x)) = 0$ uniformly for $x\in\bar{\Omega}$, where $u_{1}^{*}(t, x)$ is a globally attractive solution of system (4.1). Based on the above argument, $u_{1}(t, \cdot, \bar{\varphi})$ meets a non-autonomous system, and this system tends to periodic system (4.1) asymptotically. It is known that system (4.1) can produce a solution semiflow $\hat{P}_{t}$, $t\geq 0$ on $C([-\tau_{2}(0), 0], \mathbb{Y}^{+})$. Then $\hat{P}: = \hat{P}_{\omega}$ is a Poincaré map related to system (4.1). Obviously, $\hat{P}$ has a global attractor in $C([-\tau_{2}(0), 0], \mathbb{Y}^{+})$.

Let $\mathcal{J} = \omega(\bar{\varphi})$ be the omega limit set of $\bar{\varphi} = (\bar{\varphi}_{1}, \bar{\varphi}_{2}, \bar{\varphi}_{3})\in \mathcal{E}_{2}$ for $\hat{Q}_{t}$. Owing to $\lim\limits_{t\rightarrow \infty}u_{2}(t, x, \bar{\varphi}) = 0$ and $\lim\limits_{t\rightarrow \infty}u_{3}(t, x, \bar{\varphi}) = 0$ uniformly for $x\in\bar{ \Omega}$, one has $\mathcal{J} = J\times\{0\}\times \{\hat{0}\}$. Here, $\hat{0}$ represents function which is identical to $0$, i.e., $\hat{0}(\theta, \cdot) = 0$, $\forall \theta\in [-\tau_{2}(0), 0]$. Following Lemma 4.7, we have $\hat{0}\not\in J$. Based on [32,Lemma 1.2.1], we know that $\mathcal{J}$ is an internally chain transitive set for $\hat{Q}$, then $J$ is an internally transitive chain set for $\hat{P}$. Define $u^{0}\in C([-\tau_{2}(0), 0], \mathbb{Y}^{+})$ by $u^{0}(\theta, \cdot) = u_{1}^{*}(\theta, \cdot)$ for $\theta\in [-\tau_{2}(0), 0]$. Since $J\neq \{\hat{0}\}$ and $u^{0}$ is globally attractive in $C\left([-\tau_{2}(0), 0], \mathbb{Y}^{+}\right)\backslash \{\hat{0}\}$, one has $J\cap W^{s}(u^{0})\neq \emptyset$, where $W^{s}(u^{0})$ is the stable set of $u^{0}$. According to [32,Lemma 1.2.1], one has $J = \{u^{0}\}$. $\mathcal{J} = \{u^{0}, 0, \hat{0}\}$ is proved, thence

(ii) When $R_{0} > 1$, Lemmas 4.1, 4.4 and 4.5 indicate $r(\tilde{Q}) > 1$, consequently, $\tilde{\mu} = \frac{\ln r(\tilde{Q})}{\omega} > 0$. Let

and

For every $\bar{\varphi}\in \mathbb{P}_{0}$, Lemma 4.7 reveals that $u_{2}(t, x, \bar{\varphi}) > 0$ and $u_{3}(t, x, \bar{\varphi}) > 0$, $\forall t > 0$, $x\in \bar{\Omega}$. Thus, $\hat{Q}^{n}(\mathbb{P}_{0})\subset \mathbb{P}_{0}$, $\forall n\in \mathbb{N}$. Lemma 4.6 evidences that $\hat{Q}$ has a strong global attractor in $\mathcal{E}_{2}$.

Set

and the omega limit set of the orbit $\gamma^{+}: = \{\hat{Q}^{n}(\bar{\varphi}):\forall n\in \mathbb{N}\}$ is $\omega(\bar{\varphi})$. Denote $H = (u_{1}^{*}(t, x), 0, \hat{0})$. Next, we prove that $H$ cannot form a cycle for $\hat{Q}$ in $\partial\mathbb{P}_{0}$.

Claim 1. For every $\tilde{\phi}\in M_{\partial}$, the omega limit set $\omega(\tilde{\phi}) = H$.

For every fixed $\tilde{\phi}\in M_{\partial}$, $\hat{Q}^{n}(\tilde{\phi})\in \partial\mathbb{P}_{0}$, $\forall n\in \mathbb{N}$. Then either $u_{2}(n\omega, \cdot, \tilde{\phi})\equiv 0$ or $u_{3}(n\omega, \cdot, \tilde{\phi})\equiv 0$, for each $n\in \mathbb{N}$. Furthermore, by contradiction and Lemma 4.7, it is obvious that for each $t\geq0$, either $u_{2}(t, \cdot, \tilde{\phi})\equiv 0$ or $u_{3}(t, \cdot, \tilde{\phi})\equiv 0$. If $u_{2}(t, \cdot, \tilde{\phi})\equiv 0$ for $t\geq 0$, then $\lim\limits_{t\rightarrow \infty}\left(u_{1}(t, x, \tilde{\phi})-u_{1}^{*}(t, x)\right) = 0$ uniformly for $x\in \bar{\Omega}$. Thereby, the $u_{3}$ equation in system (2.12) meets

where $\bar{\varrho} = \min\limits_{x\in \bar{\Omega}}\varrho(x)$ and $\bar{\mu}_{h} = \min\limits_{x\in \bar{\Omega}}\mu_{h}(x)$. According to the comparison principle, one has $\lim\limits_{t\rightarrow \infty}u_{3}(t, x, \tilde{\phi}) = 0$ uniformly for $x\in\bar{\Omega}$. Suppose that $u_{2}(t_{2}, \cdot, \tilde{\phi})\neq 0$ for some $t_{2}\geq 0$, in the light of Lemma 4.7, we obtain $u_{2}(t, \cdot, \tilde{\phi}) > 0$, $\forall t\geq t_{2}$. Accordingly, $u_{3}(t, \cdot, \tilde{\phi})\equiv 0$. From the $u_{2}$ equation in system (2.12), one has $\lim\limits_{t\rightarrow \infty}u_{2}(t, x, \tilde{\phi}) = 0$ uniformly for $x\in \bar{\Omega}$. Consequently, the $u_{1}$ equation in system (2.12) abides by a nonautonomous system, which is asymptomatic to the periodic system (4.1). The theory of asymptomatically periodic system [32,Section 3.2] implies that $\lim\limits_{t\rightarrow \infty}(u_{1}(t, x, \tilde{\phi})-u_{1}^{*}(t, x)) = 0$ uniformly for $x\in \bar{\Omega}$. Therefore, $\omega(\tilde{\phi}) = H$ for any $\tilde{\phi}\in M_{\partial}$, and $H$ can not form a cycle for $\hat{Q}$ in $\partial\mathbb{P}_{0}$.

For $t > 0$, study the time-periodic parabolic system with parameter $\bar{\delta} > 0$

For every $\hat{\varphi}\in \mathcal{E}_{1}$, set $w^{\bar{\delta}}(t, x, \hat{\varphi}) = (w^{\bar{\delta}}_{1}(t, x, \hat{\varphi}), w^{\bar{\delta}}_{2}(t, x, \hat{\varphi}))$ to be the unique solution of system (4.12) with $w^{\bar{\delta}}_{0}(\hat{\varphi})(\theta, x) = (\hat{\varphi}_{1}(0, x), \hat{\varphi}_{2}(\theta, x))$ for all $\theta\in [-\tau_{2}(0), 0]$, $x\in \bar{\Omega}$, where

for any $t\geq 0$ and $x\in \bar{\Omega}$. Let $\tilde{Q}_{t}^{\bar{\delta}}:\mathcal{E}_{1}\rightarrow \mathcal{E}_{1}$ be the solution map of system (4.12), i.e., $\tilde{Q}_{t}^{\bar{\delta}}(\hat{\varphi}) = w^{\bar{\delta}}_{t}(\hat{\varphi})$, and $\tilde{Q}^{\bar{\delta}}: = \tilde{Q}_{\omega}^{\bar{\delta}}$ be the corresponding Poincaré map, for $\forall \hat{\varphi}\in \mathcal{E}_{1}$. Let $r(\tilde{Q}^{\bar{\delta}})$ be the spectral radius of $\tilde{Q}^{\bar{\delta}}$. Because $\lim\limits_{\bar{\delta}\rightarrow 0}r(\tilde{Q}^{\bar{\delta}}) = r(\tilde{Q}) > 1$, a fully small $\bar{\delta} > 0$ can be selected, such that

For the certain $\bar{\delta} > 0$, according to the continuous dependence of the solution on the initial data, there must be a constant $\delta^{*} > 0$ such that for all $\bar{\varphi}$ with $\|\bar{\varphi} -H\| < \delta^{*}$, which leads to $\|\hat{Q}_{t}(\bar{\varphi}) -\hat{Q}_{t}(H)\| < \bar{\delta}$ for all $t\in [0, \omega]$.

Claim 2. For any $\bar{\varphi}\in \mathbb{P}_{0}$, then $\limsup\limits_{n\rightarrow \infty}\|\hat{Q}^{n}(\varphi)-H\|\geq \delta^{*}$.

Assuming for some $\bar{\varphi}_{0}\in \mathbb{P}_{0}$, one has $\limsup\limits_{n\rightarrow \infty}\|\hat{Q}^{n}(\bar{\varphi}_{0})-H\| < \delta^{*}$, by contradiction. So there is $n_{2}\geq 1$ such that $\|\hat{Q}^{n}(\bar{\varphi}_{0})-H\| < \delta^{*}$ for all $n\geq n_{2}$. For each $t\geq n_{2}\omega$, set $t = n\omega+t^{\prime}$ with $n = [t/ \omega]$ and $t^{\prime}\in [0, \omega)$, one has

Following system (4.13) and Lemma 4.7, we can receive

for each $t > n_{2}\omega-\hat{\tau}_{2}$, and $x\in\bar{\Omega}$. As $t\geq n_{2}\omega$, $u_{2}(t, x, \bar{\varphi}_{0})$ and $u_{3}(t, x, \bar{\varphi_{0}})$ meet

Based on $u(t, x, \bar{\varphi}_{0})\gg 0$ for every $t\geq 0$ and $x\in \bar{\Omega}$, there must be a constant $C_{2} > 0$, such that

where $u^{*}_{\bar{\delta}}(t, x)$ is a positive $\omega$-periodic function and $e^{\tilde{\mu}_{\bar{\delta}}t}u^{*}_{\bar{\delta}}(t, x)$ is a solution of system (4.12), then $\tilde{\mu}_{\bar{\delta}} = \frac{\ln r(\tilde{Q}^{\bar{\delta}})}{\omega} > 1$. By system (4.14) and the comparison theorem

Obviously, $\tilde{\mu}_{\bar{\delta}} > 0$, then $u_{2}(t, \cdot, \bar{\varphi}_{0})\rightarrow +\infty$ and $u_{3}(t, \cdot, \bar{\varphi}_{0})\rightarrow +\infty$ as $t\rightarrow +\infty$, which leads to a contradiction.

With the above claim, it is easy to obtain that $H$ is an isolated invariant set for $\hat{Q}$ in $\mathcal{E}_{2}$, and $W^{s}(H)\cap \mathbb{P}_{0} = \emptyset$, where $W^{s}(H)$ is the stable set of $H$ for $\hat{Q}$. For every integer $n$ and $n\omega > \hat{\tau}_{2}$, $\hat{Q}^{n}: = \hat{Q}_{n\omega}$ is compact, then $\hat{Q}$ is compact, and $\hat{Q}$ is asymptotically smooth on $\mathcal{E}_{2}$. Moreover, similar to Lemma 4.6, we get that $\hat{Q}$ has a global attractor on $\mathcal{E}_{2}$. According to reference [45,Theorem 3.7], $\hat{Q}$ has a global attractor $A_{0}$ in $\mathbb{P}_{0}$. Based on the acyclicity theorem on uniform persistence for map [32,Theorem 1.3.1 and Remark 1.3.1], we obtain that $\hat{Q}$ is uniformly persistent with respect to $(\mathbb{P}_{0}, \partial \mathbb{P}_{0})$, in this sense, there exists an $\gamma_{1} > 0$, such that

Now, the practical persistence are derived. Following $A_{0} = \hat{Q}(A_{0})$, we obtain that $\bar{\varphi}_{2}(\cdot) > 0$ and $\bar{\varphi}_{3}(0, \cdot) > 0$ for any $\bar{\varphi}\in A_{0}$. Set $\mathcal{B}: = \bigcup\limits_{t\in[0, \omega]}\hat{Q}_{t}(A_{0})$. Obviously, we have $\mathcal{B}\subset\mathbb{P}_{0}$ and $\lim\limits_{t\rightarrow \infty} {\rm{d}}(\hat{Q}_{t}(\bar{\varphi}), \mathcal{B}) = 0$, $\forall \bar{\varphi}\in \mathbb{P}_{0}$. The continuous function $q:\mathcal{E}_{2}\rightarrow \mathbb{R}_{+}$ is defined by

Because $\mathcal{B}$ is a compact subset of $\mathbb{P}_{0}$, we obtain that $\inf\limits_{\bar{\varphi} \in \mathcal{B}}q(\bar{\varphi}) = \min\limits_{\bar{\varphi}\in \mathcal{B}}q(\bar{\varphi}) > 0$. Consequently, there is an $\gamma_{2} > 0$ such that

Furthermore, according to Lemma 4.7, there must be an $\gamma_{3}\in (0, \gamma_{2})$ such that

By references [29,Lemma 8] and [32,Theorem 3.5.1], for every $t > 0$, the solution map $Q_{t}: = W_{h}\rightarrow W_{h}$ of system (2.12), defined in Lemma 3.2, is a $\kappa$-contraction about an equivalent norm on $W_{h}$, where $\kappa$ is Kuratowski measure of noncompactness. Define

and

For any $\phi\in \mathbb{W}_{0}$, $Q$ is $\rho$-uniformly persistent with $\rho(\phi) = {\rm{d}}(\phi, \partial \mathbb{W}_{0})$ is easily attainable. It then follows from [45,Theorem 4.5], applicable to $Q$, that system (2.12) has an $\omega$-periodic solution $(z_{1}^{*}(t, \cdot), z_{2}^{*}(t, \cdot), z_{3}^{*}(t, \cdot))$ with $(z_{1t}^{*}, z_{2t}^{*}, z_{3t}^{*})\in \mathbb{W}_{0}$. Let $\bar{z}_{1}^{*}(\theta, \cdot) = z_{1}^{*}(\theta, \cdot)$, $\bar{z}_{2}^{*}(0, \cdot) = \bar{z}_{2}^{*}(0, \cdot)$ and $\bar{z}_{3}^{*}(\theta, \cdot) = z_{3}^{*}(\theta, \cdot)$ where $\theta\in [-\tau_{2}(0), 0]$. Combing the uniqueness of solutions and Lemma 4.7, we have that $(\bar{z}_{1}^{*}(t, \cdot), \bar{z}_{2}^{*}(t, \cdot), \bar{z}_{3}^{*}(t, \cdot))$ is periodic solution system (2.12) and it is also strictly positive.

Next, we prove the asymptomatic behaviour of $M$ and $E_{v}$ in system (2.11). By Eq (2.6), and $\Lambda_{v}(t, x)\not\equiv 0$ is nonnegative and Hölder continuous function for $t > 0$ and $x\in\bar{\Omega}$. Then there is a unique positive $\omega$-periodic solution $M^{*}(t, x)$ which is globally attractive. From Eq (3.6) and Theorem 4.8(i), when $R_{0} < 1$, one has $\lim\limits_{t\rightarrow \infty}E_{v}(t, \cdot) = 0$. With the arguments similar to those above, we can prove that if $R_{0} < 1$, then $\lim\limits_{t\rightarrow \infty}(E_{v}(t, x), I_{v}(t, x), I_{h}(t, x)) = (0, 0, 0)$ and $\lim\limits_{t\rightarrow \infty}\left((M(t, \cdot), S_{v}(t, x))-(M^{*}(t, x), u_{1}^{*}(t, x))\right) = 0$, uniformly for $x\in \bar{\Omega}$. By Eq (2.12), Theorem (4.8)(ii) and Eqs (2.6) and (3.6), then if $R_{0} > 1$, for any $\bar{\varphi}\in \mathcal{E}_{2}$ with $\bar{\varphi}_{2}(\cdot)\not\equiv 0$ and $\bar{\varphi}_{3}(0, \cdot)\not\equiv 0$, one has

uniformly for $x\in\bar{\Omega}$. Since $\Lambda_{v}(t, x)$ is Hölder continuous and non-negative function for $t > 0$ and $x\in \Omega$ from Eq (2.6), then there exists $\gamma_{4} > 0$ such that

uniformly for $x\in\bar{\Omega}$ with $M(0, x)$ satisfies compatibility condition (3.4). By the integral form Eq (3.6), then exists $\gamma_{5} > 0$ such that

with $E_{v}(0, x)$ satisfies compatibility condition (3.5). In addition, if $(S_{v}(t, \cdot), I_{v}(t, \cdot), I_{h}(t, \cdot))$ is $\omega$-periodic in $t$, then $E_{v}(t, \cdot)$ is $\omega$-periodic is easy to be checked. Therefore, the following result is obtained.

Theorem 4.9. Let $R_{0}$ be defined as in (4.4).Set $U(t, x, \psi)$ to be the solution of system (2.11) with $U_{0} = \psi$, where$(U_{1}(t, x), U_{2}(t, x),$$U_{3}(t, x), U_{4}(t, x), U_{5}(t, x)) = (M(t, x), S_{v}(t, x), E_{v}(t, x), I_{v}(t, x), I_{h}(t, x))$.One has:

(i) When $R_{0} < 1$, the disease-free $\omega$-periodic solution $(M^{*}(t, \cdot), u_{1}^{*}(t, \cdot), 0, 0, 0)$ of system (2.11) is globally attractive.

(ii) When $R_{0} > 1$, system (2.11) has at least one positive $\omega$-periodic solution $\bar{U}(t, x)$, where $\bar{U}_{2}(t, x) = \bar{z}_{1}^{\ast}(t, x)$, $\bar{U}_{4}(t, x) = \bar{z}_{2}^{\ast}(t, x)$, $\bar{U}_{5}(t, x) = \bar{z}_{3}^{\ast}(t, x)$ and there is a constant$\gamma_{6} = \max\{\gamma_{3}, \gamma_{4}, \gamma_{5}\} > 0$that makes for every $\psi\in \mathcal{D}$ with$\psi_{4}(\cdot)\not\equiv 0$, $\psi_{5}(0, \cdot)\not\equiv 0$, we have

5.   Numerical

In this part, we use numerical simulations to clarify the impact of spatial heterogeneity, periodic delays, seasonality, and vector-bias on the spread of malaria, to show how to derive some understanding of epidemiology from our analysis results.

5.1.   Numerical confirmation of theoretical results

Here, some simulations to support the analysis results built in Section 4 are provided. More precisely, the potential dynamics outcomes of system (2.11) are given. For convenience, we will focus our attention on the domain $\Omega$, which is one-dimensional, denoted by $[0, \pi]$ to simulate the long-time behavior of system (2.11). The basic reproduction number $R_{0}$ often (but not always) controls the extinction and persistence of the disease. Specifically, system (2.11) applies to the transmission of malaria in Maputo Province, Mozambique, a sub-Saharan African country where malaria is at risk of spreading in the country. The WHO report shows that the number of confirmed malaria cases has been increasing in recent years, and the condition deteriorated severely in 2014.

According to reference ^[24], suppose the total population density $N(x) = \bar{N} = 53\; ({\rm{km}}^{2})^{-1}$. The unit of time is month. Set the periodic $\omega = 1\; {\rm{year}} = 12$ months. We set $\varrho = a_{1}(2.05-\cos(2x))\; {\rm{Month}}^{-1}$, where $a_{1} = 0.0187$ means that people living in urban areas (near the center area) can get better medical services (number of doctors and hospitals, advanced medical equipment, supply of medicines) than people in rural areas. This results in a higher recovery rate near the center. See Appendix E for the values and definitions of other parameters.

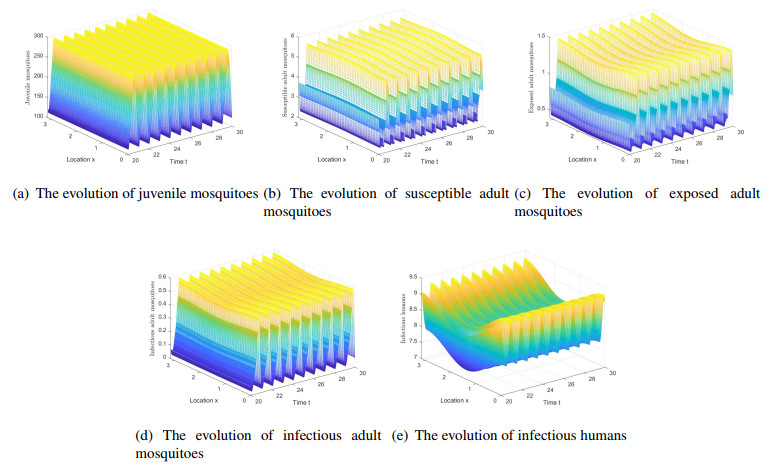
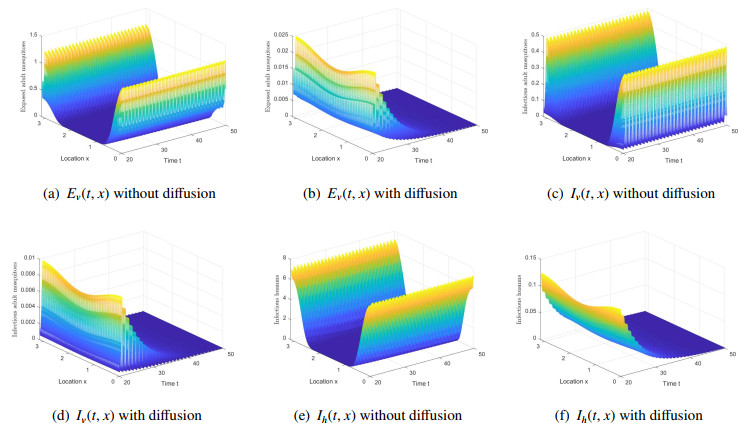
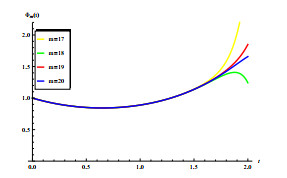
To compute $R_{0}$, we use the numerical method proposed in reference [41,Lemma 2.5 and Remark 3.2]. Using the above parameters set, the basic reproduction number can be numerically calculate as $R_{0} = 1.2233 > 1$, which implies that in mosquito and human populations, the disease persist. Figure 3 shows numerical plots of humans and mosquitoes compartments with initial data

where $\hat{u}(t, x): = (M, S_{v}, E_{v}, I_{v}, I_{h})$. This conforms to the conclusion of Theorem 4.9(ii). The time interval can be truncated ^[20,30] to prove that the existence of the positive periodic solution.

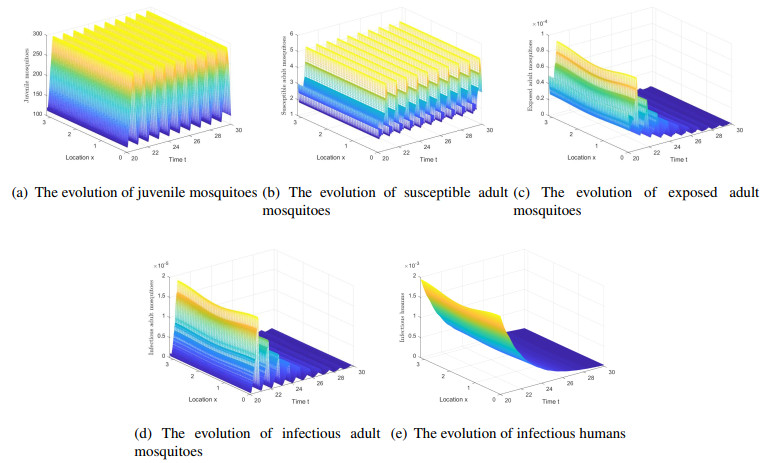
Reduce the bite rate to $0.5\beta(t)$, and increase the death rate of mosquito to $1.5\mu_{v}(t)$, which can be achieved by using insecticide-treated nets, then $R_{0} = 0.2983 < 1$. Thus, immature mosquitoes and susceptible adult mosquitoes show periodic fluctuations. The exposed adult mosquitoes, infectious adult mosquitoes and infectious humans converge to 0 (Figure 4). This is coincident with the conclusion of Theorem 4.9(i).

5.2.   Effects of parameters on $R_{0}$

We are interested in how system parameters affect the disease risk $R_{0}$. In this section, we choose the parameters that are consistent with those in Section 5.1.

5.2.1.   The impact of periodic maturity delay on disease transmission

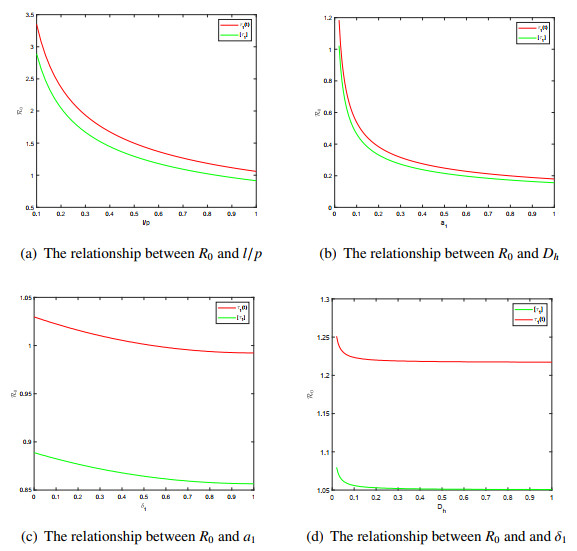
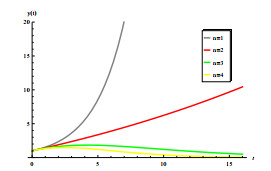
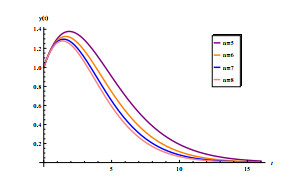
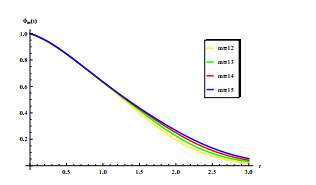
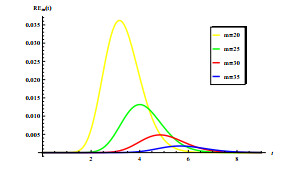
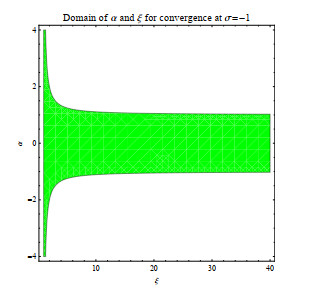
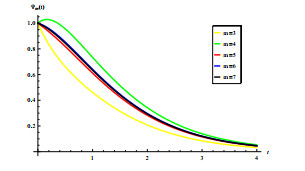
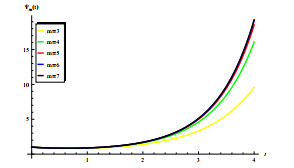
In this subsection, we explore the impact of mature period affected by seasonal climate change on malaria transmission. The results are given in Figure 5, the green one represents the time-averaged value of maturation delay $[\tau_{1}]$ in system (2.11), where $[\tau_{1}] = \frac{1}{\omega}\int_{0}^{\omega}\tau_{1}(t) {\rm{d}}t = 0.5605\; {\rm{Month}},$ and the red one indicates system (2.11) is under a time-periodic maturation delay. An intuitive result is that in these four cases, the green line is always below the red line, which fully indicates that the time-average maturity delay will underestimate the risk of malaria transmission, so the impact of climate change cannot be ignored. In the following subsections, we analyze in detail the sensitivity of $R_{0}$ to these four parameters.

5.2.2.   The relationship between $R_{0}$ and $l/p$

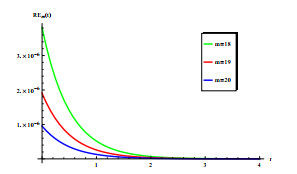
Looking at Figure 5, we let $l/p$ vary in $[0, 1]$, and other parameters are same as those in Figure 3 and explore the impact of the vector-bias effect, $l/p$ are used to represent the relative attractiveness of susceptible to infected humans. From Figure 5(a), it can be easily seen that $R_{0}$ is an increasing function of $l/p$. Therefore, ignoring the vector-bias effect will ultimately underestimate the risk of disease transmission. And this conclusion is valid regardless of whether the periodic or the time-average maturation delay is considered.

5.2.3.   The impact of interventions on $R_{0}$

In this subsection, we examine the impact of interventions on $R_{0}$. Note that in Figure 3(e), the population density of infected individuals in urban (central) areas is less than in rural (border) areas, which prompts us to explore the relationship between human recovery rate $\varrho$ and disease risk $R_{0}$ in a heterogeneous space. Since medical resources (advanced medical equipment, the number of hospitals and doctors, medicine supply) are abundant in urban areas than in rural areas, humans can get better medical services in urban areas with a higher recovery rate.

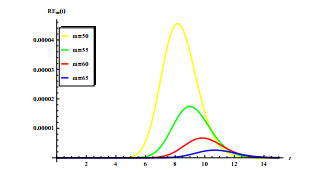
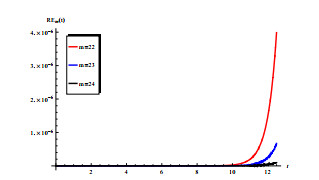
In this subsection, we analyze the impact of medical resources on the spread of malaria, including two aspects: (i) the impact of increasing medical resources; (ii) for fixed medical resources, the impact of different allocation measures on disease transmission. In Figure 5(b), we let $a_{1}$ in $\varrho$ vary in $[0.02, 0.5]$, and the other parameters are same as those in Figure 3. It proposes a strategy, i.e., in the current allocation of the medical resources, the recovery rate can be improved through efforts to develop new drugs. Figure 5(b) shows that increasing medical resources can reduce $R_{0}$ to less than 1, which means that the disease can be controlled. In this paper, we use the recovery rate $\int_{0}^{\pi}\varrho(x) {\rm{d}}x$ of the entire region to represent medical resources.

In the case of fixed medical resources, we explore the impact of different allocation on the spread of disease. Choose $a_{1} = 0.058$ and a new parameter $\delta_{1}$ is added to $\varrho$, i.e., $\varrho(x) = 0.058\times (1 -(1-\delta_{1})\cos(2x))$, where $\delta_{1}\in [0, 1]$, which measures the difference in the allocation of urban and rural medical resources. Other parameters are the same as those in Figure 3. When $\delta_{1} = 0$, the gap between rural and urban medical resources is the largest, and the recovery rate in urban area is the highest (near the center of space area, i.e., $x = \frac{\pi}{2}$). As $\delta_{1}$ changes from 0 to 1, medical resources are allocated to nearby rural area (near $x = 0$ and $x = \pi$), and the gap in medical conditions between rural and urban areas gradually narrows, and is eventually evenly distributed in space. Through calculation, it can be found that if $\delta_{1} = 0$, in order to make $R_{0}$ less than 1, $a_{1}\geq0.0637$ is needed, but if $\delta_{1} = 1$, the medical resources only need 0.0576, which can make $R_{0} < 1$. From Figure 5(c), we come to an interesting conclusion that in the case of limited medical resources, the spatial heterogeneity of the distribution of medical resources increases the risk of disease transmission. This result indicates that the distribution of medical resources dose play an important role in the design of malaria control programs.

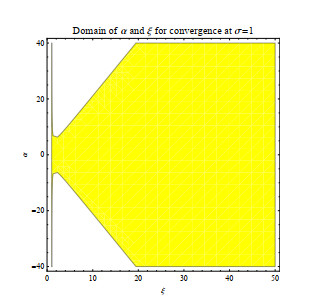
5.2.4.   The influence of $D_{h}$ on the $R_{0}$

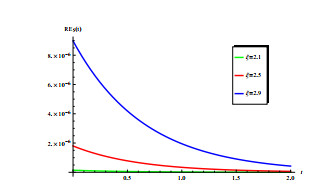
We explore the impact of human mobility on the transmission of malaria in a heterogeneous space. Let $D_{h}$ vary in $[0.02, 0.5]$ and other parameters are consistent with those in Figure 3. The result is shown in Figure 5(d), which describes the relationship between $R_{0}$ and $D_{h}$. It can be directly observed from Figure 5(d) that $R_{0}$ decreases with respect to $D_{h}$. When $D_{h}$ is very small, $R_{0}$ will drop sharply and as $D_{h}$ continues to increase, the rate of decline of $R_{0}$ will slow down. This seems to indicate that malaria cannot be controlled if no protective measures are taken and only by improving a high diffusion to avoid mosquito bites without taking any protective measures ^[49] systematically analyzes this problem.

5.3.   The impact of diffusion on the final size of malaria

In Section 5.2.4, we explore the impact of diffusion on $R_{0}$, and study the impact of diffusion on the final size of disease transmission. Set $\varrho(x) = 0.04(2.05-\cos(2x))$ and other parameters are consistent with those in Figure 3. When $D_{h} = 0.1$ and $D_{v} = 0.0125$, calculate $R_{0} = 0.8448$, the disease is extinct. However, without considering the movement of mosquitoes and humans, that is, when the diffusion coefficients are $D_{h} = 0$ and $D_{v} = 0$, it is found that $R_{0} = 1.1635$ is greater than 1, and the disease is persistent. Then, we will get the result shown in Figure 6, which shows some interesting phenomena. Under this set of parameters, if the diffusion of mosquitoes and humans is not considered, then the disease is extinct in urban areas, and is persistent in rural areas. The reason for this result is that we study spatial heterogeneity. Due to urban environment is not suitable for mosquitoes to survive, the number of mosquitoes is relatively small, and the medical resources are relatively large, so the urban disease control is better. Compared with the right column of Figure 6, the movement of mosquitoes and humans will reduce the risk of disease transmission to a certain extent, which is consistent with the conclusions in Figure 5(d) and reference ^[24]. There are two explanations: (i) The existence of diffusion indicates that the infected humans in rural areas can be treated in cities with better medical conditions. (ii) As mentioned in reference ^[24], to a certain extent, it is difficult for mosquitoes to take a blood meal among moving humans.

6.   Discussion

As we all know, in the study of malaria transmission, the combined effects of temperature-dependent EIP and maturation delay, vector-bias, spatial structure and seasonal variation are worth studying. Here, we establish and analyze a reaction-diffusion model of malaria, including periodic delays and vector-bias in a heterogeneous environment.

Using the theory proposed by Liang et al. ^[41] and Zhao ^[42], the basic reproduction number $R_{0}$ can be introduced. We first prove that in a defined phase space, linear system (4.2) generates a periodic semiflow which is eventually strongly monotonic. Then, we describe $R_{0}$ as a threshold for the extinction and persistence of malaria. It is proved that if $R_{0} < 1$, then malaria will be eliminated. When $R_{0} > 1$, there admits at least one positive $\omega$-periodic solution.

In the numerical part, data for exploring the transmission of malaria in Maputo Provence, Mozambique have been published. The numerical simulation is divided into three parts. First, we give some simulation conclusions to support the theoretical analysis. Second, we discuss the sensitivity of $R_{0}$ to the parameters in the model. (I) Our numerical results show that if we only consider the time-average maturation delay, we can underestimate the risk of malaria transmission assessed by $R_{0}$. (II) It is easy to know that $R_{0}$ is decreasing with respect to $l/p$. Thence, if the impact of vector-bias effect on malaria transmission is ignored, the risk of transmission will be underestimated. (III) We analyze the impact of intervention measures on $R_{0}$ from two aspects: (i) the impact of increasing medical resources. This case is mainly due to the uneven distribution of medical resources in rural and urban areas, which increases the impact of medical resources on $R_{0}$; (ii) for fixed medical resources, the impact of different allocation measures on disease transmission. Through the analysis of this case, we find that in the case of limited medical resources, narrowing the gap in the allocation of medical resources between rural and urban areas can better reduce the risk of malaria transmission. Third, we explore the impact of diffusion on $R_{0}$ in a spatially heterogeneous environment, assuming that the distribution of medical resources and the initial data of mosquitoes and humans depend on space. Biologically speaking, we understand this spatial heterogeneity as the difference between rural and urban areas. In addition, we also study the impact of diffusion on the final size of malaria. We find that under the set parameters, if the diffusion of mosquitoes and humans is not considered, the disease will become extinct in urban areas, and persist in rural areas. But under this set of parameters, the disease will become extinct if the diffusion is not considered.

Acknowledgments

We are very grateful to anonymous referees and editor for careful reading and helpful suggestions which led to an improvement of our original manuscript. The authors are grateful for the support and useful comments provided by Professor Xiaoqiang Zhao (Memorial University of Newfoundland). This research is supposed by National Natural Science Foundation of China (grant number: 11971013) and Postgraduate Research & Practice Innovation Program of Jiangsu Province (KYCX$21\_0176$) and Nanjing University of Aeronautics and Astronautics PhD short-term visiting scholar project (ZDGB2021027).

Conflict of interest

The authors declare there is no conflict of interest.

Appendix

A.   Proof of Lemma 3.2

Proof. Firstly, the local existence of the unique mild solution is proved. Clearly, $F$ is locally Lipschitz continuous. It is necessary to show

For all $(t, \phi)\in[0, +\infty)\times W_{h}$ and $\hat{\theta}\geq 0$, because $p\geq l > 0$, one has

for $t\geq 0$ and $x\in \bar{\Omega}$, where $\hat{\beta} = \max\limits_{t\in[0, \omega], x\in\bar{\Omega}}\beta(t, x)$ and $\tilde{N} = \min\limits_{x\in\bar{\Omega}}N(x)$, and

This implies that

Consequently, by reference [36,Corollary 4] with $K = \mathbb{Y}^{+}\times\mathbb{Y}^{+}\times\mathbb{Y}_{h}$ and $S(t, s) = T(t, s)$, system (2.12) has a unique mild solution $u(t, \cdot, \phi)$ on its maximum existence interval $t\in[0, t_{\phi})$ and $u_{0} = \phi$ where $t_{\phi}\leq \infty$, $u(t, \cdot, \phi)\in \mathbb{Y}^{+}\times\mathbb{Y}^{+}\times\mathbb{Y}_{h}$. In addition, when $t > \hat{\tau}$, $u(t, \cdot, \phi)$ is a classical solution, based on the analyticity of $T(t, s)$, $s, t\in \mathbb{R}$ and $t > s$.

Analyze the following time-periodic reaction-diffusion equation

By reference [38,Lemma 2.1], system (A.2) has a unique globally attractive positive $\omega$-periodic solution $u_{1}^{*}(t, x)$ in $\mathbb{Y}^{+}$. Since system (A.2) can dominate the first equation of (2.12), there is a $B_{1} > 0$ such that for any $\phi \in W_{h}$, a positive integer $l_{1} = l_{1}(\phi) > 0$ exists and meets $u_{1}(t, x, \phi)\leq B_{1}$ for all $t\geq l_{1}\omega$ and $x\in \bar{\Omega}$.

Next, similar to reference [46,Theorem 2.1], the ultimate boundedness of solutions can be proved. Set

for any $\phi\in W_{h}$, let $(u_{1}(t, x), u_{2}(t, x), u_{3}(t, x)): = (u_{1}(t, \phi)(x), u_{2}(t, \phi)(x), u_{3}(t, \phi)(x))$, $t\geq 0$, $x\in \bar{\Omega}$, and $\bar{u}_{i}(t) = \int_{\Omega}u_{i}(t, x) {\rm{d}}x$ where $i = 1, 2, 3$. Using the Green's formula and integrating the first equation of system (2.12), one has

that is,

By system (A.3), the property of the fundamental solutions ^[47] and Green's formula, the second equation of (2.12) are integrated to get

where $k_{1}$, $k_{2}$ and $k_{3}$ are positive numbers independent of $\phi$. Select $k_{1}\leq \bar{\mu}_{v}k_{2}$ in system (15.4), so that

which yields $\bar{u}_{2}(t)+k_{2}\bar{u}_{1}(t-\tau_{2}(t))\leq \frac{k_{2}k_{3}}{k_{1}}+1$ for $t\geq l^{\prime}_{1}\omega+\hat{\tau}$, where $l^{\prime}_{1} > l_{1}$ is some integer. Hence,

Integrating the third equation on model (2.12), and applying Green's formula, we have

Thus,

for $t\geq l_{2}\omega+\hat{\tau}$, $(l_{2}\geq l_{1})$ and $x\in \bar{\Omega}$. Therefore, we have $t_{\phi} = \infty$ for each $\phi \in W_{h}$.

Let $\{Q_{t}\}_{t\geq 0}$ be a family of operators on $W_{h}$ and $Q_{t}(\phi)(s, x) = u_{t}(s, x, \phi) = u(t+s, x, \phi)$ for $t\geq 0$, $s\in [-\hat{\tau}, 0]$, $x\in \Omega$ and $\phi \in W_{h}$. Similar to the proof of Lemma 2.1 in reference ^[38], we can show that $\{Q_{t}\}_{t\geq 0}$ is an $\omega$-periodic semiflow on $W_{h}$. From the above proofs, we conclude that $Q_{t} : W_{h} \rightarrow W_{h}$ is point dissipative. Moreover $Q: = Q_{\omega}$ is $\kappa$-contraction, where $\kappa$ is Kuratowski measure of noncompactness, and hence, $Q$ is asymptotically smooth. By references [48,Theorem 2.4.7] and [32,Theorem 1.1.2], it follows that $Q$ has a global compact attractor.

B.   Proof of Lemma 4.2

Proof. Let $\bar{\tau}_{2} = \min\limits_{t\in[0, \omega]}\tau_{2}(t)$. For all $t\in [0, \bar{\tau}_{2}]$, since $t-\tau_{2}(t)$ strictly increase with respect to $t$, one has

and therefore, $\tilde{w}_{2}(t-\tau_{2}(t), \cdot) = \hat{\psi}_{2}(t-\tau_{2}(t), \cdot)$. Thus, for any $t\in [0, \bar{\tau}_{2}]$, there holds

Fix $\hat{\psi}\in \mathcal{E}_{1}^{+}$, for $t\in [0, \bar{\tau}_{2}]$, the solution $(\tilde{w}_{1}(t, \cdot), \tilde{w}_{1}(t, \cdot))$ of the above linear system exists uniquely. To put this another way, one has $z_{1}(\theta_{3}, \cdot) = \tilde{w}_{1}(\theta_{3}, \cdot)$, where $\theta_{3}\in [0, \bar{\tau}_{2}]$ and $z_{2}(\theta_{4}, \cdot) = \tilde{w}_{2}(\theta_{4}, \cdot)$, $\theta_{4}\in [-\tau_{2}(0), \bar{\tau}_{2}]$.

By repeating the above step to $[n\bar{\tau}_{2}, (n+1)\bar{\tau}_{2}]$, we see that the solution with initial date $\hat{\psi}\in \mathcal{E}_{1}^{+}$ exists uniquely for all $t\geq 0$.

C.   Proof of Lemma 4.3

Proof. Similar to the proof of Lemma 4.2, on each interval $[n\bar{\tau}_{2}, (n+1)\bar{\tau}_{2}]$, $n\in \mathbb{N}$, one easily obtain that $\tilde{w}_{i}(t, \cdot) \geq 0$, ($i = 1, 2$) for all $t\geq 0$. Select a $K > \max\{\hat{\mu}_{v}, \hat{\mu}_{h}+\hat{\varrho}\}$, such that for every $t\in \mathbb{R}$, $g_{1}(t, \cdot, \tilde{w}_{1}): = -\mu_{v}(t, \cdot)\tilde{w}_{1}+K\tilde{w}_{1}$ is strictly increasing with respect to $\tilde{w}_{1}$, and $g_{2}(t, \cdot, \tilde{w}_{2}): = -(\mu_{h}(\cdot)+\varrho(\cdot))\tilde{w}_{2}+K\tilde{w}_{2}$ is increasing in $\tilde{w}_{2}$. Then, for $t > 0$, both $\tilde{w}_{1}$ and $\tilde{w}_{2}$ meet the following system

Therefore, for a fixed $\bar{\xi}\in \mathcal{E}_{1}^{+}$, one has

where $\tilde{T}_{1}(t, s), \tilde{T}_{2}(t, s): = \mathbb{Y}\rightarrow \mathbb{Y}$ are evolution operators related to $\frac{\partial \tilde{w}_{1}}{\partial t} = D_{v}\Delta \tilde{w}_{1}-K \tilde{w}_{1}$ and $\frac{\partial \tilde{w}_{2}}{\partial t} = D_{h}\Delta \tilde{w}_{2}-K \tilde{w}_{2}$ with Nuemann boundary condition. Since $m(t): = t-\tau_{2}(t)$ are increasing in $t\in \mathbb{R}$, it easily follows that $[-\tau_{2}(0), 0]\subseteq m([0, \hat{\tau}_{2}])$. Generally, we assume that $\xi_{2} > 0$. Then there exists an $(\theta, x_{0})\in [-\tau_{2}(0), 0]\times \Omega$ such that $\tilde{w}_{2}(\theta, x_{0}) > 0$. According to the equation of (17.1), we have $\tilde{w}_{1}(t, \cdot, \xi) > 0$ for all $t > \hat{\tau}_{2}$. If $s > 2\hat{\tau}_{2}$, then $s-\tau_{2}(s) > 2\hat{\tau}_{2}-\hat{\tau}_{2} = \hat{\tau}_{2}$. It is easy to know that $\forall t\geq 0$, $\tilde{w}_{2}(t, \cdot, \xi) > 0$ for all $t > 2\hat{\tau}_{2}$ according to the second equation of (17.1). This means that there is $\tilde{w}_{i}(t, \cdot)\geq 0$ for all $t > 2\hat{\tau}_{2}$, $i = 1, 2$, so the solution map $\tilde{Q}_{t}$ is strongly positive for all $t > 3\hat{\tau}_{2}$.

D.   Proof of Lemma 4.5

Proof. For every $\hat{\psi}\in \mathcal{E}_{1}^{+}$, let $\tilde{w}(t, x, \hat{\psi}) = (\tilde{w}_{1}(t, x, \hat{\psi}), \tilde{w}_{2}(t, x, \hat{\psi}))$ be the solution of (4.2) with $\tilde{w}_{0}(\hat{\psi}) = \hat{\psi}$. Since $\hat{\psi}\gg 0$, we get $\tilde{w}_{t}(\hat{\psi})\gg 0$ for all $t\geq 0$ will be a piece of cake. Denote

Then $w^{*}(t, x) = (w^{*}_{1}(t, x), w^{*}_{2}(t, x))\gg 0$ for $t\geq 0$, $x\in\bar{\Omega}$, and $w^{*}(t, x)$ meets the linear-periodic system with $\tilde{\mu}:$

for $t > 0$. Hence, for all $\theta\in[-\tau_{2}(0), 0]$, $x\in\bar{\Omega}$, $w^{*}(t, x)$ is the solution of the $\omega$-periodic system (D.1) with $w_{0}^{*}(\theta, x) = (w^{*}_{1}(0, x), w^{*}_{2}(\theta, x)) = \left(\hat{\psi}_{1}(x), e^{-\tilde{\mu}\theta}\hat{\psi}_{2}(\theta, x)\right)$, where $w_{t}^{*}(\cdot, \cdot) = \left(w^{*}_{1}(t, \cdot), w^{*}_{2t}(\cdot, \cdot)\right)$ for each $t\geq 0$ with

For every $\theta\in[-\tau_{2}(0), 0]$, $x\in\bar{\Omega}$, one has

Consequently, $w^{*}_{0}(\theta, \cdot) = w^{*}_{\omega}(\theta, \cdot)$ for all $\theta\in[-\tau_{2}(0), 0]$, and by the existence and uniqueness of system (D.1), one has

Thus, $w^{*}(t, x)$ is an $\omega$-periodic solution of (D.1) and $e^{\tilde{\mu}t}w^{*}(t, x)$ is a solution of (4.2).

E.   Parameter definition and value

The authors in reference ^[20] discussed the impact of seasonality on the spread of malaria including assessing the seasonal related bite rate $\beta(t)$, periodic maturity delay $\tau_{1}(t)$, periodic EIP $\tau_{2}(t)$, periodic death $\mu_{v}(t)$ and recruitment rate $\Lambda_{v}(t)$ of mosquitoes, where

Other parameter values are defined as