A continuous-time network evolution model describing $N$-interactions

1.   Introduction

Nowadays, network theory is a popular and important research field. The book by Barabási ^[1] contains several general facts on network theory. A mathematical tool to describe an evolving network is the theory of random graphs. The graph's vertices are the nodes of the network and the edges of the graph are the connections among the nodes. In real life, a connection can be a collaboration or an interaction.

In this paper, we do not want to overview the vast literature on network theory. As we intend to apply branching processes to describe a network evolution, we focus on papers using branching processes in network theory. Bollobás and Riordan in ^[2] considered several problems of random graphs and applied Galton-Watson branching processes to prove some of the theorems. Rudas et al. ^[3] as well as Rudas and Tóth ^[4] applied continuous-time branching processes to study random tree growth models. In ^[5], a preferential attachment random graph is embedded in a continuous-time branching process to find the asymptotic behavior of the graph. In ^[6], continuous-time branching processes were applied to study an estimator in sublinear preferential attachment trees. In their survey paper ^[7], Holmgren and Janson studied the asymptotics of certain trees using Crump-Mode-Jagers branching processes. In ^[8], multi-type preferential attachment trees were studied using the theory of multi-type continuous-time branching processes. Banerjee and Huang ^[9] studied growing networks via embedding into a continuous-time branching process. In ^[10], Iksanov et al. underlined that one of the main applications of the theory of branching processes is the study of evolving networks. Usually, the advanced theory of branching processes is applied to prove new results for growing networks. However, sometimes network theory inspires new research in the field of branching processes, e.g., ^[11].

Most studies in network theory concentrate on connections of two nodes. However, cooperation of more than two units is also important. There are models describing such cooperation. Backhausz and Móri studied three-interactions in ^[12], while Fazekas and Porvázsnyik in ^[13] considered $N$-interactions.

In this paper, we shall study a continuous-time network evolution model based on the cooperation of several units. Our model was motivated by the activities of teams of people. We focused on cooperation among friends, recruitment of party members, recruitment of volunteers, collaboration among scientists, and teams in social networks. In the above cases, a person can be a member of several teams at the same time, new teams can emerge and disappear, and newcomers can join an existing team.

2.   Materials and methods

In this paper, we apply similar mathematical tools as in ^[14,15], where continuous-time branching processes were used (see also ^[16]). In ^[14], the starting network is a single edge. Any edge produces several new vertices during evolution, and then the edge disappears. Any new vertex produced by an edge is joined to the endpoints of the reproducing edge with one or two new edges. In ^[14], the reproduction process of the edges is a continuous-time branching process. In ^[15], 2- and 3-cliques are considered and some results of ^[14] are extended.

In this paper, we shall study networks containing cliques (i.e., groups) of sizes $1, 2, \dots, N$, where $N$ is fixed. We shall apply multi-type branching processes, where the type is the size of a clique. The researches ^[8,17] also applied multi-type branching processes, but there the vertices had different types. We also mention, that the evolution process considered in this paper is similar to the one studied in ^[15], but we emphasize that the process in ^[15] is not a particular case of the process in the present paper.

During the evolution of the network, when a newcomer joins the network, it joins directly with certain members of an existing clique in the network. Then they will form a new clique which we shall consider as a child of the old clique. Any clique produces an offspring clique each time its driving Poisson process jumps. Then these offspring start their reproduction processes. The length of life of a clique depends on the number of offspring it has.

This paper is divided into eight sections. In Section 3, we define our model precisely. In Section 4, we present our general results. We calculate the survival function of a clique (Theorem 4.1), the mean offspring number of a clique (Corollary 4.1), the Laplace transforms (Proposition 4.1), and then we turn to the Perron root and the Malthusian parameter. We do not obtain an explicit expression for the Malthusian parameter, so we can numerically compute it. In Section 5, we prove asymptotic theorems for the number of cliques of a given size (Theorem 5.1). Each has magnitude $e^{\alpha t}$ in the event of non-extinction, where $\alpha$ is the Malthusian parameter. The proof of Theorem 5.1 is based on the asymptotic theorems of ^[18]. A most interesting question in the theory of evolving networks is the degree process of a fixed vertex. Therefore, in Section 6, we prove asymptotic theorems for the degree of a fixed vertex. For the proof, we introduce a new branching process, called the "good children" process, and then we can apply the asymptotic theorems of ^[18]. We obtain that the magnitude of the degree of a fixed vertex is $e^{{\hat{\alpha} t}}$, where $\hat{\alpha}$ is the Malthusian parameter of the "good children" process. In Section 7, we obtain the generating functions. We apply the generating functions to find the probability of extinction of the network, see Theorem 7.1. In Section 8, we show simulation results. We shall see that the simulation results support our theorems.

We mention that basic results on branching processes are contained e.g., in ^{[19,20,21,22,23]}.

3.   The model

In this paper, we shall consider the following model to describe certain evolving networks. The main ingredients of the network are teams. Any team is represented as a clique, i.e., a graph having $n$ vertices so that any two vertices are connected with one edge. The size of a clique is the number of its vertices. In our model, there are cliques of sizes $1, 2, \dots, N$, where $N$ is an arbitrarily large but fixed number. We shall describe the evolution of the network by a multi-type branching process. In terms of multi-type branching processes, see, e.g., ^[21], an $n$-clique would be a type-$n$ individual.

At the time $t = 0$ there is one team, and the size of this team can be $1, 2, \dots, N$. In terms of branching processes, we call this team the ancestor. This ancestor team produces offspring teams which can be cliques of sizes $1, 2, \dots, N$. Then these children teams also produce their own children teams, and so on. Any team has its rate of 1 Poisson process. The jumping times of this Poisson process are the reproduction times of the team. We shall suppose that the reproduction processes of different teams are independent. The reproduction processes of the teams of size $n$ are independent copies of the reproduction process of the generic team of size $n$.

Now, we identify any team with the clique representing it. The mathematical description of the evolution of the generic $n$-clique is the following. Let $\Pi_n \left(t\right)$ denote the Poisson process with parameter 1 corresponding to the generic $n$-clique. The jumping times of $\Pi_n \left(t\right)$ are the reproduction times. When $\Pi_n \left(t\right)$ jumps, then a new vertex appears and we connect it to certain vertices of the generic $n$-clique. The new vertex will be connected to $j$ vertices of the generic $n$-clique with probability $q_{n, j}$, where $0 \le q_{n, j} \le 1$, $j = 0, 1, \dots, n$, and $\sum_{j = 0}^n q_{n, j} = 1$. (We assume that $q_{N, N} = 0$ because the largest team is of size $N$.) When $j$ is chosen, then together with the new vertex, $j$ new edges appear. One endpoint of any new edge is the new vertex. The other $j$ endpoints of the $j$ new edges are chosen randomly from the vertices of the generic $n$-clique. The number of subsets having $j$ elements is $\binom{n}{j}$. We choose one of these $\binom{n}{j}$ subsets uniformly at random. The vertices of this subset are already connected, and now we connect each of them to the new vertex with one edge. So the $j$ old connected vertices chosen, the new vertex, and the $j$ new edges form a $(j+1)$-clique. This new $(j+1)$-clique is a child of the generic $n$-clique and it is the only child at this step. We should emphasize that the result of the above step is precisely one child because we shall count only this one child. The reason for this point of view is that we are interested in the number of teams, and the new sub-cliques of the new $(j+1)$-clique are not considered as teams.

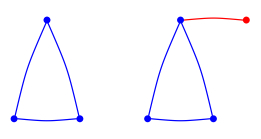
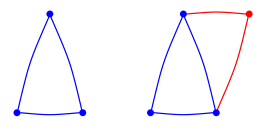
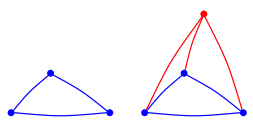
We see that the generic $n$-clique produces precisely one child clique at any birth time. If $j = 0$, this child is just one vertex, i.e., the new vertex joining the network with 0 edges. If $j = 1$, then this child is an edge, which consists of the new vertex and the old vertex connected to the new one. If $j = 2$, this child is a triangle consisting of the new vertex and two vertices of the generic $n$-clique. If $j = n < N$, this child is an $(n+1)$-clique consisting of the whole $n$-clique ancestor and the new vertex. We emphasize that when the parent is the largest possible clique, i.e., an $N$-clique, we do not allow the birth of an $(N+1)$-clique. We also see that the probability that an $i$-type ancestor produces a $j$-type child is $p_{i, j} = q_{i, j-1}$, $j = 1, 2, \dots, i+1$. The ancestor clique, the children cliques of the ancestor, and the grandchildren cliques, etc., will form an evolving network.

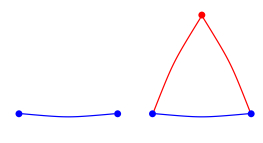
Example 3.1. We visualize four simple reproduction steps in Figures 1–4.

In our model, cliques can die. When a clique dies, it will be an inactive clique not producing children. But we do not delete its vertices and edges, because any vertex or edge can belong to several cliques. So we shall study both the number of all $j$-cliques born during the evolution process and the number of active $j$-cliques. We underline again that we are interested in the number of teams. The teams (i.e., cliques) are born during the above evolution process, i.e., the offspring of the ancestor. So we will not count those cliques that are not offspring of the ancestor clique.

Let us denote by $\xi_{i, j}(t)$ the number of type-$\! j$ children cliques of the type-$i$ generic clique up to time $t$ ($i, j = 1, 2, \dots, N$). The processes $\xi_{i, j}$ are point processes. Then

is the number of all children of the generic $i$-clique up to time $t$.

Let $\tau_i(1), \tau_i(2), \dots$ be the birth times of the generic $i$-clique and denote by $\varepsilon_i(1), \varepsilon_i(2), \dots$ the corresponding total litter sizes. In our model, $\varepsilon_i(k) \equiv 1$.

Let $\lambda_i$ be the life length of the generic $i$-clique. $\lambda_i$ is a random variable with ${{\mathbb {P}}}(0\le \lambda_i < \infty) = 1$. After its death, a clique does not produce offspring, so $\xi_i\left(t\right) = \xi_i\left(\lambda_i\right)$, when $t > \lambda_i$. So

where $\Pi_i\left(t\right)$ is the Poisson process, and $x \wedge y$ is the minimum of $\left\{x, y\right\}$.

Now we turn to the survival function of the life length of an $i$-clique. $L_i\left(t\right)$ will denote the distribution function of $\lambda_i$. Then the survival function of $\lambda_i$ is

Here $l_i\left(t\right)$ denotes the hazard rate function of $\lambda_i$.

A major assumption of this paper is that the hazard rate is determined by the total number of offspring in the following way:

where $b\ge 0$ and $c > 0$ are fixed constants.

We emphasize that the reproduction processes of the $i$-cliques are independent copies of the reproduction process of the generic $i$-clique.

4.   Preliminary results

First, we calculate the survival function of an $i$-clique.

Theorem 4.1. For any $i$, the survival function of an $i$-clique is

Proof. Using the general calculation of [15, Theorem 1], we have

where $s_j$ denotes the distribution of $\varepsilon_i$. As now $\varepsilon_i\equiv 1$, so $s_1 = 1$, and therefore the survival function for an $i$-clique is

□

Now, we turn to the mean offspring number. It is $m_{i, j}(t) = {{\mathbb {E}}} \xi_{i, j}(t)$, which is the expectation of the number of type-$\! j$ offspring of a type-$i$ parent up to time $t$.

Corollary 4.1. For any $t \geq 0$, we have

where

$0 < F(\infty) < \infty$.

Proof. Similar to the proof of [15, Corollary 1], we have

where $\varepsilon_{i, j}(k)$ is the number of type-$\! j$ children of a type-$i$ mother at her $k^{\rm{th}}$ birth event. Applying Wald's identity, we get

$\Pi$ is a rate-1 Poisson process, and $t \wedge \lambda$ is bounded, so (4.4) implies that

In our case ${{\mathbb {P}}}\left(\varepsilon_{i, j}(k) = 1 \right) = p_{i, j}$, so from (4.1) and inserting $u = 1-e^{-cs}$, we get

□

We need the Laplace transform of $m_{i, j}$,

Proposition 4.1. We have

where

$m_{i, j} (\infty) = p_{i, j} A(0)$. If $A(0) > 1$, then $A(\alpha) = 1$ for some $\alpha > 0$.

Proof. For the proof, one can use Corollary 4.1. □

Now, we shall consider the Perron root. The Laplace transform matrix is

The characteristic roots of $M(\kappa)$ are denoted by $\varrho_{l}(\kappa)$, $l = 1, \dots, N$. The Perron root is the greatest of the values $\varrho_{l}(\kappa)$. We denote it by $\varrho(\kappa)$.

We suppose that

that is, we assume that our process is supercritical.

We shall need the Malthusian parameter. $\alpha$ is called the Malthusian parameter if $\varrho(\alpha) = 1$.

If $\alpha$ is the Malthusian parameter, then we denote by ${{\mathbf{v}}} = (v_1, \dots, v_N)^\top$ the right eigenvector of $M(\alpha)$ corresponding to eigenvalue 1 and normalized as $v_1+\dots +v_N = 1$. Let ${{\mathbf{u}}} = (u_1, \dots, u_N)^\top$ be the left eigenvector of $M(\alpha)$ satisfying $u_1 v_1+\dots +u_N v_N = 1$.

We shall suppose that the stochastic matrix $\left(p_{i, j} \right)_{i, j = 1}^N$ is irreducible and acyclic. Then its Perron root is 1, so $\varrho(\kappa) = A(\kappa)$. Therefore, our branching process is supercritical if and only if $A(0) > 1$. If $A(0) > 1$, then there exists a Malthusian parameter, that is, an $\alpha > 0$ such that $A(\alpha) = 1$. We also see that ${{\mathbf{v}}} = (1/N, \dots, 1/N)^\top$.

5.   The limiting behavior of the number of cliques

For any evolving network, a basic question is the growth of the number of ingredients of the network. So, for our network, we should find the number of cliques. For the proof, we shall use powerful results on multi-type branching processes, see [18, Theorem 2.4,and Proposition 4.1]. In [15, Section 8], we summarized those results in one proposition, see [15, Proposition 4]. So here in the proof, we shall check conditions (a), (b1), (b2), (c), (d), and $(i)-(iii)$ of [15, Section 8].

We shall assume that the matrix $\left(p_{i, j} \right)$ is irreducible and acyclic. Therefore, [24, Theorem 1.4] gives that there exists a positive integer $K$, such that each element of the $K ^{\rm{th}}$ power of the matrix $\left(p_{i, j} \right)$ is positive. As $m_{i, j} (\infty) = p_{i, j} A(0)$ and $A(0) > 0$, condition (d) will be satisfied.

For condition (a), we have to show that not all measures $m_{i, j}$ are concentrated on a lattice. By Corollary 4.1, these measures are absolutely continuous, so condition (a) is fulfilled.

For (b2), we shall assume that $A(0) > 1$. As $m_{i, j} (\infty) = p_{i, j} A(0)$, it will imply (b2). Concerning condition (b1), we mention that $A(0) > 1$ implies that there exists a Malthusian parameter, that is, an $\alpha > 0$ such that $A(\alpha) = 1$. We can numerically calculate the value of $\alpha$.

We shall check condition (c) during the proof of Theorem 5.1.

Now, we shall find the denominator in the limit theorem. We can see that the denominator of $m_\infty^\Phi$ in the asymptotic expression does not depend on $\Phi$ and it has the form

It is the same as

Here $u_i$ and $v_i$ are the coordinates of the eigenvectors and we know that ${{\mathbf{v}}} = (1/N, \dots, 1/N)^\top$. Moreover, by Proposition 4.1, we can see that

So

Here

Now, we shall consider the number of the $n$-cliques.

Theorem 5.1. Assume that the matrix $\left(p_{i, j} \right)_{i, j = 1}^N$ is irreducible and acyclic. Assume that $A(0) > 1$. Let $\alpha$ be the Malthusian parameter, i.e., a finite positive solution of equation $A(\alpha) = 1$. Let $n$ be fixed, $1\le n \le N$. We denote by ${}_k T(t)$ the number of all $n$-cliques being born up to time $t$ if the ancestor of the network was a $k$-clique, $k = 1, 2, \dots, N$. Then

almost surely for $k = 1, 2, \dots, N$.

We denote by ${}_k\hat{T}(t)$ the number of all $n$-cliques alive at time $t$ if the ancestor of the network was a $k$-clique, $k = 1, 2, \dots, N$. Then

almost surely for $k = 1, 2, \dots, N$.

The quantity ${}_kW$ is a.s. non-negative, ${{\mathbb {E}}}({}_kW) = 1$, and ${}_kW$ is a.s. positive on the event of survival.

Proof. We shall use [15, Proposition 4] as in the proof of [15, Theorem 2]. To prove condition $(vi)$, it is enough to show that

where

and

At any birth, there is precisely 1 child, so

where $\tau(1), \tau(2), \dots$ are the jumping times of the Poisson process $\Pi_i$. The interarrival time ($\tau(j)-\tau({j-1})$) is exponentially distributed with rate 1, so $\tau(j)$ has $\Gamma$-distribution $\varGamma\left(j, 1\right)$. It implies that

Let $\eta_j = \tau(j)-\tau({j-1})$. Let $\eta_0$ be a random variable having an exponential distribution with parameter 1 and assume that $\eta_0$ and $M$ are independent. Then

So $e^{-\alpha \eta_0}\left(1+M\right)$ has the same distribution as that of $M$. From this and Eq (5.10), we get

So we obtain

Therefore (5.7) is true for any $i$.

To prove conditions (c) and $(iv)$, it is enough to show that $\int_0^\infty t^2 e^{-\alpha t} m_{i, j}(dt) < \infty$, for $i, j = 1, 2, \dots, N$. Now, from Corollary 4.1, we get that

as $\alpha+b$ is positive. Therefore conditions (c) and $(iv)$ are true.

Now, consider the number of $n$-cliques. To show (5.5), let $\Phi_x(t) = 1$ if $x$ is an $n$-clique, and $\Phi_x(t) = 0$ otherwise. Therefore ${{\mathbb {E}}} \Phi_n(t) = 1$ and ${{\mathbb {E}}} \Phi_j(t) = 0$ for $j\ne n$. So assumptions $(i)-(iii)$ and $(v)$ are true. Therefore, [15, Proposition 4] implies (5.5).

To prove (5.6), let $\Phi_x(t) = 1$ if $x$ is an $n$-clique and it is alive at time $t$, and let $\Phi_x(t) = 0$ otherwise. Therefore ${{\mathbb {E}}} \Phi_n(t) = 1-L_n(t)$ and ${{\mathbb {E}}} \Phi_j(t) = 0$ for $j\ne n$. So $(i)-(iii)$ and $(v)$ are fulfilled. We see that

Using [15, Proposition 4], we get (5.6). □

Remark 5.1. The process is supercritical if

If the process is supercritical, then there exists a Malthusian parameter.

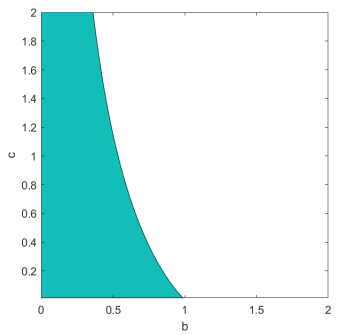
For any pair $b$, $c$, one can show whether the process is supercritical. Here we just list a few cases.

If $1\le c < 1/\ln 2$ and $0\le b \le c-1$, then the process corresponding to $b$, $c$ is supercritical. Moreover the case $b = 0$, $c = 1/2$ is also supercritical.

If $b\ge1$, $c = 1$, then the process is not supercritical. The case $b = 1$, $c = 2$ is also not supercritical.

To consider the other values, we have made a numerical investigation on a rectangle: We have considered the cases when $0\leq b \leq 2$ and $0.01\leq c \leq 2$, because the parameter $c$ is in the denominator. Figure 5 shows the set of parameters $(b, c)$ for which the process is supercritical.

Example 5.1. Consider the Leslie model. For $n = 1, 2, \dots, N-1$, when a new vertex joins to an $n$-clique, then either it joins to all vertices of the $n$-clique, or the new vertex alone creates a new clique. So $p_{n, n+1} = p_n$, $p_{n, 1} = 1- p_n$ for $n = 1, 2, \dots, N-1$. But for $n = N$, when a new vertex appears, then either it creates alone a new clique or the new vertex and $N-1$ old vertices create an $N$-clique. So $p_{N, N} = p_N$ and $p_{N, 1} = 1-p_N$.

Now, the matrix of the Laplace transforms is

We assume that $p_1 > 0, \dots, p_{N-1} > 0$, and $1-p_N > 0$. We also assume that the greatest common divisor of the set $\{ i = 1, 2, \dots, N \, : \, 1-p_i > 0 \}$ is equal to 1. So the matrix $\left(p_{i, j} \right)$ is irreducible and acyclic. Therefore its Perron root is 1. So the Perron root of $M(\kappa)$ is $A(\kappa)$, and the corresponding right eigenvector is

Direct calculations show that the coordinates of the left eigenvector are

and

Now, Theorem 5.1 gives the asymptotic number of cliques.

Consider the particular case of the Leslie model when $p_i = a$ for any $i$, where $0 < a < 1$. Then $u_N = N a^{N-1}$, and $u_n = N (1-a) a^{n-1}$, $n = 1, 2, \dots, N-1$. Inserting these values into the formulae (5.5) and (5.6), we obtain the asymptotic number of cliques. For $n$-cliques with $n = 1, 2, \dots, N-1$,

but for the $N$-cliques,

almost surely for $k = 1, 2, \dots, N$.

Similarly, for $n$-cliques with $n = 1, 2, \dots, N-1$,

and for the $N$-cliques,

We see that as $a \to 1$, then $N$-cliques dominate. It is a plausible consequence of the definition of the model.

Another particular case of the Leslie model is $p_1 = p_N = 1/2$ and $p_i = 1$ for $i = 2, \dots, N-1$. Then $u_1 = u_N = (2N)/(N+2)$, and $u_i = u_N/2$ for $i = 2, \dots, N-1$.

6.   The connected network and the degree of a fixed vertex

A basic question for any evolving network is the degree process of a fixed vertex. We study the topics of the connected network and the degree of a fixed vertex in the same chapter because both of them are studied by multi-type branching processes having $N-1$ types.

Remark 6.1. When the network is connected then it is not possible that a separated vertex is born. In that case, we can consider just the $2, 3, \dots, N$ cliques. So the possible types of our branching process will be $2, 3, \dots, N$, where the type is 2 if the clique is an edge, it is 3 if the clique is a triangle, $\dots$, and it is $N$ in the case of an $N$-clique. The probability that the new vertex will be connected to $j$ vertices of the generic $n$-clique is again $q_{n, j}$, where $0 \le q_{n, j} \le 1$, but now $j = 1, \dots, n$ and $\sum_{j = 1}^n q_{n, j} = 1$. So we should consider a multi-type branching process having $N-1$ types. Now, the probability that a type-$i$ parent gives birth to a type-$\! j$ child is $p_{i, j} = q_{i, j-1}$ for $i, j = 2, 3, \dots, N$.

The results of the previous two sections remain valid with obvious modifications. So $m_{i, j}$, $m^*_{i, j}$ are the same, but $i, j = 2, 3, \dots, N$.

We shall suppose that the stochastic matrix $\left(p_{i, j} \right)_{i, j = 2}^N$ is irreducible and acyclic. Then its Perron root is 1, so $\varrho(\kappa) = A(\kappa)$. Therefore, our branching process is supercritical if and only if $A(0) > 1$. If $A(0) > 1$, then there exists a Malthusian parameter, that is, an $\alpha > 0$ such that $A(\alpha) = 1$. ${{\mathbf{v}}} = (1/(N-1), \dots, 1/(N-1))^\top$ is the right eigenvector of $\left(p_{i, j} \right)_{i, j = 2}^N$ corresponding to eigenvalue 1. ${{\mathbf{u}}} = (u_2, \dots, u_N)^\top$ is the left eigenvector of $\left(p_{i, j} \right)_{i, j = 2}^N$ satisfying the condition $u_2 v_2+\dots +u_N v_N = 1$.

We can modify Theorem 5.1 to find the number of the $n$-cliques in the case of the connected network. Assume that the matrix $\left(p_{i, j} \right)_{i, j = 2}^N$ is irreducible and acyclic. Assume that $A(0) > 1$. Let $\alpha$ be the Malthusian parameter. Let $n$ be fixed, $2\le n \le N$. Denote by ${}_k T(t)$ the number of all $n$-cliques being born up to time $t$ if the ancestor of the population was a $k$-clique, $k = 2, 3, \dots, N$. Then

almost surely for $k = 2, 3, \dots, N$.

This is similar for the number of $n$-cliques alive at time $t$.

Now, we turn to the degree process of a fixed vertex. Let $V$ be a fixed vertex. Assume that at the beginning, $V$ is a member of an $i$-clique. We assume that $i\ge 2$, so the initial degree of $V$ is $i-1\ge 1$. We call a child a "good child" if it contains $V$. So the degree of $V$ increases by 1, when a good child is born. More precisely, the degree of $V$ increases when good children of the initial $i$-clique are born, and then good children of the good children are born, etc. Then the degree of $V$ at time $t$ is the total number of good children at that time.

Let $\hat{p}_{i, j}$ be the probability that a type-$i$ parent gives birth to a type-$\! j$ good child. Then

We see that the good children process is a branching process having types $2, 3, \dots, N$. The length of the life of an $i$-clique is the same $\lambda_i$ as in the case of our original process.

Let $\hat{\xi}_{i, j}$ be the number of type-$\! j$ good children of a type-$i$ good child. Then the average number of good children is

The Laplace transform of $\hat{m}_{i, j}(t)$ is

Let

be the matrix of the Laplace transforms. Denote by $\hat{\varrho}(\kappa)$ the Perron root of $\hat{M}(\kappa)$. We shall suppose that the good children process is supercritical, i.e., $\hat{\varrho}(0) > 1$. If the process is supercritical, then in our case there exists a positive Malthusian parameter $\hat{\alpha}$ such that $\hat{\varrho}(\hat{\alpha}) = 1$. Let $\hat{{{\mathbf{v}}}} = (\hat{v}_2, \dots, \hat{v}_N)^\top$ be the right eigenvector of $\hat{M}(\hat{\alpha})$ corresponding to eigenvalue 1 and normed according to $\hat{v}_2+\dots + \hat{v}_N = 1$. Let $\hat{{{\mathbf{u}}}} = (\hat{u}_2, \dots, \hat{u}_N)^\top$ be the left eigenvector of $\hat{M}(\hat{\alpha})$ corresponding to eigenvalue 1 and normed according to $\hat{v}_2 \hat{u}_2+\dots + \hat{v}_N\hat{u}_N = 1$.

Now, we can present our result on the asymptotic behavior of the degree of a fixed vertex.

Theorem 6.1. Assume that the matrix $\left(p_{i, j} \right)_{i, j = 2}^N$ is irreducible and acyclic. Assume that the good children process is supercritical, i.e., $\hat{\varrho}(0) > 1$. Let $\hat{\alpha}$ be the positive Malthusian parameter, so $\hat{\varrho}(\hat{\alpha}) = 1$. Let $V$ be a fixed vertex which is initially a member of an $i$-clique, $2 \le i \le N$.

Let ${}_iV(t)$ denote the degree of $V$, more precisely, the number of all edges being connected to $V$ up to time $t$. Then

almost surely.

Let ${}_i\bar{V}(t)$ denote the number of those edges, whose one endpoint is $V$ and belonging to a clique alive at time $t$. Then

almost surely.

The quantity ${}_i{\hat W}$ is a.s. non-negative, ${{\mathbb {E}}}({}_i{\hat W}) = 1$, and ${}_i{\hat W}$ is a.s. positive in the event of survival of the good children process.

Proof. Here we shall use some results obtained during the proof of Theorem 5.1. We have

where $V_{i, j}(t)$ denotes the number of type-$\! j$ good offspring of a type-$i$ mother. We shall find the limit of $V_{i, j}(t)$.

As in the proof of Theorem 5.1, we shall check the conditions of [15, Proposition 4]. Conditions (a), (c), $(iv)$, and $(vi)$ are true because they are true for the original process (see Theorem 5.1). (b1) and (b2) are true because we supposed that $\hat{\varrho}(0) > 1$. Condition (d) is true because we supposed that the matrix $\left(p_{i, j} \right)_{i, j = 2}^N$ is irreducible and acyclic.

Now, let $\Phi_x(t) = 1$, if the clique $x$ is a good $j$-clique, and $\Phi_x(t) = 0$ otherwise. Then conditions $(i)-(iii)$, and $(v)$ are satisfied. Moreover, ${{\mathbb {E}}} \Phi_j(t) = 1$ and ${{\mathbb {E}}} \Phi_l(t) = 0$ for $l\ne j$.

So [15, Proposition 4] implies

almost surely. So we obtain (6.2).

To obtain (6.3), let $\Phi_x(t) = 1$ if $x$ is a good $j$-clique and it is alive at time $t$, and let $\Phi_x(t) = 0$ otherwise. Therefore ${{\mathbb {E}}} \Phi_j(t) = 1-L_j(t)$ and ${{\mathbb {E}}} \Phi_l(t) = 0$ for $l\ne j$. Conditions $(i)-(iii)$ and $(v)$ are true. Now

Now, we can apply [15, Proposition 4]. However, in (6.3) we cannot offer equality, because an edge can belong to a clique being alive and at the same time it can belong to a clique being dead. □

7.   The extinction probability

7.1.   The joint generating function

To find the probability of the extinction of our network, we need the generating function. We calculate the joint generating function of the variables $\Pi_n \left(\lambda_n\right)$ and $\xi_{n, j}\left(\lambda_n\right)$, $j = 1, \dots, \left(n+1\right)\wedge N$, $n = 1, \dots, N$. Consider the generic $n$-clique, where $n$ is fixed with $1\le n \le N$. Consider the sequence

where $i = 0, 1, 2, \dots$, $k_j = 0, 1, 2, \dots$.

Then (7.1) describes the joint distribution of the last reproduction time and the offspring size of the generic $n$-clique during its whole lifetime. Here $\Pi_n$ is the Poisson process that describes the birth times of the generic $n$-clique and $\lambda_n$ is its life length. In other words, we can say that $w_{i, {\left\{k_j\right\}}_{j = 1}^{\left(n+1\right)\wedge N}}$ gives the probability of the event that the last birth time of the generic $n$-clique before its death is $\tau_i$ and the total number of type-$\! j$ offspring up to its death is $k_j$. That is, we can write $w_{i, {\left\{k_j\right\}}_{j = 1}^{\left(n+1\right)\wedge N}}$ in the following form:

To determine the desired joint generating function, first we consider the following sequence:

We use the notation $\tau_0 = 0$, so $u_{0, {\left\{k_j\right\}}_{j = 1}^{\left(n+1\right)\wedge N}} = 1$ if each $k_j$ is zero, but it is 0 if any $k_j$ is positive. Moreover, $u_{i, {\left\{k_j\right\}}_{j = 1}^{\left(n+1\right)\wedge N}} = 0$, if any subscript is negative. Now, for a while, assume that $\tau_i$ and $\tau_{i-1}$ are fixed and $\xi_{n, j}\left(\tau_{i-1}\right) = m$ is known. Then using the definition of the survival function of the life length given in (3.3) and by Assumption (3.4), we have

But $\tau_i$ and $\tau_{i-1}$ are random. So, a simple calculation that uses the fact that the increments of a Poisson process with intensity 1 are exponential with parameter 1 can lead us to obtain that

That is, (7.5) is the probability that the object will not die before the $i^{\rm{th}}$ birth event. Using the above calculations and the law of total probability, we can give the following recursion for the sequence $u_{i, {\left\{k_j\right\}}_{j = 1}^{\left(n+1\right)\wedge N}}$, $i = 1, 2, \dots$

Here $p_{n, j}$ is the probability that the new vertex is born with $j$ new edges. To obtain the above recursion, we also used the following. Considering the generic $n$-clique, the definition of the evolution process implies that at each birth step, exactly 1 offspring is born, the smallest possible offspring size is 1, and the maximal offspring size is $\left(n+1\right) \wedge N$. Moreover, the offspring sizes of the generic $n$-clique at any two consecutive birth steps are independent. Using (7.3) and (7.5), we can also see that

Let us consider the following sequence $v_{i, {\left\{k_j\right\}}_{j = 1}^{\left(n+1\right)\wedge N}}$, where $w_{i, {\left\{k_j\right\}}_{j = 1}^{\left(n+1\right)\wedge N}}$ is defined in (7.1):

Moreover, using the recursion (7.6), we see that the sequence $v_{i, {\left\{k_j\right\}}_{j = 1}^{\left(n+1\right)\wedge N}}$ satisfies the following recurrence relation:

where the initial values are

Let us denote by $G\left(x, \left\{x_j\right\}_{j = 1}^{\left(n+1\right)\wedge N} \right)$ the generating function of the sequence $v_{i, {\left\{k_j\right\}}_{j = 1}^{\left(n+1\right)\wedge N}}$. We have

To determine the generating function $G\left(x, \left\{x_j\right\}_{j = 1}^{\left(n+1\right)\wedge N} \right)$, we multiply with $x^i\prod_{j = 1}^{\left(n+1\right)\wedge N} x_j^{k_j}$ and then take the sum of both sides of (7.9). In this way, we obtain that

From this equation and using the definition of the generating function given by (7.11), we can obtain that

Let $h\left(t\right) = G \left(x, \left\{tx_j\right\}_{j = 1}^{\left(n+1\right)\wedge N} \right)$. By (7.10), we have the initial condition

Now, substituting $x_j$ with $tx_j$ in (7.14), we get the following first-order differential equation:

where the initial value is

The solution of the above initial value problem (7.16) and (7.17) is

Substituting $t = 1$ in (7.18), we obtain that the generating function of the sequence $v_{i, {\left\{k_j\right\}}_{j = 1}^{\left(n+1\right)\wedge N}}$ is

Now, let us denote by $g_{\Pi_n, \left\{\xi_{n, j}\right\}_{j = 1}^{\left(n+1\right)\wedge N}}$ the joint generating function of the variables $\Pi_n \left(\lambda_n\right)$ and $\xi_{n, j}\left(\lambda_n\right)$, $j = 1, \dots, \left(n+1\right)\wedge N$. Using the definitions of the sequences $w_{i, {\left\{k_j\right\}}_{j = 1}^{\left(n+1\right)\wedge N}}$ and $v_{i, {\left\{k_j\right\}}_{j = 1}^{\left(n+1\right)\wedge N}}$, by (7.14) we have

With $x = 1$ in (7.20), we obtain that the generating function of the total offspring distribution of the generic $n$-clique is

7.2.   The probability of extinction

Consider the embedded multi-type Galton-Watson process which can be constructed in the following way. At the initial time, the ancestor alone constitutes the starting generation of the Galton-Watson process. During its life, the ancestor produces a random number of offspring. All of the offspring of this ancestor form the $1 ^{\rm{st}}$ generation. Generally, the $n^{\rm{th}}$ generation is formed by the offspring of the members of the $\left(n-1\right) ^{\rm{th}}$ generation.

Under some reasonable conditions, the probability of extinction of our process is the same as the probability of extinction of the embedded multi-type Galton-Watson process, see [21, Theorem 7.1 in Chapter 3]. In our case those conditions are satisfied. Let $\mathbb{M}$ be the matrix of the expected total offspring number of our process. Then

We see that the matrix $\mathbb{M}$ contains the expected offspring numbers of the embedded Galton-Watson process.

From the theory of multi-type branching processes, we know that the probability of extinction may depend on the type of the ancestor. Moreover, the vector of extinction probabilities is the solution of a vector equation.

Theorem 7.1. Let us denote by $s_i$ the probability of extinction when the ancestor of the network is an $i$-type object. Let ${{\mathbf{s}}} = (s_1, \dots, s_N)$. Assume that $\left(p_{i, j} (\infty)\right)_{i, j = 1}^N$ is an irreducible acyclic Markov transition matrix. Denote by $\varrho$ the Perron–Frobenius root of $\mathbb{M}$. If $\varrho \leq 1$, then $s_1 = s_2 = \dots = s_N = 1$. If $\varrho > 1$, then $s_1 < 1, s_2 < 1, \dots, s_N < 1$. In any case, ${{\mathbf{s}}}$ is the smallest non-negative solution of the vector equation

where ${{\mathbf{f}}} = (f_1, \dots, f_N)$ and the functions $f_k$ are defined in (7.21).

Proof. Our conditions ensure that the matrix $\mathbb{M}$ is positively regular. Now, applying [21, Theorem 7.1 in Chapter 1], we can obtain the desired result. □

8.   Simulation results

In this section, we present some numerical results for our previously presented asymptotic theorems. We used the Julia environment because of the possibility of fast numerical computing allowed by the well-written dynamic structures. The code can be downloaded from GitHub, see ^[25].

According to Theorem 5.1, the numbers of $n$-cliques, when the process moves forward in time, are asymptotically close to a straight line on the logarithmic scale. To support numerically our Theorem 5.1, we studied the slope of the sequence of the simulated number of $n$-cliques being born up to time $t$ on the logarithmic scale.

Example 8.1. Now, we present an example of the Leslie model with $N = 5$, the transition matrix

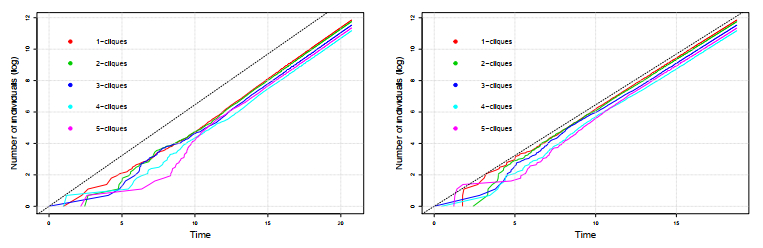
and with parameters of the hazard rate $b = 0.2$ and $c = 0.2$. In Figure 6, we illustrate the first $2^{19}$ birth steps of two different simulated processes. The five solid lines represent the number of $n$-cliques being born, for $n = 1, \ldots, 5$ on a logarithmic scale, while the dotted line's slope $\hat{\alpha}$ = 0.6462 equals the numerical approximation of the Malthusian parameter. We can see that the plotted lines are parallel straight lines for large values of $t$, which in fact gives nice feedback to our asymptotic results.

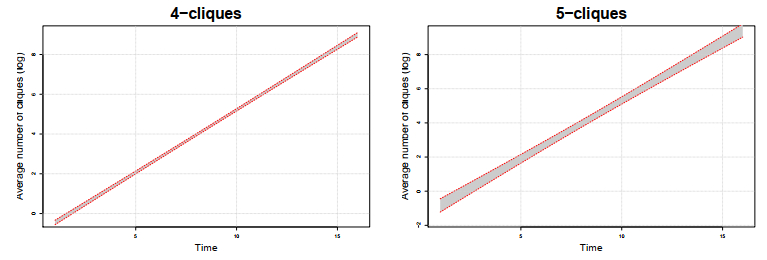
Then, to obtain statistically significant evidence, we used 100 simulated processes to construct a 99% confidence stripe for the trajectory of the number of $n$-cliques. For demonstration, in Figure 7, the 99% confidence stripes are presented for 4- and 5-cliques. The red lines are the borders of the stripes.

In Table 1, the boundaries of the 99% confidence intervals for $\alpha$ are presented. Each fixed clique size gives a confidence interval. The columns labeled with $0.5\%$ and $99.5\%$ show the lower and the upper bounds calculated from simulations. As the results show, the numerical approximation $\hat{\alpha}_1 = 0.6462$ is contained by all confidence intervals.

Example 8.2. Now, we present another example with a transition matrix

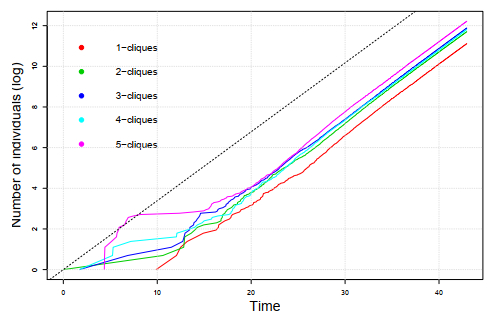
and parameters $b = 0.4$ and $c = 0.4$. In this model, a newcomer joining an $n$-clique can contact any other group members, when $n = 1, \dots, 4$. For $n = 5$, it is not possible that the newcomer joins all former clique members. In Figure 8, we show a simulated example of the process. The five solid lines represent the number of $n$-cliques being born, for $n = 1, \ldots, 5$ on a logarithmic scale, while the dotted line's slope equals $\hat{\alpha}_2 = 0.3391$. Table 2 contains the confidence intervals for the slope, using 100 simulated processes.

9.   Conclusions

We have introduced a new continuous-time network evolution model. We have proven asymptotic theorems for the number of cliques having a fixed size and the degree of a fixed node. We have obtained the probability of extinction. Besides precise mathematical proofs, we have presented simulation examples supporting our results.

Author contributions

I. Fazekas: Conceptualization, methodology for the whole paper, formal analysis, investigation, project administration, supervision, validation, writing-original draft, writing-review and editing; A. Barta: Formal analysis, investigation of Section 8, software, visualization, writing-original draft; L. Fórián: Formal analysis and investigation of Section 5, software, visualization, writing-original draft; B. Porvázsnyik: Formal analysis and investigation of Section 7, writing-original draft. All authors have read and approved the final version of the manuscript for publication.

Use of Generative-AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

The authors would like to thank the referees and the editor for their helpful remarks.

Conflict of interest

The authors declare no conflict of interest.