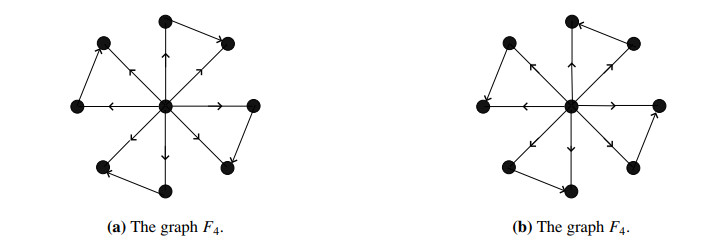On the zero forcing number and propagation time of oriented graphs

1.   Introduction

1.1.   Preliminaries

Let $G = (V, E)$ be a graph in which $V$ is the vertex set and $E\subseteq{V\choose2}$ is the edge set of $G$. An oriented graph is a graph in which some orientation to its edges are assigned. A graph is called a multigraph, if any two vertices can share more than one edge called the multiedges. A graph is called simple, if it is not directed or a multigraph.

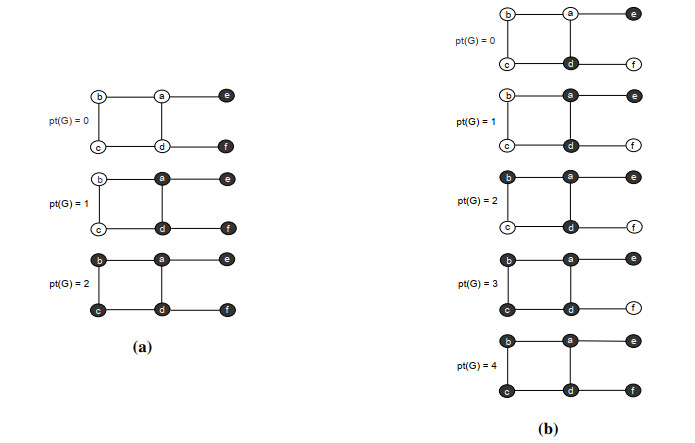
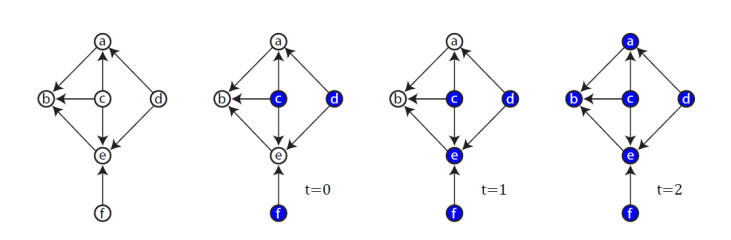
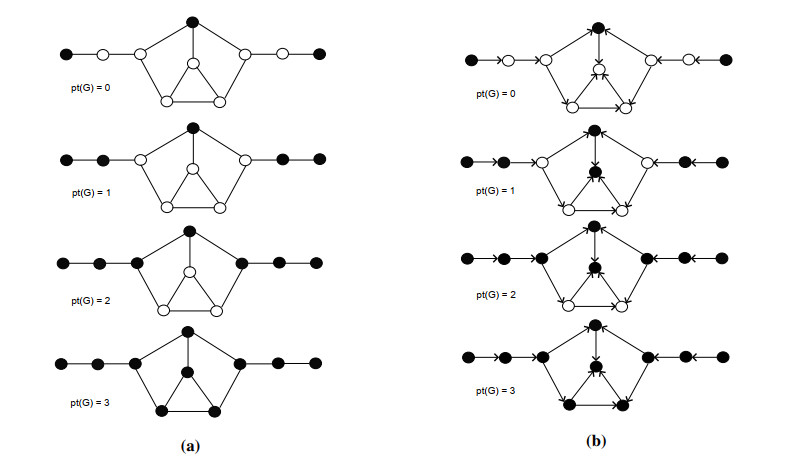
A subset $Z\subseteq V(G)$ of the vertex set of $G$ is said to be a zero forcing set if all vertices of $Z$ are filled, while the vertices in $V(G)\setminus Z$ are unfilled, but then change unfilled vertices to filled iteratively if they are the only unfilled neighbors of the filled vertices. Zero forcing is, in fact, a vertex filling rule ^[17]. According to this rule if the filled vertex has only one unfilled neighbor, the filled vertex forces the unfilled vertex to be filled. This process begins by filling some vertices and then applying the vertex filling rule. The task is to fill all vertices of graph by successive application of the vertex filling rule. Those vertices that are filled to initiate the process are known as a zero forcing set. The cardinality of a minimum zero forcing set is the zero forcing number and denoted by $Z(G)$. The minimum number of time steps, it takes to fill all vertices by minimum zero forcing set, is known as propagation time and denoted by $pt(G, Z)$. Figure 1 presents the vertex filling rule in both undirected and directed graphs. Figure 2 shows an examples of undirected graphs with $Z(G) = 3$ and $pt(G, Z) = 3$.

The propagation time, $pt(G)$, is the minimum propagation time over all minimal zero forcing sets. That is,

This is important because propagation times can vary for different zero forcing sets of the same graph, as seen in Figures 2. In Figure 2a, $Z(G) = 2$. For $B = \{e, f\}$, it takes two time steps to fill up the whole graph using the vertex filling rule. However, in Figure 2b, $Z(G) = 2$ and $B = \{d, e\}$. For this zero forcing set it takes four time steps to fill the vertices of the same undirected graph. Figure 3 shows a directed graph with the zero forcing number 3 and propagation time 2.

1.2.   Literature background

AIM Minimum Rank group ^[2] initially introduced the concept of zero forcing process for undirected graphs. They derived an interesting relationship between the zeroforcing process and the multiplicity of the eigenvalue 0 of the adjacency matrix of a graph. Barioli et al. ^[4] extended the zero forcing process to directed graphs. The authors in ^[7,8,14] studied the process of zero forcing for the class of simple digraphs. It has been shown for an undirected graph $G$ that there is relationship between its zero forcing number and the multiplicity of its eigenvalue 0 i.e. nullity of $G$. Hogben et al. ^[14] extended this relationship between the zero forcing number and the geometric multiplicity (since the adjacency matrix is not symmetric for a digraph) of the eigenvalue 0 for directed graphs. Aazami ^[1] showed that computing the zero forcing number is NP-hard. Therefore, these problems have been studied for many families of graphs. We refer the reader to a recent survey on this topic by Fallat and Hogben ^[12]. Perila et al. ^[17] obtained some results on oriented graphs such as cycles, caterpillars, star graphs and some other graphs.

Although most of the literature on the zero forcing number has its focus on its computation for different families of graphs, another natural question is to investigate the propagation time i.e the number of steps it takes to fill all the vertices. Hogben et al. ^[15] studied this problem for undirected graphs where they derived the extremal structures with respect to the propagation time (i.e. undirected graphs which propagate as slowly or as quickly as possible). Moreover, Chilakamarri et al. ^[11] determined the propagation time (they refer it as the iteration index) of certain families of graphs. In this paper, we further extend the study to other non-trivial oriented graph structures such as oriented wheel graphs, fan graphs, friendship graphs, helm graphs and generalized comb graphs. The change in propagation time while one of the edges is flipped is also investigated.

1.3.   Applications

Zero forcing and its variations have applications in different scientific areas such as graph theory ^[3,6,15], linear algebra ^[2,8], computer science ^[13], physics ^[9,10], electrical engineering ^[5], and social media^[16].

2.   Directed wheel graphs

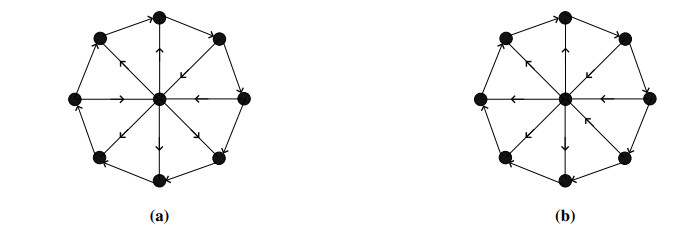
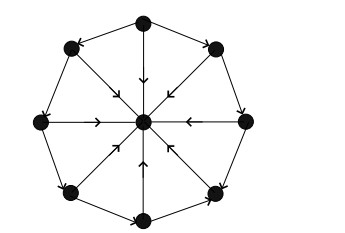
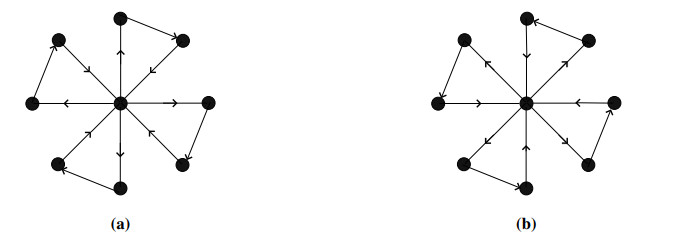
In a wheel graph, we define the orientation of all the outercycle either clockwise or anticlockwise. Moreover, the edges between the universal vertex and vertices of cycle are either introverted or extroverted. An edge directed from a vertex of cycle to universal vertex is called introverted and an edge with orientation from universal vertex to the vertex of cycle is called extroverted. Figure 4a shows an oriented wheel graph with clockwise cycle while the remain edges are extroverted. Figure 4b depicts a wheel graph with anticlockwise cycles with introverted remaining edges.

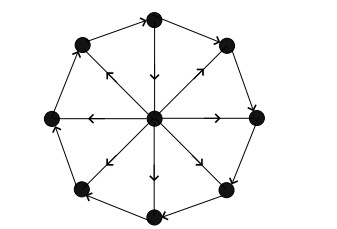
We define the wheel graph ${W}_{a_1, a_2, ..., a_i}$ of order $n+1$, in which direction of cycle is clockwise or anticlockwise and there are $a_1$ introverted edges followed by $a_2$ extroverted edges and ending with $a_i$ extroverted edges satisfying $n = a_1+a_2+...+a_i$. Figure 5a shows the graph ${W}_{2, 3, 1, 2}$. Let ${W}_{k, l} \; k, l\geq0$ be the oriented wheel graph in which direction of cycle is clockwise or anticlockwise and there are $k$ introverted edges followed by $l$ extroverted edges satisfying $n = k+l$. Note that $W_{n, 0}$ (resp. $W_{0, n}$) means that all the edges are introverted (resp. extroverted) Figure 5b (resp. Figure 6) shows the graph ${W}_{3, 5}$ (resp. ${W}_{1, 7}$).

Theorem 2.1. Let ${W}_n$ either denote ${W}_{a_1, a_2, ..., a_i}$ or ${W}_{k, l} \; k, l\geq0$ or the wheel graph of order $n+1$, in which the cycle is either clockwise or anticlockwise where the other edges are introverted or extroverted. The zero forcing number (resp. propagation time) of directed wheel graph of order $n+1$ is $Z({W}_n) = 2$ (resp. $pt ({W}_n, Z) = n-1$).

Proof. In all of the above cases of wheel graph, the zero forcing number is $2$. If in all cases the cycle is either clockwise or anticlockwise and all other edges are introverted, then we can initiate the process by filling two vertices, i.e. universal vertex and any one vertex of the cycle. If all other edges are extroverted, then we can initiate the process by any vertex of cycle but universal vertex will be unfilled thats why universal vertex has to be part of a zero forcing set. In each case, the minimum zero forcing set comprises the universal vertex and any one vertex of cycle. These vertices will force all the vertices of the wheel graph to be filled. The propagation time does not depend on the choice of edges to be introverted and extroverted. It only depends on cycle of the wheel graph. It has already been shown that the propagation time of clockwise or anticlockwise directed cycle graph is $n-1$ ^[17], which is also the propagation time of wheel graph in this case.

Theorem 2.2. In wheel graph ${W}_{k, l} \; k, l\geq1$, direction of cycle is clockwise or anticlockwise and there are $k$ introverted edges followed by $l$ extroverted edges. If $k = 1$, then the zero forcing number (resp. propagation time) is $Z({W}_{k, l}) = 1$ (resp. $pt({W}_{k, l}, Z) = n)$.

Proof. There is only one introverted edge, for $k = 1$ in wheel graph ${W}_{k, l}$. Suppose $u_0$ is the universal vertex and $u_i$ denotes any other vertex of cycle in the directed wheel graph. Since the edge $\{u_i u_0\}$ is introverted, there exists a path $u_{i+1} \rightarrow u_n \rightarrow u_i \rightarrow u_0$ of length $n$ which traverses all the vertices. If $u_{i+1}$ is initially a filled vertex, then it forces all other vertices to be filled by color change rule in $n$ iterations. So, the zero forcing number and propagation time of ${W}_{k, l}$ are respectively $Z({W}_{k, l}) = 1$ and $pt({W}_{k, l}, Z) = n.$

Figure 7 shows the directed wheel graph ${W}_8$ in which the cycle is anticlockwise and three edges are flipped on cycle.

Theorem 2.3. If some adjacent edges of cycle in the directed wheel graph of order $n+1$ are flipped, then its zero forcing number (resp. propagation time) is

Proof. If no edge of the cycle in wheel graph is flipped then its zero forcing number is $1$ or $2$ and propagation time is $n$ or $n-1$ as shown in Theorems 2.1 & 2.2. If some adjacent edges of the cycle in a wheel graph are flipped, then there exists a source vertex which is included in the zero forcing set. The universal vertex and any other vertex adjacent to the source vertex are also a part of the zero forcing set, so, the zero forcing number is $3$.

If $n$ is even and number of adjacent flipped edges of cycle are $\frac{n}{2}$, then cycle is divided into two parts and each path has $\frac{n}{2}$ number of edges and one edge of each part is not used in zero forcing process so, $pt({W}_n, Z) = \big\lceil \frac{n}{2} \big\rceil-1$ and the propagation time is $\big\lceil \frac{n}{2} \big\rceil-1 \leq pt({W}_n, Z)$, if the number of flipped edges are more or less than $\frac{n}{2}$.

If $n$ is odd and number of adjacent flipped edges of cycle are $\big \lfloor \frac{n}{2}\rfloor$, then cycle is divided into two parts. One part has $\big \lfloor \frac{n}{2} \rfloor$ number of edges and other part has $\big \lfloor \frac{n}{2} \rfloor + 1$ number of edges. Propagation time depends on larger part so, $pt ({W}_{n}, Z) = \big\lfloor \frac{n}{2} \big\rfloor$ and propagation time is $\big\lfloor \frac{n}{2} \big\rfloor \leq pt ({W}_n, Z)$. So, we obtain $\big\lceil \frac{n}{2} \big\rceil -1 \leq pt({W}_n, Z)\leq n$.

Next, we study zero forcing and propagation time for a variant of directed wheel graphs. It is known as the directed fan graphs.

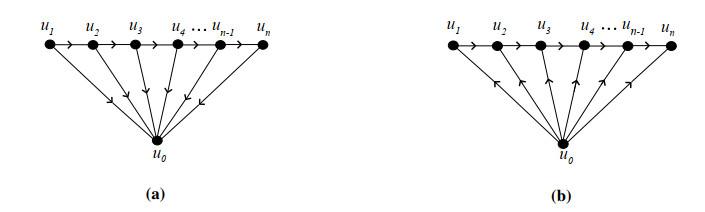
In a directed fan graph, the direction of path graph is presumably from initial vertex to terminal vertex and direction of edges between universal vertex $u_0$ and vertices of path $(u_1, u_2, \ldots, u_n)$ is introverted and extroverted. It is usually denoted by ${F}_{1, n}$. Figure 8 shows the graph $F_{1, n}$.

Theorem 2.4. If introverted edges are more than $1$ and the edge $\{u_n u_0\}$ is not introverted, then the zero forcing number (resp. propagation time) of directed fan graph is

Proof. If ${F}_{1, n}$ is constructed by joining the vertices of unidirectional path by a single vertex, then the zero forcing number is two. The universal vertex $u_0$ and initial vertex $u_1$ of unidirectional path will force all vertices of directed fan graph to be filled. Propagation time does not depend upon whether the edges are introverted or extroverted. It only depend on length of unidirectional path in ${F}_{1, n}$. The propagation time of unidirectional path graph is $n-1$ which is also the propagation time of the directed fan graph.

Figure 9 shows $F_{1, 6}$ where the only edge $u_6u_0$ is introverted.

Theorem 2.5. If the only edge $\{u_n u_0\}$ is introverted, then the zero forcing number (resp. propagation time) of directed fan graph is

Proof. In the directed fan graph, the only edge $\{u_n u_0\}$ is introverted, there exists a path $u_1 \rightarrow u_n \rightarrow u_0$ of length $n$. The vertex $u_1$ is initially filled vertex which initiate the color change rule and forces all the other vertices by taking $n$ iterations. So, the zero forcing number and propagation time of directed fan graph are respectively $Z({F}_{1, n}) = 1$ and $pt ({F}_{1, n}, Z) = n$.

Figures 10 & 11 show the graph $F_{1, 6}$ with $l = 1$ and $l = 2$.

Theorem 2.6. If there are $l$ number of adjacent flipped edges from initial or terminal side of directed path in the directed fan graph, then the zero forcing number (resp. propagation time) of directed fan graph is

Proof. If either one edge is flipped or some adjacent edges from any side of directed path graph in the directed fan graph, then two vertices of path are included in a zero forcing set. These two vertices and universal vertex are included in a zero forcing set. In this case, the zero forcing number is three. Moreover, $Z({F}_{1, n}) = 1, 2$ already explained in Theorems 2.4 & 2.5.

Upper bound on the propagation time of directed fan graph is explained in the previous theorem. If there are $\big\lfloor \frac{n-1}{2} \big\rfloor$ flipped edges from any side of directed path and all the other vertices are introverted or extroverted, then we obtain $pt({F}_{1, n}, Z) = \big\lfloor \frac{n-1}{2} \big\rfloor$ as the directed path is divided into two opposite directed paths of length $\big\lfloor \frac{n-1}{2} \big\rfloor$. Moreover, if the only edge $u_0 u_{\big\lfloor \frac{n}{2} \big\rfloor}$ or $u_0 u_{\big\lfloor \frac{n}{2} \big\rfloor+1}$ is introverted, then the length of opposite directed paths increases $1$ and propagation time is $pt({F}_{1, n}, Z) = \big\lfloor \frac{n-1}{2} \big\rfloor+1$.

If the number of flipped edges in the directed fan graph is less or more than $\big\lfloor \frac{n-1}{2} \big\rfloor$, then the propagation time will be $\big\lfloor \frac{n-1}{2} \big\rfloor \leq pt({F}_{1, n}, Z)$. This completes the proof.

3.   Generalized comb graphs

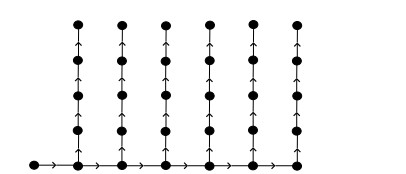
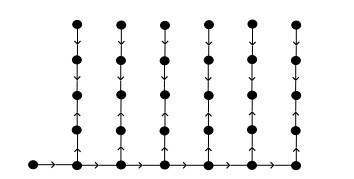
A generalized comb graph is constructed from the path $P_{n+1}$ having vertices $x_{0, 0}, x_{0, 1}, x_{0, 2}, \ldots, x_{0, n}$ by joining $n$ paths, $P_{t_i}$ of order $t_i$; $1\leq i\leq n$ with vertices $x_{0, 1}, x_{0, 2}, \ldots, x_{0, n}$ respectively. It is denoted by $Cb_n(t_i)$. By definition, $t_i > 0$, for any $i$. The order and size of the generalized comb graph are $|V(Cb_n)| = n+1+\sum_{i = 1}^{n} t_i$ and $|E(Cb_n)| = n+\sum_{i = 1}^{n}t_i$ respectively. The vertex $x_{0, 0}$ (resp. $x_{0, n}$) of $P_{n+1}$ is called its initial (resp. terminal) vertex. Moreover, for $P_{t_i}$, the vertex adjacent to $x_{0, i}$, where $1\leq i\leq n$, is called its initial vertex and, similarly, the one-degree vertex of $P_{t_i}\; (1\leq i\leq n)$ is said to be its terminal vertex. In directed generalized comb graph, the direction of each path is from the initial vertex to the terminal vertex. Figure 12 shows the graph ${Cb}_6(4)$.

Theorem 3.1. The zero forcing number (resp. propagation time) of directed generalized comb graph is $Z({Cb}_n(t_i)) = n$ (resp. $pt({Cb}_n(t_i), Z) = i+1$).

Proof. In ${Cb}_n(t_i)$, the zero forcing set contains $n$ vertices of path $P_{n+1}$ except $x_{0, 1}$. The vertex $x_{0, 0}$ is in the zero forcing set and it forces $x_{0, 1}$ to be filled and there are two ways to fill $x_{0, 1}$. Let $x_{0, 1}$ be attached with $x_{0, 2}$ and $x_{1, 1}$ so we have to include one more vertex in the zero forcing set that is why $x_{0, 2}$ is included to zero forcing set. Moreover, there are also two ways for $x_{0, 2}$ and similarly $x_{0, 3}$ is also included to the zero forcing set. In a similar fashion, $n$ vertices are included in the zero forcing set so $Z({Cb}_n(t_i)) = n$. The propagation time depends only upon the longest path in the generalized comb graph. There is a longest path, $x_{0, 0}, x_{0, 1}, x_{1, 1}, x_{2, 1}, ..., x_{i, 1}; 1\leq i\leq n$ of length $i+1$ and remaining all other paths are of length $i$ so, propagation time depends upon the path $x_{0, 0}, x_{0, 1}, x_{1, 1}, x_{2, 1}, \ldots, x_{i, 1}; 1\leq i\leq n$ and therefore, the propagation time of ${Cb}_n(t_i)$ is $pt ({Cb}_n(t_i), Z) = i+1$.

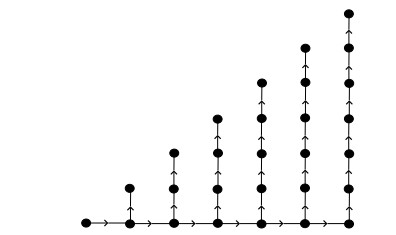
Note that there could be $l$ number of flipped edges in each path $P_{t_i}$ from terminal side. Figure 13 shows the directed graph ${Cb}_6(4)$ with $l = 2$.

Theorem 3.2. If there are $l$ number of flipped edges in each path $P_{t_i}$ from terminal side, then the zero forcing number and propagation time of ${Cb}_n(t_i)$ are

Proof. In the directed generalized comb graph ${Cb}_n(t_i)$, if one edge is flipped from all paths $P_{t_i}$, then there exist $n$ source vertices that are included in the zero forcing set. Furthermore, $n$ vertices of the path $P_{n+1}$ except $x_{0, 1}$ are also included in the zero forcing set. So the zero forcing number is $Z({Cb}_n(t_i)) = 2n$. If one edge is flipped from all paths $P_{t_i}$, then there exits a longest path $x_{0, 0}, x_{0, 1}, x_{1, 1}, x_{2, 1}, ..., x_{i-1, 1}; 1\leq i\leq n$ of length $i$ and, therefore, propagation time is $pt({Cb}_n(t_i), Z) = i-1$. If two edges are flipped from all paths $P_{t_i}$, there exits a longest path $x_{0, 0}, x_{0, 1}, x_{1, 1}, x_{2, 1}, ..., x_{i-2, 1}; 1\leq i\leq n$ of length $i-1$ and this implies that the propagation time is $pt ({Cb}_n(t_i), Z) = i-2$. Similarly, if $l$ edges are flipped from all paths $P_{t_i}$, then there exits a longest path $x_{0, 0}{Cb}_n(t_i), Z) = i-l : 1 \leq l \leq \big\lfloor \frac{i}{2}\big\rfloor$. If $l = \big\lceil\frac{i}{2} \big\rceil$ edges are flipped from all paths $P_{t_i}$, then there exits a longest path $x_{0, 0}, x_{0, 1}, x_{1, 1}, x_{2, 1}, ..., x_{i-l, 1}; 1\leq i\leq n$ of length $l+1$ and this implies that the propagation time is $pt ({Cb}_n(t_i), Z) = l$. If $\big\lceil \frac{i}{2}\big\rceil < l \leq i-1$ edges are flipped from all paths $P_{t_i}$, then there exits a longest path of length $l$ and, therefore, the propagation time is $pt({Cb}_n(t_i), Z) = l-1$.

Remark 3.3. If all the edges of a directed generalized comb graph are flipped then its zero forcing number (resp. propagation time) is $Z({Cb}_n(t_i)) = n$ (resp. $pt({Cb}_n(t_i), Z) = i+1$).

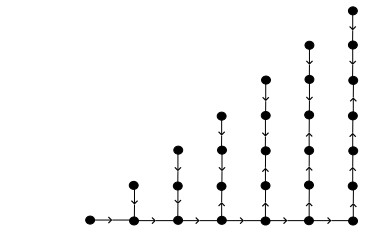
Figure 14 shows the directed graph ${Cb}_6(1, 2, 3, 4, 5, 6)$.

Theorem 3.4. The directed generalized comb graph ${Cb}_n(t_1, t_2, ..., t_n)$ have the zero forcing number and propagation time $Z\big({Cb}_n(t_1, t_2, ..., t_n)\big) = n$ and $pt\big({Cb}_n(t_1, t_2, ..., t_n), Z\big) = n$ respectively.

Proof. In the directed generalized comb graph ${Cb}_n(t_1, t_2, ..., t_n)$, a zero forcing set contains $n$ vertices of path $P_{n+1}$ except $x_{0, 1}$. The vertex $x_{0, 0}$ is in the zero forcing set and it forces $x_{0, 1}$ and there are two ways for $x_{0, 1}$. Since $x_{0, 1}$ is attached with $x_{0, 2}$ and $x_{1, 1}$ so we have to include one more vertex in the zero forcing set thats way $x_{0, 2}$ is included to the zero forcing set and there are also two ways for $x_{0, 2}$ and similarly $x_{0, 3}$ is also included in the zero forcing set. In a similar way, $n$ vertices are included in the zero forcing set, so $Z\big({Cb}_n(t_1, t_1 +1, t_1 +2, ..., t_1 + n-2, t_1 +n-1)\big) = n$. The propagation time depends upon the longest path in the generalized comb graph. There is a longest path $x_{0, n}, x_{1, n}, x_{2, n}, ..., x_{n, n}$ of length $n$ and remaining all other paths are of length $1, 2, 3, 4, ..., n-2$ and $n-1$. This implies that the propagation time depends upon the path $x_{0, n}, x_{1, n}, x_{2, n}, ..., x_{n, n}$ and, therefore, the propagation time is $pt\big({Cb}_n(t_1, t_2, ..., t_n), Z\big) = n$.

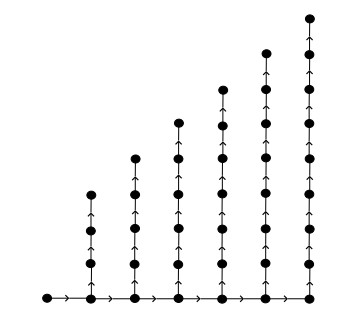
Note that there could be $l$ number of flipped edges in each path $P_{t_i}$ from terminal side. Figure 15 shows the directed graph ${Cb}_6(1, 2, 3, 4, 5, 6)$ with $l = 2$.

Theorem 3.5. If there are $l$ number of flipped edges in each path $P_{t_i}$ from terminal side, then the zero forcing number (resp. propagation time) is $Z\big({Cb}_n(t_1, t_2, \ldots, t_n)\big) = \begin{cases}n \, & l = 0; \\ 2n-l-1 & 1 \leq l \leq n-1;\\ n+1 &n-1, n.\\ \end{cases}$ $\bigg(resp. pt ({Cb}_n(t_1, t_2, ..., t_n), Z) = \begin{cases}n-l-1 \, & 1 \leq l \leq \lfloor \frac{n}{2}\rfloor -2; \\ l+3 & \lfloor \frac{n}{2}\rfloor -2 < l < n-2;\\ l+1 & l = n-1;\\ l & l = n.\\ \end{cases} \bigg)$.

Proof. In the directed generalized comb graph ${Cb}_n(t_1, t_2, ..., t_n)$, if one edge is flipped from all paths $t_1, t_2, \ldots, t_n$, then there exists $n+1$ source vertices that are included in a zero forcing set and $n-3$ vertices of path $P_{n+1}$ except $x_{0, 1}, x_{0, 2}$ and $x_{0, 3}$ are also included in the zero forcing set. This implies that the zero forcing number is $pt\big({Cb}_n(t_1, t_2, ..., t_n), Z\big) = 2n-2$. If two edges are flipped from all paths $t_1, t_2, ..., t_n$, then $n-4$ vertices of path $P_{n+1}$ except $x_{0, 1}, x_{0, 2}, x_{0, 3}$ and $x_{0, 4}$ are also included in the zero forcing set rather the source vertices. This implies that the zero forcing number is $pt({Cb}_n(t_1, t_2, \ldots, t_n), Z) = 2n-3$. If $l\; (1 \leq l < n-1)$ edges are flipped from all paths $t_1, t_2, \ldots, t_n$, then $n-l-2$ vertices of path $P_{n+1}$ are included in the zero forcing set rather than adding the source vertices. Therefore, the zero forcing number is $pt\big({Cb}_n(t_1, t_2, \ldots, t_n), Z\big) = 2n-l-1$. If $n-1$ or $n$ edges are flipped, then vertices $x_{0, 0}, x_{1, 1}, x_{2, 2}, x_{3, 3}, \ldots, x_{n, n}$ are included in $Z$ so, the zero forcing number is $pt\big({Cb}_n(t_1, t_2, \ldots, t_n), Z\big) = n+1$. Moreover, if one edge is flipped from all paths $t_1, t_2, \ldots, t_n$, then there exists a longest path $x_{0, n}, x_{1, n}, x_{2, n}, \ldots, x_{n-1, n}$ of length $n-1$ so, its propagation time is $pt\big({Cb}_n(t_1, t_2, \ldots, t_n), Z\big) = n-2$. If two edges are flipped from all paths $t_1, t_2, ..., t_n$, then there exists a longest path $x_{0, n}, x_{1, n}, x_{2, n}, ..., x_{n-2, n}$ of length $n-2$ so, in this case the propagation time is $pt\big({Cb}_n(t_1, t_2, ..., t_n), Z\big) = n-3$. Similarly, if $l\; (1 \leq l \leq \big\lfloor \frac{n}{2}\big\rfloor)$ edges are flipped from all paths $t_1, t_2, ..., t_n$, then the propagation time will be $pt\big({Cb}_n(t_1, t_2, ..., t_n), Z\big) = n-l-1$.

Remark 3.6. If all edges in the paths $P_1, P_2, \ldots, P_n$ of the directed generalized comb graph are flipped then its zero forcing number (resp. propagation time) is $Z\big({Cb}_n(t_1, t_2, ..., t_n)\big) = n$ (resp. $pt\big({Cb}_n(t_1, t_2, ..., t_n), Z\big) = n$).

Figure 16 depicts the directed graph ${Cb}_6(3, 4, 5, 6, 7, 8)$.

Theorem 3.7. For $n\geq 3$ and $|t_1| \geq 3$, the generalized directed comb graph ${Cb}_n(t_1, t_1 +1, t_1 +2, ..., t_1 + n-2, t_1 +n-1)$ has the zero forcing number and propagation time $Z\big({Cb}_n(t_1, t_1 +1, t_1 +2, ..., t_1 + n-2, t_1 +n-1)\big) = n$ and $pt\big({Cb}_n(t_1, t_1 +1, t_1 +2, ..., t_1 + n-2, t_1 +n-1), Z\big) = |t_1|+n-1$ respectively.

Proof. In the directed generalized comb graph for $n\geq 3$ and $|t_1| \geq 3$, we find a zero forcing set which contains $n$ vertices of path $P_{n+1}$ except $x_{0, 1}$. The vertex $x_{0, 0}$ is in the zero forcing set and it forces $x_{0, 1}$ and there are two ways for $x_{0, 1}$. The vertex $x_{0, 1}$ is attached with $x_{0, 2}$ and $x_{1, 1}$ so we have to include one more vertex in the zero forcing set. Therefore, we include $x_{0, 2}$ to the zero forcing set and there are also two ways for $x_{0, 2}$ and similarly $x_{0, 3}$ is also included to the zero forcing set. In a similar way, $n$ vertices are included in the zero forcing set so $Z\big({Cb}_n(t_1, t_1 +1, t_1 +2, ..., t_1 + n-2, t_1 +n-1)\big) = n$. The propagation time depends only upon the longest path in the generalized comb graph. There is a longest path $x_{0, n}, x_{1, n}, x_{2, n}, ..., x_{j, n}$ of length $| t_1 | + n - 1$ and remaining all other paths are of length $t_1, t_1 +2, ..., t_1 + n-2$ and $t_1 + n - 1$ so, the propagation time depends only upon the path $x_{0, n}, x_{1, n}, x_{2, n}, ..., x_{j, n}; 4 \leq j \leq | t_1 | + n - 1$. This implies that the propagation time is $pt({Cb}_n\big(t_1, t_1 +1, t_1 +2, \ldots, t_1 + n-2, t_1 +n-1), Z\big) = |t_1|+n-1$.

4.   Directed friendship graphs

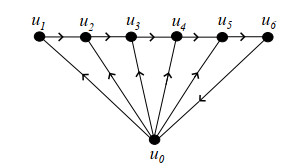
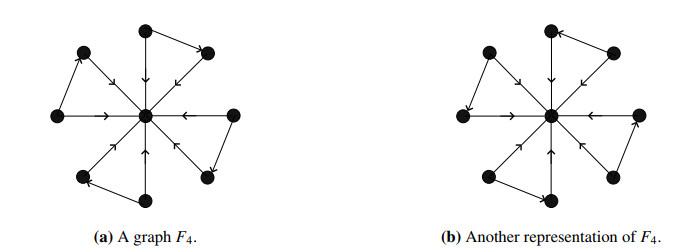
In a directed friendship graph $F_n$, we define the orientations of edges of $C_3$ in clockwise or anticlockwise. Figure 17 denotes depicts the graph ${F}_{4}$.

Theorem 4.1. Let the orientation of triangles in $F_n$ be either clockwise or anticlockwise. Then, the zero forcing number (resp. propagation time) of ${F}_{n}$ is

Proof. There are $n$ copies of $C_3$ in friendship graph and and a zero forcing set $Z$ containing one vertex from $n-1$ copies of $C_3$ other than the common vertex. Therefore, the zero forcing number is $n-1$. By using the zero forcing set $Z$, there exists a path of length $4$, therefore, the propagation time is $4$.

In directed friendship graph, we use extroverted edges and the direction of remanning edges is clockwise or anticlockwise direction and it is denoted by ${F}_n$. Figure 18 shows two examples of the graph ${F}_8$.

Theorem 4.2. Let the directed friendship graph ${F}_n$ be constructed by deleting alternative edges from directed wheel graph in which the directed cycle is either clockwise or anticlockwise, whereas, the other edges are extroverted. Then, the zero forcing number (resp. propagation time) of ${F}_n$ is

Proof. This type of friendship graph is constructed by deleting alternative edges from wheel graph in which the directed cycle is either clockwise or anticlockwise whereas the other edges are extroverted. In this graph, the common vertex is called the source vertex. A zero forcing set $Z$ contains one vertex from each cycle and the source vertex. This implies that the zero forcing number is $n+1$. By using the zero forcing set $Z$, we obtain that the propagation time is $1$ as there are $2$ vertices in the zero forcing set $Z$ from each cycle.

If we use introverted edges and the direction of remanning edges is clockwise or anticlockwise direction, then the directed friendship graph is denoted by ${F}_{n}$. See Figure 19 for two possible examples of the graph ${F}_{8}$.

Theorem 4.3. Let the directed friendship graph is constructed by deleting alternative edges from the directed wheel graph in which the directed cycle is either clockwise or anticlockwise whereas the other edges are introverted. The zero forcing number (resp. propagation time) of the directed friendship graph ${F}_{n}$ is

Proof. This type of friendship graph is constructed by deleting alternative edges from wheel graph in which the directed cycle is either clockwise or anticlockwise while the other edges are introverted. In this graph, the common vertex is called the sink vertex. A zero forcing set $Z$ contains one vertex from each cycle other than the sink vertex. This shows that its zero forcing number is $n$. By using the zero forcing set $Z$, we obtain that the propagation time is $2$ as there is only $1$ vertex in the zero forcing set $Z$ from each cycle and the remanning $2$ vertices of each cycle are forced by the vertex belonging to $Z$. This shows the theorem.

5.   Directed helm graphs

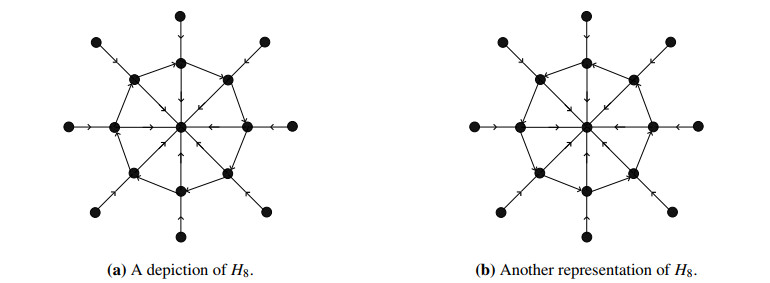
In a directed helm graph, the direction of pendant edges is same as the introverted edges or extroverted edges of the wheel graph, which in fact, contains all introverted or extroverted edges and direction of the cycle is either clockwise or anticlockwise. It is denoted by ${H}_n$.

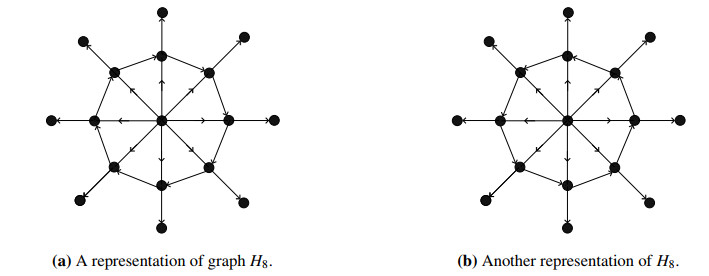
Figures 20 & 21 exhibits some possible representations of $\overrightarrow{H}_{8}$.

Theorem 5.1. Let the directed helm graph $H_n$ be constructed by orienting the cycle of the wheel graph either clockwise or anticlockwise while all the other edges be introverted (resp. extroverted) and directions of pendent edges are same as the direction of the introverted edges (resp. extroverted). Then, the zero forcing number (resp. propagation time) of directed helm graph is $Z({H}_{n}) = n$ (resp. $pt({H}_{n}, Z) = 2$).

Proof. There are two possible cases in the helm graph.

Case 1: Cycle of the wheel graph is clockwise or anticlockwise oriented while all the other edges are introverted and directions of pendent edges are same as the introverted.

In this case, there are $n$ source vertices which are included in a zero forcing set and there is no need to include any other vertex in zero forcing set. This implies that the zero forcing number is $n$. However, the propagation time of ${H}_n$ does not depend upon the direction of cycle. It depends only on the pendent edge and introverted edge having length $2$. Thus, $pt({H}_n, Z) = 2.$

Case 2: The cycle of the wheel graph is clockwise or anticlockwise oriented and all the other edges are extroverted and the direction of pendent edges is same as the extroverted.

In this case, there is one source vertex which is the universal vertex of degree $n$. Remaining $n-1$ vertices, which are attached to the universal vertex and source vertex itself are included in a zero forcing set. This implies that the zero forcing number is $n$. The propagation time of ${H}_n$ does not depend upon direction of cycle. Therefore, the propagation time depends only on extroverted edge and pendent edge with length $2$. Thus, we have $pt({H}_n, Z) = 2.$

Suppose that the direction of pendant edges in the directed helm graph is opposite to the introverted edges or extroverted edges of the wheel graph, which contains all introverted or extroverted edges and direction of cycle in wheel is clockwise or anticlockwise. We denote it by ${H}_n$. See Figure 22 for the graph ${H}_8$.

Theorem 5.2. Let the directed helm graph $H_n$ be constructed by orienting the cycle of the wheel graph either clockwise or anticlockwise while all the other edges be introverted (resp. extroverted) and directions of pendent edges are opposite to the direction of the introverted edges (resp. extroverted). Then, the zero forcing number (resp. propagation time) is $Z({H}_{n}) = n+1$ (resp. $pt({H}_{n}, Z) = 1$).

Proof. There are two cases in this helm graph.

Case 1: Cycle of the wheel graph is either clockwise or anticlockwise oriented while all the other edges are introverted and direction of pendant edges is opposite to the introverted edges.

In this case, there are $n+1$ sink vertices and $n$ vertices of cycle which have $1$ in-degree and $3$ out-degree whereas the universal vertex have $n$ in-degree. All vertices of the cycle and the universal vertex are included in a zero forcing set. Thus, the zero forcing number is $n+1$. The propagation time does not depend upon the direction of the cycle. The universal vertex and all the vertices of the cycle are included in a zero forcing set and, therefore, propagation time will be $1$ when vertices of cycle move to the pendant edges.

Case 2: Cycle of the wheel graph is either clockwise or anticlockwise directed and all the other edges are extroverted and direction of pendant edges is opposite to the extroverted edges.

In this case, there are $n+1$ source vertices which are included in the zero forcing set and no need to include any other vertex in the zero forcing set. Moreover, the zero forcing set contains $n$ pendant vertices and one universal vertex so, the zero forcing number is $n+1$. The propagation time does not depend upon direction of the cycle. All pendant edges are included in the zero forcing set. Therefore, the propagation time will be $1$ when pendant edges will move to edges of the cycle and universal vertex is in zero forcing set so, propagation time is $1$. This completes the proof.

6.   Conclusion

Zero forcing is a process of coloring a graph in a number of steps known as the propagation time. In this paper, we studied the zero forcing in certain non-trivial families of oriented graphs. We have studied the zero forcing number in oriented wheel graphs, oriented friendship graphs, oriented fan graphs and oriented generalized comb graphs. Change in propagation time has also been studied when orientation in one edge of these oriented structures is flipped. Our results significantly extend the study of Perila et al. (2017), who studied these problems for some basic oriented graph structures such as oriented paths, cycles and caterpillars.

Based on the study by Perila et al. ^[17] and our own results in this paper, we propose the following open problems:

Problem 6.1. Investigate the zero forcing and propagation time in trees, beginning with binary, circulant graphs, and Cartesian products of known graphs.

Problem 6.2. Another possible problem is studying the zero forcing and propagation time in caterpillar graph by adding more legs in it or to the original path.

Problem 6.3. Zero forcing can also be studied for more non-trivial structures such as oriented Harary graphs and oriented generalized Petersen graphs.

Problem 6.4. Study the applications of the zero forcing in social media and the graph structure of the networks.

Acknowledgments

S. Hayat and Muhammad Imran are supported by the University Program for Advanced Research (UPAR) by United Arab Emirates University (UAEU) under grant No. G00003271. The authors are grateful to the handling editor and the anonymous reviewer for a careful reading of this paper and for all their comments and remarks, which lead to a number of improvements of the paper.

Conflict of interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.