1.
Introduction
Data analysis has been received a great interest in several applied fields such as medicine, reliability analysis, engineering, environmental studies, and economics. Several authors have proposed more flexible statistical distributions to model and predict various experimental and phenomenal data encountered in applied fields.
The Fréchet (Fr) distribution is also known as the inverse-Weibull distribution and it is one of the useful distributions in extreme value theory. The Fr model has some important applications in life testing, floods, earthquakes, and wind speeds, among others. Further information about the applications of the Fr distribution can be explored in [1,2,3,4,5].
The Fr distribution is specified by the following cumulative distribution function (CDF)
Its probability density function (PDF) reduces to
where θ and λ are, respectively, the shape and scale parameters. The PDF (1.2) exhibits a unimodal shape or a decreasing shape depending on θ while its hazard rate function (HRF) is always unimodal.
There is a clear need to define and develop more flexible versions of the Fr model using the well-known families to model several datasets encountered in many applied fields such as medicine, geology, engineering, and economics, among others. Hence, many authors have proposed several generalized forms of the Fr distribution to improve its flexibility and capability in modeling real-life data. Some notable extensions are the following: the exponentiated-Fr [6], beta-Fr [7], Marshall–Olkin Fr [8], transmuted Marshall–Olkin Fr [9], Weibull–Fr [10], beta exponential-Fr [11], Burr-X Fr [12], odd Lindley–Fr [13], logarithmic-transformed Fr [14], and modified Kies–Fr distributions [15].
This article introduces a new flexible extension of the Fr distribution called the extended Weibull–Fréchet (EWFr) distribution, which provides more flexibility to model real-life data than other competing distributions. Then, the first motivation to this article is devoted to introducing the EWFr distribution as a new extension of the Fr distribution via the extended Weibull-G (EW-G) family [16]. The useful characteristics of the EWFr distribution can be summarized as follows: The EWFr distribution is a more flexible version for the Fr distribution, and it improves the fitting of real-life data; it produces more flexible kurtosis than the baseline Fr model. The HRF of the EWFr distribution can exhibit an upside-down bathtub shape, an increasing shape, and a decreasing shape. Its density function can exhibit a symmetrical shape, a unimodal shape, an asymmetrical shape, a J shape, and a reversed-J shape. Furthermore, the EWFr distribution can be adopted to model various data in the medicine and engineering sciences. This fact was illustrated by modeling two real datasets from both fields, showing its superiority fit over other competing distributions.
Another motivation to this article is to show how several classical estimators of the EWFr distribution perform for different parameter combinations and several sample sizes. Hence, the EWFr parameters are estimated using different estimation approaches including: the maximum product of spacings estimators (MPSEs), least-squares estimators (LSEs), the right-tail Anderson-Darling estimators (RADEs), the maximum likelihood estimators (MLEs), the weighted least-squares estimators (WLSEs), the percentiles estimators (PCEs), the Cramér–von Mises estimators (CRVMEs), and the Anderson–Darling estimators (ADEs). Extensive simulation results were introduced to explore the performance of these estimators. Furthermore, these estimators are compared using partial and overall ranks to determine the best method for estimation the parameters of the EWFr distribution.
The paper is organized in six sections as follows: Section 2 introduces the EWFr distribution and its related functions. The distribution properties are determined in Section 3. Section 4 presents some classical estimators of the EWFr parameters. The simulation results for the classical methods are provided in the same section. Two real-life datasets are fitted using the EWFr distribution in Section 5. Some final remarks are presented in Section 6.
2.
The EWFr distribution
The EWFr distribution is constructed based on the EW-G family [16] which is specified, for any baseline CDF G(x;ζ), by the CDF
The corresponding PDF of (2.1) takes the form
where g(x;ζ)=dG(x;ζ)/dx refers to the baseline density with parameter vector ζ.
To this end, by inserting Eq (1.1) in (2.1), the CDF of the EWFr model follows as
where η=(ϑ,φ,λ,θ)⊺. The PDF of the EWFr model reduces to
where ϑ,φ and θ are shape parameters whereas λ is a scale parameter.
2.1. Some Useful Functions and Shapes
The survival function (SF) of the EWFr distribution is given as
Long-term SF (LT-SF) is a useful feature in the modeling process, because a portion of the population may no longer be eligible to the event of interest with probability p (see [17,18]).
The general form of the LT-SF is SLT(x;p,η)=p+(1−p)S(x;η), where S(x;η) denotes the SF of any distribution and p denotes the probability of being cured. Hence, the PDF of the LT-SF can be derived as
Using Eq (2.4), the PDF of the LT-SF of the EWFr distribution takes the form
The HRF of the EWFr distribution takes the form
Its reversed HRF has the form
The odd ratio of the EWFr model is derived as
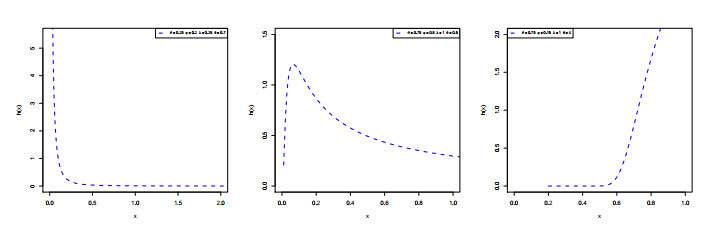
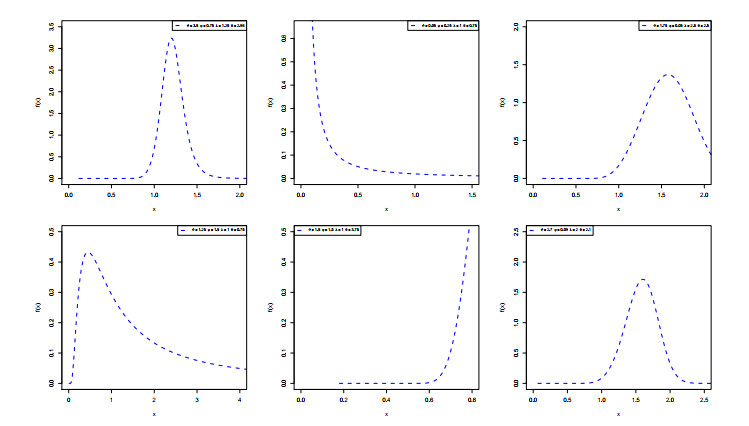
Figure 1 presents some possible shapes of the EWFr PDF for different values of its parameters. The EWFr PDF can be a symmetrical shape, a unimodal shape, an asymmetrical shape, a J shape, and a reversed-J shape. The hazard rate plots of the EWFr model are depicted in Figure 2. The EWFr HRF can be an increasing shape, a unimodal shape, and a decreasing shape.
3.
The EWFr characteristics
3.1. Quantile function and median
The quantile function (QF) of the EWFr distribution, say, Q(u), can be calculated by solving F(x)=p in (2.3) in terms of p. Then, the EWFr QF follows as
The median of the EWFr distribution follows by substituting p=0.5 in Eq (3.1).
3.2. Linear representation
A useful linear representation for the PDF of the EWFr model is provided based on [16]. Alizadeh et al. [16] introduced a simple representation for the density of the EW-G class as follows
where ψw,u=−φwΓ(ϑw+u)(−1φ)w/[w!u!Γ(ϑw)] and
is the exponentiated-G PDF with a power parameter (ϑw+u)>0. Using Eqs (1.1) and (1.2) of the Fr distribution, Eq (3.2) can be expressed as
Equation (3.3) can be rewritten as
where g(ϑw+u)(x) denotes the Fr PDF with two-parameter θ and (ϑw+u)λ. Then, the density function of the EWFr model is expressed as a linear representation of Fr densities. Let Y be a random variable having the Fr distribution in (1.1). Hence, the r−th ordinary, μ′r,Y, and incomplete moments, ϕ(r,Y)(t), of Y are, respectively, given (for r<λ, ) by
where Γ(s)=∫∞0ws−1e−wdw is the complete gamma function (GF) and γ(s,z)=∫z0ws−1e−wdw is the lower incomplete GF.
3.3. Moments and incomplete moments
This section was devoted to deriving the r−th ordinary moment and incomplete moments of the EWFr distribution.
Proposition: Based on (3.4), the r−th moment of the EWFr distribution is defined by
Setting r=1 in Eq (3.5), we get the mean of x.
The s−th incomplete moment, say ϕs(x), of the EWFr distribution takes the form
Then, we obtain (fors<θ)
The mean (μ), variance (σ2), skewness (ξ1(X)), and kurtosis (ξ2(X)) of the EWFr distribution are calculated numerically with λ=1 and different values of ϑ, φ and θ. Table 1 displays these numerical results. Table 1 shows that the EWFr model can be right-skewed and it can be leptokurtic (i.e., ξ2(X)>3).
3.4. Order statistics
Let X1,X2,…Xn be a random sample from the EWFr (2.4) and X1:n≤X2:n≤⋯≤Xn:n be their corresponding order statistics (OS). The PDF and the CDF of the of r−th OS, say, Xr:n and 1≤r≤n are, respectively, defined by
and (for k=1,2,…,n)
Using Eqs (3.6) and (3.7), the PDF and CDF of the r−th OS of the EWFr reduce to
and
4.
Estimation and simulations
In this section, the EWFr parameters ϑ, λ, φ and θ are estimated using different frequentist approaches. We also provide detailed simulation results to compare and order their performances using partial and overall ranks.
4.1. Maximum likelihood estimators
The MLEs of the parameters ϑ, λ, φ and θ of the EWFr distribution are introduced in this sub-section. Let x1,…,xn be a sample from the EWFr distribution in (2.4). Hence, the log-likelihood function of η=(ϑ,φ,λ,θ)⊺ takes the form
The MLEs follow by maximizing the above equation by several programs such as {SAS} ({PROC NLMIXED}) or {R} ({optim} function).
4.2. Ordinary and weighted least-squares estimators
Let x(1), x(2), ⋯, x(n) be the OS of a random sample from the PDF (2.4), then the LSEs [19] of the EWFr parameters are obtained by minimizing the function:
Similarly, these estimators are also obtained by solving the following equation (for k=1,2,3,4)
where
and
where wi=eλxi−θ−1. The solution of Ωk for k=1,2,3,4 may be obtained numerically.
The WLSEs of the EWFr parameters can be determined by minimizing the equation (see [19]):
4.3. Maximum product of spacing and Cramér–von Mises estimators
The uniform spacings of a random sample from the EWFr distribution are defined (for i=1,2,…,n+1) by {Di(η)=F(x(i)|η)−F(x(i−1)|η)}, where F(x(0)|η)=0, F(x(n+1)|η)=1 and ∑n+1i=1Di(η)=1. The MPSEs of the EWFr parameters can be determined by maximizing the following geometric mean (GM) of spacings
or by maximizing the logarithm of the GM of sample spacings
The CRVMEs can be obtained using the difference between the estimated and empirical CDFs. The CRVMEs [20] of the EWFr parameters are determined by minimizing
4.4. Anderson–Darling and right-tail Anderson–Darling estimators
The ADEs [21] of the EWFr parameters are calculated by minimizing
The RADEs of the EWFr parameters are calculated by minimizing
4.5. Percentile estimators
Consider the unbiased estimator of F(x(i)|η) which is defined by ui=i/(n+1). Hence, the PCEs of the EWFr parameters can be calculated by minimizing
4.6. Simulation analysis
To compare and explore the behavior of different estimators of the EWFr parameters, we presented the numerical simulation results and ranked them with respect to their: average of absolute biases (|Bias(ˆη)|), |Bias(ˆη)|= 1N∑Ni=1|ˆη−η|, average of mean relative errors (MREs), MREs=1N∑Ni=1|ˆη−η|/η, and average mean square errors (MSEs), MSEs=1N∑Ni=1(ˆη−η)2.
The following algorithm can be adopted to explore the behavior of different estimators of the EWFr parameters:
Step 1: A random sample x1,x2,…,xn of sizes n=20, 80, 200, and 500 are generated from the QF (3.1).
Step 2: The required results are obtained based on eight combinations of the parameters ϑ={0.25,0.75,1.75,3.50,3.50}, φ={0.50,0.75,2.00,2.50,3.50}, λ={0.25,0.50,1.50,3.00,4.25} and θ={0.25,1.25,2.50}.
Step 3: Each sample is replicated N=5,000 times.
Step 4: Results of the biases, MSEs, and MREs are computed for the eight combinations, and to save more space, we present just the result of 5 combinations in Tables 2–6.
All computations are obtained using R software (version 4.0.2) [22].
For each sample and each parametric combination, the EWFr parameters \vartheta , \varphi , \lambda and \theta are estimated using the eight estimators called MLEs, LSEs, WLSEs, MPSEs, CRVMEs, ADEs, PCEs, and RADEs. Simulated results are listed in Tables 2–6 which also indicate the ranks of each of the proposed estimators in each row, where the superscripts show the indicators, and the \sum Ranks illustrates the partial sum of ranks in each column for a particular sample size.
Table 7 lists the partial and overall ranks for all parametric combinations. From Tables 2–6, one can conclude that all methods of estimation illustrate the consistency property, that is, the MREs and MSEs decrease as the sample size increases, for all parametric combinations. Table 7 shows that the MPS approach has an overall score of 54, hence it outperforms other estimation methods. Therefore, we conclude and confirm the superiority of MPSEs for estimating the EWFr parameters. However, the ADEs and MLEs are approximately have a similar performance, where their overall scores are, respectively, 130.5 and 133.5.
5.
Modeling medicine and engineering data
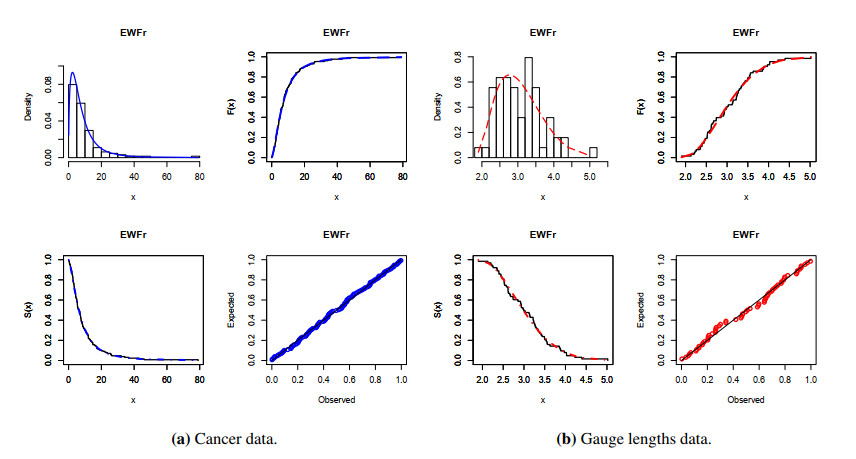
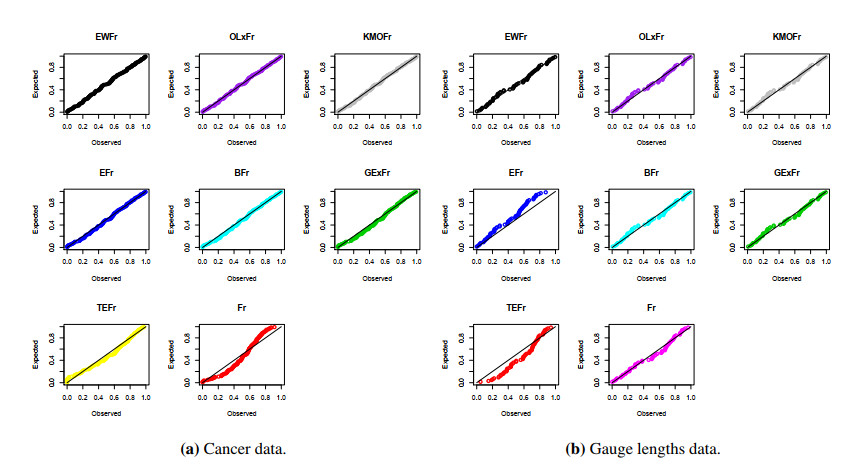
In this section, the flexibility and importance of the EWFr distribution in modeling real-life data are illustrated using two datasets from the medicine and engineering fields. The first dataset contains 128 observations and it refers to remission times (in months) for bladder cancer patients [23]. The second dataset contains 63 observations and it represents strengths for single carbon fibers of 10 mm of gauge lengths [24]. The fits of the EWFr distribution is checked and compared with some important extensions of the Fr distribution called the exponentiated-Fr (EFr) [6], beta-Fr (BFr) [7], odd Lomax-Fr (OLxFr) [25], Kumaraswamy Marshall–Olkin Fr (KMOFr) [26], gamma extended-Fr (GExFr) [27] and transmuted exponentiated-Fr (TEFr) [28] and Fr distributions.
We checked the competing distributions using some goodness-of-fit analytical measures such as AIC (Akaike information criterion), CAIC (consistent Akaike information criterion), HQIC (Hannan–Quinn information criterion), BIC (Bayesian information criterion), W^{\ast} (Cramér–Von Mises), A^{\ast} (Anderson–Darling), and KS (Kolmogorov–Smirnov) statistics with its PV (p-value).
The maximum likelihood (ML) estimates of the parameters of the fitted distributions, their standard errors (SEs), and the analytical measures are reported in Tables 8 and 9 for the cancer and gauge lengths data, respectively. The numbers in Tables 8 and 9 indicate that the EWFr distribution gives a superior fit over other competing models, since it has the lowest values for all measures and the largest PV.
Some plots including the PDF, CDF, and SF along with the PP plots of the EWFr model are displayed in Figure 3 for both datasets. The PP plots of all studied distributions are displayed in Figure 4 for the two datasets, respectively.
The estimates of the EWFr parameters under several estimation approaches and the goodness-of-fit measures for both datasets are listed in Tables 10 and 11, respectively. Based on the values of PV in Tables 10 and 11, the Anderson-Darling approach is recommended to estimate the EWFr parameters for cancer data, while the least-squares approach is recommended for gauge lengths data.
6.
Conclusions
In this paper, we introduced a more flexible four-parameter model called the extended Weibull–Fréchet (EWFr) distribution. Its basic mathematical properties are explored. The EWFr parameters are estimated using eight classical estimation methods. The simulation results showed that the maximum product of spacings approach outperforms other considered methods based on overall ranks. The importance and flexibility of the EWFr distribution over some competing extensions of the Fréchet distribution are addressed by analyzing two real-life datasets from the medicine and engineering fields. The analytical measures showed that our EWFr model returned an adequate fit in comparison with other distributions.
Acknowledgments
This study was funded by Taif University Researchers Supporting Project number (TURSP-2020/279), Taif University, Taif, Saudi Arabia. The authors would like to thank the editorial board and the three referees for their constructive comments that improved the final version of the paper.
Conflict of interest
The authors declare no conflict of interest.









 DownLoad:
DownLoad: